第23章 图形的相似 测试卷(含答案) 2025-2026学年数学华东师大版九年级上册
文档属性
| 名称 | 第23章 图形的相似 测试卷(含答案) 2025-2026学年数学华东师大版九年级上册 | 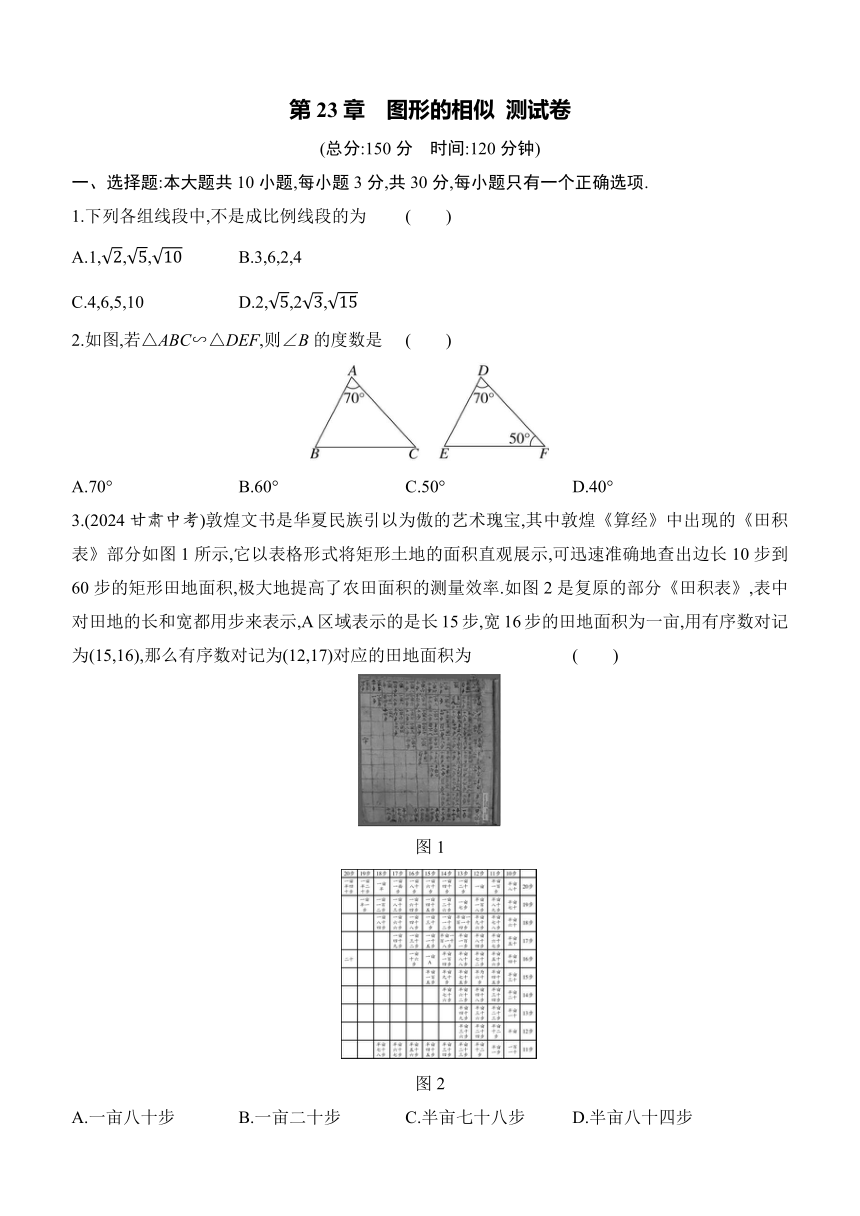 | |
| 格式 | docx | ||
| 文件大小 | 367.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 21:21:23 | ||
图片预览




文档简介
第23章 图形的相似 测试卷
(总分:150分 时间:120分钟)
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.下列各组线段中,不是成比例线段的为 ( )
A.1,,, B.3,6,2,4
C.4,6,5,10 D.2,,2,
2.如图,若△ABC∽△DEF,则∠B的度数是 ( )
A.70° B.60° C.50° D.40°
3.(2024甘肃中考)敦煌文书是华夏民族引以为傲的艺术瑰宝,其中敦煌《算经》中出现的《田积表》部分如图1所示,它以表格形式将矩形土地的面积直观展示,可迅速准确地查出边长10步到60步的矩形田地面积,极大地提高了农田面积的测量效率.如图2是复原的部分《田积表》,表中对田地的长和宽都用步来表示,A区域表示的是长15步,宽16步的田地面积为一亩,用有序数对记为(15,16),那么有序数对记为(12,17)对应的田地面积为 ( )
图1
图2
A.一亩八十步 B.一亩二十步 C.半亩七十八步 D.半亩八十四步
4.如图,已知点A、B、D的坐标分别为(1,4),(3,0),(5,0),AB∥CD,AB=CD,则点C的坐标为 ( )
A.(3,4) B.(4,3)
C.(3,5) D.(5,4)
5.(2024重庆B卷中考)若两个相似三角形的相似比为1∶4,则这两个三角形面积的比是 ( )
A.1∶2 B.1∶4 C.1∶8 D.1∶16
6.如图,小李利用镜面反射原理测树高,小李在点A处,镜子在点O处,点A、O、B在同一水平线上,小李眼睛到地面的高度CA=1.6 m,OA=2.4 m,OB=6 m,则树高BD= ( )
A.4 m B.5 m C.6 m D.7 m
第7题图 第8题图 第9题图
7.如图,已知AB∥CD∥EF,AD=3,BC=4,DF=5,则CE的长为 ( )
A.6 B. C.7 D.
8.如图,在矩形ABCD中,AB=3,BC=10,点E在BC边上,DF⊥AE,垂足为F.若DF=6,则线段EF的长为 ( )
A.2 B.3 C.4 D.5
9.如图,△ABC中,CD⊥AB于点D,有下列条件:①∠1=∠A;②;③∠B+∠2=90°;④BC∶AC∶AB=3∶4∶5;⑤AC2=AD·AB,其中一定能确定△ABC为直角三角形的条件的个数是 ( )
A.1 B.2
C.3 D.4
10.(2024南通中考)在△ABC中,∠B=∠C=α(0°<α<45°),AH⊥BC,垂足为H,D是线段HC上的动点(不与点H、C重合),将线段DH绕点D顺时针旋转2α得到线段DE.两位同学经过深入研究后,小明发现:当点E落在边AC上时,点D为HC的中点;小丽发现:连结AE,当AE的长最小时,AH2=AB·AE.下列关于两位同学的发现,说法正确的是 ( )
A.小明正确,小丽错误 B.小明错误,小丽正确
C.小明、小丽都正确 D.小明、小丽都错误
二、填空题:本大题共6小题,每小题4分,共24分.
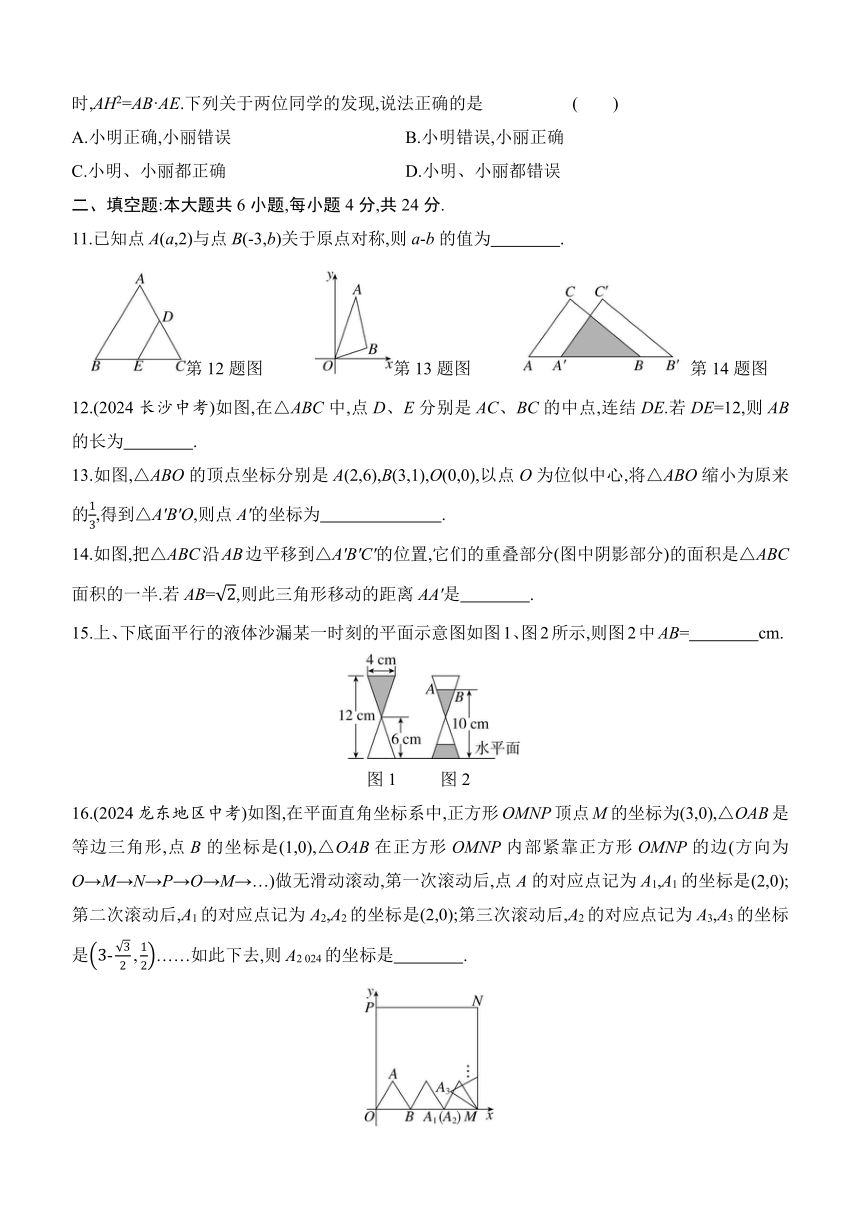
11.已知点A(a,2)与点B(-3,b)关于原点对称,则a-b的值为 .
第12题图 第13题图 第14题图
12.(2024长沙中考)如图,在△ABC中,点D、E分别是AC、BC的中点,连结DE.若DE=12,则AB的长为 .
13.如图,△ABO的顶点坐标分别是A(2,6),B(3,1),O(0,0),以点O为位似中心,将△ABO缩小为原来的,得到△A'B'O,则点A'的坐标为 .
14.如图,把△ABC沿AB边平移到△A'B'C'的位置,它们的重叠部分(图中阴影部分)的面积是△ABC面积的一半.若AB=,则此三角形移动的距离AA'是 .
15.上、下底面平行的液体沙漏某一时刻的平面示意图如图1、图2所示,则图2中AB= cm.
图1 图2
16.(2024龙东地区中考)如图,在平面直角坐标系中,正方形OMNP顶点M的坐标为(3,0),△OAB是等边三角形,点B的坐标是(1,0),△OAB在正方形OMNP内部紧靠正方形OMNP的边(方向为O→M→N→P→O→M→…)做无滑动滚动,第一次滚动后,点A的对应点记为A1,A1的坐标是(2,0);第二次滚动后,A1的对应点记为A2,A2的坐标是(2,0);第三次滚动后,A2的对应点记为A3,A3的坐标是……如此下去,则A2 024的坐标是 .
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17.(6分)如图,在由边长为1个单位的小正方形组成的网格中,△ABC的顶点均为格点(网格线的交点).
(1)请画出△ABC绕点O逆时针旋转90°后得到的图形△A1B1C1(点A、B、C的对应点分别为点A1、B1、C1).
(2)请画出一个格点三角形A2B2C2,使△A2B2C2∽△A1B1C1,且相似比为2.
18.(6分)如图,在△ABC中,点D、E分别在边BC、AC上,连结DE,若DE∥AB,CE=2AE,CD=6,求BD的长.
19.(6分)如图,点D、E分别是△ABC边AB、AC的中点,点F在DB上,且DF=2BF.连结EF并延长,与CB的延长线相交于点M.若BM=2,求线段BC的长.
20.(8分)如图,在 ABCD中,AB=10,AD=15,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=8,求△CEF的周长.
21.(10分)如图,在等边三角形ABC中,AB=4,点M、N分别是BC、AC上的点,且∠AMN=60°.
(1)求证:∠BAM=∠CMN.
(2)求点M在什么位置时,CN的长为.
22.(10分)(2025西安碑林区月考)如图,在△ABC中,D是BC边上一点,且满足AD=AB,∠ADE=∠C.
(1)求证:△ADE∽△ACD.
(2)若,且AE=4,求AB的长.
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
23.(8分)如图,在平行四边形ABCD中,对角线AC、BD交于点O.M为AD的中点,连结CM交BD于点N,且ON=1.
(1)求BD的长.
(2)若△CND的面积为2,求四边形ABNM的面积.
24.(10分)下面的方格图中,每个小方格的边长为1 cm,请按要求操作.
(1)画出图形①向右平移5格后的图形②.
(2)画出将图形①绕O点逆时针旋转180°后的图形③.
(3)画出将图形①按3∶1放大后的图形④.
(4)如果把图形①绕它的那条较长的直角边旋转一周,形成的图形是 ,这个图形的体积是
cm2(π取3.14).
25.(10分)如图所示,某测量工作人员头顶A与标杆顶点F、电视塔顶端E在同一直线上,已知此测量人员的头顶距地面的高AB为1.4 m,标杆FC的长为2.8 m,且测量人员与标杆的距离BC为3.5 m,标杆与电视塔的距离CD为6.5 m,AB⊥BC,FC⊥BD,ED⊥BD,求电视塔的高DE.
26.(10分)如图,在 ABCD中,对角线AC与BD相交于点O,∠CAB=∠ACB,过点B作BE⊥AB交AC于点E.
(1)求证:△ABO∽△BEO.
(2)若AB=10,AC=16,求OE的长.
27.(12分)(新定义试题)在平面直角坐标系中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),则称点Q是点P的“a阶智慧点”(a为常数,且a≠0).例如:点P(1,4)的“2阶智慧点”为点Q(2×1+4,1+2×4),即点Q(6,9).
(1)点A(-1,-2)的“3阶智慧点”的坐标为 .
(2)若点B的“4阶智慧点”的坐标为(-5,10),求点B的坐标.
(3)若点C(m+2,1-3m)的“-5阶智慧点”到x轴的距离为1,求m的值.
【详解答案】
1.C 解析:A.1×,是成比例线段,故本选项不符合题意;B.6×2=3×4,是成比例线段,故本选项不符合题意;C.4×10≠5×6,不是成比例线段,故本选项符合题意;D.2××2,是成比例线段,故本选项不符合题意.故选C.
2.B 解析:∵△ABC∽△DEF,∴∠B=∠E,∵∠D+∠E+∠F=180°,∠D=70°,∠F=50°,∴∠E=60°,∴∠B=∠E=60°.故选B.
3.D 解析:由题图知(12,17)对应的田地面积为半亩八十四步.故选D.
4.A 解:∵AB∥CD,AB=CD,B(3,0),D(5,0),∴AB向右平移2个单位得到CD,∵点A的坐标为(1,4),
∴点C的坐标为(1+2,4),即(3,4).故选A.
5.D 解析:若两个相似三角形的相似比为1∶4,则这两个三角形面积的比是1∶16.故选D.
6.A 解析:由题可知∠CAO=∠DBO=90°,∠COF=∠DOF,∵∠COA=90°-∠COF,∠DOB=90°-∠DOF,
∴∠COA=∠DOB,∴△ACO∽△BDO,
∴,∵AC=1.6 m,OA=2.4 m,OB=6 m,∴,解得BD=4.故选A.
7.B 解析:∵AB∥CD∥EF,∴,
∴,∴CE=.故选B.
8.B 解析:∵四边形ABCD为矩形,
∴BC=AD=10,AD∥BC,∴∠AEB=∠DAF,∵∠ABE=∠AFD=90°,∴△AFD∽△EBA,∴,∴,∴AE=5,∵DF=6,∴AF==8,∴EF=AF-AE=8-5=3.故选B.
9.D 解析:①∵CD⊥AB于D,
∴∠CDA=90°,∴∠A+∠2=90°,
∵∠1=∠A,
∴∠1+∠2=90°,即∠ACB=90°,
∴△ABC为直角三角形,故①一定能确定△ABC为直角三角形;
②∵,∴,
又∵∠CDA=∠CDB=90°,∴△ACD∽△CBD,∴∠1=∠A,∠B=∠2,
∴∠1+∠2=∠A+∠B,即∠ACB=∠A+∠B,∵∠ACB+∠A+∠B=180°,∴∠ACB+∠ACB=180°,
∴∠ACB=90°,故②一定能确定△ABC为直角三角形;
③∵CD⊥AB,∴∠CDB=90°,∴∠B+∠1=90°.∵∠B+∠2=90°,
∴∠1=∠2,∴当∠1=∠2=45°时,△ABC为直角三角形,但是根据已知条件无法得到∠1=∠2=45°,故③不一定能确定△ABC为直角三角形;
④∵BC∶AC∶AB=3∶4∶5,∴设BC=3x,AC=4x,AB=5x,∵BC2+AC2=(3x)2+(4x)2=25x2,AB2=(5x)2=25x2,∴BC2+AC2=AB2,∴△ABC为直角三角形,故④一定能确定△ABC为直角三角形;
⑤∵AC2=AD·AB,∴,
又∵∠A=∠A,∴△ADC∽△ACB,
∴∠ACB=∠ADC=90°,
∴△ABC为直角三角形,故⑤一定能确定△ABC为直角三角形.综上所述,一定能确定△ABC为直角三角形的条件是①②④⑤,共4个.故选D.
10.C 解析:∵将线段DH绕点D顺时针旋转2α得到线段DE,∴DH=DE,∠HDE=2α,当点E落在边AC上时,如图1,
图1
∵∠HDE=∠C+∠CED,∠C=α,
∴∠CED=α=∠C,∴DE=CD,
∴DH=CD,∴D为CH的中点,
故小明的说法是正确的.
连结AE、HE,如图2,
图2
∵DH=DE,∠HDE=2α,∴∠DHE=∠DEH=(180°-2α)=90°-α,
∵AH⊥BC,∴∠AHB=∠AHD=90°,
∴∠AHE=∠AHD-∠DHE=α,
∴点E在射线HE上运动,∴当AE⊥HE时,AE的长最小,∴当AE的长最小时,∠AEH=∠AHB=90°,
又∵∠B=∠C=α=∠AHE,
∴△AEH∽△AHB,∴,
∴AH2=AB·AE,故小丽的说法正确.故选C.
11.5 解析:∵点A(a,2)与点B(-3,b)关于原点对称,∴a=-(-3)=3,b=-2,∴a-b=3+2=5.
12.24 解析:∵点D、E分别是AC、BC的中点,∴DE是△ABC的中位线,
∴AB=2DE=24.
13.或
解析:∵以点O为位似中心,将△ABO缩小为原来的,得到△A'B'O,A(2,6),∴当△A'B'O在第一象限时,点A'的坐标为×2,×6,即;当△A'B'O在第三象限时,点A'的坐标为,即.综上可知,点A'的坐标为或.
14.-1 解析:设BC与A'C'交于点D(图略),∵△ABC沿AB边平移到△A'B'C'的位置,∴AC∥A'C',
∴△ABC∽△A'BD,
∴,
∴AB∶A'B=∶1,∵AB=,
∴A'B=1,∴AA'=-1.
15. 解析:如图,设沙漏的顶点为点D,上端的右端点记作F,左端点记作M,下端的右端点记作H,过点D作DC⊥AB交AB于点C,交上底边于点E,交下底边于点G.∵AB∥EF∥GH,∴DE⊥EF,DG⊥GH,△ABD∽△MFD,∴.∵EG=12 cm,DG=6 cm,CE=12-10=2(cm),MF=4 cm,∴DE=6 cm,DC=4 cm,∴,∴AB= cm.
16.(1,3) 解析:由题知,点A1的坐标为(2,0),点A2的坐标为(2,0),点A3的坐标为,点A4的坐标为(3,2),点A5的坐标为(3,2),点A6的坐标为,点A7的坐标为(1,3),点A8的坐标为(1,3),点A9的坐标为,点A10的坐标为(0,1),点A11的坐标为(0,1),点A12的坐标为,点A13的坐标为(2,0)……由此可见,点An的坐标每12个循环一次,因为2 024÷12=168……8,所以点A2 024的坐标为(1,3).
17.解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
18.解:∵DE∥AB,∴,
又∵CE=2AE,∴=2,
∴BD=3.
19.解:∵点D、E分别是边AB、AC的中点,∴DE∥BC,BC=2DE,
∴△DEF∽△BMF,∴.
∵DF=2BF,BM=2,∴=2,
∴DE=4.∴BC=2DE=8.
20.解:在 ABCD中,CD=AB=10,BC=AD=15,AB∥DC,∴∠BAF=∠F,∵AF为∠BAD的平分线,
∴∠BAF=∠DAF,∴∠DAF=∠F,
∴DF=AD=15,同理BE=AB=10,
∴CF=DF-CD=15-10=5.
∵BG⊥AE,∴AE=2AG,
在△ABG中,BG⊥AE,AB=10,BG=8,
∴AG==6,
∴AE=2AG=12,
∴△ABE的周长为10+10+12=32.
∵四边形ABCD是平行四边形,
∴AB∥CF,∴△CEF∽△BEA,
∵,∴相似比为1∶2,
∴△CEF的周长为16.
21.解:(1)证明:∵△ABC为等边三角形,
∴∠B=60°,
∴∠BAM+∠AMB=180°-∠B=120°,
∵∠AMN=60°,
∴∠CMN+∠AMB=180°-∠AMN=120°,
∴∠BAM=∠CMN.
(2)∵△ABC为等边三角形,
∴∠B=∠C=60°,AB=BC=4,
∵∠BAM=∠CMN,
∴△BAM∽△CMN,
∴,
设BM=x,则CM=BC-BM=4-x,
∴,解得x1=1,x2=3,故当BM的长为1或3时,CN的长为.
22.解:(1)证明:∵∠ADE=∠C,∠A=∠A,∴△ADE∽△ACD.
(2)∵,∴,∴,
由(1)知△ADE∽△ACD,
∴,∵AE=4,
∴,∴AD=2,
∵AD=AB,∴AB=2.
23.解:(1)在平行四边形ABCD中,AD∥BC,AD=BC,OB=OD,
∴∠DMN=∠BCN,∠MDN=∠CBN.
∴△MND∽△CNB.∴.
∵M为AD的中点,
∴MD=AD=BC,即.
∴,即BN=2DN.
设OB=OD=x,则BD=2x,BN=OB+ON=x+1,DN=OD-ON=x-1.
∴x+1=2(x-1),
解得x=3.∴BD=2x=6.
(2)由(1)得△MND∽△CNB,且相似比为1∶2,
∴MN∶CN=DN∶BN=1∶2.
∴S△MND=S△CND=1,S△NBC=2S△CND=4.∴S△ABD=S△BCD=S△CNB+S△CND=4+2=6.
∴S四边形ABNM=S△ABD-S△MND=6-1=5.
24.解:(1)如图所示,图形②即为所求.
(2)如图所示,图形③即为所求.
(3)如图所示,图形④即为所求.
(4)圆锥 12.56
25.解:过点A作AH⊥ED,交FC于点G,交ED于点H,如图,
由作图知四边形ABCG、四边形ABDH均为矩形,
∴AB=CG=DH=1.4 m,BC=AG=3.5 m,AH=BD=BC+CD=3.5+6.5=10(m),
∴FG=CF-CG=1.4 m,
∵FC⊥BD,ED⊥BD,∴FC∥DE,
∴△AGF∽△AHE,∴,
∵FG=1.4 m,∴EH=4 m,
∴DE=EH+DH=5.4 m.
答:电视塔的高DE为5.4 m.
26.解:(1)证明:∵∠CAB=∠ACB,
∴AB=CB,∴ ABCD是菱形,
∴AC⊥BD,∴∠AOB=∠BOE=90°,
∵BE⊥AB,∴∠EBA=90°,
∴∠BEO+∠BAO=∠ABO+∠BAO=90°,
∴∠BEO=∠ABO,
∴△ABO∽△BEO.
(2)∵ ABCD是菱形,
∴OA=OC=AC=8,AC⊥BD,
∴∠AOB=90°,
∴OB==6,
∵△BEO∽△ABO,∴,
即,解得OE=,
即OE的长为.
27.解:(1)(-5,-7)
(2)设点B的坐标为(x,y),∵点B的“4阶智慧点”的坐标为(-5,10),
∴解得
∴点B的坐标为(-2,3).
(3)∵点C的坐标为(m+2,1-3m),
∴点C的“-5阶智慧点”的坐标为(-8m-9,16m-3).
由题意可得|16m-3|=1,
∴16m-3=1或16m-3=-1.
解得m=或m=.
(总分:150分 时间:120分钟)
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.下列各组线段中,不是成比例线段的为 ( )
A.1,,, B.3,6,2,4
C.4,6,5,10 D.2,,2,
2.如图,若△ABC∽△DEF,则∠B的度数是 ( )
A.70° B.60° C.50° D.40°
3.(2024甘肃中考)敦煌文书是华夏民族引以为傲的艺术瑰宝,其中敦煌《算经》中出现的《田积表》部分如图1所示,它以表格形式将矩形土地的面积直观展示,可迅速准确地查出边长10步到60步的矩形田地面积,极大地提高了农田面积的测量效率.如图2是复原的部分《田积表》,表中对田地的长和宽都用步来表示,A区域表示的是长15步,宽16步的田地面积为一亩,用有序数对记为(15,16),那么有序数对记为(12,17)对应的田地面积为 ( )
图1
图2
A.一亩八十步 B.一亩二十步 C.半亩七十八步 D.半亩八十四步
4.如图,已知点A、B、D的坐标分别为(1,4),(3,0),(5,0),AB∥CD,AB=CD,则点C的坐标为 ( )
A.(3,4) B.(4,3)
C.(3,5) D.(5,4)
5.(2024重庆B卷中考)若两个相似三角形的相似比为1∶4,则这两个三角形面积的比是 ( )
A.1∶2 B.1∶4 C.1∶8 D.1∶16
6.如图,小李利用镜面反射原理测树高,小李在点A处,镜子在点O处,点A、O、B在同一水平线上,小李眼睛到地面的高度CA=1.6 m,OA=2.4 m,OB=6 m,则树高BD= ( )
A.4 m B.5 m C.6 m D.7 m
第7题图 第8题图 第9题图
7.如图,已知AB∥CD∥EF,AD=3,BC=4,DF=5,则CE的长为 ( )
A.6 B. C.7 D.
8.如图,在矩形ABCD中,AB=3,BC=10,点E在BC边上,DF⊥AE,垂足为F.若DF=6,则线段EF的长为 ( )
A.2 B.3 C.4 D.5
9.如图,△ABC中,CD⊥AB于点D,有下列条件:①∠1=∠A;②;③∠B+∠2=90°;④BC∶AC∶AB=3∶4∶5;⑤AC2=AD·AB,其中一定能确定△ABC为直角三角形的条件的个数是 ( )
A.1 B.2
C.3 D.4
10.(2024南通中考)在△ABC中,∠B=∠C=α(0°<α<45°),AH⊥BC,垂足为H,D是线段HC上的动点(不与点H、C重合),将线段DH绕点D顺时针旋转2α得到线段DE.两位同学经过深入研究后,小明发现:当点E落在边AC上时,点D为HC的中点;小丽发现:连结AE,当AE的长最小时,AH2=AB·AE.下列关于两位同学的发现,说法正确的是 ( )
A.小明正确,小丽错误 B.小明错误,小丽正确
C.小明、小丽都正确 D.小明、小丽都错误
二、填空题:本大题共6小题,每小题4分,共24分.
11.已知点A(a,2)与点B(-3,b)关于原点对称,则a-b的值为 .
第12题图 第13题图 第14题图
12.(2024长沙中考)如图,在△ABC中,点D、E分别是AC、BC的中点,连结DE.若DE=12,则AB的长为 .
13.如图,△ABO的顶点坐标分别是A(2,6),B(3,1),O(0,0),以点O为位似中心,将△ABO缩小为原来的,得到△A'B'O,则点A'的坐标为 .
14.如图,把△ABC沿AB边平移到△A'B'C'的位置,它们的重叠部分(图中阴影部分)的面积是△ABC面积的一半.若AB=,则此三角形移动的距离AA'是 .
15.上、下底面平行的液体沙漏某一时刻的平面示意图如图1、图2所示,则图2中AB= cm.
图1 图2
16.(2024龙东地区中考)如图,在平面直角坐标系中,正方形OMNP顶点M的坐标为(3,0),△OAB是等边三角形,点B的坐标是(1,0),△OAB在正方形OMNP内部紧靠正方形OMNP的边(方向为O→M→N→P→O→M→…)做无滑动滚动,第一次滚动后,点A的对应点记为A1,A1的坐标是(2,0);第二次滚动后,A1的对应点记为A2,A2的坐标是(2,0);第三次滚动后,A2的对应点记为A3,A3的坐标是……如此下去,则A2 024的坐标是 .
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17.(6分)如图,在由边长为1个单位的小正方形组成的网格中,△ABC的顶点均为格点(网格线的交点).
(1)请画出△ABC绕点O逆时针旋转90°后得到的图形△A1B1C1(点A、B、C的对应点分别为点A1、B1、C1).
(2)请画出一个格点三角形A2B2C2,使△A2B2C2∽△A1B1C1,且相似比为2.
18.(6分)如图,在△ABC中,点D、E分别在边BC、AC上,连结DE,若DE∥AB,CE=2AE,CD=6,求BD的长.
19.(6分)如图,点D、E分别是△ABC边AB、AC的中点,点F在DB上,且DF=2BF.连结EF并延长,与CB的延长线相交于点M.若BM=2,求线段BC的长.
20.(8分)如图,在 ABCD中,AB=10,AD=15,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=8,求△CEF的周长.
21.(10分)如图,在等边三角形ABC中,AB=4,点M、N分别是BC、AC上的点,且∠AMN=60°.
(1)求证:∠BAM=∠CMN.
(2)求点M在什么位置时,CN的长为.
22.(10分)(2025西安碑林区月考)如图,在△ABC中,D是BC边上一点,且满足AD=AB,∠ADE=∠C.
(1)求证:△ADE∽△ACD.
(2)若,且AE=4,求AB的长.
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
23.(8分)如图,在平行四边形ABCD中,对角线AC、BD交于点O.M为AD的中点,连结CM交BD于点N,且ON=1.
(1)求BD的长.
(2)若△CND的面积为2,求四边形ABNM的面积.
24.(10分)下面的方格图中,每个小方格的边长为1 cm,请按要求操作.
(1)画出图形①向右平移5格后的图形②.
(2)画出将图形①绕O点逆时针旋转180°后的图形③.
(3)画出将图形①按3∶1放大后的图形④.
(4)如果把图形①绕它的那条较长的直角边旋转一周,形成的图形是 ,这个图形的体积是
cm2(π取3.14).
25.(10分)如图所示,某测量工作人员头顶A与标杆顶点F、电视塔顶端E在同一直线上,已知此测量人员的头顶距地面的高AB为1.4 m,标杆FC的长为2.8 m,且测量人员与标杆的距离BC为3.5 m,标杆与电视塔的距离CD为6.5 m,AB⊥BC,FC⊥BD,ED⊥BD,求电视塔的高DE.
26.(10分)如图,在 ABCD中,对角线AC与BD相交于点O,∠CAB=∠ACB,过点B作BE⊥AB交AC于点E.
(1)求证:△ABO∽△BEO.
(2)若AB=10,AC=16,求OE的长.
27.(12分)(新定义试题)在平面直角坐标系中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),则称点Q是点P的“a阶智慧点”(a为常数,且a≠0).例如:点P(1,4)的“2阶智慧点”为点Q(2×1+4,1+2×4),即点Q(6,9).
(1)点A(-1,-2)的“3阶智慧点”的坐标为 .
(2)若点B的“4阶智慧点”的坐标为(-5,10),求点B的坐标.
(3)若点C(m+2,1-3m)的“-5阶智慧点”到x轴的距离为1,求m的值.
【详解答案】
1.C 解析:A.1×,是成比例线段,故本选项不符合题意;B.6×2=3×4,是成比例线段,故本选项不符合题意;C.4×10≠5×6,不是成比例线段,故本选项符合题意;D.2××2,是成比例线段,故本选项不符合题意.故选C.
2.B 解析:∵△ABC∽△DEF,∴∠B=∠E,∵∠D+∠E+∠F=180°,∠D=70°,∠F=50°,∴∠E=60°,∴∠B=∠E=60°.故选B.
3.D 解析:由题图知(12,17)对应的田地面积为半亩八十四步.故选D.
4.A 解:∵AB∥CD,AB=CD,B(3,0),D(5,0),∴AB向右平移2个单位得到CD,∵点A的坐标为(1,4),
∴点C的坐标为(1+2,4),即(3,4).故选A.
5.D 解析:若两个相似三角形的相似比为1∶4,则这两个三角形面积的比是1∶16.故选D.
6.A 解析:由题可知∠CAO=∠DBO=90°,∠COF=∠DOF,∵∠COA=90°-∠COF,∠DOB=90°-∠DOF,
∴∠COA=∠DOB,∴△ACO∽△BDO,
∴,∵AC=1.6 m,OA=2.4 m,OB=6 m,∴,解得BD=4.故选A.
7.B 解析:∵AB∥CD∥EF,∴,
∴,∴CE=.故选B.
8.B 解析:∵四边形ABCD为矩形,
∴BC=AD=10,AD∥BC,∴∠AEB=∠DAF,∵∠ABE=∠AFD=90°,∴△AFD∽△EBA,∴,∴,∴AE=5,∵DF=6,∴AF==8,∴EF=AF-AE=8-5=3.故选B.
9.D 解析:①∵CD⊥AB于D,
∴∠CDA=90°,∴∠A+∠2=90°,
∵∠1=∠A,
∴∠1+∠2=90°,即∠ACB=90°,
∴△ABC为直角三角形,故①一定能确定△ABC为直角三角形;
②∵,∴,
又∵∠CDA=∠CDB=90°,∴△ACD∽△CBD,∴∠1=∠A,∠B=∠2,
∴∠1+∠2=∠A+∠B,即∠ACB=∠A+∠B,∵∠ACB+∠A+∠B=180°,∴∠ACB+∠ACB=180°,
∴∠ACB=90°,故②一定能确定△ABC为直角三角形;
③∵CD⊥AB,∴∠CDB=90°,∴∠B+∠1=90°.∵∠B+∠2=90°,
∴∠1=∠2,∴当∠1=∠2=45°时,△ABC为直角三角形,但是根据已知条件无法得到∠1=∠2=45°,故③不一定能确定△ABC为直角三角形;
④∵BC∶AC∶AB=3∶4∶5,∴设BC=3x,AC=4x,AB=5x,∵BC2+AC2=(3x)2+(4x)2=25x2,AB2=(5x)2=25x2,∴BC2+AC2=AB2,∴△ABC为直角三角形,故④一定能确定△ABC为直角三角形;
⑤∵AC2=AD·AB,∴,
又∵∠A=∠A,∴△ADC∽△ACB,
∴∠ACB=∠ADC=90°,
∴△ABC为直角三角形,故⑤一定能确定△ABC为直角三角形.综上所述,一定能确定△ABC为直角三角形的条件是①②④⑤,共4个.故选D.
10.C 解析:∵将线段DH绕点D顺时针旋转2α得到线段DE,∴DH=DE,∠HDE=2α,当点E落在边AC上时,如图1,
图1
∵∠HDE=∠C+∠CED,∠C=α,
∴∠CED=α=∠C,∴DE=CD,
∴DH=CD,∴D为CH的中点,
故小明的说法是正确的.
连结AE、HE,如图2,
图2
∵DH=DE,∠HDE=2α,∴∠DHE=∠DEH=(180°-2α)=90°-α,
∵AH⊥BC,∴∠AHB=∠AHD=90°,
∴∠AHE=∠AHD-∠DHE=α,
∴点E在射线HE上运动,∴当AE⊥HE时,AE的长最小,∴当AE的长最小时,∠AEH=∠AHB=90°,
又∵∠B=∠C=α=∠AHE,
∴△AEH∽△AHB,∴,
∴AH2=AB·AE,故小丽的说法正确.故选C.
11.5 解析:∵点A(a,2)与点B(-3,b)关于原点对称,∴a=-(-3)=3,b=-2,∴a-b=3+2=5.
12.24 解析:∵点D、E分别是AC、BC的中点,∴DE是△ABC的中位线,
∴AB=2DE=24.
13.或
解析:∵以点O为位似中心,将△ABO缩小为原来的,得到△A'B'O,A(2,6),∴当△A'B'O在第一象限时,点A'的坐标为×2,×6,即;当△A'B'O在第三象限时,点A'的坐标为,即.综上可知,点A'的坐标为或.
14.-1 解析:设BC与A'C'交于点D(图略),∵△ABC沿AB边平移到△A'B'C'的位置,∴AC∥A'C',
∴△ABC∽△A'BD,
∴,
∴AB∶A'B=∶1,∵AB=,
∴A'B=1,∴AA'=-1.
15. 解析:如图,设沙漏的顶点为点D,上端的右端点记作F,左端点记作M,下端的右端点记作H,过点D作DC⊥AB交AB于点C,交上底边于点E,交下底边于点G.∵AB∥EF∥GH,∴DE⊥EF,DG⊥GH,△ABD∽△MFD,∴.∵EG=12 cm,DG=6 cm,CE=12-10=2(cm),MF=4 cm,∴DE=6 cm,DC=4 cm,∴,∴AB= cm.
16.(1,3) 解析:由题知,点A1的坐标为(2,0),点A2的坐标为(2,0),点A3的坐标为,点A4的坐标为(3,2),点A5的坐标为(3,2),点A6的坐标为,点A7的坐标为(1,3),点A8的坐标为(1,3),点A9的坐标为,点A10的坐标为(0,1),点A11的坐标为(0,1),点A12的坐标为,点A13的坐标为(2,0)……由此可见,点An的坐标每12个循环一次,因为2 024÷12=168……8,所以点A2 024的坐标为(1,3).
17.解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
18.解:∵DE∥AB,∴,
又∵CE=2AE,∴=2,
∴BD=3.
19.解:∵点D、E分别是边AB、AC的中点,∴DE∥BC,BC=2DE,
∴△DEF∽△BMF,∴.
∵DF=2BF,BM=2,∴=2,
∴DE=4.∴BC=2DE=8.
20.解:在 ABCD中,CD=AB=10,BC=AD=15,AB∥DC,∴∠BAF=∠F,∵AF为∠BAD的平分线,
∴∠BAF=∠DAF,∴∠DAF=∠F,
∴DF=AD=15,同理BE=AB=10,
∴CF=DF-CD=15-10=5.
∵BG⊥AE,∴AE=2AG,
在△ABG中,BG⊥AE,AB=10,BG=8,
∴AG==6,
∴AE=2AG=12,
∴△ABE的周长为10+10+12=32.
∵四边形ABCD是平行四边形,
∴AB∥CF,∴△CEF∽△BEA,
∵,∴相似比为1∶2,
∴△CEF的周长为16.
21.解:(1)证明:∵△ABC为等边三角形,
∴∠B=60°,
∴∠BAM+∠AMB=180°-∠B=120°,
∵∠AMN=60°,
∴∠CMN+∠AMB=180°-∠AMN=120°,
∴∠BAM=∠CMN.
(2)∵△ABC为等边三角形,
∴∠B=∠C=60°,AB=BC=4,
∵∠BAM=∠CMN,
∴△BAM∽△CMN,
∴,
设BM=x,则CM=BC-BM=4-x,
∴,解得x1=1,x2=3,故当BM的长为1或3时,CN的长为.
22.解:(1)证明:∵∠ADE=∠C,∠A=∠A,∴△ADE∽△ACD.
(2)∵,∴,∴,
由(1)知△ADE∽△ACD,
∴,∵AE=4,
∴,∴AD=2,
∵AD=AB,∴AB=2.
23.解:(1)在平行四边形ABCD中,AD∥BC,AD=BC,OB=OD,
∴∠DMN=∠BCN,∠MDN=∠CBN.
∴△MND∽△CNB.∴.
∵M为AD的中点,
∴MD=AD=BC,即.
∴,即BN=2DN.
设OB=OD=x,则BD=2x,BN=OB+ON=x+1,DN=OD-ON=x-1.
∴x+1=2(x-1),
解得x=3.∴BD=2x=6.
(2)由(1)得△MND∽△CNB,且相似比为1∶2,
∴MN∶CN=DN∶BN=1∶2.
∴S△MND=S△CND=1,S△NBC=2S△CND=4.∴S△ABD=S△BCD=S△CNB+S△CND=4+2=6.
∴S四边形ABNM=S△ABD-S△MND=6-1=5.
24.解:(1)如图所示,图形②即为所求.
(2)如图所示,图形③即为所求.
(3)如图所示,图形④即为所求.
(4)圆锥 12.56
25.解:过点A作AH⊥ED,交FC于点G,交ED于点H,如图,
由作图知四边形ABCG、四边形ABDH均为矩形,
∴AB=CG=DH=1.4 m,BC=AG=3.5 m,AH=BD=BC+CD=3.5+6.5=10(m),
∴FG=CF-CG=1.4 m,
∵FC⊥BD,ED⊥BD,∴FC∥DE,
∴△AGF∽△AHE,∴,
∵FG=1.4 m,∴EH=4 m,
∴DE=EH+DH=5.4 m.
答:电视塔的高DE为5.4 m.
26.解:(1)证明:∵∠CAB=∠ACB,
∴AB=CB,∴ ABCD是菱形,
∴AC⊥BD,∴∠AOB=∠BOE=90°,
∵BE⊥AB,∴∠EBA=90°,
∴∠BEO+∠BAO=∠ABO+∠BAO=90°,
∴∠BEO=∠ABO,
∴△ABO∽△BEO.
(2)∵ ABCD是菱形,
∴OA=OC=AC=8,AC⊥BD,
∴∠AOB=90°,
∴OB==6,
∵△BEO∽△ABO,∴,
即,解得OE=,
即OE的长为.
27.解:(1)(-5,-7)
(2)设点B的坐标为(x,y),∵点B的“4阶智慧点”的坐标为(-5,10),
∴解得
∴点B的坐标为(-2,3).
(3)∵点C的坐标为(m+2,1-3m),
∴点C的“-5阶智慧点”的坐标为(-8m-9,16m-3).
由题意可得|16m-3|=1,
∴16m-3=1或16m-3=-1.
解得m=或m=.
