第24章 解直角三角形 测试卷(含解析)2025-2026学年数学华东师大版九年级上册
文档属性
| 名称 | 第24章 解直角三角形 测试卷(含解析)2025-2026学年数学华东师大版九年级上册 | 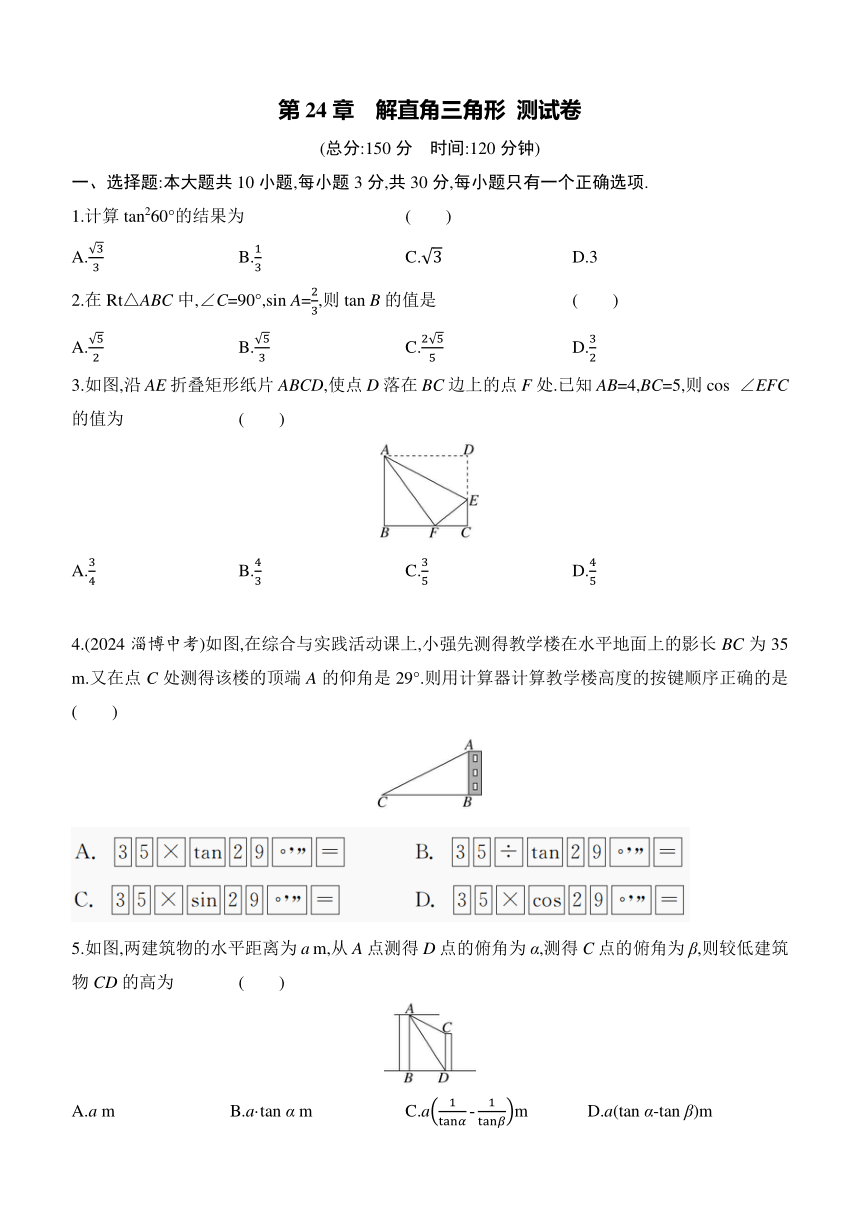 | |
| 格式 | docx | ||
| 文件大小 | 294.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-06 15:44:05 | ||
图片预览





文档简介
第24章 解直角三角形 测试卷
(总分:150分 时间:120分钟)
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.计算tan260°的结果为 ( )
A. B. C. D.3
2.在Rt△ABC中,∠C=90°,sin A=,则tan B的值是 ( )
A. B. C. D.
3.如图,沿AE折叠矩形纸片ABCD,使点D落在BC边上的点F处.已知AB=4,BC=5,则cos ∠EFC的值为 ( )
A. B. C. D.
4.(2024淄博中考)如图,在综合与实践活动课上,小强先测得教学楼在水平地面上的影长BC为35 m.又在点C处测得该楼的顶端A的仰角是29°.则用计算器计算教学楼高度的按键顺序正确的是 ( )
5.如图,两建筑物的水平距离为a m,从A点测得D点的俯角为α,测得C点的俯角为β,则较低建筑物CD的高为 ( )
A.a m B.a·tan α m C.am D.a(tan α-tan β)m
6.如图1是一种折叠桌子,示意图如图2,它是由下面的支架AD、BC与桌面构成的,已知OA=OB=OC=OD=20 cm,∠COD=60°,则点A到地面(CD所在的平面)的距离是 ( )
图1 图2
A.30 cm B.60 cm C.40 cm D.60 cm
7.在△ABC中,若+2(1-tan B)2=0,则∠C的度数是 ( )
A.45° B.60° C.75° D.105°
8.如图,钓鱼竿AC长6 m,露在水面上的鱼线BC长3 m,某垂钓者想看看鱼钩上的情况,把鱼竿AC转动到AC'的位置,此时露在水面上的鱼线B'C'为3 m,则鱼竿转过的角度是 ( )
A.60° B.45° C.15° D.90°
9.如图,某数学兴趣小组测量一棵树CD的高度,在点A处测得树顶C的仰角为45°,在点B处测得树顶C的仰角为60°,且A、B、D三点在同一直线上,若AB=(8+8)m,则这棵树CD的高度是 ( )
A.6 m B.8 m C.10 m D.12 m
10.春天是放风筝的好时节,小明为了让风筝顺利起飞,特地将风筝放在坡度为1∶2.4的山坡上,并站在视线刚好与风筝起飞点A齐平的B处,起风后小明开始往下跑26 m至坡底C处,并继续沿平地向前跑16 m到达D处后站在原地开始调整,小明将手中的线轴刚好举到与视线齐平处测得风筝的仰角是37°,此时风筝恰好升高到起飞时的正上方E处.已知小明视线距地面高度为1.5 m,图中风筝E、A、B、C、D五点在同一平面内,则风筝上升的垂直距离AE约为 ( )
(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
A.34.2 m B.32.7 m
C.31.2 m D.22.7 m
二、填空题:本大题共6小题,每小题4分,共24分.
11.在Rt△ABC中,∠ACB=90°,AC=2,BC=4,点D是AB的中点,则CD= .
12.已知α为锐角,且sin(α-10°)=0.5,则α等于 .
13.在△ABC中,∠C=90°,tan A=,△ABC的周长为60,那么AB的长为 .
14.如图,在3×3的正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫做格点.点A、B、C均在格点上,连结AB,则tan ∠ABC的值为 .
15.(2024宁夏中考)如图1是三星堆遗址出土的陶盉(hé),图2是其示意图.已知管状短流AB=2 cm,四边形BCDE是器身,BE∥CD,BC=DE=11 cm,∠ABE=120°,∠CBE=80°.器身底部CD距地面的高度为21.5 cm,则该陶盉管状短流口A距地面的高度约为 cm(结果精确到0.1 cm).(参考数据:sin 80°≈0.984 8,cos 80°≈0.173 6,tan 80°≈5.671 3,≈1.732)
图1 图2
第15题图
16.如图,已知点A(3,0),点B在y轴正半轴上,将线段AB绕点A顺时针旋转120°到线段AC,若点C的坐标为(7,h),则h= .
第16题图
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17.(6分)计算:
(1)tan 30°·tan 60°+sin245°+cos245°.
(2)2cos 30°·sin 60°-tan 45°·sin 30°.
18.(6分)如图,在△ABC中,CD⊥AB于点D,∠A=30°,BC=5,tan B=,求AC的长.
19.(6分)如图,一水库大坝的横断面为梯形ABCD,坝顶BC宽6 m,坝高20 m,斜坡AB的坡度i=1∶2.5,斜坡CD的坡角为30°,求坝底AD的长度.(结果精确到0.1 m,参考数据:≈1.414,≈1.732)
20.(8分)如图,在△ABC中,AC=,BC=,cos A=,点D在BC边上,且CD=2BD,DE⊥AB,垂足为E,连结CE.
(1)求线段AB的长.
(2)求∠CEA的正切值.
21.(10分)(2024牡丹江中考)如图,某数学活动小组用高度为1.5 m的测角仪BC,对垂直于地面CD的建筑物AD的高度进行测量,BC⊥CD于点C.在B处测得A的仰角∠ABE=45°,然后将测角仪向建筑物方向水平移动6 m至FG处,FG⊥CD于点G,测得A的仰角∠AFE=58°,BF的延长线交AD于点E,求建筑物AD的高度.(结果保留小数点后一位,参考数据:sin 58°≈0.85,cos 58°≈0.53,tan 58°≈1.60)
22.(10分)图1是一款可调节椅背的沙发椅,它可以减轻使用者的脊椎压力.图2是它的侧面示意图,椅背BC=70 cm,将椅背角度从110°调节到150°(即∠ABC=110°,∠ABD=150°)时,分别过点C、D作CE⊥AB于点E,DF⊥AB于点F,求水平方向增加的距离EF的长.(结果精确到1 cm,参考数据:sin 70°≈0.9,cos 70°≈0.3,tan 70°≈2.7,≈1.7)
图1 图2
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
23.(8分)如图,一艘轮船在A处测得灯塔M位于A的北偏东30°方向上,轮船沿着正北方向航行20 n mile到达B处,测得灯塔M位于B的北偏东60°方向上,测得港口C位于B的北偏东45°方向上.已知港口C在灯塔M的正北方向上.
(1)求灯塔M到轮船航线AB的距离(结果保留根号).
(2)求港口C与灯塔M的距离(结果保留根号).
24.(10分)(2024兴安盟、呼伦贝尔中考)综合实践活动中,数学兴趣小组利用无人机测量大楼的高度.如图,无人机在离地面40 m的D处,测得操控者A的俯角为30°,测得楼BC楼顶C处的俯角为45°,又经过人工测量得到操控者A和大楼BC之间的水平距离是80 m,则楼BC的高度是多少米 (点A、B、C、D都在同一平面内,参考数据:≈1.7)
25.(10分)(2024贵州中考)综合与实践:小星学习解直角三角形知识后,结合光的折射规律进行了如下综合性学习.
【实验操作】第一步:将长方体空水槽放置在水平桌面上,一束光线从水槽边沿A处投射到底部B处,入射光线与水槽内壁AC的夹角为∠A;
第二步:向水槽注水,水面上升到AC的中点E处时,停止注水.(直线NN'为法线,AO为入射光线,OD为折射光线)
【测量数据】如图,点A、B、C、D、E、F、O、N、N'在同一平面内,测得AC=20 cm,∠A=45°,折射角∠DON=32°.
【问题解决】根据以上实验操作和测量的数据,解答下列问题:
(1)求BC的长.
(2)求B、D之间的距离(结果精确到0.1 cm).
(参考数据:sin 32°≈0.53,cos 32°≈0.85,tan 32°≈0.62)
26.(10分)(2024广东中考)中国新能源汽车为全球应对气候变化和绿色低碳转型作出了巨大贡献.为满足新能源汽车的充电需求,某小区增设了充电站,如图是矩形PQMN充电站的平面示意图,矩形ABCD是其中一个停车位.经测量,∠ABQ=60°,AB=5.4 m,CE=1.6 m,GH⊥CD,GH是另一个车位的宽,所有车位的长宽相同,按图示并列划定.
根据以上信息回答下列问题:(结果精确到0.1 m,参考数据:≈1.73)
(1)求PQ的长.
(2)该充电站有20个停车位,求PN的长.
27.(12分)(2024济南中考)城市轨道交通发展迅猛,为市民出行带来极大方便.某校综合实践小组想测得轻轨高架站的相关距离,数据勘测组通过勘测得到了如下记录表:
综合实践活动记录表
活动内容 测量轻轨高架站的相关距离
测量工具 测倾器、红外测距仪等
过程资料 轻轨高架站示意图 相关数据及说明:图中点A、B、C、D、E、F在同一平面内,房顶AB,吊顶CF和地面DE所在的直线都平行,点F在与地面垂直的中轴线AE上,∠BCD=98°,∠CDE=97°,AE=8.5 m,CD=6.7 m
成果梳理 ……
请根据记录表提供的信息解答下列问题:
(1)求点C到地面DE的距离.
(2)求顶部线段BC的长.
(结果精确到0.01 m,参考数据:sin 15°≈0.259,cos 15°≈0.966,tan 15°≈0.268,sin 83°≈0.993,cos 83°≈0.122,tan 83°≈8.144)
【详解答案】
1.D
2.A 解析:在Rt△ABC中,sin A=,设BC=2m,则AB=3m.根据勾股定理可得AC=m.所以tan B=.故选A.
3.D 解析:∵四边形ABCD是矩形,
∴AD=BC=5,CD=AB=4,∠B=∠C=90°.由折叠的性质得AF=AD=5,EF=DE,在Rt△ABF中,由勾股定理得BF==3,
∴CF=BC-BF=5-3=2.设DE=EF=x,则CE=CD-DE=4-x,
在Rt△CEF中,由勾股定理得(4-x)2+22=x2,解得x=,即EF=,
∴cos ∠EFC==2÷.
故选D.
4.A 解析:在Rt△ABC中,∠ACB=29°,BC=35 m,∴tan ∠ACB=tan 29°=,∴AB=35×tan 29° m,∴用计算器计算教学楼高度的按键顺序为A.故选A.
5.D 解析:如图,作AE∥BD交DC的延长线于点E,
根据题意得∠DAE=α,∠CAE=β,AE=a m,∵tan α=,tan β=,
∴DE=atan α,CE=atan β,∴CD=DE-CE=a(tan α-tan β)m.故选D.
6.D 解析:如图,连结CD,过点O作OF⊥CD交于点F,延长FO交AB于点E,
由题意可知AB∥CD,∴OE⊥AB,
∵OA=OB=OC=OD=20 cm,
∠COD=∠AOB=60°,
∴△COD、△AOB为等边三角形,
△COD≌△AOB,∴∠COF=30°,
OF=OE,∴OF=OC·cos ∠COF=20=30(cm).∴EF=2OF=60 cm,即点A到地面的距离为60 cm.故选D.
7.C 解析:∵+2(1-tan B)2=0,∴cos A-=0,2(1-tan B)2=0,∴cos A=,tan B=1,∴∠A=60°,∠B=45°,∴∠C=180°-∠A-∠B=75°.故选C.
8.C 解析:∵sin ∠CAB=,∴∠CAB=45°.∵sin ∠C'AB'=,∴∠C'AB'=60°.
∴∠CAC'=60°-45°=15°,∴鱼竿转过的角度是15°.故选C.
9.B 解析:由题意得CD⊥AB,
设BD=x m,在Rt△BDC中,
∠CBD=60°,∴CD=BD·tan 60°=x(m),在Rt△ACD中,∠DAC=45°,
tan ∠DAC=1,∴AD=x(m),∵BD+AD=AB,∴x+x=8+8,解得x=8,∴CD=x=8,∴这棵树CD的高度为8 m.故选B.
10.D 解析:设小明在B处视线的点为N,延长NB交直线CD于点S,过点G作GM平行于地面交直线AE于点M,如图,
坡度为1∶2.4,BC=26 m,则SC=24 m,BS=10 m,∵AN∥SC,∴,即,解得AN=RS=3.6,AR=NS=BS+NB=10+1.5=11.5(m),则AM=10 m,MG=RD=RS+SC+CD=3.6+24+16=43.6(m),EM=MG tan 37°≈32.7 m,AE=EM-AM=32.7-10=22.7(m).故选D.
11. 解析:如图,在Rt△ABC中,
∵∠ACB=90°,AC=2,BC=4,
∴AB==2,
∵点D是AB的中点,
∴CD=AB=.
12.40° 解析:∵sin(α-10°)=0.5,α为锐角,∴α-10°=30°,∴α=40°.
13.26 解析:如图:
∵∠C=90°,tan A=,∴tan A=,设AC=5x,则BC=12x,
在Rt△ABC中,AB2=AC2+BC2=(13x)2,∴AB=13x,∵△ABC的周长为60,∴AB+AC+BC=60,∴13x+5x+12x=60,∴30x=60,∴x=2,∴AB=13x=26.
14. 解析:如图,在Rt△ABD中,AD=3,BD=2,
∴tan ∠ABC=tan ∠ABD=.
15.34.1 解析:如图,过点C作CF⊥BE,垂足为F,过点A作AG⊥EB,交EB的延长线于点G,
∵∠ABE=120°,∴∠ABG=180°-∠ABE=60°,在Rt△ABG中,AB=2 cm,∴AG=AB·sin 60°=2×(cm),在Rt△BCF中,∠EBC=80°,BC=11 cm,∴CF=BC·sin 80°≈11×0.984 8=10.832 8(cm),∵器身底部CD距地面的高度为21.5 cm,
∴该陶盉管状短流口A距地面的高度=AG+CF+21.5=+10.832 8+21.5≈34.1(cm),∴该陶盉管状短流口A距地面的高度约为34.1 cm.
16. 解析:如图,在x轴上取点D和点E,使得∠ADB=∠AEC=120°,过点C作CF⊥x轴于点F.
∵点C的坐标为(7,h),∴OF=7,CF=h.在Rt△CEF中,∠CEF=180°-∠AEC=60°,CF=h,∴EF=h,CE=h.
∵∠BAC=∠ADB=120°,∴∠BAD+∠CAE=∠BAD+∠ABD.
∴∠CAE=∠ABD.∵CA=AB,
∠CEA=∠ADB
∴△CAE≌△ABD(A.A.S.).∴AD=CE=h,AE=BD.∵点A(3,0),∴OA=3.∴OD=OA-AD=3-h.
在Rt△BOD中,∠BDO=180°-∠ADB=60°,∴BD==23-h=6-h.∴AE=BD=6-h.∵OA+AE+EF=OF,∴3+6-h+h=7,解得h=.
17.解:(1)原式==1+=2.
(2)原式=2×-1×=1.
18.解:∵tan B=,∴设CD=3x,BD=4x,∴BC==5x=5,∴x=1,∴CD=3.∵CD⊥AB,∠A=30°,∴AC=2CD=6.
19.解:如图,作BE⊥AD,CF⊥AD,垂足分别为点E、F,则四边形BCFE是矩形,
由题意得BC=EF=6 m,BE=CF=20 m,斜坡AB的坡度i为1∶2.5,
在Rt△ABE中,,
即,解得AE=50.
在Rt△CFD中,∠D=30°,
∴DF==20 m,
∴AD=AE+EF+FD=50+6+20≈90.6(m).
故坝底AD的长度约为90.6 m.
20.解:(1)如图,过点C作CF⊥AB于点F.∵AC=,cos A=,
∴AF=1.∴CF==2.
在Rt△BCF中,FB==3,
∴AB=AF+FB=1+3=4.
(2)∵CD=2BD,BC=,
∴BD=CB=.
∵FB=3,CB=,
∴cos B=,
∴BE=DB·cos B==1.
∴EF=2.
又∵CF=2,CF⊥AB,
∴tan ∠CEA=tan ∠CEF==1.
21.解:根据题意可知四边形BEDC是矩形,∠ABE=45°,∠AFE=58°,
∴DE=BC=1.5 m.
∵tan ∠ABE=,tan ∠AFE=,
∴AE=BE·tan 45°=BE,EF=.
∵BE=BF+EF,∴AE=6+,
∴AE≈16 m.
∴AD=AE+DE=17.5 m.
答:建筑物AD的高度约为17.5 m.
22.解:由题意得BC=BD=70 cm,
∵∠ABC=110°,
∴∠CBE=180°-110°=70°,
∵∠ABD=150°,
∴∠DBF=180°-150°=30°,
∵CE⊥AB,DF⊥AB,
∴BE=BC·cos ∠CBE,
BF=BD·cos ∠DBF,
∴EF=BF-BE=BD·cos ∠DBF-BC·cos ∠CBE=70×cos 30°-70×cos 70°≈39(cm).
答:水平方向增加的距离EF的长约为39 cm.
23.解:(1)如图,作CD⊥AB于点D,作ME⊥AB于点E,
∵∠DBM=∠A+∠AMB=30°+∠AMB=60°,∴∠AMB=30°,
∴△ABM是等腰三角形,
∴BM=AB=20 n mile,
在Rt△BEM中,∠EBM=60°,BM=20 n mile,∴EM=BM·sin ∠EBM=20×sin 60°=20×=10 (n mile),
∴灯塔M到轮船航线AB的距离为10 n mile.
(2)∵CD⊥AB,ME⊥AB,AB∥CM,
∴四边形CDEM是矩形,
∴CD=EM=10 n mile,DE=CM,在Rt△BEM中,∠EBM=60°,BM=20 n mile,
∴BE=BM·cos ∠EBM=20×cos 60°=20×=10 (n mile),
在Rt△CDB中,∠DBC=45°,
∴△CDB是等腰直角三角形,
∴CD=BD=10 n mile,
∴CM=DE=BD-BE=10-10=10(-1)(n mile).
∴港口C与灯塔M的距离为10(-1)n mile.
24.解:如图,过点D作DE⊥AB于点E,过点C作CF⊥DE于点F,
则四边形BCFE是矩形,
由题意得,AB=80 m,DE=40 m,
∠ADE=90°-30°=60°,∠CDF=90°-45°=45°.
在Rt△ADE中,∠AED=90°,
∵tan ∠ADE==tan 60°=,
∴AE=DE=40 m,
∴BE=AB-AE=(80-40)m,
∵四边形BCFE是矩形,
∴CF=BE=(80-40)m,
在Rt△DCF中,∠DFC=90°,
∠CDF=∠DCF=45°,
∴DF=CF=(80-40)m,
∴BC=EF=DE-DF=40-80+40≈28(m).
答:楼BC的高度约为28 m.
25.解:(1)在Rt△ABC中,∠A=45°,
∴∠B=45°,∴BC=AC=20 cm.
(2)由题可知ON=EC=AC=10 cm,
∴NB=ON=10 cm,
又∵∠DON=32°,
∴DN=ON·tan ∠DON=10·tan 32°≈10×0.62=6.2(cm),
∴BD=BN-DN=10-6.2=3.8(cm).
26.解:(1)∵四边形PQMN是矩形,
∴∠Q=∠P=90°,
在Rt△ABQ中,∠ABQ=60°,AB=5.4 m,
∴AQ=AB·sin ∠ABQ= m,
∠QAB=30°,
∵四边形ABCD是矩形,∴AD=BC,
∠BAD=∠BCD=∠ABC=∠BCE=90°,∴∠CBE=30°,
∴BC= m,
∴AD= m,
∵∠PAD=180°-30°-90°=60°,
∴AP=AD·cos ∠PAD= m,
∴PQ=AP+AQ=≈6.1(m).
(2)在Rt△BCE中,
BE==3.2 m,
在Rt△ABQ中,
BQ=AB·cos ∠ABQ=2.7 m,
∵该充电站有20个停车位,
∴QM=QB+20BE=66.7 m,
∵四边形PQMN是矩形,
∴PN=QM=66.7 m.
27.解:(1)如图,过点C作CN⊥ED,交ED的延长线于点N,
∵∠CDE=97°,∴∠CDN=83°,
在Rt△CDN中,sin ∠CDN=sin 83°=,CD=6.7 m,∴CN=CDsin 83°≈6.7×0.993≈6.65(m).
答:点C到地面DE的距离约为6.65 m.
(2)如图,过点B作BP⊥CF,垂足为P,∵CF∥DE,∴∠FCD=∠CDN=83°,∵∠BCD=98°,
∴∠BCP=∠BCD-∠FCD=15°,
∵平行线间的距离处处相等,
∴EF=CN=6.65 m,∵AE=8.5 m,
∴BP=AF=AE-EF=8.5-6.65=1.85(m),
在Rt△BCP中,sin ∠BCP=sin 15°=,
∴BC=≈≈7.14(m).
答:顶部线段BC的长约为7.14 m.
(总分:150分 时间:120分钟)
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.计算tan260°的结果为 ( )
A. B. C. D.3
2.在Rt△ABC中,∠C=90°,sin A=,则tan B的值是 ( )
A. B. C. D.
3.如图,沿AE折叠矩形纸片ABCD,使点D落在BC边上的点F处.已知AB=4,BC=5,则cos ∠EFC的值为 ( )
A. B. C. D.
4.(2024淄博中考)如图,在综合与实践活动课上,小强先测得教学楼在水平地面上的影长BC为35 m.又在点C处测得该楼的顶端A的仰角是29°.则用计算器计算教学楼高度的按键顺序正确的是 ( )
5.如图,两建筑物的水平距离为a m,从A点测得D点的俯角为α,测得C点的俯角为β,则较低建筑物CD的高为 ( )
A.a m B.a·tan α m C.am D.a(tan α-tan β)m
6.如图1是一种折叠桌子,示意图如图2,它是由下面的支架AD、BC与桌面构成的,已知OA=OB=OC=OD=20 cm,∠COD=60°,则点A到地面(CD所在的平面)的距离是 ( )
图1 图2
A.30 cm B.60 cm C.40 cm D.60 cm
7.在△ABC中,若+2(1-tan B)2=0,则∠C的度数是 ( )
A.45° B.60° C.75° D.105°
8.如图,钓鱼竿AC长6 m,露在水面上的鱼线BC长3 m,某垂钓者想看看鱼钩上的情况,把鱼竿AC转动到AC'的位置,此时露在水面上的鱼线B'C'为3 m,则鱼竿转过的角度是 ( )
A.60° B.45° C.15° D.90°
9.如图,某数学兴趣小组测量一棵树CD的高度,在点A处测得树顶C的仰角为45°,在点B处测得树顶C的仰角为60°,且A、B、D三点在同一直线上,若AB=(8+8)m,则这棵树CD的高度是 ( )
A.6 m B.8 m C.10 m D.12 m
10.春天是放风筝的好时节,小明为了让风筝顺利起飞,特地将风筝放在坡度为1∶2.4的山坡上,并站在视线刚好与风筝起飞点A齐平的B处,起风后小明开始往下跑26 m至坡底C处,并继续沿平地向前跑16 m到达D处后站在原地开始调整,小明将手中的线轴刚好举到与视线齐平处测得风筝的仰角是37°,此时风筝恰好升高到起飞时的正上方E处.已知小明视线距地面高度为1.5 m,图中风筝E、A、B、C、D五点在同一平面内,则风筝上升的垂直距离AE约为 ( )
(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
A.34.2 m B.32.7 m
C.31.2 m D.22.7 m
二、填空题:本大题共6小题,每小题4分,共24分.
11.在Rt△ABC中,∠ACB=90°,AC=2,BC=4,点D是AB的中点,则CD= .
12.已知α为锐角,且sin(α-10°)=0.5,则α等于 .
13.在△ABC中,∠C=90°,tan A=,△ABC的周长为60,那么AB的长为 .
14.如图,在3×3的正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫做格点.点A、B、C均在格点上,连结AB,则tan ∠ABC的值为 .
15.(2024宁夏中考)如图1是三星堆遗址出土的陶盉(hé),图2是其示意图.已知管状短流AB=2 cm,四边形BCDE是器身,BE∥CD,BC=DE=11 cm,∠ABE=120°,∠CBE=80°.器身底部CD距地面的高度为21.5 cm,则该陶盉管状短流口A距地面的高度约为 cm(结果精确到0.1 cm).(参考数据:sin 80°≈0.984 8,cos 80°≈0.173 6,tan 80°≈5.671 3,≈1.732)
图1 图2
第15题图
16.如图,已知点A(3,0),点B在y轴正半轴上,将线段AB绕点A顺时针旋转120°到线段AC,若点C的坐标为(7,h),则h= .
第16题图
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17.(6分)计算:
(1)tan 30°·tan 60°+sin245°+cos245°.
(2)2cos 30°·sin 60°-tan 45°·sin 30°.
18.(6分)如图,在△ABC中,CD⊥AB于点D,∠A=30°,BC=5,tan B=,求AC的长.
19.(6分)如图,一水库大坝的横断面为梯形ABCD,坝顶BC宽6 m,坝高20 m,斜坡AB的坡度i=1∶2.5,斜坡CD的坡角为30°,求坝底AD的长度.(结果精确到0.1 m,参考数据:≈1.414,≈1.732)
20.(8分)如图,在△ABC中,AC=,BC=,cos A=,点D在BC边上,且CD=2BD,DE⊥AB,垂足为E,连结CE.
(1)求线段AB的长.
(2)求∠CEA的正切值.
21.(10分)(2024牡丹江中考)如图,某数学活动小组用高度为1.5 m的测角仪BC,对垂直于地面CD的建筑物AD的高度进行测量,BC⊥CD于点C.在B处测得A的仰角∠ABE=45°,然后将测角仪向建筑物方向水平移动6 m至FG处,FG⊥CD于点G,测得A的仰角∠AFE=58°,BF的延长线交AD于点E,求建筑物AD的高度.(结果保留小数点后一位,参考数据:sin 58°≈0.85,cos 58°≈0.53,tan 58°≈1.60)
22.(10分)图1是一款可调节椅背的沙发椅,它可以减轻使用者的脊椎压力.图2是它的侧面示意图,椅背BC=70 cm,将椅背角度从110°调节到150°(即∠ABC=110°,∠ABD=150°)时,分别过点C、D作CE⊥AB于点E,DF⊥AB于点F,求水平方向增加的距离EF的长.(结果精确到1 cm,参考数据:sin 70°≈0.9,cos 70°≈0.3,tan 70°≈2.7,≈1.7)
图1 图2
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
23.(8分)如图,一艘轮船在A处测得灯塔M位于A的北偏东30°方向上,轮船沿着正北方向航行20 n mile到达B处,测得灯塔M位于B的北偏东60°方向上,测得港口C位于B的北偏东45°方向上.已知港口C在灯塔M的正北方向上.
(1)求灯塔M到轮船航线AB的距离(结果保留根号).
(2)求港口C与灯塔M的距离(结果保留根号).
24.(10分)(2024兴安盟、呼伦贝尔中考)综合实践活动中,数学兴趣小组利用无人机测量大楼的高度.如图,无人机在离地面40 m的D处,测得操控者A的俯角为30°,测得楼BC楼顶C处的俯角为45°,又经过人工测量得到操控者A和大楼BC之间的水平距离是80 m,则楼BC的高度是多少米 (点A、B、C、D都在同一平面内,参考数据:≈1.7)
25.(10分)(2024贵州中考)综合与实践:小星学习解直角三角形知识后,结合光的折射规律进行了如下综合性学习.
【实验操作】第一步:将长方体空水槽放置在水平桌面上,一束光线从水槽边沿A处投射到底部B处,入射光线与水槽内壁AC的夹角为∠A;
第二步:向水槽注水,水面上升到AC的中点E处时,停止注水.(直线NN'为法线,AO为入射光线,OD为折射光线)
【测量数据】如图,点A、B、C、D、E、F、O、N、N'在同一平面内,测得AC=20 cm,∠A=45°,折射角∠DON=32°.
【问题解决】根据以上实验操作和测量的数据,解答下列问题:
(1)求BC的长.
(2)求B、D之间的距离(结果精确到0.1 cm).
(参考数据:sin 32°≈0.53,cos 32°≈0.85,tan 32°≈0.62)
26.(10分)(2024广东中考)中国新能源汽车为全球应对气候变化和绿色低碳转型作出了巨大贡献.为满足新能源汽车的充电需求,某小区增设了充电站,如图是矩形PQMN充电站的平面示意图,矩形ABCD是其中一个停车位.经测量,∠ABQ=60°,AB=5.4 m,CE=1.6 m,GH⊥CD,GH是另一个车位的宽,所有车位的长宽相同,按图示并列划定.
根据以上信息回答下列问题:(结果精确到0.1 m,参考数据:≈1.73)
(1)求PQ的长.
(2)该充电站有20个停车位,求PN的长.
27.(12分)(2024济南中考)城市轨道交通发展迅猛,为市民出行带来极大方便.某校综合实践小组想测得轻轨高架站的相关距离,数据勘测组通过勘测得到了如下记录表:
综合实践活动记录表
活动内容 测量轻轨高架站的相关距离
测量工具 测倾器、红外测距仪等
过程资料 轻轨高架站示意图 相关数据及说明:图中点A、B、C、D、E、F在同一平面内,房顶AB,吊顶CF和地面DE所在的直线都平行,点F在与地面垂直的中轴线AE上,∠BCD=98°,∠CDE=97°,AE=8.5 m,CD=6.7 m
成果梳理 ……
请根据记录表提供的信息解答下列问题:
(1)求点C到地面DE的距离.
(2)求顶部线段BC的长.
(结果精确到0.01 m,参考数据:sin 15°≈0.259,cos 15°≈0.966,tan 15°≈0.268,sin 83°≈0.993,cos 83°≈0.122,tan 83°≈8.144)
【详解答案】
1.D
2.A 解析:在Rt△ABC中,sin A=,设BC=2m,则AB=3m.根据勾股定理可得AC=m.所以tan B=.故选A.
3.D 解析:∵四边形ABCD是矩形,
∴AD=BC=5,CD=AB=4,∠B=∠C=90°.由折叠的性质得AF=AD=5,EF=DE,在Rt△ABF中,由勾股定理得BF==3,
∴CF=BC-BF=5-3=2.设DE=EF=x,则CE=CD-DE=4-x,
在Rt△CEF中,由勾股定理得(4-x)2+22=x2,解得x=,即EF=,
∴cos ∠EFC==2÷.
故选D.
4.A 解析:在Rt△ABC中,∠ACB=29°,BC=35 m,∴tan ∠ACB=tan 29°=,∴AB=35×tan 29° m,∴用计算器计算教学楼高度的按键顺序为A.故选A.
5.D 解析:如图,作AE∥BD交DC的延长线于点E,
根据题意得∠DAE=α,∠CAE=β,AE=a m,∵tan α=,tan β=,
∴DE=atan α,CE=atan β,∴CD=DE-CE=a(tan α-tan β)m.故选D.
6.D 解析:如图,连结CD,过点O作OF⊥CD交于点F,延长FO交AB于点E,
由题意可知AB∥CD,∴OE⊥AB,
∵OA=OB=OC=OD=20 cm,
∠COD=∠AOB=60°,
∴△COD、△AOB为等边三角形,
△COD≌△AOB,∴∠COF=30°,
OF=OE,∴OF=OC·cos ∠COF=20=30(cm).∴EF=2OF=60 cm,即点A到地面的距离为60 cm.故选D.
7.C 解析:∵+2(1-tan B)2=0,∴cos A-=0,2(1-tan B)2=0,∴cos A=,tan B=1,∴∠A=60°,∠B=45°,∴∠C=180°-∠A-∠B=75°.故选C.
8.C 解析:∵sin ∠CAB=,∴∠CAB=45°.∵sin ∠C'AB'=,∴∠C'AB'=60°.
∴∠CAC'=60°-45°=15°,∴鱼竿转过的角度是15°.故选C.
9.B 解析:由题意得CD⊥AB,
设BD=x m,在Rt△BDC中,
∠CBD=60°,∴CD=BD·tan 60°=x(m),在Rt△ACD中,∠DAC=45°,
tan ∠DAC=1,∴AD=x(m),∵BD+AD=AB,∴x+x=8+8,解得x=8,∴CD=x=8,∴这棵树CD的高度为8 m.故选B.
10.D 解析:设小明在B处视线的点为N,延长NB交直线CD于点S,过点G作GM平行于地面交直线AE于点M,如图,
坡度为1∶2.4,BC=26 m,则SC=24 m,BS=10 m,∵AN∥SC,∴,即,解得AN=RS=3.6,AR=NS=BS+NB=10+1.5=11.5(m),则AM=10 m,MG=RD=RS+SC+CD=3.6+24+16=43.6(m),EM=MG tan 37°≈32.7 m,AE=EM-AM=32.7-10=22.7(m).故选D.
11. 解析:如图,在Rt△ABC中,
∵∠ACB=90°,AC=2,BC=4,
∴AB==2,
∵点D是AB的中点,
∴CD=AB=.
12.40° 解析:∵sin(α-10°)=0.5,α为锐角,∴α-10°=30°,∴α=40°.
13.26 解析:如图:
∵∠C=90°,tan A=,∴tan A=,设AC=5x,则BC=12x,
在Rt△ABC中,AB2=AC2+BC2=(13x)2,∴AB=13x,∵△ABC的周长为60,∴AB+AC+BC=60,∴13x+5x+12x=60,∴30x=60,∴x=2,∴AB=13x=26.
14. 解析:如图,在Rt△ABD中,AD=3,BD=2,
∴tan ∠ABC=tan ∠ABD=.
15.34.1 解析:如图,过点C作CF⊥BE,垂足为F,过点A作AG⊥EB,交EB的延长线于点G,
∵∠ABE=120°,∴∠ABG=180°-∠ABE=60°,在Rt△ABG中,AB=2 cm,∴AG=AB·sin 60°=2×(cm),在Rt△BCF中,∠EBC=80°,BC=11 cm,∴CF=BC·sin 80°≈11×0.984 8=10.832 8(cm),∵器身底部CD距地面的高度为21.5 cm,
∴该陶盉管状短流口A距地面的高度=AG+CF+21.5=+10.832 8+21.5≈34.1(cm),∴该陶盉管状短流口A距地面的高度约为34.1 cm.
16. 解析:如图,在x轴上取点D和点E,使得∠ADB=∠AEC=120°,过点C作CF⊥x轴于点F.
∵点C的坐标为(7,h),∴OF=7,CF=h.在Rt△CEF中,∠CEF=180°-∠AEC=60°,CF=h,∴EF=h,CE=h.
∵∠BAC=∠ADB=120°,∴∠BAD+∠CAE=∠BAD+∠ABD.
∴∠CAE=∠ABD.∵CA=AB,
∠CEA=∠ADB
∴△CAE≌△ABD(A.A.S.).∴AD=CE=h,AE=BD.∵点A(3,0),∴OA=3.∴OD=OA-AD=3-h.
在Rt△BOD中,∠BDO=180°-∠ADB=60°,∴BD==23-h=6-h.∴AE=BD=6-h.∵OA+AE+EF=OF,∴3+6-h+h=7,解得h=.
17.解:(1)原式==1+=2.
(2)原式=2×-1×=1.
18.解:∵tan B=,∴设CD=3x,BD=4x,∴BC==5x=5,∴x=1,∴CD=3.∵CD⊥AB,∠A=30°,∴AC=2CD=6.
19.解:如图,作BE⊥AD,CF⊥AD,垂足分别为点E、F,则四边形BCFE是矩形,
由题意得BC=EF=6 m,BE=CF=20 m,斜坡AB的坡度i为1∶2.5,
在Rt△ABE中,,
即,解得AE=50.
在Rt△CFD中,∠D=30°,
∴DF==20 m,
∴AD=AE+EF+FD=50+6+20≈90.6(m).
故坝底AD的长度约为90.6 m.
20.解:(1)如图,过点C作CF⊥AB于点F.∵AC=,cos A=,
∴AF=1.∴CF==2.
在Rt△BCF中,FB==3,
∴AB=AF+FB=1+3=4.
(2)∵CD=2BD,BC=,
∴BD=CB=.
∵FB=3,CB=,
∴cos B=,
∴BE=DB·cos B==1.
∴EF=2.
又∵CF=2,CF⊥AB,
∴tan ∠CEA=tan ∠CEF==1.
21.解:根据题意可知四边形BEDC是矩形,∠ABE=45°,∠AFE=58°,
∴DE=BC=1.5 m.
∵tan ∠ABE=,tan ∠AFE=,
∴AE=BE·tan 45°=BE,EF=.
∵BE=BF+EF,∴AE=6+,
∴AE≈16 m.
∴AD=AE+DE=17.5 m.
答:建筑物AD的高度约为17.5 m.
22.解:由题意得BC=BD=70 cm,
∵∠ABC=110°,
∴∠CBE=180°-110°=70°,
∵∠ABD=150°,
∴∠DBF=180°-150°=30°,
∵CE⊥AB,DF⊥AB,
∴BE=BC·cos ∠CBE,
BF=BD·cos ∠DBF,
∴EF=BF-BE=BD·cos ∠DBF-BC·cos ∠CBE=70×cos 30°-70×cos 70°≈39(cm).
答:水平方向增加的距离EF的长约为39 cm.
23.解:(1)如图,作CD⊥AB于点D,作ME⊥AB于点E,
∵∠DBM=∠A+∠AMB=30°+∠AMB=60°,∴∠AMB=30°,
∴△ABM是等腰三角形,
∴BM=AB=20 n mile,
在Rt△BEM中,∠EBM=60°,BM=20 n mile,∴EM=BM·sin ∠EBM=20×sin 60°=20×=10 (n mile),
∴灯塔M到轮船航线AB的距离为10 n mile.
(2)∵CD⊥AB,ME⊥AB,AB∥CM,
∴四边形CDEM是矩形,
∴CD=EM=10 n mile,DE=CM,在Rt△BEM中,∠EBM=60°,BM=20 n mile,
∴BE=BM·cos ∠EBM=20×cos 60°=20×=10 (n mile),
在Rt△CDB中,∠DBC=45°,
∴△CDB是等腰直角三角形,
∴CD=BD=10 n mile,
∴CM=DE=BD-BE=10-10=10(-1)(n mile).
∴港口C与灯塔M的距离为10(-1)n mile.
24.解:如图,过点D作DE⊥AB于点E,过点C作CF⊥DE于点F,
则四边形BCFE是矩形,
由题意得,AB=80 m,DE=40 m,
∠ADE=90°-30°=60°,∠CDF=90°-45°=45°.
在Rt△ADE中,∠AED=90°,
∵tan ∠ADE==tan 60°=,
∴AE=DE=40 m,
∴BE=AB-AE=(80-40)m,
∵四边形BCFE是矩形,
∴CF=BE=(80-40)m,
在Rt△DCF中,∠DFC=90°,
∠CDF=∠DCF=45°,
∴DF=CF=(80-40)m,
∴BC=EF=DE-DF=40-80+40≈28(m).
答:楼BC的高度约为28 m.
25.解:(1)在Rt△ABC中,∠A=45°,
∴∠B=45°,∴BC=AC=20 cm.
(2)由题可知ON=EC=AC=10 cm,
∴NB=ON=10 cm,
又∵∠DON=32°,
∴DN=ON·tan ∠DON=10·tan 32°≈10×0.62=6.2(cm),
∴BD=BN-DN=10-6.2=3.8(cm).
26.解:(1)∵四边形PQMN是矩形,
∴∠Q=∠P=90°,
在Rt△ABQ中,∠ABQ=60°,AB=5.4 m,
∴AQ=AB·sin ∠ABQ= m,
∠QAB=30°,
∵四边形ABCD是矩形,∴AD=BC,
∠BAD=∠BCD=∠ABC=∠BCE=90°,∴∠CBE=30°,
∴BC= m,
∴AD= m,
∵∠PAD=180°-30°-90°=60°,
∴AP=AD·cos ∠PAD= m,
∴PQ=AP+AQ=≈6.1(m).
(2)在Rt△BCE中,
BE==3.2 m,
在Rt△ABQ中,
BQ=AB·cos ∠ABQ=2.7 m,
∵该充电站有20个停车位,
∴QM=QB+20BE=66.7 m,
∵四边形PQMN是矩形,
∴PN=QM=66.7 m.
27.解:(1)如图,过点C作CN⊥ED,交ED的延长线于点N,
∵∠CDE=97°,∴∠CDN=83°,
在Rt△CDN中,sin ∠CDN=sin 83°=,CD=6.7 m,∴CN=CDsin 83°≈6.7×0.993≈6.65(m).
答:点C到地面DE的距离约为6.65 m.
(2)如图,过点B作BP⊥CF,垂足为P,∵CF∥DE,∴∠FCD=∠CDN=83°,∵∠BCD=98°,
∴∠BCP=∠BCD-∠FCD=15°,
∵平行线间的距离处处相等,
∴EF=CN=6.65 m,∵AE=8.5 m,
∴BP=AF=AE-EF=8.5-6.65=1.85(m),
在Rt△BCP中,sin ∠BCP=sin 15°=,
∴BC=≈≈7.14(m).
答:顶部线段BC的长约为7.14 m.
