期末评估测试卷(含解析)2025-2026学年数学华东师大版九年级上册
文档属性
| 名称 | 期末评估测试卷(含解析)2025-2026学年数学华东师大版九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 196.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-06 15:42:32 | ||
图片预览



文档简介
期末评估测试卷
(总分:150分 时间:120分钟)
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.若二次根式有意义,则x的取值范围是 ( )
A.x>8 B.x≥8
C.x≥0 D.x≤-8
2.方程x2+2x+1=0的根是 ( )
A.x1=x2=1 B.x1=x2=-1
C.x1=-1,x2=1 D.无实数根
3.(2024连云港中考)下列说法正确的是 ( )
A.10张票中有1张奖票,10人去摸,先摸的人摸到奖票的概率较大
B.从1,2,3,4,5中随机抽取一个数,取得偶数的可能性较大
C.小强一次掷出3颗质地均匀的骰子,3颗全是6点朝上是随机事件
D.抛一枚质地均匀的硬币,正面朝上的概率为,连续抛此硬币2次必有1次正面朝上
4.在Rt△ABC中,∠C=90°,AB=5,BC=4,则∠B的正切值为 ( )
A. B. C. D.
5.如图,以点O为位似中心,把△ABC放大为原图形的2倍得到△A'B'C',以下说法错误的是 ( )
A.S△ABC∶S△A'B'C'=1∶2
B.AB∶A'B'=1∶2
C.点A、O、A'三点在同一条直线上
D.BC∥B'C'
6.(2024山西中考)一个不透明的盒子里装有一个红球、一个白球和一个绿球,这些球除颜色外都相同.从中随机摸出一个球,记下颜色后不放回,再从中随机摸出一个球,则两次摸到的球恰好有一个红球的概率是 ( )
A. B. C. D.
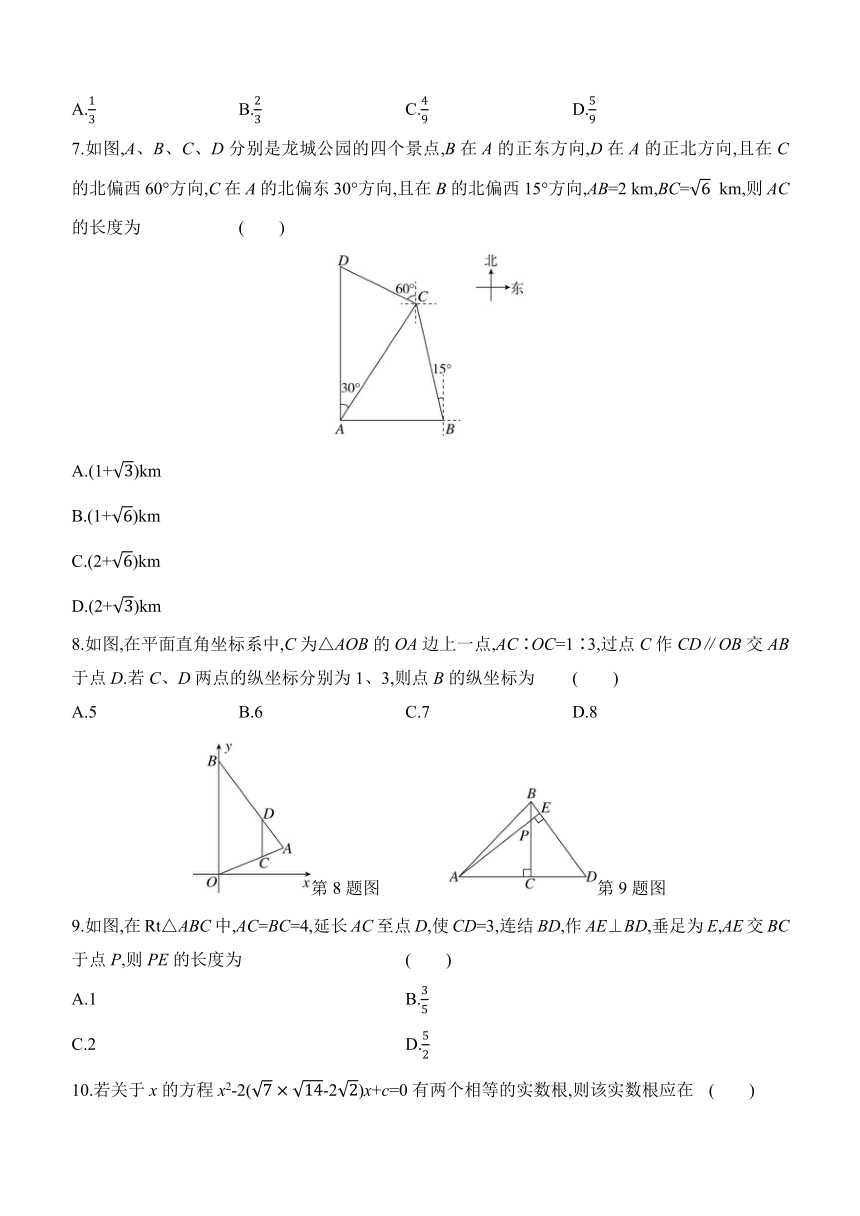
7.如图,A、B、C、D分别是龙城公园的四个景点,B在A的正东方向,D在A的正北方向,且在C的北偏西60°方向,C在A的北偏东30°方向,且在B的北偏西15°方向,AB=2 km,BC= km,则AC的长度为 ( )
A.(1+)km
B.(1+)km
C.(2+)km
D.(2+)km
8.如图,在平面直角坐标系中,C为△AOB的OA边上一点,AC∶OC=1∶3,过点C作CD∥OB交AB于点D.若C、D两点的纵坐标分别为1、3,则点B的纵坐标为 ( )
A.5 B.6 C.7 D.8
第8题图 第9题图
9.如图,在Rt△ABC中,AC=BC=4,延长AC至点D,使CD=3,连结BD,作AE⊥BD,垂足为E,AE交BC于点P,则PE的长度为 ( )
A.1 B.
C.2 D.
10.若关于x的方程x2-2(-2)x+c=0有两个相等的实数根,则该实数根应在 ( )
A.7和8之间 B.6和7之间
C.5和6之间 D.4和5之间
二、填空题:本大题共6小题,每小题4分,共24分.
11.如果一个三角形的三边长分别为5,12,13,与其相似的三角形的最长边为39,则较大的三角形的面积为 .
12.(2024重庆B卷中考)重庆在低空经济领域实现了新的突破.今年第一季度低空飞行航线安全运行了200架次,预计第三季度低空飞行航线安全运行将达到401架次.设第二、第三两个季度安全运行架次的平均增长率为x,根据题意,可列方程为 .
13.如图,在4×4的网格中,每个小正方形的边长为1,点A、B、C均在格点上,则cos ∠BAC的值是 .
14.若m=-2,则m+n的值为 .
15.如图1是小强在健身器材上进行仰卧起坐锻炼时的情景,图2是小强锻炼时上半身由ON位置运动到与地面CD垂直的OM位置时的示意图,已知ON=0.8 m,α=30°,则M、N两点间的距离是
m.
图1 图2
16.(2024牡丹江中考)如图,在正方形ABCD中,E是BC延长线上一点,AE分别交BD、CD于点F、M,过点F作NP⊥AE,分别交AD、BC于点N、P,连结MP.下列五个结论:①AM=PN;②DM+DN=DF;③若P是BC中点,AB=3,则EM=2;④BF·NF=AF·BP;⑤若PM∥BD,则CE=BC.其中正确的结论是 .(填序号)
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17.(6分)计算:|-3|+cos 30°.
18.(6分)按要求解下列方程:
(1)2x2+4x-3=0(配方法). (2)x2-3x-1=0(公式法).
19.(6分)关于x的一元二次方程x2-2(m+1)x+m2+5=0有两个实数根.
(1)求m的取值范围.
(2)若Rt△ABC的两条直角边AC、BC的长恰好是此方程的两个实数根,斜边AB=6,求△ABC的周长.
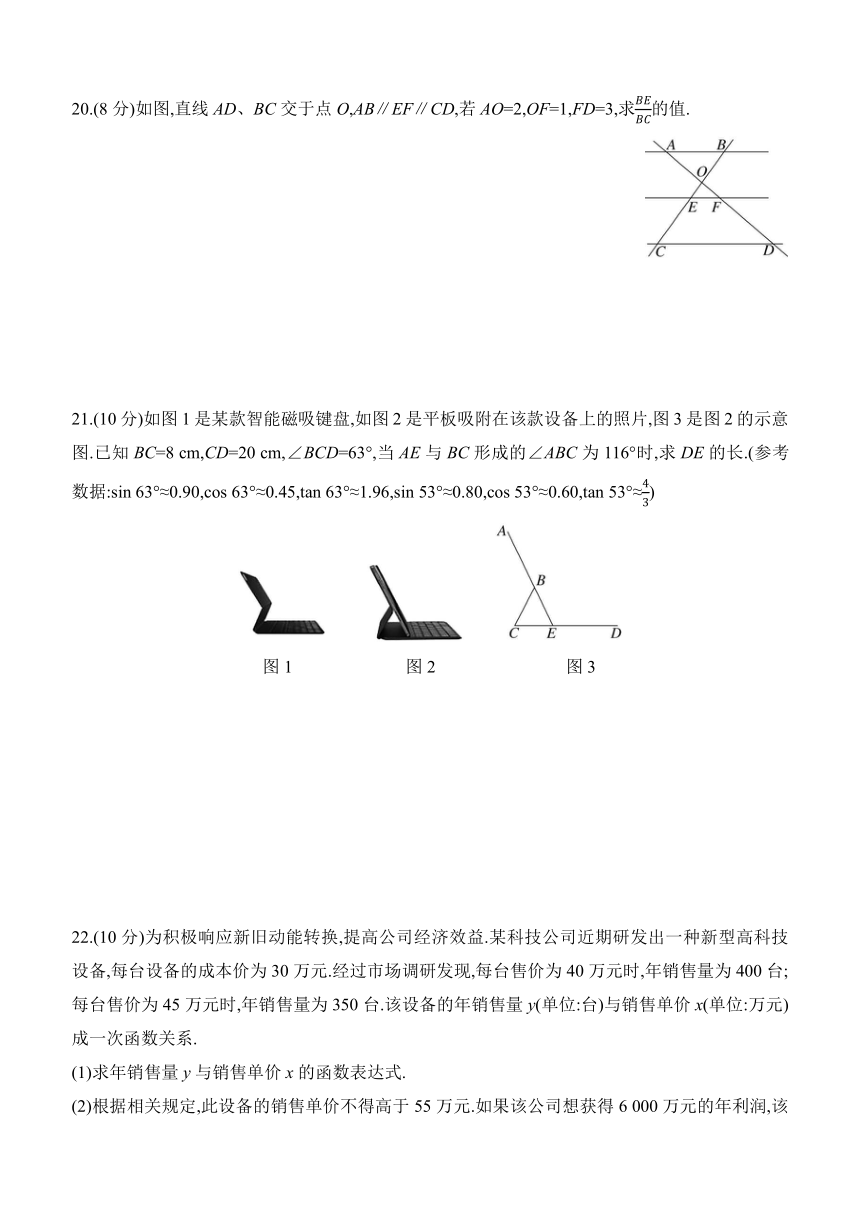
20.(8分)如图,直线AD、BC交于点O,AB∥EF∥CD,若AO=2,OF=1,FD=3,求的值.
21.(10分)如图1是某款智能磁吸键盘,如图2是平板吸附在该款设备上的照片,图3是图2的示意图.已知BC=8 cm,CD=20 cm,∠BCD=63°,当AE与BC形成的∠ABC为116°时,求DE的长.(参考数据:sin 63°≈0.90,cos 63°≈0.45,tan 63°≈1.96,sin 53°≈0.80,cos 53°≈0.60,tan 53°≈)
图1 图2 图3
22.(10分)为积极响应新旧动能转换,提高公司经济效益.某科技公司近期研发出一种新型高科技设备,每台设备的成本价为30万元.经过市场调研发现,每台售价为40万元时,年销售量为400台;每台售价为45万元时,年销售量为350台.该设备的年销售量y(单位:台)与销售单价x(单位:万元)成一次函数关系.
(1)求年销售量y与销售单价x的函数表达式.
(2)根据相关规定,此设备的销售单价不得高于55万元.如果该公司想获得6 000万元的年利润,该设备的销售单价应是多少万元
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
23.(8分)如图,在平行四边形ABCD中,AE∶BE=1∶2.
(1)求△AEF与△CDF的周长之比.
(2)若S△AEF=6 cm2,求S△CDF.
24.(10分)(2024宿迁中考)某校组织七年级学生开展以“讲好红色故事,传承红色基因”为主题的研学活动,策划了四条研学线路供学生选择:A彭雪枫纪念馆,B淮海军政大礼堂,C爱园烈士陵园,D大王庄党性教育基地,每名学生只能任意选择一条线路.
(1)小刚选择线路A的概率为 .
(2)请用画树状图或列表的方法,求小刚和小红选择同一线路的概率.
25.(10分)如图所示,在△ABC中,点D在边AB上,点E、F在边AC上,且DE∥BC,.
(1)求证:DF∥BE.
(2)把△FDE与△EBC的周长分别记作C△FDE、C△EBC,如果CF=AE,求的值.
26.(10分)(2024兰州中考)单摆是一种能够产生往复摆动的装置.某兴趣小组利用摆球和摆线进行与单摆相关的实验探究,并撰写实验报告如下.
实验主题 探究摆球运动过程中高度的变化
实验用具 摆球、摆线、支架、摄像机等
实验说明 如图1,在支架的横杆点O处用摆线悬挂一个摆球,将摆球拉高后松手,摆球开始往复运动.(摆线的长度变化忽略不计) 如图2,摆球静止时的位置为点A,拉紧摆线将摆球拉至点B处,BD⊥OA.∠BOA=64°,BD=20.5 cm;当摆球运动至点C时,∠COA=37°,CE⊥OA.(点O、A、B、C、D、E在同一平面内)
实验图示 图1 图2
解决问题:根据以上信息,求ED的长(结果精确到0.1 cm).
(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,sin 64°≈0.90,cos 64°≈0.44,tan 64°≈2.05)
27.(12分)如图,在△ABC中,∠B=90°,AB=12 cm,BC=24 cm,动点P从点A开始沿着边AB向点B以2 cm/s的速度移动(不与点B重合),动点Q从点B开始沿着边BC向点C以4 cm/s的速度移动(不与点C重合).若P、Q两点同时移动.
(1)当移动几秒时,△BPQ的面积为20 cm2
(2)当移动几秒时,四边形APQC的面积为108 cm2
(3)当移动几秒时,△BPQ与△ABC相似
【详解答案】
1.B 解析:∵二次根式有意义,∴x-8≥0,解得x≥8.故选B.
2.B 解析:∵x2+2x+1=0,∴(x+1)2=0,则x+1=0,解得x1=x2=-1,故选B.
3.C 解析:A.10张票中有1张奖票,10人去摸,先摸或者后摸的人摸到奖票的概率都一样大,故此选项不符合
题意;
B.从1,2,3,4,5中随机抽取一个数,取得奇数的可能性较大,故此选项不符合题意;
C.小强一次掷出3颗质地均匀的骰子,3颗全是6点朝上是随机事件,故此选项符合题意;
D.抛一枚质地均匀的硬币,正面朝上的概率为,连续抛此硬币2次不一定有1次正面朝上,故此选项不符合题意.故选C.
4.A 解析:由题意可得AC=
=3,∴tan B=.
故选A.
5.A 解析:∵以点O为位似中心,
把△ABC放大为原图形的2倍得到△A'B'C',∴△ABC∽△A'B'C',AB∶A'B'=1∶2,BC∥B'C',点A、O、A'三点在同一条直线上,∴S△ABC∶S△A'B'C'=1∶4,故选项A错误,符合题意,选项B、C、D正确,不符合题意.故选A.
6.B 解析:列表如下:
红 白 绿
红 — (红,白) (红,绿)
白 (白,红) — (白,绿)
绿 (绿,红) (绿,白) —
共有6种等可能的结果,其中两次摸到的球恰好有一个红球的结果有(红,白),(红,绿),(白,红),(绿,红),共4种,∴两次摸到的球恰好有一个红球的概率为.故选B.
7.A 解析:如图,过点B作BE⊥AC于点E,
∴∠AEB=∠BEC=90°,由题意得,∠CAB=90°-30°=60°,∠ABC=90°-15°=75°,∴∠ACB=180°-∠CAB-∠ABC=45°,∠ABE=90°-∠CAB=30°,在Rt△ABE中,∠AEB=90°,AB=2 km,∴AE=AB=1 km,∴BE= km,在Rt△BCE中,∠BEC=90°,∠BCE=45°,
∴△BCE是等腰直角三角形,∴CE=BE= km,∴AC=AE+CE=(1+)km.故选A.
8.D 解析:∵CD∥OB,∴∠ADC=∠ABO,又∠A=∠A,
∴△ADC∽△ABO,
∴,∵AC∶OC=1∶3,
∴,即,∵C、D两点纵坐标分别为1、3,∴CD=2,∴,解得OB=8,∴点B的坐标为(0,8).故选D.
9.B 解析:在Rt△ABC中,AC=BC=4,∴AB==4,∵∠ACB=90°,∴∠BCD=180°-∠ACB=90°,∴BD==5,∵AC=4,CD=3,
∴AD=4+3=7,∵AE⊥BD,
∴∠AEB=90°,∵△ABD的面积=AD·BC=BD·AE,∴AE=,在Rt△ABE中,BE=,
∵∠PEB=∠BCD=90°,∠PBE=∠DBC,∴△BPE∽△BDC,∴,
∴,解得PE=.故选B.
10.A 解析:∵关于x的方程x2-2(-2)x+c=0有两个相等的实数根,∴x2-2(-2)x+c能配成完全平方式,∵-2=5,∴x2-2×5x+c=x2-2×5x+(5)2=(x-5)2,
∴(x-5)2=0,∴关于x的方程x2-2(-2)x+c=0的实数根为x1=x2=5,∵72<(5)2<82,∴该实数根在7和8之间.故选A.
11.270 解析:∵52+122=132,∴三边长为5,12,13的三角形是直角三角形,其面积=×5×12=30.易得两个三角形的相似比为=3,则两个三角形的面积比为32=9,∴较大的三角形的面积为30×9=270.
12.200(1+x)2=401 解析:根据题意得200(1+x)2=401.
13. 解析:由勾股定理可得AC=
,BC==2,AB==5,∵AC2+BC2=5+20=25,AB2=25,∴AC2+BC2=AB2,∴△ABC为直角三角形,
∴∠ACB=90°,在Rt△ABC中,
cos ∠BAC=.
14.0 解析:由题意可知,n-2≥0,4-2n≥0,∴n=2,把n=2代入m=-2,得m=-2,则m+n=-2+2=0.
15. 解析:由题意得OM=ON=0.8 m,MH⊥DH,过点N作NE⊥MH于点E,如图,
∵MH⊥DH,NE⊥MH,∴NE∥DH,∠NEO=90°,∴∠ONE=α=30°,
∴OE=ON=×0.8=0.4(m),
∴ME=OM+OE=0.8+0.4=1.2(m),
在Rt△OEN中,EN=(m),
∴MN==
(m).
16.①②③⑤ 解析:∵四边形ABCD为正方形,∴∠ABC=∠BCD=∠CDA=∠DAB=90°,AB=BC=CD=AD,∠ADB=∠ABD=∠CBD=∠CDB=45°,如图1,过点P作PG⊥AD于点G,则四边形ABPG是矩形,
图1
∴PG=AB=AD,∵∠GPN+∠GNP=90°=∠GNP+∠DAM,∴∠GPN=∠DAM,又∵PG=AD,∠PGN=90°=∠ADM,∴△PGN≌△ADM(A.S.A.),
∴AM=PN,①正确,故符合要求;如图2,过点F作HF⊥DF交AD于点H,连结CF,
图2
∴∠DHF=45°=∠ADB,∴DF=HF,
∵AB=BC,∠ABF=∠CBF=45°,BF=BF,∴△ABF≌△CBF(S.A.S.),
∴AF=CF,∠BAF=∠BCF,
∵∠BPF+∠BAF=360°-∠ABP-∠AFP=180°,∠BPF+∠FPC=180°,
∴∠BAF=∠FPC,∴∠BCF=∠FPC,
∴PF=CF=AF,∴PN-PF=AM-AF,即FN=FM,
∵∠HFN+∠NFD=90°=∠DFM+∠NFD,∴∠HFN=∠DFM,
∵HF=DF,∠HFN=∠DFM,FN=FM,∴△HFN≌△DFM(S.A.S.),
∴HN=DM,由勾股定理得,DH=DF,∵DH=HN+DN=DM+DN,∴DM+DN=DF,②正确,故符合要求;∵P是BC中点,AB=3,∴BP=CP=,如图3,连结AP,
图3
由勾股定理得,AP=,AP=PF=,解得PF=,设CE=x,则PE=+x,BE=3+x,
由勾股定理得,AE==
,∵sin E=,
∴,整理得,x2-2x-24=0,解得x=6或x=-4(舍去),∴AE=3,BE=9,
∵cos E=,∴,
解得EM=2,③正确,故符合要求;由题意知,∠BPF>90°,∴△BPF、△NFA不相似,BF·NF≠AF·BP,④错误,故不符合要求;∵PM∥BD,∴∠CPM=∠CBD=45°,
∠CMP=∠CDB=45°,设PC=CM=a,BC=CD=AD=AB=b,CE=c,则DM=b-a,BE=b+c,PE=a+c,PM=a,∵AF=PF,∠AFN=90°=∠PFM,FN=FM,∴△AFN≌△PFM(S.A.S.),
∴AN=PM=a,∵∠ADM=90°=∠ECM,∠AMD=∠EMC,
∴△AMD∽△EMC,∴,即,解得a=,同理,△ANF∽△EPF,∴,即,同理,△DMF∽△BAF,
∴,即,
∴,将a=代入得,,整理得,b+c=2b+c,解得,
∴CE=BC,⑤正确,故符合要求.
故正确的结论为①②③⑤.
17.解:原式=3-+2-2=5-3-3.
18.解:(1)2x2+4x-3=0,
2x2+4x=3,
x2+2x+1=+1,
(x+1)2=,
x+1=±,
所以x1=-1,x2=--1.
(2)x2-3x-1=0,
a=1,b=-3,c=-1,
Δ=b2-4ac=9-4×1×(-1)=13>0,
∴方程有两个不相等的实数根,
∴x=,
∴x1=,x2=.
19.解:(1)∵关于x的一元二次方程x2-2(m+1)x+m2+5=0有两个实数根,
∴Δ=4(m+1)2-4(m2+5)=8m-16≥0,解得m≥2.
(2)设x1、x2是关于x的一元二次方程x2-2(m+1)x+m2+5=0的两实数根,
∴x1+x2=2(m+1),x1x2=m2+5.
∵(x1+x2)2=+2x1x2,
∴=4(m+1)2-2(m2+5)=2m2+8m-6.
根据勾股定理,得=62,
∴2m2+8m-6=36,
解得m=3或m=-7(舍去).
∴x1+x2=2(m+1)=8.
∴AC+BC=8.
∴△ABC的周长为8+6=14.
20.解:∵AO=2,OF=1,FD=3,
∴AF=AO+OF=2+1=3,
AD=AF+FD=3+3=6,
∵AB∥EF∥CD,
∴.
21.解:如图,过点B作BH⊥CE于点H,
在Rt△BCH中,∵sin 63°=≈0.90,cos 63°=≈0.45,∴BH≈7.2 cm,CH≈3.6 cm,
在Rt△BEH中,
∵∠BEH=∠ABC-∠BCE=53°,
∴tan 53°=≈,
∴HE≈5.4 cm,
∴CE=CH+EH=3.6+5.4=9(cm),
∴DE=CD-CE=20-9=11(cm).
答:DE的长为11 cm.
22.解:(1)设年销售量y与销售单价x的函数表达式为y=kx+b,根据题意,得解得
所以年销售量y与销售单价x的函数表达式为y=-10x+800.
(2)根据题意,得(-10x+800)(x-30)=6 000,解得x1=50,x2=60,
因为销售单价不得高于55万元,
所以x=50.
所以设备的销售单价是50万元.
23.解:(1)由AE∶BE=1∶2,得.又∵四边形ABCD是平行四边形,∴AB∥DC.∴△AEF∽△CDF.
由AB=CD,得.
∴△AEF与△CDF的周长比等于相似比,为1∶3.
(2)由(相似三角形面积比是相似比的平方),S△AEF=6 cm2,得S△CDF=54 cm2.
24.解:(1)
(2)列表如下:
A B C D
A (A,A) (A,B) (A,C) (A,D)
B (B,A) (B,B) (B,C) (B,D)
C (C,A) (C,B) (C,C) (C,D)
D (D,A) (D,B) (D,C) (D,D)
共有16种等可能的结果,其中小刚和小红选择同一线路的结果有4种,
∴小刚和小红选择同一线路的概率为.
25.解:(1)证明:∵DE∥BC,
∴,
∵,
∴,
∵∠DAF=∠BAE,
∴△ADF∽△ABE,
∴∠ADF=∠ABE,
∴DF∥BE.
(2)∵DF∥BE,∴∠FDE=∠DEB,
∵DE∥BC,∴∠DEB=∠EBC,
∠FED=∠C,∴∠FDE=∠EBC,
∴△FDE∽△EBC,
∴,
设FE=a,EC=b,
∵CF=AE,∴AF=CE=b,AC=AF+EF+EC=2b+a,∵,
∴,
整理得a2+ab-b2=0,
∴-1=0,
∴解得(舍去负值),
∴.
26.解:在Rt△OBD中,∠ODB=90°,
∠BOA=64°,BD=20.5 cm,
∴tan ∠BOA=,sin ∠BOA=,
∴2.05≈,0.90≈,
∴OD=10 cm,OB≈22.78 cm,
在Rt△COE中,OC=OB=22.78 cm,
∠COA=37°,∴cos ∠COA=,
即cos 37°=,∴OE≈22.78×0.80=18.224(cm),
∴ED=OE-OD≈8.2(cm),
即ED的长约为8.2 cm.
27.解:(1)设运动时间为t s(0≤t<6),
则PB=(12-2t)cm,BQ=4t cm.
由题意,得S△BPQ=PB·BQ=×(12-2t)×4t=24t-4t2=20,
解得t1=1,t2=5.
所以当移动1 s或5 s时,△BPQ的面积为20 cm2.
(2)由题意,得S四边形APQC=S△ABC-S△BPQ=·AB·BC-(24t-4t2)=4t2-24t+144=108,解得t1=t2=3.
所以当移动3 s时,四边形APQC的面积为108 cm2.
(3)可分以下两种情况讨论:
①当△BPQ∽△BAC时,,
即,解得t=3;
②当△BPQ∽△BCA时,,
即,解得t=.综上所述,当移动3 s或 s时,△BPQ与△ABC相似.
(总分:150分 时间:120分钟)
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.若二次根式有意义,则x的取值范围是 ( )
A.x>8 B.x≥8
C.x≥0 D.x≤-8
2.方程x2+2x+1=0的根是 ( )
A.x1=x2=1 B.x1=x2=-1
C.x1=-1,x2=1 D.无实数根
3.(2024连云港中考)下列说法正确的是 ( )
A.10张票中有1张奖票,10人去摸,先摸的人摸到奖票的概率较大
B.从1,2,3,4,5中随机抽取一个数,取得偶数的可能性较大
C.小强一次掷出3颗质地均匀的骰子,3颗全是6点朝上是随机事件
D.抛一枚质地均匀的硬币,正面朝上的概率为,连续抛此硬币2次必有1次正面朝上
4.在Rt△ABC中,∠C=90°,AB=5,BC=4,则∠B的正切值为 ( )
A. B. C. D.
5.如图,以点O为位似中心,把△ABC放大为原图形的2倍得到△A'B'C',以下说法错误的是 ( )
A.S△ABC∶S△A'B'C'=1∶2
B.AB∶A'B'=1∶2
C.点A、O、A'三点在同一条直线上
D.BC∥B'C'
6.(2024山西中考)一个不透明的盒子里装有一个红球、一个白球和一个绿球,这些球除颜色外都相同.从中随机摸出一个球,记下颜色后不放回,再从中随机摸出一个球,则两次摸到的球恰好有一个红球的概率是 ( )
A. B. C. D.
7.如图,A、B、C、D分别是龙城公园的四个景点,B在A的正东方向,D在A的正北方向,且在C的北偏西60°方向,C在A的北偏东30°方向,且在B的北偏西15°方向,AB=2 km,BC= km,则AC的长度为 ( )
A.(1+)km
B.(1+)km
C.(2+)km
D.(2+)km
8.如图,在平面直角坐标系中,C为△AOB的OA边上一点,AC∶OC=1∶3,过点C作CD∥OB交AB于点D.若C、D两点的纵坐标分别为1、3,则点B的纵坐标为 ( )
A.5 B.6 C.7 D.8
第8题图 第9题图
9.如图,在Rt△ABC中,AC=BC=4,延长AC至点D,使CD=3,连结BD,作AE⊥BD,垂足为E,AE交BC于点P,则PE的长度为 ( )
A.1 B.
C.2 D.
10.若关于x的方程x2-2(-2)x+c=0有两个相等的实数根,则该实数根应在 ( )
A.7和8之间 B.6和7之间
C.5和6之间 D.4和5之间
二、填空题:本大题共6小题,每小题4分,共24分.
11.如果一个三角形的三边长分别为5,12,13,与其相似的三角形的最长边为39,则较大的三角形的面积为 .
12.(2024重庆B卷中考)重庆在低空经济领域实现了新的突破.今年第一季度低空飞行航线安全运行了200架次,预计第三季度低空飞行航线安全运行将达到401架次.设第二、第三两个季度安全运行架次的平均增长率为x,根据题意,可列方程为 .
13.如图,在4×4的网格中,每个小正方形的边长为1,点A、B、C均在格点上,则cos ∠BAC的值是 .
14.若m=-2,则m+n的值为 .
15.如图1是小强在健身器材上进行仰卧起坐锻炼时的情景,图2是小强锻炼时上半身由ON位置运动到与地面CD垂直的OM位置时的示意图,已知ON=0.8 m,α=30°,则M、N两点间的距离是
m.
图1 图2
16.(2024牡丹江中考)如图,在正方形ABCD中,E是BC延长线上一点,AE分别交BD、CD于点F、M,过点F作NP⊥AE,分别交AD、BC于点N、P,连结MP.下列五个结论:①AM=PN;②DM+DN=DF;③若P是BC中点,AB=3,则EM=2;④BF·NF=AF·BP;⑤若PM∥BD,则CE=BC.其中正确的结论是 .(填序号)
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17.(6分)计算:|-3|+cos 30°.
18.(6分)按要求解下列方程:
(1)2x2+4x-3=0(配方法). (2)x2-3x-1=0(公式法).
19.(6分)关于x的一元二次方程x2-2(m+1)x+m2+5=0有两个实数根.
(1)求m的取值范围.
(2)若Rt△ABC的两条直角边AC、BC的长恰好是此方程的两个实数根,斜边AB=6,求△ABC的周长.
20.(8分)如图,直线AD、BC交于点O,AB∥EF∥CD,若AO=2,OF=1,FD=3,求的值.
21.(10分)如图1是某款智能磁吸键盘,如图2是平板吸附在该款设备上的照片,图3是图2的示意图.已知BC=8 cm,CD=20 cm,∠BCD=63°,当AE与BC形成的∠ABC为116°时,求DE的长.(参考数据:sin 63°≈0.90,cos 63°≈0.45,tan 63°≈1.96,sin 53°≈0.80,cos 53°≈0.60,tan 53°≈)
图1 图2 图3
22.(10分)为积极响应新旧动能转换,提高公司经济效益.某科技公司近期研发出一种新型高科技设备,每台设备的成本价为30万元.经过市场调研发现,每台售价为40万元时,年销售量为400台;每台售价为45万元时,年销售量为350台.该设备的年销售量y(单位:台)与销售单价x(单位:万元)成一次函数关系.
(1)求年销售量y与销售单价x的函数表达式.
(2)根据相关规定,此设备的销售单价不得高于55万元.如果该公司想获得6 000万元的年利润,该设备的销售单价应是多少万元
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
23.(8分)如图,在平行四边形ABCD中,AE∶BE=1∶2.
(1)求△AEF与△CDF的周长之比.
(2)若S△AEF=6 cm2,求S△CDF.
24.(10分)(2024宿迁中考)某校组织七年级学生开展以“讲好红色故事,传承红色基因”为主题的研学活动,策划了四条研学线路供学生选择:A彭雪枫纪念馆,B淮海军政大礼堂,C爱园烈士陵园,D大王庄党性教育基地,每名学生只能任意选择一条线路.
(1)小刚选择线路A的概率为 .
(2)请用画树状图或列表的方法,求小刚和小红选择同一线路的概率.
25.(10分)如图所示,在△ABC中,点D在边AB上,点E、F在边AC上,且DE∥BC,.
(1)求证:DF∥BE.
(2)把△FDE与△EBC的周长分别记作C△FDE、C△EBC,如果CF=AE,求的值.
26.(10分)(2024兰州中考)单摆是一种能够产生往复摆动的装置.某兴趣小组利用摆球和摆线进行与单摆相关的实验探究,并撰写实验报告如下.
实验主题 探究摆球运动过程中高度的变化
实验用具 摆球、摆线、支架、摄像机等
实验说明 如图1,在支架的横杆点O处用摆线悬挂一个摆球,将摆球拉高后松手,摆球开始往复运动.(摆线的长度变化忽略不计) 如图2,摆球静止时的位置为点A,拉紧摆线将摆球拉至点B处,BD⊥OA.∠BOA=64°,BD=20.5 cm;当摆球运动至点C时,∠COA=37°,CE⊥OA.(点O、A、B、C、D、E在同一平面内)
实验图示 图1 图2
解决问题:根据以上信息,求ED的长(结果精确到0.1 cm).
(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,sin 64°≈0.90,cos 64°≈0.44,tan 64°≈2.05)
27.(12分)如图,在△ABC中,∠B=90°,AB=12 cm,BC=24 cm,动点P从点A开始沿着边AB向点B以2 cm/s的速度移动(不与点B重合),动点Q从点B开始沿着边BC向点C以4 cm/s的速度移动(不与点C重合).若P、Q两点同时移动.
(1)当移动几秒时,△BPQ的面积为20 cm2
(2)当移动几秒时,四边形APQC的面积为108 cm2
(3)当移动几秒时,△BPQ与△ABC相似
【详解答案】
1.B 解析:∵二次根式有意义,∴x-8≥0,解得x≥8.故选B.
2.B 解析:∵x2+2x+1=0,∴(x+1)2=0,则x+1=0,解得x1=x2=-1,故选B.
3.C 解析:A.10张票中有1张奖票,10人去摸,先摸或者后摸的人摸到奖票的概率都一样大,故此选项不符合
题意;
B.从1,2,3,4,5中随机抽取一个数,取得奇数的可能性较大,故此选项不符合题意;
C.小强一次掷出3颗质地均匀的骰子,3颗全是6点朝上是随机事件,故此选项符合题意;
D.抛一枚质地均匀的硬币,正面朝上的概率为,连续抛此硬币2次不一定有1次正面朝上,故此选项不符合题意.故选C.
4.A 解析:由题意可得AC=
=3,∴tan B=.
故选A.
5.A 解析:∵以点O为位似中心,
把△ABC放大为原图形的2倍得到△A'B'C',∴△ABC∽△A'B'C',AB∶A'B'=1∶2,BC∥B'C',点A、O、A'三点在同一条直线上,∴S△ABC∶S△A'B'C'=1∶4,故选项A错误,符合题意,选项B、C、D正确,不符合题意.故选A.
6.B 解析:列表如下:
红 白 绿
红 — (红,白) (红,绿)
白 (白,红) — (白,绿)
绿 (绿,红) (绿,白) —
共有6种等可能的结果,其中两次摸到的球恰好有一个红球的结果有(红,白),(红,绿),(白,红),(绿,红),共4种,∴两次摸到的球恰好有一个红球的概率为.故选B.
7.A 解析:如图,过点B作BE⊥AC于点E,
∴∠AEB=∠BEC=90°,由题意得,∠CAB=90°-30°=60°,∠ABC=90°-15°=75°,∴∠ACB=180°-∠CAB-∠ABC=45°,∠ABE=90°-∠CAB=30°,在Rt△ABE中,∠AEB=90°,AB=2 km,∴AE=AB=1 km,∴BE= km,在Rt△BCE中,∠BEC=90°,∠BCE=45°,
∴△BCE是等腰直角三角形,∴CE=BE= km,∴AC=AE+CE=(1+)km.故选A.
8.D 解析:∵CD∥OB,∴∠ADC=∠ABO,又∠A=∠A,
∴△ADC∽△ABO,
∴,∵AC∶OC=1∶3,
∴,即,∵C、D两点纵坐标分别为1、3,∴CD=2,∴,解得OB=8,∴点B的坐标为(0,8).故选D.
9.B 解析:在Rt△ABC中,AC=BC=4,∴AB==4,∵∠ACB=90°,∴∠BCD=180°-∠ACB=90°,∴BD==5,∵AC=4,CD=3,
∴AD=4+3=7,∵AE⊥BD,
∴∠AEB=90°,∵△ABD的面积=AD·BC=BD·AE,∴AE=,在Rt△ABE中,BE=,
∵∠PEB=∠BCD=90°,∠PBE=∠DBC,∴△BPE∽△BDC,∴,
∴,解得PE=.故选B.
10.A 解析:∵关于x的方程x2-2(-2)x+c=0有两个相等的实数根,∴x2-2(-2)x+c能配成完全平方式,∵-2=5,∴x2-2×5x+c=x2-2×5x+(5)2=(x-5)2,
∴(x-5)2=0,∴关于x的方程x2-2(-2)x+c=0的实数根为x1=x2=5,∵72<(5)2<82,∴该实数根在7和8之间.故选A.
11.270 解析:∵52+122=132,∴三边长为5,12,13的三角形是直角三角形,其面积=×5×12=30.易得两个三角形的相似比为=3,则两个三角形的面积比为32=9,∴较大的三角形的面积为30×9=270.
12.200(1+x)2=401 解析:根据题意得200(1+x)2=401.
13. 解析:由勾股定理可得AC=
,BC==2,AB==5,∵AC2+BC2=5+20=25,AB2=25,∴AC2+BC2=AB2,∴△ABC为直角三角形,
∴∠ACB=90°,在Rt△ABC中,
cos ∠BAC=.
14.0 解析:由题意可知,n-2≥0,4-2n≥0,∴n=2,把n=2代入m=-2,得m=-2,则m+n=-2+2=0.
15. 解析:由题意得OM=ON=0.8 m,MH⊥DH,过点N作NE⊥MH于点E,如图,
∵MH⊥DH,NE⊥MH,∴NE∥DH,∠NEO=90°,∴∠ONE=α=30°,
∴OE=ON=×0.8=0.4(m),
∴ME=OM+OE=0.8+0.4=1.2(m),
在Rt△OEN中,EN=(m),
∴MN==
(m).
16.①②③⑤ 解析:∵四边形ABCD为正方形,∴∠ABC=∠BCD=∠CDA=∠DAB=90°,AB=BC=CD=AD,∠ADB=∠ABD=∠CBD=∠CDB=45°,如图1,过点P作PG⊥AD于点G,则四边形ABPG是矩形,
图1
∴PG=AB=AD,∵∠GPN+∠GNP=90°=∠GNP+∠DAM,∴∠GPN=∠DAM,又∵PG=AD,∠PGN=90°=∠ADM,∴△PGN≌△ADM(A.S.A.),
∴AM=PN,①正确,故符合要求;如图2,过点F作HF⊥DF交AD于点H,连结CF,
图2
∴∠DHF=45°=∠ADB,∴DF=HF,
∵AB=BC,∠ABF=∠CBF=45°,BF=BF,∴△ABF≌△CBF(S.A.S.),
∴AF=CF,∠BAF=∠BCF,
∵∠BPF+∠BAF=360°-∠ABP-∠AFP=180°,∠BPF+∠FPC=180°,
∴∠BAF=∠FPC,∴∠BCF=∠FPC,
∴PF=CF=AF,∴PN-PF=AM-AF,即FN=FM,
∵∠HFN+∠NFD=90°=∠DFM+∠NFD,∴∠HFN=∠DFM,
∵HF=DF,∠HFN=∠DFM,FN=FM,∴△HFN≌△DFM(S.A.S.),
∴HN=DM,由勾股定理得,DH=DF,∵DH=HN+DN=DM+DN,∴DM+DN=DF,②正确,故符合要求;∵P是BC中点,AB=3,∴BP=CP=,如图3,连结AP,
图3
由勾股定理得,AP=,AP=PF=,解得PF=,设CE=x,则PE=+x,BE=3+x,
由勾股定理得,AE==
,∵sin E=,
∴,整理得,x2-2x-24=0,解得x=6或x=-4(舍去),∴AE=3,BE=9,
∵cos E=,∴,
解得EM=2,③正确,故符合要求;由题意知,∠BPF>90°,∴△BPF、△NFA不相似,BF·NF≠AF·BP,④错误,故不符合要求;∵PM∥BD,∴∠CPM=∠CBD=45°,
∠CMP=∠CDB=45°,设PC=CM=a,BC=CD=AD=AB=b,CE=c,则DM=b-a,BE=b+c,PE=a+c,PM=a,∵AF=PF,∠AFN=90°=∠PFM,FN=FM,∴△AFN≌△PFM(S.A.S.),
∴AN=PM=a,∵∠ADM=90°=∠ECM,∠AMD=∠EMC,
∴△AMD∽△EMC,∴,即,解得a=,同理,△ANF∽△EPF,∴,即,同理,△DMF∽△BAF,
∴,即,
∴,将a=代入得,,整理得,b+c=2b+c,解得,
∴CE=BC,⑤正确,故符合要求.
故正确的结论为①②③⑤.
17.解:原式=3-+2-2=5-3-3.
18.解:(1)2x2+4x-3=0,
2x2+4x=3,
x2+2x+1=+1,
(x+1)2=,
x+1=±,
所以x1=-1,x2=--1.
(2)x2-3x-1=0,
a=1,b=-3,c=-1,
Δ=b2-4ac=9-4×1×(-1)=13>0,
∴方程有两个不相等的实数根,
∴x=,
∴x1=,x2=.
19.解:(1)∵关于x的一元二次方程x2-2(m+1)x+m2+5=0有两个实数根,
∴Δ=4(m+1)2-4(m2+5)=8m-16≥0,解得m≥2.
(2)设x1、x2是关于x的一元二次方程x2-2(m+1)x+m2+5=0的两实数根,
∴x1+x2=2(m+1),x1x2=m2+5.
∵(x1+x2)2=+2x1x2,
∴=4(m+1)2-2(m2+5)=2m2+8m-6.
根据勾股定理,得=62,
∴2m2+8m-6=36,
解得m=3或m=-7(舍去).
∴x1+x2=2(m+1)=8.
∴AC+BC=8.
∴△ABC的周长为8+6=14.
20.解:∵AO=2,OF=1,FD=3,
∴AF=AO+OF=2+1=3,
AD=AF+FD=3+3=6,
∵AB∥EF∥CD,
∴.
21.解:如图,过点B作BH⊥CE于点H,
在Rt△BCH中,∵sin 63°=≈0.90,cos 63°=≈0.45,∴BH≈7.2 cm,CH≈3.6 cm,
在Rt△BEH中,
∵∠BEH=∠ABC-∠BCE=53°,
∴tan 53°=≈,
∴HE≈5.4 cm,
∴CE=CH+EH=3.6+5.4=9(cm),
∴DE=CD-CE=20-9=11(cm).
答:DE的长为11 cm.
22.解:(1)设年销售量y与销售单价x的函数表达式为y=kx+b,根据题意,得解得
所以年销售量y与销售单价x的函数表达式为y=-10x+800.
(2)根据题意,得(-10x+800)(x-30)=6 000,解得x1=50,x2=60,
因为销售单价不得高于55万元,
所以x=50.
所以设备的销售单价是50万元.
23.解:(1)由AE∶BE=1∶2,得.又∵四边形ABCD是平行四边形,∴AB∥DC.∴△AEF∽△CDF.
由AB=CD,得.
∴△AEF与△CDF的周长比等于相似比,为1∶3.
(2)由(相似三角形面积比是相似比的平方),S△AEF=6 cm2,得S△CDF=54 cm2.
24.解:(1)
(2)列表如下:
A B C D
A (A,A) (A,B) (A,C) (A,D)
B (B,A) (B,B) (B,C) (B,D)
C (C,A) (C,B) (C,C) (C,D)
D (D,A) (D,B) (D,C) (D,D)
共有16种等可能的结果,其中小刚和小红选择同一线路的结果有4种,
∴小刚和小红选择同一线路的概率为.
25.解:(1)证明:∵DE∥BC,
∴,
∵,
∴,
∵∠DAF=∠BAE,
∴△ADF∽△ABE,
∴∠ADF=∠ABE,
∴DF∥BE.
(2)∵DF∥BE,∴∠FDE=∠DEB,
∵DE∥BC,∴∠DEB=∠EBC,
∠FED=∠C,∴∠FDE=∠EBC,
∴△FDE∽△EBC,
∴,
设FE=a,EC=b,
∵CF=AE,∴AF=CE=b,AC=AF+EF+EC=2b+a,∵,
∴,
整理得a2+ab-b2=0,
∴-1=0,
∴解得(舍去负值),
∴.
26.解:在Rt△OBD中,∠ODB=90°,
∠BOA=64°,BD=20.5 cm,
∴tan ∠BOA=,sin ∠BOA=,
∴2.05≈,0.90≈,
∴OD=10 cm,OB≈22.78 cm,
在Rt△COE中,OC=OB=22.78 cm,
∠COA=37°,∴cos ∠COA=,
即cos 37°=,∴OE≈22.78×0.80=18.224(cm),
∴ED=OE-OD≈8.2(cm),
即ED的长约为8.2 cm.
27.解:(1)设运动时间为t s(0≤t<6),
则PB=(12-2t)cm,BQ=4t cm.
由题意,得S△BPQ=PB·BQ=×(12-2t)×4t=24t-4t2=20,
解得t1=1,t2=5.
所以当移动1 s或5 s时,△BPQ的面积为20 cm2.
(2)由题意,得S四边形APQC=S△ABC-S△BPQ=·AB·BC-(24t-4t2)=4t2-24t+144=108,解得t1=t2=3.
所以当移动3 s时,四边形APQC的面积为108 cm2.
(3)可分以下两种情况讨论:
①当△BPQ∽△BAC时,,
即,解得t=3;
②当△BPQ∽△BCA时,,
即,解得t=.综上所述,当移动3 s或 s时,△BPQ与△ABC相似.
同课章节目录
