24.1测量 同步练习(含答案)华东师大版九年级上册
文档属性
| 名称 | 24.1测量 同步练习(含答案)华东师大版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 200.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 00:00:00 | ||
图片预览


文档简介
24.1测量
利用勾股定理进行测量
1.如图,一棵树在离地面1.2 m处断裂,树的顶部落在离底部1.6 m处,树折断之前有 ( )
A.2.2 m
B.2.8 m
.3.2 m
D.4 m
利用相似三角形的性质进行测量
2.(跨学科)如图,数学活动课上,为了测量学校旗杆的高度,小明同学在脚下水平放置一平面镜,然后向后退(保持脚、镜子和旗杆底端在同一直线上),直到他刚好在镜子中看到旗杆的顶端.已知小明的眼睛离地面高度为1.6 m,同时量得小明与镜子的水平距离为2 m,镜子与旗杆的水平距离为12 m,则旗杆高度为 ( )
A.6.4 m
B.8 m
C.6 m
D.12.5 m
3.如图,某校宣传栏BC后面12 m处种有一排与宣传栏平行的若干棵树,即BC∥ED,且相邻两棵树的间隔为2 m,一人站在距宣传栏前面的A处正好看到两端的树干,其余的树均被宣传栏挡住.已知AF⊥BC,AF=3 m,BC=10 m,该宣传栏后DE处共有 棵树.(不计宣传栏的厚度)
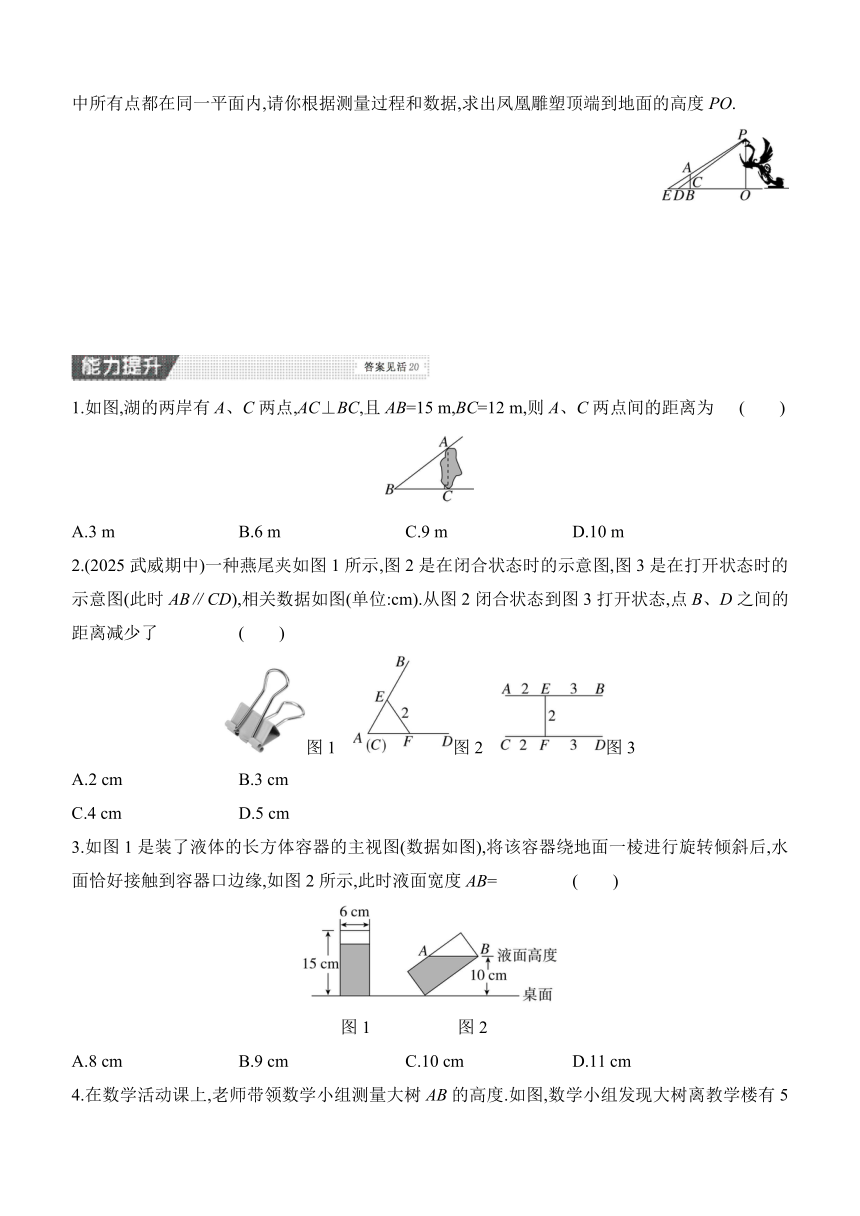
4.赵玲和张羽计划合作完成测量凤凰雕塑顶端到地面的高度PO这一任务.如图,赵玲在点B处竖立一根高3 m的标杆AB,张羽测出地面上的点D、标杆上的点C和点P在一条直线上,利用皮尺测出BC=2 m,BD=2.5 m.张羽向后退,又测出地面上的点E、标杆顶点A和点P在一条直线上,利用皮尺测出EB=3.9 m.已知AB⊥OE,PO⊥OE,点E、D、B、O在同一水平线上,点C在AB上,图中所有点都在同一平面内,请你根据测量过程和数据,求出凤凰雕塑顶端到地面的高度PO.
1.如图,湖的两岸有A、C两点,AC⊥BC,且AB=15 m,BC=12 m,则A、C两点间的距离为 ( )
A.3 m B.6 m C.9 m D.10 m
2.(2025武威期中)一种燕尾夹如图1所示,图2是在闭合状态时的示意图,图3是在打开状态时的示意图(此时AB∥CD),相关数据如图(单位:cm).从图2闭合状态到图3打开状态,点B、D之间的距离减少了 ( )
图1 图2 图3
A.2 cm B.3 cm
C.4 cm D.5 cm
3.如图1是装了液体的长方体容器的主视图(数据如图),将该容器绕地面一棱进行旋转倾斜后,水面恰好接触到容器口边缘,如图2所示,此时液面宽度AB= ( )
图1 图2
A.8 cm B.9 cm C.10 cm D.11 cm
4.在数学活动课上,老师带领数学小组测量大树AB的高度.如图,数学小组发现大树离教学楼有5 m,高1.4 m的竹竿在水平地面的影子长1 m,此时大树的影子有一部分映在地面上,还有一部分映在教学楼的墙上,墙上的影子高CD为2 m,那么这棵大树高 m.
5.(教材P101习题24.1T2变式)某校同学参与“项目式学习”综合实践活动,小明所在的数学活动小组利用所学知识测量旗杆EF的高度.如图,他在距离旗杆40 m的D处立下一根3 m高的竖直标杆CD,然后调整自己的位置,当他与标杆的距离BD为4 m时,他的眼睛、标杆顶端和旗杆顶位于同一直线上,若小明的眼睛离地面高度AB为1.6 m,求旗杆EF的高度.
6.(应用意识)某小队在探险途中发现一个深坑,小队人员为了测出坑深,采取如下方案:示意图如图所示,在深坑左侧用观测仪AB从观测出发点A观测深坑底部P,且观测视线刚好经过深坑边缘点M,在深坑右侧用观测仪CD从观测出发点C观测深坑底部P,且观测视线恰好经过深坑边缘点N(点E、B、M、N、D、F在同一水平线上).已知AB⊥EM,CD⊥NF,观测仪AB高2 m,观测仪CD高1 m,BM=1.6 m,ND=0.8 m,深坑宽度MN=8.8 m,请根据以上数据计算深坑的深度为多少米.
【详解答案】
基础达标
1.C
2.C 解析:如图,由题意得,AB=1.6 m,BC=2 m,CD=12 m,根据镜面反射可知∠ACB=∠ECD,∵AB⊥BD,DE⊥BD,∴∠ABC=∠EDC=90°,
∴△ACB∽△ECD,∴,即,∴ED=9.6 m.故选C.
3.26 解析:如图,设AF的延长线交DE于点G,∵BC∥ED,AF⊥BC,
∴△ABC∽△ADE,AG⊥DE,∴,又∵BC=10 m,AF=3 m,FG=12 m,∴AG=AF+FG=15 m,
∴,∴DE=50 m,∵50÷2=25(棵),∴25+1=26(棵),即DE处共有26棵树.
4.解:由题意可得∠ABE=∠POE=90°,
∵∠CDB=∠PDO,∠E=∠E,
∴△CBD∽△POD,△ABE∽△POE,
∴,,
∴,,
解得PO=28.
答:凤凰雕塑顶端到地面的高度PO为28 m.
能力提升
1.C 解析:∵AC⊥BC,∴∠ACB=90°.∵AB=15 m,BC=12 m,∴由勾股定理得AC==9(m),故A、C两点间的距离为9 m.故选C.
2.B 解析:连结BD,如图所示:
由题意得,,∠A=∠A,
∴△AEF∽△ABD,∴,
∴,∴BD=5 cm,∴点B、D之间的距离减少了5-2=3(cm).故选B.
3.B 解析:如图,过点B作BE⊥DE于点E,
由题意可知AC∥BD,AB∥DE,∠ACB=90°,BD=15 cm,BC=6 cm,BE=10 cm,∴∠CAB=∠ABD=∠EDB,∠ACB=∠DEB=90°,
∴△ACB∽△DEB,∴,即,解得AB=9.故选B.
4.9 解析:如图所示,过点D作DE⊥AB于点E,
则BE=CD=2 m,DE=BC=5 m.
∵同一时刻物高和影长成正比,∴,∴AE=7 m,∴AB=AE+BE=7+2=9(m),即这棵大树高9 m.
5.解:如图,过点A作AN⊥EF于点N,交CD于点M,
由题意可得AM=BD=4 m,NM=FD=40 m,CM=3-1.6=1.4(m),
∵CM∥EN,∴△ACM∽△AEN,
∴,∴,解得EN=15.4,则EF=15.4+1.6=17(m).
答:旗杆EF的高度为17 m.
6.解:过点P作PH⊥EF,垂足为H,如图,
∵AB⊥EF,PH⊥EF,CD⊥EF,
∴AB∥CD∥HP,
∴△ABM∽△PHM,△CDN∽△PHN,
∴,,
∴PH=,
∴.
设MH=x m,则NH=(8.8-x)m,
∴,
解得x=4.4,
∴PH==5.5(m),
∴深坑的深度为5.5 m.
利用勾股定理进行测量
1.如图,一棵树在离地面1.2 m处断裂,树的顶部落在离底部1.6 m处,树折断之前有 ( )
A.2.2 m
B.2.8 m
.3.2 m
D.4 m
利用相似三角形的性质进行测量
2.(跨学科)如图,数学活动课上,为了测量学校旗杆的高度,小明同学在脚下水平放置一平面镜,然后向后退(保持脚、镜子和旗杆底端在同一直线上),直到他刚好在镜子中看到旗杆的顶端.已知小明的眼睛离地面高度为1.6 m,同时量得小明与镜子的水平距离为2 m,镜子与旗杆的水平距离为12 m,则旗杆高度为 ( )
A.6.4 m
B.8 m
C.6 m
D.12.5 m
3.如图,某校宣传栏BC后面12 m处种有一排与宣传栏平行的若干棵树,即BC∥ED,且相邻两棵树的间隔为2 m,一人站在距宣传栏前面的A处正好看到两端的树干,其余的树均被宣传栏挡住.已知AF⊥BC,AF=3 m,BC=10 m,该宣传栏后DE处共有 棵树.(不计宣传栏的厚度)
4.赵玲和张羽计划合作完成测量凤凰雕塑顶端到地面的高度PO这一任务.如图,赵玲在点B处竖立一根高3 m的标杆AB,张羽测出地面上的点D、标杆上的点C和点P在一条直线上,利用皮尺测出BC=2 m,BD=2.5 m.张羽向后退,又测出地面上的点E、标杆顶点A和点P在一条直线上,利用皮尺测出EB=3.9 m.已知AB⊥OE,PO⊥OE,点E、D、B、O在同一水平线上,点C在AB上,图中所有点都在同一平面内,请你根据测量过程和数据,求出凤凰雕塑顶端到地面的高度PO.
1.如图,湖的两岸有A、C两点,AC⊥BC,且AB=15 m,BC=12 m,则A、C两点间的距离为 ( )
A.3 m B.6 m C.9 m D.10 m
2.(2025武威期中)一种燕尾夹如图1所示,图2是在闭合状态时的示意图,图3是在打开状态时的示意图(此时AB∥CD),相关数据如图(单位:cm).从图2闭合状态到图3打开状态,点B、D之间的距离减少了 ( )
图1 图2 图3
A.2 cm B.3 cm
C.4 cm D.5 cm
3.如图1是装了液体的长方体容器的主视图(数据如图),将该容器绕地面一棱进行旋转倾斜后,水面恰好接触到容器口边缘,如图2所示,此时液面宽度AB= ( )
图1 图2
A.8 cm B.9 cm C.10 cm D.11 cm
4.在数学活动课上,老师带领数学小组测量大树AB的高度.如图,数学小组发现大树离教学楼有5 m,高1.4 m的竹竿在水平地面的影子长1 m,此时大树的影子有一部分映在地面上,还有一部分映在教学楼的墙上,墙上的影子高CD为2 m,那么这棵大树高 m.
5.(教材P101习题24.1T2变式)某校同学参与“项目式学习”综合实践活动,小明所在的数学活动小组利用所学知识测量旗杆EF的高度.如图,他在距离旗杆40 m的D处立下一根3 m高的竖直标杆CD,然后调整自己的位置,当他与标杆的距离BD为4 m时,他的眼睛、标杆顶端和旗杆顶位于同一直线上,若小明的眼睛离地面高度AB为1.6 m,求旗杆EF的高度.
6.(应用意识)某小队在探险途中发现一个深坑,小队人员为了测出坑深,采取如下方案:示意图如图所示,在深坑左侧用观测仪AB从观测出发点A观测深坑底部P,且观测视线刚好经过深坑边缘点M,在深坑右侧用观测仪CD从观测出发点C观测深坑底部P,且观测视线恰好经过深坑边缘点N(点E、B、M、N、D、F在同一水平线上).已知AB⊥EM,CD⊥NF,观测仪AB高2 m,观测仪CD高1 m,BM=1.6 m,ND=0.8 m,深坑宽度MN=8.8 m,请根据以上数据计算深坑的深度为多少米.
【详解答案】
基础达标
1.C
2.C 解析:如图,由题意得,AB=1.6 m,BC=2 m,CD=12 m,根据镜面反射可知∠ACB=∠ECD,∵AB⊥BD,DE⊥BD,∴∠ABC=∠EDC=90°,
∴△ACB∽△ECD,∴,即,∴ED=9.6 m.故选C.
3.26 解析:如图,设AF的延长线交DE于点G,∵BC∥ED,AF⊥BC,
∴△ABC∽△ADE,AG⊥DE,∴,又∵BC=10 m,AF=3 m,FG=12 m,∴AG=AF+FG=15 m,
∴,∴DE=50 m,∵50÷2=25(棵),∴25+1=26(棵),即DE处共有26棵树.
4.解:由题意可得∠ABE=∠POE=90°,
∵∠CDB=∠PDO,∠E=∠E,
∴△CBD∽△POD,△ABE∽△POE,
∴,,
∴,,
解得PO=28.
答:凤凰雕塑顶端到地面的高度PO为28 m.
能力提升
1.C 解析:∵AC⊥BC,∴∠ACB=90°.∵AB=15 m,BC=12 m,∴由勾股定理得AC==9(m),故A、C两点间的距离为9 m.故选C.
2.B 解析:连结BD,如图所示:
由题意得,,∠A=∠A,
∴△AEF∽△ABD,∴,
∴,∴BD=5 cm,∴点B、D之间的距离减少了5-2=3(cm).故选B.
3.B 解析:如图,过点B作BE⊥DE于点E,
由题意可知AC∥BD,AB∥DE,∠ACB=90°,BD=15 cm,BC=6 cm,BE=10 cm,∴∠CAB=∠ABD=∠EDB,∠ACB=∠DEB=90°,
∴△ACB∽△DEB,∴,即,解得AB=9.故选B.
4.9 解析:如图所示,过点D作DE⊥AB于点E,
则BE=CD=2 m,DE=BC=5 m.
∵同一时刻物高和影长成正比,∴,∴AE=7 m,∴AB=AE+BE=7+2=9(m),即这棵大树高9 m.
5.解:如图,过点A作AN⊥EF于点N,交CD于点M,
由题意可得AM=BD=4 m,NM=FD=40 m,CM=3-1.6=1.4(m),
∵CM∥EN,∴△ACM∽△AEN,
∴,∴,解得EN=15.4,则EF=15.4+1.6=17(m).
答:旗杆EF的高度为17 m.
6.解:过点P作PH⊥EF,垂足为H,如图,
∵AB⊥EF,PH⊥EF,CD⊥EF,
∴AB∥CD∥HP,
∴△ABM∽△PHM,△CDN∽△PHN,
∴,,
∴PH=,
∴.
设MH=x m,则NH=(8.8-x)m,
∴,
解得x=4.4,
∴PH==5.5(m),
∴深坑的深度为5.5 m.
