24.3.1.1锐角三角函数的定义及关系应用 同步练习(含答案)华东师大版九年级上册
文档属性
| 名称 | 24.3.1.1锐角三角函数的定义及关系应用 同步练习(含答案)华东师大版九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 145.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 17:47:39 | ||
图片预览



文档简介
24.3锐角三角函数
1.锐角三角函数
第1课时 锐角三角函数的定义及关系应用
正弦、余弦、正切
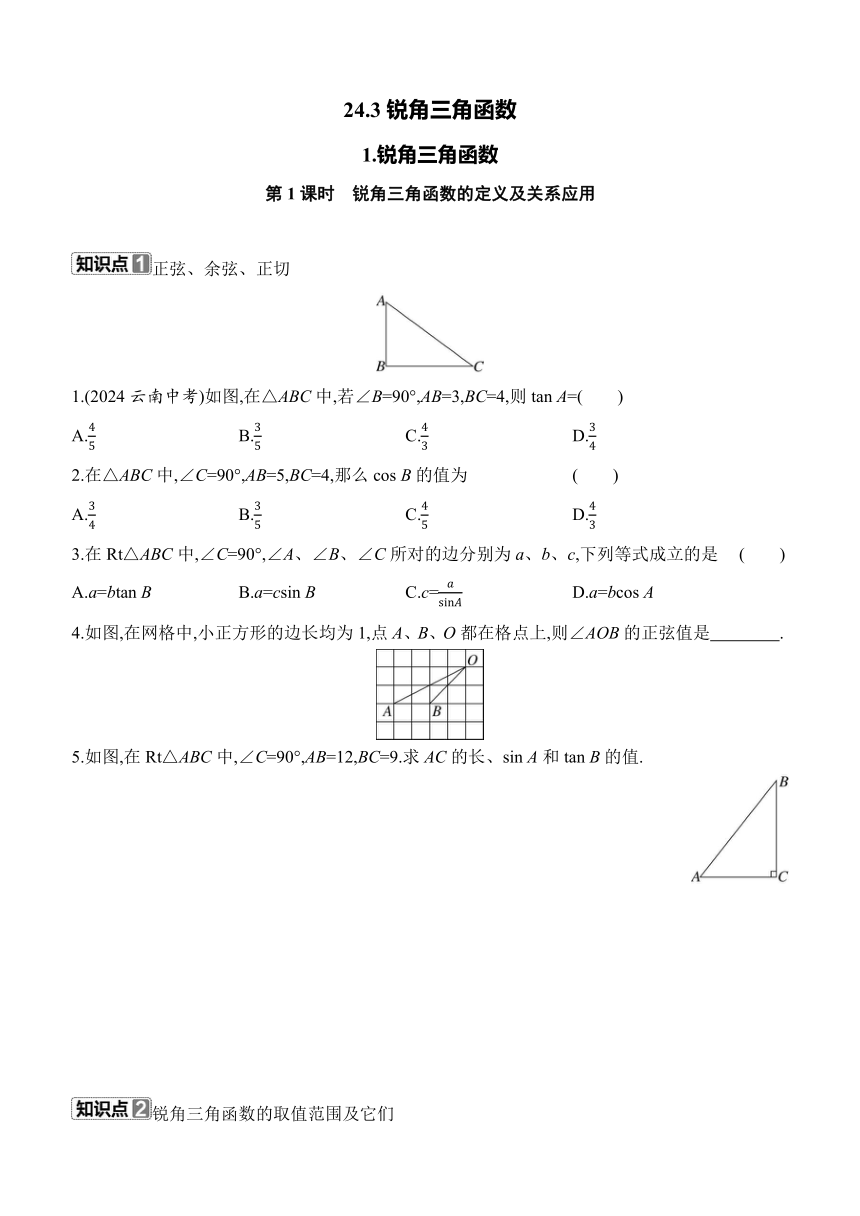
1.(2024云南中考)如图,在△ABC中,若∠B=90°,AB=3,BC=4,则tan A=( )
A. B. C. D.
2.在△ABC中,∠C=90°,AB=5,BC=4,那么cos B的值为 ( )
A. B. C. D.
3.在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,下列等式成立的是 ( )
A.a=btan B B.a=csin B C.c= D.a=bcos A
4.如图,在网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是 .
5.如图,在Rt△ABC中,∠C=90°,AB=12,BC=9.求AC的长、sin A和tan B的值.
锐角三角函数的取值范围及它们
之间的关系
6.如图,在Rt△ABC中,∠C=90°,tan B=3,则sin B的值为 ( )
A. B. C. D.3
7.已知α为锐角,sin α=2m-3,则m的取值范围是 ( )
A.m> B.m<2 C.m>2或m< D.8.在Rt△ACB中,∠C=90°,AC=8,sin A=,则BC= .
9.在Rt△ABC中,∠C=90°,cos A=,AC=12,求BC的长、tan A的值.
1.(2025泉州鲤城区月考)在Rt△ABC中,∠C=90°,现把这个三角形的三边都扩大为原来的3倍,则∠A的正弦值 ( )
A.扩大为原来的3倍
B.缩小为原来的3倍
C.不变
D.不能确定
2.(教材P107例1变式)如图,在Rt△ABC中,∠C=90°,AB=2AC,则∠B的正切值为 ( )
A.1 B. C. D.
3.在△ABC中,∠C=90°,若tan A=,则cos B的值为 ( )
A. B. C. D.
第4题图 第5题图
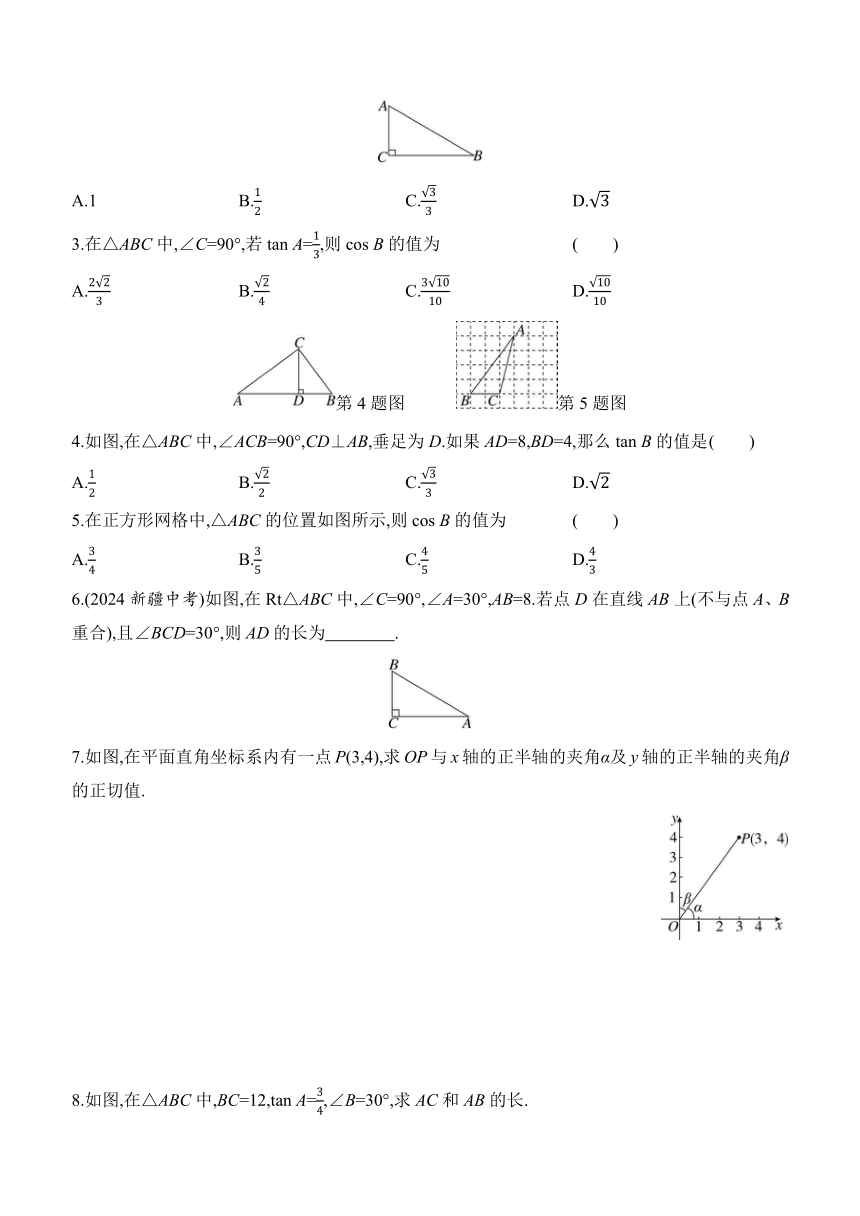
4.如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D.如果AD=8,BD=4,那么tan B的值是 ( )
A. B. C. D.
5.在正方形网格中,△ABC的位置如图所示,则cos B的值为 ( )
A. B. C. D.
6.(2024新疆中考)如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=8.若点D在直线AB上(不与点A、B重合),且∠BCD=30°,则AD的长为 .
7.如图,在平面直角坐标系内有一点P(3,4),求OP与x轴的正半轴的夹角α及y轴的正半轴的夹角β的正切值.
8.如图,在△ABC中,BC=12,tan A=,∠B=30°,求AC和AB的长.
9.(运算能力)设θ为直角三角形的一个锐角,给出θ角三角函数的两条基本性质:①tan θ=;②cos2θ+sin2θ=1,利用这些性质解答本题.已知cos θ+sin θ=,求:
(1)tan θ+.
(2)|cos θ-sin θ|.
【详解答案】
基础达标
1.C 解析:∵∠B=90°,AB=3,BC=4,∴tan A=.故选C.
2.C 解析:∵∠C=90°,∴cos B=.故选C.
3.C 解析:在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,∴tan B=,sin B=,sin A=,cos A=,
即a=,b=csin B,c=,b=ccos A.故选C.
4. 解析:设边AB上的高为h,边AO上的高为h',则h'=BO·sin ∠AOB.由题意可知,AB=2,AO==2,BO==2,∵S△ABO=AB·h=AO·BO·sin ∠AOB,∴×2×2=×2×2×sin ∠AOB,∴sin ∠AOB=.
5.解:在Rt△ABC中,∠C=90°,AB=12,BC=9,
由勾股定理得AC==3,
则sin A=,
tan B=.
6.A 解析:∵在Rt△ABC中,∠C=90°,tan B=3,∴tan B==3,
设AC=3x,则BC=x,
故AB=x,
∴sin B=.故选A.
7.D 解析:∵α为锐角,∴0∵sin α=2m-3,∴0<2m-3<1,
∴8.6 解析:∵sin A=,
∴设BC=3x,则AB=5x,∴AC==4x,∵AC=8,
∴4x=8,解得x=2,∴BC=3x=6.
9.解:∵cos A=,AC=12,
∴AB=13,∴BC==5.
∴tan A=.
能力提升
1.C 解析:在Rt△ABC中,∠C=90°,将各边长度都扩大为原来的3倍,其比值不变,∴∠A的正弦值不变.故选C.
2.C 解析:设AB=2x,AC=x,
∵∠C=90°,∴BC=x,∴tan B=.故选C.
3.D 解析:∵∠C=90°,tan A=,
∴,设BC=x,AC=3x,
故AB=x,
则cos B=.故选D.
4.D 解析:∵CD⊥AB,∴∠ADC=∠CDB=90°,∵∠ACB=90°,
∴∠ACD+∠DCB=90°,
∵∠ACD+∠A=90°,∴∠A=∠DCB,
∴△ACD∽△CBD,∴,
∵AD=8,BD=4,∴,
解得CD=4,∴tan B=.故选D.
5.B 解析:设每个小正方形的边长均为1,过点A作BC的垂线,垂足为M,如图.在Rt△ABM中,AB==5,cos B=.故选B.
6.6或12 解析:在Rt△ABC中,
∠ACB=90°,∠A=30°,
∴BC=ABsin A=4,AC=ABcos A=4.当点D在点B的左上方时,如图1所示,
图1
∵∠ACB=90°,∠A=30°,∴∠ABC=60°.又∵∠BCD=30°,∴∠BDC=60°-30°=30°,∴BD=BC=4,
∴AD=8+4=12.当点D在点B的右下方时,如图2所示,
图2
∵∠ABC=60°,∠BCD=30°,
∴∠CDA=90°,∴AD=ACcos A=6.
综上所述,AD的长为6或12.
7.解:如图,过P作PA⊥x轴于点A,PB⊥y轴于点B,∵P点坐标为(3,4),
∴OA=PB=3,OB=PA=4,
∴tan α=,tan β=.
8.解:如图,过点C作CD⊥AB于点D.
在Rt△BCD中,∵∠B=30°,BC=12,∴CD=BC=6.
根据勾股定理,得BD=
=6.
在Rt△ACD中,
∵tan A=,∴AD=8.
∴AC==10,
AB=AD+BD=8+6.
9.解:(1)∵cos θ+sin θ=,
∴(cos θ+sin θ)2=,
cos2θ+2cos θ·sin θ+sin2θ=,
cos θ·sin θ=,∴tan θ+=4.
(2)∵(cos θ-sin θ)2=cos2θ-2cos θ·sin θ+sin2θ=1-2×,
∴cos θ-sin θ=±,
∴|cos θ-sin θ|=.
1.锐角三角函数
第1课时 锐角三角函数的定义及关系应用
正弦、余弦、正切
1.(2024云南中考)如图,在△ABC中,若∠B=90°,AB=3,BC=4,则tan A=( )
A. B. C. D.
2.在△ABC中,∠C=90°,AB=5,BC=4,那么cos B的值为 ( )
A. B. C. D.
3.在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,下列等式成立的是 ( )
A.a=btan B B.a=csin B C.c= D.a=bcos A
4.如图,在网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是 .
5.如图,在Rt△ABC中,∠C=90°,AB=12,BC=9.求AC的长、sin A和tan B的值.
锐角三角函数的取值范围及它们
之间的关系
6.如图,在Rt△ABC中,∠C=90°,tan B=3,则sin B的值为 ( )
A. B. C. D.3
7.已知α为锐角,sin α=2m-3,则m的取值范围是 ( )
A.m> B.m<2 C.m>2或m< D.
9.在Rt△ABC中,∠C=90°,cos A=,AC=12,求BC的长、tan A的值.
1.(2025泉州鲤城区月考)在Rt△ABC中,∠C=90°,现把这个三角形的三边都扩大为原来的3倍,则∠A的正弦值 ( )
A.扩大为原来的3倍
B.缩小为原来的3倍
C.不变
D.不能确定
2.(教材P107例1变式)如图,在Rt△ABC中,∠C=90°,AB=2AC,则∠B的正切值为 ( )
A.1 B. C. D.
3.在△ABC中,∠C=90°,若tan A=,则cos B的值为 ( )
A. B. C. D.
第4题图 第5题图
4.如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D.如果AD=8,BD=4,那么tan B的值是 ( )
A. B. C. D.
5.在正方形网格中,△ABC的位置如图所示,则cos B的值为 ( )
A. B. C. D.
6.(2024新疆中考)如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=8.若点D在直线AB上(不与点A、B重合),且∠BCD=30°,则AD的长为 .
7.如图,在平面直角坐标系内有一点P(3,4),求OP与x轴的正半轴的夹角α及y轴的正半轴的夹角β的正切值.
8.如图,在△ABC中,BC=12,tan A=,∠B=30°,求AC和AB的长.
9.(运算能力)设θ为直角三角形的一个锐角,给出θ角三角函数的两条基本性质:①tan θ=;②cos2θ+sin2θ=1,利用这些性质解答本题.已知cos θ+sin θ=,求:
(1)tan θ+.
(2)|cos θ-sin θ|.
【详解答案】
基础达标
1.C 解析:∵∠B=90°,AB=3,BC=4,∴tan A=.故选C.
2.C 解析:∵∠C=90°,∴cos B=.故选C.
3.C 解析:在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,∴tan B=,sin B=,sin A=,cos A=,
即a=,b=csin B,c=,b=ccos A.故选C.
4. 解析:设边AB上的高为h,边AO上的高为h',则h'=BO·sin ∠AOB.由题意可知,AB=2,AO==2,BO==2,∵S△ABO=AB·h=AO·BO·sin ∠AOB,∴×2×2=×2×2×sin ∠AOB,∴sin ∠AOB=.
5.解:在Rt△ABC中,∠C=90°,AB=12,BC=9,
由勾股定理得AC==3,
则sin A=,
tan B=.
6.A 解析:∵在Rt△ABC中,∠C=90°,tan B=3,∴tan B==3,
设AC=3x,则BC=x,
故AB=x,
∴sin B=.故选A.
7.D 解析:∵α为锐角,∴0
∴
∴设BC=3x,则AB=5x,∴AC==4x,∵AC=8,
∴4x=8,解得x=2,∴BC=3x=6.
9.解:∵cos A=,AC=12,
∴AB=13,∴BC==5.
∴tan A=.
能力提升
1.C 解析:在Rt△ABC中,∠C=90°,将各边长度都扩大为原来的3倍,其比值不变,∴∠A的正弦值不变.故选C.
2.C 解析:设AB=2x,AC=x,
∵∠C=90°,∴BC=x,∴tan B=.故选C.
3.D 解析:∵∠C=90°,tan A=,
∴,设BC=x,AC=3x,
故AB=x,
则cos B=.故选D.
4.D 解析:∵CD⊥AB,∴∠ADC=∠CDB=90°,∵∠ACB=90°,
∴∠ACD+∠DCB=90°,
∵∠ACD+∠A=90°,∴∠A=∠DCB,
∴△ACD∽△CBD,∴,
∵AD=8,BD=4,∴,
解得CD=4,∴tan B=.故选D.
5.B 解析:设每个小正方形的边长均为1,过点A作BC的垂线,垂足为M,如图.在Rt△ABM中,AB==5,cos B=.故选B.
6.6或12 解析:在Rt△ABC中,
∠ACB=90°,∠A=30°,
∴BC=ABsin A=4,AC=ABcos A=4.当点D在点B的左上方时,如图1所示,
图1
∵∠ACB=90°,∠A=30°,∴∠ABC=60°.又∵∠BCD=30°,∴∠BDC=60°-30°=30°,∴BD=BC=4,
∴AD=8+4=12.当点D在点B的右下方时,如图2所示,
图2
∵∠ABC=60°,∠BCD=30°,
∴∠CDA=90°,∴AD=ACcos A=6.
综上所述,AD的长为6或12.
7.解:如图,过P作PA⊥x轴于点A,PB⊥y轴于点B,∵P点坐标为(3,4),
∴OA=PB=3,OB=PA=4,
∴tan α=,tan β=.
8.解:如图,过点C作CD⊥AB于点D.
在Rt△BCD中,∵∠B=30°,BC=12,∴CD=BC=6.
根据勾股定理,得BD=
=6.
在Rt△ACD中,
∵tan A=,∴AD=8.
∴AC==10,
AB=AD+BD=8+6.
9.解:(1)∵cos θ+sin θ=,
∴(cos θ+sin θ)2=,
cos2θ+2cos θ·sin θ+sin2θ=,
cos θ·sin θ=,∴tan θ+=4.
(2)∵(cos θ-sin θ)2=cos2θ-2cos θ·sin θ+sin2θ=1-2×,
∴cos θ-sin θ=±,
∴|cos θ-sin θ|=.
