24.4.1解直角三角形 同步练习(含答案)华东师大版九年级上册
文档属性
| 名称 | 24.4.1解直角三角形 同步练习(含答案)华东师大版九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 275.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 17:53:12 | ||
图片预览



文档简介
24.4解直角三角形
第1课时 解直角三角形
已知两边解直角三角形
1.在Rt△ABC中,∠C=90°,AC=1,BC=3,那么∠A的正弦值是 ( )
A. B. C.3 D.
2.(2025渭南富平县期末)在Rt△ABC中,∠C=90°,AB=13,AC=12,则cos A= .
3.如图,在Rt△ABC中,∠C=90°,AB=8,BC=4,求cos A和tan A的值.
已知一边一锐角(函数值)解直角三角形
4.在Rt△ACB中,∠C=90°,AB=8,sin A=,则BC的长为 ( )
A.6 B.7.5 C.8 D.12.5
5.如图,在菱形ABCD中,AE⊥BC于点E,EC=4,sin B=,则菱形的周长是 ( )
A.10 B.20 C.40 D.28
解直角三角形的简单应用
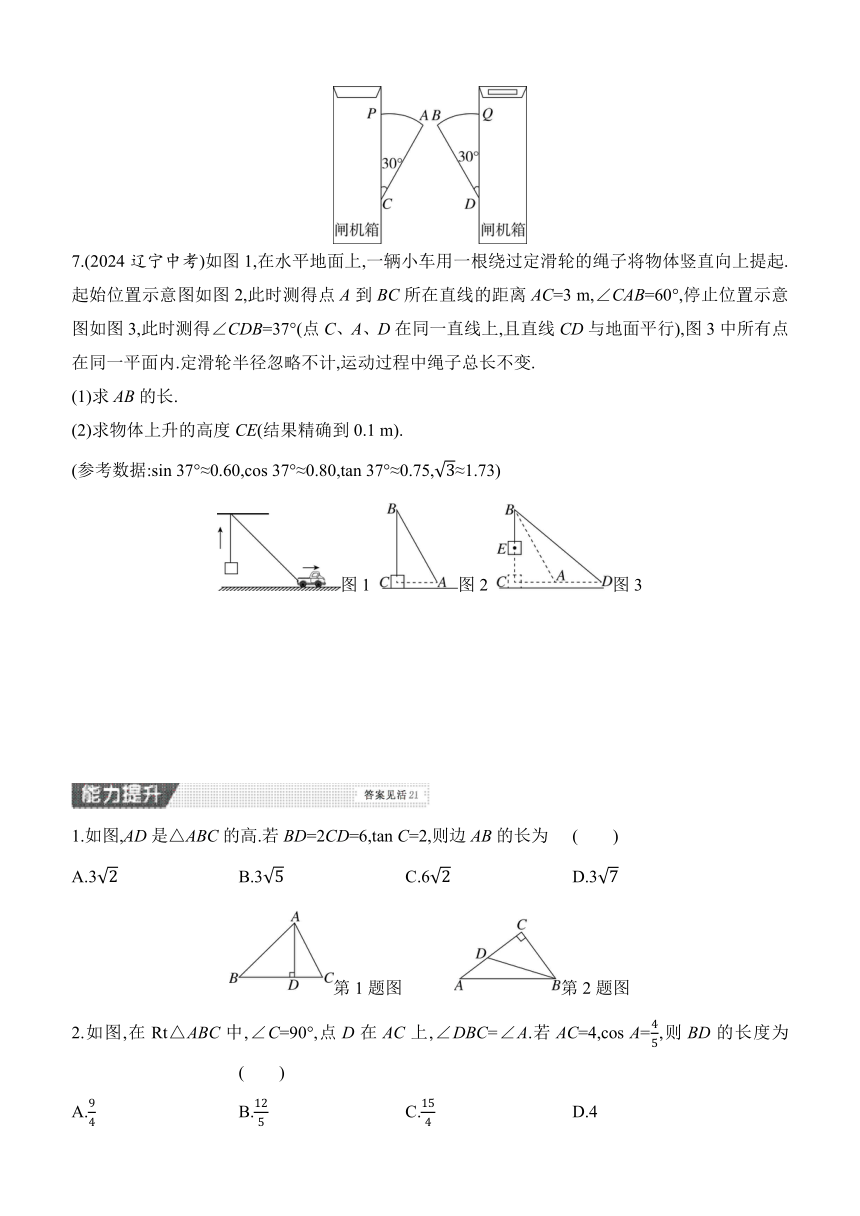
6.地铁站入口设有双翼闸机.如图,它的双翼展开时,双翼边缘的端点A与B之间的距离为10 cm,双翼的边缘AC=BD=56 cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度PQ为 cm.
7.(2024辽宁中考)如图1,在水平地面上,一辆小车用一根绕过定滑轮的绳子将物体竖直向上提起.起始位置示意图如图2,此时测得点A到BC所在直线的距离AC=3 m,∠CAB=60°,停止位置示意图如图3,此时测得∠CDB=37°(点C、A、D在同一直线上,且直线CD与地面平行),图3中所有点在同一平面内.定滑轮半径忽略不计,运动过程中绳子总长不变.
(1)求AB的长.
(2)求物体上升的高度CE(结果精确到0.1 m).
(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,≈1.73)
图1 图2 图3
1.如图,AD是△ABC的高.若BD=2CD=6,tan C=2,则边AB的长为 ( )
A.3 B.3 C.6 D.3
第1题图 第2题图
2.如图,在Rt△ABC中,∠C=90°,点D在AC上,∠DBC=∠A.若AC=4,cos A=,则BD的长度为 ( )
A. B. C. D.4
3.如图,将45°的∠AOB按下面的方式放置在一把刻度尺上:顶点O与尺下沿的左端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数为2 cm.若按相同的方式将37°的∠AOC放置在该刻度尺上,则OC与尺上沿的交点C在尺上的读数是(结果精确到0.1 cm,参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75) ( )
A.2.3 cm B.2.5 cm C.2.7 cm D.3 cm
4.如图,在网格中,每个小正方形的边长均为1,每个小正方形的顶点称为格点.点A、B、C三点都在格点上,则sin ∠ABC= .
5.(2024湖南中考)图1为《天工开物》记载的用于舂(chōng)捣谷物的工具——“碓(duì)”的结构简图,图2为其平面示意图.已知AB⊥CD于点B,AB与水平线l相交于点O,OE⊥l.若BC=4 dm,OB=12 dm,∠BOE=60°,则点C到水平线l的距离CF为 dm.(结果用含根号的式子表示)
图1 图2
6.(2025烟台蓬莱区期中)如图,AD是△ABC的中线,tan B=,cos C=,AC=.(1)求BC的长.
(2)求sin ∠ADC的值.
7.(应用意识)如图,某育苗基地为了能够最大限度地遮挡夏季炎热的阳光和充分利用冬天的光照,计划在苗圃正上方搭建一个平行于地面的遮阳篷.已知苗圃的(南北)宽AB=6.5 m,该地区一年中正午时刻太阳光与地平面的最大夹角是∠DAE=76.5°,最小夹角是∠DBE=29.5°.求遮阳篷的宽CD和到地面的距离CB.
参考数据:sin 29.5°≈,cos 29.5°≈,tan 29.5°≈,sin 76.5°≈,cos 76.5°≈,tan 76.5°≈
【详解答案】
基础达标
1.A 解析:在Rt△ABC中,∠C=90°,AC=1,BC=3,∴AB=.∴sin A=.故选A.
2. 解析:cos A=.
3.解:∵∠C=90°,AB=8,BC=4,
∴AC==4,
∴cos A=,
tan A=.
4.A 解析:如图.∵∠C=90°,AB=8,sin A=,
∴sin A=.
∴BC=6.故选A.
5.C 解析:∵sin B=,∴cos B=.
在菱形ABCD中,AE⊥BC于点E,EC=4,∴AB=BC,∴BE∶AB=(BC-EC)∶BC=3∶5,∴BC=10,
则菱形的周长=10×4=40.故选C.
6.66 解析:过点A作AE⊥PC于点E,过点B作BF⊥QD于点F,如图,
∵AC=56 cm,∠PCA=30°,∴AE=AC=28 cm,由对称性可知BF=AE,∴通过闸机的物体最大宽度为2AE+AB=56+10=66(cm).
7.解:(1)在Rt△ABC中,AC=3 m,
∠CAB=60°,∴∠ABC=30°,
∴AB=2AC=6 m,
则AB的长为6 m.
(2)在Rt△ABC中,AB=6 m,AC=3 m,∴BC==3(m),在Rt△BCD中,
sin ∠CDB=≈≈0.60,
∴BD=8.65 m,∴CE=BD-BA=8.65-6=2.65≈2.7(m),
则物体上升的高度CE约为2.7 m.
能力提升
1.C 解析:∵BD=2CD=6,∴CD=3.
∵tan C==2,∴AD=6.∴AB==6.故选C.
2.C 解析:∵∠C=90°,AC=4,cos A=,∴AB==5.∴BC==3.∵∠DBC=∠A,
∴cos ∠DBC=cos A=.
∴BD=3×.故选C.
3.C 解析:作BD⊥OA于点D,作CE⊥OA于点E,如图:
依题意得OD=2 cm,
在Rt△BOD中,∠BDO=90°,
∠BOD=45°,OD=2 cm,
∴BD=OD·tan ∠BOD=2 cm,
∵BD⊥OA,CE⊥OA,且BC∥OA,
∴CE=BD=2 cm,
在Rt△COE中,∠CEO=90°,
∠COE=37°,CE=2 cm,
∴tan ∠COE=,即tan 37°=,
解得OE≈2.7 cm,∴点C在尺上的读数约为2.7 cm.故选C.
4. 解析:如图,连结AC,
由勾股定理,得AB2=22+42=20,BC2=12+32=10,AC2=12+32=10,
则BC2+AC2=AB2,∴∠ACB=90°.
∴sin ∠ABC=.
5.(6-2) 解析:如图,延长DC交l于点H,连结OC,在Rt△OBH中,∠BOH=90°-60°=30°,OB=12 dm,∴BH=12×tan 30°=4(dm),OH=8 dm,∵S△OBH=S△OCH+S△OBC,∴OB·BH=OH·CF+OB·BC,∴×12×4×8×CF+×12×4,∴CF=(6-2)dm.
6.解:(1)过点A作AE⊥BC于点E,如图,∵cos C=,∴∠C=45°,
在Rt△ACE中,CE=AC·cos C=1,
∴AE=CE=1,
在Rt△ABE中,tan B=,即,∴BE=3AE=3,
∴BC=BE+CE=4.
(2)∵AD是△ABC的中线,
∴CD=BC=2,
∴DE=CD-CE=1,
∵AE⊥BC,DE=AE,
∴∠ADC=45°,∴sin ∠ADC=.
7.解:如图,过点D作DM⊥BE于点M,
设DM=x m,则BC=x m,
在Rt△ADM中,∵tan 76.5°=,
∴AM=.
同理BM=.
∵BM-AM=AB=6.5 m,
∴=6.5,
解得DM≈4.2,
即遮阳篷到地面的距离CB约为4.2 m.
∵tan 76.5°=,DM=4.2 m,
∴AM=≈1 m.∴CD=BM=AB+AM=6.5+1=7.5(m),
即遮阳篷的宽CD约为7.5 m.
第1课时 解直角三角形
已知两边解直角三角形
1.在Rt△ABC中,∠C=90°,AC=1,BC=3,那么∠A的正弦值是 ( )
A. B. C.3 D.
2.(2025渭南富平县期末)在Rt△ABC中,∠C=90°,AB=13,AC=12,则cos A= .
3.如图,在Rt△ABC中,∠C=90°,AB=8,BC=4,求cos A和tan A的值.
已知一边一锐角(函数值)解直角三角形
4.在Rt△ACB中,∠C=90°,AB=8,sin A=,则BC的长为 ( )
A.6 B.7.5 C.8 D.12.5
5.如图,在菱形ABCD中,AE⊥BC于点E,EC=4,sin B=,则菱形的周长是 ( )
A.10 B.20 C.40 D.28
解直角三角形的简单应用
6.地铁站入口设有双翼闸机.如图,它的双翼展开时,双翼边缘的端点A与B之间的距离为10 cm,双翼的边缘AC=BD=56 cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度PQ为 cm.
7.(2024辽宁中考)如图1,在水平地面上,一辆小车用一根绕过定滑轮的绳子将物体竖直向上提起.起始位置示意图如图2,此时测得点A到BC所在直线的距离AC=3 m,∠CAB=60°,停止位置示意图如图3,此时测得∠CDB=37°(点C、A、D在同一直线上,且直线CD与地面平行),图3中所有点在同一平面内.定滑轮半径忽略不计,运动过程中绳子总长不变.
(1)求AB的长.
(2)求物体上升的高度CE(结果精确到0.1 m).
(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,≈1.73)
图1 图2 图3
1.如图,AD是△ABC的高.若BD=2CD=6,tan C=2,则边AB的长为 ( )
A.3 B.3 C.6 D.3
第1题图 第2题图
2.如图,在Rt△ABC中,∠C=90°,点D在AC上,∠DBC=∠A.若AC=4,cos A=,则BD的长度为 ( )
A. B. C. D.4
3.如图,将45°的∠AOB按下面的方式放置在一把刻度尺上:顶点O与尺下沿的左端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数为2 cm.若按相同的方式将37°的∠AOC放置在该刻度尺上,则OC与尺上沿的交点C在尺上的读数是(结果精确到0.1 cm,参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75) ( )
A.2.3 cm B.2.5 cm C.2.7 cm D.3 cm
4.如图,在网格中,每个小正方形的边长均为1,每个小正方形的顶点称为格点.点A、B、C三点都在格点上,则sin ∠ABC= .
5.(2024湖南中考)图1为《天工开物》记载的用于舂(chōng)捣谷物的工具——“碓(duì)”的结构简图,图2为其平面示意图.已知AB⊥CD于点B,AB与水平线l相交于点O,OE⊥l.若BC=4 dm,OB=12 dm,∠BOE=60°,则点C到水平线l的距离CF为 dm.(结果用含根号的式子表示)
图1 图2
6.(2025烟台蓬莱区期中)如图,AD是△ABC的中线,tan B=,cos C=,AC=.(1)求BC的长.
(2)求sin ∠ADC的值.
7.(应用意识)如图,某育苗基地为了能够最大限度地遮挡夏季炎热的阳光和充分利用冬天的光照,计划在苗圃正上方搭建一个平行于地面的遮阳篷.已知苗圃的(南北)宽AB=6.5 m,该地区一年中正午时刻太阳光与地平面的最大夹角是∠DAE=76.5°,最小夹角是∠DBE=29.5°.求遮阳篷的宽CD和到地面的距离CB.
参考数据:sin 29.5°≈,cos 29.5°≈,tan 29.5°≈,sin 76.5°≈,cos 76.5°≈,tan 76.5°≈
【详解答案】
基础达标
1.A 解析:在Rt△ABC中,∠C=90°,AC=1,BC=3,∴AB=.∴sin A=.故选A.
2. 解析:cos A=.
3.解:∵∠C=90°,AB=8,BC=4,
∴AC==4,
∴cos A=,
tan A=.
4.A 解析:如图.∵∠C=90°,AB=8,sin A=,
∴sin A=.
∴BC=6.故选A.
5.C 解析:∵sin B=,∴cos B=.
在菱形ABCD中,AE⊥BC于点E,EC=4,∴AB=BC,∴BE∶AB=(BC-EC)∶BC=3∶5,∴BC=10,
则菱形的周长=10×4=40.故选C.
6.66 解析:过点A作AE⊥PC于点E,过点B作BF⊥QD于点F,如图,
∵AC=56 cm,∠PCA=30°,∴AE=AC=28 cm,由对称性可知BF=AE,∴通过闸机的物体最大宽度为2AE+AB=56+10=66(cm).
7.解:(1)在Rt△ABC中,AC=3 m,
∠CAB=60°,∴∠ABC=30°,
∴AB=2AC=6 m,
则AB的长为6 m.
(2)在Rt△ABC中,AB=6 m,AC=3 m,∴BC==3(m),在Rt△BCD中,
sin ∠CDB=≈≈0.60,
∴BD=8.65 m,∴CE=BD-BA=8.65-6=2.65≈2.7(m),
则物体上升的高度CE约为2.7 m.
能力提升
1.C 解析:∵BD=2CD=6,∴CD=3.
∵tan C==2,∴AD=6.∴AB==6.故选C.
2.C 解析:∵∠C=90°,AC=4,cos A=,∴AB==5.∴BC==3.∵∠DBC=∠A,
∴cos ∠DBC=cos A=.
∴BD=3×.故选C.
3.C 解析:作BD⊥OA于点D,作CE⊥OA于点E,如图:
依题意得OD=2 cm,
在Rt△BOD中,∠BDO=90°,
∠BOD=45°,OD=2 cm,
∴BD=OD·tan ∠BOD=2 cm,
∵BD⊥OA,CE⊥OA,且BC∥OA,
∴CE=BD=2 cm,
在Rt△COE中,∠CEO=90°,
∠COE=37°,CE=2 cm,
∴tan ∠COE=,即tan 37°=,
解得OE≈2.7 cm,∴点C在尺上的读数约为2.7 cm.故选C.
4. 解析:如图,连结AC,
由勾股定理,得AB2=22+42=20,BC2=12+32=10,AC2=12+32=10,
则BC2+AC2=AB2,∴∠ACB=90°.
∴sin ∠ABC=.
5.(6-2) 解析:如图,延长DC交l于点H,连结OC,在Rt△OBH中,∠BOH=90°-60°=30°,OB=12 dm,∴BH=12×tan 30°=4(dm),OH=8 dm,∵S△OBH=S△OCH+S△OBC,∴OB·BH=OH·CF+OB·BC,∴×12×4×8×CF+×12×4,∴CF=(6-2)dm.
6.解:(1)过点A作AE⊥BC于点E,如图,∵cos C=,∴∠C=45°,
在Rt△ACE中,CE=AC·cos C=1,
∴AE=CE=1,
在Rt△ABE中,tan B=,即,∴BE=3AE=3,
∴BC=BE+CE=4.
(2)∵AD是△ABC的中线,
∴CD=BC=2,
∴DE=CD-CE=1,
∵AE⊥BC,DE=AE,
∴∠ADC=45°,∴sin ∠ADC=.
7.解:如图,过点D作DM⊥BE于点M,
设DM=x m,则BC=x m,
在Rt△ADM中,∵tan 76.5°=,
∴AM=.
同理BM=.
∵BM-AM=AB=6.5 m,
∴=6.5,
解得DM≈4.2,
即遮阳篷到地面的距离CB约为4.2 m.
∵tan 76.5°=,DM=4.2 m,
∴AM=≈1 m.∴CD=BM=AB+AM=6.5+1=7.5(m),
即遮阳篷的宽CD约为7.5 m.
