24.4.2 解直角三角形的应用——方位角 同步练习(含答案)华东师大版九年级上册
文档属性
| 名称 | 24.4.2 解直角三角形的应用——方位角 同步练习(含答案)华东师大版九年级上册 | 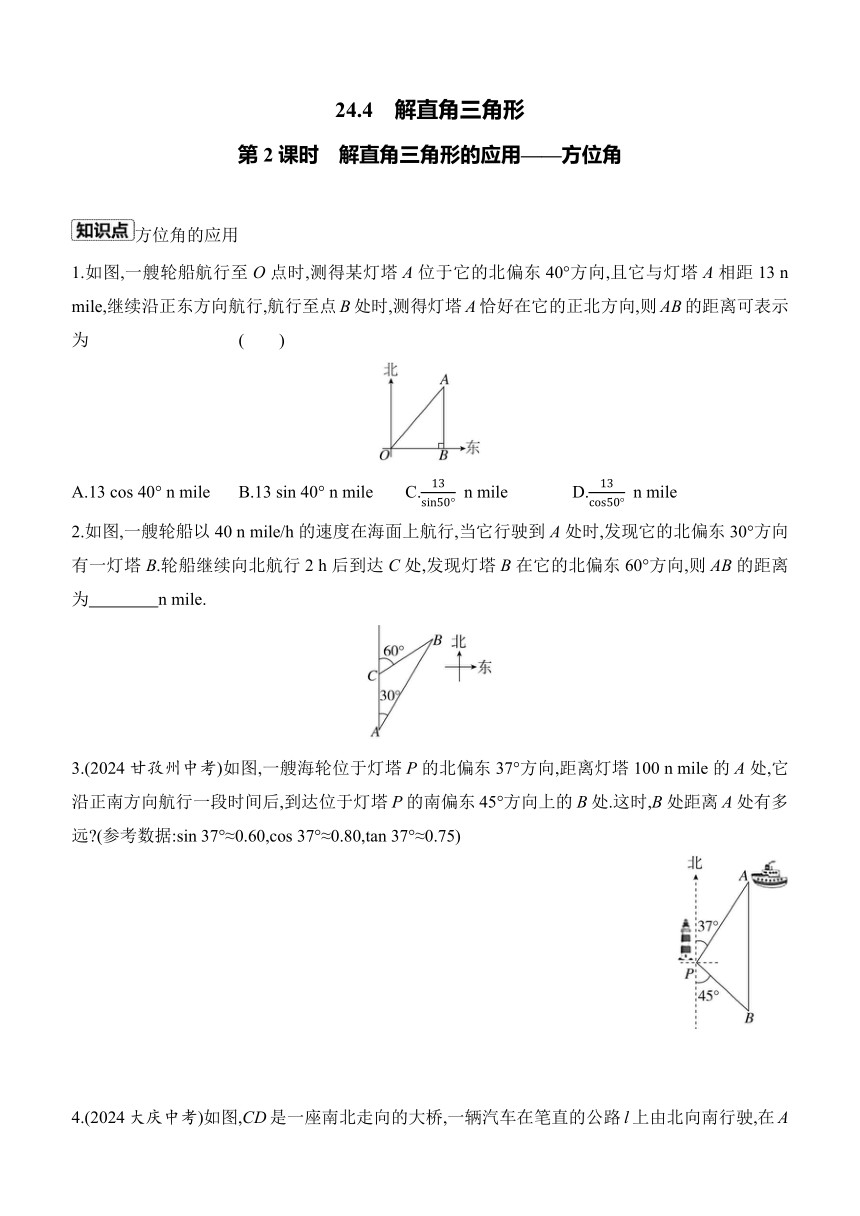 | |
| 格式 | docx | ||
| 文件大小 | 177.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 17:55:25 | ||
图片预览

文档简介
24.4 解直角三角形
第2课时 解直角三角形的应用——方位角
方位角的应用
1.如图,一艘轮船航行至O点时,测得某灯塔A位于它的北偏东40°方向,且它与灯塔A相距13 n mile,继续沿正东方向航行,航行至点B处时,测得灯塔A恰好在它的正北方向,则AB的距离可表示为 ( )
A.13 cos 40° n mile B.13 sin 40° n mile C. n mile D. n mile
2.如图,一艘轮船以40 n mile/h的速度在海面上航行,当它行驶到A处时,发现它的北偏东30°方向有一灯塔B.轮船继续向北航行2 h后到达C处,发现灯塔B在它的北偏东60°方向,则AB的距离为 n mile.
3.(2024甘孜州中考)如图,一艘海轮位于灯塔P的北偏东37°方向,距离灯塔100 n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处.这时,B处距离A处有多远 (参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
4.(2024大庆中考)如图,CD是一座南北走向的大桥,一辆汽车在笔直的公路l上由北向南行驶,在A处测得桥头C在南偏东30°方向上,继续行驶1 500 m后到达B处,测得桥头C在南偏东60°方向上,桥头D在南偏东45°方向上,求大桥CD的长度.(结果精确到1 m,参考数据:≈1.73)
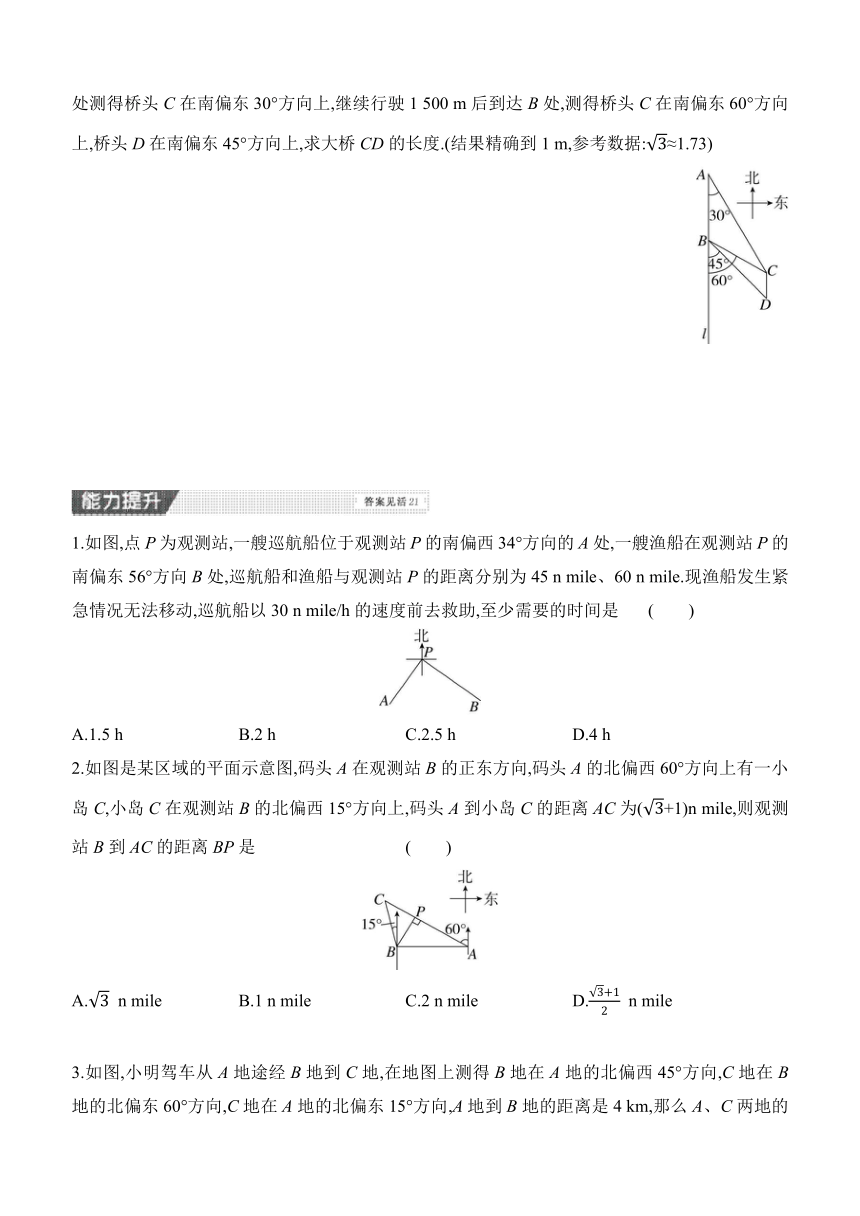
1.如图,点P为观测站,一艘巡航船位于观测站P的南偏西34°方向的A处,一艘渔船在观测站P的南偏东56°方向B处,巡航船和渔船与观测站P的距离分别为45 n mile、60 n mile.现渔船发生紧急情况无法移动,巡航船以30 n mile/h的速度前去救助,至少需要的时间是 ( )
A.1.5 h B.2 h C.2.5 h D.4 h
2.如图是某区域的平面示意图,码头A在观测站B的正东方向,码头A的北偏西60°方向上有一小岛C,小岛C在观测站B的北偏西15°方向上,码头A到小岛C的距离AC为(+1)n mile,则观测站B到AC的距离BP是 ( )
A. n mile B.1 n mile C.2 n mile D. n mile
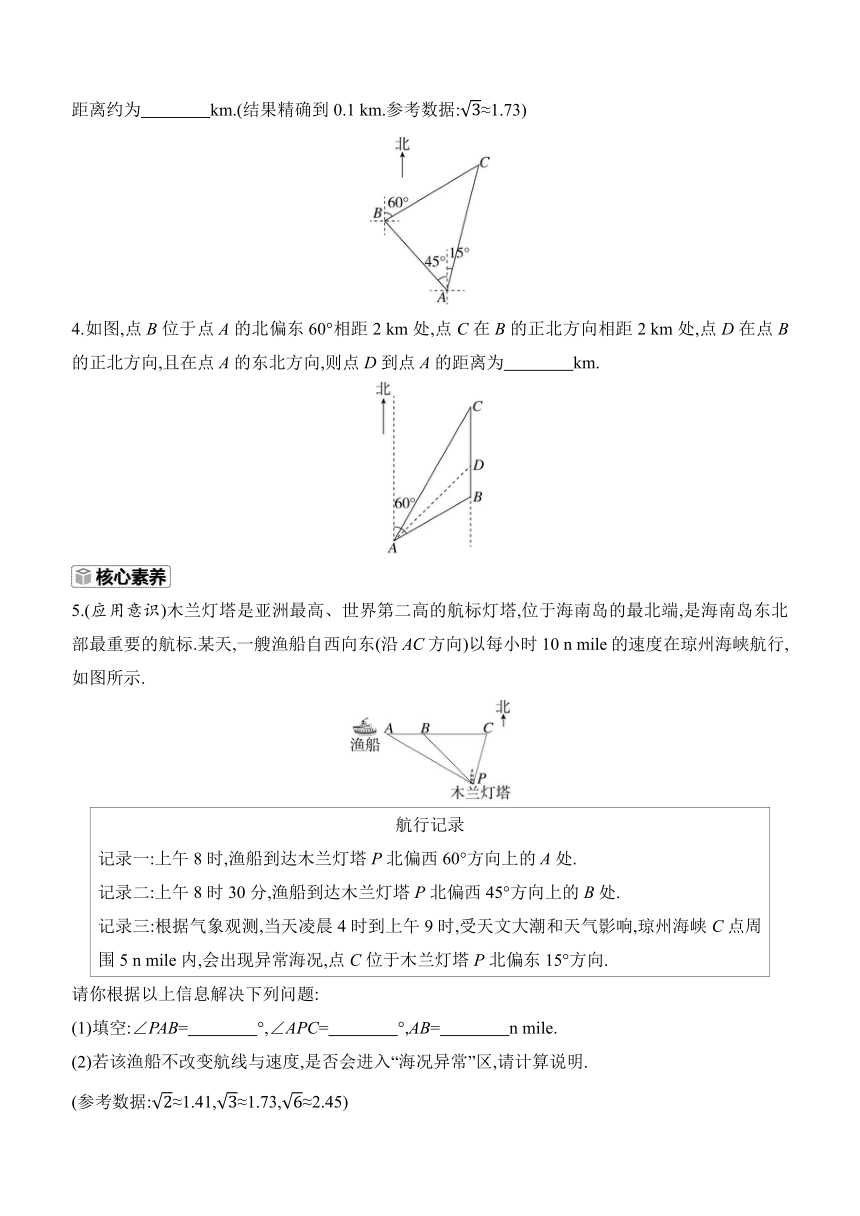
3.如图,小明驾车从A地途经B地到C地,在地图上测得B地在A地的北偏西45°方向,C地在B地的北偏东60°方向,C地在A地的北偏东15°方向,A地到B地的距离是4 km,那么A、C两地的距离约为 km.(结果精确到0.1 km.参考数据:≈1.73)
4.如图,点B位于点A的北偏东60°相距2 km处,点C在B的正北方向相距2 km处,点D在点B的正北方向,且在点A的东北方向,则点D到点A的距离为 km.
5.(应用意识)木兰灯塔是亚洲最高、世界第二高的航标灯塔,位于海南岛的最北端,是海南岛东北部最重要的航标.某天,一艘渔船自西向东(沿AC方向)以每小时10 n mile的速度在琼州海峡航行,如图所示.
航行记录 记录一:上午8时,渔船到达木兰灯塔P北偏西60°方向上的A处. 记录二:上午8时30分,渔船到达木兰灯塔P北偏西45°方向上的B处. 记录三:根据气象观测,当天凌晨4时到上午9时,受天文大潮和天气影响,琼州海峡C点周围5 n mile内,会出现异常海况,点C位于木兰灯塔P北偏东15°方向.
请你根据以上信息解决下列问题:
(1)填空:∠PAB= °,∠APC= °,AB= n mile.
(2)若该渔船不改变航线与速度,是否会进入“海况异常”区,请计算说明.
(参考数据:≈1.41,≈1.73,≈2.45)
【详解答案】
基础达标
1.A 解析:在Rt△AOB中,
OA=13 n mile,∠OAB=40°,
∵cos ∠OAB=,∴AB=OA·cos ∠OAB=13 cos 40°(n mile).故选A.
2.80 解析:如图,作BD⊥AC交AC的延长线于点D,
设CD=x n mile,在Rt△BCD中,
∠BCD=60°,∴BD=CD·tan 60°=x(n mile),在Rt△ABD中,∠A=30°,∴AD=x=3x(n mile),∴AC=AD-CD=3x-x=2x(n mile),∵AC=40×2=80(n mile),
∴2x=80,解得x=40,∴BD=x=40 n mile,∴AB=2BD=80 n mile.
3.解:如图,过P作PC⊥AB于点C,
在Rt△APC中,∠A=37°,AP=
100 n mile,∴PC=AP·sin A=100×sin 37°≈100×0.6=60(n mile),AC=AP·cos 37°≈100×0.8=80(n mile),
在Rt△PBC中,∠B=45°,∴BC=PC=60 n mile,∴AB=AC+BC=80+60=140(n mile).
答:B处距离A处有140 n mile.
4.解:如图,分别过点C和点D作AB的垂线,垂足分别为M、N,
在Rt△CBM中,tan ∠CBM=,所以CM=BM,在Rt△ACM中,tan A=,
所以,解得BM=750,
所以CM=750 m,所以DN=CM=750 m.在Rt△DBN中,
tan ∠DBN==1,
所以BN=DN=750 m,所以MN=BN-BM=(750-750)m,
则CD=MN=750-750≈548(m),
故大桥CD的长度为548 m.
能力提升
1.C 解析:如图,连结AB,
根据题意可知∠APB=34°+56°=90°,
∴△APB是直角三角形,AB=
=75(n mile),
∵巡航船的速度为30 n mile/h,∴75÷30=2.5(h),即至少需要2.5 h.故选C.
2.B 解析:由题意得∠BAC=90°-60°=30°,∠ABC=90°+15°=105°,
∴∠C=180°-∠BAC-∠ABC=45°,
∵BP⊥AC,∴∠BPA=∠BPC=90°,
∵∠C=45°,∴△BCP是等腰直角三角形,∴BP=PC,∵∠BAC=30°,
∴PA=BP,∵PA+PC=AC,
∴BP+BP=+1,解得BP=1.故选B.
3.5.5 解析:如图,过点B作BH⊥AC于点H,
由题意得∠ABC=180°-45°-60°=75°,∴∠C=180°-45°-15°-75°=45°,
在Rt△ABH中,∠BAH=60°,AB=4 km,∵sin ∠BAH=,∴BH=AB·sin ∠BAH=4×=2≈3.46(km),∵cos ∠BAH=,∴AH=AB·cos ∠BAH=4×=2(km),
在Rt△BHC中,∠C=45°,∴∠CBH=45°,∴∠CBH=∠C,∴CH=BH=3.46 km,∴AC=AH+CH=2+3.46≈5.5(km).
4. 解析:如图,过点A作AE⊥CB于点E,
则∠AEB=90°,∴∠ABE=60°,
∴∠BAE=30°,∵AB=BC=2 km,
∴AE=2cos 30°=(km),
∵点D在点B的正北方向,且在点A的东北方向,∴∠DAE=45°,
∴AD=(km).
5.解:(1)30 75 5
(2)如图,过点P作PD⊥AC于点D,设PD为x n mile,
在Rt△BPD中,∠BPD=45°,
∴∠PBD=45°,∴BD=PD=x n mile,
在Rt△APD中,∠APD=60°,
∴∠A=30°,tan ∠APD=,
cos ∠APD=,
∴AD=PD,AP=2PD,
∵AB=AD-BD,∴PD-PD=5,
∴PD=BD=(+1)n mile,∴AP=2PD=5(+1)n mile≈13.65 n mile,
在△APC中,∠A=30°,∠APC=75°,
∴∠C=180°-∠A-∠APC=75°,
∴∠C=∠APC,∴AC=AP=13.65 n mile,设上午9时渔船航行至E处,则AE=10 n mile,∴CE=AC-AE≈3.65 n mile<5 n mile,∴该渔船会进入“海况异常”区.
第2课时 解直角三角形的应用——方位角
方位角的应用
1.如图,一艘轮船航行至O点时,测得某灯塔A位于它的北偏东40°方向,且它与灯塔A相距13 n mile,继续沿正东方向航行,航行至点B处时,测得灯塔A恰好在它的正北方向,则AB的距离可表示为 ( )
A.13 cos 40° n mile B.13 sin 40° n mile C. n mile D. n mile
2.如图,一艘轮船以40 n mile/h的速度在海面上航行,当它行驶到A处时,发现它的北偏东30°方向有一灯塔B.轮船继续向北航行2 h后到达C处,发现灯塔B在它的北偏东60°方向,则AB的距离为 n mile.
3.(2024甘孜州中考)如图,一艘海轮位于灯塔P的北偏东37°方向,距离灯塔100 n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处.这时,B处距离A处有多远 (参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
4.(2024大庆中考)如图,CD是一座南北走向的大桥,一辆汽车在笔直的公路l上由北向南行驶,在A处测得桥头C在南偏东30°方向上,继续行驶1 500 m后到达B处,测得桥头C在南偏东60°方向上,桥头D在南偏东45°方向上,求大桥CD的长度.(结果精确到1 m,参考数据:≈1.73)
1.如图,点P为观测站,一艘巡航船位于观测站P的南偏西34°方向的A处,一艘渔船在观测站P的南偏东56°方向B处,巡航船和渔船与观测站P的距离分别为45 n mile、60 n mile.现渔船发生紧急情况无法移动,巡航船以30 n mile/h的速度前去救助,至少需要的时间是 ( )
A.1.5 h B.2 h C.2.5 h D.4 h
2.如图是某区域的平面示意图,码头A在观测站B的正东方向,码头A的北偏西60°方向上有一小岛C,小岛C在观测站B的北偏西15°方向上,码头A到小岛C的距离AC为(+1)n mile,则观测站B到AC的距离BP是 ( )
A. n mile B.1 n mile C.2 n mile D. n mile
3.如图,小明驾车从A地途经B地到C地,在地图上测得B地在A地的北偏西45°方向,C地在B地的北偏东60°方向,C地在A地的北偏东15°方向,A地到B地的距离是4 km,那么A、C两地的距离约为 km.(结果精确到0.1 km.参考数据:≈1.73)
4.如图,点B位于点A的北偏东60°相距2 km处,点C在B的正北方向相距2 km处,点D在点B的正北方向,且在点A的东北方向,则点D到点A的距离为 km.
5.(应用意识)木兰灯塔是亚洲最高、世界第二高的航标灯塔,位于海南岛的最北端,是海南岛东北部最重要的航标.某天,一艘渔船自西向东(沿AC方向)以每小时10 n mile的速度在琼州海峡航行,如图所示.
航行记录 记录一:上午8时,渔船到达木兰灯塔P北偏西60°方向上的A处. 记录二:上午8时30分,渔船到达木兰灯塔P北偏西45°方向上的B处. 记录三:根据气象观测,当天凌晨4时到上午9时,受天文大潮和天气影响,琼州海峡C点周围5 n mile内,会出现异常海况,点C位于木兰灯塔P北偏东15°方向.
请你根据以上信息解决下列问题:
(1)填空:∠PAB= °,∠APC= °,AB= n mile.
(2)若该渔船不改变航线与速度,是否会进入“海况异常”区,请计算说明.
(参考数据:≈1.41,≈1.73,≈2.45)
【详解答案】
基础达标
1.A 解析:在Rt△AOB中,
OA=13 n mile,∠OAB=40°,
∵cos ∠OAB=,∴AB=OA·cos ∠OAB=13 cos 40°(n mile).故选A.
2.80 解析:如图,作BD⊥AC交AC的延长线于点D,
设CD=x n mile,在Rt△BCD中,
∠BCD=60°,∴BD=CD·tan 60°=x(n mile),在Rt△ABD中,∠A=30°,∴AD=x=3x(n mile),∴AC=AD-CD=3x-x=2x(n mile),∵AC=40×2=80(n mile),
∴2x=80,解得x=40,∴BD=x=40 n mile,∴AB=2BD=80 n mile.
3.解:如图,过P作PC⊥AB于点C,
在Rt△APC中,∠A=37°,AP=
100 n mile,∴PC=AP·sin A=100×sin 37°≈100×0.6=60(n mile),AC=AP·cos 37°≈100×0.8=80(n mile),
在Rt△PBC中,∠B=45°,∴BC=PC=60 n mile,∴AB=AC+BC=80+60=140(n mile).
答:B处距离A处有140 n mile.
4.解:如图,分别过点C和点D作AB的垂线,垂足分别为M、N,
在Rt△CBM中,tan ∠CBM=,所以CM=BM,在Rt△ACM中,tan A=,
所以,解得BM=750,
所以CM=750 m,所以DN=CM=750 m.在Rt△DBN中,
tan ∠DBN==1,
所以BN=DN=750 m,所以MN=BN-BM=(750-750)m,
则CD=MN=750-750≈548(m),
故大桥CD的长度为548 m.
能力提升
1.C 解析:如图,连结AB,
根据题意可知∠APB=34°+56°=90°,
∴△APB是直角三角形,AB=
=75(n mile),
∵巡航船的速度为30 n mile/h,∴75÷30=2.5(h),即至少需要2.5 h.故选C.
2.B 解析:由题意得∠BAC=90°-60°=30°,∠ABC=90°+15°=105°,
∴∠C=180°-∠BAC-∠ABC=45°,
∵BP⊥AC,∴∠BPA=∠BPC=90°,
∵∠C=45°,∴△BCP是等腰直角三角形,∴BP=PC,∵∠BAC=30°,
∴PA=BP,∵PA+PC=AC,
∴BP+BP=+1,解得BP=1.故选B.
3.5.5 解析:如图,过点B作BH⊥AC于点H,
由题意得∠ABC=180°-45°-60°=75°,∴∠C=180°-45°-15°-75°=45°,
在Rt△ABH中,∠BAH=60°,AB=4 km,∵sin ∠BAH=,∴BH=AB·sin ∠BAH=4×=2≈3.46(km),∵cos ∠BAH=,∴AH=AB·cos ∠BAH=4×=2(km),
在Rt△BHC中,∠C=45°,∴∠CBH=45°,∴∠CBH=∠C,∴CH=BH=3.46 km,∴AC=AH+CH=2+3.46≈5.5(km).
4. 解析:如图,过点A作AE⊥CB于点E,
则∠AEB=90°,∴∠ABE=60°,
∴∠BAE=30°,∵AB=BC=2 km,
∴AE=2cos 30°=(km),
∵点D在点B的正北方向,且在点A的东北方向,∴∠DAE=45°,
∴AD=(km).
5.解:(1)30 75 5
(2)如图,过点P作PD⊥AC于点D,设PD为x n mile,
在Rt△BPD中,∠BPD=45°,
∴∠PBD=45°,∴BD=PD=x n mile,
在Rt△APD中,∠APD=60°,
∴∠A=30°,tan ∠APD=,
cos ∠APD=,
∴AD=PD,AP=2PD,
∵AB=AD-BD,∴PD-PD=5,
∴PD=BD=(+1)n mile,∴AP=2PD=5(+1)n mile≈13.65 n mile,
在△APC中,∠A=30°,∠APC=75°,
∴∠C=180°-∠A-∠APC=75°,
∴∠C=∠APC,∴AC=AP=13.65 n mile,设上午9时渔船航行至E处,则AE=10 n mile,∴CE=AC-AE≈3.65 n mile<5 n mile,∴该渔船会进入“海况异常”区.
