24.4.3 解直角三角形的应用——仰角和俯角 同步练习(含答案)华东师大版九年级上册
文档属性
| 名称 | 24.4.3 解直角三角形的应用——仰角和俯角 同步练习(含答案)华东师大版九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 169.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 17:57:15 | ||
图片预览


文档简介
24.4 解直角三角形
第3课时 解直角三角形的应用——仰角和俯角
仰角和俯角的应用
1.观测员从海面上的一艘小船上(小船和观测员高度忽略不计)观察前方高出海平面150 m的一座山崖顶端,测得仰角为60°,则小船和山崖之间的水平距离为 ( )
A.150 m B.100 m C.50 m D.300 m
2.在数学课外实践活动中,某小组测量一栋楼房CD的高度(如图),他们在A处仰望楼顶,测得仰角为30°,再往楼的方向前进50 m至B处,测得仰角为60°,那么这栋楼的高度为(人的身高忽略不计) ( )
A.25 m B.25 m C.25 m D.50 m
3.(2024德阳中考)某校学生开展综合实践活动,测量一建筑物CD的高度,在建筑物旁边有一高度为10 m的小楼房AB,小李同学在小楼房楼底B处测得C处的仰角为60°,在小楼房楼顶A处测得C处的仰角为30°(AB、CD在同一平面内,B、D在同一水平面上),则建筑物CD的高为 ( )
A.20 m
B.15 m
C.12 m
D.(10+5)m
4.(2024盐城中考)如图,小明用无人机测量教学楼的高度,将无人机垂直上升距地面30 m的点P处,测得教学楼底端点A的俯角为37°,再将无人机沿教学楼方向水平飞行26.6 m至点Q处,测得教学楼顶端点B的俯角为45°,则教学楼AB的高度约为 m.(结果精确到1 m,参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
5.(2024吉林中考)图1中的吉林省广播电视塔,又称“吉塔”.某直升机于空中A处探测到吉塔,此时飞行高度AB=873 m,如图2,从直升机上看塔尖C的俯角∠EAC=37°,看塔底D的俯角∠EAD=45°,求吉塔的高度CD.
(结果精确到0.1 m,参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
图1 图2
1.一个测量技术队员在一个高为h(忽略身高)的位置,观测一根高出此建筑物的旗杆,测出与旗杆的顶端的仰角为30°,与地面的俯角为60°,那么该旗杆的高度是 ( )
A.h B.h C.h D.h
2.(2024深圳中考)如图,为了测量某电子厂的高度,小明用高1.8 m的测量仪EF测得顶端A的仰角为45°,小军在小明的前面5 m处用高1.5 m的测量仪CD测得顶端A的仰角为53°,则电子厂AB的高度为 ( )
参考数据:sin 53°≈,cos 53°≈,tan 53°≈
A.22.7 m B.22.4 m
C.21.2 m D.23.0 m
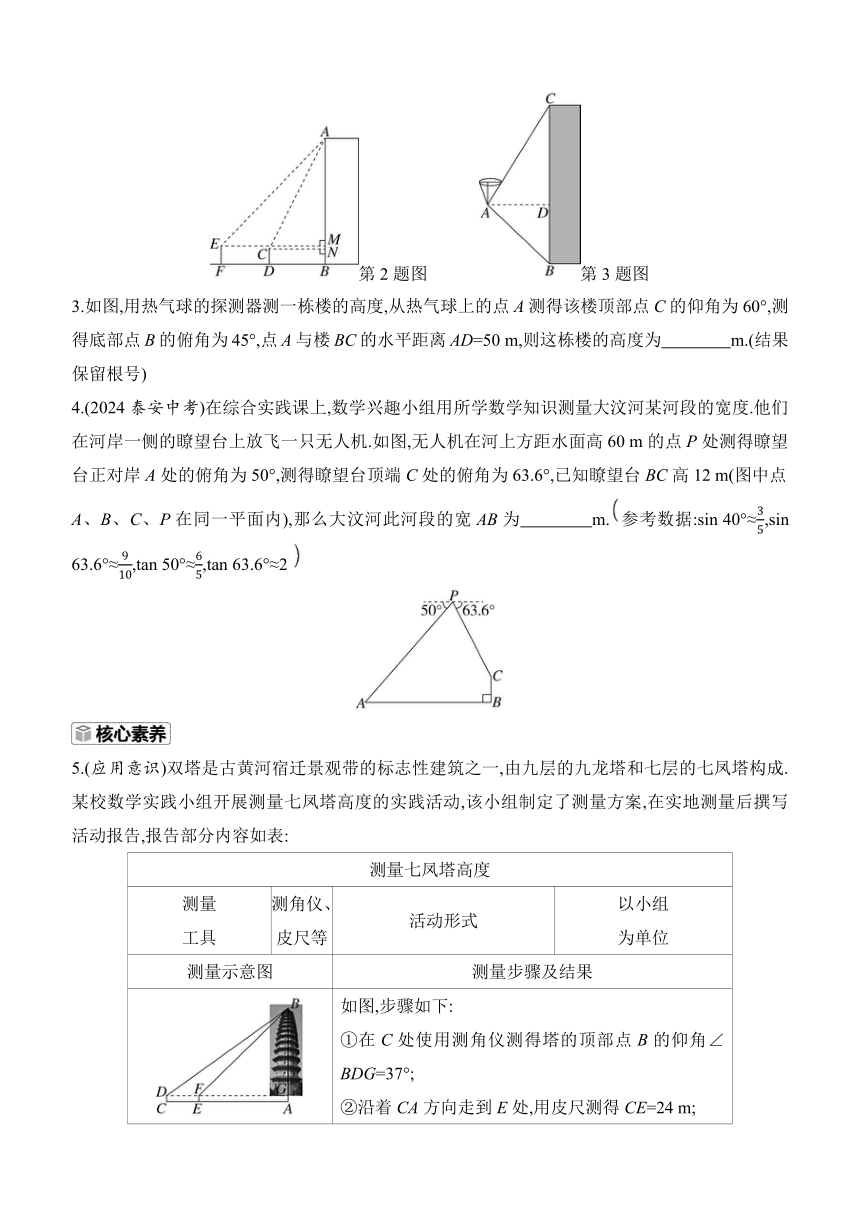
第2题图 第3题图
3.如图,用热气球的探测器测一栋楼的高度,从热气球上的点A测得该楼顶部点C的仰角为60°,测得底部点B的俯角为45°,点A与楼BC的水平距离AD=50 m,则这栋楼的高度为 m.(结果保留根号)
4.(2024泰安中考)在综合实践课上,数学兴趣小组用所学数学知识测量大汶河某河段的宽度.他们在河岸一侧的瞭望台上放飞一只无人机.如图,无人机在河上方距水面高60 m的点P处测得瞭望台正对岸A处的俯角为50°,测得瞭望台顶端C处的俯角为63.6°,已知瞭望台BC高12 m(图中点A、B、C、P在同一平面内),那么大汶河此河段的宽AB为 m.参考数据:sin 40°≈,sin 63.6°≈,tan 50°≈,tan 63.6°≈2
5.(应用意识)双塔是古黄河宿迁景观带的标志性建筑之一,由九层的九龙塔和七层的七凤塔构成.某校数学实践小组开展测量七凤塔高度的实践活动,该小组制定了测量方案,在实地测量后撰写活动报告,报告部分内容如表:
测量七凤塔高度
测量 工具 测角仪、 皮尺等 活动形式 以小组 为单位
测量示意图 测量步骤及结果
如图,步骤如下: ①在C处使用测角仪测得塔的顶部点B的仰角∠BDG=37°; ②沿着CA方向走到E处,用皮尺测得CE=24 m; ③在E处使用测角仪测得塔的顶部点B的仰角∠BFG=45°
……
已知测角仪的高度为1.2 m,点C、E、A在同一水平直线上.根据以上信息,求塔AB的高度.(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
【详解答案】
基础达标
1.C 解析:如图:
根据题意可知∠B=60°,AC=150 m,
∴BC==50(m),∴小船和山崖之间的水平距离为50 m.故选C.
2.A 解析:设DC=x m,在Rt△ACD中,∠A=30°,tan A=,即tan 30°=,整理得AC=x m,
在Rt△BCD中,∠DBC=60°,
tan ∠DBC=,即tan 60°=,
整理得BC=x m,∵AB=50 m,
∴AC-BC=50,即x-x=50,解得x=25,则这栋楼的高度为25 m.故选A.
3.B 解析:设过点A的水平线与CD交于点E,如图,
由题意知四边形ABDE是矩形,DE=AB=10 m,AE=BD,在Rt△BCD中,BD=CD,在Rt△ACE中,
AE=(CD-DE)=(CD-10),∴(CD-10)=CD,解得CD=15.故选B.
4.17 解析:如图,设AB的延长线与PQ的延长线交于点C,
由题意,知AC=30 m,PQ=26.6 m,∠APC=37°,∠BQC=45°,
在Rt△APC中,
PC=≈=40(m),
∴QC=PC-PQ=40-26.6=13.4(m),
在Rt△BQC中,BC=QC=13.4 m,
∴AB=AC-BC=30-13.4=16.6≈17(m).
5.解:如图,过点C作CF⊥AB,垂足为F.
∵AB⊥BD,CF⊥AB,DC⊥BD,
∴∠CDB=∠B=∠CFB=90°,
∴四边形CDBF是矩形,
∴BF=CD,CF=BD.
∵CF∥BD∥AE,
∴∠EAC=∠ACF=37°,
∠EAD=∠ADB=45°,∴AB=DB=CF=873 m.
在Rt△ACF中,∵tan ∠ACF=,
∴AF=tan ∠ACF·CF=tan 37°×873≈0.75×873=654.75(m).
∴CD=FB=AB-AF=873-654.75=218.25≈218.3(m).
答:吉塔的高度CD约为218.3 m.
能力提升
1.C 解析:如图,过点A作AE⊥BC于点E,
则CE=AD=h.∵在Rt△ACE中,CE=h,∴AE=h,
∵在Rt△AEB中,AE=h,∴BE=AE·tan 30°=h·h,∴BC=BE+CE=h,即旗杆的高度为h.故选C.
2.A 解析:由题意得EF=BM=1.8 m,CD=BN=1.5 m,DF=5 m,EM=BF,BD=CN,EM⊥AB,CN⊥AB,
设BD=CN=x m,∴EM=BF=DF+BD=(x+5)m,在Rt△AEM中,∠AEM=45°,∴AM=EM·tan 45°=(x+5)m,在Rt△ACN中,∠ACN=53°,∴AN=CN·tan 53°≈x m,
∵AM+BM=AN+BN=AB,∴x+5+1.8=x+1.5,解得x=15.9,
∴AN=x=21.2 m,∴AB=AN+BN=21.2+1.5=22.7(m),∴电子厂AB的高度约为22.7 m.故选A.
3.(50+50) 解析:由题意得AD⊥BC,在Rt△ACD中,∠CAD=60°,AD=50 m,∴CD=AD·tan 60°=50 m,
在Rt△ABD中,∠BAD=45°,∴BD=AD·tan 45°=50 m,∴BC=BD+CD=(50+50)m,∴这栋楼的高度为(50+50)m.
4.74 解析:如图,过点P作PE⊥AB于点E,过点C作CF⊥PE于点F,∴∠B=∠CFE=∠FEB=90°,∴四边形CBEF为矩形.由题知∠NPC=∠PCF=63.6°,∠MPA=∠BAP=50°,BC=EF=12 m,PE=60 m,∴PF=PE-EF=48 m,在Rt△PFC中,
tan 63.6°=≈2,∴CF=24 m,
∴BE=24 m,在Rt△APE中,
tan 50°=≈,∴AE=50 m,
∴AB=AE+BE=74 m.
5.解:由题意得,DF=CE=24 m,
AG=EF=CD=1.2 m,∠BDG=37°,
∠BFG=45°,
在Rt△BDG中,tan ∠BDG=tan 37°=≈0.75,∴GD=,
在Rt△BFG中,∵∠BFG=45°,
∴FG=BG,∵DF=24 m,
∴DG-FG=-BG=24,
解得BG=72,
∴AB=72+1.2=73.2(m).
答:塔AB的高度为73.2 m.
第3课时 解直角三角形的应用——仰角和俯角
仰角和俯角的应用
1.观测员从海面上的一艘小船上(小船和观测员高度忽略不计)观察前方高出海平面150 m的一座山崖顶端,测得仰角为60°,则小船和山崖之间的水平距离为 ( )
A.150 m B.100 m C.50 m D.300 m
2.在数学课外实践活动中,某小组测量一栋楼房CD的高度(如图),他们在A处仰望楼顶,测得仰角为30°,再往楼的方向前进50 m至B处,测得仰角为60°,那么这栋楼的高度为(人的身高忽略不计) ( )
A.25 m B.25 m C.25 m D.50 m
3.(2024德阳中考)某校学生开展综合实践活动,测量一建筑物CD的高度,在建筑物旁边有一高度为10 m的小楼房AB,小李同学在小楼房楼底B处测得C处的仰角为60°,在小楼房楼顶A处测得C处的仰角为30°(AB、CD在同一平面内,B、D在同一水平面上),则建筑物CD的高为 ( )
A.20 m
B.15 m
C.12 m
D.(10+5)m
4.(2024盐城中考)如图,小明用无人机测量教学楼的高度,将无人机垂直上升距地面30 m的点P处,测得教学楼底端点A的俯角为37°,再将无人机沿教学楼方向水平飞行26.6 m至点Q处,测得教学楼顶端点B的俯角为45°,则教学楼AB的高度约为 m.(结果精确到1 m,参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
5.(2024吉林中考)图1中的吉林省广播电视塔,又称“吉塔”.某直升机于空中A处探测到吉塔,此时飞行高度AB=873 m,如图2,从直升机上看塔尖C的俯角∠EAC=37°,看塔底D的俯角∠EAD=45°,求吉塔的高度CD.
(结果精确到0.1 m,参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
图1 图2
1.一个测量技术队员在一个高为h(忽略身高)的位置,观测一根高出此建筑物的旗杆,测出与旗杆的顶端的仰角为30°,与地面的俯角为60°,那么该旗杆的高度是 ( )
A.h B.h C.h D.h
2.(2024深圳中考)如图,为了测量某电子厂的高度,小明用高1.8 m的测量仪EF测得顶端A的仰角为45°,小军在小明的前面5 m处用高1.5 m的测量仪CD测得顶端A的仰角为53°,则电子厂AB的高度为 ( )
参考数据:sin 53°≈,cos 53°≈,tan 53°≈
A.22.7 m B.22.4 m
C.21.2 m D.23.0 m
第2题图 第3题图
3.如图,用热气球的探测器测一栋楼的高度,从热气球上的点A测得该楼顶部点C的仰角为60°,测得底部点B的俯角为45°,点A与楼BC的水平距离AD=50 m,则这栋楼的高度为 m.(结果保留根号)
4.(2024泰安中考)在综合实践课上,数学兴趣小组用所学数学知识测量大汶河某河段的宽度.他们在河岸一侧的瞭望台上放飞一只无人机.如图,无人机在河上方距水面高60 m的点P处测得瞭望台正对岸A处的俯角为50°,测得瞭望台顶端C处的俯角为63.6°,已知瞭望台BC高12 m(图中点A、B、C、P在同一平面内),那么大汶河此河段的宽AB为 m.参考数据:sin 40°≈,sin 63.6°≈,tan 50°≈,tan 63.6°≈2
5.(应用意识)双塔是古黄河宿迁景观带的标志性建筑之一,由九层的九龙塔和七层的七凤塔构成.某校数学实践小组开展测量七凤塔高度的实践活动,该小组制定了测量方案,在实地测量后撰写活动报告,报告部分内容如表:
测量七凤塔高度
测量 工具 测角仪、 皮尺等 活动形式 以小组 为单位
测量示意图 测量步骤及结果
如图,步骤如下: ①在C处使用测角仪测得塔的顶部点B的仰角∠BDG=37°; ②沿着CA方向走到E处,用皮尺测得CE=24 m; ③在E处使用测角仪测得塔的顶部点B的仰角∠BFG=45°
……
已知测角仪的高度为1.2 m,点C、E、A在同一水平直线上.根据以上信息,求塔AB的高度.(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
【详解答案】
基础达标
1.C 解析:如图:
根据题意可知∠B=60°,AC=150 m,
∴BC==50(m),∴小船和山崖之间的水平距离为50 m.故选C.
2.A 解析:设DC=x m,在Rt△ACD中,∠A=30°,tan A=,即tan 30°=,整理得AC=x m,
在Rt△BCD中,∠DBC=60°,
tan ∠DBC=,即tan 60°=,
整理得BC=x m,∵AB=50 m,
∴AC-BC=50,即x-x=50,解得x=25,则这栋楼的高度为25 m.故选A.
3.B 解析:设过点A的水平线与CD交于点E,如图,
由题意知四边形ABDE是矩形,DE=AB=10 m,AE=BD,在Rt△BCD中,BD=CD,在Rt△ACE中,
AE=(CD-DE)=(CD-10),∴(CD-10)=CD,解得CD=15.故选B.
4.17 解析:如图,设AB的延长线与PQ的延长线交于点C,
由题意,知AC=30 m,PQ=26.6 m,∠APC=37°,∠BQC=45°,
在Rt△APC中,
PC=≈=40(m),
∴QC=PC-PQ=40-26.6=13.4(m),
在Rt△BQC中,BC=QC=13.4 m,
∴AB=AC-BC=30-13.4=16.6≈17(m).
5.解:如图,过点C作CF⊥AB,垂足为F.
∵AB⊥BD,CF⊥AB,DC⊥BD,
∴∠CDB=∠B=∠CFB=90°,
∴四边形CDBF是矩形,
∴BF=CD,CF=BD.
∵CF∥BD∥AE,
∴∠EAC=∠ACF=37°,
∠EAD=∠ADB=45°,∴AB=DB=CF=873 m.
在Rt△ACF中,∵tan ∠ACF=,
∴AF=tan ∠ACF·CF=tan 37°×873≈0.75×873=654.75(m).
∴CD=FB=AB-AF=873-654.75=218.25≈218.3(m).
答:吉塔的高度CD约为218.3 m.
能力提升
1.C 解析:如图,过点A作AE⊥BC于点E,
则CE=AD=h.∵在Rt△ACE中,CE=h,∴AE=h,
∵在Rt△AEB中,AE=h,∴BE=AE·tan 30°=h·h,∴BC=BE+CE=h,即旗杆的高度为h.故选C.
2.A 解析:由题意得EF=BM=1.8 m,CD=BN=1.5 m,DF=5 m,EM=BF,BD=CN,EM⊥AB,CN⊥AB,
设BD=CN=x m,∴EM=BF=DF+BD=(x+5)m,在Rt△AEM中,∠AEM=45°,∴AM=EM·tan 45°=(x+5)m,在Rt△ACN中,∠ACN=53°,∴AN=CN·tan 53°≈x m,
∵AM+BM=AN+BN=AB,∴x+5+1.8=x+1.5,解得x=15.9,
∴AN=x=21.2 m,∴AB=AN+BN=21.2+1.5=22.7(m),∴电子厂AB的高度约为22.7 m.故选A.
3.(50+50) 解析:由题意得AD⊥BC,在Rt△ACD中,∠CAD=60°,AD=50 m,∴CD=AD·tan 60°=50 m,
在Rt△ABD中,∠BAD=45°,∴BD=AD·tan 45°=50 m,∴BC=BD+CD=(50+50)m,∴这栋楼的高度为(50+50)m.
4.74 解析:如图,过点P作PE⊥AB于点E,过点C作CF⊥PE于点F,∴∠B=∠CFE=∠FEB=90°,∴四边形CBEF为矩形.由题知∠NPC=∠PCF=63.6°,∠MPA=∠BAP=50°,BC=EF=12 m,PE=60 m,∴PF=PE-EF=48 m,在Rt△PFC中,
tan 63.6°=≈2,∴CF=24 m,
∴BE=24 m,在Rt△APE中,
tan 50°=≈,∴AE=50 m,
∴AB=AE+BE=74 m.
5.解:由题意得,DF=CE=24 m,
AG=EF=CD=1.2 m,∠BDG=37°,
∠BFG=45°,
在Rt△BDG中,tan ∠BDG=tan 37°=≈0.75,∴GD=,
在Rt△BFG中,∵∠BFG=45°,
∴FG=BG,∵DF=24 m,
∴DG-FG=-BG=24,
解得BG=72,
∴AB=72+1.2=73.2(m).
答:塔AB的高度为73.2 m.
