24.4.4 解直角三角形的应用——坡度和坡角 同步练习(含答案)华东师大版九年级上册
文档属性
| 名称 | 24.4.4 解直角三角形的应用——坡度和坡角 同步练习(含答案)华东师大版九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 215.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 17:58:13 | ||
图片预览


文档简介
24.4 解直角三角形
第4课时 解直角三角形的应用——坡度和坡角
坡角和坡度的应用
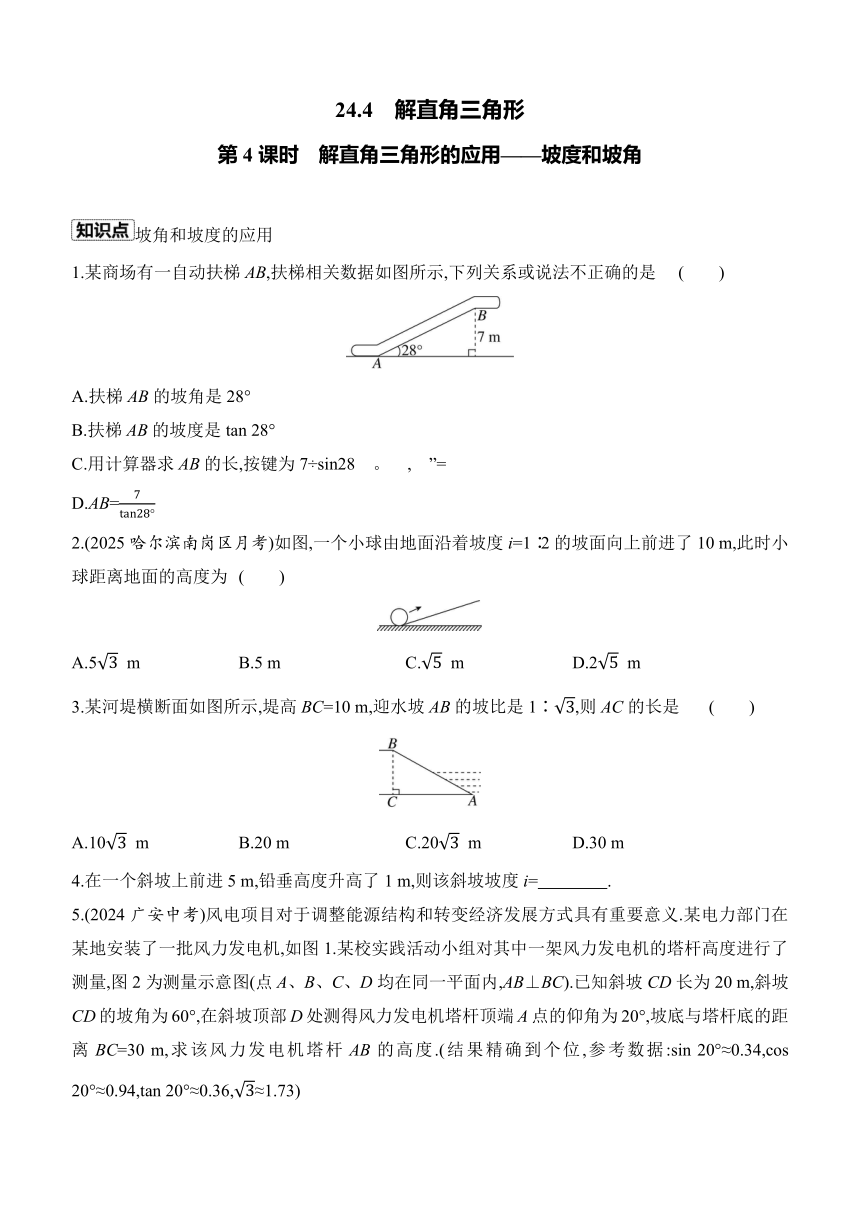
1.某商场有一自动扶梯AB,扶梯相关数据如图所示,下列关系或说法不正确的是 ( )
A.扶梯AB的坡角是28°
B.扶梯AB的坡度是tan 28°
C.用计算器求AB的长,按键为7÷sin28 。 , ”=
D.AB=
2.(2025哈尔滨南岗区月考)如图,一个小球由地面沿着坡度i=1∶2的坡面向上前进了10 m,此时小球距离地面的高度为 ( )
A.5 m B.5 m C. m D.2 m
3.某河堤横断面如图所示,堤高BC=10 m,迎水坡AB的坡比是1∶,则AC的长是 ( )
A.10 m B.20 m C.20 m D.30 m
4.在一个斜坡上前进5 m,铅垂高度升高了1 m,则该斜坡坡度i= .
5.(2024广安中考)风电项目对于调整能源结构和转变经济发展方式具有重要意义.某电力部门在某地安装了一批风力发电机,如图1.某校实践活动小组对其中一架风力发电机的塔杆高度进行了测量,图2为测量示意图(点A、B、C、D均在同一平面内,AB⊥BC).已知斜坡CD长为20 m,斜坡CD的坡角为60°,在斜坡顶部D处测得风力发电机塔杆顶端A点的仰角为20°,坡底与塔杆底的距离BC=30 m,求该风力发电机塔杆AB的高度.(结果精确到个位,参考数据:sin 20°≈0.34,cos 20°≈0.94,tan 20°≈0.36,≈1.73)
图1 图2
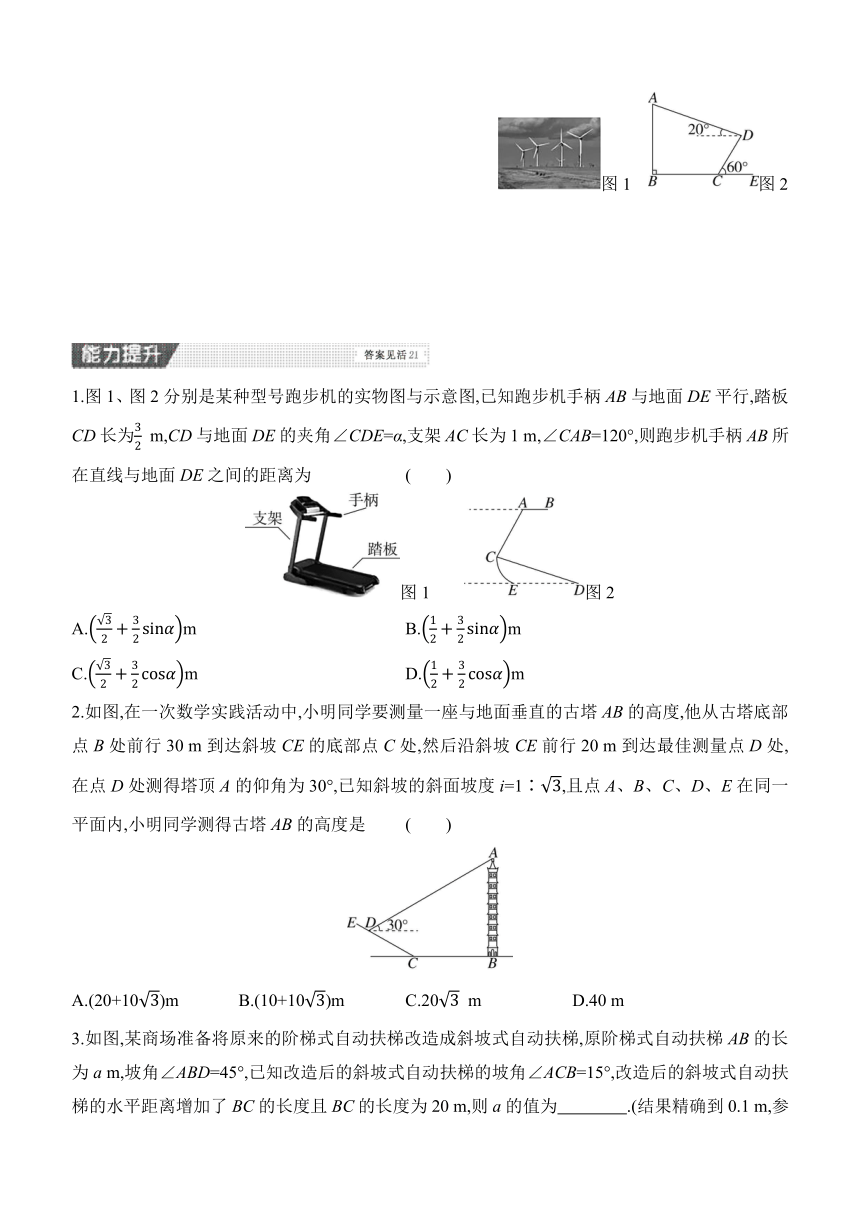
1.图1、图2分别是某种型号跑步机的实物图与示意图,已知跑步机手柄AB与地面DE平行,踏板CD长为 m,CD与地面DE的夹角∠CDE=α,支架AC长为1 m,∠CAB=120°,则跑步机手柄AB所在直线与地面DE之间的距离为 ( )
图1 图2
A.m B.m
C.m D.m
2.如图,在一次数学实践活动中,小明同学要测量一座与地面垂直的古塔AB的高度,他从古塔底部点B处前行30 m到达斜坡CE的底部点C处,然后沿斜坡CE前行20 m到达最佳测量点D处,在点D处测得塔顶A的仰角为30°,已知斜坡的斜面坡度i=1∶,且点A、B、C、D、E在同一平面内,小明同学测得古塔AB的高度是 ( )
A.(20+10)m B.(10+10)m C.20 m D.40 m
3.如图,某商场准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯,原阶梯式自动扶梯AB的长为a m,坡角∠ABD=45°,已知改造后的斜坡式自动扶梯的坡角∠ACB=15°,改造后的斜坡式自动扶梯的水平距离增加了BC的长度且BC的长度为20 m,则a的值为 .(结果精确到0.1 m,参考数据:sin 15°≈0.26,cos 15°≈0.97,tan 15°≈0.27,≈1.414)
4.(应用意识)“滑滑梯”是同学们小时候经常玩的游戏,滑梯的坡角越小,安全性越高.从安全性及适用性出发,小亮同学对所在小区的一处滑梯进行调研,制定了如下改造方案,请你帮小亮解决方案中的问题.
方案名称 滑梯安全改造
测量工具 测角仪、皮尺等
方案设计 如图,将滑梯顶端BC拓宽为BE,使CE=1 m,并将原来的滑梯CF改为EG.(图中所有点均在同一平面内,点B、C、E在同一直线上,点A、D、F、G在同一直线上)
测量数据 【步骤一】利用皮尺测量滑梯的高度CD=1.8 m; 【步骤二】在点F处用测角仪测得∠CFD=42°; 【步骤三】在点G处用测角仪测得∠EGD=32°
解决问题 调整后的滑梯会多占多长一段地面 (即求FG的长)
参考数据:sin 32°≈,cos 32°≈,tan 32°≈,sin 42°≈,cos 42°≈,tan 42°≈
【详解答案】
基础达标
1.D 解析:A.扶梯AB的坡角是28°,正确,本选项不符合题意;B.扶梯AB的坡度是tan 28°,正确,本选项不符合题意;C.用计算器求AB的长,按键为7÷sin 28 。 , ”=,正确,本选项不符合题意;D.AB=,错误,本选项符合题意.故选D.
2.D 解析:如图,过点B作BC⊥AC,垂足为C,
根据题意得tan ∠BAC=,AB=10 m,设BC=x m,则AC=2x m,由勾股定理得AB2=AC2+BC2,
即102=(2x)2+x2,解得x=2(负值舍去).故选D.
3.A 解析:∵迎水坡AB的坡比为1∶,
∴,∵堤高BC=10 m,∴AC=BC=×10=10(m).故选A.
4.1∶2 解析:设在一个斜坡上前进5 m,水平高度升高了1 m,此时水平长度为x m,根据勾股定理,得x2+12=52,解得x1=2,x2=-2(舍去),故该斜坡坡度i=1∶2.
5.解:如图,过点D作DF⊥AB于点F,作DH⊥BE于点H,
由题意得DC=20 m,∠DCH=60°,
在Rt△DCH中,
∵cos 60°=,sin 60°=,
∴CH=CD·cos 60°=10 m,
∴DH=CD·sin 60°=10 m≈17.3 m,
∵∠DFB=∠B=∠DHB=90°,
∴四边形DFBH为矩形,
∴BH=FD,BF=DH,
∵BH=BC+CH=30+10=40(m),
∴FD=40 m,
在Rt△AFD中,=tan 20°,
∴AF=FD·tan 20°≈40×0.36=14.4(m),
∴AB=BF+AF=17.3+14.4=31.7(m)≈32(m).
答:该风力发电机塔杆AB的高度为32 m.
能力提升
1.A 解析:如图,过点C作CG⊥AB,交BA的延长线于点G,交DE的延长线于点H,
∵手柄AB与地面DE平行,∴CH⊥DE,在Rt△CDH中,∠CDH=α,CD= m,∵sin ∠CDH=,
∴CH=CD·sin ∠CDH=sin α m,
∵∠CAB=120°,∴∠CAG=60°,
∴CG=AC·sin 60°= m,∴跑步机手柄AB所在直线与地面DE之间的距离为m.故选A.
2.A 解析:如图,过点D作DF⊥AB于点F,DG⊥BC,交BC的延长线于点G,
由题意得,BC=30 m,CD=20 m,
∠ADF=30°,DG=BF,DF=BG,
∵斜坡的斜面坡度i=1∶,∴,设DG=x m,则CG=x m,CD=2x m,∴2x=20,解得x=10,
∴DG=BF=10 m,CG=10 m,
∴DF=BG=CG+BC=(30+10)m,
在Rt△ADF中,tan 30°==
,解得AF=10+10,∴AB=AF+BF=(20+10)m.故选A.
3.10.5 解析:在Rt△ABD中,AB=a m,∠ABD=45°,则AD=BD=AB=a(m),∵BC=20 m,∴CD=20+am,在Rt△ACD中,∠ACD=15°,∵tan ∠ACD=,∴≈0.27,解得a≈10.5,
经检验,a≈10.5是原方程的解.
4.解:如图,过点E作EH⊥AG于点H,
则四边形CDHE为矩形,
∴EH=CD=1.8 m,DH=CE=1 m,
在Rt△CDF中,∠CFD=42°,CD=1.8 m,
则DF=≈=2(m),
∴HF=DF-DH=2-1=1(m),
在Rt△EHG中,∠EGH=32°,EH=1.8 m,
则HG=≈=2.88(m),
∴FG=HG-HF=1.88(m).
答:调整后的滑梯会多占约为1.88 m的一段地面.
第4课时 解直角三角形的应用——坡度和坡角
坡角和坡度的应用
1.某商场有一自动扶梯AB,扶梯相关数据如图所示,下列关系或说法不正确的是 ( )
A.扶梯AB的坡角是28°
B.扶梯AB的坡度是tan 28°
C.用计算器求AB的长,按键为7÷sin28 。 , ”=
D.AB=
2.(2025哈尔滨南岗区月考)如图,一个小球由地面沿着坡度i=1∶2的坡面向上前进了10 m,此时小球距离地面的高度为 ( )
A.5 m B.5 m C. m D.2 m
3.某河堤横断面如图所示,堤高BC=10 m,迎水坡AB的坡比是1∶,则AC的长是 ( )
A.10 m B.20 m C.20 m D.30 m
4.在一个斜坡上前进5 m,铅垂高度升高了1 m,则该斜坡坡度i= .
5.(2024广安中考)风电项目对于调整能源结构和转变经济发展方式具有重要意义.某电力部门在某地安装了一批风力发电机,如图1.某校实践活动小组对其中一架风力发电机的塔杆高度进行了测量,图2为测量示意图(点A、B、C、D均在同一平面内,AB⊥BC).已知斜坡CD长为20 m,斜坡CD的坡角为60°,在斜坡顶部D处测得风力发电机塔杆顶端A点的仰角为20°,坡底与塔杆底的距离BC=30 m,求该风力发电机塔杆AB的高度.(结果精确到个位,参考数据:sin 20°≈0.34,cos 20°≈0.94,tan 20°≈0.36,≈1.73)
图1 图2
1.图1、图2分别是某种型号跑步机的实物图与示意图,已知跑步机手柄AB与地面DE平行,踏板CD长为 m,CD与地面DE的夹角∠CDE=α,支架AC长为1 m,∠CAB=120°,则跑步机手柄AB所在直线与地面DE之间的距离为 ( )
图1 图2
A.m B.m
C.m D.m
2.如图,在一次数学实践活动中,小明同学要测量一座与地面垂直的古塔AB的高度,他从古塔底部点B处前行30 m到达斜坡CE的底部点C处,然后沿斜坡CE前行20 m到达最佳测量点D处,在点D处测得塔顶A的仰角为30°,已知斜坡的斜面坡度i=1∶,且点A、B、C、D、E在同一平面内,小明同学测得古塔AB的高度是 ( )
A.(20+10)m B.(10+10)m C.20 m D.40 m
3.如图,某商场准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯,原阶梯式自动扶梯AB的长为a m,坡角∠ABD=45°,已知改造后的斜坡式自动扶梯的坡角∠ACB=15°,改造后的斜坡式自动扶梯的水平距离增加了BC的长度且BC的长度为20 m,则a的值为 .(结果精确到0.1 m,参考数据:sin 15°≈0.26,cos 15°≈0.97,tan 15°≈0.27,≈1.414)
4.(应用意识)“滑滑梯”是同学们小时候经常玩的游戏,滑梯的坡角越小,安全性越高.从安全性及适用性出发,小亮同学对所在小区的一处滑梯进行调研,制定了如下改造方案,请你帮小亮解决方案中的问题.
方案名称 滑梯安全改造
测量工具 测角仪、皮尺等
方案设计 如图,将滑梯顶端BC拓宽为BE,使CE=1 m,并将原来的滑梯CF改为EG.(图中所有点均在同一平面内,点B、C、E在同一直线上,点A、D、F、G在同一直线上)
测量数据 【步骤一】利用皮尺测量滑梯的高度CD=1.8 m; 【步骤二】在点F处用测角仪测得∠CFD=42°; 【步骤三】在点G处用测角仪测得∠EGD=32°
解决问题 调整后的滑梯会多占多长一段地面 (即求FG的长)
参考数据:sin 32°≈,cos 32°≈,tan 32°≈,sin 42°≈,cos 42°≈,tan 42°≈
【详解答案】
基础达标
1.D 解析:A.扶梯AB的坡角是28°,正确,本选项不符合题意;B.扶梯AB的坡度是tan 28°,正确,本选项不符合题意;C.用计算器求AB的长,按键为7÷sin 28 。 , ”=,正确,本选项不符合题意;D.AB=,错误,本选项符合题意.故选D.
2.D 解析:如图,过点B作BC⊥AC,垂足为C,
根据题意得tan ∠BAC=,AB=10 m,设BC=x m,则AC=2x m,由勾股定理得AB2=AC2+BC2,
即102=(2x)2+x2,解得x=2(负值舍去).故选D.
3.A 解析:∵迎水坡AB的坡比为1∶,
∴,∵堤高BC=10 m,∴AC=BC=×10=10(m).故选A.
4.1∶2 解析:设在一个斜坡上前进5 m,水平高度升高了1 m,此时水平长度为x m,根据勾股定理,得x2+12=52,解得x1=2,x2=-2(舍去),故该斜坡坡度i=1∶2.
5.解:如图,过点D作DF⊥AB于点F,作DH⊥BE于点H,
由题意得DC=20 m,∠DCH=60°,
在Rt△DCH中,
∵cos 60°=,sin 60°=,
∴CH=CD·cos 60°=10 m,
∴DH=CD·sin 60°=10 m≈17.3 m,
∵∠DFB=∠B=∠DHB=90°,
∴四边形DFBH为矩形,
∴BH=FD,BF=DH,
∵BH=BC+CH=30+10=40(m),
∴FD=40 m,
在Rt△AFD中,=tan 20°,
∴AF=FD·tan 20°≈40×0.36=14.4(m),
∴AB=BF+AF=17.3+14.4=31.7(m)≈32(m).
答:该风力发电机塔杆AB的高度为32 m.
能力提升
1.A 解析:如图,过点C作CG⊥AB,交BA的延长线于点G,交DE的延长线于点H,
∵手柄AB与地面DE平行,∴CH⊥DE,在Rt△CDH中,∠CDH=α,CD= m,∵sin ∠CDH=,
∴CH=CD·sin ∠CDH=sin α m,
∵∠CAB=120°,∴∠CAG=60°,
∴CG=AC·sin 60°= m,∴跑步机手柄AB所在直线与地面DE之间的距离为m.故选A.
2.A 解析:如图,过点D作DF⊥AB于点F,DG⊥BC,交BC的延长线于点G,
由题意得,BC=30 m,CD=20 m,
∠ADF=30°,DG=BF,DF=BG,
∵斜坡的斜面坡度i=1∶,∴,设DG=x m,则CG=x m,CD=2x m,∴2x=20,解得x=10,
∴DG=BF=10 m,CG=10 m,
∴DF=BG=CG+BC=(30+10)m,
在Rt△ADF中,tan 30°==
,解得AF=10+10,∴AB=AF+BF=(20+10)m.故选A.
3.10.5 解析:在Rt△ABD中,AB=a m,∠ABD=45°,则AD=BD=AB=a(m),∵BC=20 m,∴CD=20+am,在Rt△ACD中,∠ACD=15°,∵tan ∠ACD=,∴≈0.27,解得a≈10.5,
经检验,a≈10.5是原方程的解.
4.解:如图,过点E作EH⊥AG于点H,
则四边形CDHE为矩形,
∴EH=CD=1.8 m,DH=CE=1 m,
在Rt△CDF中,∠CFD=42°,CD=1.8 m,
则DF=≈=2(m),
∴HF=DF-DH=2-1=1(m),
在Rt△EHG中,∠EGH=32°,EH=1.8 m,
则HG=≈=2.88(m),
∴FG=HG-HF=1.88(m).
答:调整后的滑梯会多占约为1.88 m的一段地面.
