第24章 解直角三角形 专题训练六 求锐角三角函数值的方法 (含答案)华东师大版九年级上册
文档属性
| 名称 | 第24章 解直角三角形 专题训练六 求锐角三角函数值的方法 (含答案)华东师大版九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 131.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 22:24:45 | ||
图片预览


文档简介
专题训练六 求锐角三角函数值的方法
定义法
1.(2025扬州期中)在Rt△ABC中,∠C=90°,AC=1,BC=2,则sin A的值为 ( )
A. B. C. D.2
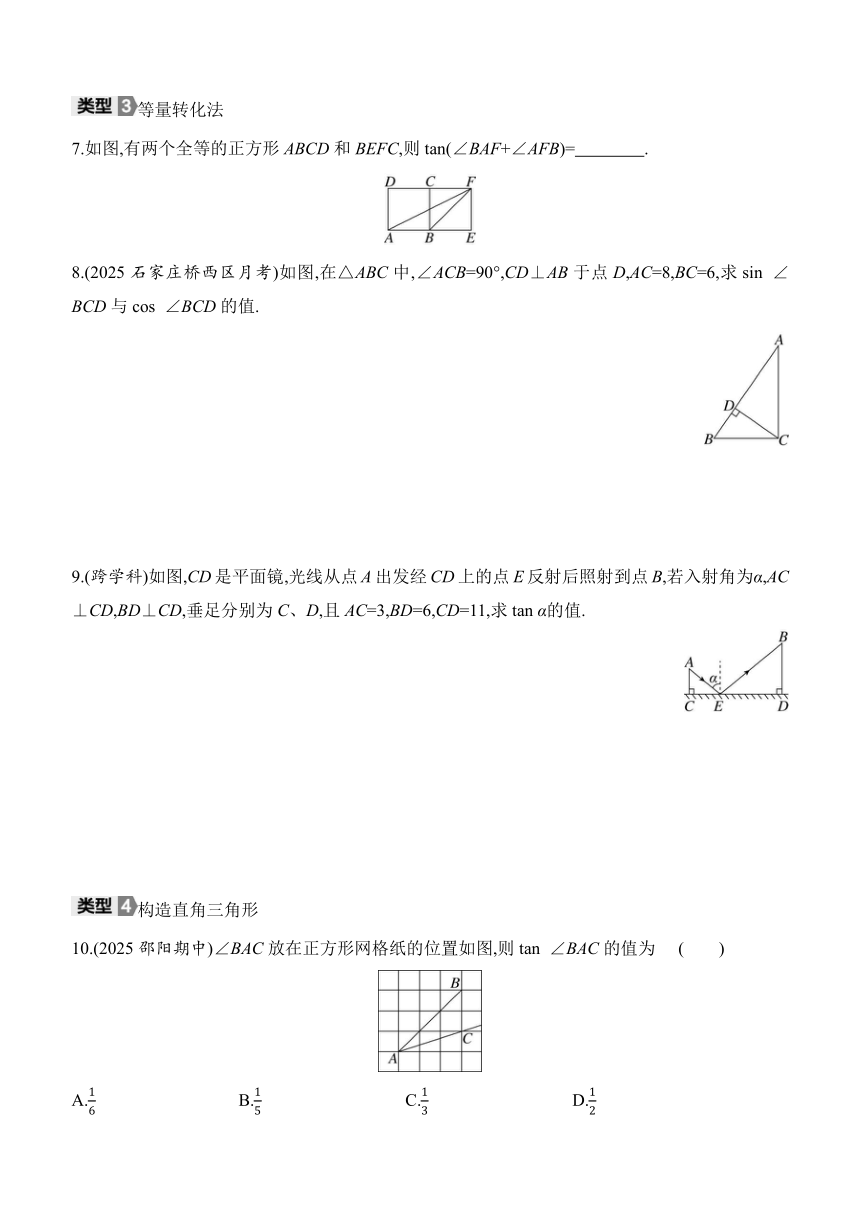
2.如图,在平面直角坐标系中,点A的坐标为(4,3),那么cos α的值是 ( )
A. B. C. D.
3.如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,求sin C、cos C、tan C的值.
4.如图,根据提供的数据回答下列问题:
图1 图2
(1)在图1中,sin A= ,cos A= ,sin2A+cos2A= ;在图2中,sin A1= ,cos A1= ,sin2A1+cos2A1= .
通过以上两个特殊的例子,你发现了什么规律 用一个一般的式子把你发现的规律表示出来,并加以证明.
(2)在图1中,tan A= ,= ;在图2中,tan A1= ,= .
通过以上两个特殊的例子,你发现了什么规律 用一个一般的式子把你发现的规律表示出来,并加以证明.
设参数
5.(2024资阳中考)第14届国际数学教育大会会标如图1所示,会标中心的图案来源于我国古代数学家赵爽的“弦图”.如图2所示的“弦图”是由四个全等的直角三角形(△ABE、△BCF、△CDG、△DAH)和一个小正方形EFGH拼成的大正方形ABCD.若EF∶AH=1∶3,则sin ∠ABE= ( )
图1 图2
A. B. C. D.
6.在Rt△ABC中,AC=2BC.
(1)求cos A的值.
(2)当AB=10时,求BC的长.
等量转化法
7.如图,有两个全等的正方形ABCD和BEFC,则tan(∠BAF+∠AFB)= .
8.(2025石家庄桥西区月考)如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,AC=8,BC=6,求sin ∠BCD与cos ∠BCD的值.
9.(跨学科)如图,CD是平面镜,光线从点A出发经CD上的点E反射后照射到点B,若入射角为α,AC⊥CD,BD⊥CD,垂足分别为C、D,且AC=3,BD=6,CD=11,求tan α的值.
构造直角三角形
10.(2025邵阳期中)∠BAC放在正方形网格纸的位置如图,则tan ∠BAC的值为 ( )
A. B. C. D.
11.如图,在平面直角坐标系中,已知点A(3,3)和点B(7,0),则sin ∠ABO的值等于 .
12.如图,在△ABC中,∠C=150°,AC=4,tan B=.
(1)求BC的长.
(2)利用此图形求tan 15°的值(结果精确到0.1,参考数据:≈1.4,≈1.7,≈2.2).
【详解答案】
1.C 解析:∵Rt△ABC中,∠C=90°,
AC=1,BC=2,∴AB=,
∴sin A=.故选C.
2.B 解析:由点A的坐标为(4,3),得OA==5,∴cos α=.故选B.
3.解:∵Rt△ABC中,∠A=90°,AB=3,AC=4,∴BC==5,
则sin C=,cos C=,tan C=.
4.解:(1) 1 1
规律:对于任意锐角α,
有sin2α+cos2α=1.
证明:如图,在Rt△ABC中,∠C=90°.
∵sin α=,cos α=,c2=a2+b2,
∴sin2α+cos2α==1.
(2)
规律:对于任意锐角α,有tan α=.
证明:如图,在Rt△ABC中,∠C=90°.∵tan α=,,
∴tan α=.
5.C 解析:根据题意,设EF=x,则AH=3x,∵△ABE≌△DAH,四边形EFGH为正方形,∴AH=BE=3x,EF=HE=x,∴AE=4x,∵∠AEB=90°,∴AB==5x,
∴sin ∠ABE=.故选C.
6.解:(1)在Rt△ABC中,AC=2BC,
设BC=x,则AC=2x,当AC是斜边时,AB=x,
则cos A=;当AC是直角边时,AB=x,
则cos A=.
综上,cos A的值为或.
(2)在Rt△ABC中,AC=2BC,
设BC=x,则AC=2x,
当AC是直角边时,(2x)2+x2=100,解得x=2(负值舍去).
当AC是斜边时,(2x)2=x2+100,解得x=(负值舍去).
综上,BC的长为或2.
7.1 解析:根据三角形外角的性质,得∠BAF+∠AFB=∠FBE.∵四边形BEFC是正方形,∴BE=EF.
∴tan(∠BAF+∠AFB)=tan ∠FBE==1.
8.解:∵∠ACB=90°,CD⊥AB,
∴∠BDC=∠ACB=90°,
∴∠B+∠BCD=90°,∠B+∠A=90°,
∴∠BCD=∠A,∵AC=8,BC=6,
∴AB==10,
∴sin ∠BCD=sin A=,cos ∠BCD=cos A=.
9.解:根据已知条件可得∠CAE=α.
∵AC⊥CD,BD⊥CD,
∴∠ACE=∠BDE=90°.
又∵∠AEC=∠BED,
∴△ACE∽△BDE,∴,
即,解得CE=.
在Rt△AEC中,
tan ∠CAE=,
即tan α=.
10.D 解析:如图,连结CD,
设每个小正方形的边长均为1,
则AD==2,
CD=,
AC=,∵(2)2+()2=()2,∴∠ADC=90°,∴tan ∠BAC=.故选D.
11. 解析:作AC⊥x轴于点C,如图,
∵点A(3,3),点B(7,0),∴OC=3,AC=3,OB=7,∴BC=4,
在Rt△ACB中,AB==5,∴sin ∠ABC=.
即sin ∠ABO的值等于.
12.解:(1)过点A作AD⊥BC,交BC的延长线于点D,如图所示.
在Rt△ADC中,AC=4,
∵∠ACB=150°,∴∠ACD=30°.
∴AD=AC=2,
CD==2.
在Rt△ABD中,tan B=,∴BD=16.
∴BC=BD-CD=16-2.
(2)在BC边上取一点M,使得CM=AC,连结AM,如图所示.
∵∠ACB=150°,
∴∠AMC=∠MAC=15°,∴tan 15°=tan ∠AMD==
=2-≈0.3.
定义法
1.(2025扬州期中)在Rt△ABC中,∠C=90°,AC=1,BC=2,则sin A的值为 ( )
A. B. C. D.2
2.如图,在平面直角坐标系中,点A的坐标为(4,3),那么cos α的值是 ( )
A. B. C. D.
3.如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,求sin C、cos C、tan C的值.
4.如图,根据提供的数据回答下列问题:
图1 图2
(1)在图1中,sin A= ,cos A= ,sin2A+cos2A= ;在图2中,sin A1= ,cos A1= ,sin2A1+cos2A1= .
通过以上两个特殊的例子,你发现了什么规律 用一个一般的式子把你发现的规律表示出来,并加以证明.
(2)在图1中,tan A= ,= ;在图2中,tan A1= ,= .
通过以上两个特殊的例子,你发现了什么规律 用一个一般的式子把你发现的规律表示出来,并加以证明.
设参数
5.(2024资阳中考)第14届国际数学教育大会会标如图1所示,会标中心的图案来源于我国古代数学家赵爽的“弦图”.如图2所示的“弦图”是由四个全等的直角三角形(△ABE、△BCF、△CDG、△DAH)和一个小正方形EFGH拼成的大正方形ABCD.若EF∶AH=1∶3,则sin ∠ABE= ( )
图1 图2
A. B. C. D.
6.在Rt△ABC中,AC=2BC.
(1)求cos A的值.
(2)当AB=10时,求BC的长.
等量转化法
7.如图,有两个全等的正方形ABCD和BEFC,则tan(∠BAF+∠AFB)= .
8.(2025石家庄桥西区月考)如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,AC=8,BC=6,求sin ∠BCD与cos ∠BCD的值.
9.(跨学科)如图,CD是平面镜,光线从点A出发经CD上的点E反射后照射到点B,若入射角为α,AC⊥CD,BD⊥CD,垂足分别为C、D,且AC=3,BD=6,CD=11,求tan α的值.
构造直角三角形
10.(2025邵阳期中)∠BAC放在正方形网格纸的位置如图,则tan ∠BAC的值为 ( )
A. B. C. D.
11.如图,在平面直角坐标系中,已知点A(3,3)和点B(7,0),则sin ∠ABO的值等于 .
12.如图,在△ABC中,∠C=150°,AC=4,tan B=.
(1)求BC的长.
(2)利用此图形求tan 15°的值(结果精确到0.1,参考数据:≈1.4,≈1.7,≈2.2).
【详解答案】
1.C 解析:∵Rt△ABC中,∠C=90°,
AC=1,BC=2,∴AB=,
∴sin A=.故选C.
2.B 解析:由点A的坐标为(4,3),得OA==5,∴cos α=.故选B.
3.解:∵Rt△ABC中,∠A=90°,AB=3,AC=4,∴BC==5,
则sin C=,cos C=,tan C=.
4.解:(1) 1 1
规律:对于任意锐角α,
有sin2α+cos2α=1.
证明:如图,在Rt△ABC中,∠C=90°.
∵sin α=,cos α=,c2=a2+b2,
∴sin2α+cos2α==1.
(2)
规律:对于任意锐角α,有tan α=.
证明:如图,在Rt△ABC中,∠C=90°.∵tan α=,,
∴tan α=.
5.C 解析:根据题意,设EF=x,则AH=3x,∵△ABE≌△DAH,四边形EFGH为正方形,∴AH=BE=3x,EF=HE=x,∴AE=4x,∵∠AEB=90°,∴AB==5x,
∴sin ∠ABE=.故选C.
6.解:(1)在Rt△ABC中,AC=2BC,
设BC=x,则AC=2x,当AC是斜边时,AB=x,
则cos A=;当AC是直角边时,AB=x,
则cos A=.
综上,cos A的值为或.
(2)在Rt△ABC中,AC=2BC,
设BC=x,则AC=2x,
当AC是直角边时,(2x)2+x2=100,解得x=2(负值舍去).
当AC是斜边时,(2x)2=x2+100,解得x=(负值舍去).
综上,BC的长为或2.
7.1 解析:根据三角形外角的性质,得∠BAF+∠AFB=∠FBE.∵四边形BEFC是正方形,∴BE=EF.
∴tan(∠BAF+∠AFB)=tan ∠FBE==1.
8.解:∵∠ACB=90°,CD⊥AB,
∴∠BDC=∠ACB=90°,
∴∠B+∠BCD=90°,∠B+∠A=90°,
∴∠BCD=∠A,∵AC=8,BC=6,
∴AB==10,
∴sin ∠BCD=sin A=,cos ∠BCD=cos A=.
9.解:根据已知条件可得∠CAE=α.
∵AC⊥CD,BD⊥CD,
∴∠ACE=∠BDE=90°.
又∵∠AEC=∠BED,
∴△ACE∽△BDE,∴,
即,解得CE=.
在Rt△AEC中,
tan ∠CAE=,
即tan α=.
10.D 解析:如图,连结CD,
设每个小正方形的边长均为1,
则AD==2,
CD=,
AC=,∵(2)2+()2=()2,∴∠ADC=90°,∴tan ∠BAC=.故选D.
11. 解析:作AC⊥x轴于点C,如图,
∵点A(3,3),点B(7,0),∴OC=3,AC=3,OB=7,∴BC=4,
在Rt△ACB中,AB==5,∴sin ∠ABC=.
即sin ∠ABO的值等于.
12.解:(1)过点A作AD⊥BC,交BC的延长线于点D,如图所示.
在Rt△ADC中,AC=4,
∵∠ACB=150°,∴∠ACD=30°.
∴AD=AC=2,
CD==2.
在Rt△ABD中,tan B=,∴BD=16.
∴BC=BD-CD=16-2.
(2)在BC边上取一点M,使得CM=AC,连结AM,如图所示.
∵∠ACB=150°,
∴∠AMC=∠MAC=15°,∴tan 15°=tan ∠AMD==
=2-≈0.3.
