第24章 解直角三角形 专题训练七 解直角三角形的常见模型(含答案)华东师大版九年级上册
文档属性
| 名称 | 第24章 解直角三角形 专题训练七 解直角三角形的常见模型(含答案)华东师大版九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 272.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 22:29:54 | ||
图片预览


文档简介
专题训练七 解直角三角形的常见模型
单直角型
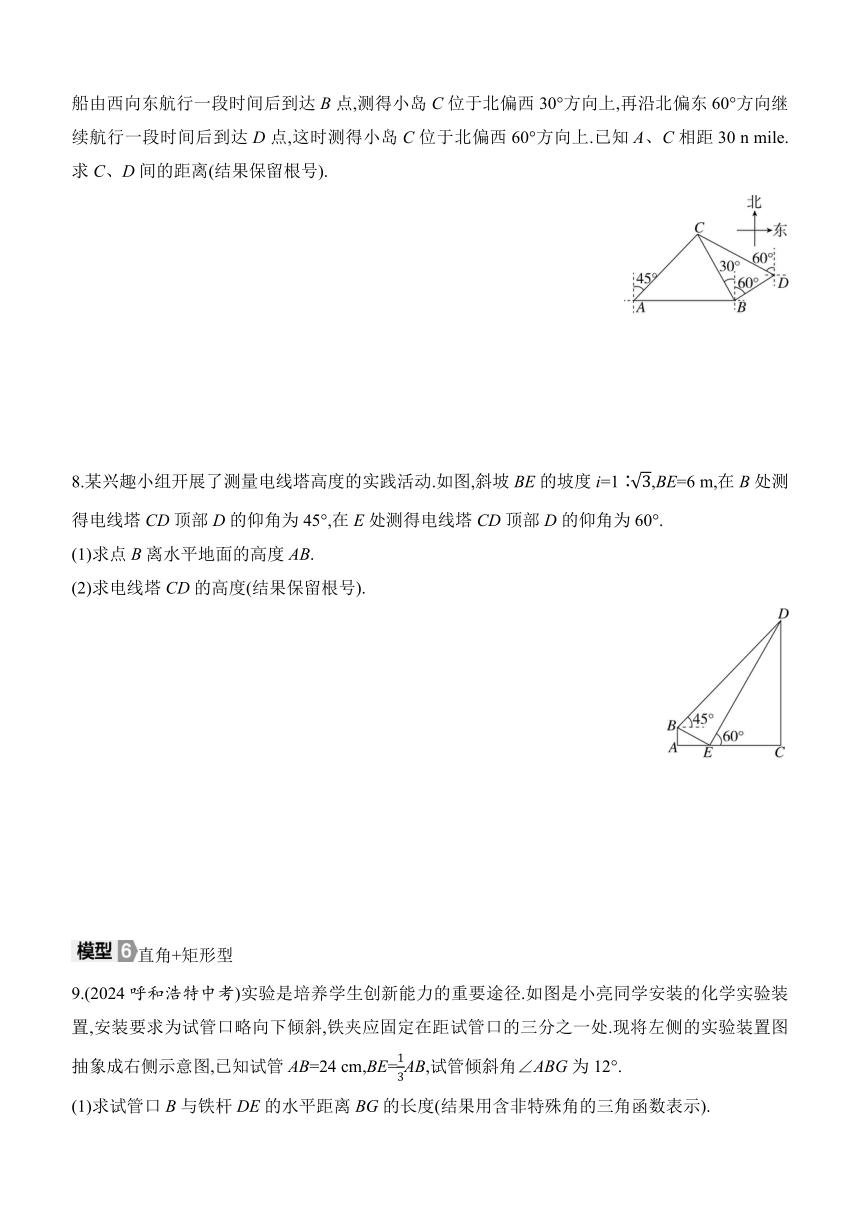
1.如图,在Rt△ABC中,∠ABC=90°,AB=4,AC=5,则cos A的值为 ( )
A. B. C. D.
2.如图1,天窗打开后,天窗边缘AC与窗框AB夹角为23°,它的示意图如图2所示.若AC长为a m,则窗角C到窗框AB的距离CD的大小为 ( )
图1 图2
A. m B. m C.acos 23° m D.asin 23° m
背靠背型
3.如图,某兴趣小组用无人机进行航拍测高,无人机从相距20 m的1号楼和2号楼的地面正中间点B垂直起飞到点A处,测得1号楼顶部E的俯角为60°,测得2号楼顶部F的俯角为45°.已知1号楼的高度为20 m,那么2号楼的高度为 m.(结果保留根号)
拥抱型
4.某地为拓宽河道和提高拦水坝,进行了现有拦水坝改造.如图所示,改造前的斜坡AB=80 m,坡度为1∶4;将斜坡AB的高度AE提高20 m(即AC=20 m)后,斜坡AB改造成斜坡CD,其坡度为1∶1.5.则改造后斜坡CD的长为 .
5.如图,在Rt△ABC中,∠ACB=90°,D是边AB的中点,BE⊥CD,垂足为点E.已知AC=6,cos A=.
(1)求线段CD的长.
(2)求cos ∠DBE的值.
母子型
6.(2024青海中考)如图,某种摄像头识别到最远点A的俯角α是17°,识别到最近点B的俯角β是45°,该摄像头安装在距地面5 m的点C处,求最远点与最近点之间的距离AB.(结果取整数,参考数据:sin 17°≈0.29,cos 17°≈0.96,tan 17°≈0.31)
牵手型
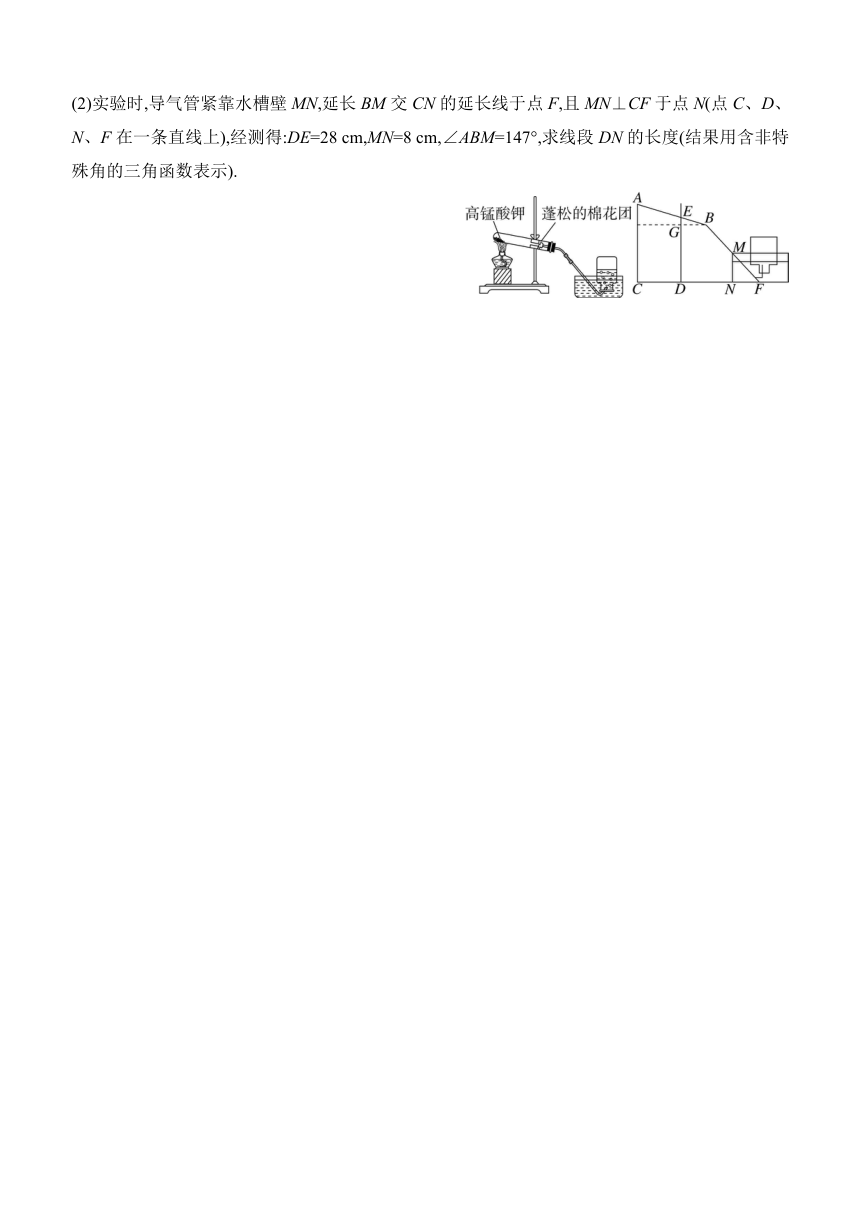
7.(2024泸州中考)如图,海中有一个小岛C,某渔船在海中的A点测得小岛C位于东北方向上,该渔船由西向东航行一段时间后到达B点,测得小岛C位于北偏西30°方向上,再沿北偏东60°方向继续航行一段时间后到达D点,这时测得小岛C位于北偏西60°方向上.已知A、C相距30 n mile.求C、D间的距离(结果保留根号).
8.某兴趣小组开展了测量电线塔高度的实践活动.如图,斜坡BE的坡度i=1∶,BE=6 m,在B处测得电线塔CD顶部D的仰角为45°,在E处测得电线塔CD顶部D的仰角为60°.
(1)求点B离水平地面的高度AB.
(2)求电线塔CD的高度(结果保留根号).
直角+矩形型
9.(2024呼和浩特中考)实验是培养学生创新能力的重要途径.如图是小亮同学安装的化学实验装置,安装要求为试管口略向下倾斜,铁夹应固定在距试管口的三分之一处.现将左侧的实验装置图抽象成右侧示意图,已知试管AB=24 cm,BE=AB,试管倾斜角∠ABG为12°.
(1)求试管口B与铁杆DE的水平距离BG的长度(结果用含非特殊角的三角函数表示).
(2)实验时,导气管紧靠水槽壁MN,延长BM交CN的延长线于点F,且MN⊥CF于点N(点C、D、N、F在一条直线上),经测得:DE=28 cm,MN=8 cm,∠ABM=147°,求线段DN的长度(结果用含非特殊角的三角函数表示).
【详解答案】
1.A 解析:∵∠ABC=90°,AB=4,
AC=5,∴cos A=.故选A.
2.D 解析:∵sin A==sin 23°,AC=a m,∴CD=AC·sin A=a sin 23°(m).故选D.
3.(50-10) 解析:如图,过点E作EG⊥AB于点G,FH⊥AB于点H,
则四边形BCEG和四边形BDFH均为矩形,∴BC=EG,HF=BD,DF=BH,由题意得CE=20 m,CD=20 m,BC=BD=10 m,∠AEG=60°,
∠AFH=45°,在Rt△AEG中,
tan ∠AEG=,∴=tan 60°=,∴AG=10=30(m),
在Rt△AFH中,
∠AHF=90°,∠AFH=45°,
∠FAH=90°-∠AFH=45°,∴AH=HF=10 m,∴DF=BH=AG+BG-AH=30+20-10=(50-10)(m),∴2号楼的高度是(50-10)m.
4.50 m 解析:在Rt△ABE中,
AB=80 m,,∴设AE=x m,BE=4x m,∴AB=x=80,∴x=80,∴AE=80 m,
∴CE=AE+AC=100 m,∵斜坡CD的坡度为1∶1.5,∴DE=150 m,由勾股定理得CD==50 m.
5.解:(1)在Rt△ABC中,∠ACB=90°,∴cos A=,∵AC=6,
∴AB=10,∵D是边AB的中点,
∴CD=AB=5.
(2)如图,过点C作CF⊥AB于点F.
∵BC==8,
∴CF=AC·BC÷AB=4.8,
∴cos ∠DCF=.
∵∠DCF=∠DBE,
∴cos ∠DBE=.
6.解:如图,由题意得CE∥AD,CD=5 m,∴∠A=α=17°,∠CBD=β=45°.
在Rt△ACD中,∵CD=5,
=tan 17°,
∴AD=≈5÷0.31≈16.1(m),
在Rt△BCD中,∵∠CBD=45°,
∴∠BCD=90°-45°=45°,
∴∠BCD=∠CBD=45°,
∴BD=CD=5 m,
∴AB=AD-BD=16.1-5=11.1≈11(m).
答:最远点与最近点之间的距离AB约是11 m.
7.解:如图,过点C作CH⊥AB于点H,
∵∠CAB=45°,AC=30 n mile,
∴AH=CH=15 n mile,
∵∠CBH=60°,
∴BC==10(n mile),
过点D作DG⊥AB交AB的延长线于点G,
∵∠DBG=180°-60°-30°-60°=30°,
∴∠BDG=60°,∴∠CDB=60°,
∴CD==20(n mile).
答:C、D间的距离为20 n mile.
8.解:(1)由题意得BA⊥AE,
∵斜坡BE的坡度i=1∶,
∴tan ∠BEA=,
∴∠BEA=30°,∵BE=6 m,
∴AB=BE=3 m,
∴点B离水平地面的高度AB为3 m.
(2)如图,过点B作BF⊥CD,垂足为F,
由题意得AB=CF=3 m,BF=AC,
由(1)得AE=AB=3 m,
设EC=x m,
∴BF=AC=AE+CE=(x+3)m,
在Rt△CDE中,∠DEC=60°,
∴CD=CE·tan 60°=x m,
在Rt△BDF中,∠DBF=45°,
∴DF=BF·tan 45°=(x+3)m,
∵DF+CF=CD,
∴x+3+3=x,
解得x=6+3,
∴CD=x=(6+9)m,
∴电线塔CD的高度为(6+9)m.
9.解:(1)∵AB=24 cm,BE=AB,
∴BE=×24=8(cm),∵cos 12°=,
∴BG=8cos 12° cm.
(2)∵sin 12°=,
∴EG=8sin 12° cm,
如图,延长GB、NM交于点H,
∴四边形DNHG是矩形,∴NH=DG=DE-EG=(28-8sin 12°)cm,∴HM=NH-MN=(20-8sin 12°)cm,
∵∠ABG=12°,∠ABM=147°,
∴∠FBG=135°,∴∠MBH=45°,
∴BH=HM=(20-8sin 12°)cm,
∴DN=GH=BG+BH=(8cos 12°+20-8sin 12°)cm.
单直角型
1.如图,在Rt△ABC中,∠ABC=90°,AB=4,AC=5,则cos A的值为 ( )
A. B. C. D.
2.如图1,天窗打开后,天窗边缘AC与窗框AB夹角为23°,它的示意图如图2所示.若AC长为a m,则窗角C到窗框AB的距离CD的大小为 ( )
图1 图2
A. m B. m C.acos 23° m D.asin 23° m
背靠背型
3.如图,某兴趣小组用无人机进行航拍测高,无人机从相距20 m的1号楼和2号楼的地面正中间点B垂直起飞到点A处,测得1号楼顶部E的俯角为60°,测得2号楼顶部F的俯角为45°.已知1号楼的高度为20 m,那么2号楼的高度为 m.(结果保留根号)
拥抱型
4.某地为拓宽河道和提高拦水坝,进行了现有拦水坝改造.如图所示,改造前的斜坡AB=80 m,坡度为1∶4;将斜坡AB的高度AE提高20 m(即AC=20 m)后,斜坡AB改造成斜坡CD,其坡度为1∶1.5.则改造后斜坡CD的长为 .
5.如图,在Rt△ABC中,∠ACB=90°,D是边AB的中点,BE⊥CD,垂足为点E.已知AC=6,cos A=.
(1)求线段CD的长.
(2)求cos ∠DBE的值.
母子型
6.(2024青海中考)如图,某种摄像头识别到最远点A的俯角α是17°,识别到最近点B的俯角β是45°,该摄像头安装在距地面5 m的点C处,求最远点与最近点之间的距离AB.(结果取整数,参考数据:sin 17°≈0.29,cos 17°≈0.96,tan 17°≈0.31)
牵手型
7.(2024泸州中考)如图,海中有一个小岛C,某渔船在海中的A点测得小岛C位于东北方向上,该渔船由西向东航行一段时间后到达B点,测得小岛C位于北偏西30°方向上,再沿北偏东60°方向继续航行一段时间后到达D点,这时测得小岛C位于北偏西60°方向上.已知A、C相距30 n mile.求C、D间的距离(结果保留根号).
8.某兴趣小组开展了测量电线塔高度的实践活动.如图,斜坡BE的坡度i=1∶,BE=6 m,在B处测得电线塔CD顶部D的仰角为45°,在E处测得电线塔CD顶部D的仰角为60°.
(1)求点B离水平地面的高度AB.
(2)求电线塔CD的高度(结果保留根号).
直角+矩形型
9.(2024呼和浩特中考)实验是培养学生创新能力的重要途径.如图是小亮同学安装的化学实验装置,安装要求为试管口略向下倾斜,铁夹应固定在距试管口的三分之一处.现将左侧的实验装置图抽象成右侧示意图,已知试管AB=24 cm,BE=AB,试管倾斜角∠ABG为12°.
(1)求试管口B与铁杆DE的水平距离BG的长度(结果用含非特殊角的三角函数表示).
(2)实验时,导气管紧靠水槽壁MN,延长BM交CN的延长线于点F,且MN⊥CF于点N(点C、D、N、F在一条直线上),经测得:DE=28 cm,MN=8 cm,∠ABM=147°,求线段DN的长度(结果用含非特殊角的三角函数表示).
【详解答案】
1.A 解析:∵∠ABC=90°,AB=4,
AC=5,∴cos A=.故选A.
2.D 解析:∵sin A==sin 23°,AC=a m,∴CD=AC·sin A=a sin 23°(m).故选D.
3.(50-10) 解析:如图,过点E作EG⊥AB于点G,FH⊥AB于点H,
则四边形BCEG和四边形BDFH均为矩形,∴BC=EG,HF=BD,DF=BH,由题意得CE=20 m,CD=20 m,BC=BD=10 m,∠AEG=60°,
∠AFH=45°,在Rt△AEG中,
tan ∠AEG=,∴=tan 60°=,∴AG=10=30(m),
在Rt△AFH中,
∠AHF=90°,∠AFH=45°,
∠FAH=90°-∠AFH=45°,∴AH=HF=10 m,∴DF=BH=AG+BG-AH=30+20-10=(50-10)(m),∴2号楼的高度是(50-10)m.
4.50 m 解析:在Rt△ABE中,
AB=80 m,,∴设AE=x m,BE=4x m,∴AB=x=80,∴x=80,∴AE=80 m,
∴CE=AE+AC=100 m,∵斜坡CD的坡度为1∶1.5,∴DE=150 m,由勾股定理得CD==50 m.
5.解:(1)在Rt△ABC中,∠ACB=90°,∴cos A=,∵AC=6,
∴AB=10,∵D是边AB的中点,
∴CD=AB=5.
(2)如图,过点C作CF⊥AB于点F.
∵BC==8,
∴CF=AC·BC÷AB=4.8,
∴cos ∠DCF=.
∵∠DCF=∠DBE,
∴cos ∠DBE=.
6.解:如图,由题意得CE∥AD,CD=5 m,∴∠A=α=17°,∠CBD=β=45°.
在Rt△ACD中,∵CD=5,
=tan 17°,
∴AD=≈5÷0.31≈16.1(m),
在Rt△BCD中,∵∠CBD=45°,
∴∠BCD=90°-45°=45°,
∴∠BCD=∠CBD=45°,
∴BD=CD=5 m,
∴AB=AD-BD=16.1-5=11.1≈11(m).
答:最远点与最近点之间的距离AB约是11 m.
7.解:如图,过点C作CH⊥AB于点H,
∵∠CAB=45°,AC=30 n mile,
∴AH=CH=15 n mile,
∵∠CBH=60°,
∴BC==10(n mile),
过点D作DG⊥AB交AB的延长线于点G,
∵∠DBG=180°-60°-30°-60°=30°,
∴∠BDG=60°,∴∠CDB=60°,
∴CD==20(n mile).
答:C、D间的距离为20 n mile.
8.解:(1)由题意得BA⊥AE,
∵斜坡BE的坡度i=1∶,
∴tan ∠BEA=,
∴∠BEA=30°,∵BE=6 m,
∴AB=BE=3 m,
∴点B离水平地面的高度AB为3 m.
(2)如图,过点B作BF⊥CD,垂足为F,
由题意得AB=CF=3 m,BF=AC,
由(1)得AE=AB=3 m,
设EC=x m,
∴BF=AC=AE+CE=(x+3)m,
在Rt△CDE中,∠DEC=60°,
∴CD=CE·tan 60°=x m,
在Rt△BDF中,∠DBF=45°,
∴DF=BF·tan 45°=(x+3)m,
∵DF+CF=CD,
∴x+3+3=x,
解得x=6+3,
∴CD=x=(6+9)m,
∴电线塔CD的高度为(6+9)m.
9.解:(1)∵AB=24 cm,BE=AB,
∴BE=×24=8(cm),∵cos 12°=,
∴BG=8cos 12° cm.
(2)∵sin 12°=,
∴EG=8sin 12° cm,
如图,延长GB、NM交于点H,
∴四边形DNHG是矩形,∴NH=DG=DE-EG=(28-8sin 12°)cm,∴HM=NH-MN=(20-8sin 12°)cm,
∵∠ABG=12°,∠ABM=147°,
∴∠FBG=135°,∴∠MBH=45°,
∴BH=HM=(20-8sin 12°)cm,
∴DN=GH=BG+BH=(8cos 12°+20-8sin 12°)cm.
