第25章 随机事件的概率 专题训练八 概率的综合应用(含答案)华东师大版九年级上册
文档属性
| 名称 | 第25章 随机事件的概率 专题训练八 概率的综合应用(含答案)华东师大版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 145.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 00:00:00 | ||
图片预览


文档简介
专题训练八 概率的综合应用
概率与数、式的综合
1.如图,三张完全相同的卡片正面分别标有数字符号a+1、2、3.将卡片置于暗箱摇匀后随机抽取两张,分别作为分子和分母,则所得代数式为分式的概率为 ( )
a+1 2 3
A. B. C. D.
2.用数字0,1,2,3组成个位数字与十位数字不同的两位数,其中是偶数的概率为 ( )
A. B. C. D.
概率与方程、不等式的综合
3.从-2,-1,1,2这四个数中任取一个作为a的值,再从余下的三个数中任取一个作为b的值,则不等式组有整数解的概率是 .
4.在课间活动时,有两个同学做了一个数字游戏:有三张正面写有数字-1,0,1的卡片,它们背面完全相同,将这三张卡片背面朝上洗匀后,其中一个同学随机抽取一张,将其正面的数字作为p的值,然后将卡片放回并洗匀,另一个同学再从这三张卡片中随机抽取一张,将其正面的数字作为q的值,两次结果为(p,q).
(1)请你帮他们用画树状图法或列表法表示(p,q)所有可能出现的结果.
(2)求满足关于x的方程x2+px+q=0没有实数根的概率.
概率与函数的综合
5.(2025南京鼓楼区月考)如图,有3张不透明的卡片,除正面写有不同的数字外,其他均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作一次函数y=kx+b中的k,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数y=kx+b中的b.
(1)写出k为负数的概率.
(2)求一次函数y=kx+b的图象经过第一、二、四象限的概率(用画树状图法或列表法求解).
概率与几何的综合
6.如图, ABCD的对角线AC、BD相交于点O,给出四个条件:①AB=BC;②∠ABC=90°;③OA=OB;④AC⊥BD.从所给的四个条件中任意选择两个,能判定 ABCD是正方形的概率是 ( )
A. B. C. D.
7.(2025廊坊期中)现有长度分别为2,3,4的三条线段,小明想从三条线段中选出两条与长度为5的线段组成一个三角形.
(1)请用画树状图或列表的方法,求小明选择的两条线段能与长度为5的线段组成一个三角形的概率.
(2)小明将每个组成的三角形分别画在背面相同的卡片上,将所有画有三角形的卡片洗匀然后背面朝上,从中任意抽取一张,则抽取的卡牌恰好画有直角三角形的概率为 .
概率与其他学科知识的综合
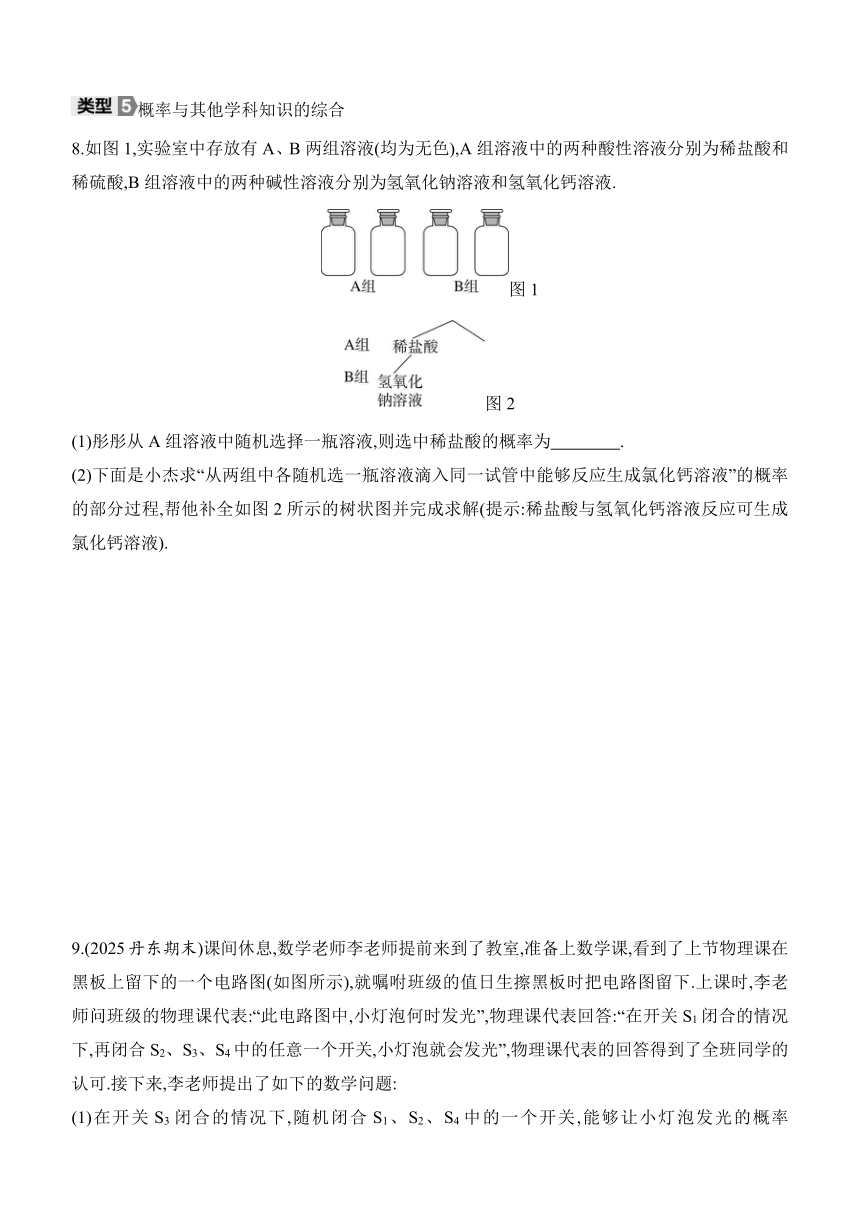
8.如图1,实验室中存放有A、B两组溶液(均为无色),A组溶液中的两种酸性溶液分别为稀盐酸和稀硫酸,B组溶液中的两种碱性溶液分别为氢氧化钠溶液和氢氧化钙溶液.
图1
图2
(1)彤彤从A组溶液中随机选择一瓶溶液,则选中稀盐酸的概率为 .
(2)下面是小杰求“从两组中各随机选一瓶溶液滴入同一试管中能够反应生成氯化钙溶液”的概率的部分过程,帮他补全如图2所示的树状图并完成求解(提示:稀盐酸与氢氧化钙溶液反应可生成氯化钙溶液).
9.(2025丹东期末)课间休息,数学老师李老师提前来到了教室,准备上数学课,看到了上节物理课在黑板上留下的一个电路图(如图所示),就嘱咐班级的值日生擦黑板时把电路图留下.上课时,李老师问班级的物理课代表:“此电路图中,小灯泡何时发光”,物理课代表回答:“在开关S1闭合的情况下,再闭合S2、S3、S4中的任意一个开关,小灯泡就会发光”,物理课代表的回答得到了全班同学的认可.接下来,李老师提出了如下的数学问题:
(1)在开关S3闭合的情况下,随机闭合S1、S2、S4中的一个开关,能够让小灯泡发光的概率为 .
(2)当随机闭合S1、S2、S3、S4中的两个开关时,请用画树状图或列表的方法求出能使小灯泡发光的概率.
【详解答案】
1.D 解析:根据题意画树状图如下:
由树状图可知,共有6种等可能的结果,其中所得代数式为分式的结果有2种,即所得代数式为分式的概率为.故选D.
2.D 解析:0不能在最高位,而且个位数字与十位数字不同,画树状图如下:
一共可以组成9个两位数,其中偶数有10、12、20、30、32,共5个,∴是偶数的概率为.故选D.
3. 解析:列表如下:
a b -2 -1 1 2
-2 — (-2,-1) (-2,1) (-2,2)
-1 (-1,-2) — (-1,1) (-1,2)
1 (1,-2) (1,-1) — (1,2)
2 (2,-2) (2,-1) (2,1) —
共有12种等可能的结果,其中满足不等式组有整数解的结果有4种,分别是(-2,1),(-2,2),(-1,1),(-1,2).所以不等式组有整数解的概率是.
4.解:(1)画树状图如图:
则共有9种等可能的结果.
(2)方程x2+px+q=0没有实数根,即Δ=p2-4q<0.
由(1)可得满足Δ=p2-4q<0的有(-1,1),(0,1),(1,1).
∴满足关于x的方程x2+px+q=0没有实数根的概率为.
5.解:(1)k为负数的概率为.
(2)画树状图如下:
共6种情况,过第一、二、四象限的有2种,∴一次函数y=kx+b的图象经过第一、二、四象限的概率为.
6.D 解析:画树状图如下:
由树状图知,共有12种等可能的结果,其中能判定 ABCD是正方形的有①②、②①、①③、③①、②④、④②、③④、④③这8种结果,∴能判定 ABCD是正方形的概率是.故选D.
7.解:(1)列表如下:
2 3 4
2 — (2,3) (2,4)
3 (3,2) — (3,4)
4 (4,2) (4,3) —
由表知,共有6种等可能的结果,其中小明选择的两条线段能与长度为5的线段组成一个三角形的有4种结果,所以小明选择的两条线段能与长度为5的线段组成一个三角形的概率为.
(2)
8.解:(1)
(2)补全树状图如图所示.
由树状图可知,共有4种等可能的结果,其中从两组中各随机选一瓶溶液滴入同一试管中能够反应生成氯化钙溶液的结果有(稀盐酸,氢氧化钙溶液),共1种,∴从两组中各随机选一瓶溶液滴入同一试管中能够反应生成氯化钙溶液的概率为.
9.解:(1)
(2)列表如下:
S1 S2 S3 S4
S1 — (S1,S2) (S1,S3) (S1,S4)
S2 (S2,S1) — (S2,S3) (S2,S4)
S3 (S3,S1) (S3,S2) — (S3,S4)
S4 (S4,S1) (S4,S2) (S4,S3) —
共有12种等可能的结果,其中能使小灯泡发光的结果有(S1,S2),(S1,S3),(S1,S4),(S2,S1),(S3,S1),(S4,S1),共6种,∴能使小灯泡发光的概率为.
概率与数、式的综合
1.如图,三张完全相同的卡片正面分别标有数字符号a+1、2、3.将卡片置于暗箱摇匀后随机抽取两张,分别作为分子和分母,则所得代数式为分式的概率为 ( )
a+1 2 3
A. B. C. D.
2.用数字0,1,2,3组成个位数字与十位数字不同的两位数,其中是偶数的概率为 ( )
A. B. C. D.
概率与方程、不等式的综合
3.从-2,-1,1,2这四个数中任取一个作为a的值,再从余下的三个数中任取一个作为b的值,则不等式组有整数解的概率是 .
4.在课间活动时,有两个同学做了一个数字游戏:有三张正面写有数字-1,0,1的卡片,它们背面完全相同,将这三张卡片背面朝上洗匀后,其中一个同学随机抽取一张,将其正面的数字作为p的值,然后将卡片放回并洗匀,另一个同学再从这三张卡片中随机抽取一张,将其正面的数字作为q的值,两次结果为(p,q).
(1)请你帮他们用画树状图法或列表法表示(p,q)所有可能出现的结果.
(2)求满足关于x的方程x2+px+q=0没有实数根的概率.
概率与函数的综合
5.(2025南京鼓楼区月考)如图,有3张不透明的卡片,除正面写有不同的数字外,其他均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作一次函数y=kx+b中的k,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数y=kx+b中的b.
(1)写出k为负数的概率.
(2)求一次函数y=kx+b的图象经过第一、二、四象限的概率(用画树状图法或列表法求解).
概率与几何的综合
6.如图, ABCD的对角线AC、BD相交于点O,给出四个条件:①AB=BC;②∠ABC=90°;③OA=OB;④AC⊥BD.从所给的四个条件中任意选择两个,能判定 ABCD是正方形的概率是 ( )
A. B. C. D.
7.(2025廊坊期中)现有长度分别为2,3,4的三条线段,小明想从三条线段中选出两条与长度为5的线段组成一个三角形.
(1)请用画树状图或列表的方法,求小明选择的两条线段能与长度为5的线段组成一个三角形的概率.
(2)小明将每个组成的三角形分别画在背面相同的卡片上,将所有画有三角形的卡片洗匀然后背面朝上,从中任意抽取一张,则抽取的卡牌恰好画有直角三角形的概率为 .
概率与其他学科知识的综合
8.如图1,实验室中存放有A、B两组溶液(均为无色),A组溶液中的两种酸性溶液分别为稀盐酸和稀硫酸,B组溶液中的两种碱性溶液分别为氢氧化钠溶液和氢氧化钙溶液.
图1
图2
(1)彤彤从A组溶液中随机选择一瓶溶液,则选中稀盐酸的概率为 .
(2)下面是小杰求“从两组中各随机选一瓶溶液滴入同一试管中能够反应生成氯化钙溶液”的概率的部分过程,帮他补全如图2所示的树状图并完成求解(提示:稀盐酸与氢氧化钙溶液反应可生成氯化钙溶液).
9.(2025丹东期末)课间休息,数学老师李老师提前来到了教室,准备上数学课,看到了上节物理课在黑板上留下的一个电路图(如图所示),就嘱咐班级的值日生擦黑板时把电路图留下.上课时,李老师问班级的物理课代表:“此电路图中,小灯泡何时发光”,物理课代表回答:“在开关S1闭合的情况下,再闭合S2、S3、S4中的任意一个开关,小灯泡就会发光”,物理课代表的回答得到了全班同学的认可.接下来,李老师提出了如下的数学问题:
(1)在开关S3闭合的情况下,随机闭合S1、S2、S4中的一个开关,能够让小灯泡发光的概率为 .
(2)当随机闭合S1、S2、S3、S4中的两个开关时,请用画树状图或列表的方法求出能使小灯泡发光的概率.
【详解答案】
1.D 解析:根据题意画树状图如下:
由树状图可知,共有6种等可能的结果,其中所得代数式为分式的结果有2种,即所得代数式为分式的概率为.故选D.
2.D 解析:0不能在最高位,而且个位数字与十位数字不同,画树状图如下:
一共可以组成9个两位数,其中偶数有10、12、20、30、32,共5个,∴是偶数的概率为.故选D.
3. 解析:列表如下:
a b -2 -1 1 2
-2 — (-2,-1) (-2,1) (-2,2)
-1 (-1,-2) — (-1,1) (-1,2)
1 (1,-2) (1,-1) — (1,2)
2 (2,-2) (2,-1) (2,1) —
共有12种等可能的结果,其中满足不等式组有整数解的结果有4种,分别是(-2,1),(-2,2),(-1,1),(-1,2).所以不等式组有整数解的概率是.
4.解:(1)画树状图如图:
则共有9种等可能的结果.
(2)方程x2+px+q=0没有实数根,即Δ=p2-4q<0.
由(1)可得满足Δ=p2-4q<0的有(-1,1),(0,1),(1,1).
∴满足关于x的方程x2+px+q=0没有实数根的概率为.
5.解:(1)k为负数的概率为.
(2)画树状图如下:
共6种情况,过第一、二、四象限的有2种,∴一次函数y=kx+b的图象经过第一、二、四象限的概率为.
6.D 解析:画树状图如下:
由树状图知,共有12种等可能的结果,其中能判定 ABCD是正方形的有①②、②①、①③、③①、②④、④②、③④、④③这8种结果,∴能判定 ABCD是正方形的概率是.故选D.
7.解:(1)列表如下:
2 3 4
2 — (2,3) (2,4)
3 (3,2) — (3,4)
4 (4,2) (4,3) —
由表知,共有6种等可能的结果,其中小明选择的两条线段能与长度为5的线段组成一个三角形的有4种结果,所以小明选择的两条线段能与长度为5的线段组成一个三角形的概率为.
(2)
8.解:(1)
(2)补全树状图如图所示.
由树状图可知,共有4种等可能的结果,其中从两组中各随机选一瓶溶液滴入同一试管中能够反应生成氯化钙溶液的结果有(稀盐酸,氢氧化钙溶液),共1种,∴从两组中各随机选一瓶溶液滴入同一试管中能够反应生成氯化钙溶液的概率为.
9.解:(1)
(2)列表如下:
S1 S2 S3 S4
S1 — (S1,S2) (S1,S3) (S1,S4)
S2 (S2,S1) — (S2,S3) (S2,S4)
S3 (S3,S1) (S3,S2) — (S3,S4)
S4 (S4,S1) (S4,S2) (S4,S3) —
共有12种等可能的结果,其中能使小灯泡发光的结果有(S1,S2),(S1,S3),(S1,S4),(S2,S1),(S3,S1),(S4,S1),共6种,∴能使小灯泡发光的概率为.
