北师大版数学八年级上册1.1 第2课时 勾股定理的验证及其简单应用 课件(共19张PPT)
文档属性
| 名称 | 北师大版数学八年级上册1.1 第2课时 勾股定理的验证及其简单应用 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 22:46:04 | ||
图片预览

文档简介
(共19张PPT)
1.1 探索勾股定理
第2课时 勾股定理的验证
及其简单应用
第一章 勾股定理
北师大版2024·八年级上册
学 习 目 标
1
2
1.学会用几种方法验证勾股定理.(重点)
2.能够运用勾股定理解决简单问题.(重点,难点)
知识回顾
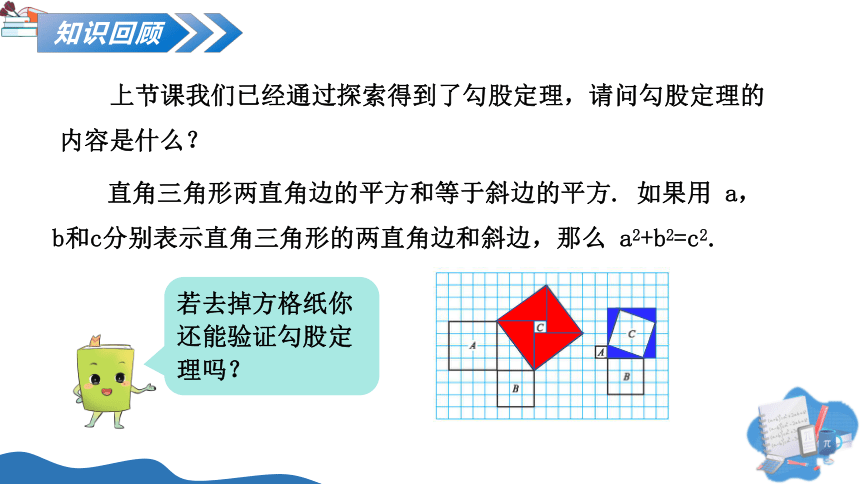
上节课我们已经通过探索得到了勾股定理,请问勾股定理的内容是什么?
直角三角形两直角边的平方和等于斜边的平方. 如果用 a,b和c分别表示直角三角形的两直角边和斜边,那么 a2+b2=c2.
若去掉方格纸你还能验证勾股定理吗?
情境导入
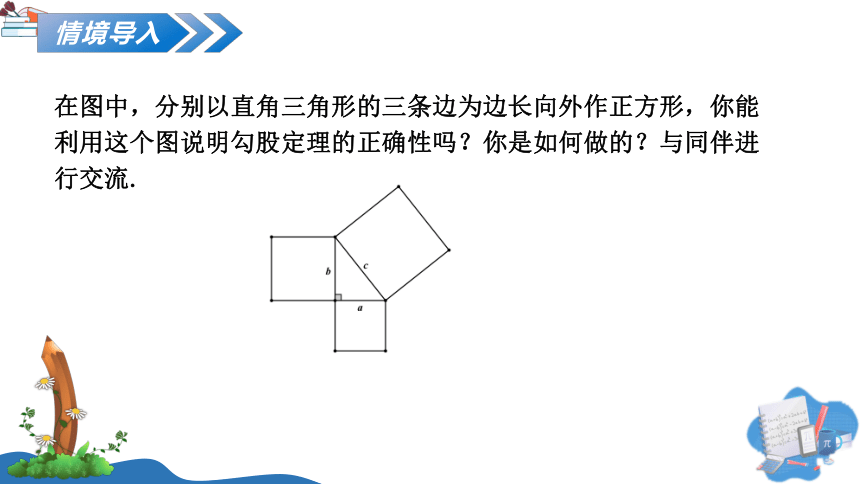
在图中,分别以直角三角形的三条边为边长向外作正方形,你能利用这个图说明勾股定理的正确性吗?你是如何做的?与同伴进行交流.
新知探究
a
a
a
a
b
b
b
b
c
c
c
c
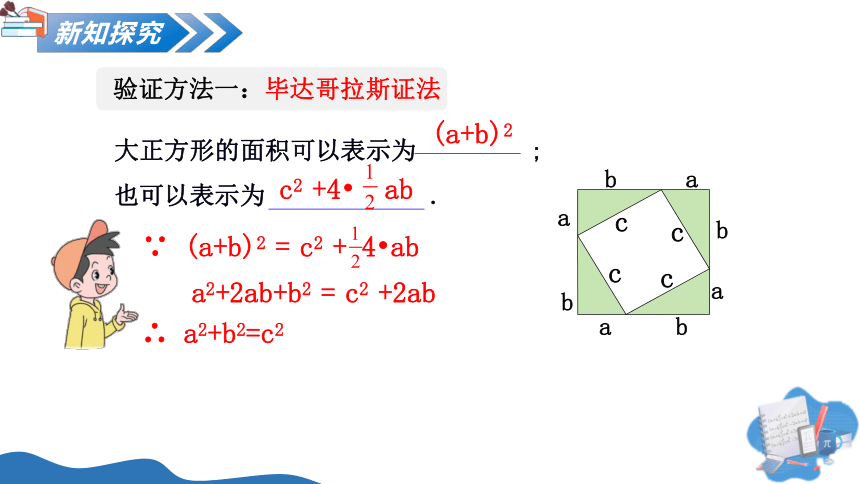
验证方法一:毕达哥拉斯证法
大正方形的面积可以表示为 ;
也可以表示为 .
(a+b)2
c2 +4 ab
∵ (a+b)2 = c2 + 4 ab
a2+2ab+b2 = c2 +2ab
∴ a2+b2=c2
新知探究
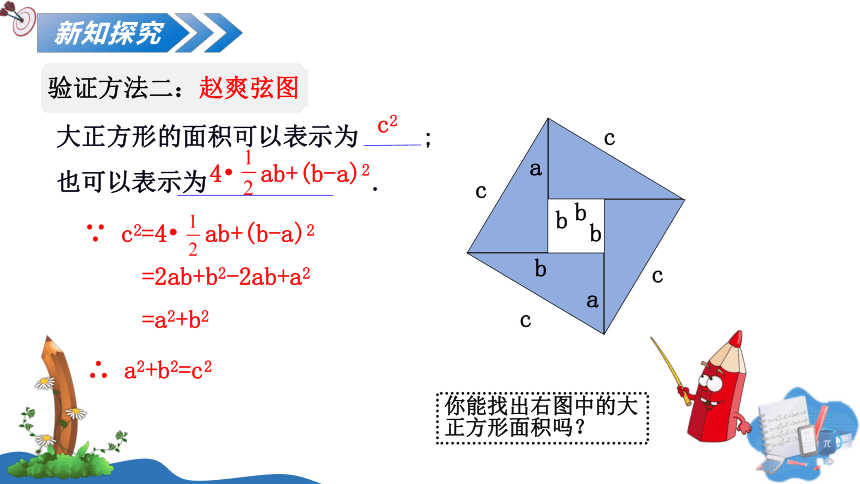
你能找出右图中的大正方形面积吗?
c
a
b
c
a
b
验证方法二:赵爽弦图
b
c
a
b
c
大正方形的面积可以表示为 ;
也可以表示为 .
∵ c2=4 ab+(b-a)2
=2ab+b2-2ab+a2
=a2+b2
∴ a2+b2=c2
c2
4 ab+(b-a)2
新知探究
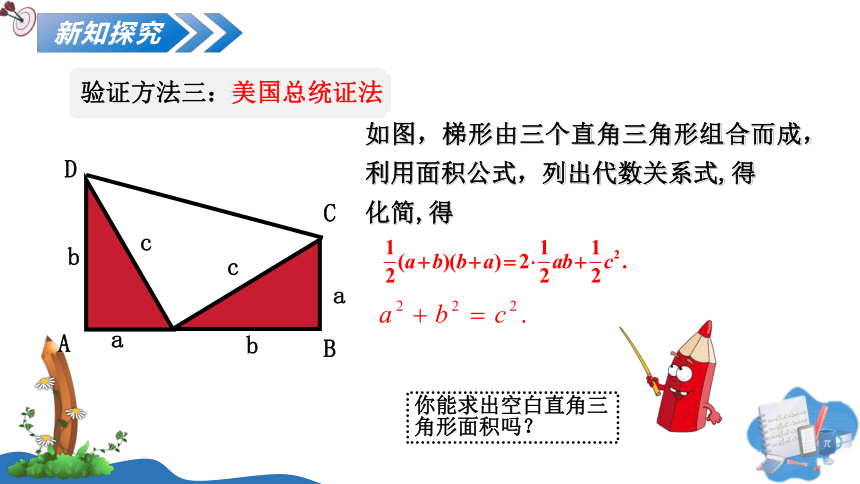
你能求出空白直角三角形面积吗?
b
c
a
b
c
a
A
B
C
D
如图,梯形由三个直角三角形组合而成,利用面积公式,列出代数关系式,得
化简,得
验证方法三:美国总统证法
新知探究
总统证法
刘徽证法
欧几里得法
新知探究
勾股定理在数学发展中起到了重大的作用,其证明方法据说有 400多种,有兴趣的同学可以继续研究,或到网上查阅勾股定理的相关资料.
典例分析
你能根据题意画出图形吗?在你画的图形中存在一个怎样的三角形?
方法技巧
解 析
例1.我方侦查员小王在距离东西向公路400m处侦查,发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距400m,10s后,汽车与他相距500m,你能帮小王计算敌方汽车的速度吗
公路
B
C
A
400m
500m
解:由勾股定理,可以得到
AB2 = BC2 + AC2,
也就是5002 = BC2 + 4002,
所以BC = 300.
敌方汽车10s行驶了300 m,那么它1 h行驶的距离为300×6×60=108000(m),
即它行驶的速度为 108 km/h.
典例分析
通过“作垂线”构造直角三角形是利用勾股定理解决实际问题常用的添加辅助线的方法.
方法技巧
例2.如图,有两棵树,一棵高10m,另一棵高4m,一只小鸟从一棵树的树梢飞到另一棵树的树梢的直线距离是 10 m,求两树相隔的距离.
典例分析
解:如图,过点 D 作 DE ⊥ AB 于点 E.
由题意知,AB=10 m,CD=4 m,AD=10 m,
易知 BE=CD=4 m,所以 AE=10-4=6(m) .
在Rt△AED 中,由勾股定理得
DE2=AD2-AE2=102-62=82,
所以 DE=8 m. 所以易得BC=DE=8 m.
所以两树相隔的距离为 8 m.
方法技巧
注意审题,找重点,在直角三角形中,用勾股定理求解;
勾股定理在实际生活中的运用
题型一
题型探究
小明
例3.某条例规定小汽车在城街路上行驶速度不得超过 70 km/h.如图,一辆小汽车在一条城街路上沿直线由东向西匀速行驶,某一时刻刚好行驶到路面车速检测仪 A 处的正前方 30 m 的 C 处,过了 2 s 后,测得小汽车在 B 处与车速检测仪 A 间距离为 50 m,这辆小汽车超速了吗?请通过计算进行说明.
方法技巧
注意审题,找重点,在直角三角形中,用勾股定理求解;
勾股定理在实际生活中的运用
题型一
题型探究
小明
解:在 Rt△ABC中,∠C=90°,AC=30 m,AB=50 m.
根据勾股定理,得 BC2=AB2-AC2=502-302=1600,
所以 BC = 40 m.
因为小汽车 2 s 行驶了40 m,
所以它的速度为 = 20 m/s.
因为 20 m/s = 72 km/h,且 72 >70,
所以这辆小汽车超速了.
40
2
课堂小结
勾股定理的验证及其简单应用
拼图验证
应用
1.拼出图形
2.写出图形面积的表达式
3.找出相等关系
4.导出勾股定理
变式训练
1.湖的两端有 A、B 两点,从与 BA 方向成直角的 BC 方向上的点 C 测得 CA = 130 米,CB = 120 米,则 AB 为 ( )
A
B
C
A. 50 米 B. 120 米 C. 100 米 D. 130 米
130
120
A
变式训练
2.如图,小亮将升旗的绳子拉到旗杆 AB 的底端 B 处,绳子末端刚好接触到地面,然后将绳子末端拉到点 D 处,发 现 此 时点 D 到 旗 杆AB 的水平距离为 8 m,点 D 到地面的距离 CD为 2 m,则 旗 杆 AB 的高度为( )
A.23 m B.17 m
C.15 m D.10 m
B
变式训练
3.如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,AD=13m,∠B=∠ACD=90°.小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问铺满这块空地共需花费多少元?
解:在Rt△ABC中,由勾股定理,
得 AC2=AB2+BC2,∴AC=5m,
在Rt△ACD中,由勾股定理,
得 CD2=AD2-AC2,∴CD=12m,
S草坪=SRt△ABC+SRt△ACD= AB BC+ AC DC = (3×4+5×12)=36 m2.
故需要的费用为36×100=3600元.
感谢聆听!
1.1 探索勾股定理
第2课时 勾股定理的验证
及其简单应用
第一章 勾股定理
北师大版2024·八年级上册
学 习 目 标
1
2
1.学会用几种方法验证勾股定理.(重点)
2.能够运用勾股定理解决简单问题.(重点,难点)
知识回顾
上节课我们已经通过探索得到了勾股定理,请问勾股定理的内容是什么?
直角三角形两直角边的平方和等于斜边的平方. 如果用 a,b和c分别表示直角三角形的两直角边和斜边,那么 a2+b2=c2.
若去掉方格纸你还能验证勾股定理吗?
情境导入
在图中,分别以直角三角形的三条边为边长向外作正方形,你能利用这个图说明勾股定理的正确性吗?你是如何做的?与同伴进行交流.
新知探究
a
a
a
a
b
b
b
b
c
c
c
c
验证方法一:毕达哥拉斯证法
大正方形的面积可以表示为 ;
也可以表示为 .
(a+b)2
c2 +4 ab
∵ (a+b)2 = c2 + 4 ab
a2+2ab+b2 = c2 +2ab
∴ a2+b2=c2
新知探究
你能找出右图中的大正方形面积吗?
c
a
b
c
a
b
验证方法二:赵爽弦图
b
c
a
b
c
大正方形的面积可以表示为 ;
也可以表示为 .
∵ c2=4 ab+(b-a)2
=2ab+b2-2ab+a2
=a2+b2
∴ a2+b2=c2
c2
4 ab+(b-a)2
新知探究
你能求出空白直角三角形面积吗?
b
c
a
b
c
a
A
B
C
D
如图,梯形由三个直角三角形组合而成,利用面积公式,列出代数关系式,得
化简,得
验证方法三:美国总统证法
新知探究
总统证法
刘徽证法
欧几里得法
新知探究
勾股定理在数学发展中起到了重大的作用,其证明方法据说有 400多种,有兴趣的同学可以继续研究,或到网上查阅勾股定理的相关资料.
典例分析
你能根据题意画出图形吗?在你画的图形中存在一个怎样的三角形?
方法技巧
解 析
例1.我方侦查员小王在距离东西向公路400m处侦查,发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距400m,10s后,汽车与他相距500m,你能帮小王计算敌方汽车的速度吗
公路
B
C
A
400m
500m
解:由勾股定理,可以得到
AB2 = BC2 + AC2,
也就是5002 = BC2 + 4002,
所以BC = 300.
敌方汽车10s行驶了300 m,那么它1 h行驶的距离为300×6×60=108000(m),
即它行驶的速度为 108 km/h.
典例分析
通过“作垂线”构造直角三角形是利用勾股定理解决实际问题常用的添加辅助线的方法.
方法技巧
例2.如图,有两棵树,一棵高10m,另一棵高4m,一只小鸟从一棵树的树梢飞到另一棵树的树梢的直线距离是 10 m,求两树相隔的距离.
典例分析
解:如图,过点 D 作 DE ⊥ AB 于点 E.
由题意知,AB=10 m,CD=4 m,AD=10 m,
易知 BE=CD=4 m,所以 AE=10-4=6(m) .
在Rt△AED 中,由勾股定理得
DE2=AD2-AE2=102-62=82,
所以 DE=8 m. 所以易得BC=DE=8 m.
所以两树相隔的距离为 8 m.
方法技巧
注意审题,找重点,在直角三角形中,用勾股定理求解;
勾股定理在实际生活中的运用
题型一
题型探究
小明
例3.某条例规定小汽车在城街路上行驶速度不得超过 70 km/h.如图,一辆小汽车在一条城街路上沿直线由东向西匀速行驶,某一时刻刚好行驶到路面车速检测仪 A 处的正前方 30 m 的 C 处,过了 2 s 后,测得小汽车在 B 处与车速检测仪 A 间距离为 50 m,这辆小汽车超速了吗?请通过计算进行说明.
方法技巧
注意审题,找重点,在直角三角形中,用勾股定理求解;
勾股定理在实际生活中的运用
题型一
题型探究
小明
解:在 Rt△ABC中,∠C=90°,AC=30 m,AB=50 m.
根据勾股定理,得 BC2=AB2-AC2=502-302=1600,
所以 BC = 40 m.
因为小汽车 2 s 行驶了40 m,
所以它的速度为 = 20 m/s.
因为 20 m/s = 72 km/h,且 72 >70,
所以这辆小汽车超速了.
40
2
课堂小结
勾股定理的验证及其简单应用
拼图验证
应用
1.拼出图形
2.写出图形面积的表达式
3.找出相等关系
4.导出勾股定理
变式训练
1.湖的两端有 A、B 两点,从与 BA 方向成直角的 BC 方向上的点 C 测得 CA = 130 米,CB = 120 米,则 AB 为 ( )
A
B
C
A. 50 米 B. 120 米 C. 100 米 D. 130 米
130
120
A
变式训练
2.如图,小亮将升旗的绳子拉到旗杆 AB 的底端 B 处,绳子末端刚好接触到地面,然后将绳子末端拉到点 D 处,发 现 此 时点 D 到 旗 杆AB 的水平距离为 8 m,点 D 到地面的距离 CD为 2 m,则 旗 杆 AB 的高度为( )
A.23 m B.17 m
C.15 m D.10 m
B
变式训练
3.如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,AD=13m,∠B=∠ACD=90°.小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问铺满这块空地共需花费多少元?
解:在Rt△ABC中,由勾股定理,
得 AC2=AB2+BC2,∴AC=5m,
在Rt△ACD中,由勾股定理,
得 CD2=AD2-AC2,∴CD=12m,
S草坪=SRt△ABC+SRt△ACD= AB BC+ AC DC = (3×4+5×12)=36 m2.
故需要的费用为36×100=3600元.
感谢聆听!
同课章节目录
