北师大2025版数学八年级上册 1.2 一定是直角三角形吗 课件(共23张PPT)
文档属性
| 名称 | 北师大2025版数学八年级上册 1.2 一定是直角三角形吗 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-08 00:00:00 | ||
图片预览



文档简介
(共23张PPT)
1.2 一定是直角三角形吗
第一章 勾股定理
北师大版2024·八年级上册
章节导读
1.1.1探索勾股定理
1.1.2 验证勾股定理
1.2一定是直角三角形吗?
1.3勾股定理的应用
勾股定理的初步认识
利用勾股定理进行计算
勾股定理的简单应用
勾股定理的验证
勾股定理的逆定理
勾股数
立体图形中两点之间的最短距离
勾股定理的实际应用
学 习 目 标
1
2
1.探索并证明勾股定理的逆定理.
2.能运用勾股定理的逆定理判定三角形是直角三角形.
知识回顾
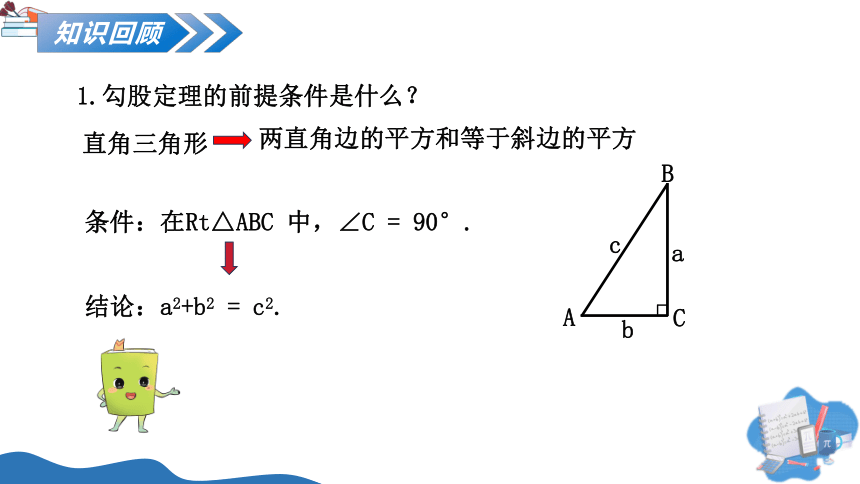
1.勾股定理的前提条件是什么?
直角三角形
两直角边的平方和等于斜边的平方
条件:在Rt△ABC 中,∠C = 90°.
结论:a2+b2 = c2.
A
B
C
c
a
b
知识回顾
A
B
C
c
a
b
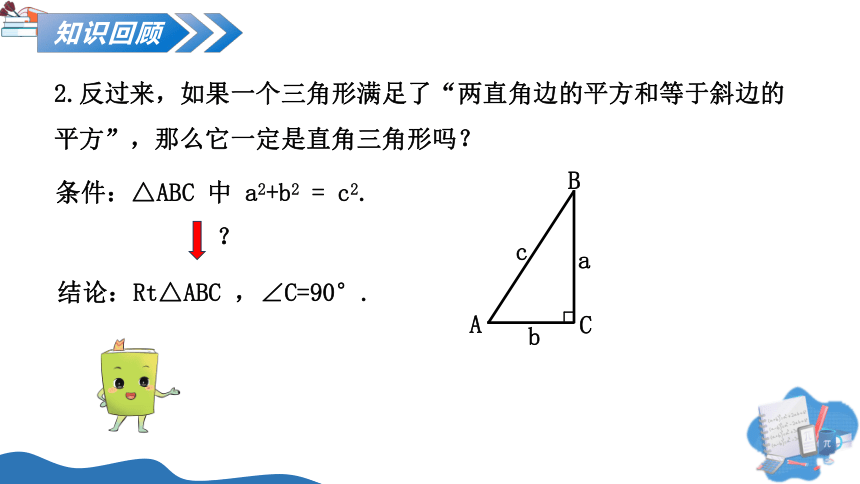
2.反过来,如果一个三角形满足了“两直角边的平方和等于斜边的平方”,那么它一定是直角三角形吗?
条件:△ABC 中 a2+b2 = c2.
?
结论:Rt△ABC ,∠C=90°.
新知探究
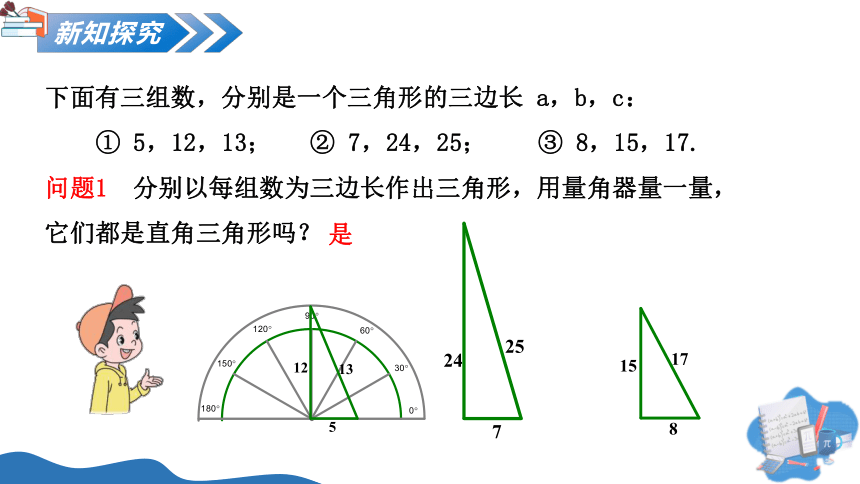
下面有三组数,分别是一个三角形的三边长 a,b,c:
① 5,12,13; ② 7,24,25; ③ 8,15,17.
问题1 分别以每组数为三边长作出三角形,用量角器量一量,它们都是直角三角形吗?
是
新知探究
这三组数在数量关系上有什么相同点?
下面有三组数分别是一个三角形的三边长 a,b,c:
① 5,12,13; ② 7,24,25; ③ 8,15,17.
① 5,12,13 满足 52 + 122 = 132,② 7,24,25 满足 72 + 242 = 252,
③ 8,15,17 满足 82 + 152 = 172.
a2 + b2 = c2
新知探究
思考:从上述问题中,能发现什么结论吗?
如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
我觉得这个猜想不准确,因为测量结果可能有误差.
我也觉得猜想不严谨,前面我们只取了几组数据,不能由部分代表整体.
新知探究
?
A
B
C
a
b
c
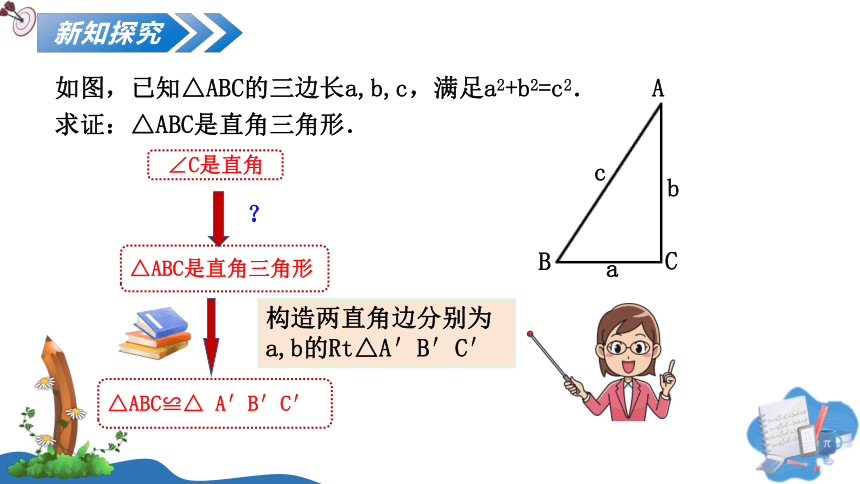
如图,已知△ABC的三边长a,b,c,满足a2+b2=c2.
求证:△ABC是直角三角形.
构造两直角边分别为a,b的Rt△A′B′C′
∠C是直角
△ABC是直角三角形
△ABC≌△ A′B′C′
新知探究
简要说明:
作一个直角∠MC1N,
在 C1M 上截取 C1B1 = a = CB,
在 C1N 上截取 C1A1 = b = CA,
连接 A1B1.
在 Rt△A1C1B1中,由勾股定理,得 A1B12 = a2 + b2 = AB2.
所以 A1B1 = AB. 所以△ABC≌△A1B1C1 (SSS).
所以∠C =∠C1 = 90°.
所以△ABC 是直角三角形.
a
c
b
A
C
B
b
C1
M
N
B1
A1
新知探究
勾股定理的逆定理:
如果三角形的三边长 a ,b ,c 满足a2+b2 =c2,
那么这个三角形是直角三角形.
A
C
B
a
b
c
特别说明:
符号语言:
在△ABC 中,若 a2 + b2 = c2
则△ABC 是直角三角形.
新知探究
满足 a2 + b2 = c2 的三个正整数,称为勾股数.
A
B
C
c
a
b
常见的勾股数:
3,4,5;5,12,13;6,8,10;7,24,25;8,15,17;9,40,41等等.
勾股数拓展性质:
一组勾股数,都扩大相同倍数 k(k 为正整数),得到一组新数,这组数同样是勾股数.
典例分析
你能根据题意画出图形吗?在你画的图形中存在一个怎样的三角形?
方法技巧
例1.一个零件的形状如图 1 所示,按规定这个零件中∠A 和∠DBC 都应为直角,工人师傅量得这个零件各边的尺寸如图 2 所示,这个零件符合要求吗
D
A
B
C
4
3
5
13
12
D
A
B
C
图1
图2
典例分析
解:在△ABD中,AB2 + AD2 = 9+16= 25=BD2,
所以△ABD 是直角三角形,∠A 是直角.
在△BCD 中,BD2 + BC2 = 25+144=169 = CD2,
所以△BCD 是直角三角形,∠DBC 是直角.
因此,这个零件符合要求.
D
A
B
C
4
3
5
13
12
典例分析
根据勾股定理及其逆定理,判断一个三角形是不是直角三角形,只要看两条较小边长的平方和是否等于最大边长的平方.
方法技巧
例2.下面以 a,b,c 为边长的三角形是不是直角三角形?如果是,那么哪一个角是直角?
(1) a = 15,b = 8,c = 17;
解:因为 152+82 = 289,172 = 289,所以 152+82 = 172,根据勾股定理的逆定理,这个三角形是直角三角形,且∠C 是直角.
(2) a = 13,b = 14,c = 15;
解:因为 132 + 142 = 365,152 = 225,所以 132 + 142 ≠ 152,不符合勾股定理的逆定理,所以这个三角形不是直角三角形.
典例分析
根据勾股定理及其逆定理,判断一个三角形是不是直角三角形,只要看两条较小边长的平方和是否等于最大边长的平方.
方法技巧
例2.下面以 a,b,c 为边长的三角形是不是直角三角形?如果是,那么哪一个角是直角?
(3) a∶b∶c = 3∶4∶5.
解:设 a = 3k,b = 4k,c = 5k。
因为 a2 + b2 = (3k)2 + (4k)2 = 25k2,c2 = (5k)2 = 25k2,
所以 a2 + b2 = c2,根据勾股定理的逆定理,这个三角形是直角三角形,∠C 是直角.
小明
方法技巧
利用勾股定理的逆定理,找出三边之间的关系,并求求CD的长
利用勾股定理及其逆定理求线段长
题型一
题型探究
小明
例3.如图,在△ABC 中,D 为 BC 边上的一点,已知AB=13,AD=12,AC=15,BD=5,求 CD 的长.
A
B
D
C
勾股定理的逆定理
△ABD为直角三角形
△ACD为直角三角形
求CD
方法技巧
勾股定理在实际生活中的运用
题型一
题型探究
小明
解:因为AB =13,AD =12,BD=5,
所以 AD2+BD2 =122+52=169=132=AB2.
所以△ABD 是直角三角形,∠ADB = 90°.
所以∠ADC = 180°-∠ADB= 90°.
所以△ACD 是直角三角形.
根据勾股定理,
得 CD2 =AC2-AD2=152-122=81,
所以 CD = 9.
A
B
D
C
利用勾股定理的逆定理,找出三边之间的关系,并求求CD的长
课堂小结
一定是直角三角形吗
勾股定理的逆定理:如果三角形的三边长 a,b,c 满足a2 + b2 = c2,
那么这个三角形是直角三角形
勾股数:满足 a2 + b2 = c2 的三个正整数 a,b,c
变式训练
1.将直角三角形的三边长扩大同样的倍数,则得到的三角形( )
A.是直角三角形 B.可能是锐角三角形
C.可能是钝角三角形 D.不可能是直角三角形
A
变式训练
2.若△ABC 的三边 a,b,c满足a2 +b2 +c2 +50=6a+8b+10c. 试判断 △ABC 的形状.
解:因为 a2 + b2 + c2 + 50 = 6a + 8b + 10c,
所以 a2 - 6a + 9 + b2 -8b+16+c2 -10c+25=0,
即 (a-3) + (b-4) + (c-5) = 0.
所以 a = 3,b = 4,c = 5.
所以 a2 + b2 = c2.
所以△ABC 是直角三角形.
变式训练
3.如图,四边形ABCD中,AB⊥AD,已知AD=3cm,AB=4cm,CD=12cm,BC=13cm,求四边形ABCD的面积.
解:连接BD.
在Rt△ABD中,由勾股定理,
得 BD2=AB2+AD2,∴BD=5m,
又∵ CD=12cm,BC=13cm
∴ BC2=CD2+BD2,∴△BDC是直角三角形.
S四边形ABCD=SRt△BCD-SRt△ABD = BD CD- AB AD
= (5×12-3×4)=24 m2.
C
B
A
D
感谢聆听!
1.2 一定是直角三角形吗
第一章 勾股定理
北师大版2024·八年级上册
章节导读
1.1.1探索勾股定理
1.1.2 验证勾股定理
1.2一定是直角三角形吗?
1.3勾股定理的应用
勾股定理的初步认识
利用勾股定理进行计算
勾股定理的简单应用
勾股定理的验证
勾股定理的逆定理
勾股数
立体图形中两点之间的最短距离
勾股定理的实际应用
学 习 目 标
1
2
1.探索并证明勾股定理的逆定理.
2.能运用勾股定理的逆定理判定三角形是直角三角形.
知识回顾
1.勾股定理的前提条件是什么?
直角三角形
两直角边的平方和等于斜边的平方
条件:在Rt△ABC 中,∠C = 90°.
结论:a2+b2 = c2.
A
B
C
c
a
b
知识回顾
A
B
C
c
a
b
2.反过来,如果一个三角形满足了“两直角边的平方和等于斜边的平方”,那么它一定是直角三角形吗?
条件:△ABC 中 a2+b2 = c2.
?
结论:Rt△ABC ,∠C=90°.
新知探究
下面有三组数,分别是一个三角形的三边长 a,b,c:
① 5,12,13; ② 7,24,25; ③ 8,15,17.
问题1 分别以每组数为三边长作出三角形,用量角器量一量,它们都是直角三角形吗?
是
新知探究
这三组数在数量关系上有什么相同点?
下面有三组数分别是一个三角形的三边长 a,b,c:
① 5,12,13; ② 7,24,25; ③ 8,15,17.
① 5,12,13 满足 52 + 122 = 132,② 7,24,25 满足 72 + 242 = 252,
③ 8,15,17 满足 82 + 152 = 172.
a2 + b2 = c2
新知探究
思考:从上述问题中,能发现什么结论吗?
如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
我觉得这个猜想不准确,因为测量结果可能有误差.
我也觉得猜想不严谨,前面我们只取了几组数据,不能由部分代表整体.
新知探究
?
A
B
C
a
b
c
如图,已知△ABC的三边长a,b,c,满足a2+b2=c2.
求证:△ABC是直角三角形.
构造两直角边分别为a,b的Rt△A′B′C′
∠C是直角
△ABC是直角三角形
△ABC≌△ A′B′C′
新知探究
简要说明:
作一个直角∠MC1N,
在 C1M 上截取 C1B1 = a = CB,
在 C1N 上截取 C1A1 = b = CA,
连接 A1B1.
在 Rt△A1C1B1中,由勾股定理,得 A1B12 = a2 + b2 = AB2.
所以 A1B1 = AB. 所以△ABC≌△A1B1C1 (SSS).
所以∠C =∠C1 = 90°.
所以△ABC 是直角三角形.
a
c
b
A
C
B
b
C1
M
N
B1
A1
新知探究
勾股定理的逆定理:
如果三角形的三边长 a ,b ,c 满足a2+b2 =c2,
那么这个三角形是直角三角形.
A
C
B
a
b
c
特别说明:
符号语言:
在△ABC 中,若 a2 + b2 = c2
则△ABC 是直角三角形.
新知探究
满足 a2 + b2 = c2 的三个正整数,称为勾股数.
A
B
C
c
a
b
常见的勾股数:
3,4,5;5,12,13;6,8,10;7,24,25;8,15,17;9,40,41等等.
勾股数拓展性质:
一组勾股数,都扩大相同倍数 k(k 为正整数),得到一组新数,这组数同样是勾股数.
典例分析
你能根据题意画出图形吗?在你画的图形中存在一个怎样的三角形?
方法技巧
例1.一个零件的形状如图 1 所示,按规定这个零件中∠A 和∠DBC 都应为直角,工人师傅量得这个零件各边的尺寸如图 2 所示,这个零件符合要求吗
D
A
B
C
4
3
5
13
12
D
A
B
C
图1
图2
典例分析
解:在△ABD中,AB2 + AD2 = 9+16= 25=BD2,
所以△ABD 是直角三角形,∠A 是直角.
在△BCD 中,BD2 + BC2 = 25+144=169 = CD2,
所以△BCD 是直角三角形,∠DBC 是直角.
因此,这个零件符合要求.
D
A
B
C
4
3
5
13
12
典例分析
根据勾股定理及其逆定理,判断一个三角形是不是直角三角形,只要看两条较小边长的平方和是否等于最大边长的平方.
方法技巧
例2.下面以 a,b,c 为边长的三角形是不是直角三角形?如果是,那么哪一个角是直角?
(1) a = 15,b = 8,c = 17;
解:因为 152+82 = 289,172 = 289,所以 152+82 = 172,根据勾股定理的逆定理,这个三角形是直角三角形,且∠C 是直角.
(2) a = 13,b = 14,c = 15;
解:因为 132 + 142 = 365,152 = 225,所以 132 + 142 ≠ 152,不符合勾股定理的逆定理,所以这个三角形不是直角三角形.
典例分析
根据勾股定理及其逆定理,判断一个三角形是不是直角三角形,只要看两条较小边长的平方和是否等于最大边长的平方.
方法技巧
例2.下面以 a,b,c 为边长的三角形是不是直角三角形?如果是,那么哪一个角是直角?
(3) a∶b∶c = 3∶4∶5.
解:设 a = 3k,b = 4k,c = 5k。
因为 a2 + b2 = (3k)2 + (4k)2 = 25k2,c2 = (5k)2 = 25k2,
所以 a2 + b2 = c2,根据勾股定理的逆定理,这个三角形是直角三角形,∠C 是直角.
小明
方法技巧
利用勾股定理的逆定理,找出三边之间的关系,并求求CD的长
利用勾股定理及其逆定理求线段长
题型一
题型探究
小明
例3.如图,在△ABC 中,D 为 BC 边上的一点,已知AB=13,AD=12,AC=15,BD=5,求 CD 的长.
A
B
D
C
勾股定理的逆定理
△ABD为直角三角形
△ACD为直角三角形
求CD
方法技巧
勾股定理在实际生活中的运用
题型一
题型探究
小明
解:因为AB =13,AD =12,BD=5,
所以 AD2+BD2 =122+52=169=132=AB2.
所以△ABD 是直角三角形,∠ADB = 90°.
所以∠ADC = 180°-∠ADB= 90°.
所以△ACD 是直角三角形.
根据勾股定理,
得 CD2 =AC2-AD2=152-122=81,
所以 CD = 9.
A
B
D
C
利用勾股定理的逆定理,找出三边之间的关系,并求求CD的长
课堂小结
一定是直角三角形吗
勾股定理的逆定理:如果三角形的三边长 a,b,c 满足a2 + b2 = c2,
那么这个三角形是直角三角形
勾股数:满足 a2 + b2 = c2 的三个正整数 a,b,c
变式训练
1.将直角三角形的三边长扩大同样的倍数,则得到的三角形( )
A.是直角三角形 B.可能是锐角三角形
C.可能是钝角三角形 D.不可能是直角三角形
A
变式训练
2.若△ABC 的三边 a,b,c满足a2 +b2 +c2 +50=6a+8b+10c. 试判断 △ABC 的形状.
解:因为 a2 + b2 + c2 + 50 = 6a + 8b + 10c,
所以 a2 - 6a + 9 + b2 -8b+16+c2 -10c+25=0,
即 (a-3) + (b-4) + (c-5) = 0.
所以 a = 3,b = 4,c = 5.
所以 a2 + b2 = c2.
所以△ABC 是直角三角形.
变式训练
3.如图,四边形ABCD中,AB⊥AD,已知AD=3cm,AB=4cm,CD=12cm,BC=13cm,求四边形ABCD的面积.
解:连接BD.
在Rt△ABD中,由勾股定理,
得 BD2=AB2+AD2,∴BD=5m,
又∵ CD=12cm,BC=13cm
∴ BC2=CD2+BD2,∴△BDC是直角三角形.
S四边形ABCD=SRt△BCD-SRt△ABD = BD CD- AB AD
= (5×12-3×4)=24 m2.
C
B
A
D
感谢聆听!
同课章节目录
