北师大2025版数学八年级上册 2.1 第2课时 认识实数 课件(共19张PPT)
文档属性
| 名称 | 北师大2025版数学八年级上册 2.1 第2课时 认识实数 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-08 09:25:44 | ||
图片预览




文档简介
(共19张PPT)
2.1 认识实数
第2课时 认识实数
第二章 实数
北师大版2024·八年级上册
学 习 目 标
1
2
通过拼图活动,感受无理数产生的实际背景和引入的必要性.
借助计算器探索无理数是无限不循环小数并从中体会无限逼近的思想.
3
会判断一个数是有理数还是无理数.
知识回顾
有理数进行分类:
正整数
零
负整数
正分数
负分数
有理数
分数
整数
有理数包括整数和分数,那么有理数范围是否能满足我们实际生活的需要呢?
新知探究
把下列各数表示成小数,你发现了什么?
3,
=0.8
=0.5
·
= 0.18
··
=﹣0.17
·
3=3.0
有理数总可以用有限小数或无限循环小数表示.反过来,任何有限小数或无限循环小数也都是有理数.
新知探究
如圆周率π=3.14159265…也是一个无限不循环小数,因此它也是一个无理数.再如0.5858858885…(相邻两个5之间8的个数逐次加1)也是无理数.
而能化成有限小数或循环小数,这些数都是有理数.
无限不循环小数称为无理数.
结论
想一想:你能找到其他的无理数吗?
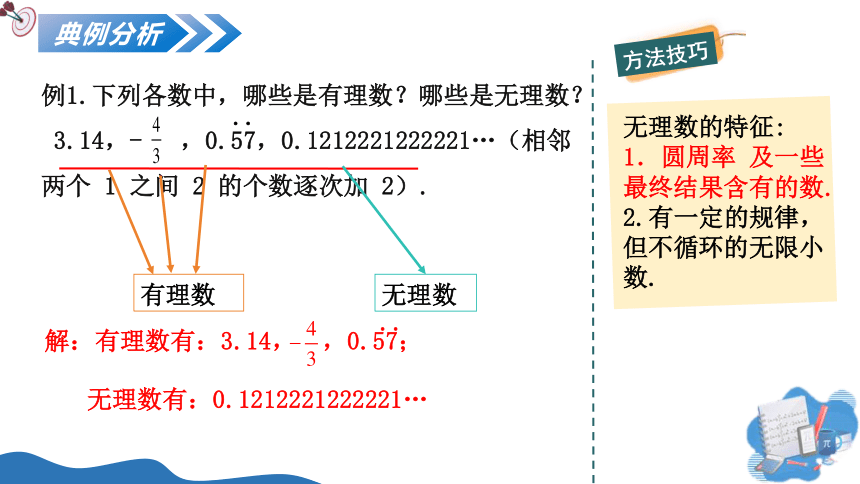
典例分析
无理数的特征:
1.圆周率 及一些最终结果含有的数.
2.有一定的规律,但不循环的无限小数.
方法技巧
例1.下列各数中,哪些是有理数?哪些是无理数?
3.14,- ,0.57,0.1212221222221…(相邻两个 1 之间 2 的个数逐次加 2).
..
解:有理数有:3.14, ,0.57;
..
无理数有:0.1212221222221…
有理数
无理数
新知探究
有理数和无理数统称为实数,即实数可以分为有理数和无理数.
问题1:你能仿照有理数的分类给实数分类吗?
新知探究
尝试思考
无理数和有理数一样,也有正负之分.如 是正的,-π是负的.
(1)你能把下面各数填入下面相应的集合内吗
0.3737737773…(相邻两个3之间的7的个数逐次加1).
新知探究
正数集合
负数集合
0.3737737773…
0.3737737773…(相邻两个3之间的7的个数逐次加1).
新知探究
负实数
正实数
数实
正有理数
负有理数
按符号分
0
正无理数
负无理数
(2) 实数还可以怎样分类?
新知探究
实数和有理数一样,可以进行加、减、乘、除、乘方运算,而且有理数的运算法则与运算律对实数仍然适用.
先算乘方(开方),再算乘除,最后算加减,同级运算按照从左到右的顺序进行,有括号先算括号里的.
归纳总结
新知探究
思考交流
前面讨论两个正方形,边长分别是a,b,且满足a2=2,b2=5.
(1) 如图,OA=OB,数轴上点 A 对应的数是什么?它介于哪两个整数之间?
-2
-1
0
1
2
A
B
O
介于整数1和2之间
新知探究
(2)你能在数轴上找到 对应的点吗?与同伴进行交流.
-2
-1
0
1
2
1
每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一点都表示一个实数.
实数和数轴上的点是一一对应的.
在数轴上,右边的点表示的数比左边的点表示的数大.
典例分析
数轴上的点与实数一一对应,结合数轴分析,可轻松得出结论.
方法技巧
例2.如图所示,数轴上 A,B 两点表示的数分别为 和 5.1,则 A,B 两点之间表示整数的点共有 ( )
A.6 个 B.5 个 C.4 个 D.3 个
∵ ≈ 1.414,∴ 和 5.1 之间的整数是 2,3,4,5. ∴ A,B 两点之间表示整数的点共有 4 个.
C
解 析
课堂小结
认识实数
有理数和无理数统称实数
在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样
实数与数轴上的点一一对应
变式训练
1.下列各数: 1, (相邻两个3之间0的个数逐次加1)中,无理数的个数是( )
A.2个 B.3个 C.4个 D.5个
A
变式训练
2.在 -3,- ,-1,0 这四个实数中,最大的是( )
A. -3 B.- C. -1 D. 0
D
变式训练
3.在数轴上找出 对应的点.
感谢聆听!
2.1 认识实数
第2课时 认识实数
第二章 实数
北师大版2024·八年级上册
学 习 目 标
1
2
通过拼图活动,感受无理数产生的实际背景和引入的必要性.
借助计算器探索无理数是无限不循环小数并从中体会无限逼近的思想.
3
会判断一个数是有理数还是无理数.
知识回顾
有理数进行分类:
正整数
零
负整数
正分数
负分数
有理数
分数
整数
有理数包括整数和分数,那么有理数范围是否能满足我们实际生活的需要呢?
新知探究
把下列各数表示成小数,你发现了什么?
3,
=0.8
=0.5
·
= 0.18
··
=﹣0.17
·
3=3.0
有理数总可以用有限小数或无限循环小数表示.反过来,任何有限小数或无限循环小数也都是有理数.
新知探究
如圆周率π=3.14159265…也是一个无限不循环小数,因此它也是一个无理数.再如0.5858858885…(相邻两个5之间8的个数逐次加1)也是无理数.
而能化成有限小数或循环小数,这些数都是有理数.
无限不循环小数称为无理数.
结论
想一想:你能找到其他的无理数吗?
典例分析
无理数的特征:
1.圆周率 及一些最终结果含有的数.
2.有一定的规律,但不循环的无限小数.
方法技巧
例1.下列各数中,哪些是有理数?哪些是无理数?
3.14,- ,0.57,0.1212221222221…(相邻两个 1 之间 2 的个数逐次加 2).
..
解:有理数有:3.14, ,0.57;
..
无理数有:0.1212221222221…
有理数
无理数
新知探究
有理数和无理数统称为实数,即实数可以分为有理数和无理数.
问题1:你能仿照有理数的分类给实数分类吗?
新知探究
尝试思考
无理数和有理数一样,也有正负之分.如 是正的,-π是负的.
(1)你能把下面各数填入下面相应的集合内吗
0.3737737773…(相邻两个3之间的7的个数逐次加1).
新知探究
正数集合
负数集合
0.3737737773…
0.3737737773…(相邻两个3之间的7的个数逐次加1).
新知探究
负实数
正实数
数实
正有理数
负有理数
按符号分
0
正无理数
负无理数
(2) 实数还可以怎样分类?
新知探究
实数和有理数一样,可以进行加、减、乘、除、乘方运算,而且有理数的运算法则与运算律对实数仍然适用.
先算乘方(开方),再算乘除,最后算加减,同级运算按照从左到右的顺序进行,有括号先算括号里的.
归纳总结
新知探究
思考交流
前面讨论两个正方形,边长分别是a,b,且满足a2=2,b2=5.
(1) 如图,OA=OB,数轴上点 A 对应的数是什么?它介于哪两个整数之间?
-2
-1
0
1
2
A
B
O
介于整数1和2之间
新知探究
(2)你能在数轴上找到 对应的点吗?与同伴进行交流.
-2
-1
0
1
2
1
每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一点都表示一个实数.
实数和数轴上的点是一一对应的.
在数轴上,右边的点表示的数比左边的点表示的数大.
典例分析
数轴上的点与实数一一对应,结合数轴分析,可轻松得出结论.
方法技巧
例2.如图所示,数轴上 A,B 两点表示的数分别为 和 5.1,则 A,B 两点之间表示整数的点共有 ( )
A.6 个 B.5 个 C.4 个 D.3 个
∵ ≈ 1.414,∴ 和 5.1 之间的整数是 2,3,4,5. ∴ A,B 两点之间表示整数的点共有 4 个.
C
解 析
课堂小结
认识实数
有理数和无理数统称实数
在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样
实数与数轴上的点一一对应
变式训练
1.下列各数: 1, (相邻两个3之间0的个数逐次加1)中,无理数的个数是( )
A.2个 B.3个 C.4个 D.5个
A
变式训练
2.在 -3,- ,-1,0 这四个实数中,最大的是( )
A. -3 B.- C. -1 D. 0
D
变式训练
3.在数轴上找出 对应的点.
感谢聆听!
同课章节目录
