北师大版数学八年级上册2.2 第1课时 算术平方根 课件(共18张ppt)
文档属性
| 名称 | 北师大版数学八年级上册2.2 第1课时 算术平方根 课件(共18张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-08 00:00:00 | ||
图片预览


文档简介
2.2 平方根与立方根
第1课时 算术平方根
第二章 实数
北师大版2024·八年级上册
学 习 目 标
1
2
了解算术平方根的概念及其性质.(重点)
会求一个数的算术平方根.(难点)
知识回顾
12=____
22=____
32=____
我们以前学过:
若x2=a,则a叫x的平方,反过来x叫a的什么呢?
1
4
9
新知探究
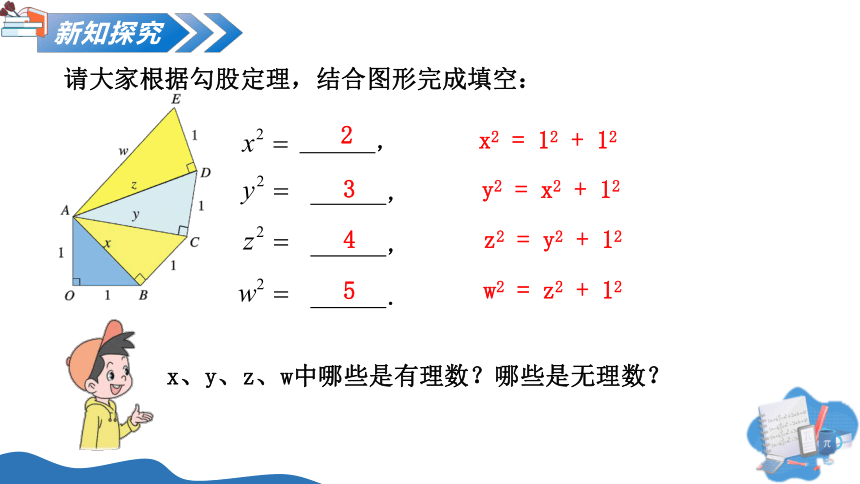
请大家根据勾股定理,结合图形完成填空:
x2 = 12 + 12
,
,
,
.
2
3
4
5
y2 = x2 + 12
z2 = y2 + 12
w2 = z2 + 12
x、y、z、w中哪些是有理数?哪些是无理数?
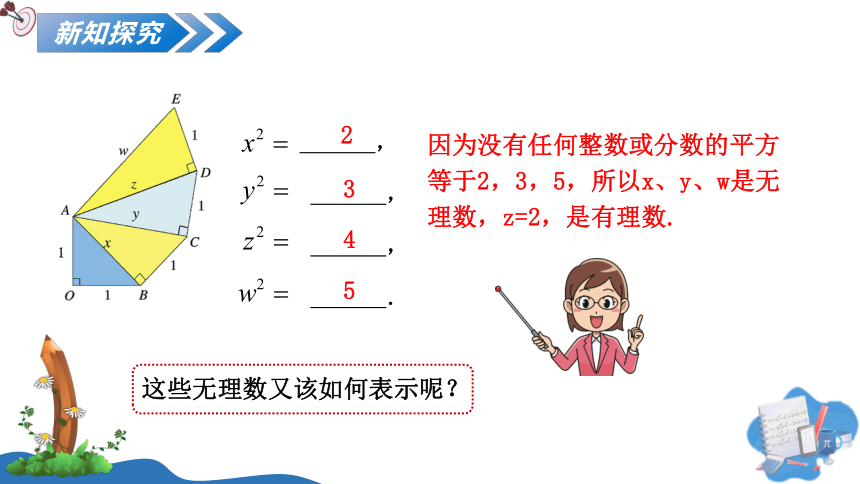
新知探究
这些无理数又该如何表示呢?
,
,
,
.
2
3
4
5
因为没有任何整数或分数的平方等于2,3,5,所以x、y、w是无理数,z=2,是有理数.
新知探究
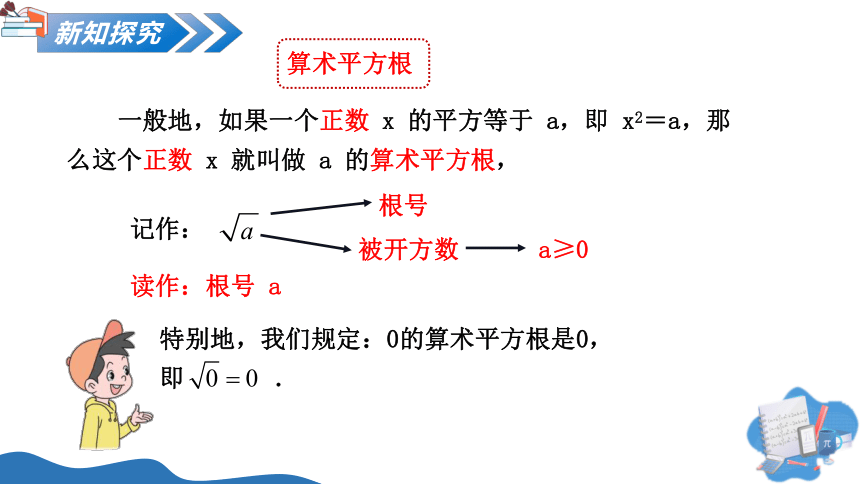
一般地,如果一个正数 x 的平方等于 a,即 x2=a,那么这个正数 x 就叫做 a 的算术平方根,
特别地,我们规定:0的算术平方根是0,即 .
记作:
根号
被开方数
a≥0
读作:根号 a
算术平方根
新知探究
1.一个正数的算术平方根有几个?
0的算术平方根有一个,是0.
2.0的算术平方有几个?
负数没有算术平方根.
3.-1有算术平方根吗?负数有算术平方根?
一个正数的算术平方根有 1 个.
正数的平方不可能是负数.
新知探究
你能根据等式122=144,说出144的算术平方根是多少吗?并用等式表示出来.
144的算术平方根是12,即
常见的平方数:
12 = 1 22 = 4 32 = 9 42 = 16 52 = 25 62 = 36
72 = 49 82 = 64 92 = 81 102 = 100 112 = 121
122 = 144 132 = 169 142 = 196 152 = 225 162 = 256
172 = 289 182 = 224 192 = 361 202 = 400
典例分析
非平方数的算术平方根只能用根号表示.
方法技巧
例1.求下列各数的算术平方根:
(1) 900; (2) 1; (3) ;(4)14 .
解 析
新知探究
1.在上面例1中,一些数的算术平方根的结果没有“√ ” 这些数有什么特点?
2.在上面例1中,????????????=30,也就是????????????=30,一般地,当a≥0时,????????=a成立吗?
3,(????)2=a成立吗?这里的a是什么数。你是怎么理解的,与同伴交流。
?
思考交流
当a<0时,????????=a还成立吗?
?
新知探究
归纳总结
当a≥0时,????????=a,(????)2=a,当a<0时,????????=-a
?
算术平方根具有双重非负性.
典例分析
求值时,要按照算术平方根的意义,写出应该满足的关系式,然后按照算术平方根的记法写出对应的值.
方法技巧
解 析
例2.自由下落物体下落的距离 s(m)与下落时间 t(s)的关系为 s = 4.9 t2. 有一铁球从 19.6m 高的建筑物上自由下落,到达地面需要多长时间?
解:将s=19.6带入公式s=4.9t2,
得t2 =4,所以t = =2(s).
即铁球到达地面需要2s.
典例分析
几个非负式的和为 0,则每个式子均为 0,现阶段学过的非负式有绝对值、平方式及算术平方根.
方法技巧
解 析
例3.若 |m-1|+ =0,求 m + n 的值.
因为|m-1|≥0, ≥0,又|m-1|+ = 0,
所以 |m-1|=0, = 0. 所以 m = 1,n = -3.
所以 m + n = 1 + (-3) = -2.
课堂小结
一般地,如果一个正数 x 的平方等于 a ,即 x2 = a,则这个正数 x 就叫作 a 的算术平方根,记作“ ”,读作“根号 a ”.
特别地,我们规定:0 的算术平方根是0,即 =0.
变式训练
1.下列运算正确的是( ?)
A. ???? =±3 B. ?????????=±3
C. (-?????)??????=-3 D. (-????)2=3
?
D
变式训练
2.求下列各数的算术平方根:
(1)169; (2) ; (3) 0.0001.
(2) 因为 ,所以 的算术平方根是 ,即
(3) 因为 0.012 =0.0001,所以 0.0001 的算术平方根是 0.01,即
解:(1) 因为 132 = 169,所以 169 的算术平方根是 13,
即 .
变式训练
3.如图,将一个长方形 ABCD 折叠,可得到一个面积为 144 cm2 的正方形 ABFE,已知正方形 ABFE 的面积等于长方形 CDEF 面积的 2 倍,求长方形 ABCD 的长和宽.
解:设正方形 ABFE 的边长为 a,
则 a2 = 144,
所以 a = =12.
所以 AB = BF = CD = 12.
设 FC = x,因为 SABFE = 2SCDEF,
所以 144 = 2×12x,解得 x = 6.
所以 BC = BF + FC = 12 + 6 = 18 (cm).
所以长方形的长为 18 cm,宽为 12 cm.
A
B
C
D
E
F
感谢聆听!
第1课时 算术平方根
第二章 实数
北师大版2024·八年级上册
学 习 目 标
1
2
了解算术平方根的概念及其性质.(重点)
会求一个数的算术平方根.(难点)
知识回顾
12=____
22=____
32=____
我们以前学过:
若x2=a,则a叫x的平方,反过来x叫a的什么呢?
1
4
9
新知探究
请大家根据勾股定理,结合图形完成填空:
x2 = 12 + 12
,
,
,
.
2
3
4
5
y2 = x2 + 12
z2 = y2 + 12
w2 = z2 + 12
x、y、z、w中哪些是有理数?哪些是无理数?
新知探究
这些无理数又该如何表示呢?
,
,
,
.
2
3
4
5
因为没有任何整数或分数的平方等于2,3,5,所以x、y、w是无理数,z=2,是有理数.
新知探究
一般地,如果一个正数 x 的平方等于 a,即 x2=a,那么这个正数 x 就叫做 a 的算术平方根,
特别地,我们规定:0的算术平方根是0,即 .
记作:
根号
被开方数
a≥0
读作:根号 a
算术平方根
新知探究
1.一个正数的算术平方根有几个?
0的算术平方根有一个,是0.
2.0的算术平方有几个?
负数没有算术平方根.
3.-1有算术平方根吗?负数有算术平方根?
一个正数的算术平方根有 1 个.
正数的平方不可能是负数.
新知探究
你能根据等式122=144,说出144的算术平方根是多少吗?并用等式表示出来.
144的算术平方根是12,即
常见的平方数:
12 = 1 22 = 4 32 = 9 42 = 16 52 = 25 62 = 36
72 = 49 82 = 64 92 = 81 102 = 100 112 = 121
122 = 144 132 = 169 142 = 196 152 = 225 162 = 256
172 = 289 182 = 224 192 = 361 202 = 400
典例分析
非平方数的算术平方根只能用根号表示.
方法技巧
例1.求下列各数的算术平方根:
(1) 900; (2) 1; (3) ;(4)14 .
解 析
新知探究
1.在上面例1中,一些数的算术平方根的结果没有“√ ” 这些数有什么特点?
2.在上面例1中,????????????=30,也就是????????????=30,一般地,当a≥0时,????????=a成立吗?
3,(????)2=a成立吗?这里的a是什么数。你是怎么理解的,与同伴交流。
?
思考交流
当a<0时,????????=a还成立吗?
?
新知探究
归纳总结
当a≥0时,????????=a,(????)2=a,当a<0时,????????=-a
?
算术平方根具有双重非负性.
典例分析
求值时,要按照算术平方根的意义,写出应该满足的关系式,然后按照算术平方根的记法写出对应的值.
方法技巧
解 析
例2.自由下落物体下落的距离 s(m)与下落时间 t(s)的关系为 s = 4.9 t2. 有一铁球从 19.6m 高的建筑物上自由下落,到达地面需要多长时间?
解:将s=19.6带入公式s=4.9t2,
得t2 =4,所以t = =2(s).
即铁球到达地面需要2s.
典例分析
几个非负式的和为 0,则每个式子均为 0,现阶段学过的非负式有绝对值、平方式及算术平方根.
方法技巧
解 析
例3.若 |m-1|+ =0,求 m + n 的值.
因为|m-1|≥0, ≥0,又|m-1|+ = 0,
所以 |m-1|=0, = 0. 所以 m = 1,n = -3.
所以 m + n = 1 + (-3) = -2.
课堂小结
一般地,如果一个正数 x 的平方等于 a ,即 x2 = a,则这个正数 x 就叫作 a 的算术平方根,记作“ ”,读作“根号 a ”.
特别地,我们规定:0 的算术平方根是0,即 =0.
变式训练
1.下列运算正确的是( ?)
A. ???? =±3 B. ?????????=±3
C. (-?????)??????=-3 D. (-????)2=3
?
D
变式训练
2.求下列各数的算术平方根:
(1)169; (2) ; (3) 0.0001.
(2) 因为 ,所以 的算术平方根是 ,即
(3) 因为 0.012 =0.0001,所以 0.0001 的算术平方根是 0.01,即
解:(1) 因为 132 = 169,所以 169 的算术平方根是 13,
即 .
变式训练
3.如图,将一个长方形 ABCD 折叠,可得到一个面积为 144 cm2 的正方形 ABFE,已知正方形 ABFE 的面积等于长方形 CDEF 面积的 2 倍,求长方形 ABCD 的长和宽.
解:设正方形 ABFE 的边长为 a,
则 a2 = 144,
所以 a = =12.
所以 AB = BF = CD = 12.
设 FC = x,因为 SABFE = 2SCDEF,
所以 144 = 2×12x,解得 x = 6.
所以 BC = BF + FC = 12 + 6 = 18 (cm).
所以长方形的长为 18 cm,宽为 12 cm.
A
B
C
D
E
F
感谢聆听!
同课章节目录
