人教A版(2019)选择性必修第三册 7.2 离散型随机变量及其分布列 课件(共18张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第三册 7.2 离散型随机变量及其分布列 课件(共18张PPT) | 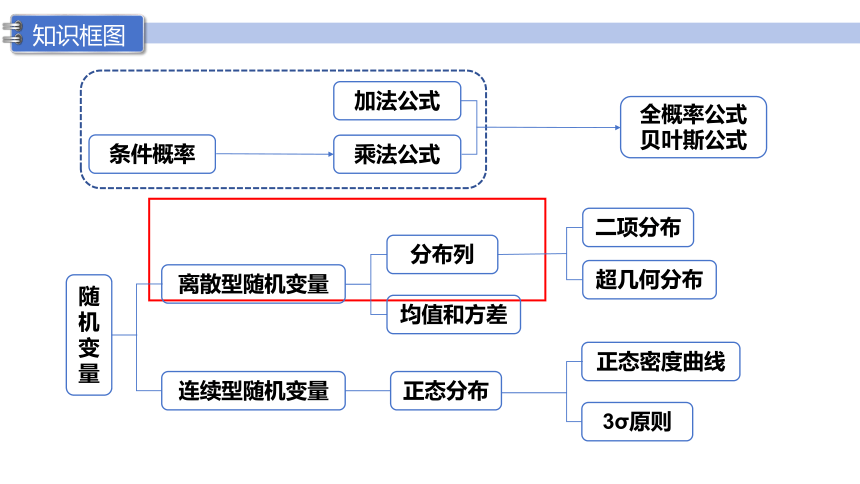 | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-06 14:56:21 | ||
图片预览







文档简介
加法公式
随机变量
全概率公式
贝叶斯公式
知识框图
条件概率
离散型随机变量
乘法公式
连续型随机变量
分布列
均值和方差
超几何分布
二项分布
正态分布
正态密度曲线
3σ原则
情境引入
(1) 掷一枚质地均匀的骰子,观察出现的点数.
(2) 某人射击一次,观察命中的环数.
(3) 掷一枚质地均匀的硬币,观察出现正、反面的情况.
(4) 一批产品共20件,其中18件正品, 2件次品,随机抽取一件观察是 正品或次品.
思考:
1.对于上述试验,可以定义不同的变量来表示这个试验结果吗?
2.任何随机试验的所有结果都可以用数字表示吗?
试验结果
实数
7.2 离散型随机变量及其分布列
数学人教A版 选择性必修第三册
新知探究
问题1:下列随机试验的样本空间是什么?样本点与变量的值是如何对应的 ?
试验1:从100个电子元件(至少含3个以上次品)中随机抽取三个进行检验,变量X 表示三个元件中的次品数;
试验2:抛掷一枚硬币直到出现正面为止,变量Y 表示需要的抛掷次数.
X=0,1,2,3
Y=1,2,3,4,…
追问1 观察两个随机试验,请你归纳试验1和试验2的样本空间中样本点与对 应变量有什么共同点?
追问2 你能类比函数中的对应关系,将样本空间中的样本点与实数的对应关 系用一般化的数学语言表达吗?
概念生成
即:用一个变量表示随机试验的结果
随机变量将随机试验的结果数量化
总结: 随机变量的特点:
①可以用数字表示;
②试验之前可以判断其可能出现的所有值;
③在试验之前不能确定取何值;
1.随机变量的概念
一般地,对于随机试验样本空间Ω中的每个样本点ω,都有唯一的实数X(ω)与之对应,我们称X为随机变量.
随机变量的概念是俄国数学家切比雪夫(也翻译为契贝晓夫)(Chebyshev,1821-1894)在19世纪中叶建立和提倡使用的.
概念生成
试验1中随机变量X的可能取值为0, 1, 2, 3, 共有4个值;试验2中随机变量Y的可能取值为1, 2, 3, ???, 有无限个取值,但可以一一列举出来.
离散型随机变量的定义:
追问3 随机变量与函数有什么异同点?
像这样,可能取值为有限个或可以一一列举的随机变量,我们称为离散型随机变量(discrete random variable).
通常用大写英文字母 表示随机变量,例如X,Y,Z;用小写英文字母表示随机变量的取值,例如x,y,z.
概念生成
2.随机变量的分类
可能取值为有限个或可以一一列出的随机变量,称为离散型随机变量.
可能取值充满某个区间、不能一一列举的随机变量,称为连续型随机变量.
如:某射击运动员射击一次可能命中的环数X;
某网页在24h内补浏览的次数Y.
如:种子含水量的测量误差X;
某品牌电视机的使用寿命Y.
新知探究
追问1 如何表示掷出的点数不大于2,
掷出偶数点呢?
追问2 抛掷一枚质地均匀的骰子,所得的点数X 取每个值的概率为多少?
问题2:抛掷一枚质地均匀的骰子,所得的点数X有哪些值?
追问3 能否用表格形式表示X的取值及相应的概率呢?
概念生成
追问4 你能根据概率的性质,研究离散型随机变量分布列的性质吗?
离散型随机变量的分布列可以用表格表示
3.离散型随机变量的分布列
一般地,设离散型随机变量????的可能取值为 ????1 ,????2 , ????3 ,?,???????? ,我们称????取每一个????????(????=1,2,3,4,?,????) 的概率
????(????=????????)=????????(????=1,2,3,?,????)
为????的概率分布列(list of probability distribution).简称分布列。
?
新知探究
追问4 你能根据概率的性质,研究离散型随机变量分布列的性质吗?
追问5 你能根据所学知识,总结出概率分布列的几种表示方法吗?
①解析式法:
③图形法:
(例)
②表格法:
????
????1
????2
?
????????
?
????????
????
????1
????2
?
????????
?
????????
????的可能取值
每个取值的概率
?
典例讲解
例1 一批产品中次品率为5%,随机抽取1件,定义
求X 的分布列.
追问 本题中离散型随机变量的分布列有什么特征 ?
课本P59
概念生成
4.两点分布
0
1
我们称X服从两点分布(two-point distribution)或0-1分布.
实际上,X为在一次试验中成功(事件A发生)的次数(0或1).像购买的彩券是否中奖,新生婴儿的性别,投篮是否命中等,都可以用两点分布来描述.
典例讲解
课本P59-60
例2 某学校高二年级有200名学生,他们的体育综合测试成绩分5个等级,每个等级对应的分数和人数如表7.2-4所示.
从这200名学生中任意选取1人,求所选同学分数X的分布列,以及????(????≥4).
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}等级
不及格
及格
中等
良
优
分数
1
2
3
4
5
人数
20
50
60
40
30
典例讲解
课本P59-60
例3 一批笔记本电脑共有10台,其中A品牌3台,B品牌7台.如果从中随机挑选2台,求这2台电脑中A品牌台数的分布列.
课堂练习
2.下列随机试验的结果能否用离散型随机变量表示?若能,请写出各随机变量可能的取值,并说明这些值所表示的随机试验的结果.
(1)抛掷2枚骰子,所得点数之和;
(2)某足球队在5次点球中射进的球数;
(3)任意抽取一瓶标有1500 mL的饮料,其实际含量与规定含量之差.
课本练习P60
1.举出两个离散型随机变量的例子.
(1)抛掷一枚质地均匀的硬币10次,正面向上的次数;
(2)某公共汽车站1分钟内等车的人数.
课堂小结
3.两点分布
只有两个可能结果的随机试验
1.随机变量的概念
4.求解离散型随机变量分布列的一般步骤
2.离散型随机变量的分布列及其性质
课后作业
1.基础性作业:
教科书第60页练习 第3,4题;
第60-61页习题7.2 第1,3,4,5题.
2.拓展性作业:
完成《同步导练》小本课时作业13 离散型随机变量的分布列.
感谢欣赏
属于持续努力与勇敢攀登的人
数学的奇峰异景
随机变量
全概率公式
贝叶斯公式
知识框图
条件概率
离散型随机变量
乘法公式
连续型随机变量
分布列
均值和方差
超几何分布
二项分布
正态分布
正态密度曲线
3σ原则
情境引入
(1) 掷一枚质地均匀的骰子,观察出现的点数.
(2) 某人射击一次,观察命中的环数.
(3) 掷一枚质地均匀的硬币,观察出现正、反面的情况.
(4) 一批产品共20件,其中18件正品, 2件次品,随机抽取一件观察是 正品或次品.
思考:
1.对于上述试验,可以定义不同的变量来表示这个试验结果吗?
2.任何随机试验的所有结果都可以用数字表示吗?
试验结果
实数
7.2 离散型随机变量及其分布列
数学人教A版 选择性必修第三册
新知探究
问题1:下列随机试验的样本空间是什么?样本点与变量的值是如何对应的 ?
试验1:从100个电子元件(至少含3个以上次品)中随机抽取三个进行检验,变量X 表示三个元件中的次品数;
试验2:抛掷一枚硬币直到出现正面为止,变量Y 表示需要的抛掷次数.
X=0,1,2,3
Y=1,2,3,4,…
追问1 观察两个随机试验,请你归纳试验1和试验2的样本空间中样本点与对 应变量有什么共同点?
追问2 你能类比函数中的对应关系,将样本空间中的样本点与实数的对应关 系用一般化的数学语言表达吗?
概念生成
即:用一个变量表示随机试验的结果
随机变量将随机试验的结果数量化
总结: 随机变量的特点:
①可以用数字表示;
②试验之前可以判断其可能出现的所有值;
③在试验之前不能确定取何值;
1.随机变量的概念
一般地,对于随机试验样本空间Ω中的每个样本点ω,都有唯一的实数X(ω)与之对应,我们称X为随机变量.
随机变量的概念是俄国数学家切比雪夫(也翻译为契贝晓夫)(Chebyshev,1821-1894)在19世纪中叶建立和提倡使用的.
概念生成
试验1中随机变量X的可能取值为0, 1, 2, 3, 共有4个值;试验2中随机变量Y的可能取值为1, 2, 3, ???, 有无限个取值,但可以一一列举出来.
离散型随机变量的定义:
追问3 随机变量与函数有什么异同点?
像这样,可能取值为有限个或可以一一列举的随机变量,我们称为离散型随机变量(discrete random variable).
通常用大写英文字母 表示随机变量,例如X,Y,Z;用小写英文字母表示随机变量的取值,例如x,y,z.
概念生成
2.随机变量的分类
可能取值为有限个或可以一一列出的随机变量,称为离散型随机变量.
可能取值充满某个区间、不能一一列举的随机变量,称为连续型随机变量.
如:某射击运动员射击一次可能命中的环数X;
某网页在24h内补浏览的次数Y.
如:种子含水量的测量误差X;
某品牌电视机的使用寿命Y.
新知探究
追问1 如何表示掷出的点数不大于2,
掷出偶数点呢?
追问2 抛掷一枚质地均匀的骰子,所得的点数X 取每个值的概率为多少?
问题2:抛掷一枚质地均匀的骰子,所得的点数X有哪些值?
追问3 能否用表格形式表示X的取值及相应的概率呢?
概念生成
追问4 你能根据概率的性质,研究离散型随机变量分布列的性质吗?
离散型随机变量的分布列可以用表格表示
3.离散型随机变量的分布列
一般地,设离散型随机变量????的可能取值为 ????1 ,????2 , ????3 ,?,???????? ,我们称????取每一个????????(????=1,2,3,4,?,????) 的概率
????(????=????????)=????????(????=1,2,3,?,????)
为????的概率分布列(list of probability distribution).简称分布列。
?
新知探究
追问4 你能根据概率的性质,研究离散型随机变量分布列的性质吗?
追问5 你能根据所学知识,总结出概率分布列的几种表示方法吗?
①解析式法:
③图形法:
(例)
②表格法:
????
????1
????2
?
????????
?
????????
????
????1
????2
?
????????
?
????????
????的可能取值
每个取值的概率
?
典例讲解
例1 一批产品中次品率为5%,随机抽取1件,定义
求X 的分布列.
追问 本题中离散型随机变量的分布列有什么特征 ?
课本P59
概念生成
4.两点分布
0
1
我们称X服从两点分布(two-point distribution)或0-1分布.
实际上,X为在一次试验中成功(事件A发生)的次数(0或1).像购买的彩券是否中奖,新生婴儿的性别,投篮是否命中等,都可以用两点分布来描述.
典例讲解
课本P59-60
例2 某学校高二年级有200名学生,他们的体育综合测试成绩分5个等级,每个等级对应的分数和人数如表7.2-4所示.
从这200名学生中任意选取1人,求所选同学分数X的分布列,以及????(????≥4).
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}等级
不及格
及格
中等
良
优
分数
1
2
3
4
5
人数
20
50
60
40
30
典例讲解
课本P59-60
例3 一批笔记本电脑共有10台,其中A品牌3台,B品牌7台.如果从中随机挑选2台,求这2台电脑中A品牌台数的分布列.
课堂练习
2.下列随机试验的结果能否用离散型随机变量表示?若能,请写出各随机变量可能的取值,并说明这些值所表示的随机试验的结果.
(1)抛掷2枚骰子,所得点数之和;
(2)某足球队在5次点球中射进的球数;
(3)任意抽取一瓶标有1500 mL的饮料,其实际含量与规定含量之差.
课本练习P60
1.举出两个离散型随机变量的例子.
(1)抛掷一枚质地均匀的硬币10次,正面向上的次数;
(2)某公共汽车站1分钟内等车的人数.
课堂小结
3.两点分布
只有两个可能结果的随机试验
1.随机变量的概念
4.求解离散型随机变量分布列的一般步骤
2.离散型随机变量的分布列及其性质
课后作业
1.基础性作业:
教科书第60页练习 第3,4题;
第60-61页习题7.2 第1,3,4,5题.
2.拓展性作业:
完成《同步导练》小本课时作业13 离散型随机变量的分布列.
感谢欣赏
属于持续努力与勇敢攀登的人
数学的奇峰异景
