人教A版(2019)选择性必修第三册 8.1 成对数据的统计相关性 课件(共29张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第三册 8.1 成对数据的统计相关性 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-06 14:59:59 | ||
图片预览





文档简介
数学人教A版 选择性必修第三册
第八章 成对数据的统计分析
8.1 成对数据的统计相关性
8.1.1 变量间的相关关系
成对数据
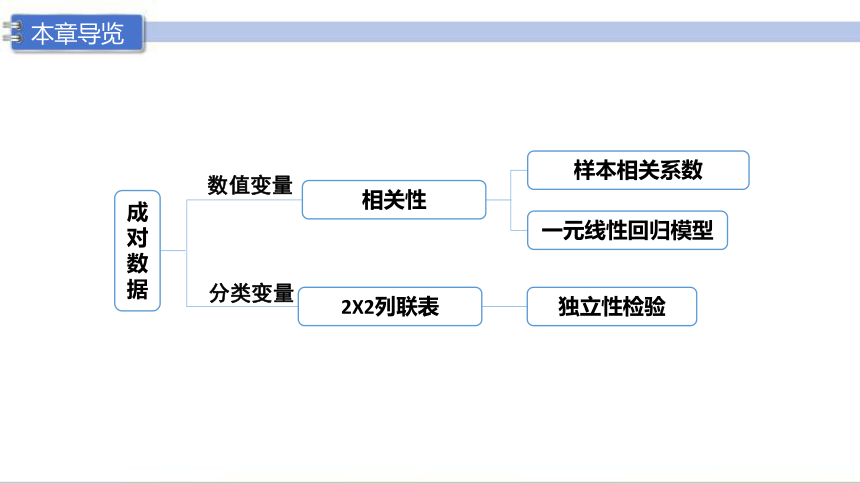
本章导览
相关性
2X2列联表
样本相关系数
一元线性回归模型
独立性检验
数值变量
分类变量
复习回顾
我们已学习了:
用直方图描述样本数据的分布规律
用均值刻画样本数据的集中趋势
用方差刻画样本数据的离散程度……
复习回顾
单个变量
的表示与特征
问题1 两个或两个以上变量之间的关系?
探究新知
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}事例
特点
1、子女身高y与父亲身高x之间的关系
2、商品销售收入y与广告支出x之间的关系
3、空气污染指数y与汽车保有量x之间的关系
4、粮食亩产量y与施肥量x之间的关系
有关系
但不确切
探究新知
两个变量有关系,但又没有确切到可由其中的一个去精确地决定另一个的程度,这种关系称为相关关系.
一、相关关系
如何研究?
案例探究:刻画人体脂肪含量和年龄的相关关系
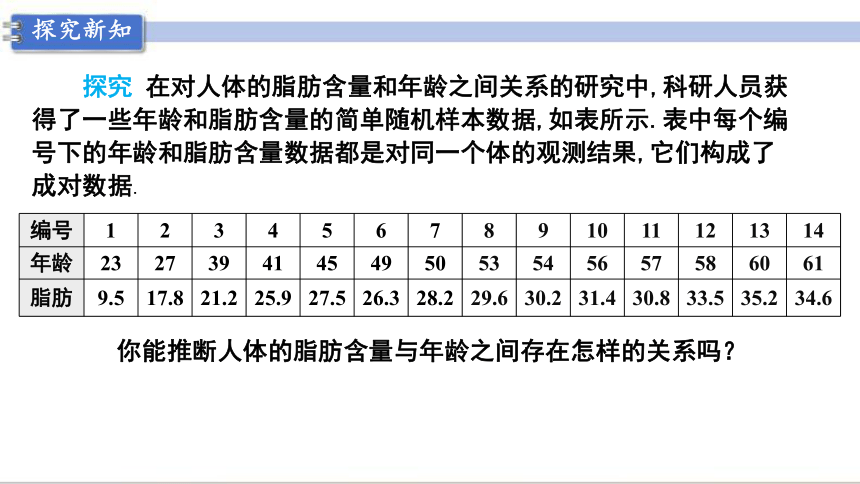
探究 在对人体的脂肪含量和年龄之间关系的研究中,科研人员获得了一些年龄和脂肪含量的简单随机样本数据,如表所示.表中每个编号下的年龄和脂肪含量数据都是对同一个体的观测结果,它们构成了成对数据.
编号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
年龄
23
27
39
41
45
49
50
53
54
56
57
58
60
61
脂肪
9.5
17.8
21.2
25.9
27.5
26.3
28.2
29.6
30.2
31.4
30.8
33.5
35.2
34.6
你能推断人体的脂肪含量与年龄之间存在怎样的关系吗?
探究新知
案例探究:刻画人体脂肪含量和年龄的相关关系
探究新知
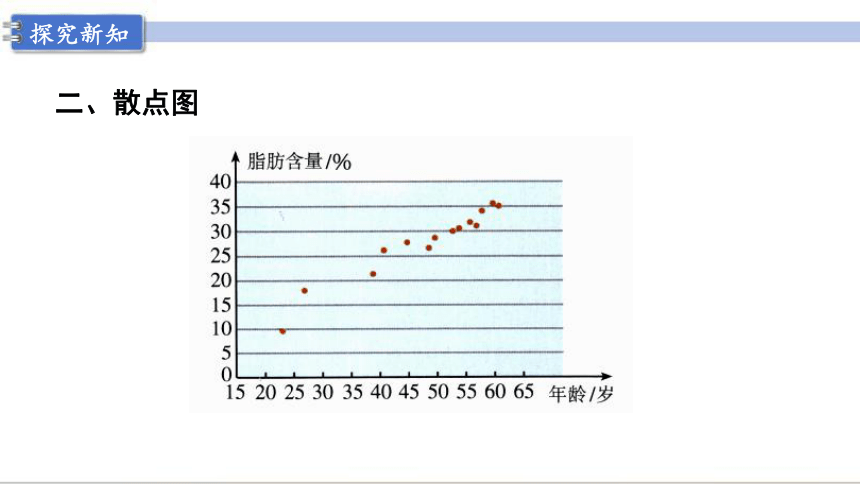
二、散点图
案例探究:刻画人体脂肪含量和年龄的相关关系
探究新知
(1)正相关和负相关
从整体上看,当一个变量的值增加时,另一个变量的相应值也呈现增加的趋势,则称两个变量正相关;
三、变量相关关系的分类
当一个变量的值增加时,另一个变量的相应值呈现减小的趋势,
则称这两个变量负相关.
探究新知
案例探究:脂肪含量和年龄的相关关系
探究新知
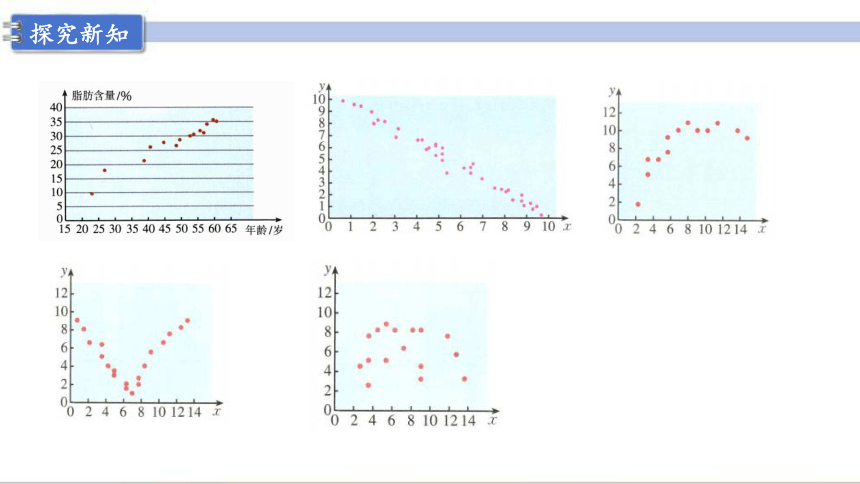
如果两个变量的取值呈现正相关或负相关,而且散点落在一条直线附近,则称这两个变量线性相关.
(2)线性相关和非线性相关
一般地,如果两个变量具有相关性,但不是线性相关,则称这两个变量非线性相关或曲线相关.
例1.在下列各个量与量的关系中:
①正方体的表面积与棱长之间的关系;②一块农田的水稻产量与施肥量之间的关系;
③家庭的收入与支出之间的关系;④某户家庭用电量与水费之间的关系.
其中是相关关系的为( ).
A.①② B.③④ C.②④ D.②③
D
例题讲解
例2.某种产品的广告支出费x与销售金额y之间有如表对应数据(单位:百万元):
x
2
4
5
6
8
y
30
40
60
50
70
①画出散点图;
②从散点图中判断销售金额与广告支出费有什么样的关系.
例题讲解
2.变量间相关关系的类型
归纳总结
案例探究:刻画人体脂肪含量和年龄的相关关系
探究新知
相关程度如何定量分析?
数学人教A版 选择性必修第三册
第八章 成对数据的统计分析
8.1 成对数据的统计相关性
8.1.2 样本相关系数
探究1:正相关和负相关的定量分析
设变量????和????经过随机抽样获得的成对样本数据为(????????,????????),(????????,????????),?,(????????,????????),其中????????,????????,?,????????和????????,????????,?,????????的均值分别为????和????.
将每个变量的观测数据减去其均值,得到成对数据为(?????????????,?????????????),(?????????????,?????????????),?,(?????????????,?????????????),并绘制散点图.
?
探究新知
中心化
????????????=??????????????????????????????????+??????????????????????????+?+??????????????????????????
?
????????????>????表明成对样本数据正相关
?
?????????????
探究新知
问题1 ????????????的大小一定能度量出成对样本数据的相关程度吗?
?
在研究体重与身高之间的相关程度时,如果体重的单位不变,
把身高单位由米改为厘米:
????′????????=??????????????????????????????????????????????????????????+??????????????????????????????????????????????????+?+??????????????????????????????????????????????????=?????????????????????????
?
单位的改变不会改变体重与身高之间的相关程度
探究新知
大小与度量单位有关
?????????????,?????????????, ?????????????,?????????????,?????????????,?????????????,…?????????????,?????????????
?
问题2:如何消除单位量级对?????????????的影响?
?
“中心化”后的
成对样本数据
除以各自的标准差,
变成无量纲的数据
????????=????????????=?????????????????????????????????=????????????=?????????????????????????
?
????????′,????????′, ????????′,????????′,????????′,????????′,…????????′,????????′
?
????????′=?????????????????????????=?????????????????????????
?
????????′=?????????????????????????=?????????????????????????
?
探究新知
标准化
????????????=??????????????????????????????????+??????????????????????????+?+??????????????????????????
?
仿造????????????的构建逻辑,构建样本相关系数
?
????=????????????????′????????′+????????′????????′+?+????????′????????′
?
=????=??????????????????????????????????????=?????????????????????????????=?????????????????????????
?
????>????表明成对样本数据正相关
?
?????
????????′=?????????????????????????=?????????????????????????
?
????????′=?????????????????????????=?????????????????????????
?
探究新知
问题3:样本相关系数????的大小与成对样本数据的相关程度有什么内在联系呢?
?
????=????????????????′????????′+????????′????????′+?+????????′????????′
?
三维向量数量积
????=(????????, ????????, ????????)
????=(????????, ????????, ????????)
????是????与????的夹角
?
=????????????????+????????????????+????????????????
?
?????????=????????????????????????
?
推广到????维
?
????维向量数量积
????=(????????, ????????, ????????,…,????????)
????=(????????, ????????, ????????,…,????????)
????是????与????的夹角
?
=????????????????+????????????????+????????????????+…+????????????????
?
?????????=????????????????????????
?
探究新知
????=????????????????′????????′+????????′????????′+?+????????′????????′
?
标准化后的数据????????′,????????′, ????????′,????????′,????????′,????????′,…????????′,????????′
?
第一组分量??????′=????????′????????′?????????′
?
第二组分量 ????′=????????′????????′?????????′
?
????=?????????????′?????′
?
=?????????????′????′????????????????
?
????????′=?????????????????????????=?????????????????????????
?
????????′=?????????????????????????=?????????????????????????
?
????=????????????????
?
?????′=????????′????+????????′????+…????????′????=????=1?????????????????21????????=1?????????????????2=????
?
?????′=????????′????+????????′????+…????????′????=????
?
探究新知
????=????????????????
?
?????≤????≤????
?
追问:当|????|=????和|????|=????时,成对样本数据之间具有怎样的关系?
?
探究新知
当|????|越接近1时,成对样本数据的线性相关程度越强
当|????|越接近0时,成对样本数据的线性相关程度越弱
?
????>????表明成对样本数据正相关
?????
当?????越接近 1时,线性正相关越强
当?????越接近-1时,线性负相关越强
?
根据样本相关系数推断变量之间的相关性
探究新知
探究新知
散点图:直观上判断成对样本数据的相关性
样本相关系数:定量刻画成对样本数据的
正负性和线性相关程度
例如:当成对样本数据呈某种曲线相关时,
计算样本相关系数就不一定有意义,
而散点图能帮助我们快速分析成对
样本数据的规律.
结合两者分析相关性
????刻画的是线性相关程度
?
探究新知
例1.根据表8.1-1中脂肪含量和年龄的样本数据,推断两个变量
是否线性相关,计算样本相关系数,并推断它们的相关程度.
例题讲解
归纳总结
本节课你学到了哪些知识?运用了哪些数学思想方法?
归纳总结
定量分析、中心化、标准化思想
变量间的相关关系
样本相关系数
相关性的实际
应用
》
》
第八章 成对数据的统计分析
8.1 成对数据的统计相关性
8.1.1 变量间的相关关系
成对数据
本章导览
相关性
2X2列联表
样本相关系数
一元线性回归模型
独立性检验
数值变量
分类变量
复习回顾
我们已学习了:
用直方图描述样本数据的分布规律
用均值刻画样本数据的集中趋势
用方差刻画样本数据的离散程度……
复习回顾
单个变量
的表示与特征
问题1 两个或两个以上变量之间的关系?
探究新知
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}事例
特点
1、子女身高y与父亲身高x之间的关系
2、商品销售收入y与广告支出x之间的关系
3、空气污染指数y与汽车保有量x之间的关系
4、粮食亩产量y与施肥量x之间的关系
有关系
但不确切
探究新知
两个变量有关系,但又没有确切到可由其中的一个去精确地决定另一个的程度,这种关系称为相关关系.
一、相关关系
如何研究?
案例探究:刻画人体脂肪含量和年龄的相关关系
探究 在对人体的脂肪含量和年龄之间关系的研究中,科研人员获得了一些年龄和脂肪含量的简单随机样本数据,如表所示.表中每个编号下的年龄和脂肪含量数据都是对同一个体的观测结果,它们构成了成对数据.
编号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
年龄
23
27
39
41
45
49
50
53
54
56
57
58
60
61
脂肪
9.5
17.8
21.2
25.9
27.5
26.3
28.2
29.6
30.2
31.4
30.8
33.5
35.2
34.6
你能推断人体的脂肪含量与年龄之间存在怎样的关系吗?
探究新知
案例探究:刻画人体脂肪含量和年龄的相关关系
探究新知
二、散点图
案例探究:刻画人体脂肪含量和年龄的相关关系
探究新知
(1)正相关和负相关
从整体上看,当一个变量的值增加时,另一个变量的相应值也呈现增加的趋势,则称两个变量正相关;
三、变量相关关系的分类
当一个变量的值增加时,另一个变量的相应值呈现减小的趋势,
则称这两个变量负相关.
探究新知
案例探究:脂肪含量和年龄的相关关系
探究新知
如果两个变量的取值呈现正相关或负相关,而且散点落在一条直线附近,则称这两个变量线性相关.
(2)线性相关和非线性相关
一般地,如果两个变量具有相关性,但不是线性相关,则称这两个变量非线性相关或曲线相关.
例1.在下列各个量与量的关系中:
①正方体的表面积与棱长之间的关系;②一块农田的水稻产量与施肥量之间的关系;
③家庭的收入与支出之间的关系;④某户家庭用电量与水费之间的关系.
其中是相关关系的为( ).
A.①② B.③④ C.②④ D.②③
D
例题讲解
例2.某种产品的广告支出费x与销售金额y之间有如表对应数据(单位:百万元):
x
2
4
5
6
8
y
30
40
60
50
70
①画出散点图;
②从散点图中判断销售金额与广告支出费有什么样的关系.
例题讲解
2.变量间相关关系的类型
归纳总结
案例探究:刻画人体脂肪含量和年龄的相关关系
探究新知
相关程度如何定量分析?
数学人教A版 选择性必修第三册
第八章 成对数据的统计分析
8.1 成对数据的统计相关性
8.1.2 样本相关系数
探究1:正相关和负相关的定量分析
设变量????和????经过随机抽样获得的成对样本数据为(????????,????????),(????????,????????),?,(????????,????????),其中????????,????????,?,????????和????????,????????,?,????????的均值分别为????和????.
将每个变量的观测数据减去其均值,得到成对数据为(?????????????,?????????????),(?????????????,?????????????),?,(?????????????,?????????????),并绘制散点图.
?
探究新知
中心化
????????????=??????????????????????????????????+??????????????????????????+?+??????????????????????????
?
????????????>????表明成对样本数据正相关
?
?????????????
探究新知
问题1 ????????????的大小一定能度量出成对样本数据的相关程度吗?
?
在研究体重与身高之间的相关程度时,如果体重的单位不变,
把身高单位由米改为厘米:
????′????????=??????????????????????????????????????????????????????????+??????????????????????????????????????????????????+?+??????????????????????????????????????????????????=?????????????????????????
?
单位的改变不会改变体重与身高之间的相关程度
探究新知
大小与度量单位有关
?????????????,?????????????, ?????????????,?????????????,?????????????,?????????????,…?????????????,?????????????
?
问题2:如何消除单位量级对?????????????的影响?
?
“中心化”后的
成对样本数据
除以各自的标准差,
变成无量纲的数据
????????=????????????=?????????????????????????????????=????????????=?????????????????????????
?
????????′,????????′, ????????′,????????′,????????′,????????′,…????????′,????????′
?
????????′=?????????????????????????=?????????????????????????
?
????????′=?????????????????????????=?????????????????????????
?
探究新知
标准化
????????????=??????????????????????????????????+??????????????????????????+?+??????????????????????????
?
仿造????????????的构建逻辑,构建样本相关系数
?
????=????????????????′????????′+????????′????????′+?+????????′????????′
?
=????=??????????????????????????????????????=?????????????????????????????=?????????????????????????
?
????>????表明成对样本数据正相关
?
?????
????????′=?????????????????????????=?????????????????????????
?
????????′=?????????????????????????=?????????????????????????
?
探究新知
问题3:样本相关系数????的大小与成对样本数据的相关程度有什么内在联系呢?
?
????=????????????????′????????′+????????′????????′+?+????????′????????′
?
三维向量数量积
????=(????????, ????????, ????????)
????=(????????, ????????, ????????)
????是????与????的夹角
?
=????????????????+????????????????+????????????????
?
?????????=????????????????????????
?
推广到????维
?
????维向量数量积
????=(????????, ????????, ????????,…,????????)
????=(????????, ????????, ????????,…,????????)
????是????与????的夹角
?
=????????????????+????????????????+????????????????+…+????????????????
?
?????????=????????????????????????
?
探究新知
????=????????????????′????????′+????????′????????′+?+????????′????????′
?
标准化后的数据????????′,????????′, ????????′,????????′,????????′,????????′,…????????′,????????′
?
第一组分量??????′=????????′????????′?????????′
?
第二组分量 ????′=????????′????????′?????????′
?
????=?????????????′?????′
?
=?????????????′????′????????????????
?
????????′=?????????????????????????=?????????????????????????
?
????????′=?????????????????????????=?????????????????????????
?
????=????????????????
?
?????′=????????′????+????????′????+…????????′????=????=1?????????????????21????????=1?????????????????2=????
?
?????′=????????′????+????????′????+…????????′????=????
?
探究新知
????=????????????????
?
?????≤????≤????
?
追问:当|????|=????和|????|=????时,成对样本数据之间具有怎样的关系?
?
探究新知
当|????|越接近1时,成对样本数据的线性相关程度越强
当|????|越接近0时,成对样本数据的线性相关程度越弱
?
????>????表明成对样本数据正相关
?????
当?????越接近 1时,线性正相关越强
当?????越接近-1时,线性负相关越强
?
根据样本相关系数推断变量之间的相关性
探究新知
探究新知
散点图:直观上判断成对样本数据的相关性
样本相关系数:定量刻画成对样本数据的
正负性和线性相关程度
例如:当成对样本数据呈某种曲线相关时,
计算样本相关系数就不一定有意义,
而散点图能帮助我们快速分析成对
样本数据的规律.
结合两者分析相关性
????刻画的是线性相关程度
?
探究新知
例1.根据表8.1-1中脂肪含量和年龄的样本数据,推断两个变量
是否线性相关,计算样本相关系数,并推断它们的相关程度.
例题讲解
归纳总结
本节课你学到了哪些知识?运用了哪些数学思想方法?
归纳总结
定量分析、中心化、标准化思想
变量间的相关关系
样本相关系数
相关性的实际
应用
》
》
