人教A版(2019)选择性必修第一册 第三章 圆锥曲线的方程 章末复习 课件(共25张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第一册 第三章 圆锥曲线的方程 章末复习 课件(共25张PPT) | 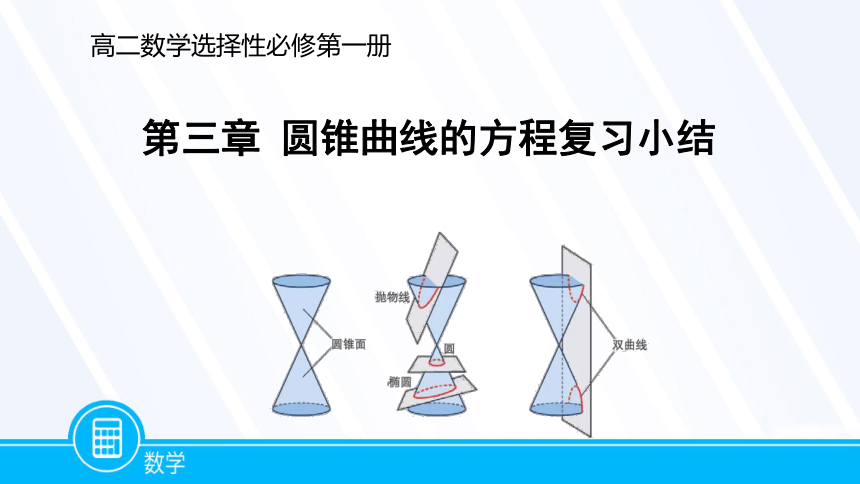 | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-06 15:05:14 | ||
图片预览





文档简介
(共25张PPT)
第三章 圆锥曲线的方程复习小结
高二数学选择性必修第一册
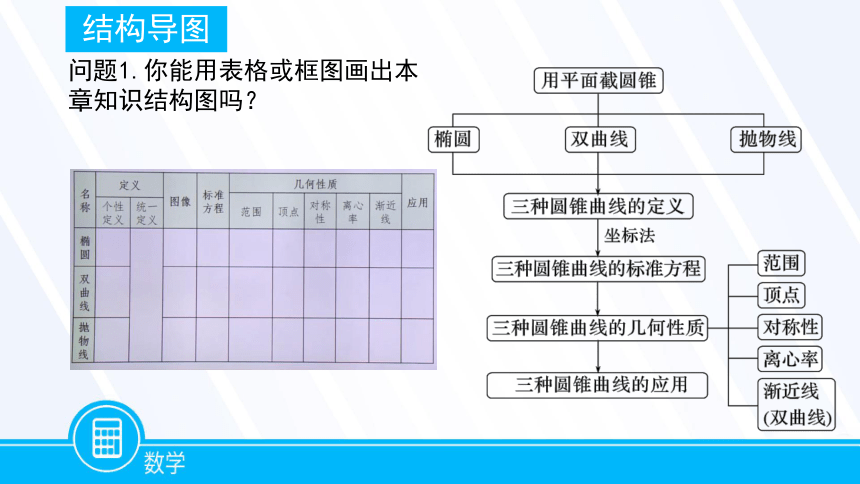
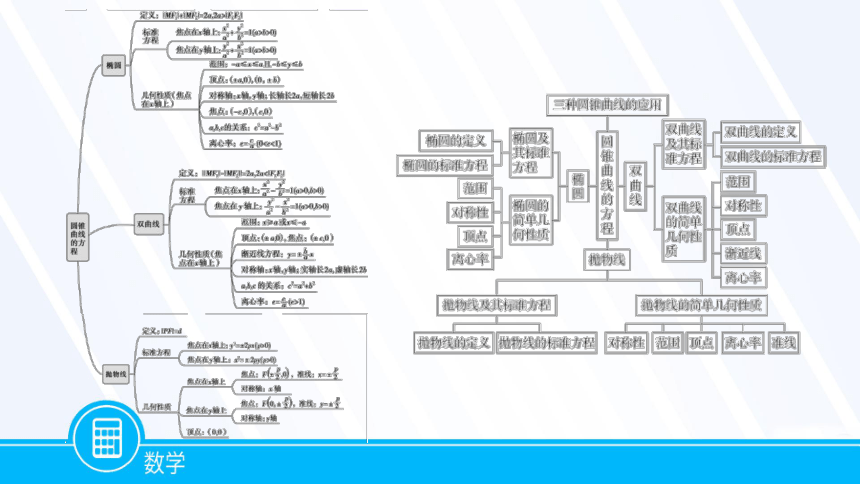
问题1.你能用表格或框图画出本章知识结构图吗?
结构导图
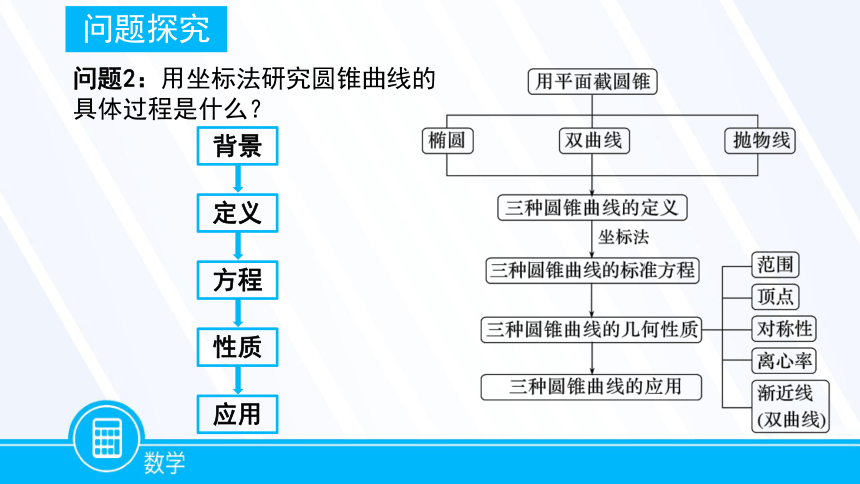
问题2:用坐标法研究圆锥曲线的具体过程是什么?
问题探究
背景
定义
方程
性质
应用
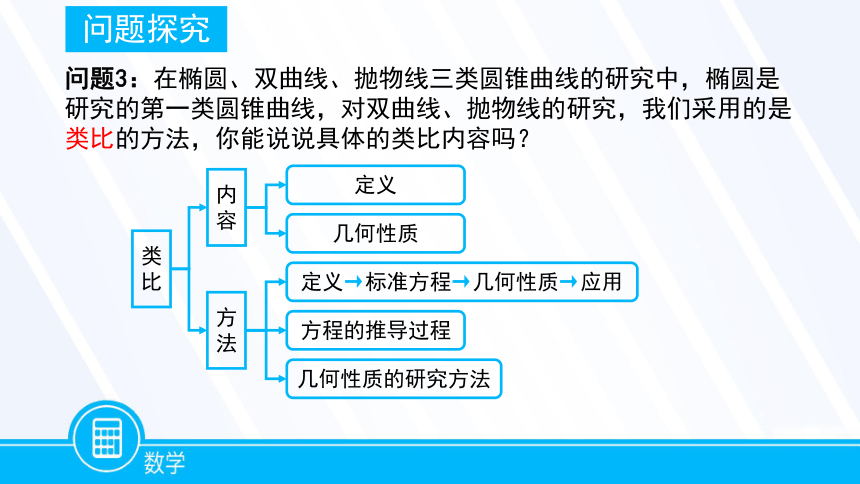
问题3:在椭圆、双曲线、抛物线三类圆锥曲线的研究中,椭圆是研究的第一类圆锥曲线,对双曲线、抛物线的研究,我们采用的是类比的方法,你能说说具体的类比内容吗?
类比
内容
方法
定义
方程的推导过程
几何性质
定义→标准方程→几何性质→应用
几何性质的研究方法
问题探究
椭圆:
平面内与两个定点的距离的和等于常数(大于)的点的轨迹.
双曲线:
平面内与两个定点的距离的差的绝对值等于非零常数(小于)的点的轨迹.
追问1:如何类比椭圆的定义研究双曲线的定义?
问题探究
追问2:我们如何类比椭圆的标准方程的推导过程,推导双曲线的标准方程?
移项
平方
化简
平方
整理
方程
问题探究
追问3:如何类比椭圆几何性质的研究过程,研究双曲线的几何性质?
问题探究
范围
.
.
问题4:圆锥曲线的“统一性”体现在哪些方面?你如何理解圆锥曲线的“统一性”?
问题探究
来源统一
定义统一
研究过程方法统一
问题探究
问题5:如何用直线与圆锥曲线的方程判断它们之间的位置关系?
问题探究
1
3
2
联立直线的方程和圆锥曲线的方程
判断位置关系
判断解的个数
例.判断直线与双曲线的交点个数.
解:联立方程,得 解得,故,
此时,故方程组的解为
故直线与双曲线有一个交点.
典例分析
练习.已知直线与双曲线的没有交点,求的取值范围.
巩固应用
直线与椭圆的位置关系
,相离
,相切
,相交
归纳小结
直线与双曲线的位置关系
一元二次方程
,相离
,相切
,相交
一元一次方程
一个根,相交
问题探究
直线与抛物线的位置关系
一元二次方程
,相离
,相切
,相交
一元一次方程
一个根,相交
问题探究
【例1】一动圆与两圆:x2+y2=1和x2+y2-6x+5=0都外切,则动圆圆心的轨迹为( )
A.抛物线 B.双曲线 C.双曲线的一支 D.椭圆
【例2】在平面直角坐标系xOy中,椭圆C的中心为原点,焦点F1,F2在x轴上,离心率为 .过F1的直线l交C于A,B两点,且△ABF2的周长为4,求椭圆C的方程.
典例分析
[解析] (1)x2+y2=1是圆心为原点,半径为1的圆,
x2+y2-6x+5=0化为标准方程为(x-3)2+y2=4,是圆心为A(3,0),半径为2的圆.
设所求动圆圆心为P,动圆半径为r,则 |PA|-|PO|=1<|AO|=3,符合双曲线的定义,所以动圆圆心的轨迹为双曲线的一支.
(2)设椭圆方程为 +=1(a>b>0),因为AB过F1且A,B在椭圆上,如图所示,
则△ABF2的周长为|AB|+|AF2|+|BF2|=|AF1|+|AF2|+|BF1|+|BF2|=4a=4,∴a=.
又离心率e==,∴c=1,∴b2=a2-c2=1,
∴椭圆C的方程为 +=1.
[答案] (1)C (2) +=1.
【类题通法】“回归定义”解题的三点应用
应用一:在求轨迹方程时,若所求轨迹符合某种圆锥曲线的定义,则根据圆锥曲线的定义,写出所求的轨迹方程;
应用二:涉及椭圆、双曲线上的点与两个定点构成的三角形问题时,常用定义结合解三角形的知识来解决;
应用三:在求有关抛物线的最值问题时,常利用定义把到焦点的距离转化为到准线的距离,结合几何图形,利用几何意义去解决.
提醒:应用定义解题时注意圆锥曲线定义中的限制条件.
【例2】已知椭圆
=1(a>b>0)的离心率为,F1,F2为左右焦点,过F1的直线l交C于A,B两点,且△ABF2的周长为4,
(1)求椭圆C的方程.
(2)若直线l过点M(,),求△ABF2的面积.
巩固应用
追问:在例2中,针对结论还可以提出哪些问题?
解:(2)∵F1(-1,0),∴直线MF1的方程为y=(x+1),
由 得2x2+2x-1=0.
∵Δ=22-4×2×(-1)=12>0,所以直线与椭圆有两个公共点,
设为A(x1,y1),B(x2,y2),则
∴|AB|=·|x1-x2|=·=·=,
又点F2到直线MF1的距离d=,故S△ABF2=|AB|·d=.
【例2】已知椭圆=1(a>b>0)的离心率为,F1,F2为左右焦点,过F1的直线l交C于A,B两点,且△ABF2的周长为4,
(1)求椭圆C的方程.
(2)若点M(,0),直线l不过点M,求△ABM的面积.
巩固应用
追问:在例2中,针对结论还可以提出哪些问题?
课堂小结
1.你能从本节课的学习中总结出“单元小结”的学习路径吗?
2.你能归纳一下本节课我们从哪些角度进行了单元小结?
3.你认为圆锥曲线的“统一性”体现了哪些数学思想方法?
从“知识结构”及圆锥曲线的“统一性”两个方面进行了单元小结.
数形结合、方程、化归与转化、分类与整合、特殊与一般等思想方法.
课后作业
完成教材—— 第145页 复习参考题3 第1,2, 3,4,5,6,7,8,9,10,11,12,13,14,15,16题
第三章 圆锥曲线的方程复习小结
高二数学选择性必修第一册
问题1.你能用表格或框图画出本章知识结构图吗?
结构导图
问题2:用坐标法研究圆锥曲线的具体过程是什么?
问题探究
背景
定义
方程
性质
应用
问题3:在椭圆、双曲线、抛物线三类圆锥曲线的研究中,椭圆是研究的第一类圆锥曲线,对双曲线、抛物线的研究,我们采用的是类比的方法,你能说说具体的类比内容吗?
类比
内容
方法
定义
方程的推导过程
几何性质
定义→标准方程→几何性质→应用
几何性质的研究方法
问题探究
椭圆:
平面内与两个定点的距离的和等于常数(大于)的点的轨迹.
双曲线:
平面内与两个定点的距离的差的绝对值等于非零常数(小于)的点的轨迹.
追问1:如何类比椭圆的定义研究双曲线的定义?
问题探究
追问2:我们如何类比椭圆的标准方程的推导过程,推导双曲线的标准方程?
移项
平方
化简
平方
整理
方程
问题探究
追问3:如何类比椭圆几何性质的研究过程,研究双曲线的几何性质?
问题探究
范围
.
.
问题4:圆锥曲线的“统一性”体现在哪些方面?你如何理解圆锥曲线的“统一性”?
问题探究
来源统一
定义统一
研究过程方法统一
问题探究
问题5:如何用直线与圆锥曲线的方程判断它们之间的位置关系?
问题探究
1
3
2
联立直线的方程和圆锥曲线的方程
判断位置关系
判断解的个数
例.判断直线与双曲线的交点个数.
解:联立方程,得 解得,故,
此时,故方程组的解为
故直线与双曲线有一个交点.
典例分析
练习.已知直线与双曲线的没有交点,求的取值范围.
巩固应用
直线与椭圆的位置关系
,相离
,相切
,相交
归纳小结
直线与双曲线的位置关系
一元二次方程
,相离
,相切
,相交
一元一次方程
一个根,相交
问题探究
直线与抛物线的位置关系
一元二次方程
,相离
,相切
,相交
一元一次方程
一个根,相交
问题探究
【例1】一动圆与两圆:x2+y2=1和x2+y2-6x+5=0都外切,则动圆圆心的轨迹为( )
A.抛物线 B.双曲线 C.双曲线的一支 D.椭圆
【例2】在平面直角坐标系xOy中,椭圆C的中心为原点,焦点F1,F2在x轴上,离心率为 .过F1的直线l交C于A,B两点,且△ABF2的周长为4,求椭圆C的方程.
典例分析
[解析] (1)x2+y2=1是圆心为原点,半径为1的圆,
x2+y2-6x+5=0化为标准方程为(x-3)2+y2=4,是圆心为A(3,0),半径为2的圆.
设所求动圆圆心为P,动圆半径为r,则 |PA|-|PO|=1<|AO|=3,符合双曲线的定义,所以动圆圆心的轨迹为双曲线的一支.
(2)设椭圆方程为 +=1(a>b>0),因为AB过F1且A,B在椭圆上,如图所示,
则△ABF2的周长为|AB|+|AF2|+|BF2|=|AF1|+|AF2|+|BF1|+|BF2|=4a=4,∴a=.
又离心率e==,∴c=1,∴b2=a2-c2=1,
∴椭圆C的方程为 +=1.
[答案] (1)C (2) +=1.
【类题通法】“回归定义”解题的三点应用
应用一:在求轨迹方程时,若所求轨迹符合某种圆锥曲线的定义,则根据圆锥曲线的定义,写出所求的轨迹方程;
应用二:涉及椭圆、双曲线上的点与两个定点构成的三角形问题时,常用定义结合解三角形的知识来解决;
应用三:在求有关抛物线的最值问题时,常利用定义把到焦点的距离转化为到准线的距离,结合几何图形,利用几何意义去解决.
提醒:应用定义解题时注意圆锥曲线定义中的限制条件.
【例2】已知椭圆
=1(a>b>0)的离心率为,F1,F2为左右焦点,过F1的直线l交C于A,B两点,且△ABF2的周长为4,
(1)求椭圆C的方程.
(2)若直线l过点M(,),求△ABF2的面积.
巩固应用
追问:在例2中,针对结论还可以提出哪些问题?
解:(2)∵F1(-1,0),∴直线MF1的方程为y=(x+1),
由 得2x2+2x-1=0.
∵Δ=22-4×2×(-1)=12>0,所以直线与椭圆有两个公共点,
设为A(x1,y1),B(x2,y2),则
∴|AB|=·|x1-x2|=·=·=,
又点F2到直线MF1的距离d=,故S△ABF2=|AB|·d=.
【例2】已知椭圆=1(a>b>0)的离心率为,F1,F2为左右焦点,过F1的直线l交C于A,B两点,且△ABF2的周长为4,
(1)求椭圆C的方程.
(2)若点M(,0),直线l不过点M,求△ABM的面积.
巩固应用
追问:在例2中,针对结论还可以提出哪些问题?
课堂小结
1.你能从本节课的学习中总结出“单元小结”的学习路径吗?
2.你能归纳一下本节课我们从哪些角度进行了单元小结?
3.你认为圆锥曲线的“统一性”体现了哪些数学思想方法?
从“知识结构”及圆锥曲线的“统一性”两个方面进行了单元小结.
数形结合、方程、化归与转化、分类与整合、特殊与一般等思想方法.
课后作业
完成教材—— 第145页 复习参考题3 第1,2, 3,4,5,6,7,8,9,10,11,12,13,14,15,16题
