人教A版(2019)选择性必修第一册 3.2.1 双曲线及其标准方程 课件(共29张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第一册 3.2.1 双曲线及其标准方程 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-06 15:06:29 | ||
图片预览




文档简介
3.2.1 双曲线及其标准方程
人教版选择性必修第一册 第三章 第二节
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
椭圆及其标准方程
圆锥曲线
椭圆的简单几何性质
椭圆
双曲线
双曲线及其标准方程
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
一
二
三
目标与素养
理解双曲线的几何特征及定义,达到数学抽象核心素养学业质量水平二的层次.
经历双曲线标准方程的推导过程,掌握双曲线的标准方程,达到逻辑推理核心素养学业质量水平二的层次.
能利用双曲线的标准方程解决问题,达到数学运算的核心所有水平学业质量水平二的层次.
双曲线的定义,几何特征与标准方程
双曲线标准方程推导及标准方程的问题
重点
难点
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
复习回顾,类比学习
我们知道,平面内与两个定点F1, F2的距离的和等于常数(大于|F1F2|)的点的轨迹是椭圆.一个自然的问题是:平面内与两个定点的距离的差等于常数的点的轨迹是什么?下面我们先用信息技术探究一下.
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
探究1:如图,在直线l上取两个定点A,B,P是直线l上的动点,在平面内, 取定点F1, F2,以点F1为圆心、线段PA为半径作圆,再以F2为圆心、线段PB为半径作圆.
创设情境,引入新课
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
A
B
P
F1
F2
M
M1
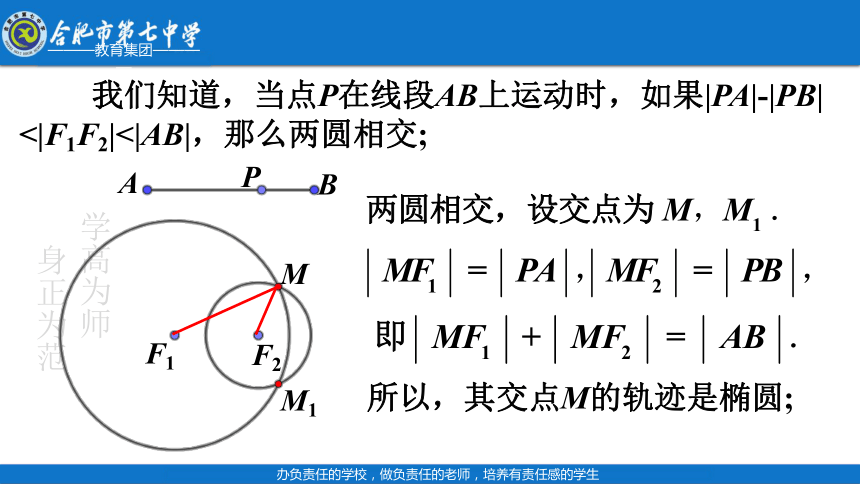
我们知道,当点P在线段AB上运动时,如果|PA|-|PB|
<|F1F2|<|AB|,那么两圆相交;
所以,其交点M的轨迹是椭圆;
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
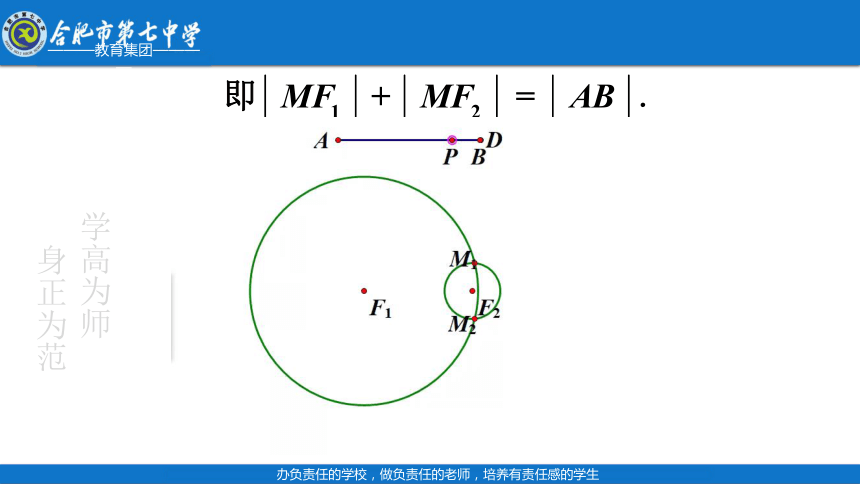
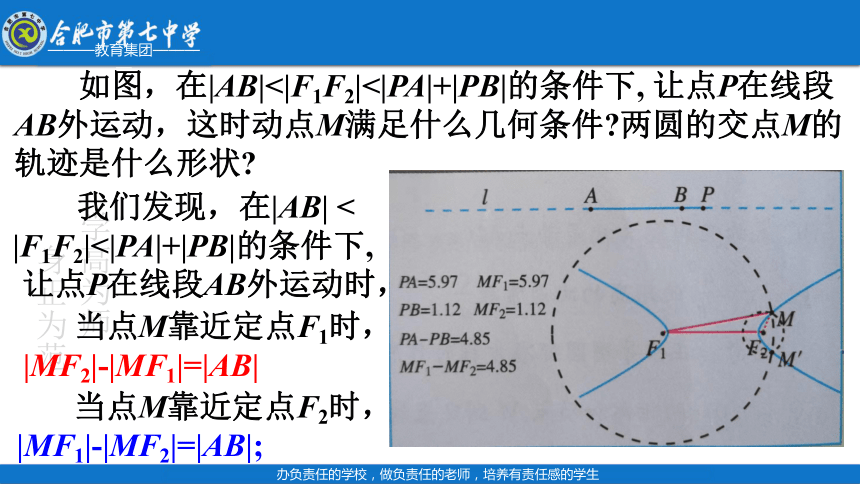
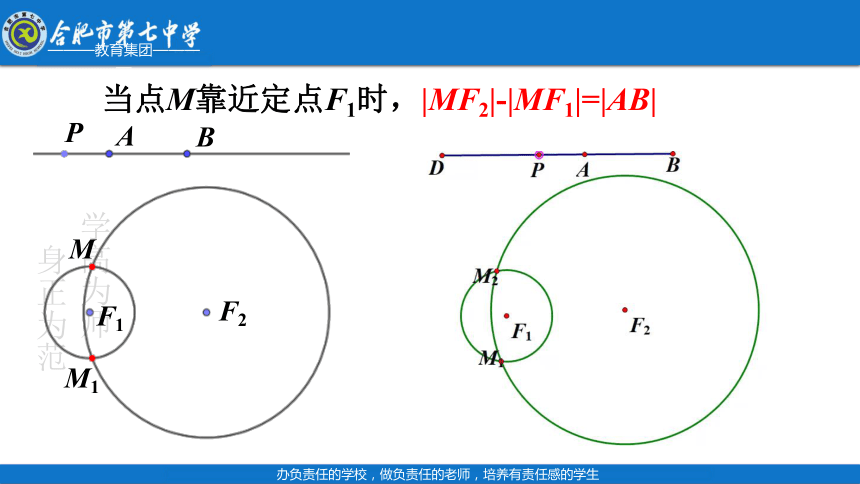
如图,在|AB|<|F1F2|<|PA|+|PB|的条件下, 让点P在线段AB外运动,这时动点M满足什么几何条件?两圆的交点M的轨迹是什么形状?
我们发现,在|AB| <
|F1F2|<|PA|+|PB|的条件下,
让点P在线段AB外运动时,
当点M靠近定点F2时,|MF1|-|MF2|=|AB|;
当点M靠近定点F1时,|MF2|-|MF1|=|AB|
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
A
B
P
F1
F2
M
M1
当点M靠近定点F1时,|MF2|-|MF1|=|AB|
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
A
B
P
F1
F2
M
M1
当点M靠近定点F2时,|MF1|-|MF2|=|AB|;
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
总之,点M与两个定点F1,F2距离的差的绝对值|AB|是一个常数(|AB|<|F1F2|),这时,点M的轨迹是不同于椭圆的曲线,它分左右两支.
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
一、双曲线定义
我们把平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹叫做双曲线.
这两个定点叫做双曲线的焦点,
两焦点间的距离叫做双曲线的焦距.
符号表述:||MF1|-|MF2||=2a<|F1F2|=2c
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
平面内与两定点的距离的差等于常数2a (2a<|F1F2| )的
轨迹是什么?
|MF2|-|MF1|=2a,图形为双曲线的左支.
|MF1|-|MF2|=2a,图形为双曲线的右支;
问1:
与两定点的距离的差的绝对值等于常数(当2a=|F1F2|时 )的轨迹是什么?
在直线F1F2上且 以F1、F2为端点向外的两条射线.
问2:
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
问3:
与两定点的距离的差的绝对值等于常数(当2a>|F1F2| )时的轨迹是什么?
不存在
问4:
当||MF1|-|MF2||= 2a=0时,
M点的轨迹是线段F1F2的垂直平分线 。
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
建立直角坐标系
列等式
设点坐标
代入坐标
化简方程
求曲线方程的一般步骤是什么?
探究2:类比求椭圆标准方程的过程,我们如何建立适当的坐标系,得出双曲线的方程?
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
设 M(x, y) 是双曲线上任意一点,
双曲线的焦距为 2c( c > 0),
则有F1(-c , 0) , F2 (c , 0).
又设||MF1|-|MF2||= 2a( a为大于0的常数, aF1
F2
M
x
y
O
我们取经过两焦点F1和F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系Oxy(如图).
由双曲线的定义,双曲线就是下列点的集合:
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
由双曲线的定义,双曲线就是下列点的集合:
????={????|||????????1|?|????????2||=2????,0<2????<|????1????2|}.
因为|????????1|=(????+????)2+????2,|????????2|=(?????????)2+????2,
所以(????+????)2+????2?(?????????)2+????2=±2????. ①
?
类比椭圆标准方程的化简过程,化简①,得
(????2?????2)????2?????2????2=????2(????2?????2),两边同时除以????2(????2?????2),得 ????2????2?????2????2?????2=1.
?
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
从上述过程中可以看到,双曲线上任意一点的坐标
(x,y)都是方程②的解;
类比椭圆标准方程的建立过程 , 令b2=c2-a2 , 其中b>0,
代入上式得:
????2????2?????2????2=1(????>0,????>0).②
?
以方程②的解为坐标的点(x,y)与双曲线的两个焦点F1(-c,0),F2(c,0)的距离之差的绝对值都为2a,即以方程②的解为坐标的点都在双曲线上.
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
二、双曲线的标准方程
我们称方程②是双曲线的方程,这个
方程叫做双曲线的标准方程.
它表示焦点在 x 轴上,两个焦点分别是 F1(- c,0),F2(c,0)的双曲线,
这里c2=a2+b2 .
????2????2?????2????2=1(????>0,????>0).②
?
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
思考: 类比焦点在y轴上的椭圆的标准方程, 焦点在y轴上的双曲线的标准方程是什么?
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
这个方程也是双曲线的标准方程.
如图,双曲线的焦距为 2c ,焦点
分别是 F1(0,- c),F2(0,c).a ,b 的
意义同上,这时双曲线的方程是
看x2,y2前的系数,哪一个为正,则焦点在哪一个轴上------焦点跟着正项走.
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
双曲线两种标准方程的特点
如果x2的系数是正的,则焦点在x轴上;
如果y2的系数是正的,则焦点在y轴上.
x
F1
F2
y
O
M(x,y)
x
y
O
M(x,y)
F1
F2
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
小试牛刀.判断正误.
(1)在双曲线标准方程????2????2?????2????2=1中,????>0,????>0,且????≠????.( )
(2)方程????22?????23=1表示焦点在????轴上的双曲线.( )
(3)方程????????2+????????2=1(????????<0)表示双曲线.( )
?
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
例1 已知双曲线的焦点F1(-5, 0), F2(5, 0), 双曲线上一点P与F1 , F2的距离差的绝对值等于6, 求双曲线的标准方程.
解:因为双曲线的焦点在x轴上,所以设它的标准方程为
所以,双曲线的标准方程为
由 2c=10,2a=6 . 即 c=5,a=3,
因此 b2=c2-a2=25-9=16.
应用举例,解难释疑
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
分析 : 先根据题意判断轨迹的形状. 由声速及A, B两处听到炮弹爆炸声的时间差, 可知A, B两处与爆炸点的距离的差为常数. 所以爆炸点在以A, B为焦点的双曲线上 . 因为爆炸点离A处比离B处远 , 所以爆炸点在靠近B处双曲线的一支上.
例2 已知A, B两地相距800m, 在A地听到炮弹爆炸声比在B地晚2s, 且声速为340m/s, 求炮弹爆炸点的轨迹方程.
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
解:如图,建立平面直角坐标系????????????,使????,????两点在????轴上,并且原点????与线段????????的中点重合.
?
设炮弹爆炸点????的坐标为(????,????),
则|????????|?|????????|=340×2=680,即2????=680,????=340.
?
又|????????|=800,所以2????=800,????=400,????2=????2?????2=44400.
?
所以,炮弹爆炸点的轨迹方程为????2115600?????244400=1(????≥340).
?
因为|????????|?|????????|=680>0,所以点的轨迹是双曲线的右支,
因此????≥340.
?
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
归纳感悟,总结提升
求双曲线标准方程的方法
一种方法:
二类方程:
三个意识:
求美意识, 求简意识,联系意识
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
教科书习题3.2 第1、2题.
基础巩固
分层作业,激发新疑
能力提升
已知圆????1:(????+3)2+????2=1和圆????2:(?????3)2+????2=9,动圆????同时与圆????1及圆????2相外切,求动圆圆心????的轨迹方程.
?
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
拓展探究:如图设 A,B 两点的坐标分别
为(-5, 0),(5, 0),直线 AM,BM 相交于点
M,且它们的斜率之积是 ????????,试求点M 的轨迹方程,并由点 M 的轨迹方程判断轨迹的形状,与3.1 例 3 比较,你有什么发现?
人教版选择性必修第一册 第三章 第二节
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
椭圆及其标准方程
圆锥曲线
椭圆的简单几何性质
椭圆
双曲线
双曲线及其标准方程
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
一
二
三
目标与素养
理解双曲线的几何特征及定义,达到数学抽象核心素养学业质量水平二的层次.
经历双曲线标准方程的推导过程,掌握双曲线的标准方程,达到逻辑推理核心素养学业质量水平二的层次.
能利用双曲线的标准方程解决问题,达到数学运算的核心所有水平学业质量水平二的层次.
双曲线的定义,几何特征与标准方程
双曲线标准方程推导及标准方程的问题
重点
难点
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
复习回顾,类比学习
我们知道,平面内与两个定点F1, F2的距离的和等于常数(大于|F1F2|)的点的轨迹是椭圆.一个自然的问题是:平面内与两个定点的距离的差等于常数的点的轨迹是什么?下面我们先用信息技术探究一下.
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
探究1:如图,在直线l上取两个定点A,B,P是直线l上的动点,在平面内, 取定点F1, F2,以点F1为圆心、线段PA为半径作圆,再以F2为圆心、线段PB为半径作圆.
创设情境,引入新课
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
A
B
P
F1
F2
M
M1
我们知道,当点P在线段AB上运动时,如果|PA|-|PB|
<|F1F2|<|AB|,那么两圆相交;
所以,其交点M的轨迹是椭圆;
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
如图,在|AB|<|F1F2|<|PA|+|PB|的条件下, 让点P在线段AB外运动,这时动点M满足什么几何条件?两圆的交点M的轨迹是什么形状?
我们发现,在|AB| <
|F1F2|<|PA|+|PB|的条件下,
让点P在线段AB外运动时,
当点M靠近定点F2时,|MF1|-|MF2|=|AB|;
当点M靠近定点F1时,|MF2|-|MF1|=|AB|
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
A
B
P
F1
F2
M
M1
当点M靠近定点F1时,|MF2|-|MF1|=|AB|
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
A
B
P
F1
F2
M
M1
当点M靠近定点F2时,|MF1|-|MF2|=|AB|;
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
总之,点M与两个定点F1,F2距离的差的绝对值|AB|是一个常数(|AB|<|F1F2|),这时,点M的轨迹是不同于椭圆的曲线,它分左右两支.
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
一、双曲线定义
我们把平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹叫做双曲线.
这两个定点叫做双曲线的焦点,
两焦点间的距离叫做双曲线的焦距.
符号表述:||MF1|-|MF2||=2a<|F1F2|=2c
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
平面内与两定点的距离的差等于常数2a (2a<|F1F2| )的
轨迹是什么?
|MF2|-|MF1|=2a,图形为双曲线的左支.
|MF1|-|MF2|=2a,图形为双曲线的右支;
问1:
与两定点的距离的差的绝对值等于常数(当2a=|F1F2|时 )的轨迹是什么?
在直线F1F2上且 以F1、F2为端点向外的两条射线.
问2:
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
问3:
与两定点的距离的差的绝对值等于常数(当2a>|F1F2| )时的轨迹是什么?
不存在
问4:
当||MF1|-|MF2||= 2a=0时,
M点的轨迹是线段F1F2的垂直平分线 。
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
建立直角坐标系
列等式
设点坐标
代入坐标
化简方程
求曲线方程的一般步骤是什么?
探究2:类比求椭圆标准方程的过程,我们如何建立适当的坐标系,得出双曲线的方程?
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
设 M(x, y) 是双曲线上任意一点,
双曲线的焦距为 2c( c > 0),
则有F1(-c , 0) , F2 (c , 0).
又设||MF1|-|MF2||= 2a( a为大于0的常数, a
F2
M
x
y
O
我们取经过两焦点F1和F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系Oxy(如图).
由双曲线的定义,双曲线就是下列点的集合:
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
由双曲线的定义,双曲线就是下列点的集合:
????={????|||????????1|?|????????2||=2????,0<2????<|????1????2|}.
因为|????????1|=(????+????)2+????2,|????????2|=(?????????)2+????2,
所以(????+????)2+????2?(?????????)2+????2=±2????. ①
?
类比椭圆标准方程的化简过程,化简①,得
(????2?????2)????2?????2????2=????2(????2?????2),两边同时除以????2(????2?????2),得 ????2????2?????2????2?????2=1.
?
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
从上述过程中可以看到,双曲线上任意一点的坐标
(x,y)都是方程②的解;
类比椭圆标准方程的建立过程 , 令b2=c2-a2 , 其中b>0,
代入上式得:
????2????2?????2????2=1(????>0,????>0).②
?
以方程②的解为坐标的点(x,y)与双曲线的两个焦点F1(-c,0),F2(c,0)的距离之差的绝对值都为2a,即以方程②的解为坐标的点都在双曲线上.
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
二、双曲线的标准方程
我们称方程②是双曲线的方程,这个
方程叫做双曲线的标准方程.
它表示焦点在 x 轴上,两个焦点分别是 F1(- c,0),F2(c,0)的双曲线,
这里c2=a2+b2 .
????2????2?????2????2=1(????>0,????>0).②
?
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
思考: 类比焦点在y轴上的椭圆的标准方程, 焦点在y轴上的双曲线的标准方程是什么?
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
这个方程也是双曲线的标准方程.
如图,双曲线的焦距为 2c ,焦点
分别是 F1(0,- c),F2(0,c).a ,b 的
意义同上,这时双曲线的方程是
看x2,y2前的系数,哪一个为正,则焦点在哪一个轴上------焦点跟着正项走.
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
双曲线两种标准方程的特点
如果x2的系数是正的,则焦点在x轴上;
如果y2的系数是正的,则焦点在y轴上.
x
F1
F2
y
O
M(x,y)
x
y
O
M(x,y)
F1
F2
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
小试牛刀.判断正误.
(1)在双曲线标准方程????2????2?????2????2=1中,????>0,????>0,且????≠????.( )
(2)方程????22?????23=1表示焦点在????轴上的双曲线.( )
(3)方程????????2+????????2=1(????????<0)表示双曲线.( )
?
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
例1 已知双曲线的焦点F1(-5, 0), F2(5, 0), 双曲线上一点P与F1 , F2的距离差的绝对值等于6, 求双曲线的标准方程.
解:因为双曲线的焦点在x轴上,所以设它的标准方程为
所以,双曲线的标准方程为
由 2c=10,2a=6 . 即 c=5,a=3,
因此 b2=c2-a2=25-9=16.
应用举例,解难释疑
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
分析 : 先根据题意判断轨迹的形状. 由声速及A, B两处听到炮弹爆炸声的时间差, 可知A, B两处与爆炸点的距离的差为常数. 所以爆炸点在以A, B为焦点的双曲线上 . 因为爆炸点离A处比离B处远 , 所以爆炸点在靠近B处双曲线的一支上.
例2 已知A, B两地相距800m, 在A地听到炮弹爆炸声比在B地晚2s, 且声速为340m/s, 求炮弹爆炸点的轨迹方程.
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
解:如图,建立平面直角坐标系????????????,使????,????两点在????轴上,并且原点????与线段????????的中点重合.
?
设炮弹爆炸点????的坐标为(????,????),
则|????????|?|????????|=340×2=680,即2????=680,????=340.
?
又|????????|=800,所以2????=800,????=400,????2=????2?????2=44400.
?
所以,炮弹爆炸点的轨迹方程为????2115600?????244400=1(????≥340).
?
因为|????????|?|????????|=680>0,所以点的轨迹是双曲线的右支,
因此????≥340.
?
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
归纳感悟,总结提升
求双曲线标准方程的方法
一种方法:
二类方程:
三个意识:
求美意识, 求简意识,联系意识
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
教科书习题3.2 第1、2题.
基础巩固
分层作业,激发新疑
能力提升
已知圆????1:(????+3)2+????2=1和圆????2:(?????3)2+????2=9,动圆????同时与圆????1及圆????2相外切,求动圆圆心????的轨迹方程.
?
———教育集团————
学高为师
身正为范
办负责任的学校,做负责任的老师,培养有责任感的学生
拓展探究:如图设 A,B 两点的坐标分别
为(-5, 0),(5, 0),直线 AM,BM 相交于点
M,且它们的斜率之积是 ????????,试求点M 的轨迹方程,并由点 M 的轨迹方程判断轨迹的形状,与3.1 例 3 比较,你有什么发现?
