2026年中考数学一轮复习 二元一次方程组(含解析)
文档属性
| 名称 | 2026年中考数学一轮复习 二元一次方程组(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1014.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-08 06:41:30 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2026年中考数学一轮复习 二元一次方程组
一.选择题(共15小题)
1.已知方程组的解x为正数,y为非负数,给出下列结论:
①﹣3<a≤1;
②当时,x=y;
③当a=﹣2时,方程组的解也是方程x+y=5+a的解;
④若x≤1,则y≥2.
其中正确的是( )
A.①② B.②③ C.③④ D.②③④
2.已知关于x,y的方程组,将此方程组的两个方程左右两边分别对应相加,得到一个新的方程,当m每取一个值时,就有一个方程,这些方程有一个公共解,这个公共解为( )
A. B. C. D.
3.我的家用小轿车配备了一种牌子的轮胎,装在前轮其可使用的距离为40000千米,装在后轮则可使用60000千米,如果将前后轮交换使用,则用这一组四个轮胎可行驶的最大距离为( )
A.44000千米 B.48000千米 C.50000千米 D.52000千米
4.在关于x,y的二元一次方程组的下列说法中,正确的是( )
①当a=3时,方程的两根互为相反数;②当且仅当a=﹣4时,解得x与y相等;③x,y满足关系式x+5y=﹣12;④若9x 27y=81,则a=10.
A.①③ B.①② C.①②③ D.①②③④
5.甲、乙、丙三家艺术中心为表彰进步学生,准备去文具店采购签字笔、笔记本、钢笔三种文具,签字笔、笔记本、钢笔单价分别为8元、10元、25元.乙艺术中心采购签字笔数量是甲的6倍,笔记本数量是甲的12倍,钢笔数量是甲的8倍,丙采购的签字笔数量是甲的3倍,笔记本数量是甲的9倍,钢笔数量和甲相同.三家艺术中心采购总费用为2850元,丙艺术中心比甲艺术中心总费用多464元,则甲艺术中心采购总费用为( )元
A.237 B.350 C.425 D.901
6.实数x、y、z且x+y+z≠0,x,z,则下列等式成立的是( )
A.x2﹣y2=z2 B.xy=z C.x2+y2=z2 D.x+y=z
7.已知关于x,y的方程组给出下列结论:
①当a=1时,方程组的解也是x+y=2a+1的解;
②无论a取何值,x,y的值不可能是互为相反数;
③x,y都为自然数的解有4对;
④若2x+y=8,则a=2.
正确的有几个( )
A.1 B.2 C.3 D.4
8.若关于x、y的二元一次方程组的解为,则方程组的解是( )
A. B. C. D.
9.已知关于x,y的二元一次方程组,给出下列结论中正确的是( )
①当这个方程组的解x,y的值互为相反数时,a=﹣2;
②当a=1时,方程组的解也是方程x+y=4+2a的解;
③无论a取什么实数,x+2y的值始终不变;
④若用x表示y,则y;
A.①② B.②③ C.②③④ D.①③④
10.普通火车从绵阳至成都历时大约2小时,成绵城际快车开通后,时间大大缩短至几十分钟,现假定普通火车与城际快车两列对开的火车于同一时刻发车,其中普通火车由成都至绵阳,城际快车由绵阳至成都,这两车在途中相遇之后,各自用了80分钟和20分钟到达自己的终点绵阳、成都,则城际快车的平均速度是普通火车平均速度的( )倍.
A.2 B.2.5 C.3 D.4
11.已知关于x,y的二元一次方程组,给出下列结论中正确的是( )
①当这个方程组的解x,y的值互为相反数时,a=﹣2;
②当a=1时,方程组的解也是方程x+y=4+2a的解;
③无论a取什么实数,x+2y的值始终不变;
④若用x表示y.则;
A.①②③ B.①②④ C.①③④ D.②③④
12.如图,长方形ABCD被分成3个正方形和2个长方形后仍是中心对称图形,设长方形ABCD的周长为l,若图中3个正方形和2个长方形的周长和为l,则标号为①的正方形的边长为( )
A.l B.l C.l D.l
13.已知关于x,y的方程组,其中﹣3≤a≤1,下列命题正确的个数为( )
①当a=﹣2时,x、y的值互为相反数;
②是方程组的解;
③当a=1时,方程组的解也是方程x+y=4﹣a的解;
④若x≤1,则1≤y≤4.
A.1个 B.2个 C.3个 D.4个
14.我们知道自行车一般是由后轮驱动,因此,后轮胎的磨损要超过前轮胎,假设前轮行驶5000千米报废,后轮行驶3000千米报废,如果在自行车行驶若干千米后,将前后轮进行对换,那么这对轮胎最多可以行驶( )
A.4000 千米 B.3750 千米 C.4250 千米 D.3250 千米
15.已知是关于x,y的二元一次方程mx+ny=7的解,则代数式4m+6n﹣3的值是( )
A.14 B.11 C.7 D.4
二.填空题(共13小题)
16.若关于x、y的二元一次方程组的解满足,则满足条件的m的所有非负整数值为 .
17.在长方形ABCD中放入六个完全相同的小长方形,所标尺寸如图所示,则小长方形的宽CE为 cm.
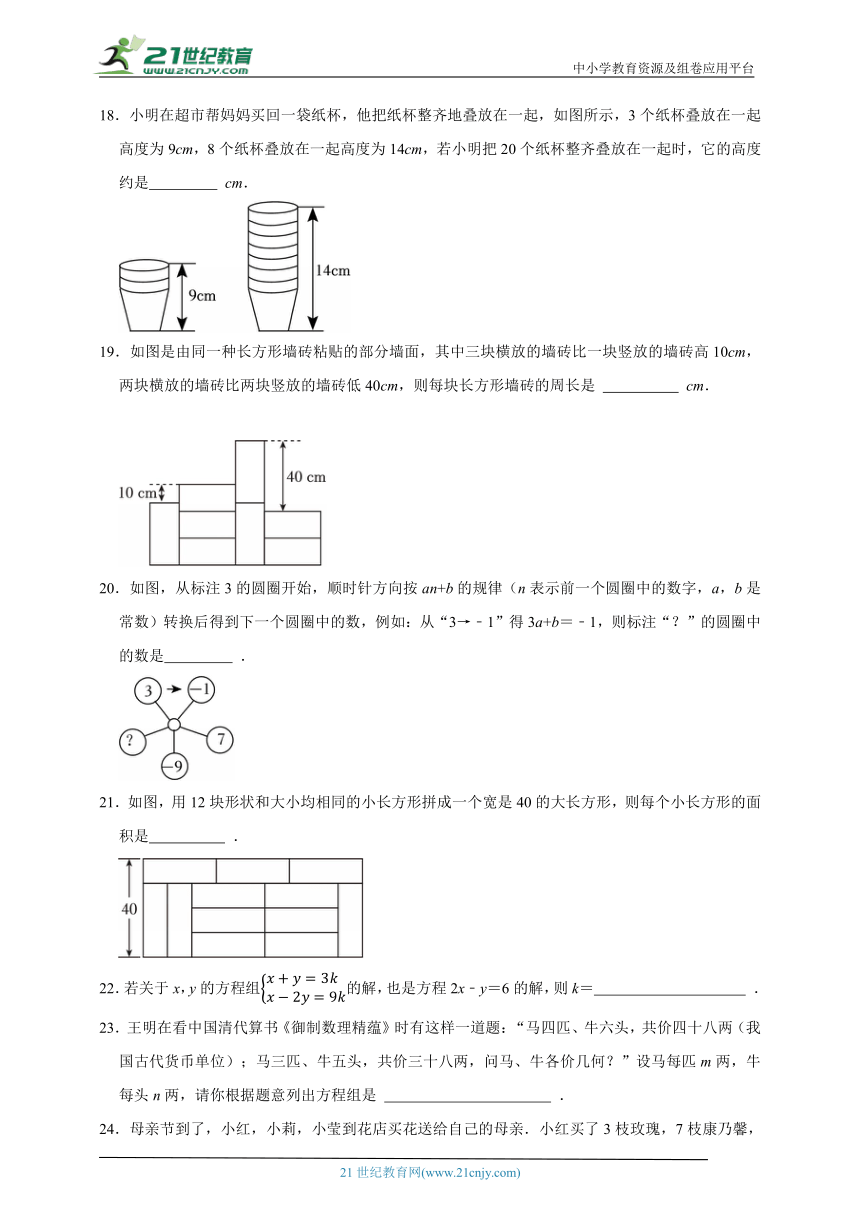
18.小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图所示,3个纸杯叠放在一起高度为9cm,8个纸杯叠放在一起高度为14cm,若小明把20个纸杯整齐叠放在一起时,它的高度约是 cm.
19.如图是由同一种长方形墙砖粘贴的部分墙面,其中三块横放的墙砖比一块竖放的墙砖高10cm,两块横放的墙砖比两块竖放的墙砖低40cm,则每块长方形墙砖的周长是 cm.
20.如图,从标注3的圆圈开始,顺时针方向按an+b的规律(n表示前一个圆圈中的数字,a,b是常数)转换后得到下一个圆圈中的数,例如:从“3→﹣1”得3a+b=﹣1,则标注“?”的圆圈中的数是 .
21.如图,用12块形状和大小均相同的小长方形拼成一个宽是40的大长方形,则每个小长方形的面积是 .
22.若关于x,y的方程组的解,也是方程2x﹣y=6的解,则k= .
23.王明在看中国清代算书《御制数理精蕴》时有这样一道题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两,问马、牛各价几何?”设马每匹m两,牛每头n两,请你根据题意列出方程组是 .
24.母亲节到了,小红,小莉,小莹到花店买花送给自己的母亲.小红买了3枝玫瑰,7枝康乃馨,1枝百合花,付了14元;小莉买了4枝玫瑰,10枝康乃馨,1枝百合花,付了16元;小莹买上面三种花各2枝,则她应付 元.
25.幻方是一种中国传统游戏,我国古代的《洛书》中记载了最早的幻方——九宫格,其规则是将数字填在正方形格子中,使每一行、每一列和两条对角线上的3个数字的和都相等.例如图①就是一个幻方.
(Ⅰ)图②是一个未完成的幻方,则x+y的结果为 ;
(Ⅱ)图③中的x为 (用含a的式子表示).
26.《九章算术》记载了这样一个问题:“今有善田一亩,价三百;恶田七亩,价五百.今并买一顷,价钱一万,问善田几何?“意思是:当下良田1亩,价值300钱;薄田7亩,价值500钱.现在共买100亩,价值10000钱.根据条件,良田买了 亩.(注:1顷=100亩)
27.用8个大小完全相同的长方形在平面直角坐标系中摆成如图所示的图案,已知点A(4,10),则点B的坐标是 .
28.我国古典数学文献《增删算法统宗 六均输》中有一个“隔沟计算”的问题:“甲乙隔沟牧放,二人暗里参详,甲云得乙九只羊,多乙一倍之上,乙说得甲九只,两家之数相当,二人闲坐恼心肠,画地算了半晌”其大意为:甲、乙两人一起放牧,两人心里暗中数羊.如果乙给甲9只羊,那么甲的羊数为乙的2倍;如果甲给乙9只羊,那么两人的羊数相同,请问甲,乙各有多少只羊?设甲有羊x只,乙有羊y只,根据题意,可列方程组为 .
三.解答题(共6小题)
29.解方程组:
(1);
(2).
30.袁隆平爷爷多次说:“中国人要把饭碗牢牢地端在自己的手里!”为扩大粮食生产规模,稻田公园生产基地计划投入一笔资金购进甲、乙两种农机,已知购进1件甲种农机和1件乙种农机共需2万元,购进2件甲种农机和3件乙种农机共需5.5万元.
(1)求购进1件甲种农机和1件乙种农机各需多少万元?
(2)若该粮食生产基地计划购进甲、乙两种农机共10件,且投入资金不少于9.5万元且不超过12万元,则有哪几种购买方案?哪种购买方案需要的资金最少,最少资金是多少?
31.秋季由于气候干燥,天气转冷,用火用电情况大量增加,起火原因增多,火灾危险性加大.为了加强秋季防火用电安全,提高同学们的安全防范意识,某学校组织了“用电安全”知识竞赛,对表现优异的班级进行奖励,学校购买了若干支钢笔和中性笔.购买5支钢笔和10支中性笔共需110元;购买8支钢笔和6支中性笔共需126元.
(1)求购买1支钢笔和1支中性笔各需多少元;
(2)若学校购买钢笔和中性笔共200支,其中钢笔的数量不得少于中性笔数量的,且总支出不超过1364元,那学校有哪几种购买方案?
32.为响应“全民植树增绿,共建美丽中国”的号召,某学校组织学生到郊外参加义务植树活动,并准备了A,B两种食品作为午餐.这两种食品每包质量均为50g,营养成分如图所示.
(1)若要从这两种食品中摄入3900KJ热量和60g蛋白质,应选用A,B两种食品各多少包?
(2)运动量大的人或青少年对蛋白质的摄入量应更多.若要从这两种食品中摄入的蛋白质含量等于80g,应选用A,B两种食品各多少包(A,B两种食品都选且不能拆分)?
33.如图是中国邮政发行的《数学之美》的邮票,其中一张圆周率邮票面值为80分,莫比乌斯带邮票面值为1.50元.小宇购买这两种邮票共7张,恰好花了7元,求小宇购买这两种邮票各多少张.
34.“脐橙结硕果,香飘引客来”,赣南脐橙以其“外表光洁美观,肉质脆嫩,风味浓甜芳香”的特点饮誉中外.现欲将一批脐橙运往外地销售,若用2辆A型车和1辆B型车载满脐橙一次可运走10吨;用1辆A型车和2辆B型车载满脐橙一次可运走11吨.现有脐橙31吨,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满脐橙.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都载满脐橙一次可分别运送多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若1辆A型车需租金100元/次,1辆B型车需租金120元/次.请选出费用最少的租车方案,并求出最少租车费.
2026年中考数学一轮复习 二元一次方程组
参考答案与试题解析
一.选择题(共15小题)
1.已知方程组的解x为正数,y为非负数,给出下列结论:
①﹣3<a≤1;
②当时,x=y;
③当a=﹣2时,方程组的解也是方程x+y=5+a的解;
④若x≤1,则y≥2.
其中正确的是( )
A.①② B.②③ C.③④ D.②③④
【答案】B
【分析】用加减法解出方程组,根据方程组的解对各个选项进行判断即可.
【解答】解:
①+②得,x=3+a,
①﹣②得,y=﹣2a﹣2,
①由题意得,3+a>0,a>﹣3,
﹣2a﹣2≥0,a≤﹣1,
∴﹣3<a≤﹣1,①不正确;
②3+a=﹣2a﹣2,a,②正确;
③a=﹣2时,x+y=1﹣a=3,5+a=3,③正确;
④x≤1时,﹣3<a≤﹣2,则4>﹣2a﹣2≥2,④错.
故选:B.
【点评】本题考查的是二元一次方程组的解法和一元一次不等式的解法,正确解出方程组是解题的关键,注意方程与不等式的综合运用.
2.已知关于x,y的方程组,将此方程组的两个方程左右两边分别对应相加,得到一个新的方程,当m每取一个值时,就有一个方程,这些方程有一个公共解,这个公共解为( )
A. B. C. D.
【答案】C
【分析】根据题意①+②得x﹣y﹣9+m(x+y﹣1)=0,然后根据题意列出方程组即可求得公共解.
【解答】解:①+②得,
x+my+mx﹣y=9+m
x﹣y﹣9+mx+my﹣m=0
x﹣y﹣9+m(x+y﹣1)=0
根据题意,这些方程有一个公共解,与m的取值无关,
解得
所以这个公共解为
故选:C.
【点评】本题考查了二元一次方程组的解法,解题关键是利用筛选法解二元一次方程组.
3.我的家用小轿车配备了一种牌子的轮胎,装在前轮其可使用的距离为40000千米,装在后轮则可使用60000千米,如果将前后轮交换使用,则用这一组四个轮胎可行驶的最大距离为( )
A.44000千米 B.48000千米 C.50000千米 D.52000千米
【答案】B
【分析】设每个新轮胎报废时的总磨损量为k,一组新轮胎交换位置前走了xkm,交换位置后走了ykm,根据交换前磨损总量和交换后的磨损总量相等,可列出方程组,解方程组即可.
【解答】解:设每个新轮胎报废时的总磨损量为k,则安装在前轮的轮胎每行驶1km磨损量为,安装在后轮的轮胎每行驶1km的磨损量为,
又设一对新轮胎交换位置前走了xkm,交换位置后走了ykm,
分别以一个轮胎的总磨损量为等量关系列方程,有
,
两式相加,得2k,
则x+y=48000,即这一组四个轮胎可行驶的最大距离为48000米.
故选:B.
【点评】本题考查了应用类问题,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解,准确地找到等量关系并用方程组表示出来是解题的关键.
4.在关于x,y的二元一次方程组的下列说法中,正确的是( )
①当a=3时,方程的两根互为相反数;②当且仅当a=﹣4时,解得x与y相等;③x,y满足关系式x+5y=﹣12;④若9x 27y=81,则a=10.
A.①③ B.①② C.①②③ D.①②③④
【答案】D
【分析】用代入消元法先求出方程组的解,①根据互为相反数的两个数的和为0,列出方程,求出a即可判断;②根据x=y列出方程,求出a即可判断;③在原方程中,我们消去a,即可得到x,y的关系;④把底数统一化成a,等式左右两边的底数相同时,指数也相同,得到x,y的方程,把方程组的解代入求出a.
【解答】解:,
由①得:x=2y+a+6③,
把③代入②中,得:y④,
把④代入③中,得:x,
∴原方程组的解为.
①∵方程的两根互为相反数,
∴x+y=0,
即,
解得:a=3,
∴①正确;
②当x与y相等时,x=y,
即,
解得:a=﹣4,
∴②正确;
③在原方程中,我们消去a,得到x,y的关系,
②﹣①×2得:x+5y=﹣12,
∴③正确;
④∵9x 27y=81,
∴(32)x (33)y=34,
∴32x 33y=34,
∴32x+3y=34,
∴2x+3y=4,
将方程组的解代入得:4,
解得:a=10,
∴④正确.
综上所述,①②③④都正确.
故选:D.
【点评】本题考查二元一次方程组的解法,考核学生的计算能力,解方程组的关键是消元,消元的常用方法是代入消元法和加减消元法.
5.甲、乙、丙三家艺术中心为表彰进步学生,准备去文具店采购签字笔、笔记本、钢笔三种文具,签字笔、笔记本、钢笔单价分别为8元、10元、25元.乙艺术中心采购签字笔数量是甲的6倍,笔记本数量是甲的12倍,钢笔数量是甲的8倍,丙采购的签字笔数量是甲的3倍,笔记本数量是甲的9倍,钢笔数量和甲相同.三家艺术中心采购总费用为2850元,丙艺术中心比甲艺术中心总费用多464元,则甲艺术中心采购总费用为( )元
A.237 B.350 C.425 D.901
【答案】A
【分析】设甲艺术中心采购签字笔数量为x,笔记本数量为y,钢笔数量为z.根据题意,通过“采购费用=采购数量×文具单价”分别求出三家艺术中心的采购费用,再根据三家艺术中心采购总费用为2850元,丙艺术中心比甲艺术中心总费用多464元,列方程组,最后结合文具数量为正整数,求出甲艺术中心的三种文具的数量,进而得出答案.
【解答】解:设甲艺术中心采购签字笔数量为x,笔记本数量为y,钢笔数量为z.则三甲艺术中心的采购费用分别如下:
甲:8x+10y+25z;
乙:8×6x+12×10y+8×25z=48x+120y+200z;
丙:3×8x+9×10y+25z=24x+90y+25z.
三家艺术中心采购费用的总和为:80x+220y+250z.
根据题意建立三元一次方程组,得
化简,得
①﹣②×8,得25z﹣18y=53,
整理,得
z.
∵x,y,z均为正整数,
∴对于②式,y只可能为1、2、3、4、5.
只有y=4时,z为正整数,故z5.
∴x=29﹣5y=29﹣5×4=9.
所以甲艺术中心的采购总费用为:8x+10y+25z=8×9+10×4+25×5=237元.
故选:A.
【点评】本题考查了三元一次方程组的实际应用.通过方程组得到变量之间的数量关系,再结合文具数量为正整数的隐含条件求解是本题的关键.
6.实数x、y、z且x+y+z≠0,x,z,则下列等式成立的是( )
A.x2﹣y2=z2 B.xy=z C.x2+y2=z2 D.x+y=z
【答案】A
【分析】分别化简这两个等式,得到y=x+z和y=x﹣z,所以x+z=x﹣z,所以z=0,代入z中得x=y,因为x+y+z≠0,所以x=y≠0,然后分别判断各选项即可.
【解答】解:∵x,
∴2x=x+y﹣z,
∴y=x+z,
∵z,
∴2z=x﹣y+z,
∴y=x﹣z,
∴x+z=x﹣z,
∴z=0,
把z=0代入z中得:x=y,
∵x+y+z≠0,
∴x=y≠0.
A.x2﹣y2=x2﹣x2=0=z2,所以A选项正确,符合题意;
B.xy≠0,z=0,所以B选项错误,不符合题意;
C.x2+y2≠0,z2=0,所以C选项错误,不符合题意;
D.x+y≠0,z=0,所以D选项错误,不符合题意.
故选:A.
【点评】本题考查了三元一次方程组的解法,求出z=0是解题的关键.
7.已知关于x,y的方程组给出下列结论:
①当a=1时,方程组的解也是x+y=2a+1的解;
②无论a取何值,x,y的值不可能是互为相反数;
③x,y都为自然数的解有4对;
④若2x+y=8,则a=2.
正确的有几个( )
A.1 B.2 C.3 D.4
【答案】D
【分析】①根据消元法解二元一次方程组,然后将解代入方程x+y=2a+1即可求解;
②根据消元法解二元一次方程组,用含有字母的式子表示x、y,再根据互为相反数的两个数相加为0即可求解;
③根据试值法求二元一次方程x+y=3的自然数解即可得结论;
④根据整体代入的方法即可求解.
【解答】解:①将a=1代入原方程组,得 解得
将x=3,y=0,a=1代入方程x+y=2a+1的左右两边,
左边=3,右边=3,
当a=1时,方程组的解也是x+y=2a+1的解;
②解原方程组,得
∴x+y=3,
无论a取何值,x,y的值不可能是互为相反数;
③∵x+y=2a+1+2﹣2a=3
∴x、y为自然数的解有,,,.
④∵2x+y=8,∴2(2a+1)+2﹣2a=8,
解得a=2.
故选:D.
【点评】本题考查了消元法解二元一次方程组,确定二元一次方程的自然数解,解题关键是用含字母的式子表示方程组的解.
8.若关于x、y的二元一次方程组的解为,则方程组的解是( )
A. B. C. D.
【答案】B
【分析】将方程组整理得,然后结合条件可得x﹣2=﹣1,y=2解方程组即可.
【解答】将方程组整理得,
∵关于x、y的二元一次方程组的解为,
∴,
∴.
故选:B.
【点评】本题考查二元一次方程组的解,将方程组进行正确的变形是解题的关键.
9.已知关于x,y的二元一次方程组,给出下列结论中正确的是( )
①当这个方程组的解x,y的值互为相反数时,a=﹣2;
②当a=1时,方程组的解也是方程x+y=4+2a的解;
③无论a取什么实数,x+2y的值始终不变;
④若用x表示y,则y;
A.①② B.②③ C.②③④ D.①③④
【答案】D
【分析】根据方程组的解法可以得到x+y=2+a,
①令x+y=0,即可求出a的值,验证即可,
②由①得x+y=0,而x+y=4+2a,求出a的值,再与a=1比较得出答案,
③解方程组可求出方程组的解,再代入x+2y求值即可,
④用含有x、y的代数式表示a,进而得出x、y的关系,
【解答】解:关于x,y的二元一次方程组,
①+②得,2x+2y=4+2a,
即:x+y=2+a,
(1)①当方程组的解x,y的值互为相反数时,即x+y=0时,即2+a=0,
∴a=﹣2,故①正确,
(2)②原方程组的解满足x+y=2+a,
当a=1时,x+y=3,
而方程x+y=4+2a的解满足x+y=6,
因此②不正确,
(3)方程组,解得,
∴x+2y=2a+1+2﹣2a=3,
因此③是正确的,
(4)方程组,
由方程①得,a=4﹣x﹣3y代入方程②得,
x﹣y=3(4﹣x﹣3y),
即;y
因此④是正确的,
故选:D.
【点评】考查二元一次方程组的解法和应用,正确的解出方程组的解是解决问题的关键.
10.普通火车从绵阳至成都历时大约2小时,成绵城际快车开通后,时间大大缩短至几十分钟,现假定普通火车与城际快车两列对开的火车于同一时刻发车,其中普通火车由成都至绵阳,城际快车由绵阳至成都,这两车在途中相遇之后,各自用了80分钟和20分钟到达自己的终点绵阳、成都,则城际快车的平均速度是普通火车平均速度的( )倍.
A.2 B.2.5 C.3 D.4
【答案】A
【分析】普通火车从绵阳至成都历时大约2小时,由速度公式表示出两地的距离;
两车在途中相遇之后,各自用了80分钟和20分钟到达自己的终点绵阳、成都,由速度公式表示出两地距离.联立两式解题即可.
【解答】解:设普通火车速度为v m/min,城际快车速度为nv m/min,
已知普通火车从绵阳至成都历时大约2h=120min,由v可得两地距离:
s=v×120,
普通火车与城际快车两列对开,途中相遇之后,各自用了80分钟和20分钟到达自己的终点绵阳、成都,
即:s普+s城=s,
所以:v×80+nv×20=s,
所以:v×80+nv×20=v×120,
解得:n=2.
故选:A.
【点评】本题考查了二元一次方程的应用,速度公式的应用,关键正确表示出两地的距离.
11.已知关于x,y的二元一次方程组,给出下列结论中正确的是( )
①当这个方程组的解x,y的值互为相反数时,a=﹣2;
②当a=1时,方程组的解也是方程x+y=4+2a的解;
③无论a取什么实数,x+2y的值始终不变;
④若用x表示y.则;
A.①②③ B.①②④ C.①③④ D.②③④
【答案】C
【分析】根据方程组的解法可以得到x+y=2+a,
①令x+y=0,即可求出a的值,验证即可,
②由①得x+y=0,而x+y=4+2a,求出a的值,再与a=1比较得出答案,
③解方程组可求出方程组的解,再代入x+2y求值即可,
④用含有x、y的代数式表示a,进而得出x、y的关系,
【解答】解:关于x,y的二元一次方程组,
①+②得,
2x+2y=4+2a,
即x+y=2+a,
①当方程组的解x,y的值互为相反数时,即x+y=0时,即2+a=0,
∴a=﹣2,故①正确;
②原方程组的解满足x+y=2+a,
当a=1时,x+y=3,
而方程x+y=4+2a的解满足x+y=6,
因此②不正确;
③方程组,
解得,
∴x+2y=2a+1+2﹣2a=3,
因此③是正确的;
④方程组,
由方程①得,a=4﹣x﹣3y,
代入方程②得,
x﹣y=3(4﹣x﹣3y),
∴y,
因此④是正确的.
故选:C.
【点评】此题考查二元一次方程组的解法和应用,正确地解出方程组的解是解决问题的关键.
12.如图,长方形ABCD被分成3个正方形和2个长方形后仍是中心对称图形,设长方形ABCD的周长为l,若图中3个正方形和2个长方形的周长和为l,则标号为①的正方形的边长为( )
A.l B.l C.l D.l
【答案】B
【分析】设两个大正方形边长为x,小正方形的边长为y,由图可知周长和列方程和方程组,解答即可.
【解答】解:长方形ABCD被分成3个正方形和2个长方形后仍是中心对称图形,
∴两个大正方形相同、2个长方形相同.
设两个大正方形边长为y,小正方形的边长为x,
∴小长方形的边长分别为(y﹣x)、(x+y),大长方形边长为(2y﹣x)、(2y+x),
∵大长方形周长=1,即:2[(2y﹣x)+(2y+x)]=1,
∴8y=1,
∴y
∵3个正方形和2个长方形的周长和为l,
即:,
∴16y+4x,
∴x,
则标号为①的正方形的边长为,
故选:B.
【点评】此题主要考查了中心对称图形的性质和二元一次方程组的应用,关键是正确理解题意,要明确中心对称的性质,找出题目中的等量关系,列出方程组.注意各个正方形的边长之间的数量关系.
13.已知关于x,y的方程组,其中﹣3≤a≤1,下列命题正确的个数为( )
①当a=﹣2时,x、y的值互为相反数;
②是方程组的解;
③当a=1时,方程组的解也是方程x+y=4﹣a的解;
④若x≤1,则1≤y≤4.
A.1个 B.2个 C.3个 D.4个
【答案】C
【分析】①先求出方程组的解,把a=﹣2代入求出x、y即可;
②把代入,求出a的值,再根据﹣3≤a≤1判断即可;
③求出方程组的解,再代入方程,看看方程左右两边是否相等即可;
④根据x≤1和x=1+2a求出a≤0,求出﹣3≤a≤0,再求出1﹣a的范围即可.
【解答】解:解方程组得:,
①当a=﹣2时,x=1+2×(﹣2)=﹣3,y=1﹣(﹣2)=3,
所以x、y互为相反数,故①正确;
②把代入,
得:,
解得:a=2,
∵﹣3≤a≤1,
∴此时a=2不符合,故②错误;
③当a=1时,
∵x=1+2a=3,y=1﹣a=0,
∴方程组的解是,
把a=1,代入方程x+y=4﹣a得:左边=右边,
即当a=1时,方程组的解也是方程x+y=4﹣a的解,故③正确;
④∵x≤1,
∴x=1+2a≤1,
即a≤0,
∴﹣3≤a≤0,
∴3≥﹣a≥0,
∴4≥1﹣a≥1,
∵y=1﹣a,
∴1≤y≤4,故④正确;
故选:C.
【点评】本题考查了解二元一次方程组,二元一次方程组的解,一元一次方程的解,解不等式组等知识点,能求出方程组的解是解此题的关键.
14.我们知道自行车一般是由后轮驱动,因此,后轮胎的磨损要超过前轮胎,假设前轮行驶5000千米报废,后轮行驶3000千米报废,如果在自行车行驶若干千米后,将前后轮进行对换,那么这对轮胎最多可以行驶( )
A.4000 千米 B.3750 千米 C.4250 千米 D.3250 千米
【答案】B
【分析】设每个新轮胎报废时的总磨损量为k,一对新轮胎交换位置前走了x km,交换位置后走了y km,根据交换前磨损总量和交换后的磨损总量相等,可列出方程组,解方程组即可.
【解答】解:设每个新轮胎报废时的总磨损量为k,
则安装在前轮的轮胎每行驶1km磨损量为,安装在后轮的轮胎每行驶1km的磨损量为,
又设一对新轮胎交换位置前走了x km,交换位置后走了y km,
分别以一个轮胎的总磨损量为等量关系列方程,
,
两式相加,得,
则 x+y=3750(千米).
故选:B.
【点评】本题考查了二元一次方程组的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.利用二元一次方程组求解的应用题一般情况下题中要给出两个等量关系,准确地找到等量关系并用方程组表示出来是解题的关键.
15.已知是关于x,y的二元一次方程mx+ny=7的解,则代数式4m+6n﹣3的值是( )
A.14 B.11 C.7 D.4
【答案】B
【分析】把代入mx+ny=7,求出2m+3n的值,再把所求代数式化成含有2m+3n的形式,最后整体代入进行计算即可.
【解答】解:把代入mx+ny=7得:2m+3n=7,
∴4m+6n﹣3
=2(2m+3n)﹣3
=2×7﹣3
=14﹣3
=11,
故选:B.
【点评】本题主要考查了二元一次方程的解,解题关键是熟练掌握二元一次方程解的定义.
二.填空题(共13小题)
16.若关于x、y的二元一次方程组的解满足,则满足条件的m的所有非负整数值为 0,1,2,3 .
【答案】0,1,2,3.
【分析】先将两个方程相加,可得3x+3y=﹣3m+6,即x+y=﹣m+2,再根据已知x+y,得出不等式,解一元一次不等式求出m的范围,进而得出答案.
【解答】解:,
①+②,得3x+3y=﹣3m+6,即x+y=﹣m+2,
∵,
∴,
去分母,得﹣2m+4>﹣3,
移项、合并同类项,得﹣2m>﹣7,
解得:,
∴满足条件的m的所有非负整数值为0,1,2,3.
故答案为:0,1,2,3.
【点评】本题考查了二元一次方程组的解,解二元一次方程组,解一元一次不等式,掌握二元一次方程组解的定义,解二元一次方程组的方法,解一元一次不等式的方法是解题的关键.
17.在长方形ABCD中放入六个完全相同的小长方形,所标尺寸如图所示,则小长方形的宽CE为 2 cm.
【答案】见试题解答内容
【分析】设小长方形的长为x cm,宽为y cm,利用长方形的对边相等,可得出关于x,y的二元一次方程组,解方程组即可.
【解答】解:设小长方形的长为x cm,宽为y cm,
则AD=x+3y,AB=x+y=5+2y,
即x﹣y=5,
根据题意,得:,
解得:,
即CE=2cm,
故答案为:2.
【点评】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
18.小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图所示,3个纸杯叠放在一起高度为9cm,8个纸杯叠放在一起高度为14cm,若小明把20个纸杯整齐叠放在一起时,它的高度约是 26 cm.
【答案】26.
【分析】根据题意设未知数,列方程组求解即可.
【解答】解:设每增加一个纸杯增加的高度为x cm,一个纸杯的高度为y cm,
由题意列二元一次方程组得:,
解得,
则20个纸杯整齐叠放在一起时,它的高度约是7+(20﹣1)×1=7+19=26(cm),
故答案为:26.
【点评】本题考查了二元一次方程组的应用,找出等量关系正确列方程组是解题关键.
19.如图是由同一种长方形墙砖粘贴的部分墙面,其中三块横放的墙砖比一块竖放的墙砖高10cm,两块横放的墙砖比两块竖放的墙砖低40cm,则每块长方形墙砖的周长是 100 cm.
【答案】100.
【分析】根据图形找到两个等量关系,求解即可.
【解答】解:设每块墙砖的长为x cm,宽为y cm,
根据题意得:.
解得:,
∴每块长方形墙砖的周长是:2×(35+15)=100(cm),
故答案为:100.
【点评】本题考查二元一次方程组的应用,关键是根据题意找到等量关系式.
20.如图,从标注3的圆圈开始,顺时针方向按an+b的规律(n表示前一个圆圈中的数字,a,b是常数)转换后得到下一个圆圈中的数,例如:从“3→﹣1”得3a+b=﹣1,则标注“?”的圆圈中的数是 23 .
【答案】23.
【分析】根据题意得,解得,则顺时针方向按﹣2n+5的规律转换,再把n=﹣9时代入求解即可.
【解答】解:根据题意得,
解得,
∴顺时针方向按﹣2n+5的规律转换后得到下一个圆圈中的数,
∴当n=﹣9时,﹣2n+5=﹣2×(﹣9)+5=18+5=23,
所以标注“?”的圆圈中的数是23,
答:标注“?”的圆圈中的数是23,
故答案为:23.
【点评】本题考查了二元一次方程组的应用,掌握知识点的应用是解题的关键.
21.如图,用12块形状和大小均相同的小长方形拼成一个宽是40的大长方形,则每个小长方形的面积是 300 .
【答案】300.
【分析】设每个小长方形的长为x,宽为y,由此列方程组得到长和宽,由面积的公式计算即可.
【解答】解:设每个小长方形的长为x,宽为y,根据题意列方程组得:
,
解得,
∴xy=30×10=300,
故答案为:300.
【点评】本题考查了二元一次方程组的运用,理解数量关系,正确列出二元一次方程组求解是关键.
22.若关于x,y的方程组的解,也是方程2x﹣y=6的解,则k= .
【答案】.
【分析】利用加减消元法解方程组,可得x=5k,y=﹣2k,把x=5k,y=﹣2k分别代入方程2x﹣y=6,得出关于k的一元一次方程,解一元一次方程即可得出答案.
【解答】解:,
①﹣②,得3y=﹣6k,
解得:y=﹣2k,
把y=﹣2k代入①,得x﹣2k=3k,
解得:x=5k,
∵关于x,y的方程组的解,也是方程2x﹣y=6的解,
∴2×5k+2k=6,
∴12k=6,
解得:.
故答案为:.
【点评】本题考查了二元一次方程组的解,解二元一次方程组,二元一次方程的解,解一元一次方程,掌握二元一次方程组解的定义,解二元一次方程组的方法,解一元一次方程的方法是解题的关键.
23.王明在看中国清代算书《御制数理精蕴》时有这样一道题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两,问马、牛各价几何?”设马每匹m两,牛每头n两,请你根据题意列出方程组是 .
【答案】.
【分析】根据题意,设马每匹m两,牛每头n两,由“马四匹、牛六头,共价四十八两;马三匹、牛五头,共价三十八两”列出方程组即可得到答案.
【解答】解:设马每匹m两,牛每头n两,由题意可得,
故答案为:.
【点评】本题考查二元一次方程组解实际应用题,读懂题意,找准等量关系列方程组是解决问题的关键.
24.母亲节到了,小红,小莉,小莹到花店买花送给自己的母亲.小红买了3枝玫瑰,7枝康乃馨,1枝百合花,付了14元;小莉买了4枝玫瑰,10枝康乃馨,1枝百合花,付了16元;小莹买上面三种花各2枝,则她应付 20 元.
【答案】见试题解答内容
【分析】如果设玫瑰、康乃馨、百合花的单价分别为x元,y元,z元,题中有两个等量关系:3枝玫瑰的价格+7枝康乃馨的价格+1枝百合花的价格=14元;4枝玫瑰的价格+10枝康乃馨的价格+1枝百合花的价格=16元,据此列出两个方程,得到三元一次方程组.在这个方程组中,把y看作常数,用含y的代数式分别表示x和z,再代入2(x+y+z),即可求出结果.
【解答】解:设玫瑰、康乃馨、百合花的单价分别为x元,y元,z元,
根据已知条件,列出方程组,
②﹣①,得x=2﹣3y.③
将③代入①,得z=8+2y.④
∴x+y+z=2﹣3y+y+8+2y=10,
∴2(x+y+z)=20.
所以,小莹应付20元.
故答案为20.
【点评】本题考查了三元一次方程组在实际中的运用.解答此题的关键是列出方程组,难点是理解不必求出每一个未知数的具体值,而只要将方程组变形,能够求出x+y+z的值即可.为此,将这个方程组中的其中一个未知数看作常数,用含有这个未知数的代数式分别表示另外两个未知数,然后代入即可.
25.幻方是一种中国传统游戏,我国古代的《洛书》中记载了最早的幻方——九宫格,其规则是将数字填在正方形格子中,使每一行、每一列和两条对角线上的3个数字的和都相等.例如图①就是一个幻方.
(Ⅰ)图②是一个未完成的幻方,则x+y的结果为 12 ;
(Ⅱ)图③中的x为 a﹣1 (用含a的式子表示).
【答案】(Ⅰ)12;
(Ⅱ)a﹣1.
【分析】(Ⅰ)先求出第1列最上面的数为4,再求出第2行中间的数为x+2或x﹣y+4,第3列最上面的数为x﹣y+6或24﹣x,然后列出二元一次方程组,解方程组即可;
(Ⅱ)先求出第1行最上面的数为x﹣2,再求出第2列中间的数为2a﹣x﹣3,第1列中间的数为2x﹣a﹣4,然后由第1列与对角线上的3个数字的和相等,列出代数式即可得出结果.
【解答】解:(Ⅰ)∵第3行的和为:x+6+20=x+26,
∴第1列最上面的数为:x+26﹣(x+22)=4,
∴第2行中间的数为:x+26﹣(4+20)=x+2或x+26﹣(y+22)=x﹣y+4,
第3列最上面的数为:x+26﹣(20+y)=x﹣y+6或x+26﹣(x+2)=24﹣x,
∴,
解得:,
∴x+y=10+2=12,
故答案为:12;
(Ⅱ)∵第3行的和为:x+a+a﹣5=x+2a﹣5,
∴第1行最上面的数为:x+2a﹣5﹣(a﹣5+a+2)=x﹣2,
∴第2列中间的数为:x+2a﹣5﹣(x﹣2+x)=2a﹣x﹣3,
∴第1列中间的数为:x+2a﹣5﹣(a+2+2a﹣x﹣3)=2x﹣a﹣4,
∴x+2x﹣a﹣4=a﹣5+2a﹣x﹣3,
解得:x=a﹣1,
故答案为:a﹣1.
【点评】本题考查了二元一次方程组的应用、列代数式,找准等量关系,正确列出二元一次方程组和代数式是解题的关键.
26.《九章算术》记载了这样一个问题:“今有善田一亩,价三百;恶田七亩,价五百.今并买一顷,价钱一万,问善田几何?“意思是:当下良田1亩,价值300钱;薄田7亩,价值500钱.现在共买100亩,价值10000钱.根据条件,良田买了 12.5 亩.(注:1顷=100亩)
【答案】12.5.
【分析】设良田买了x亩,薄田买了y亩,由“当下良田1亩,价值300钱;薄田7亩,价值500钱.现在共买100亩,价值10000钱”列出方程组,解方程组即可.
【解答】解:设良田买了x亩,薄田买了y亩,
依题意得:,
解得:,
即良田买了12.5亩,
故答案为:12.5.
【点评】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
27.用8个大小完全相同的长方形在平面直角坐标系中摆成如图所示的图案,已知点A(4,10),则点B的坐标是 (﹣6,8) .
【答案】(﹣6,8).
【分析】设小长方形纸片的长为x,宽为y,根据点A的坐标列出关于x、y二元一次方程组求得x、y的值,结合点B所在的位置即可解答.
【解答】解:8个大小完全相同的长方形在平面直角坐标系中摆成如图所示的图案,已知点A(4,10),
设小长方形纸片的长为x,宽为y,
依题意得:,
解得:,
∴x+y=6+2=8,
∵点B在第二象限内,
∴点B的坐标是(﹣6,8).
故答案为:(﹣6,8).
【点评】本题主要考查了二元一次方程组的应用、坐标与图形等知识点,设出未知数、找准等量关系,正确列出二元一次方程组是解题的关键.
28.我国古典数学文献《增删算法统宗 六均输》中有一个“隔沟计算”的问题:“甲乙隔沟牧放,二人暗里参详,甲云得乙九只羊,多乙一倍之上,乙说得甲九只,两家之数相当,二人闲坐恼心肠,画地算了半晌”其大意为:甲、乙两人一起放牧,两人心里暗中数羊.如果乙给甲9只羊,那么甲的羊数为乙的2倍;如果甲给乙9只羊,那么两人的羊数相同,请问甲,乙各有多少只羊?设甲有羊x只,乙有羊y只,根据题意,可列方程组为 .
【答案】.
【分析】设甲有羊x只,乙有羊y只,根据“如果乙给甲9只羊,那么甲的羊数为乙的2倍;如果甲给乙9只羊,那么两人的羊数相同”,即可得出关于x,y的二元一次方程组,此题得解.
【解答】解:设甲有羊x只,乙有羊y只.
∵“如果乙给甲9只羊,那么甲的羊数为乙的2倍”,
∴x+9=2(y﹣9);
∵“如果甲给乙9只羊,那么两人的羊数相同”,
∴x﹣9=y+9.
联立两方程组成方程组.
故答案为:.
【点评】本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.
三.解答题(共6小题)
29.解方程组:
(1);
(2).
【答案】见试题解答内容
【分析】(1)根据解二元一次方程组的方法,理由代入消元法解方程组即可;
(2)根据解二元一次方程组的方法,理由加减消元法解方程组即可.
【解答】解:(1),
由①,得x=y+3③,
把③代入②,得3(y+3)﹣8y=14,
去括号,得3y+9﹣8y=14,
解得:y=﹣1,
把y=﹣1代入③,得x=﹣1+3=2,
∴方程组的解为;
(2),
①×2,得6x﹣4y=8③,
②+③,得13x=26,
解得:x=2,
把x=2代入①,得3×2﹣2y=4,
解得:y=1,
∴方程组的解为.
【点评】本题考查了解二元一次方程组,掌握解二元一次方程组的方法:加减消元法和代入消元法是解题的关键.
30.袁隆平爷爷多次说:“中国人要把饭碗牢牢地端在自己的手里!”为扩大粮食生产规模,稻田公园生产基地计划投入一笔资金购进甲、乙两种农机,已知购进1件甲种农机和1件乙种农机共需2万元,购进2件甲种农机和3件乙种农机共需5.5万元.
(1)求购进1件甲种农机和1件乙种农机各需多少万元?
(2)若该粮食生产基地计划购进甲、乙两种农机共10件,且投入资金不少于9.5万元且不超过12万元,则有哪几种购买方案?哪种购买方案需要的资金最少,最少资金是多少?
【答案】(1)购进1件甲种农机0.5万元,1件乙种农机1.5万元;
(2)有3种方案:①购进甲种农机3件,购进乙种农机7件;②购进甲种农机4件,购进乙种农机6件;③购进甲种农机5件,购进乙种农机5件;购买方案需要的资金最少的是购进甲种农机5件,购进乙种农机5件,最少资金为10万元.
【分析】(1)设购进1件甲种农机m万元,1件乙种农机n万元,根据购进1件甲种农机和1件乙种农机共需2万元,购进2件甲种农机和3件乙种农机共需5.5万元,可得,即可解得答案;
(2)设购进甲种农机x件,由投入资金不少于9.5万元且不超过12万元,得9.5≤0.5x+1.5(10﹣x)≤12,解得3≤x≤5.5,故有3种方案:①购进甲种农机3件,购进乙种农机7件;②购进甲种农机4件,购进乙种农机6件;③购进甲种农机5件,购进乙种农机5件;分别算出各方案所需资金,可得需要的资金最少的方案.
【解答】解:(1)设购进1件甲种农机m万元,1件乙种农机n万元,
∵购进1件甲种农机和1件乙种农机共需2万元,购进2件甲种农机和3件乙种农机共需5.5万元,
∴,
解得,
∴购进1件甲种农机0.5万元,1件乙种农机1.5万元;
(2)设购进甲种农机x件,则购进乙种农机(10﹣x)件,
∵投入资金不少于9.5万元且不超过12万元,
∴9.5≤0.5x+1.5(10﹣x)≤12,
解得3≤x≤5.5,
∵x为整数,
∴x可取3或4或5,
∴有3种方案:①购进甲种农机3件,购进乙种农机7件,所需资金为3×0.5+7×1.5=12(万元);
②购进甲种农机4件,购进乙种农机6件,所需资金为4×0.5+6×1.5=11(万元);
③购进甲种农机5件,购进乙种农机5件,所需资金为5×0.5+5×1.5=10(万元);
∴购买方案需要的资金最少的是购进甲种农机5件,购进乙种农机5件,最少资金为10万元.
【点评】本题考查二元一次方程组的应用和一元一次不等式组的应用,解题的关键是读懂题意,列出方程组和不等式组.
31.秋季由于气候干燥,天气转冷,用火用电情况大量增加,起火原因增多,火灾危险性加大.为了加强秋季防火用电安全,提高同学们的安全防范意识,某学校组织了“用电安全”知识竞赛,对表现优异的班级进行奖励,学校购买了若干支钢笔和中性笔.购买5支钢笔和10支中性笔共需110元;购买8支钢笔和6支中性笔共需126元.
(1)求购买1支钢笔和1支中性笔各需多少元;
(2)若学校购买钢笔和中性笔共200支,其中钢笔的数量不得少于中性笔数量的,且总支出不超过1364元,那学校有哪几种购买方案?
【答案】(1)购买1支钢笔需12元,1支中性笔需5元;
(2)学校共有3种购买方案,
方案1:购买50支钢笔,150支中性笔;
方案2:购买51支钢笔,149支中性笔;
方案3:购买52支钢笔,148支中性笔.
【分析】(1)设购买1支钢笔需x元,购买1支中性笔需y元,根据“购买5支钢笔和10支中性笔共需110元;购买8支钢笔和6支中性笔共需126元”,可列出关于x,y的二元一次方程组,解之即可得出结论;
(2)设学校购买m支钢笔,则购买(200﹣m)支中性笔,根据“购买钢笔的数量不得少于中性笔数量的,且总支出不超过1364元”,可列出关于m的一元一次不等式组,解之可得出m的取值范围,再结合m为正整数,即可得出各购买方案.
【解答】解:(1)设购买1支钢笔需x元,购买1支中性笔需y元,
根据题意得:,
解得:.
答:购买1支钢笔需12元,1支中性笔需5元;
(2)设学校购买m支钢笔,则购买(200﹣m)支中性笔,
根据题意得:,
解得:50≤m≤52,
又∵m为正整数,
∴m可以为50,51,52,
∴学校共有3种购买方案,
方案1:购买50支钢笔,150支中性笔;
方案2:购买51支钢笔,149支中性笔;
方案3:购买52支钢笔,148支中性笔.
【点评】本题考查了二元一次方程组的应用以及一元一次不等式组的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式组.
32.为响应“全民植树增绿,共建美丽中国”的号召,某学校组织学生到郊外参加义务植树活动,并准备了A,B两种食品作为午餐.这两种食品每包质量均为50g,营养成分如图所示.
(1)若要从这两种食品中摄入3900KJ热量和60g蛋白质,应选用A,B两种食品各多少包?
(2)运动量大的人或青少年对蛋白质的摄入量应更多.若要从这两种食品中摄入的蛋白质含量等于80g,应选用A,B两种食品各多少包(A,B两种食品都选且不能拆分)?
【答案】(1)应选用A种食品3包,B种食品2包;
(2)应选用A,B两种食品各5包,2包或2包,4包.
【分析】(1)设应选用A种食品x包,B种食品y包,根据要从这两种食品中摄入3900KJ热量和60g蛋白质,可列出关于x,y的二元一次方程组,解之即可得出结论;
(2)设应选用A种食品m包,B种食品n包,根据要从这两种食品中摄入的蛋白质含量等于80g,可列出关于m,n的二元一次方程,结合m,n均为正整数,即可得出结论.
【解答】解:(1)设应选用A种食品x包,B种食品y包,
根据题意得:,
解得:.
答:应选用A种食品3包,B种食品2包;
(2)设应选用A种食品m包,B种食品n包,
根据题意得:10m+15n=80,
∴m=8n,
又∵m,n均为正整数,
∴或.
答:应选用A,B两种食品各5包,2包或2包,4包.
【点评】本题考查了二元一次方程组的应用以及二元一次方程的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)找准等量关系,正确列出二元一次方程.
33.如图是中国邮政发行的《数学之美》的邮票,其中一张圆周率邮票面值为80分,莫比乌斯带邮票面值为1.50元.小宇购买这两种邮票共7张,恰好花了7元,求小宇购买这两种邮票各多少张.
【答案】小宇购买圆周率邮票5张,莫比乌斯带邮票2张.
【分析】设小宇购买圆周率邮票x张,莫比乌斯带邮票y张,根据题意,列出二元一次方程组,求出x与y,即可解答.
【解答】解:设小宇购买圆周率邮票x张,莫比乌斯带邮票y张,依题意得,
,
解得.
即小宇购买圆周率邮票5张,莫比乌斯带邮票2张,
答:小宇购买圆周率邮票5张,莫比乌斯带邮票2张.
【点评】本题考查二元一次方程组的应用,找到等量关系是解题的关键.
34.“脐橙结硕果,香飘引客来”,赣南脐橙以其“外表光洁美观,肉质脆嫩,风味浓甜芳香”的特点饮誉中外.现欲将一批脐橙运往外地销售,若用2辆A型车和1辆B型车载满脐橙一次可运走10吨;用1辆A型车和2辆B型车载满脐橙一次可运走11吨.现有脐橙31吨,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满脐橙.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都载满脐橙一次可分别运送多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若1辆A型车需租金100元/次,1辆B型车需租金120元/次.请选出费用最少的租车方案,并求出最少租车费.
【答案】见试题解答内容
【分析】(1)设1辆A型车载满脐橙一次可运送x吨,1辆B型车载满脐橙一次可运送y吨,根据“用2辆A型车和1辆B型车载满脐橙一次可运走10吨;用1辆A型车和2辆B型车载满脐橙一次可运走11吨”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)根据一次运送脐橙31吨,即可得出关于a,b的二元一次方程,结合a,b均为正整数,即可得出各租车方案;
(3)根据总租金=每辆车的租金×租车辆数,分别求出三个租车方案所需租金,比较后即可得出结论.
【解答】解:(1)设1辆A型车载满脐橙一次可运送x吨,1辆B型车载满脐橙一次可运送y吨,
依题意,得:,
解得:.
答:1辆A型车载满脐橙一次可运送3吨,1辆B型车载满脐橙一次可运送4吨.
(2)依题意,得:3a+4b=31,
∵a,b均为正整数,
∴或或.
∴一共有3种租车方案,方案一:租A型车1辆,B型车7辆;方案二:租A型车5辆,B型车4辆;方案三:租A型车9辆,B型车1辆.
(3)方案一所需租金为100×1+120×7=940(元);
方案二所需租金为100×5+120×4=980(元);
方案三所需租金为100×9+120×1=1020(元).
∵940<980<1020,
∴最省钱的租车方案是方案一,即租A型车1辆,B型车7辆,最少租车费为940元.
【点评】本题考查了二元一次方程组的应用以及二元一次方程的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)找准等量关系,正确列出二元一次方程;(3)根据各数量之间的关系,分别求出三个租车方案所需租金.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2026年中考数学一轮复习 二元一次方程组
一.选择题(共15小题)
1.已知方程组的解x为正数,y为非负数,给出下列结论:
①﹣3<a≤1;
②当时,x=y;
③当a=﹣2时,方程组的解也是方程x+y=5+a的解;
④若x≤1,则y≥2.
其中正确的是( )
A.①② B.②③ C.③④ D.②③④
2.已知关于x,y的方程组,将此方程组的两个方程左右两边分别对应相加,得到一个新的方程,当m每取一个值时,就有一个方程,这些方程有一个公共解,这个公共解为( )
A. B. C. D.
3.我的家用小轿车配备了一种牌子的轮胎,装在前轮其可使用的距离为40000千米,装在后轮则可使用60000千米,如果将前后轮交换使用,则用这一组四个轮胎可行驶的最大距离为( )
A.44000千米 B.48000千米 C.50000千米 D.52000千米
4.在关于x,y的二元一次方程组的下列说法中,正确的是( )
①当a=3时,方程的两根互为相反数;②当且仅当a=﹣4时,解得x与y相等;③x,y满足关系式x+5y=﹣12;④若9x 27y=81,则a=10.
A.①③ B.①② C.①②③ D.①②③④
5.甲、乙、丙三家艺术中心为表彰进步学生,准备去文具店采购签字笔、笔记本、钢笔三种文具,签字笔、笔记本、钢笔单价分别为8元、10元、25元.乙艺术中心采购签字笔数量是甲的6倍,笔记本数量是甲的12倍,钢笔数量是甲的8倍,丙采购的签字笔数量是甲的3倍,笔记本数量是甲的9倍,钢笔数量和甲相同.三家艺术中心采购总费用为2850元,丙艺术中心比甲艺术中心总费用多464元,则甲艺术中心采购总费用为( )元
A.237 B.350 C.425 D.901
6.实数x、y、z且x+y+z≠0,x,z,则下列等式成立的是( )
A.x2﹣y2=z2 B.xy=z C.x2+y2=z2 D.x+y=z
7.已知关于x,y的方程组给出下列结论:
①当a=1时,方程组的解也是x+y=2a+1的解;
②无论a取何值,x,y的值不可能是互为相反数;
③x,y都为自然数的解有4对;
④若2x+y=8,则a=2.
正确的有几个( )
A.1 B.2 C.3 D.4
8.若关于x、y的二元一次方程组的解为,则方程组的解是( )
A. B. C. D.
9.已知关于x,y的二元一次方程组,给出下列结论中正确的是( )
①当这个方程组的解x,y的值互为相反数时,a=﹣2;
②当a=1时,方程组的解也是方程x+y=4+2a的解;
③无论a取什么实数,x+2y的值始终不变;
④若用x表示y,则y;
A.①② B.②③ C.②③④ D.①③④
10.普通火车从绵阳至成都历时大约2小时,成绵城际快车开通后,时间大大缩短至几十分钟,现假定普通火车与城际快车两列对开的火车于同一时刻发车,其中普通火车由成都至绵阳,城际快车由绵阳至成都,这两车在途中相遇之后,各自用了80分钟和20分钟到达自己的终点绵阳、成都,则城际快车的平均速度是普通火车平均速度的( )倍.
A.2 B.2.5 C.3 D.4
11.已知关于x,y的二元一次方程组,给出下列结论中正确的是( )
①当这个方程组的解x,y的值互为相反数时,a=﹣2;
②当a=1时,方程组的解也是方程x+y=4+2a的解;
③无论a取什么实数,x+2y的值始终不变;
④若用x表示y.则;
A.①②③ B.①②④ C.①③④ D.②③④
12.如图,长方形ABCD被分成3个正方形和2个长方形后仍是中心对称图形,设长方形ABCD的周长为l,若图中3个正方形和2个长方形的周长和为l,则标号为①的正方形的边长为( )
A.l B.l C.l D.l
13.已知关于x,y的方程组,其中﹣3≤a≤1,下列命题正确的个数为( )
①当a=﹣2时,x、y的值互为相反数;
②是方程组的解;
③当a=1时,方程组的解也是方程x+y=4﹣a的解;
④若x≤1,则1≤y≤4.
A.1个 B.2个 C.3个 D.4个
14.我们知道自行车一般是由后轮驱动,因此,后轮胎的磨损要超过前轮胎,假设前轮行驶5000千米报废,后轮行驶3000千米报废,如果在自行车行驶若干千米后,将前后轮进行对换,那么这对轮胎最多可以行驶( )
A.4000 千米 B.3750 千米 C.4250 千米 D.3250 千米
15.已知是关于x,y的二元一次方程mx+ny=7的解,则代数式4m+6n﹣3的值是( )
A.14 B.11 C.7 D.4
二.填空题(共13小题)
16.若关于x、y的二元一次方程组的解满足,则满足条件的m的所有非负整数值为 .
17.在长方形ABCD中放入六个完全相同的小长方形,所标尺寸如图所示,则小长方形的宽CE为 cm.
18.小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图所示,3个纸杯叠放在一起高度为9cm,8个纸杯叠放在一起高度为14cm,若小明把20个纸杯整齐叠放在一起时,它的高度约是 cm.
19.如图是由同一种长方形墙砖粘贴的部分墙面,其中三块横放的墙砖比一块竖放的墙砖高10cm,两块横放的墙砖比两块竖放的墙砖低40cm,则每块长方形墙砖的周长是 cm.
20.如图,从标注3的圆圈开始,顺时针方向按an+b的规律(n表示前一个圆圈中的数字,a,b是常数)转换后得到下一个圆圈中的数,例如:从“3→﹣1”得3a+b=﹣1,则标注“?”的圆圈中的数是 .
21.如图,用12块形状和大小均相同的小长方形拼成一个宽是40的大长方形,则每个小长方形的面积是 .
22.若关于x,y的方程组的解,也是方程2x﹣y=6的解,则k= .
23.王明在看中国清代算书《御制数理精蕴》时有这样一道题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两,问马、牛各价几何?”设马每匹m两,牛每头n两,请你根据题意列出方程组是 .
24.母亲节到了,小红,小莉,小莹到花店买花送给自己的母亲.小红买了3枝玫瑰,7枝康乃馨,1枝百合花,付了14元;小莉买了4枝玫瑰,10枝康乃馨,1枝百合花,付了16元;小莹买上面三种花各2枝,则她应付 元.
25.幻方是一种中国传统游戏,我国古代的《洛书》中记载了最早的幻方——九宫格,其规则是将数字填在正方形格子中,使每一行、每一列和两条对角线上的3个数字的和都相等.例如图①就是一个幻方.
(Ⅰ)图②是一个未完成的幻方,则x+y的结果为 ;
(Ⅱ)图③中的x为 (用含a的式子表示).
26.《九章算术》记载了这样一个问题:“今有善田一亩,价三百;恶田七亩,价五百.今并买一顷,价钱一万,问善田几何?“意思是:当下良田1亩,价值300钱;薄田7亩,价值500钱.现在共买100亩,价值10000钱.根据条件,良田买了 亩.(注:1顷=100亩)
27.用8个大小完全相同的长方形在平面直角坐标系中摆成如图所示的图案,已知点A(4,10),则点B的坐标是 .
28.我国古典数学文献《增删算法统宗 六均输》中有一个“隔沟计算”的问题:“甲乙隔沟牧放,二人暗里参详,甲云得乙九只羊,多乙一倍之上,乙说得甲九只,两家之数相当,二人闲坐恼心肠,画地算了半晌”其大意为:甲、乙两人一起放牧,两人心里暗中数羊.如果乙给甲9只羊,那么甲的羊数为乙的2倍;如果甲给乙9只羊,那么两人的羊数相同,请问甲,乙各有多少只羊?设甲有羊x只,乙有羊y只,根据题意,可列方程组为 .
三.解答题(共6小题)
29.解方程组:
(1);
(2).
30.袁隆平爷爷多次说:“中国人要把饭碗牢牢地端在自己的手里!”为扩大粮食生产规模,稻田公园生产基地计划投入一笔资金购进甲、乙两种农机,已知购进1件甲种农机和1件乙种农机共需2万元,购进2件甲种农机和3件乙种农机共需5.5万元.
(1)求购进1件甲种农机和1件乙种农机各需多少万元?
(2)若该粮食生产基地计划购进甲、乙两种农机共10件,且投入资金不少于9.5万元且不超过12万元,则有哪几种购买方案?哪种购买方案需要的资金最少,最少资金是多少?
31.秋季由于气候干燥,天气转冷,用火用电情况大量增加,起火原因增多,火灾危险性加大.为了加强秋季防火用电安全,提高同学们的安全防范意识,某学校组织了“用电安全”知识竞赛,对表现优异的班级进行奖励,学校购买了若干支钢笔和中性笔.购买5支钢笔和10支中性笔共需110元;购买8支钢笔和6支中性笔共需126元.
(1)求购买1支钢笔和1支中性笔各需多少元;
(2)若学校购买钢笔和中性笔共200支,其中钢笔的数量不得少于中性笔数量的,且总支出不超过1364元,那学校有哪几种购买方案?
32.为响应“全民植树增绿,共建美丽中国”的号召,某学校组织学生到郊外参加义务植树活动,并准备了A,B两种食品作为午餐.这两种食品每包质量均为50g,营养成分如图所示.
(1)若要从这两种食品中摄入3900KJ热量和60g蛋白质,应选用A,B两种食品各多少包?
(2)运动量大的人或青少年对蛋白质的摄入量应更多.若要从这两种食品中摄入的蛋白质含量等于80g,应选用A,B两种食品各多少包(A,B两种食品都选且不能拆分)?
33.如图是中国邮政发行的《数学之美》的邮票,其中一张圆周率邮票面值为80分,莫比乌斯带邮票面值为1.50元.小宇购买这两种邮票共7张,恰好花了7元,求小宇购买这两种邮票各多少张.
34.“脐橙结硕果,香飘引客来”,赣南脐橙以其“外表光洁美观,肉质脆嫩,风味浓甜芳香”的特点饮誉中外.现欲将一批脐橙运往外地销售,若用2辆A型车和1辆B型车载满脐橙一次可运走10吨;用1辆A型车和2辆B型车载满脐橙一次可运走11吨.现有脐橙31吨,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满脐橙.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都载满脐橙一次可分别运送多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若1辆A型车需租金100元/次,1辆B型车需租金120元/次.请选出费用最少的租车方案,并求出最少租车费.
2026年中考数学一轮复习 二元一次方程组
参考答案与试题解析
一.选择题(共15小题)
1.已知方程组的解x为正数,y为非负数,给出下列结论:
①﹣3<a≤1;
②当时,x=y;
③当a=﹣2时,方程组的解也是方程x+y=5+a的解;
④若x≤1,则y≥2.
其中正确的是( )
A.①② B.②③ C.③④ D.②③④
【答案】B
【分析】用加减法解出方程组,根据方程组的解对各个选项进行判断即可.
【解答】解:
①+②得,x=3+a,
①﹣②得,y=﹣2a﹣2,
①由题意得,3+a>0,a>﹣3,
﹣2a﹣2≥0,a≤﹣1,
∴﹣3<a≤﹣1,①不正确;
②3+a=﹣2a﹣2,a,②正确;
③a=﹣2时,x+y=1﹣a=3,5+a=3,③正确;
④x≤1时,﹣3<a≤﹣2,则4>﹣2a﹣2≥2,④错.
故选:B.
【点评】本题考查的是二元一次方程组的解法和一元一次不等式的解法,正确解出方程组是解题的关键,注意方程与不等式的综合运用.
2.已知关于x,y的方程组,将此方程组的两个方程左右两边分别对应相加,得到一个新的方程,当m每取一个值时,就有一个方程,这些方程有一个公共解,这个公共解为( )
A. B. C. D.
【答案】C
【分析】根据题意①+②得x﹣y﹣9+m(x+y﹣1)=0,然后根据题意列出方程组即可求得公共解.
【解答】解:①+②得,
x+my+mx﹣y=9+m
x﹣y﹣9+mx+my﹣m=0
x﹣y﹣9+m(x+y﹣1)=0
根据题意,这些方程有一个公共解,与m的取值无关,
解得
所以这个公共解为
故选:C.
【点评】本题考查了二元一次方程组的解法,解题关键是利用筛选法解二元一次方程组.
3.我的家用小轿车配备了一种牌子的轮胎,装在前轮其可使用的距离为40000千米,装在后轮则可使用60000千米,如果将前后轮交换使用,则用这一组四个轮胎可行驶的最大距离为( )
A.44000千米 B.48000千米 C.50000千米 D.52000千米
【答案】B
【分析】设每个新轮胎报废时的总磨损量为k,一组新轮胎交换位置前走了xkm,交换位置后走了ykm,根据交换前磨损总量和交换后的磨损总量相等,可列出方程组,解方程组即可.
【解答】解:设每个新轮胎报废时的总磨损量为k,则安装在前轮的轮胎每行驶1km磨损量为,安装在后轮的轮胎每行驶1km的磨损量为,
又设一对新轮胎交换位置前走了xkm,交换位置后走了ykm,
分别以一个轮胎的总磨损量为等量关系列方程,有
,
两式相加,得2k,
则x+y=48000,即这一组四个轮胎可行驶的最大距离为48000米.
故选:B.
【点评】本题考查了应用类问题,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解,准确地找到等量关系并用方程组表示出来是解题的关键.
4.在关于x,y的二元一次方程组的下列说法中,正确的是( )
①当a=3时,方程的两根互为相反数;②当且仅当a=﹣4时,解得x与y相等;③x,y满足关系式x+5y=﹣12;④若9x 27y=81,则a=10.
A.①③ B.①② C.①②③ D.①②③④
【答案】D
【分析】用代入消元法先求出方程组的解,①根据互为相反数的两个数的和为0,列出方程,求出a即可判断;②根据x=y列出方程,求出a即可判断;③在原方程中,我们消去a,即可得到x,y的关系;④把底数统一化成a,等式左右两边的底数相同时,指数也相同,得到x,y的方程,把方程组的解代入求出a.
【解答】解:,
由①得:x=2y+a+6③,
把③代入②中,得:y④,
把④代入③中,得:x,
∴原方程组的解为.
①∵方程的两根互为相反数,
∴x+y=0,
即,
解得:a=3,
∴①正确;
②当x与y相等时,x=y,
即,
解得:a=﹣4,
∴②正确;
③在原方程中,我们消去a,得到x,y的关系,
②﹣①×2得:x+5y=﹣12,
∴③正确;
④∵9x 27y=81,
∴(32)x (33)y=34,
∴32x 33y=34,
∴32x+3y=34,
∴2x+3y=4,
将方程组的解代入得:4,
解得:a=10,
∴④正确.
综上所述,①②③④都正确.
故选:D.
【点评】本题考查二元一次方程组的解法,考核学生的计算能力,解方程组的关键是消元,消元的常用方法是代入消元法和加减消元法.
5.甲、乙、丙三家艺术中心为表彰进步学生,准备去文具店采购签字笔、笔记本、钢笔三种文具,签字笔、笔记本、钢笔单价分别为8元、10元、25元.乙艺术中心采购签字笔数量是甲的6倍,笔记本数量是甲的12倍,钢笔数量是甲的8倍,丙采购的签字笔数量是甲的3倍,笔记本数量是甲的9倍,钢笔数量和甲相同.三家艺术中心采购总费用为2850元,丙艺术中心比甲艺术中心总费用多464元,则甲艺术中心采购总费用为( )元
A.237 B.350 C.425 D.901
【答案】A
【分析】设甲艺术中心采购签字笔数量为x,笔记本数量为y,钢笔数量为z.根据题意,通过“采购费用=采购数量×文具单价”分别求出三家艺术中心的采购费用,再根据三家艺术中心采购总费用为2850元,丙艺术中心比甲艺术中心总费用多464元,列方程组,最后结合文具数量为正整数,求出甲艺术中心的三种文具的数量,进而得出答案.
【解答】解:设甲艺术中心采购签字笔数量为x,笔记本数量为y,钢笔数量为z.则三甲艺术中心的采购费用分别如下:
甲:8x+10y+25z;
乙:8×6x+12×10y+8×25z=48x+120y+200z;
丙:3×8x+9×10y+25z=24x+90y+25z.
三家艺术中心采购费用的总和为:80x+220y+250z.
根据题意建立三元一次方程组,得
化简,得
①﹣②×8,得25z﹣18y=53,
整理,得
z.
∵x,y,z均为正整数,
∴对于②式,y只可能为1、2、3、4、5.
只有y=4时,z为正整数,故z5.
∴x=29﹣5y=29﹣5×4=9.
所以甲艺术中心的采购总费用为:8x+10y+25z=8×9+10×4+25×5=237元.
故选:A.
【点评】本题考查了三元一次方程组的实际应用.通过方程组得到变量之间的数量关系,再结合文具数量为正整数的隐含条件求解是本题的关键.
6.实数x、y、z且x+y+z≠0,x,z,则下列等式成立的是( )
A.x2﹣y2=z2 B.xy=z C.x2+y2=z2 D.x+y=z
【答案】A
【分析】分别化简这两个等式,得到y=x+z和y=x﹣z,所以x+z=x﹣z,所以z=0,代入z中得x=y,因为x+y+z≠0,所以x=y≠0,然后分别判断各选项即可.
【解答】解:∵x,
∴2x=x+y﹣z,
∴y=x+z,
∵z,
∴2z=x﹣y+z,
∴y=x﹣z,
∴x+z=x﹣z,
∴z=0,
把z=0代入z中得:x=y,
∵x+y+z≠0,
∴x=y≠0.
A.x2﹣y2=x2﹣x2=0=z2,所以A选项正确,符合题意;
B.xy≠0,z=0,所以B选项错误,不符合题意;
C.x2+y2≠0,z2=0,所以C选项错误,不符合题意;
D.x+y≠0,z=0,所以D选项错误,不符合题意.
故选:A.
【点评】本题考查了三元一次方程组的解法,求出z=0是解题的关键.
7.已知关于x,y的方程组给出下列结论:
①当a=1时,方程组的解也是x+y=2a+1的解;
②无论a取何值,x,y的值不可能是互为相反数;
③x,y都为自然数的解有4对;
④若2x+y=8,则a=2.
正确的有几个( )
A.1 B.2 C.3 D.4
【答案】D
【分析】①根据消元法解二元一次方程组,然后将解代入方程x+y=2a+1即可求解;
②根据消元法解二元一次方程组,用含有字母的式子表示x、y,再根据互为相反数的两个数相加为0即可求解;
③根据试值法求二元一次方程x+y=3的自然数解即可得结论;
④根据整体代入的方法即可求解.
【解答】解:①将a=1代入原方程组,得 解得
将x=3,y=0,a=1代入方程x+y=2a+1的左右两边,
左边=3,右边=3,
当a=1时,方程组的解也是x+y=2a+1的解;
②解原方程组,得
∴x+y=3,
无论a取何值,x,y的值不可能是互为相反数;
③∵x+y=2a+1+2﹣2a=3
∴x、y为自然数的解有,,,.
④∵2x+y=8,∴2(2a+1)+2﹣2a=8,
解得a=2.
故选:D.
【点评】本题考查了消元法解二元一次方程组,确定二元一次方程的自然数解,解题关键是用含字母的式子表示方程组的解.
8.若关于x、y的二元一次方程组的解为,则方程组的解是( )
A. B. C. D.
【答案】B
【分析】将方程组整理得,然后结合条件可得x﹣2=﹣1,y=2解方程组即可.
【解答】将方程组整理得,
∵关于x、y的二元一次方程组的解为,
∴,
∴.
故选:B.
【点评】本题考查二元一次方程组的解,将方程组进行正确的变形是解题的关键.
9.已知关于x,y的二元一次方程组,给出下列结论中正确的是( )
①当这个方程组的解x,y的值互为相反数时,a=﹣2;
②当a=1时,方程组的解也是方程x+y=4+2a的解;
③无论a取什么实数,x+2y的值始终不变;
④若用x表示y,则y;
A.①② B.②③ C.②③④ D.①③④
【答案】D
【分析】根据方程组的解法可以得到x+y=2+a,
①令x+y=0,即可求出a的值,验证即可,
②由①得x+y=0,而x+y=4+2a,求出a的值,再与a=1比较得出答案,
③解方程组可求出方程组的解,再代入x+2y求值即可,
④用含有x、y的代数式表示a,进而得出x、y的关系,
【解答】解:关于x,y的二元一次方程组,
①+②得,2x+2y=4+2a,
即:x+y=2+a,
(1)①当方程组的解x,y的值互为相反数时,即x+y=0时,即2+a=0,
∴a=﹣2,故①正确,
(2)②原方程组的解满足x+y=2+a,
当a=1时,x+y=3,
而方程x+y=4+2a的解满足x+y=6,
因此②不正确,
(3)方程组,解得,
∴x+2y=2a+1+2﹣2a=3,
因此③是正确的,
(4)方程组,
由方程①得,a=4﹣x﹣3y代入方程②得,
x﹣y=3(4﹣x﹣3y),
即;y
因此④是正确的,
故选:D.
【点评】考查二元一次方程组的解法和应用,正确的解出方程组的解是解决问题的关键.
10.普通火车从绵阳至成都历时大约2小时,成绵城际快车开通后,时间大大缩短至几十分钟,现假定普通火车与城际快车两列对开的火车于同一时刻发车,其中普通火车由成都至绵阳,城际快车由绵阳至成都,这两车在途中相遇之后,各自用了80分钟和20分钟到达自己的终点绵阳、成都,则城际快车的平均速度是普通火车平均速度的( )倍.
A.2 B.2.5 C.3 D.4
【答案】A
【分析】普通火车从绵阳至成都历时大约2小时,由速度公式表示出两地的距离;
两车在途中相遇之后,各自用了80分钟和20分钟到达自己的终点绵阳、成都,由速度公式表示出两地距离.联立两式解题即可.
【解答】解:设普通火车速度为v m/min,城际快车速度为nv m/min,
已知普通火车从绵阳至成都历时大约2h=120min,由v可得两地距离:
s=v×120,
普通火车与城际快车两列对开,途中相遇之后,各自用了80分钟和20分钟到达自己的终点绵阳、成都,
即:s普+s城=s,
所以:v×80+nv×20=s,
所以:v×80+nv×20=v×120,
解得:n=2.
故选:A.
【点评】本题考查了二元一次方程的应用,速度公式的应用,关键正确表示出两地的距离.
11.已知关于x,y的二元一次方程组,给出下列结论中正确的是( )
①当这个方程组的解x,y的值互为相反数时,a=﹣2;
②当a=1时,方程组的解也是方程x+y=4+2a的解;
③无论a取什么实数,x+2y的值始终不变;
④若用x表示y.则;
A.①②③ B.①②④ C.①③④ D.②③④
【答案】C
【分析】根据方程组的解法可以得到x+y=2+a,
①令x+y=0,即可求出a的值,验证即可,
②由①得x+y=0,而x+y=4+2a,求出a的值,再与a=1比较得出答案,
③解方程组可求出方程组的解,再代入x+2y求值即可,
④用含有x、y的代数式表示a,进而得出x、y的关系,
【解答】解:关于x,y的二元一次方程组,
①+②得,
2x+2y=4+2a,
即x+y=2+a,
①当方程组的解x,y的值互为相反数时,即x+y=0时,即2+a=0,
∴a=﹣2,故①正确;
②原方程组的解满足x+y=2+a,
当a=1时,x+y=3,
而方程x+y=4+2a的解满足x+y=6,
因此②不正确;
③方程组,
解得,
∴x+2y=2a+1+2﹣2a=3,
因此③是正确的;
④方程组,
由方程①得,a=4﹣x﹣3y,
代入方程②得,
x﹣y=3(4﹣x﹣3y),
∴y,
因此④是正确的.
故选:C.
【点评】此题考查二元一次方程组的解法和应用,正确地解出方程组的解是解决问题的关键.
12.如图,长方形ABCD被分成3个正方形和2个长方形后仍是中心对称图形,设长方形ABCD的周长为l,若图中3个正方形和2个长方形的周长和为l,则标号为①的正方形的边长为( )
A.l B.l C.l D.l
【答案】B
【分析】设两个大正方形边长为x,小正方形的边长为y,由图可知周长和列方程和方程组,解答即可.
【解答】解:长方形ABCD被分成3个正方形和2个长方形后仍是中心对称图形,
∴两个大正方形相同、2个长方形相同.
设两个大正方形边长为y,小正方形的边长为x,
∴小长方形的边长分别为(y﹣x)、(x+y),大长方形边长为(2y﹣x)、(2y+x),
∵大长方形周长=1,即:2[(2y﹣x)+(2y+x)]=1,
∴8y=1,
∴y
∵3个正方形和2个长方形的周长和为l,
即:,
∴16y+4x,
∴x,
则标号为①的正方形的边长为,
故选:B.
【点评】此题主要考查了中心对称图形的性质和二元一次方程组的应用,关键是正确理解题意,要明确中心对称的性质,找出题目中的等量关系,列出方程组.注意各个正方形的边长之间的数量关系.
13.已知关于x,y的方程组,其中﹣3≤a≤1,下列命题正确的个数为( )
①当a=﹣2时,x、y的值互为相反数;
②是方程组的解;
③当a=1时,方程组的解也是方程x+y=4﹣a的解;
④若x≤1,则1≤y≤4.
A.1个 B.2个 C.3个 D.4个
【答案】C
【分析】①先求出方程组的解,把a=﹣2代入求出x、y即可;
②把代入,求出a的值,再根据﹣3≤a≤1判断即可;
③求出方程组的解,再代入方程,看看方程左右两边是否相等即可;
④根据x≤1和x=1+2a求出a≤0,求出﹣3≤a≤0,再求出1﹣a的范围即可.
【解答】解:解方程组得:,
①当a=﹣2时,x=1+2×(﹣2)=﹣3,y=1﹣(﹣2)=3,
所以x、y互为相反数,故①正确;
②把代入,
得:,
解得:a=2,
∵﹣3≤a≤1,
∴此时a=2不符合,故②错误;
③当a=1时,
∵x=1+2a=3,y=1﹣a=0,
∴方程组的解是,
把a=1,代入方程x+y=4﹣a得:左边=右边,
即当a=1时,方程组的解也是方程x+y=4﹣a的解,故③正确;
④∵x≤1,
∴x=1+2a≤1,
即a≤0,
∴﹣3≤a≤0,
∴3≥﹣a≥0,
∴4≥1﹣a≥1,
∵y=1﹣a,
∴1≤y≤4,故④正确;
故选:C.
【点评】本题考查了解二元一次方程组,二元一次方程组的解,一元一次方程的解,解不等式组等知识点,能求出方程组的解是解此题的关键.
14.我们知道自行车一般是由后轮驱动,因此,后轮胎的磨损要超过前轮胎,假设前轮行驶5000千米报废,后轮行驶3000千米报废,如果在自行车行驶若干千米后,将前后轮进行对换,那么这对轮胎最多可以行驶( )
A.4000 千米 B.3750 千米 C.4250 千米 D.3250 千米
【答案】B
【分析】设每个新轮胎报废时的总磨损量为k,一对新轮胎交换位置前走了x km,交换位置后走了y km,根据交换前磨损总量和交换后的磨损总量相等,可列出方程组,解方程组即可.
【解答】解:设每个新轮胎报废时的总磨损量为k,
则安装在前轮的轮胎每行驶1km磨损量为,安装在后轮的轮胎每行驶1km的磨损量为,
又设一对新轮胎交换位置前走了x km,交换位置后走了y km,
分别以一个轮胎的总磨损量为等量关系列方程,
,
两式相加,得,
则 x+y=3750(千米).
故选:B.
【点评】本题考查了二元一次方程组的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.利用二元一次方程组求解的应用题一般情况下题中要给出两个等量关系,准确地找到等量关系并用方程组表示出来是解题的关键.
15.已知是关于x,y的二元一次方程mx+ny=7的解,则代数式4m+6n﹣3的值是( )
A.14 B.11 C.7 D.4
【答案】B
【分析】把代入mx+ny=7,求出2m+3n的值,再把所求代数式化成含有2m+3n的形式,最后整体代入进行计算即可.
【解答】解:把代入mx+ny=7得:2m+3n=7,
∴4m+6n﹣3
=2(2m+3n)﹣3
=2×7﹣3
=14﹣3
=11,
故选:B.
【点评】本题主要考查了二元一次方程的解,解题关键是熟练掌握二元一次方程解的定义.
二.填空题(共13小题)
16.若关于x、y的二元一次方程组的解满足,则满足条件的m的所有非负整数值为 0,1,2,3 .
【答案】0,1,2,3.
【分析】先将两个方程相加,可得3x+3y=﹣3m+6,即x+y=﹣m+2,再根据已知x+y,得出不等式,解一元一次不等式求出m的范围,进而得出答案.
【解答】解:,
①+②,得3x+3y=﹣3m+6,即x+y=﹣m+2,
∵,
∴,
去分母,得﹣2m+4>﹣3,
移项、合并同类项,得﹣2m>﹣7,
解得:,
∴满足条件的m的所有非负整数值为0,1,2,3.
故答案为:0,1,2,3.
【点评】本题考查了二元一次方程组的解,解二元一次方程组,解一元一次不等式,掌握二元一次方程组解的定义,解二元一次方程组的方法,解一元一次不等式的方法是解题的关键.
17.在长方形ABCD中放入六个完全相同的小长方形,所标尺寸如图所示,则小长方形的宽CE为 2 cm.
【答案】见试题解答内容
【分析】设小长方形的长为x cm,宽为y cm,利用长方形的对边相等,可得出关于x,y的二元一次方程组,解方程组即可.
【解答】解:设小长方形的长为x cm,宽为y cm,
则AD=x+3y,AB=x+y=5+2y,
即x﹣y=5,
根据题意,得:,
解得:,
即CE=2cm,
故答案为:2.
【点评】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
18.小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图所示,3个纸杯叠放在一起高度为9cm,8个纸杯叠放在一起高度为14cm,若小明把20个纸杯整齐叠放在一起时,它的高度约是 26 cm.
【答案】26.
【分析】根据题意设未知数,列方程组求解即可.
【解答】解:设每增加一个纸杯增加的高度为x cm,一个纸杯的高度为y cm,
由题意列二元一次方程组得:,
解得,
则20个纸杯整齐叠放在一起时,它的高度约是7+(20﹣1)×1=7+19=26(cm),
故答案为:26.
【点评】本题考查了二元一次方程组的应用,找出等量关系正确列方程组是解题关键.
19.如图是由同一种长方形墙砖粘贴的部分墙面,其中三块横放的墙砖比一块竖放的墙砖高10cm,两块横放的墙砖比两块竖放的墙砖低40cm,则每块长方形墙砖的周长是 100 cm.
【答案】100.
【分析】根据图形找到两个等量关系,求解即可.
【解答】解:设每块墙砖的长为x cm,宽为y cm,
根据题意得:.
解得:,
∴每块长方形墙砖的周长是:2×(35+15)=100(cm),
故答案为:100.
【点评】本题考查二元一次方程组的应用,关键是根据题意找到等量关系式.
20.如图,从标注3的圆圈开始,顺时针方向按an+b的规律(n表示前一个圆圈中的数字,a,b是常数)转换后得到下一个圆圈中的数,例如:从“3→﹣1”得3a+b=﹣1,则标注“?”的圆圈中的数是 23 .
【答案】23.
【分析】根据题意得,解得,则顺时针方向按﹣2n+5的规律转换,再把n=﹣9时代入求解即可.
【解答】解:根据题意得,
解得,
∴顺时针方向按﹣2n+5的规律转换后得到下一个圆圈中的数,
∴当n=﹣9时,﹣2n+5=﹣2×(﹣9)+5=18+5=23,
所以标注“?”的圆圈中的数是23,
答:标注“?”的圆圈中的数是23,
故答案为:23.
【点评】本题考查了二元一次方程组的应用,掌握知识点的应用是解题的关键.
21.如图,用12块形状和大小均相同的小长方形拼成一个宽是40的大长方形,则每个小长方形的面积是 300 .
【答案】300.
【分析】设每个小长方形的长为x,宽为y,由此列方程组得到长和宽,由面积的公式计算即可.
【解答】解:设每个小长方形的长为x,宽为y,根据题意列方程组得:
,
解得,
∴xy=30×10=300,
故答案为:300.
【点评】本题考查了二元一次方程组的运用,理解数量关系,正确列出二元一次方程组求解是关键.
22.若关于x,y的方程组的解,也是方程2x﹣y=6的解,则k= .
【答案】.
【分析】利用加减消元法解方程组,可得x=5k,y=﹣2k,把x=5k,y=﹣2k分别代入方程2x﹣y=6,得出关于k的一元一次方程,解一元一次方程即可得出答案.
【解答】解:,
①﹣②,得3y=﹣6k,
解得:y=﹣2k,
把y=﹣2k代入①,得x﹣2k=3k,
解得:x=5k,
∵关于x,y的方程组的解,也是方程2x﹣y=6的解,
∴2×5k+2k=6,
∴12k=6,
解得:.
故答案为:.
【点评】本题考查了二元一次方程组的解,解二元一次方程组,二元一次方程的解,解一元一次方程,掌握二元一次方程组解的定义,解二元一次方程组的方法,解一元一次方程的方法是解题的关键.
23.王明在看中国清代算书《御制数理精蕴》时有这样一道题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两,问马、牛各价几何?”设马每匹m两,牛每头n两,请你根据题意列出方程组是 .
【答案】.
【分析】根据题意,设马每匹m两,牛每头n两,由“马四匹、牛六头,共价四十八两;马三匹、牛五头,共价三十八两”列出方程组即可得到答案.
【解答】解:设马每匹m两,牛每头n两,由题意可得,
故答案为:.
【点评】本题考查二元一次方程组解实际应用题,读懂题意,找准等量关系列方程组是解决问题的关键.
24.母亲节到了,小红,小莉,小莹到花店买花送给自己的母亲.小红买了3枝玫瑰,7枝康乃馨,1枝百合花,付了14元;小莉买了4枝玫瑰,10枝康乃馨,1枝百合花,付了16元;小莹买上面三种花各2枝,则她应付 20 元.
【答案】见试题解答内容
【分析】如果设玫瑰、康乃馨、百合花的单价分别为x元,y元,z元,题中有两个等量关系:3枝玫瑰的价格+7枝康乃馨的价格+1枝百合花的价格=14元;4枝玫瑰的价格+10枝康乃馨的价格+1枝百合花的价格=16元,据此列出两个方程,得到三元一次方程组.在这个方程组中,把y看作常数,用含y的代数式分别表示x和z,再代入2(x+y+z),即可求出结果.
【解答】解:设玫瑰、康乃馨、百合花的单价分别为x元,y元,z元,
根据已知条件,列出方程组,
②﹣①,得x=2﹣3y.③
将③代入①,得z=8+2y.④
∴x+y+z=2﹣3y+y+8+2y=10,
∴2(x+y+z)=20.
所以,小莹应付20元.
故答案为20.
【点评】本题考查了三元一次方程组在实际中的运用.解答此题的关键是列出方程组,难点是理解不必求出每一个未知数的具体值,而只要将方程组变形,能够求出x+y+z的值即可.为此,将这个方程组中的其中一个未知数看作常数,用含有这个未知数的代数式分别表示另外两个未知数,然后代入即可.
25.幻方是一种中国传统游戏,我国古代的《洛书》中记载了最早的幻方——九宫格,其规则是将数字填在正方形格子中,使每一行、每一列和两条对角线上的3个数字的和都相等.例如图①就是一个幻方.
(Ⅰ)图②是一个未完成的幻方,则x+y的结果为 12 ;
(Ⅱ)图③中的x为 a﹣1 (用含a的式子表示).
【答案】(Ⅰ)12;
(Ⅱ)a﹣1.
【分析】(Ⅰ)先求出第1列最上面的数为4,再求出第2行中间的数为x+2或x﹣y+4,第3列最上面的数为x﹣y+6或24﹣x,然后列出二元一次方程组,解方程组即可;
(Ⅱ)先求出第1行最上面的数为x﹣2,再求出第2列中间的数为2a﹣x﹣3,第1列中间的数为2x﹣a﹣4,然后由第1列与对角线上的3个数字的和相等,列出代数式即可得出结果.
【解答】解:(Ⅰ)∵第3行的和为:x+6+20=x+26,
∴第1列最上面的数为:x+26﹣(x+22)=4,
∴第2行中间的数为:x+26﹣(4+20)=x+2或x+26﹣(y+22)=x﹣y+4,
第3列最上面的数为:x+26﹣(20+y)=x﹣y+6或x+26﹣(x+2)=24﹣x,
∴,
解得:,
∴x+y=10+2=12,
故答案为:12;
(Ⅱ)∵第3行的和为:x+a+a﹣5=x+2a﹣5,
∴第1行最上面的数为:x+2a﹣5﹣(a﹣5+a+2)=x﹣2,
∴第2列中间的数为:x+2a﹣5﹣(x﹣2+x)=2a﹣x﹣3,
∴第1列中间的数为:x+2a﹣5﹣(a+2+2a﹣x﹣3)=2x﹣a﹣4,
∴x+2x﹣a﹣4=a﹣5+2a﹣x﹣3,
解得:x=a﹣1,
故答案为:a﹣1.
【点评】本题考查了二元一次方程组的应用、列代数式,找准等量关系,正确列出二元一次方程组和代数式是解题的关键.
26.《九章算术》记载了这样一个问题:“今有善田一亩,价三百;恶田七亩,价五百.今并买一顷,价钱一万,问善田几何?“意思是:当下良田1亩,价值300钱;薄田7亩,价值500钱.现在共买100亩,价值10000钱.根据条件,良田买了 12.5 亩.(注:1顷=100亩)
【答案】12.5.
【分析】设良田买了x亩,薄田买了y亩,由“当下良田1亩,价值300钱;薄田7亩,价值500钱.现在共买100亩,价值10000钱”列出方程组,解方程组即可.
【解答】解:设良田买了x亩,薄田买了y亩,
依题意得:,
解得:,
即良田买了12.5亩,
故答案为:12.5.
【点评】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
27.用8个大小完全相同的长方形在平面直角坐标系中摆成如图所示的图案,已知点A(4,10),则点B的坐标是 (﹣6,8) .
【答案】(﹣6,8).
【分析】设小长方形纸片的长为x,宽为y,根据点A的坐标列出关于x、y二元一次方程组求得x、y的值,结合点B所在的位置即可解答.
【解答】解:8个大小完全相同的长方形在平面直角坐标系中摆成如图所示的图案,已知点A(4,10),
设小长方形纸片的长为x,宽为y,
依题意得:,
解得:,
∴x+y=6+2=8,
∵点B在第二象限内,
∴点B的坐标是(﹣6,8).
故答案为:(﹣6,8).
【点评】本题主要考查了二元一次方程组的应用、坐标与图形等知识点,设出未知数、找准等量关系,正确列出二元一次方程组是解题的关键.
28.我国古典数学文献《增删算法统宗 六均输》中有一个“隔沟计算”的问题:“甲乙隔沟牧放,二人暗里参详,甲云得乙九只羊,多乙一倍之上,乙说得甲九只,两家之数相当,二人闲坐恼心肠,画地算了半晌”其大意为:甲、乙两人一起放牧,两人心里暗中数羊.如果乙给甲9只羊,那么甲的羊数为乙的2倍;如果甲给乙9只羊,那么两人的羊数相同,请问甲,乙各有多少只羊?设甲有羊x只,乙有羊y只,根据题意,可列方程组为 .
【答案】.
【分析】设甲有羊x只,乙有羊y只,根据“如果乙给甲9只羊,那么甲的羊数为乙的2倍;如果甲给乙9只羊,那么两人的羊数相同”,即可得出关于x,y的二元一次方程组,此题得解.
【解答】解:设甲有羊x只,乙有羊y只.
∵“如果乙给甲9只羊,那么甲的羊数为乙的2倍”,
∴x+9=2(y﹣9);
∵“如果甲给乙9只羊,那么两人的羊数相同”,
∴x﹣9=y+9.
联立两方程组成方程组.
故答案为:.
【点评】本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.
三.解答题(共6小题)
29.解方程组:
(1);
(2).
【答案】见试题解答内容
【分析】(1)根据解二元一次方程组的方法,理由代入消元法解方程组即可;
(2)根据解二元一次方程组的方法,理由加减消元法解方程组即可.
【解答】解:(1),
由①,得x=y+3③,
把③代入②,得3(y+3)﹣8y=14,
去括号,得3y+9﹣8y=14,
解得:y=﹣1,
把y=﹣1代入③,得x=﹣1+3=2,
∴方程组的解为;
(2),
①×2,得6x﹣4y=8③,
②+③,得13x=26,
解得:x=2,
把x=2代入①,得3×2﹣2y=4,
解得:y=1,
∴方程组的解为.
【点评】本题考查了解二元一次方程组,掌握解二元一次方程组的方法:加减消元法和代入消元法是解题的关键.
30.袁隆平爷爷多次说:“中国人要把饭碗牢牢地端在自己的手里!”为扩大粮食生产规模,稻田公园生产基地计划投入一笔资金购进甲、乙两种农机,已知购进1件甲种农机和1件乙种农机共需2万元,购进2件甲种农机和3件乙种农机共需5.5万元.
(1)求购进1件甲种农机和1件乙种农机各需多少万元?
(2)若该粮食生产基地计划购进甲、乙两种农机共10件,且投入资金不少于9.5万元且不超过12万元,则有哪几种购买方案?哪种购买方案需要的资金最少,最少资金是多少?
【答案】(1)购进1件甲种农机0.5万元,1件乙种农机1.5万元;
(2)有3种方案:①购进甲种农机3件,购进乙种农机7件;②购进甲种农机4件,购进乙种农机6件;③购进甲种农机5件,购进乙种农机5件;购买方案需要的资金最少的是购进甲种农机5件,购进乙种农机5件,最少资金为10万元.
【分析】(1)设购进1件甲种农机m万元,1件乙种农机n万元,根据购进1件甲种农机和1件乙种农机共需2万元,购进2件甲种农机和3件乙种农机共需5.5万元,可得,即可解得答案;
(2)设购进甲种农机x件,由投入资金不少于9.5万元且不超过12万元,得9.5≤0.5x+1.5(10﹣x)≤12,解得3≤x≤5.5,故有3种方案:①购进甲种农机3件,购进乙种农机7件;②购进甲种农机4件,购进乙种农机6件;③购进甲种农机5件,购进乙种农机5件;分别算出各方案所需资金,可得需要的资金最少的方案.
【解答】解:(1)设购进1件甲种农机m万元,1件乙种农机n万元,
∵购进1件甲种农机和1件乙种农机共需2万元,购进2件甲种农机和3件乙种农机共需5.5万元,
∴,
解得,
∴购进1件甲种农机0.5万元,1件乙种农机1.5万元;
(2)设购进甲种农机x件,则购进乙种农机(10﹣x)件,
∵投入资金不少于9.5万元且不超过12万元,
∴9.5≤0.5x+1.5(10﹣x)≤12,
解得3≤x≤5.5,
∵x为整数,
∴x可取3或4或5,
∴有3种方案:①购进甲种农机3件,购进乙种农机7件,所需资金为3×0.5+7×1.5=12(万元);
②购进甲种农机4件,购进乙种农机6件,所需资金为4×0.5+6×1.5=11(万元);
③购进甲种农机5件,购进乙种农机5件,所需资金为5×0.5+5×1.5=10(万元);
∴购买方案需要的资金最少的是购进甲种农机5件,购进乙种农机5件,最少资金为10万元.
【点评】本题考查二元一次方程组的应用和一元一次不等式组的应用,解题的关键是读懂题意,列出方程组和不等式组.
31.秋季由于气候干燥,天气转冷,用火用电情况大量增加,起火原因增多,火灾危险性加大.为了加强秋季防火用电安全,提高同学们的安全防范意识,某学校组织了“用电安全”知识竞赛,对表现优异的班级进行奖励,学校购买了若干支钢笔和中性笔.购买5支钢笔和10支中性笔共需110元;购买8支钢笔和6支中性笔共需126元.
(1)求购买1支钢笔和1支中性笔各需多少元;
(2)若学校购买钢笔和中性笔共200支,其中钢笔的数量不得少于中性笔数量的,且总支出不超过1364元,那学校有哪几种购买方案?
【答案】(1)购买1支钢笔需12元,1支中性笔需5元;
(2)学校共有3种购买方案,
方案1:购买50支钢笔,150支中性笔;
方案2:购买51支钢笔,149支中性笔;
方案3:购买52支钢笔,148支中性笔.
【分析】(1)设购买1支钢笔需x元,购买1支中性笔需y元,根据“购买5支钢笔和10支中性笔共需110元;购买8支钢笔和6支中性笔共需126元”,可列出关于x,y的二元一次方程组,解之即可得出结论;
(2)设学校购买m支钢笔,则购买(200﹣m)支中性笔,根据“购买钢笔的数量不得少于中性笔数量的,且总支出不超过1364元”,可列出关于m的一元一次不等式组,解之可得出m的取值范围,再结合m为正整数,即可得出各购买方案.
【解答】解:(1)设购买1支钢笔需x元,购买1支中性笔需y元,
根据题意得:,
解得:.
答:购买1支钢笔需12元,1支中性笔需5元;
(2)设学校购买m支钢笔,则购买(200﹣m)支中性笔,
根据题意得:,
解得:50≤m≤52,
又∵m为正整数,
∴m可以为50,51,52,
∴学校共有3种购买方案,
方案1:购买50支钢笔,150支中性笔;
方案2:购买51支钢笔,149支中性笔;
方案3:购买52支钢笔,148支中性笔.
【点评】本题考查了二元一次方程组的应用以及一元一次不等式组的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式组.
32.为响应“全民植树增绿,共建美丽中国”的号召,某学校组织学生到郊外参加义务植树活动,并准备了A,B两种食品作为午餐.这两种食品每包质量均为50g,营养成分如图所示.
(1)若要从这两种食品中摄入3900KJ热量和60g蛋白质,应选用A,B两种食品各多少包?
(2)运动量大的人或青少年对蛋白质的摄入量应更多.若要从这两种食品中摄入的蛋白质含量等于80g,应选用A,B两种食品各多少包(A,B两种食品都选且不能拆分)?
【答案】(1)应选用A种食品3包,B种食品2包;
(2)应选用A,B两种食品各5包,2包或2包,4包.
【分析】(1)设应选用A种食品x包,B种食品y包,根据要从这两种食品中摄入3900KJ热量和60g蛋白质,可列出关于x,y的二元一次方程组,解之即可得出结论;
(2)设应选用A种食品m包,B种食品n包,根据要从这两种食品中摄入的蛋白质含量等于80g,可列出关于m,n的二元一次方程,结合m,n均为正整数,即可得出结论.
【解答】解:(1)设应选用A种食品x包,B种食品y包,
根据题意得:,
解得:.
答:应选用A种食品3包,B种食品2包;
(2)设应选用A种食品m包,B种食品n包,
根据题意得:10m+15n=80,
∴m=8n,
又∵m,n均为正整数,
∴或.
答:应选用A,B两种食品各5包,2包或2包,4包.
【点评】本题考查了二元一次方程组的应用以及二元一次方程的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)找准等量关系,正确列出二元一次方程.
33.如图是中国邮政发行的《数学之美》的邮票,其中一张圆周率邮票面值为80分,莫比乌斯带邮票面值为1.50元.小宇购买这两种邮票共7张,恰好花了7元,求小宇购买这两种邮票各多少张.
【答案】小宇购买圆周率邮票5张,莫比乌斯带邮票2张.
【分析】设小宇购买圆周率邮票x张,莫比乌斯带邮票y张,根据题意,列出二元一次方程组,求出x与y,即可解答.
【解答】解:设小宇购买圆周率邮票x张,莫比乌斯带邮票y张,依题意得,
,
解得.
即小宇购买圆周率邮票5张,莫比乌斯带邮票2张,
答:小宇购买圆周率邮票5张,莫比乌斯带邮票2张.
【点评】本题考查二元一次方程组的应用,找到等量关系是解题的关键.
34.“脐橙结硕果,香飘引客来”,赣南脐橙以其“外表光洁美观,肉质脆嫩,风味浓甜芳香”的特点饮誉中外.现欲将一批脐橙运往外地销售,若用2辆A型车和1辆B型车载满脐橙一次可运走10吨;用1辆A型车和2辆B型车载满脐橙一次可运走11吨.现有脐橙31吨,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满脐橙.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都载满脐橙一次可分别运送多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若1辆A型车需租金100元/次,1辆B型车需租金120元/次.请选出费用最少的租车方案,并求出最少租车费.
【答案】见试题解答内容
【分析】(1)设1辆A型车载满脐橙一次可运送x吨,1辆B型车载满脐橙一次可运送y吨,根据“用2辆A型车和1辆B型车载满脐橙一次可运走10吨;用1辆A型车和2辆B型车载满脐橙一次可运走11吨”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)根据一次运送脐橙31吨,即可得出关于a,b的二元一次方程,结合a,b均为正整数,即可得出各租车方案;
(3)根据总租金=每辆车的租金×租车辆数,分别求出三个租车方案所需租金,比较后即可得出结论.
【解答】解:(1)设1辆A型车载满脐橙一次可运送x吨,1辆B型车载满脐橙一次可运送y吨,
依题意,得:,
解得:.
答:1辆A型车载满脐橙一次可运送3吨,1辆B型车载满脐橙一次可运送4吨.
(2)依题意,得:3a+4b=31,
∵a,b均为正整数,
∴或或.
∴一共有3种租车方案,方案一:租A型车1辆,B型车7辆;方案二:租A型车5辆,B型车4辆;方案三:租A型车9辆,B型车1辆.
(3)方案一所需租金为100×1+120×7=940(元);
方案二所需租金为100×5+120×4=980(元);
方案三所需租金为100×9+120×1=1020(元).
∵940<980<1020,
∴最省钱的租车方案是方案一,即租A型车1辆,B型车7辆,最少租车费为940元.
【点评】本题考查了二元一次方程组的应用以及二元一次方程的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)找准等量关系,正确列出二元一次方程;(3)根据各数量之间的关系,分别求出三个租车方案所需租金.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
