2026年中考数学一轮复习 整式(含解析)
文档属性
| 名称 | 2026年中考数学一轮复习 整式(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 184.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-06 14:56:02 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2026年中考数学一轮复习 整式
一.选择题(共10小题)
1.(2025 天河区校级四模)下列计算正确的是( )
A.a3+a4=a7 B.( a3)2=﹣a6
C.﹣4a8÷a4=﹣4a4 D.a3 a3=a9
2.(2025 武汉)下列计算正确的是( )
A.a2+a3=a5 B.a2 a3=a6 C.(﹣a3)2=a6 D.a8÷a2=a4
3.(2025 广东模拟)多项式2a2b﹣ab﹣1的次数是( )
A.5 B.3 C.2 D.1
4.(2025 椒江区校级模拟)下列运算中,计算结果正确的是( )
A.a2 a3=a6 B.a2+a3=a5 C.(a2)3=a6 D.a8÷a4=a2
5.(2025 沛县校级一模)下列计算中,结果正确的是( )
A.a2+a2=a4 B.a2 a3=a5 C.(a2)3=a5 D.a3﹣a3=a
6.(2025 淮安区校级一模)下列计算正确的是( )
A.(a2)3=a6 B.a8÷a2=a4 C.a2 a3=a6 D.2x+3y=5xy
7.(2025 泰兴市校级三模)下列式子运算结果最小的是( )
A.2002+1 B.199×201
C.1992+2×199+1 D.2012﹣2×201+1
8.(2025 汝阳县模拟)下列计算正确的是( )
A.3mn﹣mn=2 B.(m+2n)2=m2+2mn+2n2
C.(m﹣n)2=m2﹣n2 D.(﹣m)3 m=﹣m4
9.(2025 包河区二模)下列运算正确的是( )
A.a2 a3=a6 B.(﹣a)5÷(﹣a)4=a
C. D.(﹣2a)2=4a2
10.(2025 沭阳县校级一模)下列计算正确的是( )
A.a3 a3=a6 B.(﹣2a2)3=﹣6a6
C.a2 a3=a6 D.2a2+2a2=2a4
二.填空题(共5小题)
11.(2025 昌邑区校级三模)若a2﹣ab=2,ab﹣b2=1,则(a﹣b)2= .
12.(2025 蓬江区校级三模)多项式2x3y+xy+1的次数是 .
13.(2025 城东区校级三模)定义新运算:a※b=ab+b2,则(﹣2m)※m的运算结果是 .
14.(2025 阳西县二模)多项式2a2﹣3b+ab2的次数是 .
15.(2025 广西模拟)观察以下等式:
(x+2y)2+(2x﹣y)2=5(x2+y2);
(2x+3y)2+(3x﹣2y)2=13(x2+y2);
(3x+4y)2+(4x﹣3y)2=25(x2+y2);
(4x+6y)2+(6x﹣4y)2=52(x2+y2).
运用你所发现的规律解决以下问题:已知x,y为实数,x2+y2=1,则(6x+8y)2的最大值为 .
三.解答题(共5小题)
16.(2025 常州校级一模)先化简,再求值:(2x+1)2﹣x(4﹣x),其中x=﹣2.
17.(2025 定西模拟)先化简,再求值:(x﹣2y)2﹣4x(2x﹣y),其中x=﹣1,y=2.
18.(2025 雁塔区校级模拟)先化简,再求值:(2x﹣y)2﹣2x(x﹣2y),其中x=2,y=﹣1.
19.(2025 新华区校级一模)把1,3,5,7,9…这一组数按如下规律排放在表格中,任意选定如图所示方框中4个数,进行交叉相乘再相减的运算,即bc﹣ad,例如:9×17﹣7×19=20.完成下列各题:
(1)计算:3×11﹣1×13= ;
(2)猜想:bc﹣ad= ;
(3)验证:请你利用整式的运算对以上的规律加以证明.
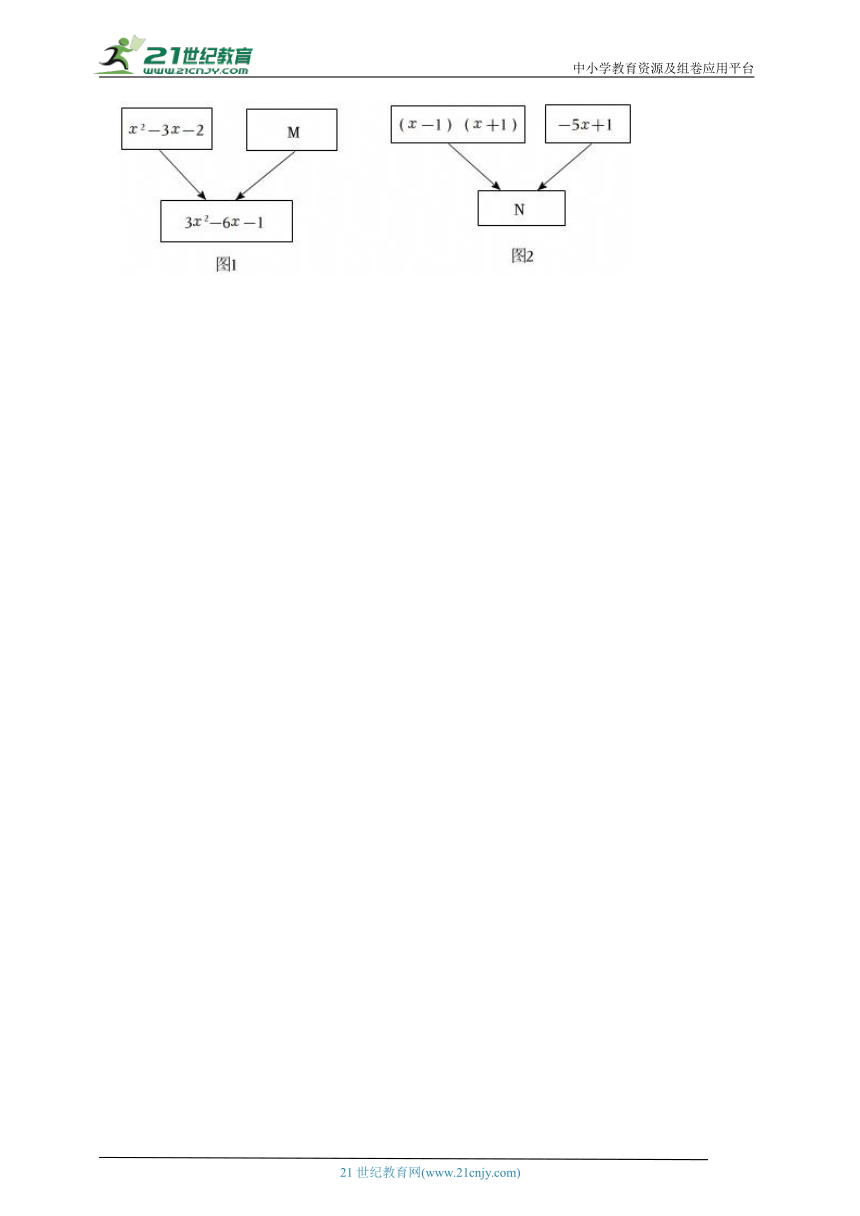
20.(2025 安次区校级二模)如图1和图2,约定:上方相邻两代数式之和等于这两代数式下方箭头共同指向的代数式.
(1)先求出代数式M,再计算当x=﹣1时,代数式M的值;
(2)嘉淇说:“只要x的值不取﹣1,M的值就一定大于N的值.”你同意她的说法吗?说明理由.
2026年中考数学一轮复习 整式
参考答案与试题解析
一.选择题(共10小题)
1.(2025 天河区校级四模)下列计算正确的是( )
A.a3+a4=a7 B.( a3)2=﹣a6
C.﹣4a8÷a4=﹣4a4 D.a3 a3=a9
【考点】整式的除法;合并同类项;同底数幂的乘法;幂的乘方与积的乘方.
【专题】整式;运算能力.
【答案】C
【分析】根据合并同类项法则、幂的乘方与积的乘方法则、单项式除以单项式法则、同底数幂的乘法法则分别计算判断即可.
【解答】解:A、a3与a4不是同类项,不能合并,故此选项不符合题意;
B、( a3)2=a6,故此选项不符合题意;
C、﹣4a8÷a4=﹣4a4,故此选项符合题意;
D、a3 a3=a6,故此选项不符合题意;
故选:C.
【点评】本题考查了整式的除法,幂的乘方与积的乘方,同底数幂的乘法,合并同类项,熟练掌握运算法则是解题的关键.
2.(2025 武汉)下列计算正确的是( )
A.a2+a3=a5 B.a2 a3=a6 C.(﹣a3)2=a6 D.a8÷a2=a4
【考点】同底数幂的除法;合并同类项;同底数幂的乘法;幂的乘方与积的乘方.
【专题】整式;运算能力.
【答案】C
【分析】利用同底数幂乘法及除法,合并同类项,幂的乘方法则逐项判断即可.
【解答】解:a2与a3不是同类项,无法合并,则A不符合题意,
a2 a3=a5,则B不符合题意,
(﹣a3)2=a6,则C符合题意,
a8÷a2=a6,则D不符合题意,
故选:C.
【点评】本题考查同底数幂乘法及除法,合并同类项,幂的乘方,熟练掌握相关运算法则是解题的关键.
3.(2025 广东模拟)多项式2a2b﹣ab﹣1的次数是( )
A.5 B.3 C.2 D.1
【考点】多项式.
【专题】整式;符号意识.
【答案】B.
【分析】根据多项式次数的定义求解.
【解答】解:多项式2a2b﹣ab﹣1中最高次项是2a2b,次数是3.
故选:B.
【点评】此题考查的是多项式的定义,多项式中每个单项式叫做多项式的项,这些单项式中的最高次数,就是这个多项式的次数.
4.(2025 椒江区校级模拟)下列运算中,计算结果正确的是( )
A.a2 a3=a6 B.a2+a3=a5 C.(a2)3=a6 D.a8÷a4=a2
【考点】同底数幂的除法;合并同类项;同底数幂的乘法;幂的乘方与积的乘方.
【专题】整式;运算能力.
【答案】C
【分析】根据同底数幂的乘除法法则、合并同类项的方法、幂的乘方与积的乘方法则进行逐项计算即可.
【解答】解:A、a2 a3=a5,故该项不正确,不符合题意;
B、a3与a2不是同类项,不能进行合并,该项不正确,不符合题意;
C、(a2)3=a6,该项正确,符合题意;
D、a8÷a4=a4,该项不正确,不符合题意;
故选:C.
【点评】本题考查同底数幂的乘除法、合并同类项、幂的乘方与积的乘方,熟练掌握运算法则是解题的关键.
5.(2025 沛县校级一模)下列计算中,结果正确的是( )
A.a2+a2=a4 B.a2 a3=a5 C.(a2)3=a5 D.a3﹣a3=a
【考点】幂的乘方与积的乘方;合并同类项;同底数幂的乘法.
【专题】整式;运算能力.
【答案】B
【分析】A、D选项均根据合并同类项法则进行计算,然后判断即可;
B.根据同底数幂的乘法法则进行计算,然后判断即可;
C.根据幂的乘方法则进行计算,然后判断即可.
【解答】解:A.∵a2+a2=2a2,∴此选项的计算错误,故此选项不符合题意;
B.∵a2 a3=a5,∴此选项的计算正确,故此选项符合题意;
C.∵(a2)3=a6,∴此选项的计算错误,故此选项不符合题意;
D.∵a3﹣a3=0,∴此选项的计算错误,故此选项不符合题意;
故选:B.
【点评】本题主要考查了整式的有关运算,解题关键是熟练掌握同底数幂的乘法法则、幂的乘方法则和合并同类项法则.
6.(2025 淮安区校级一模)下列计算正确的是( )
A.(a2)3=a6 B.a8÷a2=a4 C.a2 a3=a6 D.2x+3y=5xy
【考点】同底数幂的除法;合并同类项;同底数幂的乘法;幂的乘方与积的乘方.
【答案】A
【分析】根据幂的乘方,底数不变,指数相乘;同底数幂相除,底数不变,指数相减;同底数幂相乘,底数不变,指数相加;合并同类项法则;对各选项分析判断后利用排除法求解.
【解答】解:A、(a2)3=a6,故此选项符合题意;
B、a8÷a2=a6,故此选项不符合题意;
C、a2 a3=a5,故此选项不符合题意;
D、2x与3y不是同类项,不能合并,故此选项不符合题意;
故选:A.
【点评】本题考查合并同类项、同底数幂的乘法、幂的乘方与积的乘方、同底数幂的除法,熟练掌握运算性质和法则是解题的关键.
7.(2025 泰兴市校级三模)下列式子运算结果最小的是( )
A.2002+1 B.199×201
C.1992+2×199+1 D.2012﹣2×201+1
【考点】平方差公式.
【专题】整式;运算能力.
【答案】B
【分析】利用平方差公式、完全平方公式分别计算各选项,再比算即可.
【解答】解:根据平方差公式、完全平方公式逐项分析计算比较可得:
199×201=2002﹣1,
1992+2×199+1=(199+1)2=2002,
2012﹣2×201+1=(201﹣1)2=2002,
∴199×201最小,
故选:B.
【点评】本题考查了有理数的混合运算,平方差公式、完全平方公式的运用,熟练掌握以上知识点是关键.
8.(2025 汝阳县模拟)下列计算正确的是( )
A.3mn﹣mn=2 B.(m+2n)2=m2+2mn+2n2
C.(m﹣n)2=m2﹣n2 D.(﹣m)3 m=﹣m4
【考点】完全平方公式;合并同类项;同底数幂的乘法.
【专题】整式;运算能力.
【答案】D
【分析】根据合并同类项法则、完全平方公式、单项式乘单项式的运算法则分别计算判断即可.
【解答】解:A、3mn﹣mn=2mn,故此选项不符合题意;
B、(m+2n)2=m2+4mn+4n2,故此选项不符合题意;
C、(m﹣n)2=m2﹣2mn+n2,故此选项不符合题意;
D、(﹣m)3 m=﹣m3 m=﹣m4,故此选项符合题意;
故选:D.
【点评】本题考查了完全平方公式、合并同类项法则、单项式乘单项式,熟练掌握运算法则是解题的关键.
9.(2025 包河区二模)下列运算正确的是( )
A.a2 a3=a6 B.(﹣a)5÷(﹣a)4=a
C. D.(﹣2a)2=4a2
【考点】同底数幂的除法;同底数幂的乘法;幂的乘方与积的乘方.
【专题】整式;运算能力.
【答案】D
【分析】根据幂的运算性质逐项化简判断即可.
【解答】解:A、a2 a3=a5,故A选项错误;
B、(﹣a)5÷(﹣a)4=﹣a,故B选项错误;
C、(am)2=a2m,故C选项错误;
D、(﹣2a)2=4a2,故D选项正确.
故选:D.
【点评】本题考查了同底数幂的除法,同底数幂的乘法,幂的乘方与积的乘方,熟练掌握幂的运算性质是解题的关键.
10.(2025 沭阳县校级一模)下列计算正确的是( )
A.a3 a3=a6 B.(﹣2a2)3=﹣6a6
C.a2 a3=a6 D.2a2+2a2=2a4
【考点】幂的乘方与积的乘方;合并同类项;同底数幂的乘法.
【专题】整式;运算能力.
【答案】A
【分析】利用合并同类项的法则,同底数幂的乘法的法则,积的乘方的法则对各项进行运算即可.
【解答】解:A、a3 a3=a6,符合题意;
B、(﹣2a2)3=﹣8a6,不符合题意;
C、a2 a3=a5,不符合题意;
D、2a2+2a2=4a2,不符合题意.
故选:A.
【点评】本题主要考查合并同类项,积的乘方,同底数幂的乘法,解答的关键是对相应的运算法则的掌握.
二.填空题(共5小题)
11.(2025 昌邑区校级三模)若a2﹣ab=2,ab﹣b2=1,则(a﹣b)2= 1 .
【考点】完全平方公式.
【专题】整式;运算能力.
【答案】1.
【分析】根据题意可得a(a﹣b)=2,b(a﹣b)=1,则可推出a=2b,进而得到b2=1,再把a=2b代入所求式子中计算求解即可.
【解答】解:根据题意可知,a(a﹣b)=2,b(a﹣b)=1,
∴a=2b,
∴2b(2b﹣b)=2,即b2=1,
∴(a﹣b)2=(2b﹣b)2=b2=1.
故答案为:1.
【点评】本题主要考查了完全平方根,掌握完全平方根的定义是关键.
12.(2025 蓬江区校级三模)多项式2x3y+xy+1的次数是 4 .
【考点】多项式.
【专题】整式;符号意识.
【答案】4.
【分析】根据多项式次数的定义求解.
【解答】解:多项式2x3y+xy+1中最高次项是2x3y,次数是4.
故答案为:4.
【点评】此题考查的是多项式的定义,多项式中每个单项式叫做多项式的项,这些单项式中的最高次数,就是这个多项式的次数.
13.(2025 城东区校级三模)定义新运算:a※b=ab+b2,则(﹣2m)※m的运算结果是 ﹣m2 .
【考点】整式的混合运算.
【专题】整式;运算能力.
【答案】﹣m2.
【分析】根据新定义,列出算式,利用单项式乘单项式的法则,以及合并同类项的法则,进行计算即可.
【解答】解:根据新定义可得:
原式=﹣2m m+m2=﹣m2;
故答案为:﹣m2.
【点评】本题考查整式的运算,理解新定义是关键.
14.(2025 阳西县二模)多项式2a2﹣3b+ab2的次数是 3 .
【考点】多项式.
【专题】整式;符号意识.
【答案】3.
【分析】根据多项式次数的定义求解.
【解答】解:多项式2a2﹣3b+ab2中最高次项是ab2,次数是3.
故答案为:3.
【点评】此题考查的是多项式的定义,多项式中每个单项式叫做多项式的项,这些单项式中的最高次数,就是这个多项式的次数.
15.(2025 广西模拟)观察以下等式:
(x+2y)2+(2x﹣y)2=5(x2+y2);
(2x+3y)2+(3x﹣2y)2=13(x2+y2);
(3x+4y)2+(4x﹣3y)2=25(x2+y2);
(4x+6y)2+(6x﹣4y)2=52(x2+y2).
运用你所发现的规律解决以下问题:已知x,y为实数,x2+y2=1,则(6x+8y)2的最大值为 100 .
【考点】完全平方公式;非负数的性质:偶次方;规律型:数字的变化类.
【专题】整式;运算能力.
【答案】100.
【分析】根据已知得到(6x+8y)2+(8x﹣6y)2=(62+82)(x2+y2)=100(x2+y2),再根据偶次方的非负性求出最大值.
【解答】解:由等式可知:(6x+8y)2+(8x﹣6y)2=(62+82)(x2+y2)=100(x2+y2)
∴(6x+8y)2=100(x2+y2)﹣(8x﹣6y)2
∵x2+y2=1,
∴(6x+8y)2=100﹣(8x﹣6y)2
∵(8x﹣6y)2≥0,
∴0≤100﹣(8x﹣6y)2≤100,
∴(6x+8y)2的最大值为100,
故答案为:100.
【点评】本题主要考查了多项式运算中的规律探索,根据已知等式得到计算规律,并解决问题是解题的关键,
三.解答题(共5小题)
16.(2025 常州校级一模)先化简,再求值:(2x+1)2﹣x(4﹣x),其中x=﹣2.
【考点】整式的混合运算—化简求值.
【专题】整式;运算能力.
【答案】5x2+1,21.
【分析】先根据完全平方公式和去括号计算,然合并同类项化简,最后代值计算即可.
【解答】解:原式=4x2+4x+1﹣4x+x2
=5x2+1,
当x=﹣2时,原式=5×(﹣2)2+1=21.
【点评】本题主要考查了整式的化简求值,熟知完全平方公式是解题的关键.
17.(2025 定西模拟)先化简,再求值:(x﹣2y)2﹣4x(2x﹣y),其中x=﹣1,y=2.
【考点】整式的混合运算—化简求值.
【专题】整式;运算能力.
【答案】﹣7x2+4y2,9.
【分析】根据完全平方公式、单项式乘多项式、合并同类项把原式化简,把x、y的值代入计算得到答案.
【解答】解:(x﹣2y)2﹣4x(2x﹣y)
=x2﹣4xy+4y2﹣(8x2﹣4xy)
=x2﹣4xy+4y2﹣8x2+4xy
=﹣7x2+4y2,
当x=﹣1,y=2时,原式=﹣7×(﹣1)2+4×22=﹣7+16=9.
【点评】本题考查的是整式的混合运算﹣化简求值,掌握整式的混合运算法则是解题的关键.
18.(2025 雁塔区校级模拟)先化简,再求值:(2x﹣y)2﹣2x(x﹣2y),其中x=2,y=﹣1.
【考点】整式的混合运算—化简求值.
【专题】整式;运算能力.
【答案】2x2+y2,原式=9.
【分析】先利用完全平方公式,单项式乘多项式的法则进行计算,然后把x,y的值代入化简后的式子进行计算,即可解答.
【解答】解:(2x﹣y)2﹣2x(x﹣2y)
=4x2﹣4xy+y2﹣2x2+4xy
=2x2+y2,
当x=2,y=﹣1时,原式=2×22+(﹣1)2=2×4+1=8+1=9.
【点评】本题考查了整式的混合运算﹣化简求值,准确熟练地进行计算是解题的关键.
19.(2025 新华区校级一模)把1,3,5,7,9…这一组数按如下规律排放在表格中,任意选定如图所示方框中4个数,进行交叉相乘再相减的运算,即bc﹣ad,例如:9×17﹣7×19=20.完成下列各题:
(1)计算:3×11﹣1×13= 20 ;
(2)猜想:bc﹣ad= 20 ;
(3)验证:请你利用整式的运算对以上的规律加以证明.
【考点】整式的混合运算;有理数的混合运算;规律型:数字的变化类.
【专题】猜想归纳;实数;整式;运算能力.
【答案】(1)20;
(2)20;
(3)见解析.
【分析】(1)先算乘法,再算减法即可;
(2)根据表格中的数据及(1)中求得的结果总结规律即可;
(3)由图表可得b=a+2,c=a+10,d=a+12,然后列得算式并计算即可.
【解答】解:(1)3×11﹣1×13
=33﹣13
=20,
故答案为:20;
(2)猜想:bc﹣ad=20,
故答案为:20;
(3)由图表可得b=a+2,c=a+10,d=a+12,
则bc﹣ad=(a+2)(a+10)﹣a(a+12)
=a2+10a+2a+20﹣(a2+12a)
=a2+10a+2a+20﹣a2﹣12a
=20,
∴bc﹣ad=20正确.
【点评】本题考查整式的混合运算,有理数的混合运算,数式规律问题,理解题意并总结出规律是解题的关键.
20.(2025 安次区校级二模)如图1和图2,约定:上方相邻两代数式之和等于这两代数式下方箭头共同指向的代数式.
(1)先求出代数式M,再计算当x=﹣1时,代数式M的值;
(2)嘉淇说:“只要x的值不取﹣1,M的值就一定大于N的值.”你同意她的说法吗?说明理由.
【考点】整式的加减;代数式求值.
【专题】整式;运算能力.
【答案】(1)2x2﹣3x+1;当x=﹣1时,M=6;(2)同意,理由见解析.
【分析】(1)由题意可得M=3x2﹣6x﹣1﹣(x2﹣3x﹣2),再根据去括号、合并同类项法则计算即可化简,最后代入x=﹣1计算即可得解;
(2)先求出N=x2﹣5x,再计算出M﹣N=(x+1)2,分情况讨论即可得解.
【解答】解:(1)根据题意可知,x2﹣3x﹣2+M=3x2﹣6x﹣1,
∴M=3x2﹣6x﹣1﹣(x2﹣3x﹣2)
=3x2﹣6x﹣1﹣x2+3x+2
=2x2﹣3x+1,
当x=﹣1时,
2x2﹣3x+1
=2×(﹣1)2﹣3×(﹣1)+1
=2+3+1
=6;
(2)同意,理由如下:
根据题意可知,(x﹣1)(x+1)﹣5x+1=N,
∴N=x2﹣1﹣5x+1=x2﹣5x,
∴M﹣N=2x2﹣3x+1﹣(x2﹣5x)
=2x2﹣3x+1﹣x2+5x
=x2+2x+1
=(x+1)2,
当x=﹣1时,(x+1)2=0,此时M﹣N=0,M=N;
当x不取﹣1,(x+1)2恒大于0,M的值就一定大于N的值.
【点评】本题考查了整式的加减,代数式求值,掌握相应的运算法则是关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2026年中考数学一轮复习 整式
一.选择题(共10小题)
1.(2025 天河区校级四模)下列计算正确的是( )
A.a3+a4=a7 B.( a3)2=﹣a6
C.﹣4a8÷a4=﹣4a4 D.a3 a3=a9
2.(2025 武汉)下列计算正确的是( )
A.a2+a3=a5 B.a2 a3=a6 C.(﹣a3)2=a6 D.a8÷a2=a4
3.(2025 广东模拟)多项式2a2b﹣ab﹣1的次数是( )
A.5 B.3 C.2 D.1
4.(2025 椒江区校级模拟)下列运算中,计算结果正确的是( )
A.a2 a3=a6 B.a2+a3=a5 C.(a2)3=a6 D.a8÷a4=a2
5.(2025 沛县校级一模)下列计算中,结果正确的是( )
A.a2+a2=a4 B.a2 a3=a5 C.(a2)3=a5 D.a3﹣a3=a
6.(2025 淮安区校级一模)下列计算正确的是( )
A.(a2)3=a6 B.a8÷a2=a4 C.a2 a3=a6 D.2x+3y=5xy
7.(2025 泰兴市校级三模)下列式子运算结果最小的是( )
A.2002+1 B.199×201
C.1992+2×199+1 D.2012﹣2×201+1
8.(2025 汝阳县模拟)下列计算正确的是( )
A.3mn﹣mn=2 B.(m+2n)2=m2+2mn+2n2
C.(m﹣n)2=m2﹣n2 D.(﹣m)3 m=﹣m4
9.(2025 包河区二模)下列运算正确的是( )
A.a2 a3=a6 B.(﹣a)5÷(﹣a)4=a
C. D.(﹣2a)2=4a2
10.(2025 沭阳县校级一模)下列计算正确的是( )
A.a3 a3=a6 B.(﹣2a2)3=﹣6a6
C.a2 a3=a6 D.2a2+2a2=2a4
二.填空题(共5小题)
11.(2025 昌邑区校级三模)若a2﹣ab=2,ab﹣b2=1,则(a﹣b)2= .
12.(2025 蓬江区校级三模)多项式2x3y+xy+1的次数是 .
13.(2025 城东区校级三模)定义新运算:a※b=ab+b2,则(﹣2m)※m的运算结果是 .
14.(2025 阳西县二模)多项式2a2﹣3b+ab2的次数是 .
15.(2025 广西模拟)观察以下等式:
(x+2y)2+(2x﹣y)2=5(x2+y2);
(2x+3y)2+(3x﹣2y)2=13(x2+y2);
(3x+4y)2+(4x﹣3y)2=25(x2+y2);
(4x+6y)2+(6x﹣4y)2=52(x2+y2).
运用你所发现的规律解决以下问题:已知x,y为实数,x2+y2=1,则(6x+8y)2的最大值为 .
三.解答题(共5小题)
16.(2025 常州校级一模)先化简,再求值:(2x+1)2﹣x(4﹣x),其中x=﹣2.
17.(2025 定西模拟)先化简,再求值:(x﹣2y)2﹣4x(2x﹣y),其中x=﹣1,y=2.
18.(2025 雁塔区校级模拟)先化简,再求值:(2x﹣y)2﹣2x(x﹣2y),其中x=2,y=﹣1.
19.(2025 新华区校级一模)把1,3,5,7,9…这一组数按如下规律排放在表格中,任意选定如图所示方框中4个数,进行交叉相乘再相减的运算,即bc﹣ad,例如:9×17﹣7×19=20.完成下列各题:
(1)计算:3×11﹣1×13= ;
(2)猜想:bc﹣ad= ;
(3)验证:请你利用整式的运算对以上的规律加以证明.
20.(2025 安次区校级二模)如图1和图2,约定:上方相邻两代数式之和等于这两代数式下方箭头共同指向的代数式.
(1)先求出代数式M,再计算当x=﹣1时,代数式M的值;
(2)嘉淇说:“只要x的值不取﹣1,M的值就一定大于N的值.”你同意她的说法吗?说明理由.
2026年中考数学一轮复习 整式
参考答案与试题解析
一.选择题(共10小题)
1.(2025 天河区校级四模)下列计算正确的是( )
A.a3+a4=a7 B.( a3)2=﹣a6
C.﹣4a8÷a4=﹣4a4 D.a3 a3=a9
【考点】整式的除法;合并同类项;同底数幂的乘法;幂的乘方与积的乘方.
【专题】整式;运算能力.
【答案】C
【分析】根据合并同类项法则、幂的乘方与积的乘方法则、单项式除以单项式法则、同底数幂的乘法法则分别计算判断即可.
【解答】解:A、a3与a4不是同类项,不能合并,故此选项不符合题意;
B、( a3)2=a6,故此选项不符合题意;
C、﹣4a8÷a4=﹣4a4,故此选项符合题意;
D、a3 a3=a6,故此选项不符合题意;
故选:C.
【点评】本题考查了整式的除法,幂的乘方与积的乘方,同底数幂的乘法,合并同类项,熟练掌握运算法则是解题的关键.
2.(2025 武汉)下列计算正确的是( )
A.a2+a3=a5 B.a2 a3=a6 C.(﹣a3)2=a6 D.a8÷a2=a4
【考点】同底数幂的除法;合并同类项;同底数幂的乘法;幂的乘方与积的乘方.
【专题】整式;运算能力.
【答案】C
【分析】利用同底数幂乘法及除法,合并同类项,幂的乘方法则逐项判断即可.
【解答】解:a2与a3不是同类项,无法合并,则A不符合题意,
a2 a3=a5,则B不符合题意,
(﹣a3)2=a6,则C符合题意,
a8÷a2=a6,则D不符合题意,
故选:C.
【点评】本题考查同底数幂乘法及除法,合并同类项,幂的乘方,熟练掌握相关运算法则是解题的关键.
3.(2025 广东模拟)多项式2a2b﹣ab﹣1的次数是( )
A.5 B.3 C.2 D.1
【考点】多项式.
【专题】整式;符号意识.
【答案】B.
【分析】根据多项式次数的定义求解.
【解答】解:多项式2a2b﹣ab﹣1中最高次项是2a2b,次数是3.
故选:B.
【点评】此题考查的是多项式的定义,多项式中每个单项式叫做多项式的项,这些单项式中的最高次数,就是这个多项式的次数.
4.(2025 椒江区校级模拟)下列运算中,计算结果正确的是( )
A.a2 a3=a6 B.a2+a3=a5 C.(a2)3=a6 D.a8÷a4=a2
【考点】同底数幂的除法;合并同类项;同底数幂的乘法;幂的乘方与积的乘方.
【专题】整式;运算能力.
【答案】C
【分析】根据同底数幂的乘除法法则、合并同类项的方法、幂的乘方与积的乘方法则进行逐项计算即可.
【解答】解:A、a2 a3=a5,故该项不正确,不符合题意;
B、a3与a2不是同类项,不能进行合并,该项不正确,不符合题意;
C、(a2)3=a6,该项正确,符合题意;
D、a8÷a4=a4,该项不正确,不符合题意;
故选:C.
【点评】本题考查同底数幂的乘除法、合并同类项、幂的乘方与积的乘方,熟练掌握运算法则是解题的关键.
5.(2025 沛县校级一模)下列计算中,结果正确的是( )
A.a2+a2=a4 B.a2 a3=a5 C.(a2)3=a5 D.a3﹣a3=a
【考点】幂的乘方与积的乘方;合并同类项;同底数幂的乘法.
【专题】整式;运算能力.
【答案】B
【分析】A、D选项均根据合并同类项法则进行计算,然后判断即可;
B.根据同底数幂的乘法法则进行计算,然后判断即可;
C.根据幂的乘方法则进行计算,然后判断即可.
【解答】解:A.∵a2+a2=2a2,∴此选项的计算错误,故此选项不符合题意;
B.∵a2 a3=a5,∴此选项的计算正确,故此选项符合题意;
C.∵(a2)3=a6,∴此选项的计算错误,故此选项不符合题意;
D.∵a3﹣a3=0,∴此选项的计算错误,故此选项不符合题意;
故选:B.
【点评】本题主要考查了整式的有关运算,解题关键是熟练掌握同底数幂的乘法法则、幂的乘方法则和合并同类项法则.
6.(2025 淮安区校级一模)下列计算正确的是( )
A.(a2)3=a6 B.a8÷a2=a4 C.a2 a3=a6 D.2x+3y=5xy
【考点】同底数幂的除法;合并同类项;同底数幂的乘法;幂的乘方与积的乘方.
【答案】A
【分析】根据幂的乘方,底数不变,指数相乘;同底数幂相除,底数不变,指数相减;同底数幂相乘,底数不变,指数相加;合并同类项法则;对各选项分析判断后利用排除法求解.
【解答】解:A、(a2)3=a6,故此选项符合题意;
B、a8÷a2=a6,故此选项不符合题意;
C、a2 a3=a5,故此选项不符合题意;
D、2x与3y不是同类项,不能合并,故此选项不符合题意;
故选:A.
【点评】本题考查合并同类项、同底数幂的乘法、幂的乘方与积的乘方、同底数幂的除法,熟练掌握运算性质和法则是解题的关键.
7.(2025 泰兴市校级三模)下列式子运算结果最小的是( )
A.2002+1 B.199×201
C.1992+2×199+1 D.2012﹣2×201+1
【考点】平方差公式.
【专题】整式;运算能力.
【答案】B
【分析】利用平方差公式、完全平方公式分别计算各选项,再比算即可.
【解答】解:根据平方差公式、完全平方公式逐项分析计算比较可得:
199×201=2002﹣1,
1992+2×199+1=(199+1)2=2002,
2012﹣2×201+1=(201﹣1)2=2002,
∴199×201最小,
故选:B.
【点评】本题考查了有理数的混合运算,平方差公式、完全平方公式的运用,熟练掌握以上知识点是关键.
8.(2025 汝阳县模拟)下列计算正确的是( )
A.3mn﹣mn=2 B.(m+2n)2=m2+2mn+2n2
C.(m﹣n)2=m2﹣n2 D.(﹣m)3 m=﹣m4
【考点】完全平方公式;合并同类项;同底数幂的乘法.
【专题】整式;运算能力.
【答案】D
【分析】根据合并同类项法则、完全平方公式、单项式乘单项式的运算法则分别计算判断即可.
【解答】解:A、3mn﹣mn=2mn,故此选项不符合题意;
B、(m+2n)2=m2+4mn+4n2,故此选项不符合题意;
C、(m﹣n)2=m2﹣2mn+n2,故此选项不符合题意;
D、(﹣m)3 m=﹣m3 m=﹣m4,故此选项符合题意;
故选:D.
【点评】本题考查了完全平方公式、合并同类项法则、单项式乘单项式,熟练掌握运算法则是解题的关键.
9.(2025 包河区二模)下列运算正确的是( )
A.a2 a3=a6 B.(﹣a)5÷(﹣a)4=a
C. D.(﹣2a)2=4a2
【考点】同底数幂的除法;同底数幂的乘法;幂的乘方与积的乘方.
【专题】整式;运算能力.
【答案】D
【分析】根据幂的运算性质逐项化简判断即可.
【解答】解:A、a2 a3=a5,故A选项错误;
B、(﹣a)5÷(﹣a)4=﹣a,故B选项错误;
C、(am)2=a2m,故C选项错误;
D、(﹣2a)2=4a2,故D选项正确.
故选:D.
【点评】本题考查了同底数幂的除法,同底数幂的乘法,幂的乘方与积的乘方,熟练掌握幂的运算性质是解题的关键.
10.(2025 沭阳县校级一模)下列计算正确的是( )
A.a3 a3=a6 B.(﹣2a2)3=﹣6a6
C.a2 a3=a6 D.2a2+2a2=2a4
【考点】幂的乘方与积的乘方;合并同类项;同底数幂的乘法.
【专题】整式;运算能力.
【答案】A
【分析】利用合并同类项的法则,同底数幂的乘法的法则,积的乘方的法则对各项进行运算即可.
【解答】解:A、a3 a3=a6,符合题意;
B、(﹣2a2)3=﹣8a6,不符合题意;
C、a2 a3=a5,不符合题意;
D、2a2+2a2=4a2,不符合题意.
故选:A.
【点评】本题主要考查合并同类项,积的乘方,同底数幂的乘法,解答的关键是对相应的运算法则的掌握.
二.填空题(共5小题)
11.(2025 昌邑区校级三模)若a2﹣ab=2,ab﹣b2=1,则(a﹣b)2= 1 .
【考点】完全平方公式.
【专题】整式;运算能力.
【答案】1.
【分析】根据题意可得a(a﹣b)=2,b(a﹣b)=1,则可推出a=2b,进而得到b2=1,再把a=2b代入所求式子中计算求解即可.
【解答】解:根据题意可知,a(a﹣b)=2,b(a﹣b)=1,
∴a=2b,
∴2b(2b﹣b)=2,即b2=1,
∴(a﹣b)2=(2b﹣b)2=b2=1.
故答案为:1.
【点评】本题主要考查了完全平方根,掌握完全平方根的定义是关键.
12.(2025 蓬江区校级三模)多项式2x3y+xy+1的次数是 4 .
【考点】多项式.
【专题】整式;符号意识.
【答案】4.
【分析】根据多项式次数的定义求解.
【解答】解:多项式2x3y+xy+1中最高次项是2x3y,次数是4.
故答案为:4.
【点评】此题考查的是多项式的定义,多项式中每个单项式叫做多项式的项,这些单项式中的最高次数,就是这个多项式的次数.
13.(2025 城东区校级三模)定义新运算:a※b=ab+b2,则(﹣2m)※m的运算结果是 ﹣m2 .
【考点】整式的混合运算.
【专题】整式;运算能力.
【答案】﹣m2.
【分析】根据新定义,列出算式,利用单项式乘单项式的法则,以及合并同类项的法则,进行计算即可.
【解答】解:根据新定义可得:
原式=﹣2m m+m2=﹣m2;
故答案为:﹣m2.
【点评】本题考查整式的运算,理解新定义是关键.
14.(2025 阳西县二模)多项式2a2﹣3b+ab2的次数是 3 .
【考点】多项式.
【专题】整式;符号意识.
【答案】3.
【分析】根据多项式次数的定义求解.
【解答】解:多项式2a2﹣3b+ab2中最高次项是ab2,次数是3.
故答案为:3.
【点评】此题考查的是多项式的定义,多项式中每个单项式叫做多项式的项,这些单项式中的最高次数,就是这个多项式的次数.
15.(2025 广西模拟)观察以下等式:
(x+2y)2+(2x﹣y)2=5(x2+y2);
(2x+3y)2+(3x﹣2y)2=13(x2+y2);
(3x+4y)2+(4x﹣3y)2=25(x2+y2);
(4x+6y)2+(6x﹣4y)2=52(x2+y2).
运用你所发现的规律解决以下问题:已知x,y为实数,x2+y2=1,则(6x+8y)2的最大值为 100 .
【考点】完全平方公式;非负数的性质:偶次方;规律型:数字的变化类.
【专题】整式;运算能力.
【答案】100.
【分析】根据已知得到(6x+8y)2+(8x﹣6y)2=(62+82)(x2+y2)=100(x2+y2),再根据偶次方的非负性求出最大值.
【解答】解:由等式可知:(6x+8y)2+(8x﹣6y)2=(62+82)(x2+y2)=100(x2+y2)
∴(6x+8y)2=100(x2+y2)﹣(8x﹣6y)2
∵x2+y2=1,
∴(6x+8y)2=100﹣(8x﹣6y)2
∵(8x﹣6y)2≥0,
∴0≤100﹣(8x﹣6y)2≤100,
∴(6x+8y)2的最大值为100,
故答案为:100.
【点评】本题主要考查了多项式运算中的规律探索,根据已知等式得到计算规律,并解决问题是解题的关键,
三.解答题(共5小题)
16.(2025 常州校级一模)先化简,再求值:(2x+1)2﹣x(4﹣x),其中x=﹣2.
【考点】整式的混合运算—化简求值.
【专题】整式;运算能力.
【答案】5x2+1,21.
【分析】先根据完全平方公式和去括号计算,然合并同类项化简,最后代值计算即可.
【解答】解:原式=4x2+4x+1﹣4x+x2
=5x2+1,
当x=﹣2时,原式=5×(﹣2)2+1=21.
【点评】本题主要考查了整式的化简求值,熟知完全平方公式是解题的关键.
17.(2025 定西模拟)先化简,再求值:(x﹣2y)2﹣4x(2x﹣y),其中x=﹣1,y=2.
【考点】整式的混合运算—化简求值.
【专题】整式;运算能力.
【答案】﹣7x2+4y2,9.
【分析】根据完全平方公式、单项式乘多项式、合并同类项把原式化简,把x、y的值代入计算得到答案.
【解答】解:(x﹣2y)2﹣4x(2x﹣y)
=x2﹣4xy+4y2﹣(8x2﹣4xy)
=x2﹣4xy+4y2﹣8x2+4xy
=﹣7x2+4y2,
当x=﹣1,y=2时,原式=﹣7×(﹣1)2+4×22=﹣7+16=9.
【点评】本题考查的是整式的混合运算﹣化简求值,掌握整式的混合运算法则是解题的关键.
18.(2025 雁塔区校级模拟)先化简,再求值:(2x﹣y)2﹣2x(x﹣2y),其中x=2,y=﹣1.
【考点】整式的混合运算—化简求值.
【专题】整式;运算能力.
【答案】2x2+y2,原式=9.
【分析】先利用完全平方公式,单项式乘多项式的法则进行计算,然后把x,y的值代入化简后的式子进行计算,即可解答.
【解答】解:(2x﹣y)2﹣2x(x﹣2y)
=4x2﹣4xy+y2﹣2x2+4xy
=2x2+y2,
当x=2,y=﹣1时,原式=2×22+(﹣1)2=2×4+1=8+1=9.
【点评】本题考查了整式的混合运算﹣化简求值,准确熟练地进行计算是解题的关键.
19.(2025 新华区校级一模)把1,3,5,7,9…这一组数按如下规律排放在表格中,任意选定如图所示方框中4个数,进行交叉相乘再相减的运算,即bc﹣ad,例如:9×17﹣7×19=20.完成下列各题:
(1)计算:3×11﹣1×13= 20 ;
(2)猜想:bc﹣ad= 20 ;
(3)验证:请你利用整式的运算对以上的规律加以证明.
【考点】整式的混合运算;有理数的混合运算;规律型:数字的变化类.
【专题】猜想归纳;实数;整式;运算能力.
【答案】(1)20;
(2)20;
(3)见解析.
【分析】(1)先算乘法,再算减法即可;
(2)根据表格中的数据及(1)中求得的结果总结规律即可;
(3)由图表可得b=a+2,c=a+10,d=a+12,然后列得算式并计算即可.
【解答】解:(1)3×11﹣1×13
=33﹣13
=20,
故答案为:20;
(2)猜想:bc﹣ad=20,
故答案为:20;
(3)由图表可得b=a+2,c=a+10,d=a+12,
则bc﹣ad=(a+2)(a+10)﹣a(a+12)
=a2+10a+2a+20﹣(a2+12a)
=a2+10a+2a+20﹣a2﹣12a
=20,
∴bc﹣ad=20正确.
【点评】本题考查整式的混合运算,有理数的混合运算,数式规律问题,理解题意并总结出规律是解题的关键.
20.(2025 安次区校级二模)如图1和图2,约定:上方相邻两代数式之和等于这两代数式下方箭头共同指向的代数式.
(1)先求出代数式M,再计算当x=﹣1时,代数式M的值;
(2)嘉淇说:“只要x的值不取﹣1,M的值就一定大于N的值.”你同意她的说法吗?说明理由.
【考点】整式的加减;代数式求值.
【专题】整式;运算能力.
【答案】(1)2x2﹣3x+1;当x=﹣1时,M=6;(2)同意,理由见解析.
【分析】(1)由题意可得M=3x2﹣6x﹣1﹣(x2﹣3x﹣2),再根据去括号、合并同类项法则计算即可化简,最后代入x=﹣1计算即可得解;
(2)先求出N=x2﹣5x,再计算出M﹣N=(x+1)2,分情况讨论即可得解.
【解答】解:(1)根据题意可知,x2﹣3x﹣2+M=3x2﹣6x﹣1,
∴M=3x2﹣6x﹣1﹣(x2﹣3x﹣2)
=3x2﹣6x﹣1﹣x2+3x+2
=2x2﹣3x+1,
当x=﹣1时,
2x2﹣3x+1
=2×(﹣1)2﹣3×(﹣1)+1
=2+3+1
=6;
(2)同意,理由如下:
根据题意可知,(x﹣1)(x+1)﹣5x+1=N,
∴N=x2﹣1﹣5x+1=x2﹣5x,
∴M﹣N=2x2﹣3x+1﹣(x2﹣5x)
=2x2﹣3x+1﹣x2+5x
=x2+2x+1
=(x+1)2,
当x=﹣1时,(x+1)2=0,此时M﹣N=0,M=N;
当x不取﹣1,(x+1)2恒大于0,M的值就一定大于N的值.
【点评】本题考查了整式的加减,代数式求值,掌握相应的运算法则是关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
