2026年中考数学一轮复习 尺规作图(含解析)
文档属性
| 名称 | 2026年中考数学一轮复习 尺规作图(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-06 15:04:15 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2026年中考数学一轮复习 尺规作图
一.选择题(共10小题)
1.(2025 碧江区 校级模拟)在Rt△ABC中,∠B=90°,AB=BC,以点A为圆心,适当长为半径画弧,分别交AC,AB于点D,E,分别以D,E为圆心大于为半径画弧,两弧交于点P,连接BP交BC于点F,则∠AFB的度数为( )
A.60° B.67.5° C.77.5° D.80°
2.(2025 凌河区校级三模)如图,已知∠MAN,以点A为圆心,以适当长为半径作弧,分别与AM、AN相交于点B、C;分别以B、C为圆心,以大于BC的长为半径作弧,两弧在∠MAN内部相交于点P,作射线AP.分别以A、B为圆心,以大于AB的长为半径作弧,两弧相交于点D、E,作直线DE分别与AB、AP、AN相交于点F、Q、H.若AB=4,∠PQE=67.5°,则AH的长为( )
A.2 B.2 C.2 D.4
3.(2025 门头沟区一模)下面是“作∠AOB的角平分线”的尺规作图方法:
(1)以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N. (2)分别以点M,N为圆心,大于长为半径画弧,两弧在∠AOB内部交于点C. (3)画射线OC,射线OC即为所求.
上述方法是通过判定△OMC≌△ONC得到∠MOC=∠NOC的,其中判定△OMC≌△ONC的依据是( )
A.两边及其夹角分别相等的两个三角形全等
B.三边分别相等的两个三角形全等
C.两角及其夹边分别相等的两个三角形全等
D.两角分别相等且其中一组等角的对边相等的两个三角形全等
4.(2025 阳山县一模)如图,在△ABC中,AB=AC,分别以点A、B为圆心,以适当的长为半径作弧,两弧分别交于E,F,作直线EF,D为BC的中点,M为直线EF上任意一点.若BC=4,△ABC面积为10,则BM+MD长度的最小值为( )
A. B.3 C.4 D.5
5.(2025 滨海新区校级模拟)如图,在△ABC中,∠C=60°,∠B=50°.以点A为圆心,适当长为半径画弧,交AB于点D,交AC于点E;再分别以点D,E为圆心,大于的长为半径画弧,两弧(所在圆的半径相等)相交于点P,作射线AP,与边BC相交于点F,则∠AFB的大小为( )
A.80° B.85° C.90° D.95°
6.(2025 海淀区一模)已知:如图,四边形ABCD是平行四边形,点E为AD上的一点(不与点A,D重合),连接CE.
求作:点F,使得点F在BC上,且AF∥CE.
甲、乙、丙三名同学的尺规作图方法如下:
甲:以点C为圆心,AE的长为半径画弧,交BC于点F,连接AF;
乙:以点A为圆心,CE的长为半径画弧,交BC于点F,连接AF;
丙:以点B为圆心,DE的长为半径画弧,交BC于点F,连接AF.
上述三名同学的作法一定正确的是( )
A.甲、乙 B.乙、丙 C.甲、丙 D.甲、乙、丙
7.(2025 门头沟区二模)下面是小明设计的“过直线外一点作这条直线平行线”的尺规作图过程:
已知:如图1,直线BC及直线BC外一点P. 求作:直线PE,使得PE∥BC. 作法:如图2,①在直线BC上取一点A,连接PA. ②作∠PAC的平分线AD. ③以点P为圆心,PA长为半径画弧,交射线AD于点E. ④作直线PE. ∴直线PE就是所求作的直线.
上述的方法是通过判定∠PEA=∠EAC得到PE∥BC的,其中判定PE∥BC的依据是( )
A.同位角相等,两直线平行
B.两直线平行,同位角相等
C.内错角相等,两直线平行
D.两直线平行,内错角相等
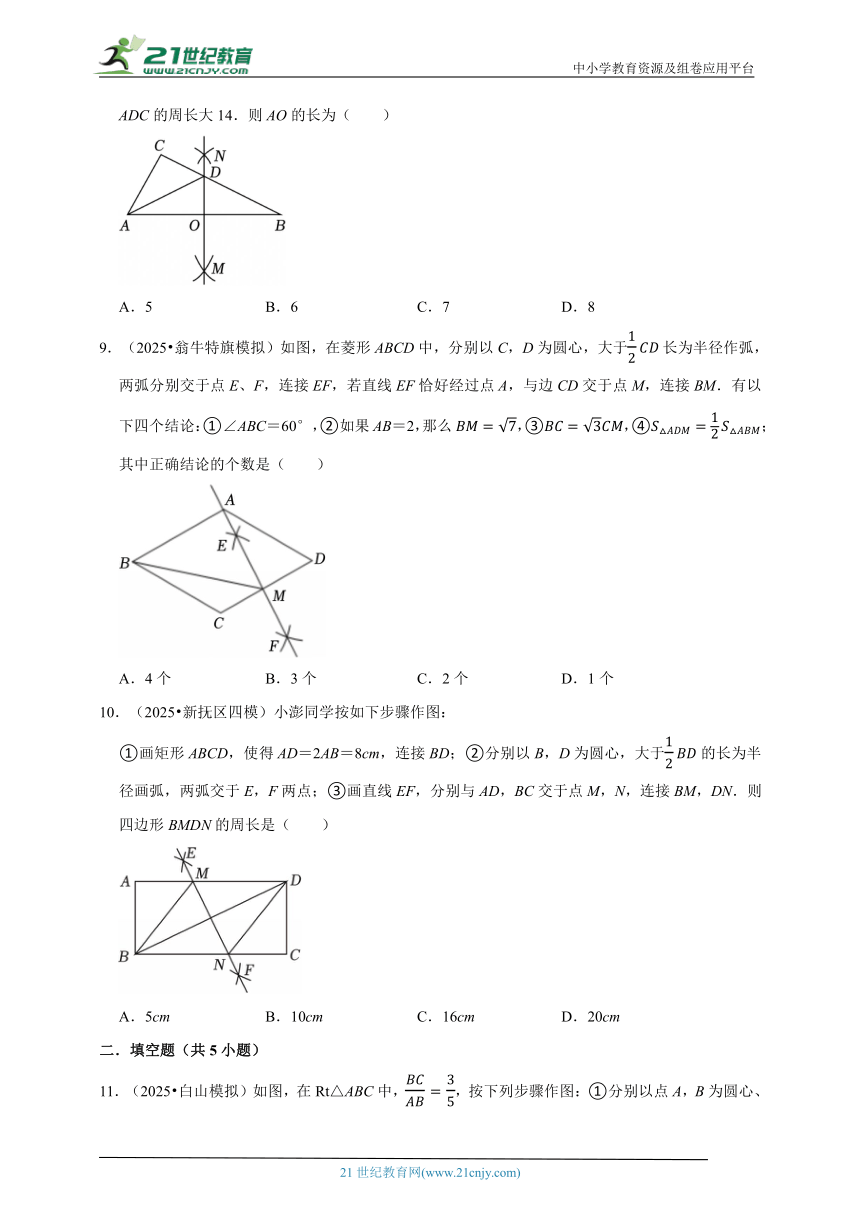
8.(2025 东明县三模)如图,在△ABC中,分别以点A,B为圆心,大于的长为半径作弧,两弧相交于点M,N,作直线MN交BC于点D,交AB于点O,连接AD,若△ABC的周长比△ADC的周长大14.则AO的长为( )
A.5 B.6 C.7 D.8
9.(2025 翁牛特旗模拟)如图,在菱形ABCD中,分别以C,D为圆心,大于长为半径作弧,两弧分别交于点E、F,连接EF,若直线EF恰好经过点A,与边CD交于点M,连接BM.有以下四个结论:①∠ABC=60°,②如果AB=2,那么,③,④;其中正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
10.(2025 新抚区四模)小澎同学按如下步骤作图:
①画矩形ABCD,使得AD=2AB=8cm,连接BD;②分别以B,D为圆心,大于的长为半径画弧,两弧交于E,F两点;③画直线EF,分别与AD,BC交于点M,N,连接BM,DN.则四边形BMDN的周长是( )
A.5cm B.10cm C.16cm D.20cm
二.填空题(共5小题)
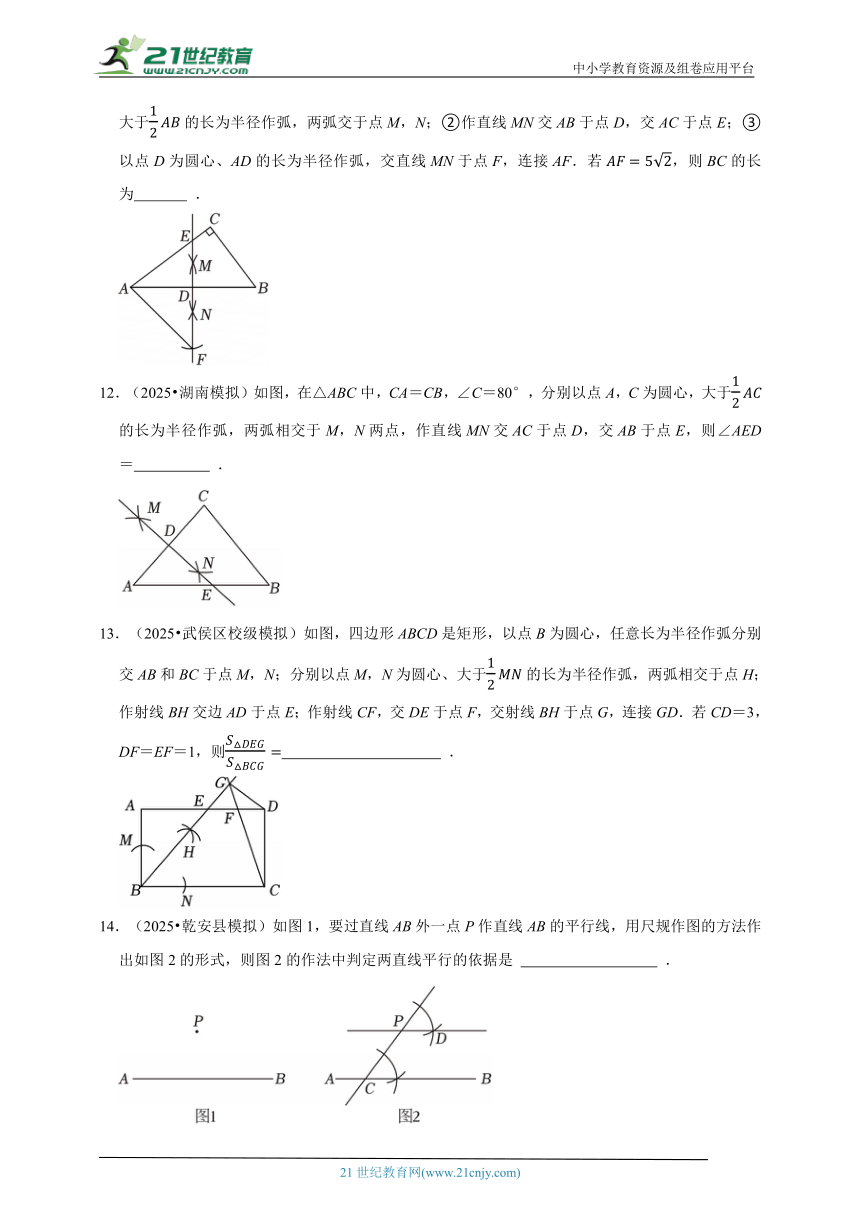
11.(2025 白山模拟)如图,在Rt△ABC中,,按下列步骤作图:①分别以点A,B为圆心、大于的长为半径作弧,两弧交于点M,N;②作直线MN交AB于点D,交AC于点E;③以点D为圆心、AD的长为半径作弧,交直线MN于点F,连接AF.若,则BC的长为 .
12.(2025 湖南模拟)如图,在△ABC中,CA=CB,∠C=80°,分别以点A,C为圆心,大于的长为半径作弧,两弧相交于M,N两点,作直线MN交AC于点D,交AB于点E,则∠AED= .
13.(2025 武侯区校级模拟)如图,四边形ABCD是矩形,以点B为圆心,任意长为半径作弧分别交AB和BC于点M,N;分别以点M,N为圆心、大于的长为半径作弧,两弧相交于点H;作射线BH交边AD于点E;作射线CF,交DE于点F,交射线BH于点G,连接GD.若CD=3,DF=EF=1,则 .
14.(2025 乾安县模拟)如图1,要过直线AB外一点P作直线AB的平行线,用尺规作图的方法作出如图2的形式,则图2的作法中判定两直线平行的依据是 .
15.(2025 祁阳市校级一模)如图,在平行四边形ABCD中,AB⊥AC,AB=6,AC=8,分别以A,C为圆心,大于的长为半径画弧,两弧相交于点M,N,作直线MN与BC交于点E,与AD交于点F,连接AE,CF,则四边形AECF的周长为 .
三.解答题(共5小题)
16.(2025 天河区校级四模)如图,在△ABC中,∠A=90°.
(1)尺规作图:在边AC上取点O,以O为圆心画圆,使得⊙O与边BC、BA相切(保留作图痕迹,不写作法);
(2)在(1)所作的图中,若,AB=6,求OB的长.
17.(2025 昌邑区校级三模)如图,均是5×5的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1,点A,B,C,D均在格点上.
(1)如图①,若连接AB,CD交于点P,则的值为 .
(2)如图②,在AB上找一点Q,使(仅用无刻度的直尺,在给定的正方形网格中,按要求作图,保留作图痕迹,不要求写作法).
18.(2025 永寿县校级模拟)如图,在△ABC中,AB=AC,请用尺规作图法,求作一个菱形AEFG,使得点E,F,G分别在AB,BC,AC边上.(保留作图痕迹,不写作法)
19.(2025 椒江区校级模拟)如图,在正方形网格中,点A为格点(网格线的交点),点B在网格线上,仅使用无刻度的直尺作图,保留作图痕迹.
(1)如图1,在直线m上找到一点P,使得AP+BP的值最小;
(2)如图2,部分网格被墨汁污染,在仅剩的网格中,标出格点Q,使线段BQ的长度等于(1)中的最小值.
20.(2025 萍乡一模)如图,点E是正方形ABCD内一点,且EB=EC.请仅用无刻度的直尺按要求作图(保留画图痕迹,不写作法).
(1)在图1中,作出BC边的中点.
(2)在图2中,作出CD边的中点.
2026年中考数学一轮复习 尺规作图
参考答案与试题解析
一.选择题(共10小题)
1.(2025 碧江区 校级模拟)在Rt△ABC中,∠B=90°,AB=BC,以点A为圆心,适当长为半径画弧,分别交AC,AB于点D,E,分别以D,E为圆心大于为半径画弧,两弧交于点P,连接BP交BC于点F,则∠AFB的度数为( )
A.60° B.67.5° C.77.5° D.80°
【考点】作图—基本作图;线段垂直平分线的性质;等腰直角三角形.
【专题】作图题;等腰三角形与直角三角形;几何直观;推理能力.
【答案】B
【分析】先根据三角形内角和定理求出∠CAB的度数,再由AF是∠BAC的平分线得出,根据直角三角形的性质可知∠AFB=90°﹣∠BAF=67.5°.
【解答】解:在Rt△ABC中,∠B=90°,AB=BC,
∴∠CAB=45°.
由题意得:AF是∠BAC的角平分线,
∴,
∴∠AFB=90°﹣∠BAF=67.5°.
故选:B.
【点评】本题主要考查作图﹣基本作图,线段垂直平分线的性质,等腰直角三角形,掌握相关定义是解题的关键.
2.(2025 凌河区校级三模)如图,已知∠MAN,以点A为圆心,以适当长为半径作弧,分别与AM、AN相交于点B、C;分别以B、C为圆心,以大于BC的长为半径作弧,两弧在∠MAN内部相交于点P,作射线AP.分别以A、B为圆心,以大于AB的长为半径作弧,两弧相交于点D、E,作直线DE分别与AB、AP、AN相交于点F、Q、H.若AB=4,∠PQE=67.5°,则AH的长为( )
A.2 B.2 C.2 D.4
【考点】作图—基本作图;角平分线的定义;线段垂直平分线的性质.
【专题】作图题;几何直观;运算能力.
【答案】A
【分析】证明∠FAH=45°,推出AHAF可得结论.
【解答】解:由作图可得:∠BAP=∠CAP,DE⊥AB,AF=FBAB=2,
∵∠PQE=67.5°,
∴∠AQF=67.5°,
∴∠BAP=∠CAP=90°﹣67.5°=22.5°,
∴∠FAH=45°,
∴AHAF=2.
故选:A.
【点评】本题考查作图﹣基本作图,角平分线的定义,线段垂直平分线的性质,就提到过房间数理解题意,灵活运用所学知识解决问题.
3.(2025 门头沟区一模)下面是“作∠AOB的角平分线”的尺规作图方法:
(1)以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N. (2)分别以点M,N为圆心,大于长为半径画弧,两弧在∠AOB内部交于点C. (3)画射线OC,射线OC即为所求.
上述方法是通过判定△OMC≌△ONC得到∠MOC=∠NOC的,其中判定△OMC≌△ONC的依据是( )
A.两边及其夹角分别相等的两个三角形全等
B.三边分别相等的两个三角形全等
C.两角及其夹边分别相等的两个三角形全等
D.两角分别相等且其中一组等角的对边相等的两个三角形全等
【考点】作图—基本作图;全等三角形的判定;角平分线的性质.
【专题】作图题;图形的全等;几何直观;推理能力.
【答案】B
【分析】根据SSS证明三角形全等即可.
【解答】解:在△COM和△CON中,
,
∴△COM≌△CON(SSS),
∴∠COM=∠CON,
∴射线OC平分∠AOB.
故选:B.
【点评】本题考查作图﹣基本作图,全等三角形的判定,解题的关键是理解题意,灵活运用所学知识解决问题.
4.(2025 阳山县一模)如图,在△ABC中,AB=AC,分别以点A、B为圆心,以适当的长为半径作弧,两弧分别交于E,F,作直线EF,D为BC的中点,M为直线EF上任意一点.若BC=4,△ABC面积为10,则BM+MD长度的最小值为( )
A. B.3 C.4 D.5
【考点】作图—基本作图;线段垂直平分线的性质;等腰三角形的性质.
【专题】等腰三角形与直角三角形;尺规作图;几何直观.
【答案】D
【分析】连接AD,交直线EF于点N,设EF交AB于点G,当点M与点N重合时,BM+MD长度最小,最小值即为AD的长,结合已知条件求出AD即可.
【解答】解:连接AD,交直线EF于点N,设EF交AB于点G,
由题意得,直线EF为线段AB的垂直平分线,
∴AG=BG,EF⊥AB,
∴当点M与点N重合时,BM+MD长度最小,最小值即为AD的长.
∵AB=AC,D为BC的中点,
∴AD⊥BC,
∵BC=4,△ABC面积为10,
∴10,
解得AD=5.
故选:D.
【点评】本题考查作图﹣基本作图、线段垂直平分线的性质、等腰三角形的性质、轴对称﹣最短路径问题,熟练掌握线段垂直平分线的性质、等腰三角形的性质、轴对称﹣最短路径问题是解答本题的关键.
5.(2025 滨海新区校级模拟)如图,在△ABC中,∠C=60°,∠B=50°.以点A为圆心,适当长为半径画弧,交AB于点D,交AC于点E;再分别以点D,E为圆心,大于的长为半径画弧,两弧(所在圆的半径相等)相交于点P,作射线AP,与边BC相交于点F,则∠AFB的大小为( )
A.80° B.85° C.90° D.95°
【考点】作图—基本作图;三角形内角和定理.
【专题】作图题.
【答案】D
【分析】由三角形内角和可得∠BAC=70°,再根据作图过程可得AP平分∠BAC,即∠BAF=35°,然后根据三角形内角和定理即可解答.
【解答】解:∵在△ABC中,∠C=60°,∠B=50°,
∴∠BAC=180°﹣∠C﹣∠B=70°,
由作图过程可得:AP平分∠BAC,
∴,
∴∠AFB=180°﹣∠B﹣∠BAF=95°.
故选:D.
【点评】本题主要考查了角平分线的作法、三角形内角和定理等知识点,掌握角平分线的尺规作图法成为解题的关键.
6.(2025 海淀区一模)已知:如图,四边形ABCD是平行四边形,点E为AD上的一点(不与点A,D重合),连接CE.
求作:点F,使得点F在BC上,且AF∥CE.
甲、乙、丙三名同学的尺规作图方法如下:
甲:以点C为圆心,AE的长为半径画弧,交BC于点F,连接AF;
乙:以点A为圆心,CE的长为半径画弧,交BC于点F,连接AF;
丙:以点B为圆心,DE的长为半径画弧,交BC于点F,连接AF.
上述三名同学的作法一定正确的是( )
A.甲、乙 B.乙、丙 C.甲、丙 D.甲、乙、丙
【考点】作图—复杂作图;平行四边形的判定与性质.
【专题】多边形与平行四边形;尺规作图;几何直观.
【答案】C
【分析】由甲同学的尺规作图方法可得CF=AE,结合平行四边形的性质可得AD∥BC,进而可得四边形AECF为平行四边形,则AF∥CE;由乙同学的尺规作图方法可得AF=CE,不能得出AF∥CE;由丙同学的尺规作图方法可得BF=DE,结合平行四边形的性质可得AD∥BC,AD=BC,则AE=CF,进而可得四边形AECF为平行四边形,则AF∥CE.
【解答】解:由甲同学的尺规作图方法可得CF=AE,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴四边形AECF为平行四边形,
∴AF∥CE.
故甲同学的作法正确,符合题意;
由乙同学的尺规作图方法可得AF=CE,
不能得出AF∥CE,
故乙同学的作法不正确,不符合题意;
由丙同学的尺规作图方法可得BF=DE,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴AE=CF,
∴四边形AECF为平行四边形,
∴AF∥CE.
故丙同学的作法正确,符合题意.
综上所述,三名同学的作法一定正确的是甲、丙.
故选:C.
【点评】本题考查作图—复杂作图、平行四边形的判定与性质,熟练掌握平行四边形的判定与性质是解答本题的关键.
7.(2025 门头沟区二模)下面是小明设计的“过直线外一点作这条直线平行线”的尺规作图过程:
已知:如图1,直线BC及直线BC外一点P. 求作:直线PE,使得PE∥BC. 作法:如图2,①在直线BC上取一点A,连接PA. ②作∠PAC的平分线AD. ③以点P为圆心,PA长为半径画弧,交射线AD于点E. ④作直线PE. ∴直线PE就是所求作的直线.
上述的方法是通过判定∠PEA=∠EAC得到PE∥BC的,其中判定PE∥BC的依据是( )
A.同位角相等,两直线平行
B.两直线平行,同位角相等
C.内错角相等,两直线平行
D.两直线平行,内错角相等
【考点】作图—复杂作图;平行线的判定与性质.
【专题】线段、角、相交线与平行线;尺规作图;应用意识.
【答案】C
【分析】结合平行线的判定可得答案.
【解答】解:∵AD为∠PAC的平分线,
∴∠PAE=∠CAE.
∵由作图过程可得,PE=PA,
∴∠PEA=∠PAE,
∴∠PEA=∠CAE,
∴PE∥BC,
∴判定PE∥BC的依据是内错角相等,两直线平行.
故选:C.
【点评】本题考查作图—复杂作图、平行线的判定与性质,熟练掌握平行线的判定是解答本题的关键.
8.(2025 东明县三模)如图,在△ABC中,分别以点A,B为圆心,大于的长为半径作弧,两弧相交于点M,N,作直线MN交BC于点D,交AB于点O,连接AD,若△ABC的周长比△ADC的周长大14.则AO的长为( )
A.5 B.6 C.7 D.8
【考点】作图—基本作图;线段垂直平分线的性质.
【专题】作图题;线段、角、相交线与平行线;运算能力;推理能力.
【答案】C
【分析】利用基本作图得到DE垂直平分AB,则DA=DB,AO=BO,利用等量代换得到△ADC的周长,再利用△ABC的周长比△ADC的周长大14得到AB=8,从而得到AO的长.
【解答】解:由作法得DO垂直平分AB,
∴DA=DB,AO=BO,
∴△ADC的周长=AC+BC,
∵△ABC的周长=AC+BC+AB,△ABC的周长比△ADC的周长大14,
∴AB=14,
∴AOAB=7.
故选:C.
【点评】本题考查了作图﹣基本作图,线段垂直平分线的性质,解决本题的关键是熟练掌握线段的垂直平分线的作法.
9.(2025 翁牛特旗模拟)如图,在菱形ABCD中,分别以C,D为圆心,大于长为半径作弧,两弧分别交于点E、F,连接EF,若直线EF恰好经过点A,与边CD交于点M,连接BM.有以下四个结论:①∠ABC=60°,②如果AB=2,那么,③,④;其中正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
【考点】作图—基本作图;线段垂直平分线的性质;等边三角形的判定与性质;菱形的性质.
【专题】作图题;几何直观;推理能力.
【答案】B
【分析】连接AC,如图,先利用基本作图可判断AM垂直平分CD,则根据线段垂直平分线的性质得到AC=AD,CM=DM,AM⊥CD,再利用菱形的性质得到AD=AB=BC=CD,AB∥CD,则可判断△ABC和△ADC都为等边三角形,从而可对①进行判断;利用勾股定理在Rt△ADM中计算出AM,接着在Rt△BAM中计算出BM,从而可对②进行判断;利用BC=2,CM=1可对③进行判断;最后根据三角形面积公式可对④进行判断.
【解答】解:连接AC,如图,
由作法得AM垂直平分CD,
∴AC=AD,CM=DM,AM⊥CD,
∵四边形ABCD为菱形,
∴AD=AB=BC=CD,AB∥CD,
∴AB=AC=BC=CD=AD,
∴△ABC和△ADC都为等边三角形,
∴∠ABC=60°,所以①正确;
∵AB=2,
∴AD=CD=2,DM=1,
在Rt△ADM中,AM,
∵AM⊥CD,AB∥CD,
∴AM⊥AB,
∴∠BAM=90°,
∴BM,所以②正确;
∵BC=2,CM=1,
∴BC=2CM,所以③错误;
∵S△ADMAM DM,S△ABMAM AB,
而DMAB,
∴S△ADMS△ABM,所以④正确.
故选:B.
【点评】本题考查了作图﹣基本作图:熟练掌握5种基本作图是解决问题的关键.也考查了线段垂直平分线的性质、等边三角形的判定与性质和菱形的性质.
10.(2025 新抚区四模)小澎同学按如下步骤作图:
①画矩形ABCD,使得AD=2AB=8cm,连接BD;②分别以B,D为圆心,大于的长为半径画弧,两弧交于E,F两点;③画直线EF,分别与AD,BC交于点M,N,连接BM,DN.则四边形BMDN的周长是( )
A.5cm B.10cm C.16cm D.20cm
【考点】作图—复杂作图;线段垂直平分线的性质;矩形的判定.
【专题】作图题;线段、角、相交线与平行线;矩形 菱形 正方形;推理能力.
【答案】D
【分析】利用基本作图可判断MN垂直平分BD,则MB=MD,NB=ND,设MD=x,则BM=x,AM=8﹣x,在Rt△ABM中利用勾股定理得到42+(8﹣x)2=x2,解方程得到BM=DM=5,同理可得NB=ND=5,然后计算四边形MBND的周长.
【解答】解:由作法得MN垂直平分BD,
∴MB=MD,NB=ND,
设MD=x,则BM=x,AM=8﹣x,
由条件可知∠A=∠C=90°,
由勾股定理可得42+(8﹣x)2=x2,
解得x=5,
即BM=DM=5,
同理可得NB=ND=5,
∴四边形MBND的周长为5+5+5+5=20.
故选:D.
【点评】本题考查了线段垂直平分线的作图和性质、矩形的性质、勾股定理等知识.熟练掌握以上知识点是关键.
二.填空题(共5小题)
11.(2025 白山模拟)如图,在Rt△ABC中,,按下列步骤作图:①分别以点A,B为圆心、大于的长为半径作弧,两弧交于点M,N;②作直线MN交AB于点D,交AC于点E;③以点D为圆心、AD的长为半径作弧,交直线MN于点F,连接AF.若,则BC的长为 6 .
【考点】作图—基本作图;线段垂直平分线的性质;勾股定理.
【专题】等腰三角形与直角三角形;尺规作图;几何直观;推理能力.
【答案】6.
【分析】由作图可得EF垂直平分AB,AD=DF,根据勾股定理得到AD2+DF2=AF2=50,求得AD=DF=5,结合,即可求解.
【解答】解:由题意得:EF是线段AB的垂直平分线,AD=DF,
∴∠ADF=90°,
在直角三角形ADF中,由勾股定理得:AD2+DF2=AF2=50,
解得:AD=DF=5,
∴AB=AD+DB=10,
∵,
∴,
故答案为:6.
【点评】本题考查了作图﹣基本作图,线段垂直平分线的性质,勾股定理,解答本题的关键是熟练掌握勾股定理.
12.(2025 湖南模拟)如图,在△ABC中,CA=CB,∠C=80°,分别以点A,C为圆心,大于的长为半径作弧,两弧相交于M,N两点,作直线MN交AC于点D,交AB于点E,则∠AED= 40° .
【考点】作图—基本作图;三角形内角和定理;线段垂直平分线的性质;等腰三角形的性质.
【专题】作图题;几何直观.
【答案】40°.
【分析】由作图可知,MN垂直平分AC,得出∠ADE=90°,再根据等腰三角形的性质即可求解.
【解答】解:由作图可知,MN垂直平分AC,
∴∠ADE=90°,
又∵CA=CB,∠C=80°,
∴∠A50°,
∴∠AED=90°﹣50°=40°,
故答案为:40°.
【点评】本题考查了作图﹣基本作图,线段垂直平分线的性质,等腰三角形的性质,熟记线段垂直平分线的作法是解题的关键.
13.(2025 武侯区校级模拟)如图,四边形ABCD是矩形,以点B为圆心,任意长为半径作弧分别交AB和BC于点M,N;分别以点M,N为圆心、大于的长为半径作弧,两弧相交于点H;作射线BH交边AD于点E;作射线CF,交DE于点F,交射线BH于点G,连接GD.若CD=3,DF=EF=1,则 .
【考点】作图—基本作图;相似三角形的判定与性质;角平分线的定义;等腰三角形的判定与性质;矩形的性质.
【专题】作图题;等腰三角形与直角三角形;矩形 菱形 正方形;图形的相似;推理能力.
【答案】.
【分析】根据角平分线的定义得到∠ABE=∠CBE,根据矩形的性质得到AD=BC,AD∥BC,AB=CD=3,求得 AE=AB=3,得到AD=BC=5,根据相似三角形的判定和性质定理即可得到结论.
【解答】解:由作图知,BG平分∠ABC,
∴∠ABE=∠CBE,
∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,AB=CD=3,
∴∠AEB=∠CBE,
∴∠ABE=∠AEB,
∴AE=AB=3,
∵DF=EF=1,
∴AD=BC=5,
∵EF∥BC,
∴△GEF∽△GBC,
∴,
∵EF=DF,
∴S△DEG=2S△GEF,
∴,
故答案为:.
【点评】本题考查了作图﹣基本作图,矩形的性质,相似三角形的判定和性质,角平分线的定义,等腰三角形的判定和性质,熟练掌握等腰三角形的判定和性质以及相似三角形的判定和性质定理是解题的关键.
14.(2025 乾安县模拟)如图1,要过直线AB外一点P作直线AB的平行线,用尺规作图的方法作出如图2的形式,则图2的作法中判定两直线平行的依据是 同位角相等,两直线平行 .
【考点】作图—复杂作图;平行线的判定.
【专题】作图题;几何直观.
【答案】见试题解答内容
【分析】根据同位角相等两直线平行,判断即可.
【解答】解:由作图可知:∠MPD=∠MCB,
∴PD∥AB(同位角相等,两直线平行),
故答案为:同位角相等,两直线平行.
【点评】本题考查作图—复杂作图,平行线的判定等知识,解题的关键是读懂图象信息,掌握平行线的判定.
15.(2025 祁阳市校级一模)如图,在平行四边形ABCD中,AB⊥AC,AB=6,AC=8,分别以A,C为圆心,大于的长为半径画弧,两弧相交于点M,N,作直线MN与BC交于点E,与AD交于点F,连接AE,CF,则四边形AECF的周长为 20 .
【考点】作图—基本作图;线段垂直平分线的性质;勾股定理;平行四边形的性质.
【专题】等腰三角形与直角三角形;多边形与平行四边形;运算能力;推理能力.
【答案】20.
【分析】根据勾股定理得到BC10,由作图可知,MN是线段AC的垂直平分线,求得EC=EA,AF=CF,推出AE=CEBC=5,根据平行四边形的性质得到AD=BC=10,CD=AB=6,∠ACD=∠BAC=90°,同理证得AF=CF=5,于是得到结论.
【解答】解:∵AB⊥AC,AB=6,AC=8,
∴BC10,
由作图可知,MN是线段AC的垂直平分线,
∴EC=EA,AF=CF,
∴∠EAC=∠ACE,
∵∠B+∠ACB=∠BAE+∠CAE=90°,
∴∠B=∠BAE,
∴AE=BE,
∴AE=CEBC=5,
∵四边形ABCD是平行四边形,
∴AD=BC=10,CD=AB=6,∠ACD=∠BAC=90°,
同理证得AF=CF=5,
∴四边形AECF的周长=EC+EA+AF+CF=20,
故答案为:20.
【点评】本题考查了平行四边形的性质,作图﹣基本作图,勾股定理,线段垂直平分线的性质.利用勾股定理列出方程是解题的关键.
三.解答题(共5小题)
16.(2025 天河区校级四模)如图,在△ABC中,∠A=90°.
(1)尺规作图:在边AC上取点O,以O为圆心画圆,使得⊙O与边BC、BA相切(保留作图痕迹,不写作法);
(2)在(1)所作的图中,若,AB=6,求OB的长.
【考点】作图—复杂作图;解直角三角形;勾股定理;圆周角定理;切线的判定与性质.
【专题】作图题;几何直观.
【答案】(1)见解析;
(2).
【分析】(1)作BO平分∠ABC,BO交AC于点O,以O为圆心,OA为半径作⊙O即可;
(2)设BC与⊙O相切于点K,连接OK,则BA=BK=6,CK=BC﹣BK=10﹣6=4,设OA=OK=r,利用勾股定理构建方程求解.
【解答】解:(1)如图,⊙O即为所求;
(2)在Rt△ABC中,sin∠ACB,AB=6,
∴BC=10,
∴AC8,
设BC与⊙O相切于点K,连接OK,则BA=BK=6,CK=BC﹣BK=10﹣6=4,设OA=OK=r,
则有(8﹣r)2=r2+42,
解得r=5,
∴OB.
【点评】你本题考查作图﹣复杂作图,勾股定理,切线的判定和性质,解直角三角形,解题的关键是学会利用参数构建方程解决问题.
17.(2025 昌邑区校级三模)如图,均是5×5的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1,点A,B,C,D均在格点上.
(1)如图①,若连接AB,CD交于点P,则的值为 .
(2)如图②,在AB上找一点Q,使(仅用无刻度的直尺,在给定的正方形网格中,按要求作图,保留作图痕迹,不要求写作法).
【考点】作图—应用与设计作图;相似三角形的判定与性质;平行线的性质;勾股定理.
【专题】作图题;等腰三角形与直角三角形;图形的相似;几何直观;推理能力.
【答案】(1);
(2)作图见解析.
【分析】(1)如图,连接AD,BC,证明△PAD∽△PBC,由相似三角形的性质可得结论;
(2)如图,取格点M、N,连接MN交AB于点Q即可,
【解答】解:(1)如图①是5×5的正方形网格,每个小正方形的边长均为1,点A,B,C,D均在格点上,连接AD,BC,
∴AD∥BC,AD=3,BC=5,
∴∠PAD=∠PBC,∠PDA=∠PCB,
∴△PAD∽△PBC,
∴,
∴的值为,
故答案为:;
(2)如图②是5×5的正方形网格,每个小正方形的边长均为1,点A,B,C,D均在格点上,取格点M、N,连接MN交AB于点Q,连接BM、AN,
∴AN∥BM,AN=3,BM=1,
由勾股定理得:,
∴∠QAN=∠QBM,∠QNA=∠QMB,
∴△QAN∽△QBM,
∴,
∴,
则点Q即为所作.
【点评】本题考查作图﹣应用与设计作图,平行线的性质,相似三角形的判定与性质,勾股定理等知识,解题的关键是理解题意,学会利用数形结合的思想解决问题,
18.(2025 永寿县校级模拟)如图,在△ABC中,AB=AC,请用尺规作图法,求作一个菱形AEFG,使得点E,F,G分别在AB,BC,AC边上.(保留作图痕迹,不写作法)
【考点】作图—复杂作图;线段垂直平分线的性质;等腰三角形的性质;菱形的判定.
【专题】作图题;几何直观.
【答案】见解析.
【分析】作AF⊥BC于点F,作线段AF的垂直平分线交AB于点E,交AC于点G,连接EF,GF,四边形AEFG即为所求.
【解答】解:如图,菱形AEFG即为所求.
【点评】本题考查作图﹣复杂作图,线段垂直平分线的性质,菱形的判定,等腰三角形的性质,解题的关键是掌握相关知识解决问题.
19.(2025 椒江区校级模拟)如图,在正方形网格中,点A为格点(网格线的交点),点B在网格线上,仅使用无刻度的直尺作图,保留作图痕迹.
(1)如图1,在直线m上找到一点P,使得AP+BP的值最小;
(2)如图2,部分网格被墨汁污染,在仅剩的网格中,标出格点Q,使线段BQ的长度等于(1)中的最小值.
【考点】作图—应用与设计作图;轴对称﹣最短路线问题;勾股定理.
【专题】作图题;几何直观.
【答案】见解析.
【分析】(1)作点A关于直线m的对称点A′,连接BA′交直线m于点P,连接AP,点P即为所求;
(2)取格点A″,作点A″关于直线m的对称点Q,连接BQ,线段BQ即为所求.
【解答】解:(1)如图,点P即为所求;
(2)如图2中,线段BQ即为所求.
【点评】本题考查作图﹣应用与设计作图,勾股定理,轴对称最短问题,解题的关键是掌握轴对称最短问题.
20.(2025 萍乡一模)如图,点E是正方形ABCD内一点,且EB=EC.请仅用无刻度的直尺按要求作图(保留画图痕迹,不写作法).
(1)在图1中,作出BC边的中点.
(2)在图2中,作出CD边的中点.
【考点】作图—复杂作图;线段垂直平分线的性质;正方形的性质.
【专题】作图题;几何直观.
【答案】见试题解答内容
【分析】(1)连接AC、BD,它们相交于O点,连接EO并延长交BC于F,则F点满足条件;
(2)FE交AD于H,连接CH交BD于G,则AG的延长线交CD于P,则P点满足条件.
【解答】解:(1)如图1,点F为所作;
(2)如图2,点P为所作.
【点评】本题考查了作图﹣复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了正方形的性质.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2026年中考数学一轮复习 尺规作图
一.选择题(共10小题)
1.(2025 碧江区 校级模拟)在Rt△ABC中,∠B=90°,AB=BC,以点A为圆心,适当长为半径画弧,分别交AC,AB于点D,E,分别以D,E为圆心大于为半径画弧,两弧交于点P,连接BP交BC于点F,则∠AFB的度数为( )
A.60° B.67.5° C.77.5° D.80°
2.(2025 凌河区校级三模)如图,已知∠MAN,以点A为圆心,以适当长为半径作弧,分别与AM、AN相交于点B、C;分别以B、C为圆心,以大于BC的长为半径作弧,两弧在∠MAN内部相交于点P,作射线AP.分别以A、B为圆心,以大于AB的长为半径作弧,两弧相交于点D、E,作直线DE分别与AB、AP、AN相交于点F、Q、H.若AB=4,∠PQE=67.5°,则AH的长为( )
A.2 B.2 C.2 D.4
3.(2025 门头沟区一模)下面是“作∠AOB的角平分线”的尺规作图方法:
(1)以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N. (2)分别以点M,N为圆心,大于长为半径画弧,两弧在∠AOB内部交于点C. (3)画射线OC,射线OC即为所求.
上述方法是通过判定△OMC≌△ONC得到∠MOC=∠NOC的,其中判定△OMC≌△ONC的依据是( )
A.两边及其夹角分别相等的两个三角形全等
B.三边分别相等的两个三角形全等
C.两角及其夹边分别相等的两个三角形全等
D.两角分别相等且其中一组等角的对边相等的两个三角形全等
4.(2025 阳山县一模)如图,在△ABC中,AB=AC,分别以点A、B为圆心,以适当的长为半径作弧,两弧分别交于E,F,作直线EF,D为BC的中点,M为直线EF上任意一点.若BC=4,△ABC面积为10,则BM+MD长度的最小值为( )
A. B.3 C.4 D.5
5.(2025 滨海新区校级模拟)如图,在△ABC中,∠C=60°,∠B=50°.以点A为圆心,适当长为半径画弧,交AB于点D,交AC于点E;再分别以点D,E为圆心,大于的长为半径画弧,两弧(所在圆的半径相等)相交于点P,作射线AP,与边BC相交于点F,则∠AFB的大小为( )
A.80° B.85° C.90° D.95°
6.(2025 海淀区一模)已知:如图,四边形ABCD是平行四边形,点E为AD上的一点(不与点A,D重合),连接CE.
求作:点F,使得点F在BC上,且AF∥CE.
甲、乙、丙三名同学的尺规作图方法如下:
甲:以点C为圆心,AE的长为半径画弧,交BC于点F,连接AF;
乙:以点A为圆心,CE的长为半径画弧,交BC于点F,连接AF;
丙:以点B为圆心,DE的长为半径画弧,交BC于点F,连接AF.
上述三名同学的作法一定正确的是( )
A.甲、乙 B.乙、丙 C.甲、丙 D.甲、乙、丙
7.(2025 门头沟区二模)下面是小明设计的“过直线外一点作这条直线平行线”的尺规作图过程:
已知:如图1,直线BC及直线BC外一点P. 求作:直线PE,使得PE∥BC. 作法:如图2,①在直线BC上取一点A,连接PA. ②作∠PAC的平分线AD. ③以点P为圆心,PA长为半径画弧,交射线AD于点E. ④作直线PE. ∴直线PE就是所求作的直线.
上述的方法是通过判定∠PEA=∠EAC得到PE∥BC的,其中判定PE∥BC的依据是( )
A.同位角相等,两直线平行
B.两直线平行,同位角相等
C.内错角相等,两直线平行
D.两直线平行,内错角相等
8.(2025 东明县三模)如图,在△ABC中,分别以点A,B为圆心,大于的长为半径作弧,两弧相交于点M,N,作直线MN交BC于点D,交AB于点O,连接AD,若△ABC的周长比△ADC的周长大14.则AO的长为( )
A.5 B.6 C.7 D.8
9.(2025 翁牛特旗模拟)如图,在菱形ABCD中,分别以C,D为圆心,大于长为半径作弧,两弧分别交于点E、F,连接EF,若直线EF恰好经过点A,与边CD交于点M,连接BM.有以下四个结论:①∠ABC=60°,②如果AB=2,那么,③,④;其中正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
10.(2025 新抚区四模)小澎同学按如下步骤作图:
①画矩形ABCD,使得AD=2AB=8cm,连接BD;②分别以B,D为圆心,大于的长为半径画弧,两弧交于E,F两点;③画直线EF,分别与AD,BC交于点M,N,连接BM,DN.则四边形BMDN的周长是( )
A.5cm B.10cm C.16cm D.20cm
二.填空题(共5小题)
11.(2025 白山模拟)如图,在Rt△ABC中,,按下列步骤作图:①分别以点A,B为圆心、大于的长为半径作弧,两弧交于点M,N;②作直线MN交AB于点D,交AC于点E;③以点D为圆心、AD的长为半径作弧,交直线MN于点F,连接AF.若,则BC的长为 .
12.(2025 湖南模拟)如图,在△ABC中,CA=CB,∠C=80°,分别以点A,C为圆心,大于的长为半径作弧,两弧相交于M,N两点,作直线MN交AC于点D,交AB于点E,则∠AED= .
13.(2025 武侯区校级模拟)如图,四边形ABCD是矩形,以点B为圆心,任意长为半径作弧分别交AB和BC于点M,N;分别以点M,N为圆心、大于的长为半径作弧,两弧相交于点H;作射线BH交边AD于点E;作射线CF,交DE于点F,交射线BH于点G,连接GD.若CD=3,DF=EF=1,则 .
14.(2025 乾安县模拟)如图1,要过直线AB外一点P作直线AB的平行线,用尺规作图的方法作出如图2的形式,则图2的作法中判定两直线平行的依据是 .
15.(2025 祁阳市校级一模)如图,在平行四边形ABCD中,AB⊥AC,AB=6,AC=8,分别以A,C为圆心,大于的长为半径画弧,两弧相交于点M,N,作直线MN与BC交于点E,与AD交于点F,连接AE,CF,则四边形AECF的周长为 .
三.解答题(共5小题)
16.(2025 天河区校级四模)如图,在△ABC中,∠A=90°.
(1)尺规作图:在边AC上取点O,以O为圆心画圆,使得⊙O与边BC、BA相切(保留作图痕迹,不写作法);
(2)在(1)所作的图中,若,AB=6,求OB的长.
17.(2025 昌邑区校级三模)如图,均是5×5的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1,点A,B,C,D均在格点上.
(1)如图①,若连接AB,CD交于点P,则的值为 .
(2)如图②,在AB上找一点Q,使(仅用无刻度的直尺,在给定的正方形网格中,按要求作图,保留作图痕迹,不要求写作法).
18.(2025 永寿县校级模拟)如图,在△ABC中,AB=AC,请用尺规作图法,求作一个菱形AEFG,使得点E,F,G分别在AB,BC,AC边上.(保留作图痕迹,不写作法)
19.(2025 椒江区校级模拟)如图,在正方形网格中,点A为格点(网格线的交点),点B在网格线上,仅使用无刻度的直尺作图,保留作图痕迹.
(1)如图1,在直线m上找到一点P,使得AP+BP的值最小;
(2)如图2,部分网格被墨汁污染,在仅剩的网格中,标出格点Q,使线段BQ的长度等于(1)中的最小值.
20.(2025 萍乡一模)如图,点E是正方形ABCD内一点,且EB=EC.请仅用无刻度的直尺按要求作图(保留画图痕迹,不写作法).
(1)在图1中,作出BC边的中点.
(2)在图2中,作出CD边的中点.
2026年中考数学一轮复习 尺规作图
参考答案与试题解析
一.选择题(共10小题)
1.(2025 碧江区 校级模拟)在Rt△ABC中,∠B=90°,AB=BC,以点A为圆心,适当长为半径画弧,分别交AC,AB于点D,E,分别以D,E为圆心大于为半径画弧,两弧交于点P,连接BP交BC于点F,则∠AFB的度数为( )
A.60° B.67.5° C.77.5° D.80°
【考点】作图—基本作图;线段垂直平分线的性质;等腰直角三角形.
【专题】作图题;等腰三角形与直角三角形;几何直观;推理能力.
【答案】B
【分析】先根据三角形内角和定理求出∠CAB的度数,再由AF是∠BAC的平分线得出,根据直角三角形的性质可知∠AFB=90°﹣∠BAF=67.5°.
【解答】解:在Rt△ABC中,∠B=90°,AB=BC,
∴∠CAB=45°.
由题意得:AF是∠BAC的角平分线,
∴,
∴∠AFB=90°﹣∠BAF=67.5°.
故选:B.
【点评】本题主要考查作图﹣基本作图,线段垂直平分线的性质,等腰直角三角形,掌握相关定义是解题的关键.
2.(2025 凌河区校级三模)如图,已知∠MAN,以点A为圆心,以适当长为半径作弧,分别与AM、AN相交于点B、C;分别以B、C为圆心,以大于BC的长为半径作弧,两弧在∠MAN内部相交于点P,作射线AP.分别以A、B为圆心,以大于AB的长为半径作弧,两弧相交于点D、E,作直线DE分别与AB、AP、AN相交于点F、Q、H.若AB=4,∠PQE=67.5°,则AH的长为( )
A.2 B.2 C.2 D.4
【考点】作图—基本作图;角平分线的定义;线段垂直平分线的性质.
【专题】作图题;几何直观;运算能力.
【答案】A
【分析】证明∠FAH=45°,推出AHAF可得结论.
【解答】解:由作图可得:∠BAP=∠CAP,DE⊥AB,AF=FBAB=2,
∵∠PQE=67.5°,
∴∠AQF=67.5°,
∴∠BAP=∠CAP=90°﹣67.5°=22.5°,
∴∠FAH=45°,
∴AHAF=2.
故选:A.
【点评】本题考查作图﹣基本作图,角平分线的定义,线段垂直平分线的性质,就提到过房间数理解题意,灵活运用所学知识解决问题.
3.(2025 门头沟区一模)下面是“作∠AOB的角平分线”的尺规作图方法:
(1)以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N. (2)分别以点M,N为圆心,大于长为半径画弧,两弧在∠AOB内部交于点C. (3)画射线OC,射线OC即为所求.
上述方法是通过判定△OMC≌△ONC得到∠MOC=∠NOC的,其中判定△OMC≌△ONC的依据是( )
A.两边及其夹角分别相等的两个三角形全等
B.三边分别相等的两个三角形全等
C.两角及其夹边分别相等的两个三角形全等
D.两角分别相等且其中一组等角的对边相等的两个三角形全等
【考点】作图—基本作图;全等三角形的判定;角平分线的性质.
【专题】作图题;图形的全等;几何直观;推理能力.
【答案】B
【分析】根据SSS证明三角形全等即可.
【解答】解:在△COM和△CON中,
,
∴△COM≌△CON(SSS),
∴∠COM=∠CON,
∴射线OC平分∠AOB.
故选:B.
【点评】本题考查作图﹣基本作图,全等三角形的判定,解题的关键是理解题意,灵活运用所学知识解决问题.
4.(2025 阳山县一模)如图,在△ABC中,AB=AC,分别以点A、B为圆心,以适当的长为半径作弧,两弧分别交于E,F,作直线EF,D为BC的中点,M为直线EF上任意一点.若BC=4,△ABC面积为10,则BM+MD长度的最小值为( )
A. B.3 C.4 D.5
【考点】作图—基本作图;线段垂直平分线的性质;等腰三角形的性质.
【专题】等腰三角形与直角三角形;尺规作图;几何直观.
【答案】D
【分析】连接AD,交直线EF于点N,设EF交AB于点G,当点M与点N重合时,BM+MD长度最小,最小值即为AD的长,结合已知条件求出AD即可.
【解答】解:连接AD,交直线EF于点N,设EF交AB于点G,
由题意得,直线EF为线段AB的垂直平分线,
∴AG=BG,EF⊥AB,
∴当点M与点N重合时,BM+MD长度最小,最小值即为AD的长.
∵AB=AC,D为BC的中点,
∴AD⊥BC,
∵BC=4,△ABC面积为10,
∴10,
解得AD=5.
故选:D.
【点评】本题考查作图﹣基本作图、线段垂直平分线的性质、等腰三角形的性质、轴对称﹣最短路径问题,熟练掌握线段垂直平分线的性质、等腰三角形的性质、轴对称﹣最短路径问题是解答本题的关键.
5.(2025 滨海新区校级模拟)如图,在△ABC中,∠C=60°,∠B=50°.以点A为圆心,适当长为半径画弧,交AB于点D,交AC于点E;再分别以点D,E为圆心,大于的长为半径画弧,两弧(所在圆的半径相等)相交于点P,作射线AP,与边BC相交于点F,则∠AFB的大小为( )
A.80° B.85° C.90° D.95°
【考点】作图—基本作图;三角形内角和定理.
【专题】作图题.
【答案】D
【分析】由三角形内角和可得∠BAC=70°,再根据作图过程可得AP平分∠BAC,即∠BAF=35°,然后根据三角形内角和定理即可解答.
【解答】解:∵在△ABC中,∠C=60°,∠B=50°,
∴∠BAC=180°﹣∠C﹣∠B=70°,
由作图过程可得:AP平分∠BAC,
∴,
∴∠AFB=180°﹣∠B﹣∠BAF=95°.
故选:D.
【点评】本题主要考查了角平分线的作法、三角形内角和定理等知识点,掌握角平分线的尺规作图法成为解题的关键.
6.(2025 海淀区一模)已知:如图,四边形ABCD是平行四边形,点E为AD上的一点(不与点A,D重合),连接CE.
求作:点F,使得点F在BC上,且AF∥CE.
甲、乙、丙三名同学的尺规作图方法如下:
甲:以点C为圆心,AE的长为半径画弧,交BC于点F,连接AF;
乙:以点A为圆心,CE的长为半径画弧,交BC于点F,连接AF;
丙:以点B为圆心,DE的长为半径画弧,交BC于点F,连接AF.
上述三名同学的作法一定正确的是( )
A.甲、乙 B.乙、丙 C.甲、丙 D.甲、乙、丙
【考点】作图—复杂作图;平行四边形的判定与性质.
【专题】多边形与平行四边形;尺规作图;几何直观.
【答案】C
【分析】由甲同学的尺规作图方法可得CF=AE,结合平行四边形的性质可得AD∥BC,进而可得四边形AECF为平行四边形,则AF∥CE;由乙同学的尺规作图方法可得AF=CE,不能得出AF∥CE;由丙同学的尺规作图方法可得BF=DE,结合平行四边形的性质可得AD∥BC,AD=BC,则AE=CF,进而可得四边形AECF为平行四边形,则AF∥CE.
【解答】解:由甲同学的尺规作图方法可得CF=AE,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴四边形AECF为平行四边形,
∴AF∥CE.
故甲同学的作法正确,符合题意;
由乙同学的尺规作图方法可得AF=CE,
不能得出AF∥CE,
故乙同学的作法不正确,不符合题意;
由丙同学的尺规作图方法可得BF=DE,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴AE=CF,
∴四边形AECF为平行四边形,
∴AF∥CE.
故丙同学的作法正确,符合题意.
综上所述,三名同学的作法一定正确的是甲、丙.
故选:C.
【点评】本题考查作图—复杂作图、平行四边形的判定与性质,熟练掌握平行四边形的判定与性质是解答本题的关键.
7.(2025 门头沟区二模)下面是小明设计的“过直线外一点作这条直线平行线”的尺规作图过程:
已知:如图1,直线BC及直线BC外一点P. 求作:直线PE,使得PE∥BC. 作法:如图2,①在直线BC上取一点A,连接PA. ②作∠PAC的平分线AD. ③以点P为圆心,PA长为半径画弧,交射线AD于点E. ④作直线PE. ∴直线PE就是所求作的直线.
上述的方法是通过判定∠PEA=∠EAC得到PE∥BC的,其中判定PE∥BC的依据是( )
A.同位角相等,两直线平行
B.两直线平行,同位角相等
C.内错角相等,两直线平行
D.两直线平行,内错角相等
【考点】作图—复杂作图;平行线的判定与性质.
【专题】线段、角、相交线与平行线;尺规作图;应用意识.
【答案】C
【分析】结合平行线的判定可得答案.
【解答】解:∵AD为∠PAC的平分线,
∴∠PAE=∠CAE.
∵由作图过程可得,PE=PA,
∴∠PEA=∠PAE,
∴∠PEA=∠CAE,
∴PE∥BC,
∴判定PE∥BC的依据是内错角相等,两直线平行.
故选:C.
【点评】本题考查作图—复杂作图、平行线的判定与性质,熟练掌握平行线的判定是解答本题的关键.
8.(2025 东明县三模)如图,在△ABC中,分别以点A,B为圆心,大于的长为半径作弧,两弧相交于点M,N,作直线MN交BC于点D,交AB于点O,连接AD,若△ABC的周长比△ADC的周长大14.则AO的长为( )
A.5 B.6 C.7 D.8
【考点】作图—基本作图;线段垂直平分线的性质.
【专题】作图题;线段、角、相交线与平行线;运算能力;推理能力.
【答案】C
【分析】利用基本作图得到DE垂直平分AB,则DA=DB,AO=BO,利用等量代换得到△ADC的周长,再利用△ABC的周长比△ADC的周长大14得到AB=8,从而得到AO的长.
【解答】解:由作法得DO垂直平分AB,
∴DA=DB,AO=BO,
∴△ADC的周长=AC+BC,
∵△ABC的周长=AC+BC+AB,△ABC的周长比△ADC的周长大14,
∴AB=14,
∴AOAB=7.
故选:C.
【点评】本题考查了作图﹣基本作图,线段垂直平分线的性质,解决本题的关键是熟练掌握线段的垂直平分线的作法.
9.(2025 翁牛特旗模拟)如图,在菱形ABCD中,分别以C,D为圆心,大于长为半径作弧,两弧分别交于点E、F,连接EF,若直线EF恰好经过点A,与边CD交于点M,连接BM.有以下四个结论:①∠ABC=60°,②如果AB=2,那么,③,④;其中正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
【考点】作图—基本作图;线段垂直平分线的性质;等边三角形的判定与性质;菱形的性质.
【专题】作图题;几何直观;推理能力.
【答案】B
【分析】连接AC,如图,先利用基本作图可判断AM垂直平分CD,则根据线段垂直平分线的性质得到AC=AD,CM=DM,AM⊥CD,再利用菱形的性质得到AD=AB=BC=CD,AB∥CD,则可判断△ABC和△ADC都为等边三角形,从而可对①进行判断;利用勾股定理在Rt△ADM中计算出AM,接着在Rt△BAM中计算出BM,从而可对②进行判断;利用BC=2,CM=1可对③进行判断;最后根据三角形面积公式可对④进行判断.
【解答】解:连接AC,如图,
由作法得AM垂直平分CD,
∴AC=AD,CM=DM,AM⊥CD,
∵四边形ABCD为菱形,
∴AD=AB=BC=CD,AB∥CD,
∴AB=AC=BC=CD=AD,
∴△ABC和△ADC都为等边三角形,
∴∠ABC=60°,所以①正确;
∵AB=2,
∴AD=CD=2,DM=1,
在Rt△ADM中,AM,
∵AM⊥CD,AB∥CD,
∴AM⊥AB,
∴∠BAM=90°,
∴BM,所以②正确;
∵BC=2,CM=1,
∴BC=2CM,所以③错误;
∵S△ADMAM DM,S△ABMAM AB,
而DMAB,
∴S△ADMS△ABM,所以④正确.
故选:B.
【点评】本题考查了作图﹣基本作图:熟练掌握5种基本作图是解决问题的关键.也考查了线段垂直平分线的性质、等边三角形的判定与性质和菱形的性质.
10.(2025 新抚区四模)小澎同学按如下步骤作图:
①画矩形ABCD,使得AD=2AB=8cm,连接BD;②分别以B,D为圆心,大于的长为半径画弧,两弧交于E,F两点;③画直线EF,分别与AD,BC交于点M,N,连接BM,DN.则四边形BMDN的周长是( )
A.5cm B.10cm C.16cm D.20cm
【考点】作图—复杂作图;线段垂直平分线的性质;矩形的判定.
【专题】作图题;线段、角、相交线与平行线;矩形 菱形 正方形;推理能力.
【答案】D
【分析】利用基本作图可判断MN垂直平分BD,则MB=MD,NB=ND,设MD=x,则BM=x,AM=8﹣x,在Rt△ABM中利用勾股定理得到42+(8﹣x)2=x2,解方程得到BM=DM=5,同理可得NB=ND=5,然后计算四边形MBND的周长.
【解答】解:由作法得MN垂直平分BD,
∴MB=MD,NB=ND,
设MD=x,则BM=x,AM=8﹣x,
由条件可知∠A=∠C=90°,
由勾股定理可得42+(8﹣x)2=x2,
解得x=5,
即BM=DM=5,
同理可得NB=ND=5,
∴四边形MBND的周长为5+5+5+5=20.
故选:D.
【点评】本题考查了线段垂直平分线的作图和性质、矩形的性质、勾股定理等知识.熟练掌握以上知识点是关键.
二.填空题(共5小题)
11.(2025 白山模拟)如图,在Rt△ABC中,,按下列步骤作图:①分别以点A,B为圆心、大于的长为半径作弧,两弧交于点M,N;②作直线MN交AB于点D,交AC于点E;③以点D为圆心、AD的长为半径作弧,交直线MN于点F,连接AF.若,则BC的长为 6 .
【考点】作图—基本作图;线段垂直平分线的性质;勾股定理.
【专题】等腰三角形与直角三角形;尺规作图;几何直观;推理能力.
【答案】6.
【分析】由作图可得EF垂直平分AB,AD=DF,根据勾股定理得到AD2+DF2=AF2=50,求得AD=DF=5,结合,即可求解.
【解答】解:由题意得:EF是线段AB的垂直平分线,AD=DF,
∴∠ADF=90°,
在直角三角形ADF中,由勾股定理得:AD2+DF2=AF2=50,
解得:AD=DF=5,
∴AB=AD+DB=10,
∵,
∴,
故答案为:6.
【点评】本题考查了作图﹣基本作图,线段垂直平分线的性质,勾股定理,解答本题的关键是熟练掌握勾股定理.
12.(2025 湖南模拟)如图,在△ABC中,CA=CB,∠C=80°,分别以点A,C为圆心,大于的长为半径作弧,两弧相交于M,N两点,作直线MN交AC于点D,交AB于点E,则∠AED= 40° .
【考点】作图—基本作图;三角形内角和定理;线段垂直平分线的性质;等腰三角形的性质.
【专题】作图题;几何直观.
【答案】40°.
【分析】由作图可知,MN垂直平分AC,得出∠ADE=90°,再根据等腰三角形的性质即可求解.
【解答】解:由作图可知,MN垂直平分AC,
∴∠ADE=90°,
又∵CA=CB,∠C=80°,
∴∠A50°,
∴∠AED=90°﹣50°=40°,
故答案为:40°.
【点评】本题考查了作图﹣基本作图,线段垂直平分线的性质,等腰三角形的性质,熟记线段垂直平分线的作法是解题的关键.
13.(2025 武侯区校级模拟)如图,四边形ABCD是矩形,以点B为圆心,任意长为半径作弧分别交AB和BC于点M,N;分别以点M,N为圆心、大于的长为半径作弧,两弧相交于点H;作射线BH交边AD于点E;作射线CF,交DE于点F,交射线BH于点G,连接GD.若CD=3,DF=EF=1,则 .
【考点】作图—基本作图;相似三角形的判定与性质;角平分线的定义;等腰三角形的判定与性质;矩形的性质.
【专题】作图题;等腰三角形与直角三角形;矩形 菱形 正方形;图形的相似;推理能力.
【答案】.
【分析】根据角平分线的定义得到∠ABE=∠CBE,根据矩形的性质得到AD=BC,AD∥BC,AB=CD=3,求得 AE=AB=3,得到AD=BC=5,根据相似三角形的判定和性质定理即可得到结论.
【解答】解:由作图知,BG平分∠ABC,
∴∠ABE=∠CBE,
∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,AB=CD=3,
∴∠AEB=∠CBE,
∴∠ABE=∠AEB,
∴AE=AB=3,
∵DF=EF=1,
∴AD=BC=5,
∵EF∥BC,
∴△GEF∽△GBC,
∴,
∵EF=DF,
∴S△DEG=2S△GEF,
∴,
故答案为:.
【点评】本题考查了作图﹣基本作图,矩形的性质,相似三角形的判定和性质,角平分线的定义,等腰三角形的判定和性质,熟练掌握等腰三角形的判定和性质以及相似三角形的判定和性质定理是解题的关键.
14.(2025 乾安县模拟)如图1,要过直线AB外一点P作直线AB的平行线,用尺规作图的方法作出如图2的形式,则图2的作法中判定两直线平行的依据是 同位角相等,两直线平行 .
【考点】作图—复杂作图;平行线的判定.
【专题】作图题;几何直观.
【答案】见试题解答内容
【分析】根据同位角相等两直线平行,判断即可.
【解答】解:由作图可知:∠MPD=∠MCB,
∴PD∥AB(同位角相等,两直线平行),
故答案为:同位角相等,两直线平行.
【点评】本题考查作图—复杂作图,平行线的判定等知识,解题的关键是读懂图象信息,掌握平行线的判定.
15.(2025 祁阳市校级一模)如图,在平行四边形ABCD中,AB⊥AC,AB=6,AC=8,分别以A,C为圆心,大于的长为半径画弧,两弧相交于点M,N,作直线MN与BC交于点E,与AD交于点F,连接AE,CF,则四边形AECF的周长为 20 .
【考点】作图—基本作图;线段垂直平分线的性质;勾股定理;平行四边形的性质.
【专题】等腰三角形与直角三角形;多边形与平行四边形;运算能力;推理能力.
【答案】20.
【分析】根据勾股定理得到BC10,由作图可知,MN是线段AC的垂直平分线,求得EC=EA,AF=CF,推出AE=CEBC=5,根据平行四边形的性质得到AD=BC=10,CD=AB=6,∠ACD=∠BAC=90°,同理证得AF=CF=5,于是得到结论.
【解答】解:∵AB⊥AC,AB=6,AC=8,
∴BC10,
由作图可知,MN是线段AC的垂直平分线,
∴EC=EA,AF=CF,
∴∠EAC=∠ACE,
∵∠B+∠ACB=∠BAE+∠CAE=90°,
∴∠B=∠BAE,
∴AE=BE,
∴AE=CEBC=5,
∵四边形ABCD是平行四边形,
∴AD=BC=10,CD=AB=6,∠ACD=∠BAC=90°,
同理证得AF=CF=5,
∴四边形AECF的周长=EC+EA+AF+CF=20,
故答案为:20.
【点评】本题考查了平行四边形的性质,作图﹣基本作图,勾股定理,线段垂直平分线的性质.利用勾股定理列出方程是解题的关键.
三.解答题(共5小题)
16.(2025 天河区校级四模)如图,在△ABC中,∠A=90°.
(1)尺规作图:在边AC上取点O,以O为圆心画圆,使得⊙O与边BC、BA相切(保留作图痕迹,不写作法);
(2)在(1)所作的图中,若,AB=6,求OB的长.
【考点】作图—复杂作图;解直角三角形;勾股定理;圆周角定理;切线的判定与性质.
【专题】作图题;几何直观.
【答案】(1)见解析;
(2).
【分析】(1)作BO平分∠ABC,BO交AC于点O,以O为圆心,OA为半径作⊙O即可;
(2)设BC与⊙O相切于点K,连接OK,则BA=BK=6,CK=BC﹣BK=10﹣6=4,设OA=OK=r,利用勾股定理构建方程求解.
【解答】解:(1)如图,⊙O即为所求;
(2)在Rt△ABC中,sin∠ACB,AB=6,
∴BC=10,
∴AC8,
设BC与⊙O相切于点K,连接OK,则BA=BK=6,CK=BC﹣BK=10﹣6=4,设OA=OK=r,
则有(8﹣r)2=r2+42,
解得r=5,
∴OB.
【点评】你本题考查作图﹣复杂作图,勾股定理,切线的判定和性质,解直角三角形,解题的关键是学会利用参数构建方程解决问题.
17.(2025 昌邑区校级三模)如图,均是5×5的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1,点A,B,C,D均在格点上.
(1)如图①,若连接AB,CD交于点P,则的值为 .
(2)如图②,在AB上找一点Q,使(仅用无刻度的直尺,在给定的正方形网格中,按要求作图,保留作图痕迹,不要求写作法).
【考点】作图—应用与设计作图;相似三角形的判定与性质;平行线的性质;勾股定理.
【专题】作图题;等腰三角形与直角三角形;图形的相似;几何直观;推理能力.
【答案】(1);
(2)作图见解析.
【分析】(1)如图,连接AD,BC,证明△PAD∽△PBC,由相似三角形的性质可得结论;
(2)如图,取格点M、N,连接MN交AB于点Q即可,
【解答】解:(1)如图①是5×5的正方形网格,每个小正方形的边长均为1,点A,B,C,D均在格点上,连接AD,BC,
∴AD∥BC,AD=3,BC=5,
∴∠PAD=∠PBC,∠PDA=∠PCB,
∴△PAD∽△PBC,
∴,
∴的值为,
故答案为:;
(2)如图②是5×5的正方形网格,每个小正方形的边长均为1,点A,B,C,D均在格点上,取格点M、N,连接MN交AB于点Q,连接BM、AN,
∴AN∥BM,AN=3,BM=1,
由勾股定理得:,
∴∠QAN=∠QBM,∠QNA=∠QMB,
∴△QAN∽△QBM,
∴,
∴,
则点Q即为所作.
【点评】本题考查作图﹣应用与设计作图,平行线的性质,相似三角形的判定与性质,勾股定理等知识,解题的关键是理解题意,学会利用数形结合的思想解决问题,
18.(2025 永寿县校级模拟)如图,在△ABC中,AB=AC,请用尺规作图法,求作一个菱形AEFG,使得点E,F,G分别在AB,BC,AC边上.(保留作图痕迹,不写作法)
【考点】作图—复杂作图;线段垂直平分线的性质;等腰三角形的性质;菱形的判定.
【专题】作图题;几何直观.
【答案】见解析.
【分析】作AF⊥BC于点F,作线段AF的垂直平分线交AB于点E,交AC于点G,连接EF,GF,四边形AEFG即为所求.
【解答】解:如图,菱形AEFG即为所求.
【点评】本题考查作图﹣复杂作图,线段垂直平分线的性质,菱形的判定,等腰三角形的性质,解题的关键是掌握相关知识解决问题.
19.(2025 椒江区校级模拟)如图,在正方形网格中,点A为格点(网格线的交点),点B在网格线上,仅使用无刻度的直尺作图,保留作图痕迹.
(1)如图1,在直线m上找到一点P,使得AP+BP的值最小;
(2)如图2,部分网格被墨汁污染,在仅剩的网格中,标出格点Q,使线段BQ的长度等于(1)中的最小值.
【考点】作图—应用与设计作图;轴对称﹣最短路线问题;勾股定理.
【专题】作图题;几何直观.
【答案】见解析.
【分析】(1)作点A关于直线m的对称点A′,连接BA′交直线m于点P,连接AP,点P即为所求;
(2)取格点A″,作点A″关于直线m的对称点Q,连接BQ,线段BQ即为所求.
【解答】解:(1)如图,点P即为所求;
(2)如图2中,线段BQ即为所求.
【点评】本题考查作图﹣应用与设计作图,勾股定理,轴对称最短问题,解题的关键是掌握轴对称最短问题.
20.(2025 萍乡一模)如图,点E是正方形ABCD内一点,且EB=EC.请仅用无刻度的直尺按要求作图(保留画图痕迹,不写作法).
(1)在图1中,作出BC边的中点.
(2)在图2中,作出CD边的中点.
【考点】作图—复杂作图;线段垂直平分线的性质;正方形的性质.
【专题】作图题;几何直观.
【答案】见试题解答内容
【分析】(1)连接AC、BD,它们相交于O点,连接EO并延长交BC于F,则F点满足条件;
(2)FE交AD于H,连接CH交BD于G,则AG的延长线交CD于P,则P点满足条件.
【解答】解:(1)如图1,点F为所作;
(2)如图2,点P为所作.
【点评】本题考查了作图﹣复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了正方形的性质.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
