第七章 相交线与平行线(暑假复习.含解析)-2024-2025学年七年级下册数学人教版(2024)
文档属性
| 名称 | 第七章 相交线与平行线(暑假复习.含解析)-2024-2025学年七年级下册数学人教版(2024) | 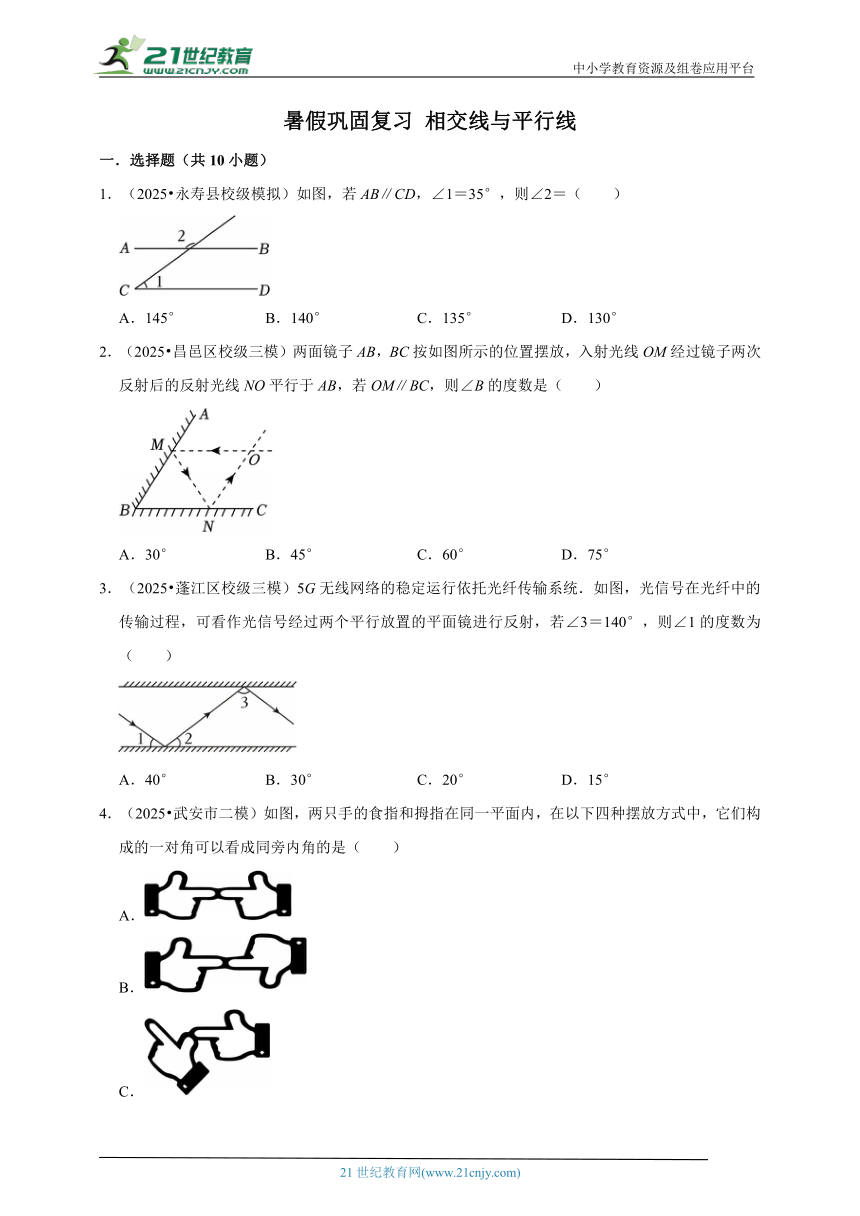 | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-06 15:06:22 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
暑假巩固复习 相交线与平行线
一.选择题(共10小题)
1.(2025 永寿县校级模拟)如图,若AB∥CD,∠1=35°,则∠2=( )
A.145° B.140° C.135° D.130°
2.(2025 昌邑区校级三模)两面镜子AB,BC按如图所示的位置摆放,入射光线OM经过镜子两次反射后的反射光线NO平行于AB,若OM∥BC,则∠B的度数是( )
A.30° B.45° C.60° D.75°
3.(2025 蓬江区校级三模)5G无线网络的稳定运行依托光纤传输系统.如图,光信号在光纤中的传输过程,可看作光信号经过两个平行放置的平面镜进行反射,若∠3=140°,则∠1的度数为( )
A.40° B.30° C.20° D.15°
4.(2025 武安市二模)如图,两只手的食指和拇指在同一平面内,在以下四种摆放方式中,它们构成的一对角可以看成同旁内角的是( )
A.
B.
C.
D.
5.(2025 定西模拟)如图,街道AB与CD平行,∠ABC=130°,则∠BCD等于( )
A.150° B.130° C.120° D.50°
6.(2025 花垣县校级模拟)如图,a∥b,∠1=55°,则∠2的度数是( )
A.135° B.55° C.115° D.125°
7.(2025 孝义市三模)如图,从点光源A发出平行于主光轴的光线,在凸透镜B处折射后经过焦点F1射出,从点光源A发出的光线经过光心O后沿原方向射出,两束光线汇聚于点C.若∠ABF1=160°,∠AOF2=12°.则∠BCO的度数为( )
A.8° B.10° C.12° D.20°
8.(2025 朝阳区校级二模)划船是一项涉及全身的协调运动,正确的划船动作需要保持正确的姿势和体态.如图,AB∥CD,AC∥ED,若∠MDE=136°,则∠FAC的大小为( )
A.44° B.54° C.136° D.46°
9.(2025 二七区校级三模)如图,已知直线a∥b,c⊥a,∠1=35°,则∠2的度数为( )
A.35° B.45° C.55° D.50°
10.(2025 铜陵三模)一等腰三角板和一直尺如图放置,若∠1=60°,则∠2的度数是( )
A.105° B.110° C.115° D.120°
二.填空题(共5小题)
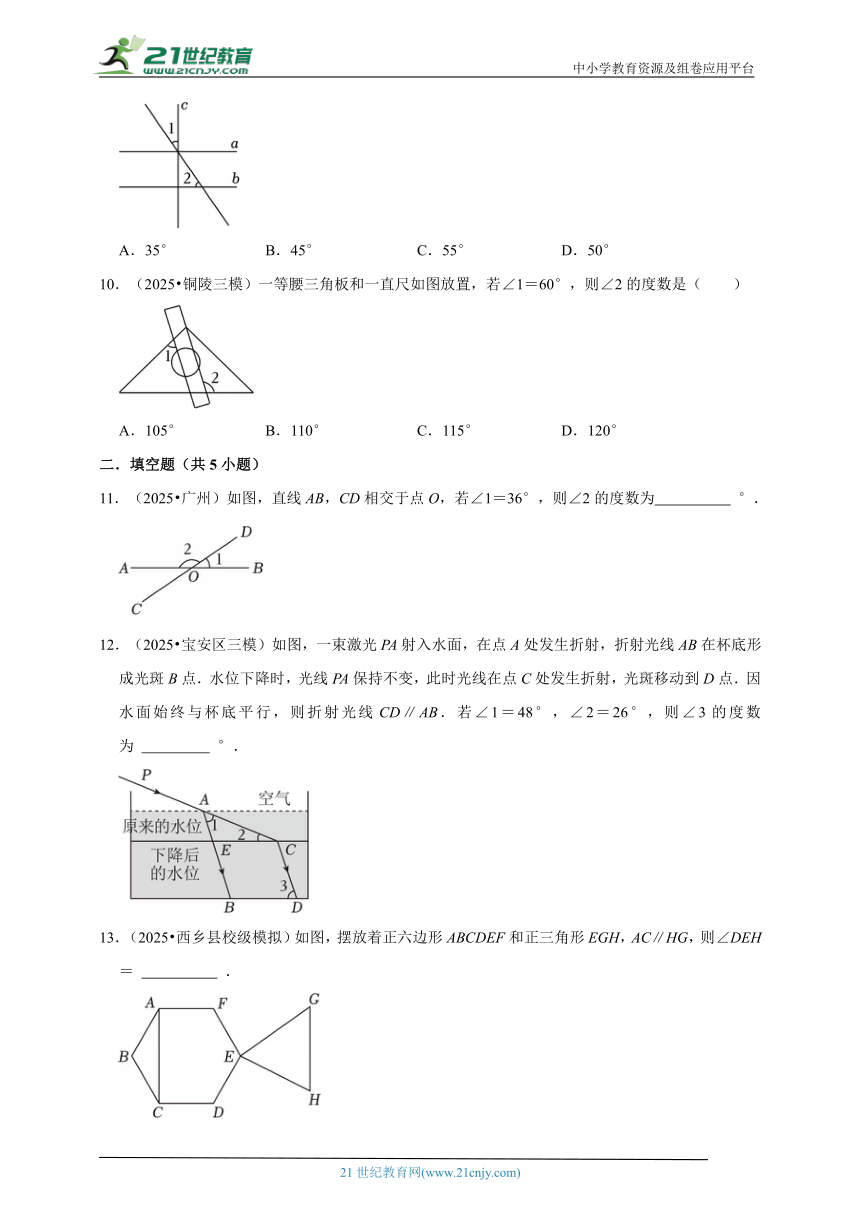
11.(2025 广州)如图,直线AB,CD相交于点O,若∠1=36°,则∠2的度数为 °.
12.(2025 宝安区三模)如图,一束激光PA射入水面,在点A处发生折射,折射光线AB在杯底形成光斑B点.水位下降时,光线PA保持不变,此时光线在点C处发生折射,光斑移动到D点.因水面始终与杯底平行,则折射光线CD∥AB.若∠1=48°,∠2=26°,则∠3的度数为 °.
13.(2025 西乡县校级模拟)如图,摆放着正六边形ABCDEF和正三角形EGH,AC∥HG,则∠DEH= .
14.(2025 东台市一模)如图,烧杯内液体表面AB与烧杯下底部CD平行,光线EF从液体中射向空气时发生折射,光线变成FH,点G在射线EF上.已知∠HFB=19°,∠FED=55°,则∠GFH的度数为 .
15.(2025 番禺区二模)图①是用一根吸管吸吮纸杯中的豆浆,图②是其截面图,已知AB∥CD,c表示吸管.若∠1=76°,则∠2= 度.
三.解答题(共5小题)
16.(2025 武汉三模)如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DE∥BA,DF∥CA.
求证:∠FDE=∠A.
17.(2025 长安区校级模拟)如图,三条直线AB,CD,EF相交于点O,且CD⊥EF,∠AOE=70°,若OG平分∠BOF.求∠DOG的度数.
18.(2025 长安区校级模拟)如图,直线AC,BD被直线BC所截,连接AB,CD,BA平分∠CBD,且与线段CD相交于点E,F是线段AC上一点,连接EF.若∠A=∠ABC,∠AFE+∠CBD=180°.求证:EF∥BC.
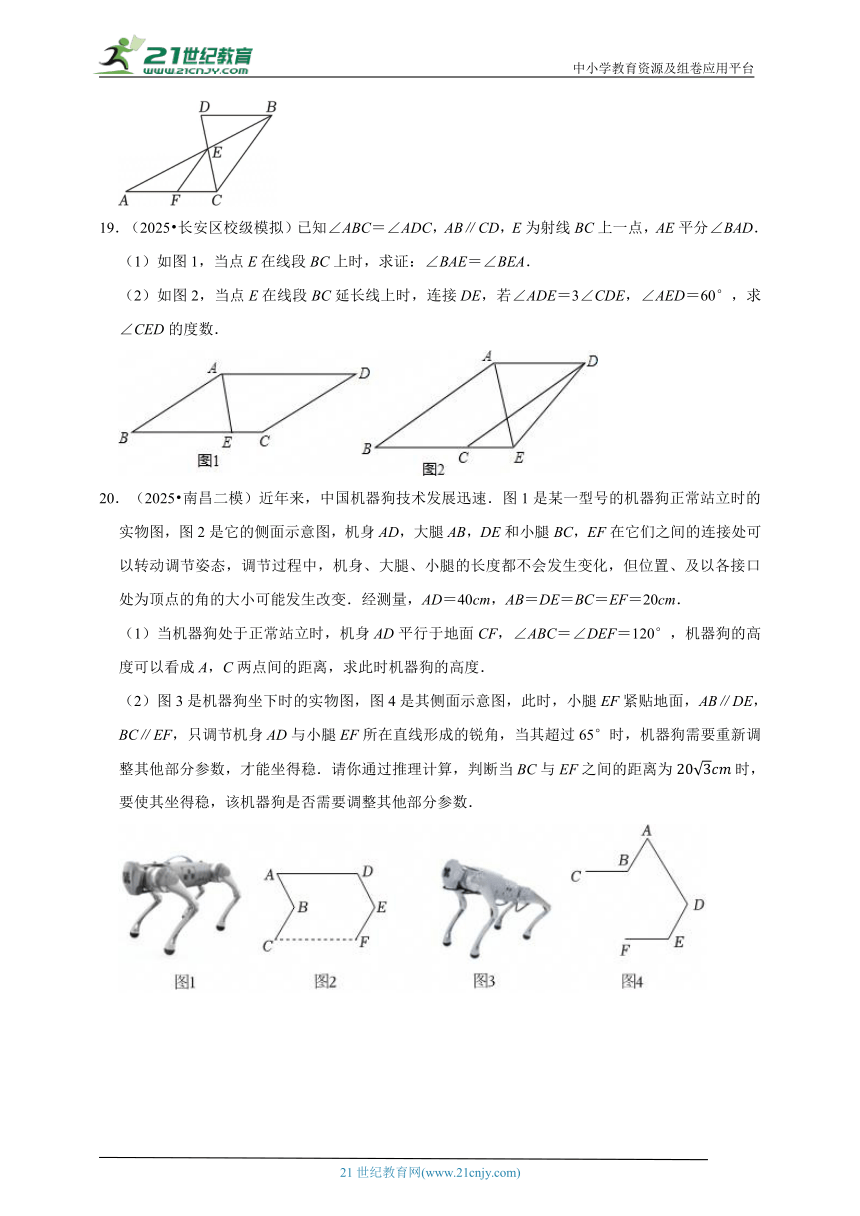
19.(2025 长安区校级模拟)已知∠ABC=∠ADC,AB∥CD,E为射线BC上一点,AE平分∠BAD.
(1)如图1,当点E在线段BC上时,求证:∠BAE=∠BEA.
(2)如图2,当点E在线段BC延长线上时,连接DE,若∠ADE=3∠CDE,∠AED=60°,求∠CED的度数.
20.(2025 南昌二模)近年来,中国机器狗技术发展迅速.图1是某一型号的机器狗正常站立时的实物图,图2是它的侧面示意图,机身AD,大腿AB,DE和小腿BC,EF在它们之间的连接处可以转动调节姿态,调节过程中,机身、大腿、小腿的长度都不会发生变化,但位置、及以各接口处为顶点的角的大小可能发生改变.经测量,AD=40cm,AB=DE=BC=EF=20cm.
(1)当机器狗处于正常站立时,机身AD平行于地面CF,∠ABC=∠DEF=120°,机器狗的高度可以看成A,C两点间的距离,求此时机器狗的高度.
(2)图3是机器狗坐下时的实物图,图4是其侧面示意图,此时,小腿EF紧贴地面,AB∥DE,BC∥EF,只调节机身AD与小腿EF所在直线形成的锐角,当其超过65°时,机器狗需要重新调整其他部分参数,才能坐得稳.请你通过推理计算,判断当BC与EF之间的距离为时,要使其坐得稳,该机器狗是否需要调整其他部分参数.
暑假巩固复习 相交线与平行线
参考答案与试题解析
一.选择题(共10小题)
1.(2025 永寿县校级模拟)如图,若AB∥CD,∠1=35°,则∠2=( )
A.145° B.140° C.135° D.130°
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】A
【分析】根据两直线平行,同位角相等得出∠1=∠3=35°,即可求出∠2的度数.
【解答】解:如图,
∵AB∥CD,
∴∠1=∠3,
∵∠1=35°,
∴∠3=35°,
∴∠2=180°﹣∠3=180°﹣35°=145°,
故选:A.
【点评】本题考查了平行线的性质,熟练掌握两直线平行,同位角相等是解题的关键.
2.(2025 昌邑区校级三模)两面镜子AB,BC按如图所示的位置摆放,入射光线OM经过镜子两次反射后的反射光线NO平行于AB,若OM∥BC,则∠B的度数是( )
A.30° B.45° C.60° D.75°
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】C
【分析】根据已知条件,得到∠AMO=∠BMN,∠MNB=∠CNO,由平行线的性质得到∠AMO=∠MBC,∠MBC=∠CNO,∠MNO=∠BMN,推出∠B=∠MNB=∠MNO=∠CNO,再根据∠MNB+∠MNO+∠CNO=180°,进行求解即可.
【解答】解:根据题意得到∠AMO=∠BMN,∠MNB=∠CNO,
∵OM∥BC,NO∥AB,
∴∠AMO=∠B,∠MBC=∠CNO,∠MNO=∠BMN,
∴∠B=∠MNB=∠MNO=∠CNO,
∵∠MNB+∠MNO+∠CNO=180°,
∴∠B=∠MNB=∠MNO=∠CNO=180°÷3=60°,
即∠B的度数是60°,
故选:C.
【点评】本题考查平行线的性质,关键是平行线性质的熟练掌握.
3.(2025 蓬江区校级三模)5G无线网络的稳定运行依托光纤传输系统.如图,光信号在光纤中的传输过程,可看作光信号经过两个平行放置的平面镜进行反射,若∠3=140°,则∠1的度数为( )
A.40° B.30° C.20° D.15°
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】C
【分析】由光的反射定律可知∠5=∠4,∠1=∠2,再由平行线的性质推出∠4=∠2,从而得出结论.
【解答】解:如图:
由光的反射定律可知∠5=∠4,
∵∠3=140°,
∴∠5=∠4(180°﹣140°)=20°,
∵两平面镜平行,
∴∠4=∠2=20°(两直线平行,内错角相等),
由光的反射定律可知∠1=∠2=20°,
故选:C.
【点评】本题考查平行线的性质,解题的关键是由平行线的性质推出∠4=∠2.
4.(2025 武安市二模)如图,两只手的食指和拇指在同一平面内,在以下四种摆放方式中,它们构成的一对角可以看成同旁内角的是( )
A.
B.
C.
D.
【考点】同位角、内错角、同旁内角.
【专题】线段、角、相交线与平行线;运算能力.
【答案】A
【分析】根据同位角,同旁内角,内错角的定义,进行判断即可.
【解答】解:根据相关概念逐项分析判断如下:
A、可以看成同旁内角,符合题意;
B、可以看成内错角,不符合题意;
C、不是内错角,不是同位角,不是同旁内角,不符合题意;
D、可以看成同位角,不符合题意;
故选:A.
【点评】本题考查三线八角.熟练掌握同位角,同旁内角,内错角的定义是解题的关键.
5.(2025 定西模拟)如图,街道AB与CD平行,∠ABC=130°,则∠BCD等于( )
A.150° B.130° C.120° D.50°
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】B
【分析】由街道AB与CD平行,∠ABC=130°,根据两直线平行,内错角相等,即可求得∠BCD的度数.
【解答】解:∵AB∥CD,∠ABC=130°,
∴∠BCD=∠ABC=130°.
故选:B.
【点评】此题考查了平行线的性质.此题比较简单,注意掌握两直线平行,内错角相等定理的应用,注意数形结合思想的应用.
6.(2025 花垣县校级模拟)如图,a∥b,∠1=55°,则∠2的度数是( )
A.135° B.55° C.115° D.125°
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;运算能力.
【答案】D
【分析】根据平行线的性质求出∠3的度数,再由平角的定义即可得到答案.
【解答】解;如图所示,
∵a∥b,∠1=55°,
平行线的性质求出∠3的度数,
∴∠3=∠1=55°,
∴∠2=180°﹣∠3=125°.
故选:D.
【点评】本题主要考查了平行线的性质,平角的定义,正确记忆相关知识点是解题关键.
7.(2025 孝义市三模)如图,从点光源A发出平行于主光轴的光线,在凸透镜B处折射后经过焦点F1射出,从点光源A发出的光线经过光心O后沿原方向射出,两束光线汇聚于点C.若∠ABF1=160°,∠AOF2=12°.则∠BCO的度数为( )
A.8° B.10° C.12° D.20°
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】A
【分析】由平行线的性质得出∠BF1O=180°﹣∠ABF1=20°,由对顶角相等得出∠COF1=∠AOF2=12°,最后由三角形外角的性质即可得出答案.
【解答】解:∵AB∥OF1,∠ABF1=160°,
∴∠BF1O+∠ABF1=180°,
∴∠BF1O=180°﹣∠ABF1=20°,
∵∠COF1=∠AOF2=12°,
∴∠BCO=∠BF1O﹣∠COF1=20°﹣12°=8°,
故选:A.
【点评】本题考查了平行线的性质,掌握对顶角相等、三角形外角的性质是解题的关键.
8.(2025 朝阳区校级二模)划船是一项涉及全身的协调运动,正确的划船动作需要保持正确的姿势和体态.如图,AB∥CD,AC∥ED,若∠MDE=136°,则∠FAC的大小为( )
A.44° B.54° C.136° D.46°
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】A
【分析】根据平行线的性质定理求解即可.
【解答】解:∵∠MDE=136°,
∴∠CDE=180°﹣136°=44°,
∵AC∥ED,
∴∠CDE=∠ACD=44°,
∵AB∥CD,
∴∠ACD=∠FAC=44°,
故选:A.
【点评】此题考查了平行线的性质,熟记“两直线平行,内错角相等”是解题的关键.
9.(2025 二七区校级三模)如图,已知直线a∥b,c⊥a,∠1=35°,则∠2的度数为( )
A.35° B.45° C.55° D.50°
【考点】平行线的性质;三角形内角和定理;余角和补角;对顶角、邻补角;垂线.
【专题】线段、角、相交线与平行线;推理能力.
【答案】C
【分析】根据题意得出c⊥b,又∠1=∠3=35°,即可求解.
【解答】解:∵a∥b,c⊥a,
∴c⊥b,
∴∠ABC=90°,
∵∠1=35°,
∴∠1=∠3=35°,
∴∠2=90°﹣35°=55°,
故选:C.
【点评】本题考查了平行线的性质,对顶角、邻补角,三角形内角和定理,垂线,余角和补角,熟记以上知识并准确识图是解题的关键.
10.(2025 铜陵三模)一等腰三角板和一直尺如图放置,若∠1=60°,则∠2的度数是( )
A.105° B.110° C.115° D.120°
【考点】平行线的性质;余角和补角.
【专题】线段、角、相交线与平行线;推理能力.
【答案】A
【分析】结合等腰直角三角形性质,先由三角形内角和定理求出∠3,再由平行线性质及邻补角定义,数形结合即可得到答案.
【解答】解:如图所示:
由三角形内角和定理可知∠3=180°﹣60°﹣45°=75°,
∴由平行线性质可知∠4=∠3=75°(两直线平行,同位角相等),
∴∠2=180°﹣∠4=180°﹣75°=105°,
故选:A.
【点评】本题考查平行线的性质,余角和补角,熟练掌握相关几何性质,数形结合是解决问题的关键.
二.填空题(共5小题)
11.(2025 广州)如图,直线AB,CD相交于点O,若∠1=36°,则∠2的度数为 144 °.
【考点】对顶角、邻补角.
【专题】线段、角、相交线与平行线;几何直观;运算能力.
【答案】144.
【分析】根据邻补角的定义进行计算即可.
【解答】解:∵∠1+∠2=180°,而∠1=36°,
∴∠2=180°﹣36°=144°,
故答案为:144.
【点评】本题考查对顶角、邻补角,理解邻补角的定义是正确解答的关键.
12.(2025 宝安区三模)如图,一束激光PA射入水面,在点A处发生折射,折射光线AB在杯底形成光斑B点.水位下降时,光线PA保持不变,此时光线在点C处发生折射,光斑移动到D点.因水面始终与杯底平行,则折射光线CD∥AB.若∠1=48°,∠2=26°,则∠3的度数为 74 °.
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】见试题解答内容
【分析】由三角形的外角性质求出∠CEB=74°,判定四边形BDCE是平行四边形,推出∠3=∠CEB=74°.
【解答】解:∵∠1=48°,∠2=26°,
∴∠CEB=∠1+∠2=74°,
∵EC∥BD,BE∥CD,
∴四边形BDCE是平行四边形,
∴∠3=∠CEB=74°.
故答案为:74.
【点评】本题考查平行线的性质,关键是由三角形的外角性质得到∠CEB=∠1+∠2,判定四边形BDCE是平行四边形,推出∠3=∠CEB.
13.(2025 西乡县校级模拟)如图,摆放着正六边形ABCDEF和正三角形EGH,AC∥HG,则∠DEH= 90° .
【考点】平行线的性质;等边三角形的性质;多边形内角与外角.
【专题】线段、角、相交线与平行线;等腰三角形与直角三角形;正多边形与圆;推理能力.
【答案】90°.
【分析】连接DF,过E作EK∥DF,由正多边形的性质得到FE=ED,∠DEF=∠AFE=120°,判定DF⊥AF,CA⊥AF,推出DF∥AC,得到DF∥GH,EK∥GH,推出∠DEK=∠FDE=30°,∠HEK=∠H,即可求出∠DEH=∠DEK+∠HEK=90°.
【解答】解:连接DF,过E作EK∥DF,
∵六边形ABCDEF是正六边形,
∴FE=ED,∠DEF=∠AFE120°,
∴∠DFE=∠FDE(180°﹣120°)=30°,
∴∠AFD=∠AFE﹣∠DFE=90°,
∴DF⊥AF,
同理:CA⊥AF,
∴DF∥AC,
∵AC∥GH,
∴DF∥GH,
∴EK∥GH,
∴∠DEK=∠FDE=30°,∠HEK=∠H,
∵△EGH是等边三角形,
∴∠H=60°,
∴∠HEK=60°,
∴∠DEH=∠DEK+∠HEK=90°.
故答案为:90°.
【点评】本题考查平行线的性质,等边三角形的性质,多边形的内角和外角,关键是由正六边形的性质判定DF∥GH,得到EK∥GH,由平行线的性质来解决问题.
14.(2025 东台市一模)如图,烧杯内液体表面AB与烧杯下底部CD平行,光线EF从液体中射向空气时发生折射,光线变成FH,点G在射线EF上.已知∠HFB=19°,∠FED=55°,则∠GFH的度数为 36° .
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】36°.
【分析】先根据两直线平行,同位角相等得出∠GFB=∠FED=55°,再根据∠GFH=∠GFB﹣∠HFB计算即可.
【解答】解:∵AB∥CD,∠FED=55°,
∴∠GFB=∠FED=55°,
∵∠HFB=19°,
∴∠GFH=∠GFB﹣∠HFB=55°﹣19°=36°.
故答案为:36°.
【点评】本题考查了平行线的性质,熟练掌握平行线的性质定理是解题的关键.
15.(2025 番禺区二模)图①是用一根吸管吸吮纸杯中的豆浆,图②是其截面图,已知AB∥CD,c表示吸管.若∠1=76°,则∠2= 104 度.
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】104.
【分析】依据题意,由已知条件AB∥CD,可得∠1=∠3=76°,又由于∠2与∠3是邻补角,则可得∠2的度数.
【解答】解:如图所示,
∵AB∥CD,
∴∠1=∠3=76°.
∵∠2与∠3是邻补角,
∴∠2+∠3=180°.
∴∠2=180°﹣∠3=180°﹣76°=104°.
故答案为:104.
【点评】本题考查了平行线的性质及邻补角的性质,需要熟悉角之间的转化是解题的关键.
三.解答题(共5小题)
16.(2025 武汉三模)如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DE∥BA,DF∥CA.
求证:∠FDE=∠A.
【考点】平行线的性质.
【专题】证明题.
【答案】见试题解答内容
【分析】根据平行线的性质证明即可.
【解答】证明:∵DE∥BA,
∴∠FDE=∠BFD;
∵DF∥CA,
∴∠A=∠BFD,
∴∠FDE=∠A.
【点评】本题考查了平行线性质定理:定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.定理2:两条平行线被第三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.定理3:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.
17.(2025 长安区校级模拟)如图,三条直线AB,CD,EF相交于点O,且CD⊥EF,∠AOE=70°,若OG平分∠BOF.求∠DOG的度数.
【考点】垂线;角平分线的定义.
【专题】线段、角、相交线与平行线;推理能力.
【答案】55°.
【分析】根据对顶角相等可得∠BOF=∠AOE=70°,由CD⊥EF可得∠DOF=90°,再根据角平分线的性质求得∠GOF,进而根据∠DOG=∠DOF﹣∠GOF计算即可.
【解答】解:∵三条直线AB,CD,EF相交于点O,∠AOE=70°,
∴∠BOF=∠AOE=70°,
∵CD⊥EF,
∴∠DOF=90°,
∵OG平分∠BOF,
∴,
∴∠DOG=∠DOF﹣∠GOF=90°﹣35°=55°.
【点评】本题考查了几何图形中角的和差计算,对顶角的性质,角平分线的定义,垂线的定义,熟练掌握知识点是解题的关键.
18.(2025 长安区校级模拟)如图,直线AC,BD被直线BC所截,连接AB,CD,BA平分∠CBD,且与线段CD相交于点E,F是线段AC上一点,连接EF.若∠A=∠ABC,∠AFE+∠CBD=180°.求证:EF∥BC.
【考点】平行线的判定.
【专题】线段、角、相交线与平行线;推理能力.
【答案】见解析.
【分析】根据角平分线的定义和平行线的判定定理即可得到结论.
【解答】证明:∵AB平分∠CBD,
∴∠ABD=∠ABC,
∵∠A=∠ABC,
∴∠ABD=∠A,
∴BD∥AC,
∴∠ACB+∠CBD=180°,
∵∠AFE+∠CBD=180°,
∴∠ACB=∠AFE,
∴EF∥BC.
【点评】本题考查了平行线的判定,角平分线的定义,熟练掌握平行线的判定定理是解题的关键.
19.(2025 长安区校级模拟)已知∠ABC=∠ADC,AB∥CD,E为射线BC上一点,AE平分∠BAD.
(1)如图1,当点E在线段BC上时,求证:∠BAE=∠BEA.
(2)如图2,当点E在线段BC延长线上时,连接DE,若∠ADE=3∠CDE,∠AED=60°,求∠CED的度数.
【考点】平行线的判定与性质;三角形内角和定理;三角形的外角性质.
【答案】见试题解答内容
【分析】(1)根据平行线的性质求出∠B+∠C=180°,推出∠C+∠D=180°,根据平行线的判定得出AD∥BC,求出∠DAE=∠BEA即可;
(2)根据∠ADE=3∠CDE,设∠CDE=x°,∠ADE=3x°,∠ADC=2x°,根据平行线的性质得出方程90﹣x+60+3x=180,求出x即可.
【解答】(1)证明:∵AB∥CD,
∴∠B+∠C=180°,
∵∠B=∠D,
∴∠C+∠D=180°,
∴AD∥BC,
∴∠DAE=∠BEA,
∵AE平分∠BAD,
∴∠DAE=∠BAE,
∴∠BAE=∠BEA;
(2)解:∵∠ADE=3∠CDE,设∠CDE=x°,
∴∠ADE=3x°,∠ADC=2x°,
∵AB∥CD,
∴∠BAD+∠ADC=180°,
∴∠DAB=180°﹣2x°,
由(1)可知:∠DAE=∠BAE=∠BEA=90°﹣x°,
∵AD∥BC,
∴∠BED+∠ADE=180°,
∵∠AED=60°,
即90﹣x+60+3x=180,
∴∠CDE=x°=15°,∠ADE=45°,
∵AD∥BC,
∴∠CED=180°﹣∠ADE=135°.
【点评】本题考查了平行线的性质和判定的应用,用了方程的思想,能运用平行线的性质和判定进行推理是解此题的关键.
20.(2025 南昌二模)近年来,中国机器狗技术发展迅速.图1是某一型号的机器狗正常站立时的实物图,图2是它的侧面示意图,机身AD,大腿AB,DE和小腿BC,EF在它们之间的连接处可以转动调节姿态,调节过程中,机身、大腿、小腿的长度都不会发生变化,但位置、及以各接口处为顶点的角的大小可能发生改变.经测量,AD=40cm,AB=DE=BC=EF=20cm.
(1)当机器狗处于正常站立时,机身AD平行于地面CF,∠ABC=∠DEF=120°,机器狗的高度可以看成A,C两点间的距离,求此时机器狗的高度.
(2)图3是机器狗坐下时的实物图,图4是其侧面示意图,此时,小腿EF紧贴地面,AB∥DE,BC∥EF,只调节机身AD与小腿EF所在直线形成的锐角,当其超过65°时,机器狗需要重新调整其他部分参数,才能坐得稳.请你通过推理计算,判断当BC与EF之间的距离为时,要使其坐得稳,该机器狗是否需要调整其他部分参数.
【考点】平行线之间的距离;平行四边形的判定与性质;解直角三角形的应用.
【专题】线段、角、相交线与平行线;等腰三角形与直角三角形;多边形与平行四边形;运算能力;推理能力.
【答案】(1)此时机器狗的高度为;
(2)不需要调整其他部分参数.
【分析】(1)连接AC,过点B作BG⊥AC于点G,则AC=2AG,∠ABG=60°,解直角三角形求出AG的长即可得到答案;
(2)连接BE,过点B作BM⊥EF于点M,可证明四边形ABED是平行四边形.则BE=AD=40cm,BE∥AD.解直角三角形得到∠BEM=60°,即可得到结论.
【解答】解:(1)如图,连接AC,过点B作BG⊥AC于点G,
∵AB=BC=20cm,∠ABC=120°,
∴AC=2AG,∠ABG=60°,
∴,
∴.
答:此时机器狗的高度为;
(2)如图,连接BE,过点B作BM⊥EF于点M,
∵AB∥DE,AB=DE,
∴四边形ABED是平行四边形.
∴BE=AD=40cm,BE∥AD.
∴∠BEF的度数就是直线AD与EF的夹角的度数.
∵.
∴.
∴∠BEM=60°,
∵65°>60°,
∴不需要调整其他部分参数.
【点评】本题主要考查了解直角三角形的实际应用,三线合一定理,平行四边形的性质与判定,正确作出辅助线是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
暑假巩固复习 相交线与平行线
一.选择题(共10小题)
1.(2025 永寿县校级模拟)如图,若AB∥CD,∠1=35°,则∠2=( )
A.145° B.140° C.135° D.130°
2.(2025 昌邑区校级三模)两面镜子AB,BC按如图所示的位置摆放,入射光线OM经过镜子两次反射后的反射光线NO平行于AB,若OM∥BC,则∠B的度数是( )
A.30° B.45° C.60° D.75°
3.(2025 蓬江区校级三模)5G无线网络的稳定运行依托光纤传输系统.如图,光信号在光纤中的传输过程,可看作光信号经过两个平行放置的平面镜进行反射,若∠3=140°,则∠1的度数为( )
A.40° B.30° C.20° D.15°
4.(2025 武安市二模)如图,两只手的食指和拇指在同一平面内,在以下四种摆放方式中,它们构成的一对角可以看成同旁内角的是( )
A.
B.
C.
D.
5.(2025 定西模拟)如图,街道AB与CD平行,∠ABC=130°,则∠BCD等于( )
A.150° B.130° C.120° D.50°
6.(2025 花垣县校级模拟)如图,a∥b,∠1=55°,则∠2的度数是( )
A.135° B.55° C.115° D.125°
7.(2025 孝义市三模)如图,从点光源A发出平行于主光轴的光线,在凸透镜B处折射后经过焦点F1射出,从点光源A发出的光线经过光心O后沿原方向射出,两束光线汇聚于点C.若∠ABF1=160°,∠AOF2=12°.则∠BCO的度数为( )
A.8° B.10° C.12° D.20°
8.(2025 朝阳区校级二模)划船是一项涉及全身的协调运动,正确的划船动作需要保持正确的姿势和体态.如图,AB∥CD,AC∥ED,若∠MDE=136°,则∠FAC的大小为( )
A.44° B.54° C.136° D.46°
9.(2025 二七区校级三模)如图,已知直线a∥b,c⊥a,∠1=35°,则∠2的度数为( )
A.35° B.45° C.55° D.50°
10.(2025 铜陵三模)一等腰三角板和一直尺如图放置,若∠1=60°,则∠2的度数是( )
A.105° B.110° C.115° D.120°
二.填空题(共5小题)
11.(2025 广州)如图,直线AB,CD相交于点O,若∠1=36°,则∠2的度数为 °.
12.(2025 宝安区三模)如图,一束激光PA射入水面,在点A处发生折射,折射光线AB在杯底形成光斑B点.水位下降时,光线PA保持不变,此时光线在点C处发生折射,光斑移动到D点.因水面始终与杯底平行,则折射光线CD∥AB.若∠1=48°,∠2=26°,则∠3的度数为 °.
13.(2025 西乡县校级模拟)如图,摆放着正六边形ABCDEF和正三角形EGH,AC∥HG,则∠DEH= .
14.(2025 东台市一模)如图,烧杯内液体表面AB与烧杯下底部CD平行,光线EF从液体中射向空气时发生折射,光线变成FH,点G在射线EF上.已知∠HFB=19°,∠FED=55°,则∠GFH的度数为 .
15.(2025 番禺区二模)图①是用一根吸管吸吮纸杯中的豆浆,图②是其截面图,已知AB∥CD,c表示吸管.若∠1=76°,则∠2= 度.
三.解答题(共5小题)
16.(2025 武汉三模)如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DE∥BA,DF∥CA.
求证:∠FDE=∠A.
17.(2025 长安区校级模拟)如图,三条直线AB,CD,EF相交于点O,且CD⊥EF,∠AOE=70°,若OG平分∠BOF.求∠DOG的度数.
18.(2025 长安区校级模拟)如图,直线AC,BD被直线BC所截,连接AB,CD,BA平分∠CBD,且与线段CD相交于点E,F是线段AC上一点,连接EF.若∠A=∠ABC,∠AFE+∠CBD=180°.求证:EF∥BC.
19.(2025 长安区校级模拟)已知∠ABC=∠ADC,AB∥CD,E为射线BC上一点,AE平分∠BAD.
(1)如图1,当点E在线段BC上时,求证:∠BAE=∠BEA.
(2)如图2,当点E在线段BC延长线上时,连接DE,若∠ADE=3∠CDE,∠AED=60°,求∠CED的度数.
20.(2025 南昌二模)近年来,中国机器狗技术发展迅速.图1是某一型号的机器狗正常站立时的实物图,图2是它的侧面示意图,机身AD,大腿AB,DE和小腿BC,EF在它们之间的连接处可以转动调节姿态,调节过程中,机身、大腿、小腿的长度都不会发生变化,但位置、及以各接口处为顶点的角的大小可能发生改变.经测量,AD=40cm,AB=DE=BC=EF=20cm.
(1)当机器狗处于正常站立时,机身AD平行于地面CF,∠ABC=∠DEF=120°,机器狗的高度可以看成A,C两点间的距离,求此时机器狗的高度.
(2)图3是机器狗坐下时的实物图,图4是其侧面示意图,此时,小腿EF紧贴地面,AB∥DE,BC∥EF,只调节机身AD与小腿EF所在直线形成的锐角,当其超过65°时,机器狗需要重新调整其他部分参数,才能坐得稳.请你通过推理计算,判断当BC与EF之间的距离为时,要使其坐得稳,该机器狗是否需要调整其他部分参数.
暑假巩固复习 相交线与平行线
参考答案与试题解析
一.选择题(共10小题)
1.(2025 永寿县校级模拟)如图,若AB∥CD,∠1=35°,则∠2=( )
A.145° B.140° C.135° D.130°
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】A
【分析】根据两直线平行,同位角相等得出∠1=∠3=35°,即可求出∠2的度数.
【解答】解:如图,
∵AB∥CD,
∴∠1=∠3,
∵∠1=35°,
∴∠3=35°,
∴∠2=180°﹣∠3=180°﹣35°=145°,
故选:A.
【点评】本题考查了平行线的性质,熟练掌握两直线平行,同位角相等是解题的关键.
2.(2025 昌邑区校级三模)两面镜子AB,BC按如图所示的位置摆放,入射光线OM经过镜子两次反射后的反射光线NO平行于AB,若OM∥BC,则∠B的度数是( )
A.30° B.45° C.60° D.75°
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】C
【分析】根据已知条件,得到∠AMO=∠BMN,∠MNB=∠CNO,由平行线的性质得到∠AMO=∠MBC,∠MBC=∠CNO,∠MNO=∠BMN,推出∠B=∠MNB=∠MNO=∠CNO,再根据∠MNB+∠MNO+∠CNO=180°,进行求解即可.
【解答】解:根据题意得到∠AMO=∠BMN,∠MNB=∠CNO,
∵OM∥BC,NO∥AB,
∴∠AMO=∠B,∠MBC=∠CNO,∠MNO=∠BMN,
∴∠B=∠MNB=∠MNO=∠CNO,
∵∠MNB+∠MNO+∠CNO=180°,
∴∠B=∠MNB=∠MNO=∠CNO=180°÷3=60°,
即∠B的度数是60°,
故选:C.
【点评】本题考查平行线的性质,关键是平行线性质的熟练掌握.
3.(2025 蓬江区校级三模)5G无线网络的稳定运行依托光纤传输系统.如图,光信号在光纤中的传输过程,可看作光信号经过两个平行放置的平面镜进行反射,若∠3=140°,则∠1的度数为( )
A.40° B.30° C.20° D.15°
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】C
【分析】由光的反射定律可知∠5=∠4,∠1=∠2,再由平行线的性质推出∠4=∠2,从而得出结论.
【解答】解:如图:
由光的反射定律可知∠5=∠4,
∵∠3=140°,
∴∠5=∠4(180°﹣140°)=20°,
∵两平面镜平行,
∴∠4=∠2=20°(两直线平行,内错角相等),
由光的反射定律可知∠1=∠2=20°,
故选:C.
【点评】本题考查平行线的性质,解题的关键是由平行线的性质推出∠4=∠2.
4.(2025 武安市二模)如图,两只手的食指和拇指在同一平面内,在以下四种摆放方式中,它们构成的一对角可以看成同旁内角的是( )
A.
B.
C.
D.
【考点】同位角、内错角、同旁内角.
【专题】线段、角、相交线与平行线;运算能力.
【答案】A
【分析】根据同位角,同旁内角,内错角的定义,进行判断即可.
【解答】解:根据相关概念逐项分析判断如下:
A、可以看成同旁内角,符合题意;
B、可以看成内错角,不符合题意;
C、不是内错角,不是同位角,不是同旁内角,不符合题意;
D、可以看成同位角,不符合题意;
故选:A.
【点评】本题考查三线八角.熟练掌握同位角,同旁内角,内错角的定义是解题的关键.
5.(2025 定西模拟)如图,街道AB与CD平行,∠ABC=130°,则∠BCD等于( )
A.150° B.130° C.120° D.50°
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】B
【分析】由街道AB与CD平行,∠ABC=130°,根据两直线平行,内错角相等,即可求得∠BCD的度数.
【解答】解:∵AB∥CD,∠ABC=130°,
∴∠BCD=∠ABC=130°.
故选:B.
【点评】此题考查了平行线的性质.此题比较简单,注意掌握两直线平行,内错角相等定理的应用,注意数形结合思想的应用.
6.(2025 花垣县校级模拟)如图,a∥b,∠1=55°,则∠2的度数是( )
A.135° B.55° C.115° D.125°
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;运算能力.
【答案】D
【分析】根据平行线的性质求出∠3的度数,再由平角的定义即可得到答案.
【解答】解;如图所示,
∵a∥b,∠1=55°,
平行线的性质求出∠3的度数,
∴∠3=∠1=55°,
∴∠2=180°﹣∠3=125°.
故选:D.
【点评】本题主要考查了平行线的性质,平角的定义,正确记忆相关知识点是解题关键.
7.(2025 孝义市三模)如图,从点光源A发出平行于主光轴的光线,在凸透镜B处折射后经过焦点F1射出,从点光源A发出的光线经过光心O后沿原方向射出,两束光线汇聚于点C.若∠ABF1=160°,∠AOF2=12°.则∠BCO的度数为( )
A.8° B.10° C.12° D.20°
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】A
【分析】由平行线的性质得出∠BF1O=180°﹣∠ABF1=20°,由对顶角相等得出∠COF1=∠AOF2=12°,最后由三角形外角的性质即可得出答案.
【解答】解:∵AB∥OF1,∠ABF1=160°,
∴∠BF1O+∠ABF1=180°,
∴∠BF1O=180°﹣∠ABF1=20°,
∵∠COF1=∠AOF2=12°,
∴∠BCO=∠BF1O﹣∠COF1=20°﹣12°=8°,
故选:A.
【点评】本题考查了平行线的性质,掌握对顶角相等、三角形外角的性质是解题的关键.
8.(2025 朝阳区校级二模)划船是一项涉及全身的协调运动,正确的划船动作需要保持正确的姿势和体态.如图,AB∥CD,AC∥ED,若∠MDE=136°,则∠FAC的大小为( )
A.44° B.54° C.136° D.46°
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】A
【分析】根据平行线的性质定理求解即可.
【解答】解:∵∠MDE=136°,
∴∠CDE=180°﹣136°=44°,
∵AC∥ED,
∴∠CDE=∠ACD=44°,
∵AB∥CD,
∴∠ACD=∠FAC=44°,
故选:A.
【点评】此题考查了平行线的性质,熟记“两直线平行,内错角相等”是解题的关键.
9.(2025 二七区校级三模)如图,已知直线a∥b,c⊥a,∠1=35°,则∠2的度数为( )
A.35° B.45° C.55° D.50°
【考点】平行线的性质;三角形内角和定理;余角和补角;对顶角、邻补角;垂线.
【专题】线段、角、相交线与平行线;推理能力.
【答案】C
【分析】根据题意得出c⊥b,又∠1=∠3=35°,即可求解.
【解答】解:∵a∥b,c⊥a,
∴c⊥b,
∴∠ABC=90°,
∵∠1=35°,
∴∠1=∠3=35°,
∴∠2=90°﹣35°=55°,
故选:C.
【点评】本题考查了平行线的性质,对顶角、邻补角,三角形内角和定理,垂线,余角和补角,熟记以上知识并准确识图是解题的关键.
10.(2025 铜陵三模)一等腰三角板和一直尺如图放置,若∠1=60°,则∠2的度数是( )
A.105° B.110° C.115° D.120°
【考点】平行线的性质;余角和补角.
【专题】线段、角、相交线与平行线;推理能力.
【答案】A
【分析】结合等腰直角三角形性质,先由三角形内角和定理求出∠3,再由平行线性质及邻补角定义,数形结合即可得到答案.
【解答】解:如图所示:
由三角形内角和定理可知∠3=180°﹣60°﹣45°=75°,
∴由平行线性质可知∠4=∠3=75°(两直线平行,同位角相等),
∴∠2=180°﹣∠4=180°﹣75°=105°,
故选:A.
【点评】本题考查平行线的性质,余角和补角,熟练掌握相关几何性质,数形结合是解决问题的关键.
二.填空题(共5小题)
11.(2025 广州)如图,直线AB,CD相交于点O,若∠1=36°,则∠2的度数为 144 °.
【考点】对顶角、邻补角.
【专题】线段、角、相交线与平行线;几何直观;运算能力.
【答案】144.
【分析】根据邻补角的定义进行计算即可.
【解答】解:∵∠1+∠2=180°,而∠1=36°,
∴∠2=180°﹣36°=144°,
故答案为:144.
【点评】本题考查对顶角、邻补角,理解邻补角的定义是正确解答的关键.
12.(2025 宝安区三模)如图,一束激光PA射入水面,在点A处发生折射,折射光线AB在杯底形成光斑B点.水位下降时,光线PA保持不变,此时光线在点C处发生折射,光斑移动到D点.因水面始终与杯底平行,则折射光线CD∥AB.若∠1=48°,∠2=26°,则∠3的度数为 74 °.
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】见试题解答内容
【分析】由三角形的外角性质求出∠CEB=74°,判定四边形BDCE是平行四边形,推出∠3=∠CEB=74°.
【解答】解:∵∠1=48°,∠2=26°,
∴∠CEB=∠1+∠2=74°,
∵EC∥BD,BE∥CD,
∴四边形BDCE是平行四边形,
∴∠3=∠CEB=74°.
故答案为:74.
【点评】本题考查平行线的性质,关键是由三角形的外角性质得到∠CEB=∠1+∠2,判定四边形BDCE是平行四边形,推出∠3=∠CEB.
13.(2025 西乡县校级模拟)如图,摆放着正六边形ABCDEF和正三角形EGH,AC∥HG,则∠DEH= 90° .
【考点】平行线的性质;等边三角形的性质;多边形内角与外角.
【专题】线段、角、相交线与平行线;等腰三角形与直角三角形;正多边形与圆;推理能力.
【答案】90°.
【分析】连接DF,过E作EK∥DF,由正多边形的性质得到FE=ED,∠DEF=∠AFE=120°,判定DF⊥AF,CA⊥AF,推出DF∥AC,得到DF∥GH,EK∥GH,推出∠DEK=∠FDE=30°,∠HEK=∠H,即可求出∠DEH=∠DEK+∠HEK=90°.
【解答】解:连接DF,过E作EK∥DF,
∵六边形ABCDEF是正六边形,
∴FE=ED,∠DEF=∠AFE120°,
∴∠DFE=∠FDE(180°﹣120°)=30°,
∴∠AFD=∠AFE﹣∠DFE=90°,
∴DF⊥AF,
同理:CA⊥AF,
∴DF∥AC,
∵AC∥GH,
∴DF∥GH,
∴EK∥GH,
∴∠DEK=∠FDE=30°,∠HEK=∠H,
∵△EGH是等边三角形,
∴∠H=60°,
∴∠HEK=60°,
∴∠DEH=∠DEK+∠HEK=90°.
故答案为:90°.
【点评】本题考查平行线的性质,等边三角形的性质,多边形的内角和外角,关键是由正六边形的性质判定DF∥GH,得到EK∥GH,由平行线的性质来解决问题.
14.(2025 东台市一模)如图,烧杯内液体表面AB与烧杯下底部CD平行,光线EF从液体中射向空气时发生折射,光线变成FH,点G在射线EF上.已知∠HFB=19°,∠FED=55°,则∠GFH的度数为 36° .
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】36°.
【分析】先根据两直线平行,同位角相等得出∠GFB=∠FED=55°,再根据∠GFH=∠GFB﹣∠HFB计算即可.
【解答】解:∵AB∥CD,∠FED=55°,
∴∠GFB=∠FED=55°,
∵∠HFB=19°,
∴∠GFH=∠GFB﹣∠HFB=55°﹣19°=36°.
故答案为:36°.
【点评】本题考查了平行线的性质,熟练掌握平行线的性质定理是解题的关键.
15.(2025 番禺区二模)图①是用一根吸管吸吮纸杯中的豆浆,图②是其截面图,已知AB∥CD,c表示吸管.若∠1=76°,则∠2= 104 度.
【考点】平行线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】104.
【分析】依据题意,由已知条件AB∥CD,可得∠1=∠3=76°,又由于∠2与∠3是邻补角,则可得∠2的度数.
【解答】解:如图所示,
∵AB∥CD,
∴∠1=∠3=76°.
∵∠2与∠3是邻补角,
∴∠2+∠3=180°.
∴∠2=180°﹣∠3=180°﹣76°=104°.
故答案为:104.
【点评】本题考查了平行线的性质及邻补角的性质,需要熟悉角之间的转化是解题的关键.
三.解答题(共5小题)
16.(2025 武汉三模)如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DE∥BA,DF∥CA.
求证:∠FDE=∠A.
【考点】平行线的性质.
【专题】证明题.
【答案】见试题解答内容
【分析】根据平行线的性质证明即可.
【解答】证明:∵DE∥BA,
∴∠FDE=∠BFD;
∵DF∥CA,
∴∠A=∠BFD,
∴∠FDE=∠A.
【点评】本题考查了平行线性质定理:定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.定理2:两条平行线被第三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.定理3:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.
17.(2025 长安区校级模拟)如图,三条直线AB,CD,EF相交于点O,且CD⊥EF,∠AOE=70°,若OG平分∠BOF.求∠DOG的度数.
【考点】垂线;角平分线的定义.
【专题】线段、角、相交线与平行线;推理能力.
【答案】55°.
【分析】根据对顶角相等可得∠BOF=∠AOE=70°,由CD⊥EF可得∠DOF=90°,再根据角平分线的性质求得∠GOF,进而根据∠DOG=∠DOF﹣∠GOF计算即可.
【解答】解:∵三条直线AB,CD,EF相交于点O,∠AOE=70°,
∴∠BOF=∠AOE=70°,
∵CD⊥EF,
∴∠DOF=90°,
∵OG平分∠BOF,
∴,
∴∠DOG=∠DOF﹣∠GOF=90°﹣35°=55°.
【点评】本题考查了几何图形中角的和差计算,对顶角的性质,角平分线的定义,垂线的定义,熟练掌握知识点是解题的关键.
18.(2025 长安区校级模拟)如图,直线AC,BD被直线BC所截,连接AB,CD,BA平分∠CBD,且与线段CD相交于点E,F是线段AC上一点,连接EF.若∠A=∠ABC,∠AFE+∠CBD=180°.求证:EF∥BC.
【考点】平行线的判定.
【专题】线段、角、相交线与平行线;推理能力.
【答案】见解析.
【分析】根据角平分线的定义和平行线的判定定理即可得到结论.
【解答】证明:∵AB平分∠CBD,
∴∠ABD=∠ABC,
∵∠A=∠ABC,
∴∠ABD=∠A,
∴BD∥AC,
∴∠ACB+∠CBD=180°,
∵∠AFE+∠CBD=180°,
∴∠ACB=∠AFE,
∴EF∥BC.
【点评】本题考查了平行线的判定,角平分线的定义,熟练掌握平行线的判定定理是解题的关键.
19.(2025 长安区校级模拟)已知∠ABC=∠ADC,AB∥CD,E为射线BC上一点,AE平分∠BAD.
(1)如图1,当点E在线段BC上时,求证:∠BAE=∠BEA.
(2)如图2,当点E在线段BC延长线上时,连接DE,若∠ADE=3∠CDE,∠AED=60°,求∠CED的度数.
【考点】平行线的判定与性质;三角形内角和定理;三角形的外角性质.
【答案】见试题解答内容
【分析】(1)根据平行线的性质求出∠B+∠C=180°,推出∠C+∠D=180°,根据平行线的判定得出AD∥BC,求出∠DAE=∠BEA即可;
(2)根据∠ADE=3∠CDE,设∠CDE=x°,∠ADE=3x°,∠ADC=2x°,根据平行线的性质得出方程90﹣x+60+3x=180,求出x即可.
【解答】(1)证明:∵AB∥CD,
∴∠B+∠C=180°,
∵∠B=∠D,
∴∠C+∠D=180°,
∴AD∥BC,
∴∠DAE=∠BEA,
∵AE平分∠BAD,
∴∠DAE=∠BAE,
∴∠BAE=∠BEA;
(2)解:∵∠ADE=3∠CDE,设∠CDE=x°,
∴∠ADE=3x°,∠ADC=2x°,
∵AB∥CD,
∴∠BAD+∠ADC=180°,
∴∠DAB=180°﹣2x°,
由(1)可知:∠DAE=∠BAE=∠BEA=90°﹣x°,
∵AD∥BC,
∴∠BED+∠ADE=180°,
∵∠AED=60°,
即90﹣x+60+3x=180,
∴∠CDE=x°=15°,∠ADE=45°,
∵AD∥BC,
∴∠CED=180°﹣∠ADE=135°.
【点评】本题考查了平行线的性质和判定的应用,用了方程的思想,能运用平行线的性质和判定进行推理是解此题的关键.
20.(2025 南昌二模)近年来,中国机器狗技术发展迅速.图1是某一型号的机器狗正常站立时的实物图,图2是它的侧面示意图,机身AD,大腿AB,DE和小腿BC,EF在它们之间的连接处可以转动调节姿态,调节过程中,机身、大腿、小腿的长度都不会发生变化,但位置、及以各接口处为顶点的角的大小可能发生改变.经测量,AD=40cm,AB=DE=BC=EF=20cm.
(1)当机器狗处于正常站立时,机身AD平行于地面CF,∠ABC=∠DEF=120°,机器狗的高度可以看成A,C两点间的距离,求此时机器狗的高度.
(2)图3是机器狗坐下时的实物图,图4是其侧面示意图,此时,小腿EF紧贴地面,AB∥DE,BC∥EF,只调节机身AD与小腿EF所在直线形成的锐角,当其超过65°时,机器狗需要重新调整其他部分参数,才能坐得稳.请你通过推理计算,判断当BC与EF之间的距离为时,要使其坐得稳,该机器狗是否需要调整其他部分参数.
【考点】平行线之间的距离;平行四边形的判定与性质;解直角三角形的应用.
【专题】线段、角、相交线与平行线;等腰三角形与直角三角形;多边形与平行四边形;运算能力;推理能力.
【答案】(1)此时机器狗的高度为;
(2)不需要调整其他部分参数.
【分析】(1)连接AC,过点B作BG⊥AC于点G,则AC=2AG,∠ABG=60°,解直角三角形求出AG的长即可得到答案;
(2)连接BE,过点B作BM⊥EF于点M,可证明四边形ABED是平行四边形.则BE=AD=40cm,BE∥AD.解直角三角形得到∠BEM=60°,即可得到结论.
【解答】解:(1)如图,连接AC,过点B作BG⊥AC于点G,
∵AB=BC=20cm,∠ABC=120°,
∴AC=2AG,∠ABG=60°,
∴,
∴.
答:此时机器狗的高度为;
(2)如图,连接BE,过点B作BM⊥EF于点M,
∵AB∥DE,AB=DE,
∴四边形ABED是平行四边形.
∴BE=AD=40cm,BE∥AD.
∴∠BEF的度数就是直线AD与EF的夹角的度数.
∵.
∴.
∴∠BEM=60°,
∵65°>60°,
∴不需要调整其他部分参数.
【点评】本题主要考查了解直角三角形的实际应用,三线合一定理,平行四边形的性质与判定,正确作出辅助线是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
