第十九章 一次函数(暑假复习.含解析)-2024-2025学年八年级下册数学人教版
文档属性
| 名称 | 第十九章 一次函数(暑假复习.含解析)-2024-2025学年八年级下册数学人教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-06 15:06:31 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
暑假巩固复习 一次函数
一.选择题(共10小题)
1.(2025 永寿县校级模拟)已知A(4,a)和B(﹣1,b)是一次函数y=kx﹣4(k≠0)图象上的两点,若a<b,则该一次函数的图象还可能经过的点是( )
A.(﹣4,0) B.(4,0) C.(0,4) D.(1,﹣3)
2.(2025 广州)如图,在平面直角坐标系中,点A(﹣3,1),点B(﹣1,1),若将直线y=x向上平移d个单位长度后与线段AB有交点,则d的取值范围是( )
A.﹣3≤d≤﹣1 B.1≤d≤3 C.﹣4≤d≤﹣2 D.2≤d≤4
3.(2025 定西模拟)下列四点中,在函数y=3x+2的图象上的点是( )
A.(﹣1,1) B.(﹣1,﹣1) C.(2,0) D.(0,﹣1.5)
4.(2025 湖南模拟)已知A(m,﹣1),B(n,2)是一次函数y=﹣2x+b图象上的两点,则m和n的大小关系是( )
A.m=n B.m≤n C.m<n D.m>n
5.(2025 许昌二模)甲无人机从地面起飞,乙无人机从距离地面20m高的楼顶起飞,两架无人机同时匀速上升10s.甲、乙两架无人机所在的位置距离地面的高度y(单位:m)与无人机上升的时间x(单位:s)之间的关系如图所示.下列说法:①甲无人机上升的速度为8m/s;②5s时,两架无人机都上升了40m;③8s时,乙无人机距离地面的高度是64m;④10s时,两架无人机的高度差为20m.正确的是( )
A.①③ B.①④ C.②③ D.②④
6.(2025 旬邑县校级模拟)在同一平面直角坐标系中,函数y=mx和y=﹣mx+m(m为常数,m≠0)的图象可能是( )
A. B.
C. D.
7.(2025 碧江区 校级模拟)已知一次函数y=kx+b(k≠0),如下表是x与y的一些对应数值,则下列结论中正确的是( )
x … ﹣1.5 0 1 2 …
y … 6 3 1 0 ﹣1 …
A.y随x的增大而增大
B.与y轴的交点是(0,﹣3)
C.关于x的方程kx+b=1的解是x=1
D.图象与x轴的交点是
8.(2025 蓬江区校级一模)我国著名数学家华罗庚说过“数缺形时少直观,形少数时难入微”,数形结合是解决数学问题的重要思想方法.为了了解关于x的不等式﹣x+2>mx+n的解集,某同学绘制了y=﹣x+2与y=mx+n(m,n为常数,m≠0)的函数图象如图所示,通过观察图象发现,该不等式的解集在数轴上表示正确的是( )
A.
B.
C.
D.
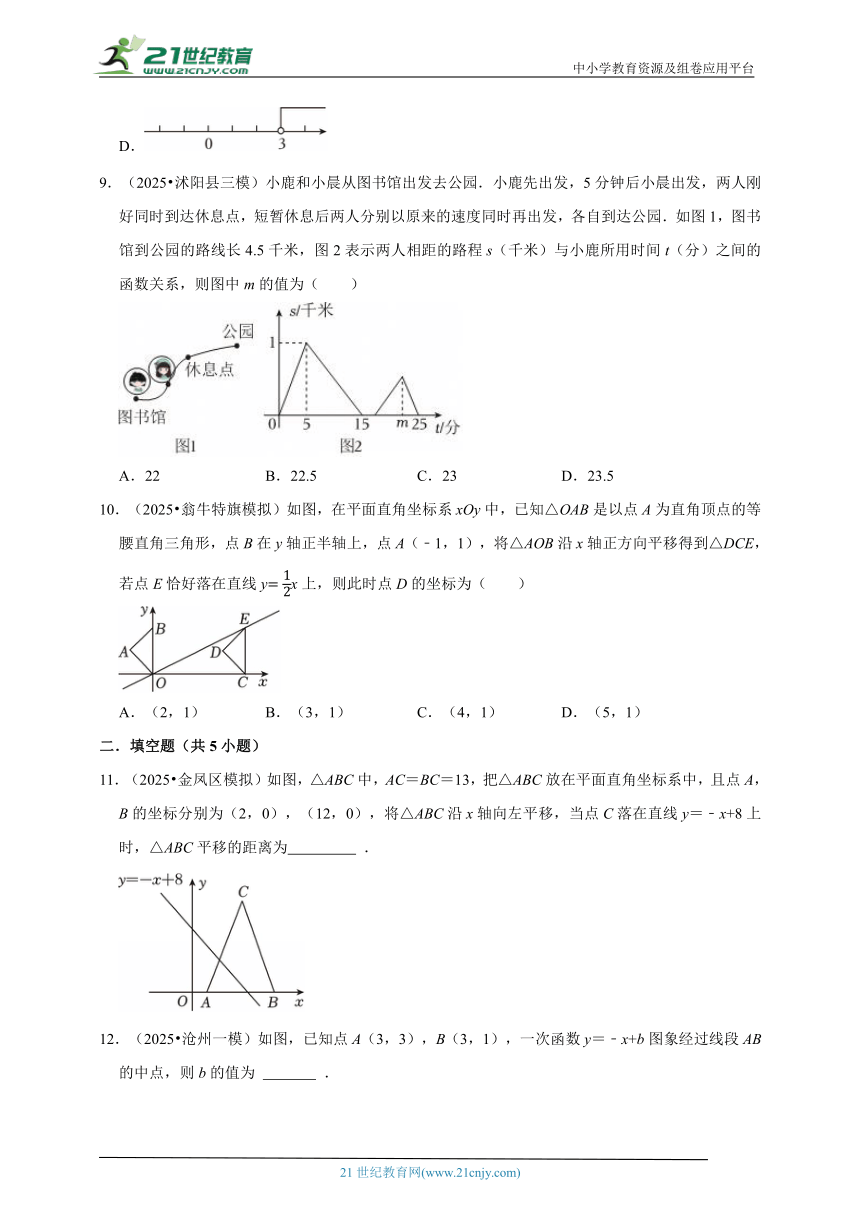
9.(2025 沭阳县三模)小鹿和小晨从图书馆出发去公园.小鹿先出发,5分钟后小晨出发,两人刚好同时到达休息点,短暂休息后两人分别以原来的速度同时再出发,各自到达公园.如图1,图书馆到公园的路线长4.5千米,图2表示两人相距的路程s(千米)与小鹿所用时间t(分)之间的函数关系,则图中m的值为( )
A.22 B.22.5 C.23 D.23.5
10.(2025 翁牛特旗模拟)如图,在平面直角坐标系xOy中,已知△OAB是以点A为直角顶点的等腰直角三角形,点B在y轴正半轴上,点A(﹣1,1),将△AOB沿x轴正方向平移得到△DCE,若点E恰好落在直线yx上,则此时点D的坐标为( )
A.(2,1) B.(3,1) C.(4,1) D.(5,1)
二.填空题(共5小题)
11.(2025 金凤区模拟)如图,△ABC中,AC=BC=13,把△ABC放在平面直角坐标系中,且点A,B的坐标分别为(2,0),(12,0),将△ABC沿x轴向左平移,当点C落在直线y=﹣x+8上时,△ABC平移的距离为 .
12.(2025 沧州一模)如图,已知点A(3,3),B(3,1),一次函数y=﹣x+b图象经过线段AB的中点,则b的值为 .
13.(2025 白城模拟)关于函数y=(k+1)x+2k,给出下列结论:①当k≠﹣1时,此函数是一次函数;②无论k为何值,函数图象必经过点(﹣2,﹣2);③已知点A(1,2),B(2,3),若函数图象与线段AB始终有交点,则k的取值范围是;④已知点C(x1,y1),D(x2,y2)是该函数图象上的任意两点,且(x1﹣x2)(y1﹣y2)>0恒成立,则图象必经过第二、第四象限.其中正确的是 .(写所有正确的结论的序号)
14.(2025 越秀区校级二模)甲、乙两人在一次赛跑中,路程s(米)与时间t(秒)的关系如图所示.当第一个人到达终点时,第二个人距离终点还剩 米.
15.(2025 陇南模拟)已知一次函数y=kx+b与x轴的交点坐标的横坐标是3,且平行于函数y=﹣3x,那么这个一次函数解析式是 .
三.解答题(共5小题)
16.(2025 前进区校级二模)某商场准备购进A和B两种款式的书包,每个A款式书包比B款式书包的进价多25元,用20000元购进A款式书包的数量与用15000元购进B款式书包的数量相同,请解决下列问题:
(1)A款式书包和B款式书包每个的进价各是多少元?
(2)若每个A款式书包的售价为140元,每个B款式书包的售价为100元,商场决定同时购A款式书包、B款式书包共500个,且全部售出,请求出所获利润y(单位:元)与A款式书包的数量x(单位:个)的函数关系式,若商场用不低于40000元且不高于40250元的资金购进A和B两种款式的书包,则有几种购买方案?
(3)在(2)的条件下,商场用获得的最大利润的全部用于福利院的慈善,其中购买文具花费915元,其余部分全部再次购进A、B两种款式的书包送给福利院,请直接写出捐赠A款式书包、B款式书包各是多少个?
17.(2025 永寿县校级模拟)随着年龄的增长,人体的代谢能力下降,心脏的收缩力也会减弱,再加上血管的硬化和肌肉组织的流失,会导致最大心率降低.研究发现,最大心率y(次/分钟)是年龄x(岁)的一次函数.已知15岁时的最大心率为205次/分钟,36岁时的最大心率为184次/分钟.
(1)求y与x之间的函数表达式;
(2)燃烧脂肪时运动心率为最大心率的60%~70%,已知小丽燃烧脂肪时的运动心率最大为140次/分钟,求小丽的年龄.
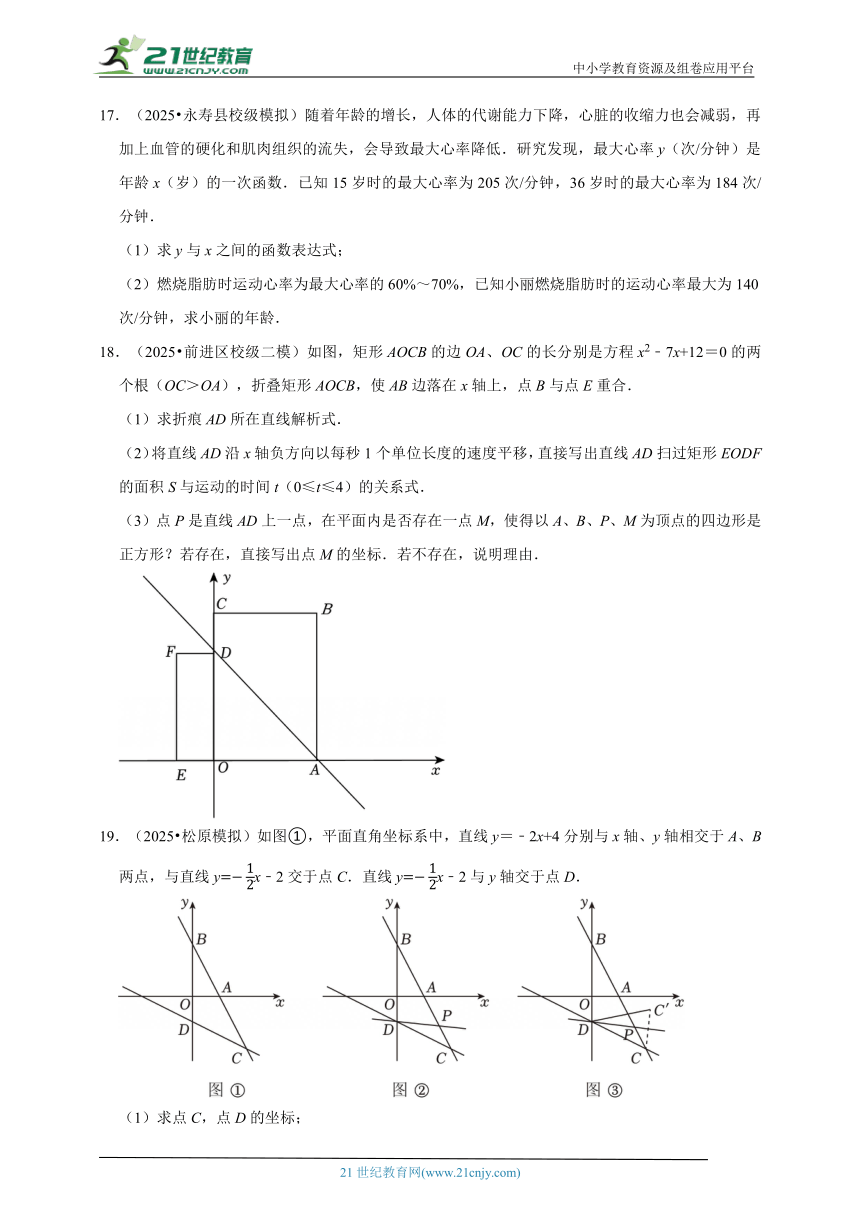
18.(2025 前进区校级二模)如图,矩形AOCB的边OA、OC的长分别是方程x2﹣7x+12=0的两个根(OC>OA),折叠矩形AOCB,使AB边落在x轴上,点B与点E重合.
(1)求折痕AD所在直线解析式.
(2)将直线AD沿x轴负方向以每秒1个单位长度的速度平移,直接写出直线AD扫过矩形EODF的面积S与运动的时间t(0≤t≤4)的关系式.
(3)点P是直线AD上一点,在平面内是否存在一点M,使得以A、B、P、M为顶点的四边形是正方形?若存在,直接写出点M的坐标.若不存在,说明理由.
19.(2025 松原模拟)如图①,平面直角坐标系中,直线y=﹣2x+4分别与x轴、y轴相交于A、B两点,与直线yx﹣2交于点C.直线yx﹣2与y轴交于点D.
(1)求点C,点D的坐标;
(2)如图②,P为直线BC上的一个动点,当S△PBD,求点P坐标;
(3)如图③,P为线段BC上的一个动点,点C关于直线DP的对称点为C′,当C′恰好落在x轴上时,直接写出点P的坐标.
20.(2025 西湖区二模)小敏和小慧去西湖风景区游玩,约好在少年宫广场见面.如图1,A地、B地、少年宫广场在一条直线上.小敏从A地出发,先匀速步行至车站,再坐公交车前往少年宫广场.同时,小慧从B地出发,骑车去少年宫广场,平均速度为200米/分钟.两人距离A地的路程s(米)和所经过的时间t(分)之间的函数关系如图2所示.(公交车的停车时间忽略不计)
(1)求公交车的平均速度.
(2)求同时出发后,经过多少时间小敏追上小慧.
(3)在小敏坐公交车的过程中,当她与小慧相距400米时,求t的值.
暑假巩固复习 一次函数
参考答案与试题解析
一.选择题(共10小题)
1.(2025 永寿县校级模拟)已知A(4,a)和B(﹣1,b)是一次函数y=kx﹣4(k≠0)图象上的两点,若a<b,则该一次函数的图象还可能经过的点是( )
A.(﹣4,0) B.(4,0) C.(0,4) D.(1,﹣3)
【考点】一次函数与一元一次不等式.
【答案】A
【分析】利用一次函数的增减性得到k<0,然后分别把四个选项的点的坐标代入解析式求得k的值,即可判断.
【解答】解:∵A(4,a)和B(﹣1,b)是一次函数y=kx﹣4(k≠0)图象上的两点,且a<b,
∴y随x的增大而减小,
∴k<0,
A、将(﹣4,0)代入y=kx﹣4得,﹣4k﹣4=0,
∴k=﹣1<0,符合题意;
B、将(4,0)代入y=kx﹣4得,4k﹣4=0,
∴k=1>0,不符合题意;
C、x=0时,y=kx﹣4=﹣4,
∴(0,﹣4)在一次函数y=kx﹣4(k≠0)图象上,故不符合题意;
D、将(1,﹣3)代入y=kx﹣4得,k﹣4=﹣3,
∴k=1>0,不符合题意;
故选:A.
【点评】本题考查一次函数的性质,一次函数图象上点的坐标特征,解题的关键是熟练掌握基本知识,属于中考常考题型.
2.(2025 广州)如图,在平面直角坐标系中,点A(﹣3,1),点B(﹣1,1),若将直线y=x向上平移d个单位长度后与线段AB有交点,则d的取值范围是( )
A.﹣3≤d≤﹣1 B.1≤d≤3 C.﹣4≤d≤﹣2 D.2≤d≤4
【考点】一次函数图象与几何变换;正比例函数的性质.
【专题】一次函数及其应用;运算能力;应用意识.
【答案】D
【分析】求得平移后的解析式为y=x+d,分别代入A、B的坐标,求得对应的d的值,根据题意得到2≤d≤4.
【解答】解:把直线y=x向上平移d个单位长度后得到y=x+d,
若直线过A(﹣3,1),则﹣3+d=1,解得d=4,
若直线过B(﹣1,1),则﹣1+d=1,解得d=2,
∴若将直线y=x向上平移d个单位长度后与线段AB有交点,则2≤d≤4,
故选:D.
【点评】本题考查了一次函数图象与几何变换,一次函数的性质,根据题意列出关于d的不等式组是解题的关键.
3.(2025 定西模拟)下列四点中,在函数y=3x+2的图象上的点是( )
A.(﹣1,1) B.(﹣1,﹣1) C.(2,0) D.(0,﹣1.5)
【考点】一次函数图象上点的坐标特征.
【专题】计算题.
【答案】B
【分析】只要把点的坐标代入一次函数的解析式,若左边=右边,则点在函数的图象上,反之就不在函数的图象上,代入检验即可.
【解答】解:A、把(﹣1,1)代入y=3x+2得:左边=1,右边=3×(﹣1)+2=﹣1,左边≠右边,故A选项错误;
B、把(﹣1,﹣1)代入y=3x+2得:左边=﹣1,右边=3×(﹣1)+2=﹣1,左边=右边,故B选项正确;
C、把(2,0)代入y=3x+2得:左边=0,右边=3×2+2=8,左边≠右边,故C选项错误;
D、把(0,﹣1.5)代入y=3x+2得:左边=﹣1.5,右边=3×0+2=2,左边≠右边,故D选项错误.
故选:B.
【点评】本题主要考查对一次函数图象上点的坐标特征的理解和掌握,能根据点的坐标判断是否在函数的图象上是解此题的关键.
4.(2025 湖南模拟)已知A(m,﹣1),B(n,2)是一次函数y=﹣2x+b图象上的两点,则m和n的大小关系是( )
A.m=n B.m≤n C.m<n D.m>n
【考点】一次函数与一元一次不等式.
【专题】一次函数及其应用;运算能力.
【答案】D
【分析】根据一次函数的增减性即可判断即可.
【解答】解:∵k=﹣2<0,
∴一次函数y=﹣2x+b中y随x的增大而减小,
∵﹣1<2,
∴m>n,
故选:D.
【点评】本题考查了一次函数图象上点的坐标特征,掌握一次函数图象上点的坐标特征是解题的关键.
5.(2025 许昌二模)甲无人机从地面起飞,乙无人机从距离地面20m高的楼顶起飞,两架无人机同时匀速上升10s.甲、乙两架无人机所在的位置距离地面的高度y(单位:m)与无人机上升的时间x(单位:s)之间的关系如图所示.下列说法:①甲无人机上升的速度为8m/s;②5s时,两架无人机都上升了40m;③8s时,乙无人机距离地面的高度是64m;④10s时,两架无人机的高度差为20m.正确的是( )
A.①③ B.①④ C.②③ D.②④
【考点】一次函数的应用;有理数的加减混合运算.
【专题】一次函数及其应用;运算能力.
【答案】B
【分析】根据题意和函数图象中的数据,可以计算出甲、乙两架无人机的速度,然后即可判断各个选项中的说法是否正确.
【解答】解:根据题意和函数图象中的数据逐项分析判断如下:
甲无人机上升的速度为40÷5=8(m/s),故①正确;
5s时,甲、乙两架无人机距离底面的高度都为40m,则甲无人机上升了40m,乙无人机上升了40﹣20=20m,故②错误;
乙无人机的速度为:(40﹣20)÷5=4(m/s),
∴8s时,乙无人机距离地面的高度是20+4×8=52(m),故③错误;
10s时,两架无人机的高度差为:(8×10)﹣(20+4×10)=20(m),故④正确;
故选:B.
【点评】本题主要考查了从函数图象获取信息,熟练掌握该知识点是关键.
6.(2025 旬邑县校级模拟)在同一平面直角坐标系中,函数y=mx和y=﹣mx+m(m为常数,m≠0)的图象可能是( )
A. B.
C. D.
【考点】正比例函数的图象;一次函数的图象.
【专题】一次函数及其应用;几何直观.
【答案】A
【分析】根据m的正负情况,分别写出函数y=mx和y=﹣mx+m经过的象限,即可判断哪个选项符合题意.
【解答】解:当m>0时,
正比例函数y=mx的图象上y的值随x值的增大而增大,经过第一、三象限,
﹣m<0,一次函数y=﹣mx+m的图象过第一、二、四象限,故选项B,D不符合题意;
当m<0时,
正比例函数y=mx的图象上y的值随x值的增大而减小,经过第二、四象限,
﹣m>0,一次函数 y=﹣mx+m的图象过第一、三、四象限,故选项C不符合题意,选项A符合题意.
故选:A.
【点评】本题考查正比例函数的图象和一次函数的图象,解答本题的关键是明确它们的性质,写出函数经过的象限.
7.(2025 碧江区 校级模拟)已知一次函数y=kx+b(k≠0),如下表是x与y的一些对应数值,则下列结论中正确的是( )
x … ﹣1.5 0 1 2 …
y … 6 3 1 0 ﹣1 …
A.y随x的增大而增大
B.与y轴的交点是(0,﹣3)
C.关于x的方程kx+b=1的解是x=1
D.图象与x轴的交点是
【考点】一次函数与一元一次方程;一次函数的性质;一次函数图象上点的坐标特征.
【专题】一次函数及其应用;运算能力.
【答案】C
【分析】先求出一次函数的解析式,再根据k的符号得出增减,可判断A;再求出与y轴的交点,可判断B;根据当x=1时,y=1,可判断C;求出与x轴的交点,可判断D.
【解答】解:一次函数y=kx+b(k≠0),
则,
解得:,
所以一次函数解析式为y=﹣2x+3,
因为k=﹣2<0,
所以y随x的增大而减小,故A选项不符合题意;
由表格可知,当x=0时,y=3,
所以与y轴的交点是(0,3),故B选项不符合题意;
因为当x=1时,y=1,
所以关于x的方程kx+b=1的解是x=1,故C选项符合题意;
由表格可知,当y=0时,,
所以图象与x轴的交点是,故D选项不符合题意,
故选:C.
【点评】本题考查了一次函数的性质,一次函数与坐标轴的交点,一次函数与一次方程的关系,解题关键是利用待定系数法求出一次函数解析式.
8.(2025 蓬江区校级一模)我国著名数学家华罗庚说过“数缺形时少直观,形少数时难入微”,数形结合是解决数学问题的重要思想方法.为了了解关于x的不等式﹣x+2>mx+n的解集,某同学绘制了y=﹣x+2与y=mx+n(m,n为常数,m≠0)的函数图象如图所示,通过观察图象发现,该不等式的解集在数轴上表示正确的是( )
A.
B.
C.
D.
【考点】一次函数与一元一次不等式;在数轴上表示不等式的解集;一次函数的图象.
【专题】一次函数及其应用;运算能力.
【答案】C
【分析】直接根据一次函数的图象即可得出结论.
【解答】解:由条件可知关于x的不等式﹣x+2>mx+n的解集是x<﹣1.
在数轴上表示x<﹣1的解集,只有选项C符合,
故选:C.
【点评】本题考查了一次函数与一元一次不等式,在数轴上表示不等式的解集,能利用数形结合求出不等式的解集是解题的关键.
9.(2025 沭阳县三模)小鹿和小晨从图书馆出发去公园.小鹿先出发,5分钟后小晨出发,两人刚好同时到达休息点,短暂休息后两人分别以原来的速度同时再出发,各自到达公园.如图1,图书馆到公园的路线长4.5千米,图2表示两人相距的路程s(千米)与小鹿所用时间t(分)之间的函数关系,则图中m的值为( )
A.22 B.22.5 C.23 D.23.5
【考点】一次函数的应用.
【专题】一次函数及其应用;运算能力;应用意识.
【答案】B
【分析】求出小鹿的速度,从而求出二人共同休息的时间,设小晨的速度为v千米/分,根据二人同时到达休息点时距离图书馆的路程相等列关于v的方程并求解,进而求出m的值即可.
【解答】解:小鹿的速度为1÷5(千米/分),
则二人共同休息的时间为25﹣4.52.5(分),
设小晨的速度为v千米/分,
则二人同时到达休息点时,得(15﹣5)v15,
解得v,
5+2.5+4.522.5(分),
∴m=22.5.
故选:B.
【点评】本题考查一次函数的应用,掌握时间、速度和路程之间的关系是解题的关键.
10.(2025 翁牛特旗模拟)如图,在平面直角坐标系xOy中,已知△OAB是以点A为直角顶点的等腰直角三角形,点B在y轴正半轴上,点A(﹣1,1),将△AOB沿x轴正方向平移得到△DCE,若点E恰好落在直线yx上,则此时点D的坐标为( )
A.(2,1) B.(3,1) C.(4,1) D.(5,1)
【考点】一次函数图象上点的坐标特征;等腰直角三角形;坐标与图形变化﹣平移.
【专题】一次函数及其应用;平移、旋转与对称;运算能力;推理能力.
【答案】B
【分析】由点A的坐标,可得出OA的长,结合等腰直角三角形的性质,可得出AB的长,由平移的性质,可知点E的纵坐标为2,利用一次函数图象上点的坐标特征,可得出点E的坐标,结合点B的坐标,可得出点E是点B向右平移4个单位长度得到的点,进而可得出点D是点A向右平移4个单位长度得到的点,再结合点A的坐标,即可得出点D的坐标.
【解答】解:∵点A的坐标为(﹣1,1),
∴OA,
∵△OAB是以点A为直角顶点的等腰直角三角形,
∴ABOA=2,
∴点B的坐标为(0,2).
∵点E是点B向右平移得到的点,
∴点E的纵坐标为2.
当y=2时,x=2,
解得:x=4,
∴点E的坐标为(4,2),
∴点E是点B向右平移4个单位长度得到的点,
∴点D是点A向右平移4个单位长度得到的点,
∴点D的坐标为(3,1).
故选:B.
【点评】本题考查了一次函数图象上点的坐标特征、等腰直角三角形以及坐标与图形变化﹣平移,利用平移的性质及一次函数图象上点的坐标特征,找出点E的坐标是解题的关键.
二.填空题(共5小题)
11.(2025 金凤区模拟)如图,△ABC中,AC=BC=13,把△ABC放在平面直角坐标系中,且点A,B的坐标分别为(2,0),(12,0),将△ABC沿x轴向左平移,当点C落在直线y=﹣x+8上时,△ABC平移的距离为 11 .
【考点】一次函数图象上点的坐标特征;等腰三角形的性质;坐标与图形变化﹣平移.
【专题】一次函数及其应用;运算能力.
【答案】11.
【分析】过点C作CD⊥x轴于点D,由点A、B的坐标利用勾股定理可求出点C的坐标,再利用一次函数图象上点的坐标特征可求出点C移动后的坐标,即可得△ABC平移的距离.
【解答】解:过点C作CD⊥x轴于点D,如图所示.
由条件可知AD=BDAB=5,
∴.
∴点C的坐标为(7,12).
当y=12时,有12=﹣x+8,
解得:x=﹣4,
∴点C平移后的坐标为(﹣4,12).
∴△ABC沿x轴向左平移7﹣(﹣4)=11个单位长度.
故答案为:11.
【点评】本题考查了一次函数图象上点的坐标特征、等腰三角形的性质、坐标与图形变化中的平移以及勾股定理,利用一次函数图象上点的坐标特征求出点C平移后的坐标是解题的关键.
12.(2025 沧州一模)如图,已知点A(3,3),B(3,1),一次函数y=﹣x+b图象经过线段AB的中点,则b的值为 5 .
【考点】一次函数图象上点的坐标特征.
【专题】一次函数及其应用;推理能力.
【答案】5.
【分析】求出线段AB的中点,代入一次函数y=﹣x+b,求出b的值即可.
【解答】解:∵A(3,3),B(3,1),
∴线段AB的中点坐标为(3,2),
∵一次函数y=﹣x+b图象经过线段AB的中点,
∴2=﹣3+b,
∴b=5,
故答案为:5.
【点评】本题考查了一次函数图象上点的坐标特征,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解题的关键.
13.(2025 白城模拟)关于函数y=(k+1)x+2k,给出下列结论:①当k≠﹣1时,此函数是一次函数;②无论k为何值,函数图象必经过点(﹣2,﹣2);③已知点A(1,2),B(2,3),若函数图象与线段AB始终有交点,则k的取值范围是;④已知点C(x1,y1),D(x2,y2)是该函数图象上的任意两点,且(x1﹣x2)(y1﹣y2)>0恒成立,则图象必经过第二、第四象限.其中正确的是 ①② .(写所有正确的结论的序号)
【考点】一次函数图象上点的坐标特征;一次函数的性质.
【专题】一次函数及其应用;运算能力.
【答案】①②.
【分析】根据一次函数的定义可判断①;根据当x=﹣2时,y=﹣2可判断②;求出当函数y=(k+1)x+2k恰好经过A(1,2)时,当函数y=(k+1)x+2k恰好经过B(2,3)时k的值即可判断③;根据题意可得当x1>x2时,y1>y2,当x1<x2时,y1<y2,则y随x增大而增大,即可得到图象必经过第一、第三象限,可判断④.
【解答】解:①当k≠﹣1时,此函数是一次函数,原说法正确;
②∵y=(k+1)x+2k=(x+2)k+x,
∴当x=﹣2时,y=﹣2,
∴无论k为何值,函数图象必经过点(﹣2,﹣2),原说法正确;
③当函数y=(k+1)x+2k恰好经过A(1,2)时,则k+1+2k=2,解得,
当函数y=(k+1)x+2k恰好经过B(2,3)时,则2(k+1)+2k=3,解得;
∴若函数图象与线段AB始终有交点,则k的取值范围是,原说法错误;
④∵(x1﹣x2)(y1﹣y2)>0,
∴或,
∴当x1>x2时,y1>y2,当x1<x2时,y1<y2,
∴y随x增大而增大,
∴图象必经过第一、第三象限,原说法错误;
故答案为:①②.
【点评】本题主要考查了考查了一次函数的定义和一次函数的性质,正确记忆相关知识点是解题关键.
14.(2025 越秀区校级二模)甲、乙两人在一次赛跑中,路程s(米)与时间t(秒)的关系如图所示.当第一个人到达终点时,第二个人距离终点还剩 4 米.
【考点】一次函数的应用.
【专题】一次函数及其应用;应用意识.
【答案】见试题解答内容
【分析】根据图形列出算式,再求出即可.
【解答】解:1004(米),
即当第一个人到达终点时,第二个人距离终点还剩4米,
故答案为:4.
【点评】本题考查了一次函数的应用,能根据图形得出正确的信息是解此题的关键,数形结合思想的应用.
15.(2025 陇南模拟)已知一次函数y=kx+b与x轴的交点坐标的横坐标是3,且平行于函数y=﹣3x,那么这个一次函数解析式是 y=﹣3x+9 .
【考点】两条直线相交或平行问题.
【答案】见试题解答内容
【分析】根据平行直线解析式的k值相等可得k=﹣3,再将与x轴的交点代入求出b的值,然后写出函数解析式即可.
【解答】解:∵一次函数y=kx+b平行于函数y=﹣3x,
∴k=﹣3,
∵一次函数y=kx+b与x轴的交点坐标的横坐标是3,
∴与x轴的交点坐标为(3,0),
∴﹣3×3+b=0,
解得b=9,
∴这个一次函数解析式是y=﹣3x+9.
故答案为:y=﹣3x+9.
【点评】本题考查了两直线平行的问题,主要利用了两平行直线解析式的k值相等,难点在于求出直线与x轴的交点坐标.
三.解答题(共5小题)
16.(2025 前进区校级二模)某商场准备购进A和B两种款式的书包,每个A款式书包比B款式书包的进价多25元,用20000元购进A款式书包的数量与用15000元购进B款式书包的数量相同,请解决下列问题:
(1)A款式书包和B款式书包每个的进价各是多少元?
(2)若每个A款式书包的售价为140元,每个B款式书包的售价为100元,商场决定同时购A款式书包、B款式书包共500个,且全部售出,请求出所获利润y(单位:元)与A款式书包的数量x(单位:个)的函数关系式,若商场用不低于40000元且不高于40250元的资金购进A和B两种款式的书包,则有几种购买方案?
(3)在(2)的条件下,商场用获得的最大利润的全部用于福利院的慈善,其中购买文具花费915元,其余部分全部再次购进A、B两种款式的书包送给福利院,请直接写出捐赠A款式书包、B款式书包各是多少个?
【考点】一次函数的应用;分式方程的应用;一元一次不等式组的应用.
【专题】分式方程及应用;一元一次不等式(组)及应用;一次函数及其应用;运算能力;应用意识.
【答案】(1)100,75;
(2)11;
(3)2,4.
【分析】(1)设A款式书包每个的进价为a元,则B款式书包每个的进价为(a﹣25)元,根据题意列关于a的分式方程并求解即可;
(2)购买B款式书包(500﹣x)个,根据所获利润=A款式书包的利润+B款式书包的利润写出y与x的函数关系式,根据题意列关于x的一元一次不等式组并求其解集,x的符合条件的取值的个数即为购买方案的数量;
(3)根据一次函数的增减性求出y的最大值,设购买A款式书包m个、B款式书包n个,根据题意写出关于m和n的二元一次方程并求其正整数解即可.
【解答】解:(1)设A款式书包每个的进价为a元,则B款式书包每个的进价为(a﹣25)元.
根据题意,得,
解得a=100,
经检验,a=100是所列分式方程的根,
100﹣25=75(元).
答:A款式书包每个的进价为100元,则B款式书包每个的进价为75元.
(2)购买B款式书包(500﹣x)个,
则y=(140﹣100)x+(100﹣75)(500﹣x)=15x+12500,
∴y与x的函数关系式为y=15x+12500,
根据题意,得,
解得100≤x≤110,
∵x为整数,
∴有11种购买方案.
(3)∵15>0,
∴y随x的增大而增大,
∵100≤x≤110,
∴当x=110时y值最大,y最大=15×110+12500=14150,
141501415(元),
设购买A款式书包m个、B款式书包n个,
则100m+75n=1415﹣915,
经整理,得4m+3n=20,
该方程的正整数解为,
∴捐赠A款式书包2个、B款式书包4个.
【点评】本题考查一次函数的应用、分式方程的应用、一元一次不等式组的应用,掌握分式方程、一元一次不等式组的解法及一次函数的增减性是解题的关键.
17.(2025 永寿县校级模拟)随着年龄的增长,人体的代谢能力下降,心脏的收缩力也会减弱,再加上血管的硬化和肌肉组织的流失,会导致最大心率降低.研究发现,最大心率y(次/分钟)是年龄x(岁)的一次函数.已知15岁时的最大心率为205次/分钟,36岁时的最大心率为184次/分钟.
(1)求y与x之间的函数表达式;
(2)燃烧脂肪时运动心率为最大心率的60%~70%,已知小丽燃烧脂肪时的运动心率最大为140次/分钟,求小丽的年龄.
【考点】一次函数的应用.
【专题】一次函数及其应用;运算能力;应用意识.
【答案】(1)y=﹣x+220;
(2)20岁.
【分析】(1)根据待定系数法计算即可;
(2)求出小丽的最大心率并作为x的值代入y与x之间的函数表达式,求出对应y的值即可.
【解答】解:(1)设y与x之间的函数表达式为y=kx+b(k、b为常数,且k≠0).
将x=15,y=205和x=36,y=184分别代入y=kx+b,
得,
解得,
∴y与x之间的函数表达式y=﹣x+220.
(2)燃烧脂肪时的运动心率最大为140次/分钟时,小丽的最大心率为140÷70%=200(次/分钟),
当x=200时,y=﹣200+220=20.
答:小丽的年龄为20岁.
【点评】本题考查一次函数的应用,掌握待定系数法求一次函数的关系式是解题的关键.
18.(2025 前进区校级二模)如图,矩形AOCB的边OA、OC的长分别是方程x2﹣7x+12=0的两个根(OC>OA),折叠矩形AOCB,使AB边落在x轴上,点B与点E重合.
(1)求折痕AD所在直线解析式.
(2)将直线AD沿x轴负方向以每秒1个单位长度的速度平移,直接写出直线AD扫过矩形EODF的面积S与运动的时间t(0≤t≤4)的关系式.
(3)点P是直线AD上一点,在平面内是否存在一点M,使得以A、B、P、M为顶点的四边形是正方形?若存在,直接写出点M的坐标.若不存在,说明理由.
【考点】一次函数综合题.
【专题】一次函数及其应用;运算能力;推理能力.
【答案】(1)y=﹣x+3;
(2);
(3)M(﹣1,0)或M(5,2).
【分析】(1)求出D(0,3),A(3,0),再用待定系数法求函数的解析式即可;
(2)当0≤t≤1时,直线AD扫过矩形EODF的区域为等腰直角三角形;当1<t≤3时,直线AD扫过矩形EODF的区域为一个等腰直角三角形加平行四边形;当3<t≤4时,直线AD扫过矩形EODF的区域面积为矩形EODF的面积减去底部未扫过三角形的面积;
(3)分两种情况讨论:当AB⊥BP时,此时P(﹣1,4),M(﹣1,0);当BP⊥AD时,此时P(1,2),M(5,2).
【解答】解:(1)当y=0时,x2﹣7x+12=0,
解得x1=3,x2=4,
∵OA、OC的长分别是方程x2﹣7x+12=0的两个根(OC>OA),
∴OC=4,OA=3,
由折叠可知,BC=EF=OD=3,
∴D(0,3),A(3,0),
设直线AD的解析式为y=kx+3,
∴3k+3=0,
解得k=﹣1,
∴直线AD的直线解析式为y=﹣x+3;
(2)当0≤t≤1时,直线AD扫过矩形EODF的区域为等腰直角三角形,故;
当1<t≤3时,直线AD扫过矩形EODF的区域为一个等腰直角三角形加平行四边形,故;
当3<t≤4时,直线AD扫过矩形EODF的区域面积为矩形EODF的面积减去底部未扫过三角形的面积,即;
综上,直线AD扫过矩形EODF的面积S与运动的时间t的关系式为;
(3)当AB⊥BP时,P(﹣1,4),此时BP=AB=4,
∴M(﹣1,0);
当BP⊥AD时,
∵OA=OD,
∴∠OAD=45°,
∵∠BAO=90°,
∴∠BAD=45°,
∴P(1,2),
∴M点与P点关于AB对称,
∴M(5,2);
综上所述:M(﹣1,0)或M(5,2).
【点评】本题考查了待定系数法求一次函数的解析式,矩形的性质,动点引出的几何图形面积与函数问题,两点间距离公式,一元二次方程,正方形的判定,等腰三角形的判定,掌握以上内容是解题关键.
19.(2025 松原模拟)如图①,平面直角坐标系中,直线y=﹣2x+4分别与x轴、y轴相交于A、B两点,与直线yx﹣2交于点C.直线yx﹣2与y轴交于点D.
(1)求点C,点D的坐标;
(2)如图②,P为直线BC上的一个动点,当S△PBD,求点P坐标;
(3)如图③,P为线段BC上的一个动点,点C关于直线DP的对称点为C′,当C′恰好落在x轴上时,直接写出点P的坐标.
【考点】一次函数综合题.
【专题】代数几何综合题;几何直观;运算能力;推理能力.
【答案】(1)C(4,﹣4),D(0,﹣2);
(2)P(1,2)或P(﹣1,6);
(3)P(3,﹣2)或.
【分析】(1)联立两个解析式求出C点坐标,令x=0,求出的函数值,得到D点坐标即可;
(2)求出B点坐标,设P(m,﹣2m+4),根据,列出方程进行求解即可;
(3)设C′(n,0),根据对称的性质,得到CD=C′D求出C′的坐标,进而求出C′,C的中点坐标,求出直线DP的解析式,联立直线DP和直线y=﹣2x+4,求出P点坐标即可.
【解答】解:(1)∵直线y=﹣2x+4与直线yx﹣2交于点C,
联立得:,
解得:,
∴C(4,﹣4),
∵直线yx﹣2与y轴交于点D.
当x=0时,得:y=﹣2,
∴D(0,﹣2);
(2)∵直线y=﹣2x+4分别与x轴、y轴相交于A、B两点,
当x=0时,得:y=4,
∴B(0,4),
∵C(4,﹣4),D(0,﹣2),
∴BD=6,
∴S△BCD6×4=12,
设P(m,﹣2m+4),
∴S△PBD6×|m|S△BCD=3,
∴|m|=1,
∴m=1或﹣1,
∴P(1,2)或P(﹣1,6);
(3)点P的坐标为P(3,﹣2)或.理由如下:
如图③,
设C′(n,0),
∵点C关于直线DP的对称点为C′,
∴CD=C′D,
∵C(4,﹣4),D(0,﹣2),
∴n2+4=42+(4﹣2)2,
解得:n=±4,
∴C′(4,0)或C′(﹣4,0),
当C′(4,0)时,C,C′的中点坐标为(4,﹣2),
∵D(0,﹣2),
∴DP∥x轴,
∴yP=﹣2,
此时﹣2x+4=﹣2,
解得:x=3,
∴P(3,﹣2),
当C′(﹣4,0)时,C,C′的中点坐标为:(0,﹣2),即为D点,
设直线DP与x轴交于点E(a,0),则EC=EC′,
∴(a+4)2=(4﹣a)2+42,
解得:a=1,
∴E(1,0),
设直线DE的解析式为:y=cx﹣2,把E(1,0)代入得:
0=c﹣2,
解得:c=2,
∴y=2x﹣2,
联立得:,
解得:,
∴.
综上所述,点P的坐标为P(3,﹣2)或.
【点评】本题属于一次函数综合题,主要考查一次函数与几何的综合应用,熟练掌握一次函数的图象和性质,利用数形结合和分类讨论的思想进行求解是解题的关键:
20.(2025 西湖区二模)小敏和小慧去西湖风景区游玩,约好在少年宫广场见面.如图1,A地、B地、少年宫广场在一条直线上.小敏从A地出发,先匀速步行至车站,再坐公交车前往少年宫广场.同时,小慧从B地出发,骑车去少年宫广场,平均速度为200米/分钟.两人距离A地的路程s(米)和所经过的时间t(分)之间的函数关系如图2所示.(公交车的停车时间忽略不计)
(1)求公交车的平均速度.
(2)求同时出发后,经过多少时间小敏追上小慧.
(3)在小敏坐公交车的过程中,当她与小慧相距400米时,求t的值.
【考点】一次函数的应用.
【专题】一次函数及其应用;运算能力;应用意识.
【答案】(1)400米/分;
(2)25分;
(3)23或27.
【分析】(1)根据速度=路程÷时间计算即可;
(2)分别写出当10≤t≤30时小敏距离A地的路程s和所经过的时间t之间的函数关系式、小慧距离A地的路程s和所经过的时间t之间的函数关系式,令两函数值相等列关于t的一元一次方程并求解即可;
(3)当10≤t≤30时,令两函数值差的绝对值为400,列关于t的方程并求解即可.
【解答】解:(1)(8800﹣800)÷(30﹣10)=400(米/分).
答:公交车的平均速度是400米/分.
(2)当10≤t≤30时,小敏距离A地的路程s和所经过的时间t之间的函数关系式为s=800+400(t﹣10)=400t﹣3200,
小慧距离A地的路程s和所经过的时间t之间的函数关系式为s=200t+1800,
当小敏追上小慧时,得400t﹣3200=200t+1800,
解得t=25.
答:同时出发后,经过25分小敏追上小慧.
(3)当10≤t≤30时,得|400t﹣3200﹣(200t+1800)|=400,
解得t=23或27.
答:小敏坐公交车的过程中,当她与小慧相距400米时,求t的值为23或27.
【点评】本题考查一次函数的应用,掌握时间、速度和路程之间的关系是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
暑假巩固复习 一次函数
一.选择题(共10小题)
1.(2025 永寿县校级模拟)已知A(4,a)和B(﹣1,b)是一次函数y=kx﹣4(k≠0)图象上的两点,若a<b,则该一次函数的图象还可能经过的点是( )
A.(﹣4,0) B.(4,0) C.(0,4) D.(1,﹣3)
2.(2025 广州)如图,在平面直角坐标系中,点A(﹣3,1),点B(﹣1,1),若将直线y=x向上平移d个单位长度后与线段AB有交点,则d的取值范围是( )
A.﹣3≤d≤﹣1 B.1≤d≤3 C.﹣4≤d≤﹣2 D.2≤d≤4
3.(2025 定西模拟)下列四点中,在函数y=3x+2的图象上的点是( )
A.(﹣1,1) B.(﹣1,﹣1) C.(2,0) D.(0,﹣1.5)
4.(2025 湖南模拟)已知A(m,﹣1),B(n,2)是一次函数y=﹣2x+b图象上的两点,则m和n的大小关系是( )
A.m=n B.m≤n C.m<n D.m>n
5.(2025 许昌二模)甲无人机从地面起飞,乙无人机从距离地面20m高的楼顶起飞,两架无人机同时匀速上升10s.甲、乙两架无人机所在的位置距离地面的高度y(单位:m)与无人机上升的时间x(单位:s)之间的关系如图所示.下列说法:①甲无人机上升的速度为8m/s;②5s时,两架无人机都上升了40m;③8s时,乙无人机距离地面的高度是64m;④10s时,两架无人机的高度差为20m.正确的是( )
A.①③ B.①④ C.②③ D.②④
6.(2025 旬邑县校级模拟)在同一平面直角坐标系中,函数y=mx和y=﹣mx+m(m为常数,m≠0)的图象可能是( )
A. B.
C. D.
7.(2025 碧江区 校级模拟)已知一次函数y=kx+b(k≠0),如下表是x与y的一些对应数值,则下列结论中正确的是( )
x … ﹣1.5 0 1 2 …
y … 6 3 1 0 ﹣1 …
A.y随x的增大而增大
B.与y轴的交点是(0,﹣3)
C.关于x的方程kx+b=1的解是x=1
D.图象与x轴的交点是
8.(2025 蓬江区校级一模)我国著名数学家华罗庚说过“数缺形时少直观,形少数时难入微”,数形结合是解决数学问题的重要思想方法.为了了解关于x的不等式﹣x+2>mx+n的解集,某同学绘制了y=﹣x+2与y=mx+n(m,n为常数,m≠0)的函数图象如图所示,通过观察图象发现,该不等式的解集在数轴上表示正确的是( )
A.
B.
C.
D.
9.(2025 沭阳县三模)小鹿和小晨从图书馆出发去公园.小鹿先出发,5分钟后小晨出发,两人刚好同时到达休息点,短暂休息后两人分别以原来的速度同时再出发,各自到达公园.如图1,图书馆到公园的路线长4.5千米,图2表示两人相距的路程s(千米)与小鹿所用时间t(分)之间的函数关系,则图中m的值为( )
A.22 B.22.5 C.23 D.23.5
10.(2025 翁牛特旗模拟)如图,在平面直角坐标系xOy中,已知△OAB是以点A为直角顶点的等腰直角三角形,点B在y轴正半轴上,点A(﹣1,1),将△AOB沿x轴正方向平移得到△DCE,若点E恰好落在直线yx上,则此时点D的坐标为( )
A.(2,1) B.(3,1) C.(4,1) D.(5,1)
二.填空题(共5小题)
11.(2025 金凤区模拟)如图,△ABC中,AC=BC=13,把△ABC放在平面直角坐标系中,且点A,B的坐标分别为(2,0),(12,0),将△ABC沿x轴向左平移,当点C落在直线y=﹣x+8上时,△ABC平移的距离为 .
12.(2025 沧州一模)如图,已知点A(3,3),B(3,1),一次函数y=﹣x+b图象经过线段AB的中点,则b的值为 .
13.(2025 白城模拟)关于函数y=(k+1)x+2k,给出下列结论:①当k≠﹣1时,此函数是一次函数;②无论k为何值,函数图象必经过点(﹣2,﹣2);③已知点A(1,2),B(2,3),若函数图象与线段AB始终有交点,则k的取值范围是;④已知点C(x1,y1),D(x2,y2)是该函数图象上的任意两点,且(x1﹣x2)(y1﹣y2)>0恒成立,则图象必经过第二、第四象限.其中正确的是 .(写所有正确的结论的序号)
14.(2025 越秀区校级二模)甲、乙两人在一次赛跑中,路程s(米)与时间t(秒)的关系如图所示.当第一个人到达终点时,第二个人距离终点还剩 米.
15.(2025 陇南模拟)已知一次函数y=kx+b与x轴的交点坐标的横坐标是3,且平行于函数y=﹣3x,那么这个一次函数解析式是 .
三.解答题(共5小题)
16.(2025 前进区校级二模)某商场准备购进A和B两种款式的书包,每个A款式书包比B款式书包的进价多25元,用20000元购进A款式书包的数量与用15000元购进B款式书包的数量相同,请解决下列问题:
(1)A款式书包和B款式书包每个的进价各是多少元?
(2)若每个A款式书包的售价为140元,每个B款式书包的售价为100元,商场决定同时购A款式书包、B款式书包共500个,且全部售出,请求出所获利润y(单位:元)与A款式书包的数量x(单位:个)的函数关系式,若商场用不低于40000元且不高于40250元的资金购进A和B两种款式的书包,则有几种购买方案?
(3)在(2)的条件下,商场用获得的最大利润的全部用于福利院的慈善,其中购买文具花费915元,其余部分全部再次购进A、B两种款式的书包送给福利院,请直接写出捐赠A款式书包、B款式书包各是多少个?
17.(2025 永寿县校级模拟)随着年龄的增长,人体的代谢能力下降,心脏的收缩力也会减弱,再加上血管的硬化和肌肉组织的流失,会导致最大心率降低.研究发现,最大心率y(次/分钟)是年龄x(岁)的一次函数.已知15岁时的最大心率为205次/分钟,36岁时的最大心率为184次/分钟.
(1)求y与x之间的函数表达式;
(2)燃烧脂肪时运动心率为最大心率的60%~70%,已知小丽燃烧脂肪时的运动心率最大为140次/分钟,求小丽的年龄.
18.(2025 前进区校级二模)如图,矩形AOCB的边OA、OC的长分别是方程x2﹣7x+12=0的两个根(OC>OA),折叠矩形AOCB,使AB边落在x轴上,点B与点E重合.
(1)求折痕AD所在直线解析式.
(2)将直线AD沿x轴负方向以每秒1个单位长度的速度平移,直接写出直线AD扫过矩形EODF的面积S与运动的时间t(0≤t≤4)的关系式.
(3)点P是直线AD上一点,在平面内是否存在一点M,使得以A、B、P、M为顶点的四边形是正方形?若存在,直接写出点M的坐标.若不存在,说明理由.
19.(2025 松原模拟)如图①,平面直角坐标系中,直线y=﹣2x+4分别与x轴、y轴相交于A、B两点,与直线yx﹣2交于点C.直线yx﹣2与y轴交于点D.
(1)求点C,点D的坐标;
(2)如图②,P为直线BC上的一个动点,当S△PBD,求点P坐标;
(3)如图③,P为线段BC上的一个动点,点C关于直线DP的对称点为C′,当C′恰好落在x轴上时,直接写出点P的坐标.
20.(2025 西湖区二模)小敏和小慧去西湖风景区游玩,约好在少年宫广场见面.如图1,A地、B地、少年宫广场在一条直线上.小敏从A地出发,先匀速步行至车站,再坐公交车前往少年宫广场.同时,小慧从B地出发,骑车去少年宫广场,平均速度为200米/分钟.两人距离A地的路程s(米)和所经过的时间t(分)之间的函数关系如图2所示.(公交车的停车时间忽略不计)
(1)求公交车的平均速度.
(2)求同时出发后,经过多少时间小敏追上小慧.
(3)在小敏坐公交车的过程中,当她与小慧相距400米时,求t的值.
暑假巩固复习 一次函数
参考答案与试题解析
一.选择题(共10小题)
1.(2025 永寿县校级模拟)已知A(4,a)和B(﹣1,b)是一次函数y=kx﹣4(k≠0)图象上的两点,若a<b,则该一次函数的图象还可能经过的点是( )
A.(﹣4,0) B.(4,0) C.(0,4) D.(1,﹣3)
【考点】一次函数与一元一次不等式.
【答案】A
【分析】利用一次函数的增减性得到k<0,然后分别把四个选项的点的坐标代入解析式求得k的值,即可判断.
【解答】解:∵A(4,a)和B(﹣1,b)是一次函数y=kx﹣4(k≠0)图象上的两点,且a<b,
∴y随x的增大而减小,
∴k<0,
A、将(﹣4,0)代入y=kx﹣4得,﹣4k﹣4=0,
∴k=﹣1<0,符合题意;
B、将(4,0)代入y=kx﹣4得,4k﹣4=0,
∴k=1>0,不符合题意;
C、x=0时,y=kx﹣4=﹣4,
∴(0,﹣4)在一次函数y=kx﹣4(k≠0)图象上,故不符合题意;
D、将(1,﹣3)代入y=kx﹣4得,k﹣4=﹣3,
∴k=1>0,不符合题意;
故选:A.
【点评】本题考查一次函数的性质,一次函数图象上点的坐标特征,解题的关键是熟练掌握基本知识,属于中考常考题型.
2.(2025 广州)如图,在平面直角坐标系中,点A(﹣3,1),点B(﹣1,1),若将直线y=x向上平移d个单位长度后与线段AB有交点,则d的取值范围是( )
A.﹣3≤d≤﹣1 B.1≤d≤3 C.﹣4≤d≤﹣2 D.2≤d≤4
【考点】一次函数图象与几何变换;正比例函数的性质.
【专题】一次函数及其应用;运算能力;应用意识.
【答案】D
【分析】求得平移后的解析式为y=x+d,分别代入A、B的坐标,求得对应的d的值,根据题意得到2≤d≤4.
【解答】解:把直线y=x向上平移d个单位长度后得到y=x+d,
若直线过A(﹣3,1),则﹣3+d=1,解得d=4,
若直线过B(﹣1,1),则﹣1+d=1,解得d=2,
∴若将直线y=x向上平移d个单位长度后与线段AB有交点,则2≤d≤4,
故选:D.
【点评】本题考查了一次函数图象与几何变换,一次函数的性质,根据题意列出关于d的不等式组是解题的关键.
3.(2025 定西模拟)下列四点中,在函数y=3x+2的图象上的点是( )
A.(﹣1,1) B.(﹣1,﹣1) C.(2,0) D.(0,﹣1.5)
【考点】一次函数图象上点的坐标特征.
【专题】计算题.
【答案】B
【分析】只要把点的坐标代入一次函数的解析式,若左边=右边,则点在函数的图象上,反之就不在函数的图象上,代入检验即可.
【解答】解:A、把(﹣1,1)代入y=3x+2得:左边=1,右边=3×(﹣1)+2=﹣1,左边≠右边,故A选项错误;
B、把(﹣1,﹣1)代入y=3x+2得:左边=﹣1,右边=3×(﹣1)+2=﹣1,左边=右边,故B选项正确;
C、把(2,0)代入y=3x+2得:左边=0,右边=3×2+2=8,左边≠右边,故C选项错误;
D、把(0,﹣1.5)代入y=3x+2得:左边=﹣1.5,右边=3×0+2=2,左边≠右边,故D选项错误.
故选:B.
【点评】本题主要考查对一次函数图象上点的坐标特征的理解和掌握,能根据点的坐标判断是否在函数的图象上是解此题的关键.
4.(2025 湖南模拟)已知A(m,﹣1),B(n,2)是一次函数y=﹣2x+b图象上的两点,则m和n的大小关系是( )
A.m=n B.m≤n C.m<n D.m>n
【考点】一次函数与一元一次不等式.
【专题】一次函数及其应用;运算能力.
【答案】D
【分析】根据一次函数的增减性即可判断即可.
【解答】解:∵k=﹣2<0,
∴一次函数y=﹣2x+b中y随x的增大而减小,
∵﹣1<2,
∴m>n,
故选:D.
【点评】本题考查了一次函数图象上点的坐标特征,掌握一次函数图象上点的坐标特征是解题的关键.
5.(2025 许昌二模)甲无人机从地面起飞,乙无人机从距离地面20m高的楼顶起飞,两架无人机同时匀速上升10s.甲、乙两架无人机所在的位置距离地面的高度y(单位:m)与无人机上升的时间x(单位:s)之间的关系如图所示.下列说法:①甲无人机上升的速度为8m/s;②5s时,两架无人机都上升了40m;③8s时,乙无人机距离地面的高度是64m;④10s时,两架无人机的高度差为20m.正确的是( )
A.①③ B.①④ C.②③ D.②④
【考点】一次函数的应用;有理数的加减混合运算.
【专题】一次函数及其应用;运算能力.
【答案】B
【分析】根据题意和函数图象中的数据,可以计算出甲、乙两架无人机的速度,然后即可判断各个选项中的说法是否正确.
【解答】解:根据题意和函数图象中的数据逐项分析判断如下:
甲无人机上升的速度为40÷5=8(m/s),故①正确;
5s时,甲、乙两架无人机距离底面的高度都为40m,则甲无人机上升了40m,乙无人机上升了40﹣20=20m,故②错误;
乙无人机的速度为:(40﹣20)÷5=4(m/s),
∴8s时,乙无人机距离地面的高度是20+4×8=52(m),故③错误;
10s时,两架无人机的高度差为:(8×10)﹣(20+4×10)=20(m),故④正确;
故选:B.
【点评】本题主要考查了从函数图象获取信息,熟练掌握该知识点是关键.
6.(2025 旬邑县校级模拟)在同一平面直角坐标系中,函数y=mx和y=﹣mx+m(m为常数,m≠0)的图象可能是( )
A. B.
C. D.
【考点】正比例函数的图象;一次函数的图象.
【专题】一次函数及其应用;几何直观.
【答案】A
【分析】根据m的正负情况,分别写出函数y=mx和y=﹣mx+m经过的象限,即可判断哪个选项符合题意.
【解答】解:当m>0时,
正比例函数y=mx的图象上y的值随x值的增大而增大,经过第一、三象限,
﹣m<0,一次函数y=﹣mx+m的图象过第一、二、四象限,故选项B,D不符合题意;
当m<0时,
正比例函数y=mx的图象上y的值随x值的增大而减小,经过第二、四象限,
﹣m>0,一次函数 y=﹣mx+m的图象过第一、三、四象限,故选项C不符合题意,选项A符合题意.
故选:A.
【点评】本题考查正比例函数的图象和一次函数的图象,解答本题的关键是明确它们的性质,写出函数经过的象限.
7.(2025 碧江区 校级模拟)已知一次函数y=kx+b(k≠0),如下表是x与y的一些对应数值,则下列结论中正确的是( )
x … ﹣1.5 0 1 2 …
y … 6 3 1 0 ﹣1 …
A.y随x的增大而增大
B.与y轴的交点是(0,﹣3)
C.关于x的方程kx+b=1的解是x=1
D.图象与x轴的交点是
【考点】一次函数与一元一次方程;一次函数的性质;一次函数图象上点的坐标特征.
【专题】一次函数及其应用;运算能力.
【答案】C
【分析】先求出一次函数的解析式,再根据k的符号得出增减,可判断A;再求出与y轴的交点,可判断B;根据当x=1时,y=1,可判断C;求出与x轴的交点,可判断D.
【解答】解:一次函数y=kx+b(k≠0),
则,
解得:,
所以一次函数解析式为y=﹣2x+3,
因为k=﹣2<0,
所以y随x的增大而减小,故A选项不符合题意;
由表格可知,当x=0时,y=3,
所以与y轴的交点是(0,3),故B选项不符合题意;
因为当x=1时,y=1,
所以关于x的方程kx+b=1的解是x=1,故C选项符合题意;
由表格可知,当y=0时,,
所以图象与x轴的交点是,故D选项不符合题意,
故选:C.
【点评】本题考查了一次函数的性质,一次函数与坐标轴的交点,一次函数与一次方程的关系,解题关键是利用待定系数法求出一次函数解析式.
8.(2025 蓬江区校级一模)我国著名数学家华罗庚说过“数缺形时少直观,形少数时难入微”,数形结合是解决数学问题的重要思想方法.为了了解关于x的不等式﹣x+2>mx+n的解集,某同学绘制了y=﹣x+2与y=mx+n(m,n为常数,m≠0)的函数图象如图所示,通过观察图象发现,该不等式的解集在数轴上表示正确的是( )
A.
B.
C.
D.
【考点】一次函数与一元一次不等式;在数轴上表示不等式的解集;一次函数的图象.
【专题】一次函数及其应用;运算能力.
【答案】C
【分析】直接根据一次函数的图象即可得出结论.
【解答】解:由条件可知关于x的不等式﹣x+2>mx+n的解集是x<﹣1.
在数轴上表示x<﹣1的解集,只有选项C符合,
故选:C.
【点评】本题考查了一次函数与一元一次不等式,在数轴上表示不等式的解集,能利用数形结合求出不等式的解集是解题的关键.
9.(2025 沭阳县三模)小鹿和小晨从图书馆出发去公园.小鹿先出发,5分钟后小晨出发,两人刚好同时到达休息点,短暂休息后两人分别以原来的速度同时再出发,各自到达公园.如图1,图书馆到公园的路线长4.5千米,图2表示两人相距的路程s(千米)与小鹿所用时间t(分)之间的函数关系,则图中m的值为( )
A.22 B.22.5 C.23 D.23.5
【考点】一次函数的应用.
【专题】一次函数及其应用;运算能力;应用意识.
【答案】B
【分析】求出小鹿的速度,从而求出二人共同休息的时间,设小晨的速度为v千米/分,根据二人同时到达休息点时距离图书馆的路程相等列关于v的方程并求解,进而求出m的值即可.
【解答】解:小鹿的速度为1÷5(千米/分),
则二人共同休息的时间为25﹣4.52.5(分),
设小晨的速度为v千米/分,
则二人同时到达休息点时,得(15﹣5)v15,
解得v,
5+2.5+4.522.5(分),
∴m=22.5.
故选:B.
【点评】本题考查一次函数的应用,掌握时间、速度和路程之间的关系是解题的关键.
10.(2025 翁牛特旗模拟)如图,在平面直角坐标系xOy中,已知△OAB是以点A为直角顶点的等腰直角三角形,点B在y轴正半轴上,点A(﹣1,1),将△AOB沿x轴正方向平移得到△DCE,若点E恰好落在直线yx上,则此时点D的坐标为( )
A.(2,1) B.(3,1) C.(4,1) D.(5,1)
【考点】一次函数图象上点的坐标特征;等腰直角三角形;坐标与图形变化﹣平移.
【专题】一次函数及其应用;平移、旋转与对称;运算能力;推理能力.
【答案】B
【分析】由点A的坐标,可得出OA的长,结合等腰直角三角形的性质,可得出AB的长,由平移的性质,可知点E的纵坐标为2,利用一次函数图象上点的坐标特征,可得出点E的坐标,结合点B的坐标,可得出点E是点B向右平移4个单位长度得到的点,进而可得出点D是点A向右平移4个单位长度得到的点,再结合点A的坐标,即可得出点D的坐标.
【解答】解:∵点A的坐标为(﹣1,1),
∴OA,
∵△OAB是以点A为直角顶点的等腰直角三角形,
∴ABOA=2,
∴点B的坐标为(0,2).
∵点E是点B向右平移得到的点,
∴点E的纵坐标为2.
当y=2时,x=2,
解得:x=4,
∴点E的坐标为(4,2),
∴点E是点B向右平移4个单位长度得到的点,
∴点D是点A向右平移4个单位长度得到的点,
∴点D的坐标为(3,1).
故选:B.
【点评】本题考查了一次函数图象上点的坐标特征、等腰直角三角形以及坐标与图形变化﹣平移,利用平移的性质及一次函数图象上点的坐标特征,找出点E的坐标是解题的关键.
二.填空题(共5小题)
11.(2025 金凤区模拟)如图,△ABC中,AC=BC=13,把△ABC放在平面直角坐标系中,且点A,B的坐标分别为(2,0),(12,0),将△ABC沿x轴向左平移,当点C落在直线y=﹣x+8上时,△ABC平移的距离为 11 .
【考点】一次函数图象上点的坐标特征;等腰三角形的性质;坐标与图形变化﹣平移.
【专题】一次函数及其应用;运算能力.
【答案】11.
【分析】过点C作CD⊥x轴于点D,由点A、B的坐标利用勾股定理可求出点C的坐标,再利用一次函数图象上点的坐标特征可求出点C移动后的坐标,即可得△ABC平移的距离.
【解答】解:过点C作CD⊥x轴于点D,如图所示.
由条件可知AD=BDAB=5,
∴.
∴点C的坐标为(7,12).
当y=12时,有12=﹣x+8,
解得:x=﹣4,
∴点C平移后的坐标为(﹣4,12).
∴△ABC沿x轴向左平移7﹣(﹣4)=11个单位长度.
故答案为:11.
【点评】本题考查了一次函数图象上点的坐标特征、等腰三角形的性质、坐标与图形变化中的平移以及勾股定理,利用一次函数图象上点的坐标特征求出点C平移后的坐标是解题的关键.
12.(2025 沧州一模)如图,已知点A(3,3),B(3,1),一次函数y=﹣x+b图象经过线段AB的中点,则b的值为 5 .
【考点】一次函数图象上点的坐标特征.
【专题】一次函数及其应用;推理能力.
【答案】5.
【分析】求出线段AB的中点,代入一次函数y=﹣x+b,求出b的值即可.
【解答】解:∵A(3,3),B(3,1),
∴线段AB的中点坐标为(3,2),
∵一次函数y=﹣x+b图象经过线段AB的中点,
∴2=﹣3+b,
∴b=5,
故答案为:5.
【点评】本题考查了一次函数图象上点的坐标特征,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解题的关键.
13.(2025 白城模拟)关于函数y=(k+1)x+2k,给出下列结论:①当k≠﹣1时,此函数是一次函数;②无论k为何值,函数图象必经过点(﹣2,﹣2);③已知点A(1,2),B(2,3),若函数图象与线段AB始终有交点,则k的取值范围是;④已知点C(x1,y1),D(x2,y2)是该函数图象上的任意两点,且(x1﹣x2)(y1﹣y2)>0恒成立,则图象必经过第二、第四象限.其中正确的是 ①② .(写所有正确的结论的序号)
【考点】一次函数图象上点的坐标特征;一次函数的性质.
【专题】一次函数及其应用;运算能力.
【答案】①②.
【分析】根据一次函数的定义可判断①;根据当x=﹣2时,y=﹣2可判断②;求出当函数y=(k+1)x+2k恰好经过A(1,2)时,当函数y=(k+1)x+2k恰好经过B(2,3)时k的值即可判断③;根据题意可得当x1>x2时,y1>y2,当x1<x2时,y1<y2,则y随x增大而增大,即可得到图象必经过第一、第三象限,可判断④.
【解答】解:①当k≠﹣1时,此函数是一次函数,原说法正确;
②∵y=(k+1)x+2k=(x+2)k+x,
∴当x=﹣2时,y=﹣2,
∴无论k为何值,函数图象必经过点(﹣2,﹣2),原说法正确;
③当函数y=(k+1)x+2k恰好经过A(1,2)时,则k+1+2k=2,解得,
当函数y=(k+1)x+2k恰好经过B(2,3)时,则2(k+1)+2k=3,解得;
∴若函数图象与线段AB始终有交点,则k的取值范围是,原说法错误;
④∵(x1﹣x2)(y1﹣y2)>0,
∴或,
∴当x1>x2时,y1>y2,当x1<x2时,y1<y2,
∴y随x增大而增大,
∴图象必经过第一、第三象限,原说法错误;
故答案为:①②.
【点评】本题主要考查了考查了一次函数的定义和一次函数的性质,正确记忆相关知识点是解题关键.
14.(2025 越秀区校级二模)甲、乙两人在一次赛跑中,路程s(米)与时间t(秒)的关系如图所示.当第一个人到达终点时,第二个人距离终点还剩 4 米.
【考点】一次函数的应用.
【专题】一次函数及其应用;应用意识.
【答案】见试题解答内容
【分析】根据图形列出算式,再求出即可.
【解答】解:1004(米),
即当第一个人到达终点时,第二个人距离终点还剩4米,
故答案为:4.
【点评】本题考查了一次函数的应用,能根据图形得出正确的信息是解此题的关键,数形结合思想的应用.
15.(2025 陇南模拟)已知一次函数y=kx+b与x轴的交点坐标的横坐标是3,且平行于函数y=﹣3x,那么这个一次函数解析式是 y=﹣3x+9 .
【考点】两条直线相交或平行问题.
【答案】见试题解答内容
【分析】根据平行直线解析式的k值相等可得k=﹣3,再将与x轴的交点代入求出b的值,然后写出函数解析式即可.
【解答】解:∵一次函数y=kx+b平行于函数y=﹣3x,
∴k=﹣3,
∵一次函数y=kx+b与x轴的交点坐标的横坐标是3,
∴与x轴的交点坐标为(3,0),
∴﹣3×3+b=0,
解得b=9,
∴这个一次函数解析式是y=﹣3x+9.
故答案为:y=﹣3x+9.
【点评】本题考查了两直线平行的问题,主要利用了两平行直线解析式的k值相等,难点在于求出直线与x轴的交点坐标.
三.解答题(共5小题)
16.(2025 前进区校级二模)某商场准备购进A和B两种款式的书包,每个A款式书包比B款式书包的进价多25元,用20000元购进A款式书包的数量与用15000元购进B款式书包的数量相同,请解决下列问题:
(1)A款式书包和B款式书包每个的进价各是多少元?
(2)若每个A款式书包的售价为140元,每个B款式书包的售价为100元,商场决定同时购A款式书包、B款式书包共500个,且全部售出,请求出所获利润y(单位:元)与A款式书包的数量x(单位:个)的函数关系式,若商场用不低于40000元且不高于40250元的资金购进A和B两种款式的书包,则有几种购买方案?
(3)在(2)的条件下,商场用获得的最大利润的全部用于福利院的慈善,其中购买文具花费915元,其余部分全部再次购进A、B两种款式的书包送给福利院,请直接写出捐赠A款式书包、B款式书包各是多少个?
【考点】一次函数的应用;分式方程的应用;一元一次不等式组的应用.
【专题】分式方程及应用;一元一次不等式(组)及应用;一次函数及其应用;运算能力;应用意识.
【答案】(1)100,75;
(2)11;
(3)2,4.
【分析】(1)设A款式书包每个的进价为a元,则B款式书包每个的进价为(a﹣25)元,根据题意列关于a的分式方程并求解即可;
(2)购买B款式书包(500﹣x)个,根据所获利润=A款式书包的利润+B款式书包的利润写出y与x的函数关系式,根据题意列关于x的一元一次不等式组并求其解集,x的符合条件的取值的个数即为购买方案的数量;
(3)根据一次函数的增减性求出y的最大值,设购买A款式书包m个、B款式书包n个,根据题意写出关于m和n的二元一次方程并求其正整数解即可.
【解答】解:(1)设A款式书包每个的进价为a元,则B款式书包每个的进价为(a﹣25)元.
根据题意,得,
解得a=100,
经检验,a=100是所列分式方程的根,
100﹣25=75(元).
答:A款式书包每个的进价为100元,则B款式书包每个的进价为75元.
(2)购买B款式书包(500﹣x)个,
则y=(140﹣100)x+(100﹣75)(500﹣x)=15x+12500,
∴y与x的函数关系式为y=15x+12500,
根据题意,得,
解得100≤x≤110,
∵x为整数,
∴有11种购买方案.
(3)∵15>0,
∴y随x的增大而增大,
∵100≤x≤110,
∴当x=110时y值最大,y最大=15×110+12500=14150,
141501415(元),
设购买A款式书包m个、B款式书包n个,
则100m+75n=1415﹣915,
经整理,得4m+3n=20,
该方程的正整数解为,
∴捐赠A款式书包2个、B款式书包4个.
【点评】本题考查一次函数的应用、分式方程的应用、一元一次不等式组的应用,掌握分式方程、一元一次不等式组的解法及一次函数的增减性是解题的关键.
17.(2025 永寿县校级模拟)随着年龄的增长,人体的代谢能力下降,心脏的收缩力也会减弱,再加上血管的硬化和肌肉组织的流失,会导致最大心率降低.研究发现,最大心率y(次/分钟)是年龄x(岁)的一次函数.已知15岁时的最大心率为205次/分钟,36岁时的最大心率为184次/分钟.
(1)求y与x之间的函数表达式;
(2)燃烧脂肪时运动心率为最大心率的60%~70%,已知小丽燃烧脂肪时的运动心率最大为140次/分钟,求小丽的年龄.
【考点】一次函数的应用.
【专题】一次函数及其应用;运算能力;应用意识.
【答案】(1)y=﹣x+220;
(2)20岁.
【分析】(1)根据待定系数法计算即可;
(2)求出小丽的最大心率并作为x的值代入y与x之间的函数表达式,求出对应y的值即可.
【解答】解:(1)设y与x之间的函数表达式为y=kx+b(k、b为常数,且k≠0).
将x=15,y=205和x=36,y=184分别代入y=kx+b,
得,
解得,
∴y与x之间的函数表达式y=﹣x+220.
(2)燃烧脂肪时的运动心率最大为140次/分钟时,小丽的最大心率为140÷70%=200(次/分钟),
当x=200时,y=﹣200+220=20.
答:小丽的年龄为20岁.
【点评】本题考查一次函数的应用,掌握待定系数法求一次函数的关系式是解题的关键.
18.(2025 前进区校级二模)如图,矩形AOCB的边OA、OC的长分别是方程x2﹣7x+12=0的两个根(OC>OA),折叠矩形AOCB,使AB边落在x轴上,点B与点E重合.
(1)求折痕AD所在直线解析式.
(2)将直线AD沿x轴负方向以每秒1个单位长度的速度平移,直接写出直线AD扫过矩形EODF的面积S与运动的时间t(0≤t≤4)的关系式.
(3)点P是直线AD上一点,在平面内是否存在一点M,使得以A、B、P、M为顶点的四边形是正方形?若存在,直接写出点M的坐标.若不存在,说明理由.
【考点】一次函数综合题.
【专题】一次函数及其应用;运算能力;推理能力.
【答案】(1)y=﹣x+3;
(2);
(3)M(﹣1,0)或M(5,2).
【分析】(1)求出D(0,3),A(3,0),再用待定系数法求函数的解析式即可;
(2)当0≤t≤1时,直线AD扫过矩形EODF的区域为等腰直角三角形;当1<t≤3时,直线AD扫过矩形EODF的区域为一个等腰直角三角形加平行四边形;当3<t≤4时,直线AD扫过矩形EODF的区域面积为矩形EODF的面积减去底部未扫过三角形的面积;
(3)分两种情况讨论:当AB⊥BP时,此时P(﹣1,4),M(﹣1,0);当BP⊥AD时,此时P(1,2),M(5,2).
【解答】解:(1)当y=0时,x2﹣7x+12=0,
解得x1=3,x2=4,
∵OA、OC的长分别是方程x2﹣7x+12=0的两个根(OC>OA),
∴OC=4,OA=3,
由折叠可知,BC=EF=OD=3,
∴D(0,3),A(3,0),
设直线AD的解析式为y=kx+3,
∴3k+3=0,
解得k=﹣1,
∴直线AD的直线解析式为y=﹣x+3;
(2)当0≤t≤1时,直线AD扫过矩形EODF的区域为等腰直角三角形,故;
当1<t≤3时,直线AD扫过矩形EODF的区域为一个等腰直角三角形加平行四边形,故;
当3<t≤4时,直线AD扫过矩形EODF的区域面积为矩形EODF的面积减去底部未扫过三角形的面积,即;
综上,直线AD扫过矩形EODF的面积S与运动的时间t的关系式为;
(3)当AB⊥BP时,P(﹣1,4),此时BP=AB=4,
∴M(﹣1,0);
当BP⊥AD时,
∵OA=OD,
∴∠OAD=45°,
∵∠BAO=90°,
∴∠BAD=45°,
∴P(1,2),
∴M点与P点关于AB对称,
∴M(5,2);
综上所述:M(﹣1,0)或M(5,2).
【点评】本题考查了待定系数法求一次函数的解析式,矩形的性质,动点引出的几何图形面积与函数问题,两点间距离公式,一元二次方程,正方形的判定,等腰三角形的判定,掌握以上内容是解题关键.
19.(2025 松原模拟)如图①,平面直角坐标系中,直线y=﹣2x+4分别与x轴、y轴相交于A、B两点,与直线yx﹣2交于点C.直线yx﹣2与y轴交于点D.
(1)求点C,点D的坐标;
(2)如图②,P为直线BC上的一个动点,当S△PBD,求点P坐标;
(3)如图③,P为线段BC上的一个动点,点C关于直线DP的对称点为C′,当C′恰好落在x轴上时,直接写出点P的坐标.
【考点】一次函数综合题.
【专题】代数几何综合题;几何直观;运算能力;推理能力.
【答案】(1)C(4,﹣4),D(0,﹣2);
(2)P(1,2)或P(﹣1,6);
(3)P(3,﹣2)或.
【分析】(1)联立两个解析式求出C点坐标,令x=0,求出的函数值,得到D点坐标即可;
(2)求出B点坐标,设P(m,﹣2m+4),根据,列出方程进行求解即可;
(3)设C′(n,0),根据对称的性质,得到CD=C′D求出C′的坐标,进而求出C′,C的中点坐标,求出直线DP的解析式,联立直线DP和直线y=﹣2x+4,求出P点坐标即可.
【解答】解:(1)∵直线y=﹣2x+4与直线yx﹣2交于点C,
联立得:,
解得:,
∴C(4,﹣4),
∵直线yx﹣2与y轴交于点D.
当x=0时,得:y=﹣2,
∴D(0,﹣2);
(2)∵直线y=﹣2x+4分别与x轴、y轴相交于A、B两点,
当x=0时,得:y=4,
∴B(0,4),
∵C(4,﹣4),D(0,﹣2),
∴BD=6,
∴S△BCD6×4=12,
设P(m,﹣2m+4),
∴S△PBD6×|m|S△BCD=3,
∴|m|=1,
∴m=1或﹣1,
∴P(1,2)或P(﹣1,6);
(3)点P的坐标为P(3,﹣2)或.理由如下:
如图③,
设C′(n,0),
∵点C关于直线DP的对称点为C′,
∴CD=C′D,
∵C(4,﹣4),D(0,﹣2),
∴n2+4=42+(4﹣2)2,
解得:n=±4,
∴C′(4,0)或C′(﹣4,0),
当C′(4,0)时,C,C′的中点坐标为(4,﹣2),
∵D(0,﹣2),
∴DP∥x轴,
∴yP=﹣2,
此时﹣2x+4=﹣2,
解得:x=3,
∴P(3,﹣2),
当C′(﹣4,0)时,C,C′的中点坐标为:(0,﹣2),即为D点,
设直线DP与x轴交于点E(a,0),则EC=EC′,
∴(a+4)2=(4﹣a)2+42,
解得:a=1,
∴E(1,0),
设直线DE的解析式为:y=cx﹣2,把E(1,0)代入得:
0=c﹣2,
解得:c=2,
∴y=2x﹣2,
联立得:,
解得:,
∴.
综上所述,点P的坐标为P(3,﹣2)或.
【点评】本题属于一次函数综合题,主要考查一次函数与几何的综合应用,熟练掌握一次函数的图象和性质,利用数形结合和分类讨论的思想进行求解是解题的关键:
20.(2025 西湖区二模)小敏和小慧去西湖风景区游玩,约好在少年宫广场见面.如图1,A地、B地、少年宫广场在一条直线上.小敏从A地出发,先匀速步行至车站,再坐公交车前往少年宫广场.同时,小慧从B地出发,骑车去少年宫广场,平均速度为200米/分钟.两人距离A地的路程s(米)和所经过的时间t(分)之间的函数关系如图2所示.(公交车的停车时间忽略不计)
(1)求公交车的平均速度.
(2)求同时出发后,经过多少时间小敏追上小慧.
(3)在小敏坐公交车的过程中,当她与小慧相距400米时,求t的值.
【考点】一次函数的应用.
【专题】一次函数及其应用;运算能力;应用意识.
【答案】(1)400米/分;
(2)25分;
(3)23或27.
【分析】(1)根据速度=路程÷时间计算即可;
(2)分别写出当10≤t≤30时小敏距离A地的路程s和所经过的时间t之间的函数关系式、小慧距离A地的路程s和所经过的时间t之间的函数关系式,令两函数值相等列关于t的一元一次方程并求解即可;
(3)当10≤t≤30时,令两函数值差的绝对值为400,列关于t的方程并求解即可.
【解答】解:(1)(8800﹣800)÷(30﹣10)=400(米/分).
答:公交车的平均速度是400米/分.
(2)当10≤t≤30时,小敏距离A地的路程s和所经过的时间t之间的函数关系式为s=800+400(t﹣10)=400t﹣3200,
小慧距离A地的路程s和所经过的时间t之间的函数关系式为s=200t+1800,
当小敏追上小慧时,得400t﹣3200=200t+1800,
解得t=25.
答:同时出发后,经过25分小敏追上小慧.
(3)当10≤t≤30时,得|400t﹣3200﹣(200t+1800)|=400,
解得t=23或27.
答:小敏坐公交车的过程中,当她与小慧相距400米时,求t的值为23或27.
【点评】本题考查一次函数的应用,掌握时间、速度和路程之间的关系是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
