第十章 二元一次方程组(暑假复习.含解析)-2024-2025学年七年级下册数学人教版(2024)
文档属性
| 名称 | 第十章 二元一次方程组(暑假复习.含解析)-2024-2025学年七年级下册数学人教版(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 630.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-06 15:06:15 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
暑假巩固复习 二元一次方程组
一.选择题(共10小题)
1.(2025 鸡西一模)为积极响应“环保垃圾分类”政策,某小区计划采购A、B两种类型的垃圾桶,用于提升小区垃圾分类的效率和质量.已知A型垃圾桶每个80元,B型垃圾桶每个60元.小区准备投入1200元资金全部用于购买这两种垃圾桶(两种垃圾桶都要买),则共有( )种购买方案
A.6 B.5 C.4 D.3
2.(2025 淅川县三模)我国古代著作《增删算法统宗》中记载了一首古算诗:“庭前孩童闹如簇,不知人数不知梨,每人四梨多十二,每人六梨恰齐足.”其大意:“孩童们在庭院玩耍,不知有多少人和梨,每人分4个梨,多12个梨;每人分6个梨,恰好分完.”设有x个梨,y个孩童,则可列方程组为( )
A. B.
C. D.
3.(2025 甘州区一模)古代数学趣题:老头提篮去赶集,一共花去七十七;满满装了一菜篮,十斤大肉三斤鱼;买好未曾问单价,只因回家心里急;道旁行人告诉他,九斤肉钱五斤鱼.意思是:77元钱共买了10斤肉和3斤鱼,9斤肉的钱等于5斤鱼的钱,问每斤肉和鱼各是多少钱?设每斤肉x元,每斤鱼y元,可列方程组为( )
A. B.
C. D.
4.(2025 齐齐哈尔四模)在数学知识竞赛中,为奖励成绩突出的学生,班级计划用100元钱购买甲,乙,丙三种奖品,三种奖品都要购买,甲种奖品每个5元,乙种奖品每个10元,丙种奖品每个15元,在丙种奖品不超过两个且钱全部用完的情况下,购买方案有( )
A.12种 B.15种 C.16种 D.14种
5.(2025 沿河县三模)若关于x,y的方程组与有相同的解,则m+n的值为( )
A.﹣2 B.﹣1 C.3 D.﹣5
6.(2025 河北区二模)《九章算术》共收有246个数学问题,分为九章,其中第八章“方程”篇中记载了这样一道题:“今有甲乙二人持钱不知其数,甲得乙半而钱八十,乙得甲太半而钱亦八十.问甲、乙持钱各几何?”题目大意是:甲、乙两人各带了若干钱,如果甲得到乙所有钱的一半,那么甲共有钱80.如果乙得到甲所有钱的,那么乙也共有钱80.若设甲、乙原本各持钱x,y,则根据题意可列方程组为( )
A. B.
C. D.
7.(2025 赤坎区校级四模)方程组的解是( )
A. B.
C. D.
8.(2025 孝感模拟)《孙子算经》是中国古代重要的数学著作,书中记载有这样一个问题:“今有三人共车,二车空;二人共车,九人步.问:人与车各几何?”其意思是:“今有3人坐一辆车,则有2辆车是空的;2人坐一辆车,则有9人需要步行.问:人与车各多少?”若设有x个人,y辆车,则可列方程组是( )
A. B.
C. D.
9.(2025 和平区二模)幻方起源于中国,是我国古代数学的杰作之一,是一种将数字安排在正方形格子中,使每一横行、每一竖列以及两条斜对角线上的数字和都相等的方法.如图①就是一个幻方,图②是一个未完成的幻方,则可以列出的方程组为( )
A.
B.
C.
D.
10.(2025 武安市三模)若x4﹣3|m|+y|n|﹣2=2025是关于x,y的二元一次方程,且mn<0,﹣5<m﹣n<﹣3,则m+n的值是( )
A.﹣4 B.2 C.4 D.﹣2
二.填空题(共5小题)
11.(2025 泸县校级二模)已知关于x,y的方程组,且x﹣y=2,则k= .
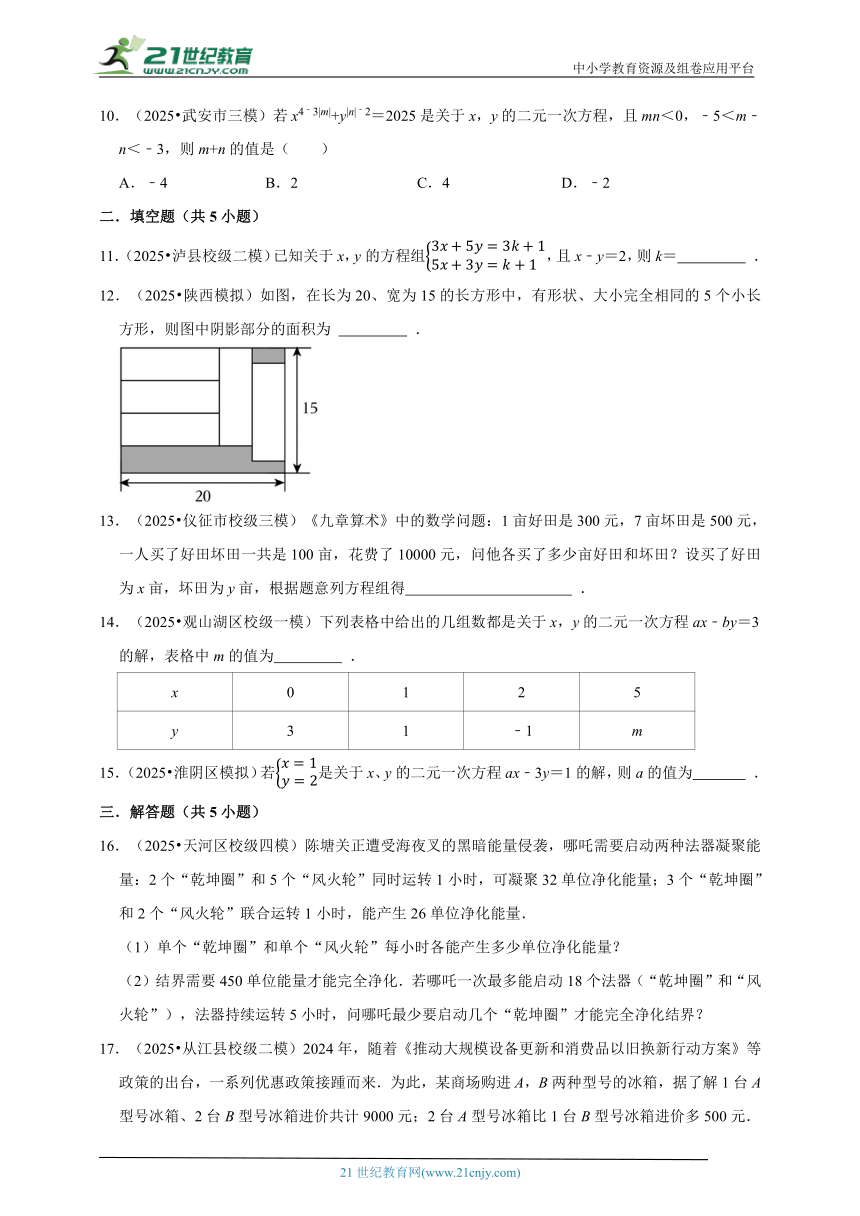
12.(2025 陕西模拟)如图,在长为20、宽为15的长方形中,有形状、大小完全相同的5个小长方形,则图中阴影部分的面积为 .
13.(2025 仪征市校级三模)《九章算术》中的数学问题:1亩好田是300元,7亩坏田是500元,一人买了好田坏田一共是100亩,花费了10000元,问他各买了多少亩好田和坏田?设买了好田为x亩,坏田为y亩,根据题意列方程组得 .
14.(2025 观山湖区校级一模)下列表格中给出的几组数都是关于x,y的二元一次方程ax﹣by=3的解,表格中m的值为 .
x 0 1 2 5
y 3 1 ﹣1 m
15.(2025 淮阴区模拟)若是关于x、y的二元一次方程ax﹣3y=1的解,则a的值为 .
三.解答题(共5小题)
16.(2025 天河区校级四模)陈塘关正遭受海夜叉的黑暗能量侵袭,哪吒需要启动两种法器凝聚能量:2个“乾坤圈”和5个“风火轮”同时运转1小时,可凝聚32单位净化能量;3个“乾坤圈”和2个“风火轮”联合运转1小时,能产生26单位净化能量.
(1)单个“乾坤圈”和单个“风火轮”每小时各能产生多少单位净化能量?
(2)结界需要450单位能量才能完全净化.若哪吒一次最多能启动18个法器(“乾坤圈”和“风火轮”),法器持续运转5小时,问哪吒最少要启动几个“乾坤圈”才能完全净化结界?
17.(2025 从江县校级二模)2024年,随着《推动大规模设备更新和消费品以旧换新行动方案》等政策的出台,一系列优惠政策接踵而来.为此,某商场购进A,B两种型号的冰箱,据了解1台A型号冰箱、2台B型号冰箱进价共计9000元;2台A型号冰箱比1台B型号冰箱进价多500元.
(1)求A,B两种型号的冰箱每台的进价;
(2)由于需求不断增大,该商场准备购进两种型号的冰箱共100台,已知A型号冰箱的售价为2500元/台,B型号冰箱的售价为4100元/台,若购进A型号冰箱的数量不少于40台,设购进a台A型号冰箱,100台冰箱全部售完获利W(元),该商场应购进A,B两种型号的冰箱各多少台才能使W最大?W最大为多少元?
18.(2025 东莞市校级三模)嘉嘉坚持每天做运动.已知某两组运动都由波比跳和深蹲组成,每个波比跳耗时5秒,每个深蹲也耗时5秒.运动软件显示,完成第一组运动,嘉嘉做了20个波比跳和40个深蹲,共消耗热量132大卡;完成第二组运动,嘉嘉做了20个波比跳和70个深蹲,共消耗热量156大卡.每个动作之间的衔接时间忽略不计.
(1)每个波比跳和每个深蹲各消耗热量多少大卡?
(2)若嘉嘉只做波比跳和深蹲两个动作,花10分钟,消耗至少200大卡,嘉嘉至少要做多少个波比跳?
19.(2025 雁塔区校级一模)《九章算术》是人类科学史上应用数学的“算经之首”,书中记载:今有三人共车,二车空;二人共车,九人步.问:人与车各几何?译文:若3人坐一辆车,则两辆车是空的;若2人坐一辆车,则9人需要步行.问:人与车各多少?
20.(2025 怀仁市模拟)超市购物车使我们的购物方式更方便、快捷,如图为购物车叠放在一起的示意图.3辆超市购物车叠放在一起的长度为1.4m,6辆超市购物车叠放在一起的长度为2m.
(1)求每一辆超市购物车的长度;
(2)若该超市只有扶手电梯,且倾斜长度为12米,工作人员可以通过电梯转运超市购物车.为安全起见,规定电梯一次只能转运1列超市购物车,并且不能超过电梯总长度的,则工作人员一次最多可以转运多少辆超市购物车?
暑假巩固复习 二元一次方程组
参考答案与试题解析
一.选择题(共10小题)
1.(2025 鸡西一模)为积极响应“环保垃圾分类”政策,某小区计划采购A、B两种类型的垃圾桶,用于提升小区垃圾分类的效率和质量.已知A型垃圾桶每个80元,B型垃圾桶每个60元.小区准备投入1200元资金全部用于购买这两种垃圾桶(两种垃圾桶都要买),则共有( )种购买方案
A.6 B.5 C.4 D.3
【考点】二元一次方程的应用.
【专题】一次方程(组)及应用;应用意识.
【答案】C
【分析】购买x个A型垃圾桶,y个B型垃圾桶,利用总价=单价×数量,可列出关于x,y的二元一次方程,结合x,y均为正整数,可得出共有4种购买方案.
【解答】解:购买x个A型垃圾桶,y个B型垃圾桶,
根据题意得:80x+60y=1200,
∴y=20x,
又∵x,y均为正整数,
∴或或或,
∴共有4种购买方案.
故选:C.
【点评】本题考查了二元一次方程的应用,找准等量关系,正确列出二元一次方程是解题的关键.
2.(2025 淅川县三模)我国古代著作《增删算法统宗》中记载了一首古算诗:“庭前孩童闹如簇,不知人数不知梨,每人四梨多十二,每人六梨恰齐足.”其大意:“孩童们在庭院玩耍,不知有多少人和梨,每人分4个梨,多12个梨;每人分6个梨,恰好分完.”设有x个梨,y个孩童,则可列方程组为( )
A. B.
C. D.
【考点】由实际问题抽象出二元一次方程组.
【专题】方程与不等式;运算能力.
【答案】A
【分析】根据“每人分4个梨,多12个梨;每人分6个梨,恰好分完.”列方程组即可.
【解答】解:由题意可设有x个梨,y个孩童,
∴,
∴A选项符合,
故选:A.
【点评】本题考查由实际问题抽象出二元一次方程组,理解题意,找到等量关系是解题关键.
3.(2025 甘州区一模)古代数学趣题:老头提篮去赶集,一共花去七十七;满满装了一菜篮,十斤大肉三斤鱼;买好未曾问单价,只因回家心里急;道旁行人告诉他,九斤肉钱五斤鱼.意思是:77元钱共买了10斤肉和3斤鱼,9斤肉的钱等于5斤鱼的钱,问每斤肉和鱼各是多少钱?设每斤肉x元,每斤鱼y元,可列方程组为( )
A. B.
C. D.
【考点】由实际问题抽象出二元一次方程组.
【专题】一次方程(组)及应用;应用意识.
【答案】A
【分析】根据“77元钱共买了10斤肉和3斤鱼,9斤肉的钱等于5斤鱼的钱”,即可列出关于x,y的二元一次方程组,此题得解.
【解答】解:∵77元钱共买了10斤肉和3斤鱼
∴10x+3y=77;
∵9斤肉的钱等于5斤鱼的钱,
∴9x=5y.
∴根据题意可列出方程组.
故选:A.
【点评】本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.
4.(2025 齐齐哈尔四模)在数学知识竞赛中,为奖励成绩突出的学生,班级计划用100元钱购买甲,乙,丙三种奖品,三种奖品都要购买,甲种奖品每个5元,乙种奖品每个10元,丙种奖品每个15元,在丙种奖品不超过两个且钱全部用完的情况下,购买方案有( )
A.12种 B.15种 C.16种 D.14种
【考点】三元一次方程组的应用.
【专题】一次方程(组)及应用;运算能力.
【答案】D
【分析】设购买A、B、C三种奖品分别为x,y,z个,根据题意列方程得5x+10y+15z=100,化简后根据x,y,z均为正整数,结合C种奖品不超过两个分类讨论,确定解的个数即可.
【解答】解:设购买A、B、C三种奖品分别为x,y,z个,
根据题意列方程得5x+10y+15z=100,
即x+2y+3z=20,
由题意得x,y,z均为正整数.
①当z=1时,x+2y=17,
∴,
∴y分别取1,3,5,7,9,11,13,15共8种情况时,x为正整数;
②当z=2时,x+2y=14,
∴,
∴y可以分别取2,4,6,8,10,12共6种情况,x为正整数;
综上所述:共有8+6=14种购买方案,
综上所述,只有选项D正确,符合题意.
故选:D.
【点评】本题考查了三元一次方程组的应用,根据题意列出方程,并确定方程组的解为正整数是解题关键.
5.(2025 沿河县三模)若关于x,y的方程组与有相同的解,则m+n的值为( )
A.﹣2 B.﹣1 C.3 D.﹣5
【考点】二元一次方程组的解.
【专题】一次方程(组)及应用;运算能力.
【答案】A
【分析】先根据题意得出相同的解是,然后分别代入方程mx+ny=1和方程nx+my=﹣7中得到关于m、n的方程组,直接相加即可求解.
【解答】解:根据题意得两个方程组相同的解是,
把代入方程mx+ny=1和方程nx+my=﹣7中,得,,
①+②,得3m+3n=﹣6,
∴m+n=﹣2,
故选:A.
【点评】本题考查了二元一次方程组的解,熟练掌握二元一次方程组的解的定义是解题的关键.
6.(2025 河北区二模)《九章算术》共收有246个数学问题,分为九章,其中第八章“方程”篇中记载了这样一道题:“今有甲乙二人持钱不知其数,甲得乙半而钱八十,乙得甲太半而钱亦八十.问甲、乙持钱各几何?”题目大意是:甲、乙两人各带了若干钱,如果甲得到乙所有钱的一半,那么甲共有钱80.如果乙得到甲所有钱的,那么乙也共有钱80.若设甲、乙原本各持钱x,y,则根据题意可列方程组为( )
A. B.
C. D.
【考点】由实际问题抽象出二元一次方程组;数学常识.
【专题】一次方程(组)及应用;应用意识.
【答案】D
【分析】根据题意可得,甲的钱+乙所有钱的一半=80,乙的钱+甲所有钱的80,据此列方程组可得.
【解答】解:根据题意,得:,
故选:D.
【点评】本题考查了由实际问题抽象出二元一次方程组,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列出方程组.
7.(2025 赤坎区校级四模)方程组的解是( )
A. B.
C. D.
【考点】解二元一次方程组.
【专题】一次方程(组)及应用;运算能力.
【答案】B
【分析】用加减消元法解方程组即可.
【解答】解:将方程标号得,
②﹣①得x=2,
将x=2代入①得2+y=6,
解得y=4,
∴,
故选:B.
【点评】本题考查了解一元二次方程,熟练掌握该知识点是关键.
8.(2025 孝感模拟)《孙子算经》是中国古代重要的数学著作,书中记载有这样一个问题:“今有三人共车,二车空;二人共车,九人步.问:人与车各几何?”其意思是:“今有3人坐一辆车,则有2辆车是空的;2人坐一辆车,则有9人需要步行.问:人与车各多少?”若设有x个人,y辆车,则可列方程组是( )
A. B.
C. D.
【考点】二元一次方程组的应用.
【专题】一次方程(组)及应用;应用意识.
【答案】C
【分析】根据今有3人坐一辆车,则有2辆车是空的;2人坐一辆车,则有9人需要步行;列出二元一次方程组即可.
【解答】解:根据题意得:,
故选:C.
【点评】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
9.(2025 和平区二模)幻方起源于中国,是我国古代数学的杰作之一,是一种将数字安排在正方形格子中,使每一横行、每一竖列以及两条斜对角线上的数字和都相等的方法.如图①就是一个幻方,图②是一个未完成的幻方,则可以列出的方程组为( )
A.
B.
C.
D.
【考点】由实际问题抽象出二元一次方程组.
【专题】一次方程(组)及应用;运算能力.
【答案】A
【分析】根据第一行与第三列的和相等,斜对角线与第一行的和相等,列出方程组即可.
【解答】解:根据第一行与第三列的和相等,斜对角线与第一行的和相等,列出方程组得:
;
故选:A.
【点评】本题考查了列二元一次方程组,理解题意是解题的关键.
10.(2025 武安市三模)若x4﹣3|m|+y|n|﹣2=2025是关于x,y的二元一次方程,且mn<0,﹣5<m﹣n<﹣3,则m+n的值是( )
A.﹣4 B.2 C.4 D.﹣2
【考点】二元一次方程的定义;绝对值.
【专题】一次方程(组)及应用;运算能力.
【答案】B
【分析】二元一次方程满足的条件:含有2个未知数,未知数的项的次数是1的整式方程.
【解答】解:由x4﹣3|m|+y|n|﹣2=2025是关于x,y的二元一次方程,得
.
解得m=±1,n=±3.
由mn<0,﹣5<m﹣n<﹣3,得
m=﹣1,n=3.
m+n=﹣1+3=2,
故选:B.
【点评】主要考查二元一次方程的概念,要求熟悉二元一次方程的形式及其特点:含有2个未知数,未知数的项的次数是1的整式方程.
二.填空题(共5小题)
11.(2025 泸县校级二模)已知关于x,y的方程组,且x﹣y=2,则k= ﹣2 .
【考点】解二元一次方程组.
【专题】一次方程(组)及应用;运算能力.
【答案】﹣2.
【分析】根据题意,两个方程相减,整理得x﹣y=﹣k,再根据x﹣y=2,进而得出答案.
【解答】解:,
②﹣①,得2x﹣2y=﹣2k,
∴x﹣y=﹣k,
∵x﹣y=2,
∴﹣k=2,即k=﹣2.
故答案为:﹣2.
【点评】本题考查了解二元一次方程组,掌握解二元一次方程组是方法解题的关键.
12.(2025 陕西模拟)如图,在长为20、宽为15的长方形中,有形状、大小完全相同的5个小长方形,则图中阴影部分的面积为 60 .
【考点】二元一次方程组的应用.
【专题】一次方程(组)及应用;应用意识.
【答案】60
【分析】设小长方形的长为x,宽为y,由图形列出方程组,即可求解.
【解答】解:设小长方形的长为x,宽为y,
由题意可得:,
解得:,
∴阴影部分的面积=15×20﹣5×12×4=60,
故答案为:60.
【点评】本题考查了二元一次方程组的应用,找到正确的数量共线是解题的关键.
13.(2025 仪征市校级三模)《九章算术》中的数学问题:1亩好田是300元,7亩坏田是500元,一人买了好田坏田一共是100亩,花费了10000元,问他各买了多少亩好田和坏田?设买了好田为x亩,坏田为y亩,根据题意列方程组得 .
【考点】由实际问题抽象出二元一次方程组.
【专题】一次方程(组)及应用;应用意识.
【答案】,
【分析】利用总价=单价×数量,结合“一人买了好田坏田一共是100亩,花费了10000元”,即可列出关于x,y的二元一次方程组,此题得解.
【解答】解:∵好田坏田一共买了100亩,
∴x+y=100;
∵1亩好田是300元,7亩坏田是500元,且共花费了10000元,
∴300x+500×(y÷7)=10000.
∴根据题意可列出方程,
故答案为:.
【点评】本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.
14.(2025 观山湖区校级一模)下列表格中给出的几组数都是关于x,y的二元一次方程ax﹣by=3的解,表格中m的值为 ﹣7 .
x 0 1 2 5
y 3 1 ﹣1 m
【考点】二元一次方程的解.
【专题】一次方程(组)及应用;运算能力.
【答案】见试题解答内容
【分析】由表格可知当x=0时y=3,x=1时y=1,于是得到关于a、b的方程组,求出a、b的值,即可写出这个二元一次方程,再把x=5代入即可求出m的值.
【解答】解:由表格可知当x=0时y=3,x=1时y=1,
∴,
解得,
∴关于x,y的二元一次方程ax﹣by=3为2x+y=3,
当x=5时,2×5+m=3,
∴m=﹣7,
故答案为:﹣7.
【点评】本题考查了二元一次方程的解,熟练掌握二元一次方程的解的定义是解题的关键.
15.(2025 淮阴区模拟)若是关于x、y的二元一次方程ax﹣3y=1的解,则a的值为 7 .
【考点】二元一次方程的解.
【答案】见试题解答内容
【分析】把方程的解代入二元一次方程,然后解关于a的一元一次方程即可.
【解答】解:把代入ax﹣3y=1得,a﹣3×2=1,
解得a=7.
故答案为:7.
【点评】本题考查了二元一次方程的解,熟记方程的解就是使方程的左右两边相等的未知数的值把方程的解是解题的关键.
三.解答题(共5小题)
16.(2025 天河区校级四模)陈塘关正遭受海夜叉的黑暗能量侵袭,哪吒需要启动两种法器凝聚能量:2个“乾坤圈”和5个“风火轮”同时运转1小时,可凝聚32单位净化能量;3个“乾坤圈”和2个“风火轮”联合运转1小时,能产生26单位净化能量.
(1)单个“乾坤圈”和单个“风火轮”每小时各能产生多少单位净化能量?
(2)结界需要450单位能量才能完全净化.若哪吒一次最多能启动18个法器(“乾坤圈”和“风火轮”),法器持续运转5小时,问哪吒最少要启动几个“乾坤圈”才能完全净化结界?
【考点】二元一次方程组的应用;一元一次不等式的应用.
【专题】一次方程(组)及应用;一元一次不等式(组)及应用;应用意识.
【答案】(1)单个“乾坤圈”每小时能产生6单位净化能量,单个“风火轮”每小时能产生4单位净化能量;
(2)哪吒最少要启动9个“乾坤圈”才能完全净化结界.
【分析】(1)设单个“乾坤圈”每小时能产生x单位净化能量,单个“风火轮”每小时能产生y单位净化能量,根据“2个'乾坤圈'和5个'风火轮'同时运转1小时,可凝聚32单位净化能量;3个'乾坤圈'和2个'风火轮'联合运转1小时,能产生26单位净化能量”,可列出关于x,y的二元一次方程组,解之即可得出结论;
(2)设哪吒启动m个“乾坤圈”,则启动(18﹣m)个“风火轮”,根据5个小时至少产生450单位能量,可列出关于m的一元一次不等式,解之取其中的最小值,即可得出结论.
【解答】解:(1)设单个“乾坤圈”每小时能产生x单位净化能量,单个“风火轮”每小时能产生y单位净化能量,
根据题意得:,
解得:.
答:单个“乾坤圈”每小时能产生6单位净化能量,单个“风火轮”每小时能产生4单位净化能量;
(2)设哪吒启动m个“乾坤圈”,则启动(18﹣m)个“风火轮”,
根据题意得:5[6m+4(18﹣m)]≥450,
解得:m≥9,
∴m的最小值为9.
答:哪吒最少要启动9个“乾坤圈”才能完全净化结界.
【点评】本题考查了二元一次方程组的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式.
17.(2025 从江县校级二模)2024年,随着《推动大规模设备更新和消费品以旧换新行动方案》等政策的出台,一系列优惠政策接踵而来.为此,某商场购进A,B两种型号的冰箱,据了解1台A型号冰箱、2台B型号冰箱进价共计9000元;2台A型号冰箱比1台B型号冰箱进价多500元.
(1)求A,B两种型号的冰箱每台的进价;
(2)由于需求不断增大,该商场准备购进两种型号的冰箱共100台,已知A型号冰箱的售价为2500元/台,B型号冰箱的售价为4100元/台,若购进A型号冰箱的数量不少于40台,设购进a台A型号冰箱,100台冰箱全部售完获利W(元),该商场应购进A,B两种型号的冰箱各多少台才能使W最大?W最大为多少元?
【考点】二元一次方程组的应用;一次函数的应用.
【专题】一次方程(组)及应用;一次函数及其应用;运算能力;应用意识.
【答案】(1)A型号的冰箱每台的进价为2000元,B型号的冰箱每台的进价为3500元;
(2)该商场应购进A、B两种型号的冰箱分别为40台、60台才能使W最大,W最大为56000元.
【分析】(1)设A型号的冰箱每台的进价为x元,B型号的冰箱每台的进价为y元,根据1台A型号冰箱、2台B型号冰箱进价共计9000元;2台A型号冰箱比1台B型号冰箱进价多500元,列出二元一次方程组,解方程组即可;
(2)设购进a台A型号冰箱,则设购进B型号冰箱(100﹣a)台,根据利润=(售价﹣进价)×数量,列出一次函数关系式,然后由一次函数的性质即可得出结果.
【解答】解:(1)设A型号的冰箱每台的进价为x元,B型号的冰箱每台的进价为y元,
由题意得:,
解得:,
答:A型号的冰箱每台的进价为2000元,B型号的冰箱每台的进价为3500元;
(2)设购进a台A型号冰箱,则设购进B型号冰箱(100﹣a)台,
由题意得:W=(2500﹣2000)a+(4100﹣3500)(100﹣a)=﹣100a+60000,
∵﹣100<0,
∴W随a的增大而减少,
∵a≥40,
∴a=40时,W最大,W最大为:﹣100×40+60000=56000(元),
此时,100﹣a=100﹣40=60,
答:该商场应购进A、B两种型号的冰箱分别为40台、60台才能使W最大,W最大为56000元.
【点评】本题考查了二元一次方程组的应用以及一次函数的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一次函数关系式.
18.(2025 东莞市校级三模)嘉嘉坚持每天做运动.已知某两组运动都由波比跳和深蹲组成,每个波比跳耗时5秒,每个深蹲也耗时5秒.运动软件显示,完成第一组运动,嘉嘉做了20个波比跳和40个深蹲,共消耗热量132大卡;完成第二组运动,嘉嘉做了20个波比跳和70个深蹲,共消耗热量156大卡.每个动作之间的衔接时间忽略不计.
(1)每个波比跳和每个深蹲各消耗热量多少大卡?
(2)若嘉嘉只做波比跳和深蹲两个动作,花10分钟,消耗至少200大卡,嘉嘉至少要做多少个波比跳?
【考点】二元一次方程组的应用;一元一次不等式的应用.
【专题】一次方程(组)及应用;一元一次不等式(组)及应用;应用意识.
【答案】(1)每个波比跳消耗热量5大卡,每个深蹲消耗热量0.8大卡;
(2)嘉嘉至少要做25个波比跳.
【分析】(1)设每个波比跳消耗热量x大卡,每个深蹲消耗热量y大卡,根据“嘉嘉做了20个波比跳和40个深蹲,共消耗热量132大卡;嘉嘉做了20个波比跳和70个深蹲,共消耗热量156大卡”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设要做m个波比跳,则要做(120﹣m)个深蹲,利用消耗总热量=每个波比跳消耗热量×做波比跳的数量+每个深蹲消耗热量×做深蹲的数量,结合要消耗至少200大卡,即可得出关于m的一元一次不等式,解之即可得出m的取值范围,再取其中的最小整数值即可得出结论.
【解答】解:(1)设每个波比跳消耗热量x大卡,每个深蹲消耗热量y大卡,
依题意得:,
解得:.
答:每个波比跳消耗热量5大卡,每个深蹲消耗热量0.8大卡.
(2)设要做m个波比跳,则要做(120﹣m)个深蹲,
依题意得:5m+0.8(120﹣m)≥200,
解得:m≥24.
又∵m为整数,
∴m的最小值为25.
答:嘉嘉至少要做25个波比跳.
【点评】本题考查了二元一次方程组的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式.
19.(2025 雁塔区校级一模)《九章算术》是人类科学史上应用数学的“算经之首”,书中记载:今有三人共车,二车空;二人共车,九人步.问:人与车各几何?译文:若3人坐一辆车,则两辆车是空的;若2人坐一辆车,则9人需要步行.问:人与车各多少?
【考点】二元一次方程组的应用.
【专题】一次方程(组)及应用;应用意识.
【答案】共有39人,15辆车.
【分析】设共有x人,y辆车,根据“今有三人共车,二车空;二人共车,九人步”,即可得出关于x,y的二元一次方程组,解之即可得出结论.
【解答】解:设共有x人,y辆车,
依题意得:,
解得:.
答:共有39人,15辆车.
【点评】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
20.(2025 怀仁市模拟)超市购物车使我们的购物方式更方便、快捷,如图为购物车叠放在一起的示意图.3辆超市购物车叠放在一起的长度为1.4m,6辆超市购物车叠放在一起的长度为2m.
(1)求每一辆超市购物车的长度;
(2)若该超市只有扶手电梯,且倾斜长度为12米,工作人员可以通过电梯转运超市购物车.为安全起见,规定电梯一次只能转运1列超市购物车,并且不能超过电梯总长度的,则工作人员一次最多可以转运多少辆超市购物车?
【考点】二元一次方程组的应用;一元一次不等式的应用.
【专题】一次方程(组)及应用;一元一次不等式(组)及应用;运算能力.
【答案】(1)每一辆超市购物车的长度为1米;
(2)工作人员一次最多可以转运16辆超市购物车.
【分析】(1)设每一辆超市购物车的长度为x米,两辆超市购物车重叠部分的长度为y米,根据3辆超市购物车叠放在一起的长度为1.4m,6辆超市购物车叠放在一起的长度为2m建立方程组求解即可;
(2)设一次最多可以转运m辆超市购物车,则购物车的总长度为[m 1﹣0.8(m﹣1)]m,再根据购物车的总长度不能超过电梯总长度的建立不等式求解即可.
【解答】解:(1)设每一辆超市购物车的长度为x米,两辆超市购物车重叠部分的长度为y米,
根据题意列二元一次方程得,,
解得,
即每一辆超市购物车的长度为1米,
答:每一辆超市购物车的长度为1米;
(2)设一次最多可以转运m辆超市购物车,
根据题意列一元一次不等式得,,
解得m≤16,
∵m取最大正整数,
∴m的值为16.
答:工作人员一次最多可以转运16辆超市购物车.
【点评】本题主要考查了二元一次方程组的应用,一元一次不等式的实际应用,正确理解题意列出方程组和不等式是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
暑假巩固复习 二元一次方程组
一.选择题(共10小题)
1.(2025 鸡西一模)为积极响应“环保垃圾分类”政策,某小区计划采购A、B两种类型的垃圾桶,用于提升小区垃圾分类的效率和质量.已知A型垃圾桶每个80元,B型垃圾桶每个60元.小区准备投入1200元资金全部用于购买这两种垃圾桶(两种垃圾桶都要买),则共有( )种购买方案
A.6 B.5 C.4 D.3
2.(2025 淅川县三模)我国古代著作《增删算法统宗》中记载了一首古算诗:“庭前孩童闹如簇,不知人数不知梨,每人四梨多十二,每人六梨恰齐足.”其大意:“孩童们在庭院玩耍,不知有多少人和梨,每人分4个梨,多12个梨;每人分6个梨,恰好分完.”设有x个梨,y个孩童,则可列方程组为( )
A. B.
C. D.
3.(2025 甘州区一模)古代数学趣题:老头提篮去赶集,一共花去七十七;满满装了一菜篮,十斤大肉三斤鱼;买好未曾问单价,只因回家心里急;道旁行人告诉他,九斤肉钱五斤鱼.意思是:77元钱共买了10斤肉和3斤鱼,9斤肉的钱等于5斤鱼的钱,问每斤肉和鱼各是多少钱?设每斤肉x元,每斤鱼y元,可列方程组为( )
A. B.
C. D.
4.(2025 齐齐哈尔四模)在数学知识竞赛中,为奖励成绩突出的学生,班级计划用100元钱购买甲,乙,丙三种奖品,三种奖品都要购买,甲种奖品每个5元,乙种奖品每个10元,丙种奖品每个15元,在丙种奖品不超过两个且钱全部用完的情况下,购买方案有( )
A.12种 B.15种 C.16种 D.14种
5.(2025 沿河县三模)若关于x,y的方程组与有相同的解,则m+n的值为( )
A.﹣2 B.﹣1 C.3 D.﹣5
6.(2025 河北区二模)《九章算术》共收有246个数学问题,分为九章,其中第八章“方程”篇中记载了这样一道题:“今有甲乙二人持钱不知其数,甲得乙半而钱八十,乙得甲太半而钱亦八十.问甲、乙持钱各几何?”题目大意是:甲、乙两人各带了若干钱,如果甲得到乙所有钱的一半,那么甲共有钱80.如果乙得到甲所有钱的,那么乙也共有钱80.若设甲、乙原本各持钱x,y,则根据题意可列方程组为( )
A. B.
C. D.
7.(2025 赤坎区校级四模)方程组的解是( )
A. B.
C. D.
8.(2025 孝感模拟)《孙子算经》是中国古代重要的数学著作,书中记载有这样一个问题:“今有三人共车,二车空;二人共车,九人步.问:人与车各几何?”其意思是:“今有3人坐一辆车,则有2辆车是空的;2人坐一辆车,则有9人需要步行.问:人与车各多少?”若设有x个人,y辆车,则可列方程组是( )
A. B.
C. D.
9.(2025 和平区二模)幻方起源于中国,是我国古代数学的杰作之一,是一种将数字安排在正方形格子中,使每一横行、每一竖列以及两条斜对角线上的数字和都相等的方法.如图①就是一个幻方,图②是一个未完成的幻方,则可以列出的方程组为( )
A.
B.
C.
D.
10.(2025 武安市三模)若x4﹣3|m|+y|n|﹣2=2025是关于x,y的二元一次方程,且mn<0,﹣5<m﹣n<﹣3,则m+n的值是( )
A.﹣4 B.2 C.4 D.﹣2
二.填空题(共5小题)
11.(2025 泸县校级二模)已知关于x,y的方程组,且x﹣y=2,则k= .
12.(2025 陕西模拟)如图,在长为20、宽为15的长方形中,有形状、大小完全相同的5个小长方形,则图中阴影部分的面积为 .
13.(2025 仪征市校级三模)《九章算术》中的数学问题:1亩好田是300元,7亩坏田是500元,一人买了好田坏田一共是100亩,花费了10000元,问他各买了多少亩好田和坏田?设买了好田为x亩,坏田为y亩,根据题意列方程组得 .
14.(2025 观山湖区校级一模)下列表格中给出的几组数都是关于x,y的二元一次方程ax﹣by=3的解,表格中m的值为 .
x 0 1 2 5
y 3 1 ﹣1 m
15.(2025 淮阴区模拟)若是关于x、y的二元一次方程ax﹣3y=1的解,则a的值为 .
三.解答题(共5小题)
16.(2025 天河区校级四模)陈塘关正遭受海夜叉的黑暗能量侵袭,哪吒需要启动两种法器凝聚能量:2个“乾坤圈”和5个“风火轮”同时运转1小时,可凝聚32单位净化能量;3个“乾坤圈”和2个“风火轮”联合运转1小时,能产生26单位净化能量.
(1)单个“乾坤圈”和单个“风火轮”每小时各能产生多少单位净化能量?
(2)结界需要450单位能量才能完全净化.若哪吒一次最多能启动18个法器(“乾坤圈”和“风火轮”),法器持续运转5小时,问哪吒最少要启动几个“乾坤圈”才能完全净化结界?
17.(2025 从江县校级二模)2024年,随着《推动大规模设备更新和消费品以旧换新行动方案》等政策的出台,一系列优惠政策接踵而来.为此,某商场购进A,B两种型号的冰箱,据了解1台A型号冰箱、2台B型号冰箱进价共计9000元;2台A型号冰箱比1台B型号冰箱进价多500元.
(1)求A,B两种型号的冰箱每台的进价;
(2)由于需求不断增大,该商场准备购进两种型号的冰箱共100台,已知A型号冰箱的售价为2500元/台,B型号冰箱的售价为4100元/台,若购进A型号冰箱的数量不少于40台,设购进a台A型号冰箱,100台冰箱全部售完获利W(元),该商场应购进A,B两种型号的冰箱各多少台才能使W最大?W最大为多少元?
18.(2025 东莞市校级三模)嘉嘉坚持每天做运动.已知某两组运动都由波比跳和深蹲组成,每个波比跳耗时5秒,每个深蹲也耗时5秒.运动软件显示,完成第一组运动,嘉嘉做了20个波比跳和40个深蹲,共消耗热量132大卡;完成第二组运动,嘉嘉做了20个波比跳和70个深蹲,共消耗热量156大卡.每个动作之间的衔接时间忽略不计.
(1)每个波比跳和每个深蹲各消耗热量多少大卡?
(2)若嘉嘉只做波比跳和深蹲两个动作,花10分钟,消耗至少200大卡,嘉嘉至少要做多少个波比跳?
19.(2025 雁塔区校级一模)《九章算术》是人类科学史上应用数学的“算经之首”,书中记载:今有三人共车,二车空;二人共车,九人步.问:人与车各几何?译文:若3人坐一辆车,则两辆车是空的;若2人坐一辆车,则9人需要步行.问:人与车各多少?
20.(2025 怀仁市模拟)超市购物车使我们的购物方式更方便、快捷,如图为购物车叠放在一起的示意图.3辆超市购物车叠放在一起的长度为1.4m,6辆超市购物车叠放在一起的长度为2m.
(1)求每一辆超市购物车的长度;
(2)若该超市只有扶手电梯,且倾斜长度为12米,工作人员可以通过电梯转运超市购物车.为安全起见,规定电梯一次只能转运1列超市购物车,并且不能超过电梯总长度的,则工作人员一次最多可以转运多少辆超市购物车?
暑假巩固复习 二元一次方程组
参考答案与试题解析
一.选择题(共10小题)
1.(2025 鸡西一模)为积极响应“环保垃圾分类”政策,某小区计划采购A、B两种类型的垃圾桶,用于提升小区垃圾分类的效率和质量.已知A型垃圾桶每个80元,B型垃圾桶每个60元.小区准备投入1200元资金全部用于购买这两种垃圾桶(两种垃圾桶都要买),则共有( )种购买方案
A.6 B.5 C.4 D.3
【考点】二元一次方程的应用.
【专题】一次方程(组)及应用;应用意识.
【答案】C
【分析】购买x个A型垃圾桶,y个B型垃圾桶,利用总价=单价×数量,可列出关于x,y的二元一次方程,结合x,y均为正整数,可得出共有4种购买方案.
【解答】解:购买x个A型垃圾桶,y个B型垃圾桶,
根据题意得:80x+60y=1200,
∴y=20x,
又∵x,y均为正整数,
∴或或或,
∴共有4种购买方案.
故选:C.
【点评】本题考查了二元一次方程的应用,找准等量关系,正确列出二元一次方程是解题的关键.
2.(2025 淅川县三模)我国古代著作《增删算法统宗》中记载了一首古算诗:“庭前孩童闹如簇,不知人数不知梨,每人四梨多十二,每人六梨恰齐足.”其大意:“孩童们在庭院玩耍,不知有多少人和梨,每人分4个梨,多12个梨;每人分6个梨,恰好分完.”设有x个梨,y个孩童,则可列方程组为( )
A. B.
C. D.
【考点】由实际问题抽象出二元一次方程组.
【专题】方程与不等式;运算能力.
【答案】A
【分析】根据“每人分4个梨,多12个梨;每人分6个梨,恰好分完.”列方程组即可.
【解答】解:由题意可设有x个梨,y个孩童,
∴,
∴A选项符合,
故选:A.
【点评】本题考查由实际问题抽象出二元一次方程组,理解题意,找到等量关系是解题关键.
3.(2025 甘州区一模)古代数学趣题:老头提篮去赶集,一共花去七十七;满满装了一菜篮,十斤大肉三斤鱼;买好未曾问单价,只因回家心里急;道旁行人告诉他,九斤肉钱五斤鱼.意思是:77元钱共买了10斤肉和3斤鱼,9斤肉的钱等于5斤鱼的钱,问每斤肉和鱼各是多少钱?设每斤肉x元,每斤鱼y元,可列方程组为( )
A. B.
C. D.
【考点】由实际问题抽象出二元一次方程组.
【专题】一次方程(组)及应用;应用意识.
【答案】A
【分析】根据“77元钱共买了10斤肉和3斤鱼,9斤肉的钱等于5斤鱼的钱”,即可列出关于x,y的二元一次方程组,此题得解.
【解答】解:∵77元钱共买了10斤肉和3斤鱼
∴10x+3y=77;
∵9斤肉的钱等于5斤鱼的钱,
∴9x=5y.
∴根据题意可列出方程组.
故选:A.
【点评】本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.
4.(2025 齐齐哈尔四模)在数学知识竞赛中,为奖励成绩突出的学生,班级计划用100元钱购买甲,乙,丙三种奖品,三种奖品都要购买,甲种奖品每个5元,乙种奖品每个10元,丙种奖品每个15元,在丙种奖品不超过两个且钱全部用完的情况下,购买方案有( )
A.12种 B.15种 C.16种 D.14种
【考点】三元一次方程组的应用.
【专题】一次方程(组)及应用;运算能力.
【答案】D
【分析】设购买A、B、C三种奖品分别为x,y,z个,根据题意列方程得5x+10y+15z=100,化简后根据x,y,z均为正整数,结合C种奖品不超过两个分类讨论,确定解的个数即可.
【解答】解:设购买A、B、C三种奖品分别为x,y,z个,
根据题意列方程得5x+10y+15z=100,
即x+2y+3z=20,
由题意得x,y,z均为正整数.
①当z=1时,x+2y=17,
∴,
∴y分别取1,3,5,7,9,11,13,15共8种情况时,x为正整数;
②当z=2时,x+2y=14,
∴,
∴y可以分别取2,4,6,8,10,12共6种情况,x为正整数;
综上所述:共有8+6=14种购买方案,
综上所述,只有选项D正确,符合题意.
故选:D.
【点评】本题考查了三元一次方程组的应用,根据题意列出方程,并确定方程组的解为正整数是解题关键.
5.(2025 沿河县三模)若关于x,y的方程组与有相同的解,则m+n的值为( )
A.﹣2 B.﹣1 C.3 D.﹣5
【考点】二元一次方程组的解.
【专题】一次方程(组)及应用;运算能力.
【答案】A
【分析】先根据题意得出相同的解是,然后分别代入方程mx+ny=1和方程nx+my=﹣7中得到关于m、n的方程组,直接相加即可求解.
【解答】解:根据题意得两个方程组相同的解是,
把代入方程mx+ny=1和方程nx+my=﹣7中,得,,
①+②,得3m+3n=﹣6,
∴m+n=﹣2,
故选:A.
【点评】本题考查了二元一次方程组的解,熟练掌握二元一次方程组的解的定义是解题的关键.
6.(2025 河北区二模)《九章算术》共收有246个数学问题,分为九章,其中第八章“方程”篇中记载了这样一道题:“今有甲乙二人持钱不知其数,甲得乙半而钱八十,乙得甲太半而钱亦八十.问甲、乙持钱各几何?”题目大意是:甲、乙两人各带了若干钱,如果甲得到乙所有钱的一半,那么甲共有钱80.如果乙得到甲所有钱的,那么乙也共有钱80.若设甲、乙原本各持钱x,y,则根据题意可列方程组为( )
A. B.
C. D.
【考点】由实际问题抽象出二元一次方程组;数学常识.
【专题】一次方程(组)及应用;应用意识.
【答案】D
【分析】根据题意可得,甲的钱+乙所有钱的一半=80,乙的钱+甲所有钱的80,据此列方程组可得.
【解答】解:根据题意,得:,
故选:D.
【点评】本题考查了由实际问题抽象出二元一次方程组,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列出方程组.
7.(2025 赤坎区校级四模)方程组的解是( )
A. B.
C. D.
【考点】解二元一次方程组.
【专题】一次方程(组)及应用;运算能力.
【答案】B
【分析】用加减消元法解方程组即可.
【解答】解:将方程标号得,
②﹣①得x=2,
将x=2代入①得2+y=6,
解得y=4,
∴,
故选:B.
【点评】本题考查了解一元二次方程,熟练掌握该知识点是关键.
8.(2025 孝感模拟)《孙子算经》是中国古代重要的数学著作,书中记载有这样一个问题:“今有三人共车,二车空;二人共车,九人步.问:人与车各几何?”其意思是:“今有3人坐一辆车,则有2辆车是空的;2人坐一辆车,则有9人需要步行.问:人与车各多少?”若设有x个人,y辆车,则可列方程组是( )
A. B.
C. D.
【考点】二元一次方程组的应用.
【专题】一次方程(组)及应用;应用意识.
【答案】C
【分析】根据今有3人坐一辆车,则有2辆车是空的;2人坐一辆车,则有9人需要步行;列出二元一次方程组即可.
【解答】解:根据题意得:,
故选:C.
【点评】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
9.(2025 和平区二模)幻方起源于中国,是我国古代数学的杰作之一,是一种将数字安排在正方形格子中,使每一横行、每一竖列以及两条斜对角线上的数字和都相等的方法.如图①就是一个幻方,图②是一个未完成的幻方,则可以列出的方程组为( )
A.
B.
C.
D.
【考点】由实际问题抽象出二元一次方程组.
【专题】一次方程(组)及应用;运算能力.
【答案】A
【分析】根据第一行与第三列的和相等,斜对角线与第一行的和相等,列出方程组即可.
【解答】解:根据第一行与第三列的和相等,斜对角线与第一行的和相等,列出方程组得:
;
故选:A.
【点评】本题考查了列二元一次方程组,理解题意是解题的关键.
10.(2025 武安市三模)若x4﹣3|m|+y|n|﹣2=2025是关于x,y的二元一次方程,且mn<0,﹣5<m﹣n<﹣3,则m+n的值是( )
A.﹣4 B.2 C.4 D.﹣2
【考点】二元一次方程的定义;绝对值.
【专题】一次方程(组)及应用;运算能力.
【答案】B
【分析】二元一次方程满足的条件:含有2个未知数,未知数的项的次数是1的整式方程.
【解答】解:由x4﹣3|m|+y|n|﹣2=2025是关于x,y的二元一次方程,得
.
解得m=±1,n=±3.
由mn<0,﹣5<m﹣n<﹣3,得
m=﹣1,n=3.
m+n=﹣1+3=2,
故选:B.
【点评】主要考查二元一次方程的概念,要求熟悉二元一次方程的形式及其特点:含有2个未知数,未知数的项的次数是1的整式方程.
二.填空题(共5小题)
11.(2025 泸县校级二模)已知关于x,y的方程组,且x﹣y=2,则k= ﹣2 .
【考点】解二元一次方程组.
【专题】一次方程(组)及应用;运算能力.
【答案】﹣2.
【分析】根据题意,两个方程相减,整理得x﹣y=﹣k,再根据x﹣y=2,进而得出答案.
【解答】解:,
②﹣①,得2x﹣2y=﹣2k,
∴x﹣y=﹣k,
∵x﹣y=2,
∴﹣k=2,即k=﹣2.
故答案为:﹣2.
【点评】本题考查了解二元一次方程组,掌握解二元一次方程组是方法解题的关键.
12.(2025 陕西模拟)如图,在长为20、宽为15的长方形中,有形状、大小完全相同的5个小长方形,则图中阴影部分的面积为 60 .
【考点】二元一次方程组的应用.
【专题】一次方程(组)及应用;应用意识.
【答案】60
【分析】设小长方形的长为x,宽为y,由图形列出方程组,即可求解.
【解答】解:设小长方形的长为x,宽为y,
由题意可得:,
解得:,
∴阴影部分的面积=15×20﹣5×12×4=60,
故答案为:60.
【点评】本题考查了二元一次方程组的应用,找到正确的数量共线是解题的关键.
13.(2025 仪征市校级三模)《九章算术》中的数学问题:1亩好田是300元,7亩坏田是500元,一人买了好田坏田一共是100亩,花费了10000元,问他各买了多少亩好田和坏田?设买了好田为x亩,坏田为y亩,根据题意列方程组得 .
【考点】由实际问题抽象出二元一次方程组.
【专题】一次方程(组)及应用;应用意识.
【答案】,
【分析】利用总价=单价×数量,结合“一人买了好田坏田一共是100亩,花费了10000元”,即可列出关于x,y的二元一次方程组,此题得解.
【解答】解:∵好田坏田一共买了100亩,
∴x+y=100;
∵1亩好田是300元,7亩坏田是500元,且共花费了10000元,
∴300x+500×(y÷7)=10000.
∴根据题意可列出方程,
故答案为:.
【点评】本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.
14.(2025 观山湖区校级一模)下列表格中给出的几组数都是关于x,y的二元一次方程ax﹣by=3的解,表格中m的值为 ﹣7 .
x 0 1 2 5
y 3 1 ﹣1 m
【考点】二元一次方程的解.
【专题】一次方程(组)及应用;运算能力.
【答案】见试题解答内容
【分析】由表格可知当x=0时y=3,x=1时y=1,于是得到关于a、b的方程组,求出a、b的值,即可写出这个二元一次方程,再把x=5代入即可求出m的值.
【解答】解:由表格可知当x=0时y=3,x=1时y=1,
∴,
解得,
∴关于x,y的二元一次方程ax﹣by=3为2x+y=3,
当x=5时,2×5+m=3,
∴m=﹣7,
故答案为:﹣7.
【点评】本题考查了二元一次方程的解,熟练掌握二元一次方程的解的定义是解题的关键.
15.(2025 淮阴区模拟)若是关于x、y的二元一次方程ax﹣3y=1的解,则a的值为 7 .
【考点】二元一次方程的解.
【答案】见试题解答内容
【分析】把方程的解代入二元一次方程,然后解关于a的一元一次方程即可.
【解答】解:把代入ax﹣3y=1得,a﹣3×2=1,
解得a=7.
故答案为:7.
【点评】本题考查了二元一次方程的解,熟记方程的解就是使方程的左右两边相等的未知数的值把方程的解是解题的关键.
三.解答题(共5小题)
16.(2025 天河区校级四模)陈塘关正遭受海夜叉的黑暗能量侵袭,哪吒需要启动两种法器凝聚能量:2个“乾坤圈”和5个“风火轮”同时运转1小时,可凝聚32单位净化能量;3个“乾坤圈”和2个“风火轮”联合运转1小时,能产生26单位净化能量.
(1)单个“乾坤圈”和单个“风火轮”每小时各能产生多少单位净化能量?
(2)结界需要450单位能量才能完全净化.若哪吒一次最多能启动18个法器(“乾坤圈”和“风火轮”),法器持续运转5小时,问哪吒最少要启动几个“乾坤圈”才能完全净化结界?
【考点】二元一次方程组的应用;一元一次不等式的应用.
【专题】一次方程(组)及应用;一元一次不等式(组)及应用;应用意识.
【答案】(1)单个“乾坤圈”每小时能产生6单位净化能量,单个“风火轮”每小时能产生4单位净化能量;
(2)哪吒最少要启动9个“乾坤圈”才能完全净化结界.
【分析】(1)设单个“乾坤圈”每小时能产生x单位净化能量,单个“风火轮”每小时能产生y单位净化能量,根据“2个'乾坤圈'和5个'风火轮'同时运转1小时,可凝聚32单位净化能量;3个'乾坤圈'和2个'风火轮'联合运转1小时,能产生26单位净化能量”,可列出关于x,y的二元一次方程组,解之即可得出结论;
(2)设哪吒启动m个“乾坤圈”,则启动(18﹣m)个“风火轮”,根据5个小时至少产生450单位能量,可列出关于m的一元一次不等式,解之取其中的最小值,即可得出结论.
【解答】解:(1)设单个“乾坤圈”每小时能产生x单位净化能量,单个“风火轮”每小时能产生y单位净化能量,
根据题意得:,
解得:.
答:单个“乾坤圈”每小时能产生6单位净化能量,单个“风火轮”每小时能产生4单位净化能量;
(2)设哪吒启动m个“乾坤圈”,则启动(18﹣m)个“风火轮”,
根据题意得:5[6m+4(18﹣m)]≥450,
解得:m≥9,
∴m的最小值为9.
答:哪吒最少要启动9个“乾坤圈”才能完全净化结界.
【点评】本题考查了二元一次方程组的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式.
17.(2025 从江县校级二模)2024年,随着《推动大规模设备更新和消费品以旧换新行动方案》等政策的出台,一系列优惠政策接踵而来.为此,某商场购进A,B两种型号的冰箱,据了解1台A型号冰箱、2台B型号冰箱进价共计9000元;2台A型号冰箱比1台B型号冰箱进价多500元.
(1)求A,B两种型号的冰箱每台的进价;
(2)由于需求不断增大,该商场准备购进两种型号的冰箱共100台,已知A型号冰箱的售价为2500元/台,B型号冰箱的售价为4100元/台,若购进A型号冰箱的数量不少于40台,设购进a台A型号冰箱,100台冰箱全部售完获利W(元),该商场应购进A,B两种型号的冰箱各多少台才能使W最大?W最大为多少元?
【考点】二元一次方程组的应用;一次函数的应用.
【专题】一次方程(组)及应用;一次函数及其应用;运算能力;应用意识.
【答案】(1)A型号的冰箱每台的进价为2000元,B型号的冰箱每台的进价为3500元;
(2)该商场应购进A、B两种型号的冰箱分别为40台、60台才能使W最大,W最大为56000元.
【分析】(1)设A型号的冰箱每台的进价为x元,B型号的冰箱每台的进价为y元,根据1台A型号冰箱、2台B型号冰箱进价共计9000元;2台A型号冰箱比1台B型号冰箱进价多500元,列出二元一次方程组,解方程组即可;
(2)设购进a台A型号冰箱,则设购进B型号冰箱(100﹣a)台,根据利润=(售价﹣进价)×数量,列出一次函数关系式,然后由一次函数的性质即可得出结果.
【解答】解:(1)设A型号的冰箱每台的进价为x元,B型号的冰箱每台的进价为y元,
由题意得:,
解得:,
答:A型号的冰箱每台的进价为2000元,B型号的冰箱每台的进价为3500元;
(2)设购进a台A型号冰箱,则设购进B型号冰箱(100﹣a)台,
由题意得:W=(2500﹣2000)a+(4100﹣3500)(100﹣a)=﹣100a+60000,
∵﹣100<0,
∴W随a的增大而减少,
∵a≥40,
∴a=40时,W最大,W最大为:﹣100×40+60000=56000(元),
此时,100﹣a=100﹣40=60,
答:该商场应购进A、B两种型号的冰箱分别为40台、60台才能使W最大,W最大为56000元.
【点评】本题考查了二元一次方程组的应用以及一次函数的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一次函数关系式.
18.(2025 东莞市校级三模)嘉嘉坚持每天做运动.已知某两组运动都由波比跳和深蹲组成,每个波比跳耗时5秒,每个深蹲也耗时5秒.运动软件显示,完成第一组运动,嘉嘉做了20个波比跳和40个深蹲,共消耗热量132大卡;完成第二组运动,嘉嘉做了20个波比跳和70个深蹲,共消耗热量156大卡.每个动作之间的衔接时间忽略不计.
(1)每个波比跳和每个深蹲各消耗热量多少大卡?
(2)若嘉嘉只做波比跳和深蹲两个动作,花10分钟,消耗至少200大卡,嘉嘉至少要做多少个波比跳?
【考点】二元一次方程组的应用;一元一次不等式的应用.
【专题】一次方程(组)及应用;一元一次不等式(组)及应用;应用意识.
【答案】(1)每个波比跳消耗热量5大卡,每个深蹲消耗热量0.8大卡;
(2)嘉嘉至少要做25个波比跳.
【分析】(1)设每个波比跳消耗热量x大卡,每个深蹲消耗热量y大卡,根据“嘉嘉做了20个波比跳和40个深蹲,共消耗热量132大卡;嘉嘉做了20个波比跳和70个深蹲,共消耗热量156大卡”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设要做m个波比跳,则要做(120﹣m)个深蹲,利用消耗总热量=每个波比跳消耗热量×做波比跳的数量+每个深蹲消耗热量×做深蹲的数量,结合要消耗至少200大卡,即可得出关于m的一元一次不等式,解之即可得出m的取值范围,再取其中的最小整数值即可得出结论.
【解答】解:(1)设每个波比跳消耗热量x大卡,每个深蹲消耗热量y大卡,
依题意得:,
解得:.
答:每个波比跳消耗热量5大卡,每个深蹲消耗热量0.8大卡.
(2)设要做m个波比跳,则要做(120﹣m)个深蹲,
依题意得:5m+0.8(120﹣m)≥200,
解得:m≥24.
又∵m为整数,
∴m的最小值为25.
答:嘉嘉至少要做25个波比跳.
【点评】本题考查了二元一次方程组的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式.
19.(2025 雁塔区校级一模)《九章算术》是人类科学史上应用数学的“算经之首”,书中记载:今有三人共车,二车空;二人共车,九人步.问:人与车各几何?译文:若3人坐一辆车,则两辆车是空的;若2人坐一辆车,则9人需要步行.问:人与车各多少?
【考点】二元一次方程组的应用.
【专题】一次方程(组)及应用;应用意识.
【答案】共有39人,15辆车.
【分析】设共有x人,y辆车,根据“今有三人共车,二车空;二人共车,九人步”,即可得出关于x,y的二元一次方程组,解之即可得出结论.
【解答】解:设共有x人,y辆车,
依题意得:,
解得:.
答:共有39人,15辆车.
【点评】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
20.(2025 怀仁市模拟)超市购物车使我们的购物方式更方便、快捷,如图为购物车叠放在一起的示意图.3辆超市购物车叠放在一起的长度为1.4m,6辆超市购物车叠放在一起的长度为2m.
(1)求每一辆超市购物车的长度;
(2)若该超市只有扶手电梯,且倾斜长度为12米,工作人员可以通过电梯转运超市购物车.为安全起见,规定电梯一次只能转运1列超市购物车,并且不能超过电梯总长度的,则工作人员一次最多可以转运多少辆超市购物车?
【考点】二元一次方程组的应用;一元一次不等式的应用.
【专题】一次方程(组)及应用;一元一次不等式(组)及应用;运算能力.
【答案】(1)每一辆超市购物车的长度为1米;
(2)工作人员一次最多可以转运16辆超市购物车.
【分析】(1)设每一辆超市购物车的长度为x米,两辆超市购物车重叠部分的长度为y米,根据3辆超市购物车叠放在一起的长度为1.4m,6辆超市购物车叠放在一起的长度为2m建立方程组求解即可;
(2)设一次最多可以转运m辆超市购物车,则购物车的总长度为[m 1﹣0.8(m﹣1)]m,再根据购物车的总长度不能超过电梯总长度的建立不等式求解即可.
【解答】解:(1)设每一辆超市购物车的长度为x米,两辆超市购物车重叠部分的长度为y米,
根据题意列二元一次方程得,,
解得,
即每一辆超市购物车的长度为1米,
答:每一辆超市购物车的长度为1米;
(2)设一次最多可以转运m辆超市购物车,
根据题意列一元一次不等式得,,
解得m≤16,
∵m取最大正整数,
∴m的值为16.
答:工作人员一次最多可以转运16辆超市购物车.
【点评】本题主要考查了二元一次方程组的应用,一元一次不等式的实际应用,正确理解题意列出方程组和不等式是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
