第二十六章 反比例函数(暑假复习.含解析)-2024-2025学年九年级下册数学人教版
文档属性
| 名称 | 第二十六章 反比例函数(暑假复习.含解析)-2024-2025学年九年级下册数学人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-06 14:57:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
暑假巩固复习 反比例函数
一.选择题(共10小题)
1.(2025 天河区校级四模)如图,在平面直角坐标系中,从坐标原点出发的两条射线OA,OB.且OA⊥OB,两射线分别与函数和相交,交点分别为A,B,连接AB,则sin∠ABO的值为( )
A. B. C. D.
2.(2025 高要区校级三模)机器狗是一种模拟真实犬只形态和部分行为的机器装置,最快移动速度v(m/s)是载重后总质量M(kg)的反比例函数.已知一款机器狗(如图所示)载重后总质量M=30kg时,它的最快移动速度v=2m/s;当其载重后总质量M=60kg时,它的最快移动速度v=( )m/s.
A.4 B.3 C.2 D.1
3.(2025 广州)若|k|=﹣k(k≠0),则反比例函数y的图象在( )
A.第一、二象限 B.第一、三象限
C.第二、四象限 D.第三、四象限
4.(2025 孝义市三模)已知点A(x1,y1),B(x2,y2)都在反比例函数的图象上,且当x1<0<x2时,y1>y2,则k的取值范围是( )
A.k≤﹣1 B.k≥1 C.k<1 D.k>1
5.(2025 金安区校级一模)如图,直线y=mx+n交反比例函数y(x>0)的图象于点A和点B,交x轴于点C,,过点A作AD⊥x轴于点D,连接BD并延长,交y轴于点P,连接PC.若△PCD的面积为6,则k的值为( )
A.6 B.8 C.9 D.18
6.(2025 永州模拟)在一个密闭的容器内装有一定质量的某种气体,当它的容积V改变时,气体的密度ρ也随之改变,ρ与V之间在一定范围内满足,如图所示.当ρ为2.4kg/m3时,V的值是( )
A.3m3 B.3.4m3 C.5m3 D.7.2m3
7.(2025 厦门校级模拟)在平面直角坐标系中,反比例函数的图象如图所示,点A,B不在该反比例函数的图象上,则k的值可以为( )
A.﹣1 B.﹣2 C.﹣3 D.﹣4
8.(2025 淅川县三模)某教材《阅读与思考》中的部分内容如下:
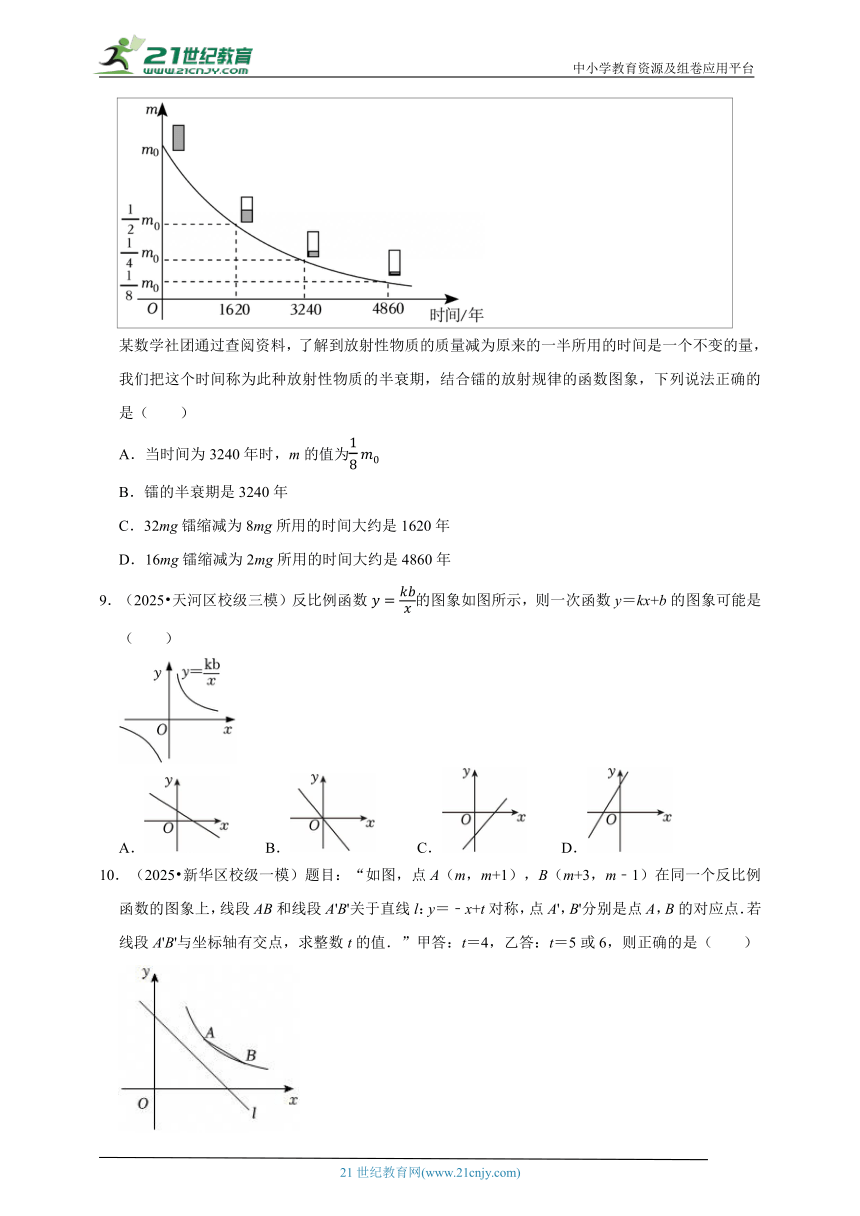
科学家如何测算岩石的年龄 你知道科学家如何测算岩石的年龄吗?解决这个问题时也用到函数这个数学工具. 1903年,英国物理学家卢瑟福通过实验证实,放射性物质在放出射线后,这种物质的质量将减少,减少的速度开始较快,后来较慢.物质所剩的质量与时间成某种函数关系,如图为表示镭的放射规律的函数图象.
某数学社团通过查阅资料,了解到放射性物质的质量减为原来的一半所用的时间是一个不变的量,我们把这个时间称为此种放射性物质的半衰期,结合镭的放射规律的函数图象,下列说法正确的是( )
A.当时间为3240年时,m的值为
B.镭的半衰期是3240年
C.32mg镭缩减为8mg所用的时间大约是1620年
D.16mg镭缩减为2mg所用的时间大约是4860年
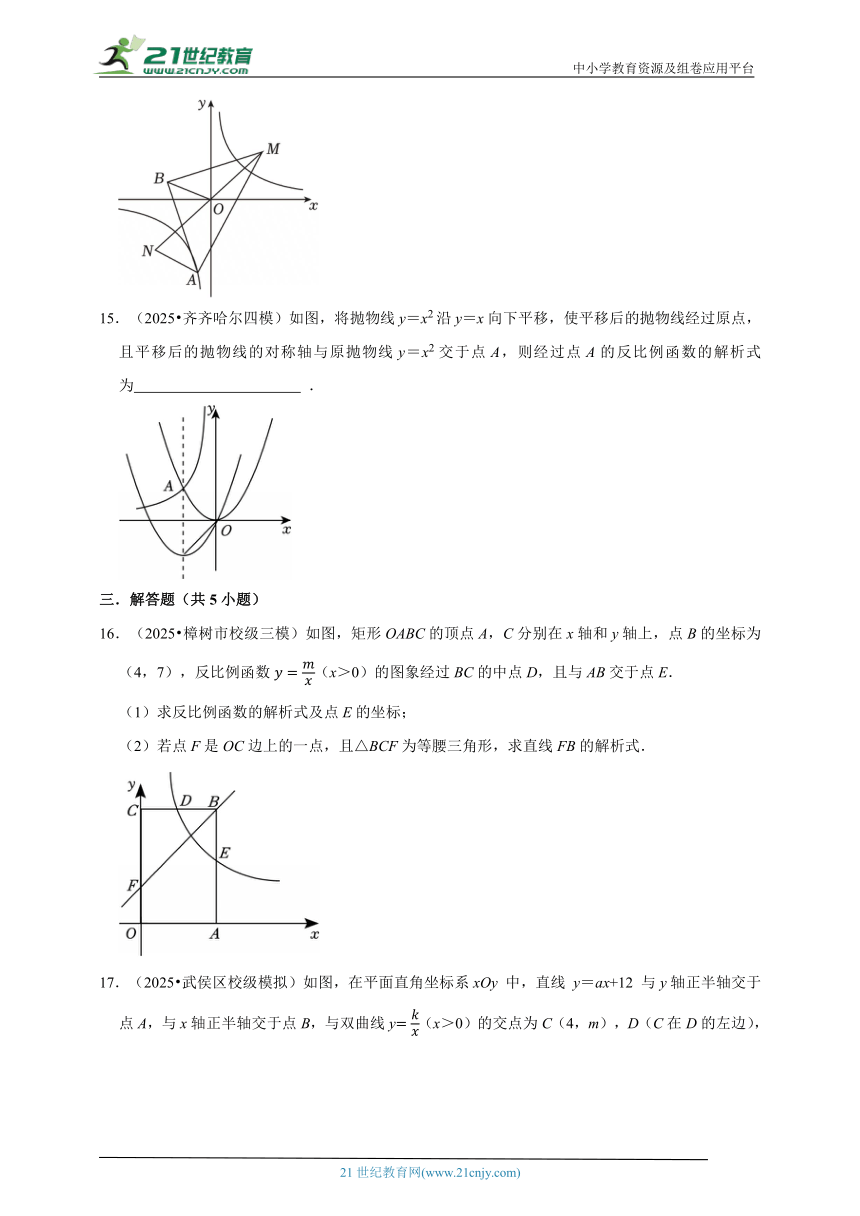
9.(2025 天河区校级三模)反比例函数的图象如图所示,则一次函数y=kx+b的图象可能是( )
A. B. C. D.
10.(2025 新华区校级一模)题目:“如图,点A(m,m+1),B(m+3,m﹣1)在同一个反比例函数的图象上,线段AB和线段A'B'关于直线l:y=﹣x+t对称,点A',B'分别是点A,B的对应点.若线段A'B'与坐标轴有交点,求整数t的值.”甲答:t=4,乙答:t=5或6,则正确的是( )
A.只有甲答的对
B.只有乙答的对
C.两人答案合在一起才完整
D.两人答案合在一起也不完整
二.填空题(共5小题)
11.(2025 武汉)在平面直角坐标系中,某反比例函数y的图象分别位于第一、第三象限.写出一个满足条件的k的值是 .
12.(2025 大同模拟)近视眼镜的度数y(度)与镜片焦距x(米)之间有如图所示的反比例函数关系,王老师计划配一副近视眼镜,测得镜片的焦距为0.16米,则王老师镜片的度数为 度.
13.(2025 普兰店区一模)我们称关于x的二次函数y=px2+qx+k为一次函数y=px+q和反比例函数的“非对称韦达函数”,一次函数y=px+q和反比例函数的交点称为二次函数y=px2+qx+k的“韦达点”,若一次函数y=ax+2b和反比例函数的“非对称韦达函数”的两个“韦达点”的横坐标为s,t,其中实数a>b>c,a+b+c=0.则的取值范围为 .
14.(2025 武安市二模)对于反比例函数y(k>0),称M(,),N(,)为该反比例函数图象的两个“焦点”,且若P为反比例函数图象上的任意一点,则恒有|PM﹣PN|=2.如图,M,N为反比例函数y(k>0)的图象的两个焦点,A为该反比例函数在第三象限的图象上的一个动点,B为∠NAM的平分线上的一点,且AB⊥BM,OB=2,则k的值为 .
15.(2025 齐齐哈尔四模)如图,将抛物线y=x2沿y=x向下平移,使平移后的抛物线经过原点,且平移后的抛物线的对称轴与原抛物线y=x2交于点A,则经过点A的反比例函数的解析式为 .
三.解答题(共5小题)
16.(2025 樟树市校级三模)如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(4,7),反比例函数(x>0)的图象经过BC的中点D,且与AB交于点E.
(1)求反比例函数的解析式及点E的坐标;
(2)若点F是OC边上的一点,且△BCF为等腰三角形,求直线FB的解析式.
17.(2025 武侯区校级模拟)如图,在平面直角坐标系xOy 中,直线 y=ax+12 与y轴正半轴交于点A,与x轴正半轴交于点B,与双曲线y(x>0)的交点为C(4,m),D(C在D的左边),且C,D恰好是线段AB的三等分点.
(1)求a,k的值;
(2)P是线段OB上一点,连接CP.
①若CP将△AOB 的面积分成5:7两部分,求点P的坐标;
②将直线CP沿直线AB进行翻折,与双曲线交于另一点E,连接PE,若 CE=2CP,求点P的坐标.
18.(2025 广州)如图,曲线G:y(x>0)经过点P(4,t).
(1)求t的值;
(2)直线l:y=﹣x+b也经过点P,求l与y轴交点的坐标,并在图中画出直线l;
(3)在(2)的条件下,若在l与两坐标轴围成的三角形内部(不包含边界)随机取一个格点(横、纵坐标都是整数的点),求该格点在曲线G上的概率.
19.(2025 巴中模拟)如图,在平面直角坐标系xOy中,一次函数y=kx+b与反比例函数y(x>0)的图象交于点A(2,6),B(n,3),与x轴,y轴分别交于C,D两点.
(1)求一次函数和反比例函数的表达式;
(2)请根据图象直接写出关于x的不等式kx+b(x>0)的解集;
(3)在直线CD上有点P,△PCO的面积为12,求点P的坐标.
20.(2025 浙江模拟)如图,在平面直角坐标系中,点C,D都在反比例函数的图象上,CE⊥x轴于点E,DB⊥x轴于点B,OC与BD的延长线相交于点A.
(1)若△OCE的面积为6.
①求反比例函数的表达式.
②当y≤4时,求自变量x的取值范围.
(2)已知CE=4,BD,求AB的长.
暑假巩固复习 反比例函数
参考答案与试题解析
一.选择题(共10小题)
1.(2025 天河区校级四模)如图,在平面直角坐标系中,从坐标原点出发的两条射线OA,OB.且OA⊥OB,两射线分别与函数和相交,交点分别为A,B,连接AB,则sin∠ABO的值为( )
A. B. C. D.
【考点】反比例函数图象上点的坐标特征;解直角三角形;反比例函数的性质.
【专题】函数及其图象;运算能力.
【答案】D
【分析】分别过点A,B作AC⊥x轴于点C,BD⊥x轴于点D,△OAC∽△BOD,结合反比例函数k的几何意义,求出,再利用勾股定理求出,最后利用正弦的定义即可求解.
【解答】解:分别过点A,B作AC⊥x轴于点C,BD⊥x轴于点D,如图所示:
因为OA⊥OB,
所以∠AOB=90°,∠AOC+∠OAC=∠AOC+∠BOD=90°,
所以∠OAC=∠BOD,
又因为∠ACO=∠BDO=90°,
所以△OAC∽△BOD,,
因为
所以,(负值舍去),
所以,
所以,
故选:D.
【点评】本题考查了反比例函数k的几何意义,相似三角形的判定与性质,正弦的定义及勾股定理,正确计算是解题关键.
2.(2025 高要区校级三模)机器狗是一种模拟真实犬只形态和部分行为的机器装置,最快移动速度v(m/s)是载重后总质量M(kg)的反比例函数.已知一款机器狗(如图所示)载重后总质量M=30kg时,它的最快移动速度v=2m/s;当其载重后总质量M=60kg时,它的最快移动速度v=( )m/s.
A.4 B.3 C.2 D.1
【考点】反比例函数的应用.
【专题】反比例函数及其应用;运算能力;应用意识.
【答案】D
【分析】根据待定系数法求出v与M的函数关系式,当M=60时,求出对应v的值即可.
【解答】解:设v与M的函数关系式为v(k为常数,且k≠0).
将M=30,v=2代入v,
得2,
解得k=60,
∴v与M的函数关系式为v,
当M=60时,v1,
∴当其载重后总质量M=60kg时,它的最快移动速度v=1m/s.
故选:D.
【点评】本题考查反比例函数的应用,掌握待定系数法求出反比例函数的关系式是解题的关键.
3.(2025 广州)若|k|=﹣k(k≠0),则反比例函数y的图象在( )
A.第一、二象限 B.第一、三象限
C.第二、四象限 D.第三、四象限
【考点】反比例函数的性质;反比例函数的图象.
【专题】反比例函数及其应用;运算能力.
【答案】C
【分析】根据绝对值的性质得k<0,再根据反比例函数的图象与k的关系即可得出答案.
【解答】解:∵|k|=﹣k(k≠0),
∴k<0,
∴反比例函数y的图象在第二、四象限.
故选:C.
【点评】本题主要考查反比例函数的图象和性质,熟练掌握反比例函数的图象和性质是解题的关键.
4.(2025 孝义市三模)已知点A(x1,y1),B(x2,y2)都在反比例函数的图象上,且当x1<0<x2时,y1>y2,则k的取值范围是( )
A.k≤﹣1 B.k≥1 C.k<1 D.k>1
【考点】反比例函数图象上点的坐标特征.
【专题】反比例函数及其应用;运算能力.
【答案】D
【分析】根据反比例函数图象上点的坐标特征解答即可.
【解答】解:∵点A(x1,y1),B(x2,y2)都在反比例函数的图象上,且当x1<0<x2时,y1>y2,
∴点A在第二象限,点B在第四象限,
∴反比例函数的图象分布在第二、四象限,
∴1﹣k<0,解得k>1,
故选:D.
【点评】本题考查了反比例函数图象上点的坐标特征,熟练掌握该知识点是关键.
5.(2025 金安区校级一模)如图,直线y=mx+n交反比例函数y(x>0)的图象于点A和点B,交x轴于点C,,过点A作AD⊥x轴于点D,连接BD并延长,交y轴于点P,连接PC.若△PCD的面积为6,则k的值为( )
A.6 B.8 C.9 D.18
【考点】反比例函数与一次函数的交点问题.
【专题】一次函数及其应用;反比例函数及其应用;运算能力;推理能力.
【答案】D
【分析】证明△CNB∽△CDA,得到,即,求出点A(a,b),则点D(,0),由S△PCD OP即可求解.
【解答】解:过点B分别作BM⊥AD于点M,BN⊥CD于点N,
设点B(a,b),k=ab,
则BN∥AD,则△CNB∽△CDA,
则,即,
∴ADb,
则k=abb xA,则xAa,
则点A(a,b),则点D(,0),
由点B、D的坐标得,直线BD的表达式为:yx,
则点P(0,b);
由点A、B的坐标得,直线AB的表达式为:yxb,
则点C(,0),则CD=a,
∵S△PCD OP6,
则ab=18=k,
故选:D.
【点评】本题为反比例函数综合题,考查了三角形相似、用字母表示坐标等基本数学知识,利用了数形结合的数学思想.
6.(2025 永州模拟)在一个密闭的容器内装有一定质量的某种气体,当它的容积V改变时,气体的密度ρ也随之改变,ρ与V之间在一定范围内满足,如图所示.当ρ为2.4kg/m3时,V的值是( )
A.3m3 B.3.4m3 C.5m3 D.7.2m3
【考点】反比例函数的图象.
【专题】反比例函数及其应用;运算能力.
【答案】A
【分析】由反比例函数图象可知m=1.8×4=7.2,得到反比例函数解析式,继而求出当ρ为2.4kg/m3时,V的值即可.
【解答】解:由反比例函数图象上的点(4,1.8),
∴m=1.8×4=7.2,
∴反比例函数解析式为ρ,
当ρ为2.4kg/m3时,V3(m3).
故选:A.
【点评】本题考查了反比例函数的图象,熟练掌握待定系数法求反比例函数解析式是关键.
7.(2025 厦门校级模拟)在平面直角坐标系中,反比例函数的图象如图所示,点A,B不在该反比例函数的图象上,则k的值可以为( )
A.﹣1 B.﹣2 C.﹣3 D.﹣4
【考点】反比例函数图象上点的坐标特征;反比例函数的图象.
【专题】反比例函数及其应用;运算能力.
【答案】C
【分析】根据点A(﹣2,2)关于原点的对称点为点A′(2,﹣2),所以可得2×(﹣2)<k<1×(﹣2),即﹣4<k<﹣2,即可得出答案.
【解答】解:∵点A(﹣2,2)关于原点的对称点为点A′(2,﹣2),
∴2×(﹣2)<k<1×(﹣2),
即﹣4<k<﹣2,
∴k的值可以为﹣3.
故选:C.
【点评】本题考查反比例函数的图象及反比例函数图象上点的坐标特征,熟练掌握反比例函数图象上点的坐标特征是解题的关键.
8.(2025 淅川县三模)某教材《阅读与思考》中的部分内容如下:
科学家如何测算岩石的年龄 你知道科学家如何测算岩石的年龄吗?解决这个问题时也用到函数这个数学工具. 1903年,英国物理学家卢瑟福通过实验证实,放射性物质在放出射线后,这种物质的质量将减少,减少的速度开始较快,后来较慢.物质所剩的质量与时间成某种函数关系,如图为表示镭的放射规律的函数图象.
某数学社团通过查阅资料,了解到放射性物质的质量减为原来的一半所用的时间是一个不变的量,我们把这个时间称为此种放射性物质的半衰期,结合镭的放射规律的函数图象,下列说法正确的是( )
A.当时间为3240年时,m的值为
B.镭的半衰期是3240年
C.32mg镭缩减为8mg所用的时间大约是1620年
D.16mg镭缩减为2mg所用的时间大约是4860年
【考点】反比例函数的应用.
【专题】反比例函数及其应用.
【答案】D
【分析】根据函数图象以及题意,逐项分析判断,即可求解.
【解答】解:A.由图象可得,当时间为3240年时,m的值为,故该选项错误,不符合题意;
B.根据题意,结合图象可得镭的半衰期是1620年,故该选项错误,不符合题意;
C.32mg镭缩减至16mg需一个半衰期,缩减至8mg需两个半衰期,即1620×2=3240(年),故该选项错误,不符合题意;
D.16mg缩减至8mg需一个半衰期,缩减至4mg需两个半衰期,缩减至2mg需三个半衰期,即1620×3=4860(年),故该选项正确,符合题意;
故选:D.
【点评】本题考查了根据函数图象获取信息,掌握其性质是解题的关键.
9.(2025 天河区校级三模)反比例函数的图象如图所示,则一次函数y=kx+b的图象可能是( )
A. B. C. D.
【考点】反比例函数的图象;一次函数的图象.
【专题】一次函数及其应用;反比例函数及其应用;几何直观.
【答案】D
【分析】由反比例函数的图象可知:kb>0,然后分情况讨论k、b与0的大小关系即可.
【解答】解:由反比例函数的图象可知:kb>0,
当k>0,b>0时,
∴直线经过一、三、四象限,
当k<0,b<0时,
∴直线经过一、二、四象限,
故选:D.
【点评】本题考查一次函数的图象,解题的关键是通过反比例函数得出kb<0,本题属于基础题型.
10.(2025 新华区校级一模)题目:“如图,点A(m,m+1),B(m+3,m﹣1)在同一个反比例函数的图象上,线段AB和线段A'B'关于直线l:y=﹣x+t对称,点A',B'分别是点A,B的对应点.若线段A'B'与坐标轴有交点,求整数t的值.”甲答:t=4,乙答:t=5或6,则正确的是( )
A.只有甲答的对
B.只有乙答的对
C.两人答案合在一起才完整
D.两人答案合在一起也不完整
【考点】反比例函数图象上点的坐标特征;坐标与图形变化﹣对称;一次函数的性质;一次函数图象上点的坐标特征;反比例函数的图象;反比例函数的性质.
【专题】函数及其图象;推理能力.
【答案】D
【分析】先根据AB两点都在同一反比例函数图象上得到关于m的方程:m(m+1)=(m+3)(m﹣1),解方程求出m的值,通过作直线l1和l2求出线段AA′和BB′的中点坐标,再根据线段A′B′与y轴有交点时,xA′≤0≤xB′,或线段A′B′与x轴有交点时,yB′≤0≤yA′,即可确定t的取值范围.
【解答】解:根据题意作出点A和点B关于直线l的对称点:点A′和点B′.直线l交y轴于点P,交x轴于点Q,如图:
∵点A和点B在同一个反比例函数图象上,
∴xA yA=xB yB,即:m(m+1)=(m+3)(m﹣1).
解得:m=3.
∴点A坐标为(3,4),点B坐标为(6,2)
过点A作直线l2⊥l交l于点C,过点B作l3⊥l交l于点D,
根据点A的坐标可得,点A在直线l1:y=x+1上;根据点B的坐标可知点B在直线l2:y=x﹣4上.
由求解出点C的坐标为(,);
由求解出点D的坐标为(,).
根据轴对称的性质,点C是线段AA′的中点,点D是线段BB′的中点.
∵xC,yC.
则xA′=t﹣4,yA′=t﹣3.
同理可得:xB′=t﹣2,yB′=t﹣6.
当线段A′B′与y轴有交点时,xA′≤0≤xB′,即:t﹣4≤0≤t﹣2,解得:2≤t≤4.
当线段A′B′与x轴有交点时,yB′≤0≤yA′,即:t﹣6≤0≤t﹣3,解得:3≤t≤6.
∴2≤t≤6,整数t的值为2,3,4,5,6.
故答案为:D.
【点评】本题考查了反比例函数的图象和性质,一次函数的图象和性质,轴对称图形的性质,一元一次不等式组,求出AB两点关于直线l的对称点坐标是解答本题的难点.
二.填空题(共5小题)
11.(2025 武汉)在平面直角坐标系中,某反比例函数y的图象分别位于第一、第三象限.写出一个满足条件的k的值是 1(答案不唯一) .
【考点】反比例函数的性质;反比例函数的图象.
【专题】反比例函数及其应用;几何直观.
【答案】1(答案不唯一).
【分析】根据反比例函数图象分布确定k的取值范围,在k的取值范围内选取一个数即可.
【解答】解:∵反比例函数y的图象分别位于第一、第三象限,
∴k>0,
不妨令k=1.
故答案为:1(答案不唯一).
【点评】本题考查了反比例函数的图象与性质,熟练掌握反比例函数的性质是关键.
12.(2025 大同模拟)近视眼镜的度数y(度)与镜片焦距x(米)之间有如图所示的反比例函数关系,王老师计划配一副近视眼镜,测得镜片的焦距为0.16米,则王老师镜片的度数为 625 度.
【考点】反比例函数的应用.
【专题】反比例函数及其应用.
【答案】625.
【分析】首先求出反比例函数解析式,然后把x=0.16代入计算即可.
【解答】解:设反比例函数解析式为,
将(0.4,250)代入得,,
解得k=100,
∴反比例函数解析式为,
把x=0.16代入,得度,
故答案为:625.
【点评】本题考查了求反比例函数值,反比例函数的应用,掌握以上性质是解题的关键.
13.(2025 普兰店区一模)我们称关于x的二次函数y=px2+qx+k为一次函数y=px+q和反比例函数的“非对称韦达函数”,一次函数y=px+q和反比例函数的交点称为二次函数y=px2+qx+k的“韦达点”,若一次函数y=ax+2b和反比例函数的“非对称韦达函数”的两个“韦达点”的横坐标为s,t,其中实数a>b>c,a+b+c=0.则的取值范围为 .
【考点】反比例函数图象上点的坐标特征;二次函数的性质;二次函数图象上点的坐标特征;二次函数图象与几何变换;一次函数图象与几何变换;反比例函数的性质.
【专题】一次函数及其应用;反比例函数及其应用;二次函数图象及其性质;运算能力.
【答案】.
【分析】联立方程组,根据根与系数的故选求出的值,在根据a,b,c的取值求出的取值范围即可.
【解答】解:∵a>b>c,a+b+c=0,
∴a>0,c<0,a+a+c>0,a+c+c<0,
∴﹣2,
∵一次函数y=ax+2b和反比例函数的“非对称韦达函数”的两个“韦达点”的横坐标为s,t,
∴s,t是方程ax+2b,即ax2+2bx+c=0的两根,
∴s+tst,
∵
=2,
=2
=2
=2,
∵﹣2,
∴2,
即.
故答案为:.
【点评】本题主要考查了反比例函数图象上点的坐标特征一次函数图象与几何变换,二次函数的性质,二次函数图象与几何变换,根据题干所给定义结合根与系数的关系来求解是本题解题的关键.
14.(2025 武安市二模)对于反比例函数y(k>0),称M(,),N(,)为该反比例函数图象的两个“焦点”,且若P为反比例函数图象上的任意一点,则恒有|PM﹣PN|=2.如图,M,N为反比例函数y(k>0)的图象的两个焦点,A为该反比例函数在第三象限的图象上的一个动点,B为∠NAM的平分线上的一点,且AB⊥BM,OB=2,则k的值为 2 .
【考点】反比例函数图象上点的坐标特征;反比例函数的图象.
【专题】反比例函数及其应用;运算能力.
【答案】2.
【分析】依据题意,延长AN,MB相交于点H.由AB平分∠MAN,且BM⊥AB,可得AH=AM,再由利用“焦点”的结论,得|AM﹣AN|=2,结合点O,B分别为MN,MH的中点,可得2,进而可以判断得解.
【解答】解:如图,延长AN,MB相交于点H.∵AB平分∠MAN,且BM⊥AB,
∴AH=AM,点B为HM的中点.利用“焦点”的结论,得
|AM﹣AN|=2.
∵点O,B分别为MN,MH的中点,
∴2,
∴k=2.
故答案为:2.
【点评】本题主要考查了反比例函数的应用,解题时要熟练掌握并能灵活运用反比例函数的性质是关键.
15.(2025 齐齐哈尔四模)如图,将抛物线y=x2沿y=x向下平移,使平移后的抛物线经过原点,且平移后的抛物线的对称轴与原抛物线y=x2交于点A,则经过点A的反比例函数的解析式为 .
【考点】反比例函数图象上点的坐标特征;二次函数的性质;二次函数图象上点的坐标特征;二次函数图象与几何变换;一次函数图象上点的坐标特征.
【专题】反比例函数及其应用;二次函数图象及其性质;运算能力.
【答案】.
【分析】根据题意可设将抛物线y=x2向下平移t(t>0)个单位长度,向左平移t个长度可得到新抛物线,则新抛物线解析式为y=(x+t)2﹣t,利用待定系数法可求出平移后的抛物线解析式为y=(x+1)2﹣1,进而可求出点A的坐标,再利用待定系数法求出对应的反比例函数解析式即可.
【解答】解:可设将抛物线y=x2向下平移t(t>0)个单位长度,向左平移t个长度可得到新抛物线,
∴新抛物线解析式为y=(x+t)2﹣t,
∵平移后的抛物线经过原点,
∴0=(0+t)2﹣t,
解得t=1或t=0(舍去),
∴平移后的抛物线解析式为y=(x+1)2﹣1,
∴平移后的抛物线对称轴为直线x=﹣1,
在y=x2中,当x=﹣1时,y=1,
∴A(﹣1,1),
设经过点A的反比例函数解析式为,
∴,
∴k=﹣1,
∴经过点A的反比例函数解析式为,
故答案为:.
【点评】本题主要考查了二次函数图象的平移问题,求反比例函数解析式,熟练掌握以上知识点是关键.
三.解答题(共5小题)
16.(2025 樟树市校级三模)如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(4,7),反比例函数(x>0)的图象经过BC的中点D,且与AB交于点E.
(1)求反比例函数的解析式及点E的坐标;
(2)若点F是OC边上的一点,且△BCF为等腰三角形,求直线FB的解析式.
【考点】反比例函数综合题.
【专题】代数几何综合题;运算能力;推理能力.
【答案】(1)y(x>0).(4,);
(2)y=x+3.
【分析】(1)先根据点B的坐标为(4,7)求出D点坐标,代入反比例函数y(x>0)即可求出m的值,进而得出解析式,再把x=4代入求出y的值即可得出E点坐标;
(2)根据△BCF为等腰三角形得出CF的长,进而得出F点的坐标,利用待定系数法求出直线FB的解析式即可.
【解答】解:(1)∵点B的坐标为(4,7),点D是BC的中点,
∴D(2,7),
∵点D在反比例函数y(x>0)上,
∴7,
解得:m=14,
∴反比例函数的解析式为y(x>0).
∵四边形OABC是矩形,点B的坐标为(4,7),
∴点E的横坐标为4,
把x=4代入y得y,
∴点E的坐标为(4,);
(2)∵△BCF为等腰三角形,点B的坐标为(4,7),∠BCF=90°,
∴BC=CF=4,
∴F(0,3),
设直线BF的解析式为y=ax+b(a≠0),
∴将点B(4,7),F(0,3)代入,得,
解得,
∴直线FB的解析式为y=x+3.
【点评】本题考查的是反比例函数综合题,熟知反比例函数图象上点的坐标特点、矩形的性质、一次函数的性质等知识是解答此题的关键.
17.(2025 武侯区校级模拟)如图,在平面直角坐标系xOy 中,直线 y=ax+12 与y轴正半轴交于点A,与x轴正半轴交于点B,与双曲线y(x>0)的交点为C(4,m),D(C在D的左边),且C,D恰好是线段AB的三等分点.
(1)求a,k的值;
(2)P是线段OB上一点,连接CP.
①若CP将△AOB 的面积分成5:7两部分,求点P的坐标;
②将直线CP沿直线AB进行翻折,与双曲线交于另一点E,连接PE,若 CE=2CP,求点P的坐标.
【考点】反比例函数与一次函数的交点问题.
【专题】一次函数及其应用;反比例函数及其应用;三角形;图形的相似;几何直观;运算能力;推理能力.
【答案】(1)a=﹣1,k=32;
(2)①(1.5,0)或(4.5,0);②(7.2,0).
【分析】(1)过点C作CH⊥x轴于点H,则CH∥OA,依题意设AC=CD=DB=t,则AB=3t,BC=2t,再求出点A(0,12)得AO=12,证明△BCH和△BOA相似,由相似三角形性质得CH=8,进而得点C(4,8),将点C(4,8)代入y=ax+12,得a=﹣1,将点C(4,8)代入y得k=32;
(2)①求出点B(12,0)得S△AOBAO BO=72,设点P的坐标为(m,0),则BP=12﹣m,进而得S△BPCCH BP=48﹣4m,S四边形AOPC=S△AOB﹣S△BPC=24+4m,再分两种情况讨论如下:(ⅰ)当S四边形AOPC:S△BPC=5:7时,则(24+4m):(48﹣4m)=5:7,由此得m=1.5,则点P(1.5,0);(ⅱ)当S△BPC:S四边形AOPC=5:7时,则(48﹣4m):(24+4m)=5:7,由此得m=4.5,则点P(4.5,0),综上所述即可得出答案;
②直线CP沿直线AB进行翻折后点P的对应点为Q,连接BQ,过点E作EF⊥x轴于点F,证明△AOB是等腰直角三角形得∠OBA=45°,由翻折的性质得BC是线段PQ的垂直平分线得CP=CQ=EQ,进而得△BPQ是等腰三角形,则∠PBQ=90°,根据由此得CH∥BQ∥EF,根据平行线分线段成比例定理得BH=BF=8,则OF=20,从而得点E(20,1.6),则CE2=296.96,设点P(n,0)得CP2=(n﹣4)2+82,再根据CE=2CP得296.96=4[(n﹣4)2+82],据此解出n=7.2,继而可得点P的坐标.
【解答】解:(1)过点C作CH⊥x轴于点H,如图1所示:
∵∠CHB=∠AOB=90°,
∴CH∥OA,
∵C,D恰好是线段AB的三等分点,
∴设AC=CD=DB=t,
∴AB=3t,BC=2t,
对于直线y=ax+12,当x=0时,y=12,
∴点A的坐标为(0,12),
∴AO=12,
∵CH∥OA,
∴△BCH∽△BOA,
∴,
∴,
∴CH=8,
∴点C的坐标为(4,8),
将点C(4,8)代入y=ax+12,得:4a+12=8,
解得:a=﹣1,
将点C(4,8)代入y,得:k=4×8=32;
(2)①由(1)可知:直线AB的表达式为:y=﹣x+12,
∴当y=0时,x=12,
∴点B的坐标为(12,0),
∴BO=12,
∵点A(0,12),
∴AO=12,
∴S△AOBAO BO12×12=72,
∵点P在线段OB上,
∴设点P的坐标为(m,0),
∴OP=m,
∴BP=OB﹣OP=12﹣m,
∴S△BPCCH BP8(12﹣m)=48﹣4m,
∴S四边形AOPC=S△AOB﹣S△BPC=72﹣(48﹣4m)=24+4m,
当CP将△AOB的面积分成5:7两部分时,有以下两种情况:
(ⅰ)当S四边形AOPC:S△BPC=5:7时,
∴(24+4m):(48﹣4m)=5:7,
解得:m=1.5,
此时点P的坐标为(1.5,0);
(ⅱ)当S△BPC:S四边形AOPC=5:7时,
∴(48﹣4m):(24+4m)=5:7,
解得:m=4.5,
此时点P的坐标为(4.5,0),
综上所述:点P的坐标为(1.5,0)或(4.5,0);
②直线CP沿直线AB进行翻折后点P的对应点为Q,连接BQ,过点E作EF⊥x轴于点F,如图2所示:
∵BO=AO=12,
∴△AOB是等腰直角三角形,
∴∠OBA=45°,
由翻折的性质得:CP=AQ,PQ⊥AB,
∴BC是线段PQ的垂直平分线,
∴BP=BQ,
∴△BPQ是等腰三角形,
∵PQ⊥AB,
∴∠QBC=∠OBA=45°,
∴∠PBQ=∠QBC+∠OBA=90°,
∴BQ⊥x轴,
∵CE=AQ+EQ=CP+EQ,CE=2CP,
∴CP+EQ=2CP,
∴EQ=CP=CQ,
∵CH⊥x轴,BQ⊥x轴,EF⊥x轴,
∴CH∥BQ∥EF,
根据平行线分线段成比例定理得:BH=BF,
由(1)可知:反比例函数的表达式为:y(x>0),点C(4,8),
∴OH=4,
∵OB=12,
∴BH=OB﹣OH=8,
∴BH=BF=8,
即HF=16,
∴OF=OH+HF=20,
∴点E的横坐标为20,
∵点E在反比例y(x>0)的图象上,
∴点E的坐标为(20,1.6),
∴CE2=(4﹣20)2+(8﹣1.6)2=296.96,
设点P的坐标为(n,0),
∴CP2=(n﹣4)2+82,
∵CE=2CP,
∴CE2=4CP2,
∴296.96=4[(n﹣4)2+82],
整理得:(n﹣4)2=10.24,
∴n﹣4=±3.2,
由n﹣4=3.2,解得:n=7.2,
∴点P的坐标为(7.2,0);
由n﹣4=﹣3.2,解得:n=0.8,
∴点P的坐标为(0.8,0),此时CP沿AB翻折后与双曲线y(x>0)没有交点,故不合题意,舍去,
∴点P的坐标为(7.2,0).
【点评】此题主要考查了反比例函数与一次函数的交点,图形的翻折变换及其性质,三角形的面积,熟练掌握图形的翻折变换及其性质,相似三角形的判定和性质,三角形的面积公式是解决问题的关键,分类讨论是解决问题的易错点.
18.(2025 广州)如图,曲线G:y(x>0)经过点P(4,t).
(1)求t的值;
(2)直线l:y=﹣x+b也经过点P,求l与y轴交点的坐标,并在图中画出直线l;
(3)在(2)的条件下,若在l与两坐标轴围成的三角形内部(不包含边界)随机取一个格点(横、纵坐标都是整数的点),求该格点在曲线G上的概率.
【考点】反比例函数与一次函数的交点问题.
【专题】函数及其图象;一次函数及其应用;概率及其应用;模型思想.
【答案】(1);
(2)l与y轴交点的坐标为(0,4.5),图中画出直线l见解答;
(3).
【分析】(1)直接把(4,t)代入y进行计算,得t;
(2)先得出P(4,),再代入直线l:y=﹣x+4.5,即可求出t与y轴交点的坐标,再由两点确定一直线画出直线l的函数图象;
(3)先得出格点共有6个,分别是(1,3),(1,2),(1,1),(2,1),(2,2),(3,1),再分析所得格点(1,2),(2,1)在曲线G上,即有两个格点在曲线G上,最后由概率公式解答即可.
【解答】解:(1)曲线G:y过点P(4,t),
∴t;
(2)由(1)得t,
故P(4,),
∵直线l:y=﹣x+b也经过点P,
∴把(4,)代入y=﹣x+b,得,
解得b=4.5,
∴y=﹣x+4.5,
令x=0,则y=0+4.5=4.5,
∴l与y轴交点的坐标为(0,4.5),
直线的函数图象,如图所示:
(3)根据题意,在l与两坐标轴围成的三角形内部(不包括边界)的格点共有6个,分别是(1,3),(1,2),(1,1),(2,1),(2,2),(3,1),
∵曲线G:y(x>0),
则1×3=3≠2,1×2=2,1×1≠2,2×1=2,2×2=4≠2,3×1=3≠2,
∴格点(1,2),(2,1)在曲线G上,即有两个格点在曲线G上,
∴该格点在曲线G上的概率.
【点评】本题考查了概率公式,反比例函数的性质,一次函数的性质,画函数图象,掌握相关性质是解答本题的关键.
19.(2025 巴中模拟)如图,在平面直角坐标系xOy中,一次函数y=kx+b与反比例函数y(x>0)的图象交于点A(2,6),B(n,3),与x轴,y轴分别交于C,D两点.
(1)求一次函数和反比例函数的表达式;
(2)请根据图象直接写出关于x的不等式kx+b(x>0)的解集;
(3)在直线CD上有点P,△PCO的面积为12,求点P的坐标.
【考点】反比例函数与一次函数的交点问题.
【专题】一次函数及其应用;反比例函数及其应用;运算能力.
【答案】(1),;
(2)0<x<2或x>4;
(3)点P的坐标为或.
【分析】(1)先把A(2,6)代入得m=12,再把B(n,3)代入,求出B(4,3),运用待定系数法进行求一次函数的解析式,即可作答.
(2)认真观察图象,且结合A(2,6),B(4,3),运用数形结合思想得不等式的解集0<x<2或x>4,即可作答.
(3)先求出C(6,0),得OC=6,设,运用三角形面积公式列式计算,即可作答.
【解答】解:(1)由条件可得,
∴m=12,
∴,
把B(n,3)代入,得,
∴n=4,
则B(4,3),
把A(2,6)和B(4,3)分别代入y=kx+b,
得,
解得,
∴.
(2)由(1)得,B(4,3),,
∵一次函数与反比例函数的图象交于点A(2,6),B(4,3),
∴不等式的解集0<x<2或x>4;
(3)依题意,与x轴交于C点,
∴当y=0时,则,
解得x=6,
∴C(6,0),
∴OC=6,
∵直线CD上有点P,
设,
∵△PCO的面积为12,
∴,
则,
∴或,
解得或,
则或.
【点评】本题考查了反比例函数与一次函数的交点,求反比例函数的解析式,求一次函数的解析式,一次函数与几何综合,正确掌握相关性质内容是解题的关键.
20.(2025 浙江模拟)如图,在平面直角坐标系中,点C,D都在反比例函数的图象上,CE⊥x轴于点E,DB⊥x轴于点B,OC与BD的延长线相交于点A.
(1)若△OCE的面积为6.
①求反比例函数的表达式.
②当y≤4时,求自变量x的取值范围.
(2)已知CE=4,BD,求AB的长.
【考点】待定系数法求反比例函数解析式;反比例函数的性质;反比例函数系数k的几何意义;反比例函数图象上点的坐标特征.
【专题】反比例函数及其应用;运算能力;推理能力.
【答案】见试题解答内容
【分析】(1)①利用反比例函数系数k的几何意义即可求解;
②求得y=4时,自变量x的值,然后根据图象即可求解;
【解答】解:(1)①点C在反比例函数的图象上,CE⊥x轴于点E,
∴S△OCE|k|,
∵△OCE的面积为6,
∴|k|=6,
∵k>0,
∴k=12,
∴反比例函数的表达式为y;
②当y=4时,则4,解得x=3,
由图象可知,当y≤4时,x≥3.
(2)∵点C,D都在反比例函数的图象上,CE⊥x轴于点E,DB⊥x轴于点B,OC与BD的延长线相交于点A,
∴CE∥BD,,
∵CE=4,BD,
∴4OEOB,
∴,
∵CE∥AB,
∴,
∴AB=3CE=3×4=12.
【点评】本题考查了反比例函数系数k的几何意义,反比例函数图象上点的坐标特征,反比例函数的性质,平行线分线段成比例定理,数形结合是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
暑假巩固复习 反比例函数
一.选择题(共10小题)
1.(2025 天河区校级四模)如图,在平面直角坐标系中,从坐标原点出发的两条射线OA,OB.且OA⊥OB,两射线分别与函数和相交,交点分别为A,B,连接AB,则sin∠ABO的值为( )
A. B. C. D.
2.(2025 高要区校级三模)机器狗是一种模拟真实犬只形态和部分行为的机器装置,最快移动速度v(m/s)是载重后总质量M(kg)的反比例函数.已知一款机器狗(如图所示)载重后总质量M=30kg时,它的最快移动速度v=2m/s;当其载重后总质量M=60kg时,它的最快移动速度v=( )m/s.
A.4 B.3 C.2 D.1
3.(2025 广州)若|k|=﹣k(k≠0),则反比例函数y的图象在( )
A.第一、二象限 B.第一、三象限
C.第二、四象限 D.第三、四象限
4.(2025 孝义市三模)已知点A(x1,y1),B(x2,y2)都在反比例函数的图象上,且当x1<0<x2时,y1>y2,则k的取值范围是( )
A.k≤﹣1 B.k≥1 C.k<1 D.k>1
5.(2025 金安区校级一模)如图,直线y=mx+n交反比例函数y(x>0)的图象于点A和点B,交x轴于点C,,过点A作AD⊥x轴于点D,连接BD并延长,交y轴于点P,连接PC.若△PCD的面积为6,则k的值为( )
A.6 B.8 C.9 D.18
6.(2025 永州模拟)在一个密闭的容器内装有一定质量的某种气体,当它的容积V改变时,气体的密度ρ也随之改变,ρ与V之间在一定范围内满足,如图所示.当ρ为2.4kg/m3时,V的值是( )
A.3m3 B.3.4m3 C.5m3 D.7.2m3
7.(2025 厦门校级模拟)在平面直角坐标系中,反比例函数的图象如图所示,点A,B不在该反比例函数的图象上,则k的值可以为( )
A.﹣1 B.﹣2 C.﹣3 D.﹣4
8.(2025 淅川县三模)某教材《阅读与思考》中的部分内容如下:
科学家如何测算岩石的年龄 你知道科学家如何测算岩石的年龄吗?解决这个问题时也用到函数这个数学工具. 1903年,英国物理学家卢瑟福通过实验证实,放射性物质在放出射线后,这种物质的质量将减少,减少的速度开始较快,后来较慢.物质所剩的质量与时间成某种函数关系,如图为表示镭的放射规律的函数图象.
某数学社团通过查阅资料,了解到放射性物质的质量减为原来的一半所用的时间是一个不变的量,我们把这个时间称为此种放射性物质的半衰期,结合镭的放射规律的函数图象,下列说法正确的是( )
A.当时间为3240年时,m的值为
B.镭的半衰期是3240年
C.32mg镭缩减为8mg所用的时间大约是1620年
D.16mg镭缩减为2mg所用的时间大约是4860年
9.(2025 天河区校级三模)反比例函数的图象如图所示,则一次函数y=kx+b的图象可能是( )
A. B. C. D.
10.(2025 新华区校级一模)题目:“如图,点A(m,m+1),B(m+3,m﹣1)在同一个反比例函数的图象上,线段AB和线段A'B'关于直线l:y=﹣x+t对称,点A',B'分别是点A,B的对应点.若线段A'B'与坐标轴有交点,求整数t的值.”甲答:t=4,乙答:t=5或6,则正确的是( )
A.只有甲答的对
B.只有乙答的对
C.两人答案合在一起才完整
D.两人答案合在一起也不完整
二.填空题(共5小题)
11.(2025 武汉)在平面直角坐标系中,某反比例函数y的图象分别位于第一、第三象限.写出一个满足条件的k的值是 .
12.(2025 大同模拟)近视眼镜的度数y(度)与镜片焦距x(米)之间有如图所示的反比例函数关系,王老师计划配一副近视眼镜,测得镜片的焦距为0.16米,则王老师镜片的度数为 度.
13.(2025 普兰店区一模)我们称关于x的二次函数y=px2+qx+k为一次函数y=px+q和反比例函数的“非对称韦达函数”,一次函数y=px+q和反比例函数的交点称为二次函数y=px2+qx+k的“韦达点”,若一次函数y=ax+2b和反比例函数的“非对称韦达函数”的两个“韦达点”的横坐标为s,t,其中实数a>b>c,a+b+c=0.则的取值范围为 .
14.(2025 武安市二模)对于反比例函数y(k>0),称M(,),N(,)为该反比例函数图象的两个“焦点”,且若P为反比例函数图象上的任意一点,则恒有|PM﹣PN|=2.如图,M,N为反比例函数y(k>0)的图象的两个焦点,A为该反比例函数在第三象限的图象上的一个动点,B为∠NAM的平分线上的一点,且AB⊥BM,OB=2,则k的值为 .
15.(2025 齐齐哈尔四模)如图,将抛物线y=x2沿y=x向下平移,使平移后的抛物线经过原点,且平移后的抛物线的对称轴与原抛物线y=x2交于点A,则经过点A的反比例函数的解析式为 .
三.解答题(共5小题)
16.(2025 樟树市校级三模)如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(4,7),反比例函数(x>0)的图象经过BC的中点D,且与AB交于点E.
(1)求反比例函数的解析式及点E的坐标;
(2)若点F是OC边上的一点,且△BCF为等腰三角形,求直线FB的解析式.
17.(2025 武侯区校级模拟)如图,在平面直角坐标系xOy 中,直线 y=ax+12 与y轴正半轴交于点A,与x轴正半轴交于点B,与双曲线y(x>0)的交点为C(4,m),D(C在D的左边),且C,D恰好是线段AB的三等分点.
(1)求a,k的值;
(2)P是线段OB上一点,连接CP.
①若CP将△AOB 的面积分成5:7两部分,求点P的坐标;
②将直线CP沿直线AB进行翻折,与双曲线交于另一点E,连接PE,若 CE=2CP,求点P的坐标.
18.(2025 广州)如图,曲线G:y(x>0)经过点P(4,t).
(1)求t的值;
(2)直线l:y=﹣x+b也经过点P,求l与y轴交点的坐标,并在图中画出直线l;
(3)在(2)的条件下,若在l与两坐标轴围成的三角形内部(不包含边界)随机取一个格点(横、纵坐标都是整数的点),求该格点在曲线G上的概率.
19.(2025 巴中模拟)如图,在平面直角坐标系xOy中,一次函数y=kx+b与反比例函数y(x>0)的图象交于点A(2,6),B(n,3),与x轴,y轴分别交于C,D两点.
(1)求一次函数和反比例函数的表达式;
(2)请根据图象直接写出关于x的不等式kx+b(x>0)的解集;
(3)在直线CD上有点P,△PCO的面积为12,求点P的坐标.
20.(2025 浙江模拟)如图,在平面直角坐标系中,点C,D都在反比例函数的图象上,CE⊥x轴于点E,DB⊥x轴于点B,OC与BD的延长线相交于点A.
(1)若△OCE的面积为6.
①求反比例函数的表达式.
②当y≤4时,求自变量x的取值范围.
(2)已知CE=4,BD,求AB的长.
暑假巩固复习 反比例函数
参考答案与试题解析
一.选择题(共10小题)
1.(2025 天河区校级四模)如图,在平面直角坐标系中,从坐标原点出发的两条射线OA,OB.且OA⊥OB,两射线分别与函数和相交,交点分别为A,B,连接AB,则sin∠ABO的值为( )
A. B. C. D.
【考点】反比例函数图象上点的坐标特征;解直角三角形;反比例函数的性质.
【专题】函数及其图象;运算能力.
【答案】D
【分析】分别过点A,B作AC⊥x轴于点C,BD⊥x轴于点D,△OAC∽△BOD,结合反比例函数k的几何意义,求出,再利用勾股定理求出,最后利用正弦的定义即可求解.
【解答】解:分别过点A,B作AC⊥x轴于点C,BD⊥x轴于点D,如图所示:
因为OA⊥OB,
所以∠AOB=90°,∠AOC+∠OAC=∠AOC+∠BOD=90°,
所以∠OAC=∠BOD,
又因为∠ACO=∠BDO=90°,
所以△OAC∽△BOD,,
因为
所以,(负值舍去),
所以,
所以,
故选:D.
【点评】本题考查了反比例函数k的几何意义,相似三角形的判定与性质,正弦的定义及勾股定理,正确计算是解题关键.
2.(2025 高要区校级三模)机器狗是一种模拟真实犬只形态和部分行为的机器装置,最快移动速度v(m/s)是载重后总质量M(kg)的反比例函数.已知一款机器狗(如图所示)载重后总质量M=30kg时,它的最快移动速度v=2m/s;当其载重后总质量M=60kg时,它的最快移动速度v=( )m/s.
A.4 B.3 C.2 D.1
【考点】反比例函数的应用.
【专题】反比例函数及其应用;运算能力;应用意识.
【答案】D
【分析】根据待定系数法求出v与M的函数关系式,当M=60时,求出对应v的值即可.
【解答】解:设v与M的函数关系式为v(k为常数,且k≠0).
将M=30,v=2代入v,
得2,
解得k=60,
∴v与M的函数关系式为v,
当M=60时,v1,
∴当其载重后总质量M=60kg时,它的最快移动速度v=1m/s.
故选:D.
【点评】本题考查反比例函数的应用,掌握待定系数法求出反比例函数的关系式是解题的关键.
3.(2025 广州)若|k|=﹣k(k≠0),则反比例函数y的图象在( )
A.第一、二象限 B.第一、三象限
C.第二、四象限 D.第三、四象限
【考点】反比例函数的性质;反比例函数的图象.
【专题】反比例函数及其应用;运算能力.
【答案】C
【分析】根据绝对值的性质得k<0,再根据反比例函数的图象与k的关系即可得出答案.
【解答】解:∵|k|=﹣k(k≠0),
∴k<0,
∴反比例函数y的图象在第二、四象限.
故选:C.
【点评】本题主要考查反比例函数的图象和性质,熟练掌握反比例函数的图象和性质是解题的关键.
4.(2025 孝义市三模)已知点A(x1,y1),B(x2,y2)都在反比例函数的图象上,且当x1<0<x2时,y1>y2,则k的取值范围是( )
A.k≤﹣1 B.k≥1 C.k<1 D.k>1
【考点】反比例函数图象上点的坐标特征.
【专题】反比例函数及其应用;运算能力.
【答案】D
【分析】根据反比例函数图象上点的坐标特征解答即可.
【解答】解:∵点A(x1,y1),B(x2,y2)都在反比例函数的图象上,且当x1<0<x2时,y1>y2,
∴点A在第二象限,点B在第四象限,
∴反比例函数的图象分布在第二、四象限,
∴1﹣k<0,解得k>1,
故选:D.
【点评】本题考查了反比例函数图象上点的坐标特征,熟练掌握该知识点是关键.
5.(2025 金安区校级一模)如图,直线y=mx+n交反比例函数y(x>0)的图象于点A和点B,交x轴于点C,,过点A作AD⊥x轴于点D,连接BD并延长,交y轴于点P,连接PC.若△PCD的面积为6,则k的值为( )
A.6 B.8 C.9 D.18
【考点】反比例函数与一次函数的交点问题.
【专题】一次函数及其应用;反比例函数及其应用;运算能力;推理能力.
【答案】D
【分析】证明△CNB∽△CDA,得到,即,求出点A(a,b),则点D(,0),由S△PCD OP即可求解.
【解答】解:过点B分别作BM⊥AD于点M,BN⊥CD于点N,
设点B(a,b),k=ab,
则BN∥AD,则△CNB∽△CDA,
则,即,
∴ADb,
则k=abb xA,则xAa,
则点A(a,b),则点D(,0),
由点B、D的坐标得,直线BD的表达式为:yx,
则点P(0,b);
由点A、B的坐标得,直线AB的表达式为:yxb,
则点C(,0),则CD=a,
∵S△PCD OP6,
则ab=18=k,
故选:D.
【点评】本题为反比例函数综合题,考查了三角形相似、用字母表示坐标等基本数学知识,利用了数形结合的数学思想.
6.(2025 永州模拟)在一个密闭的容器内装有一定质量的某种气体,当它的容积V改变时,气体的密度ρ也随之改变,ρ与V之间在一定范围内满足,如图所示.当ρ为2.4kg/m3时,V的值是( )
A.3m3 B.3.4m3 C.5m3 D.7.2m3
【考点】反比例函数的图象.
【专题】反比例函数及其应用;运算能力.
【答案】A
【分析】由反比例函数图象可知m=1.8×4=7.2,得到反比例函数解析式,继而求出当ρ为2.4kg/m3时,V的值即可.
【解答】解:由反比例函数图象上的点(4,1.8),
∴m=1.8×4=7.2,
∴反比例函数解析式为ρ,
当ρ为2.4kg/m3时,V3(m3).
故选:A.
【点评】本题考查了反比例函数的图象,熟练掌握待定系数法求反比例函数解析式是关键.
7.(2025 厦门校级模拟)在平面直角坐标系中,反比例函数的图象如图所示,点A,B不在该反比例函数的图象上,则k的值可以为( )
A.﹣1 B.﹣2 C.﹣3 D.﹣4
【考点】反比例函数图象上点的坐标特征;反比例函数的图象.
【专题】反比例函数及其应用;运算能力.
【答案】C
【分析】根据点A(﹣2,2)关于原点的对称点为点A′(2,﹣2),所以可得2×(﹣2)<k<1×(﹣2),即﹣4<k<﹣2,即可得出答案.
【解答】解:∵点A(﹣2,2)关于原点的对称点为点A′(2,﹣2),
∴2×(﹣2)<k<1×(﹣2),
即﹣4<k<﹣2,
∴k的值可以为﹣3.
故选:C.
【点评】本题考查反比例函数的图象及反比例函数图象上点的坐标特征,熟练掌握反比例函数图象上点的坐标特征是解题的关键.
8.(2025 淅川县三模)某教材《阅读与思考》中的部分内容如下:
科学家如何测算岩石的年龄 你知道科学家如何测算岩石的年龄吗?解决这个问题时也用到函数这个数学工具. 1903年,英国物理学家卢瑟福通过实验证实,放射性物质在放出射线后,这种物质的质量将减少,减少的速度开始较快,后来较慢.物质所剩的质量与时间成某种函数关系,如图为表示镭的放射规律的函数图象.
某数学社团通过查阅资料,了解到放射性物质的质量减为原来的一半所用的时间是一个不变的量,我们把这个时间称为此种放射性物质的半衰期,结合镭的放射规律的函数图象,下列说法正确的是( )
A.当时间为3240年时,m的值为
B.镭的半衰期是3240年
C.32mg镭缩减为8mg所用的时间大约是1620年
D.16mg镭缩减为2mg所用的时间大约是4860年
【考点】反比例函数的应用.
【专题】反比例函数及其应用.
【答案】D
【分析】根据函数图象以及题意,逐项分析判断,即可求解.
【解答】解:A.由图象可得,当时间为3240年时,m的值为,故该选项错误,不符合题意;
B.根据题意,结合图象可得镭的半衰期是1620年,故该选项错误,不符合题意;
C.32mg镭缩减至16mg需一个半衰期,缩减至8mg需两个半衰期,即1620×2=3240(年),故该选项错误,不符合题意;
D.16mg缩减至8mg需一个半衰期,缩减至4mg需两个半衰期,缩减至2mg需三个半衰期,即1620×3=4860(年),故该选项正确,符合题意;
故选:D.
【点评】本题考查了根据函数图象获取信息,掌握其性质是解题的关键.
9.(2025 天河区校级三模)反比例函数的图象如图所示,则一次函数y=kx+b的图象可能是( )
A. B. C. D.
【考点】反比例函数的图象;一次函数的图象.
【专题】一次函数及其应用;反比例函数及其应用;几何直观.
【答案】D
【分析】由反比例函数的图象可知:kb>0,然后分情况讨论k、b与0的大小关系即可.
【解答】解:由反比例函数的图象可知:kb>0,
当k>0,b>0时,
∴直线经过一、三、四象限,
当k<0,b<0时,
∴直线经过一、二、四象限,
故选:D.
【点评】本题考查一次函数的图象,解题的关键是通过反比例函数得出kb<0,本题属于基础题型.
10.(2025 新华区校级一模)题目:“如图,点A(m,m+1),B(m+3,m﹣1)在同一个反比例函数的图象上,线段AB和线段A'B'关于直线l:y=﹣x+t对称,点A',B'分别是点A,B的对应点.若线段A'B'与坐标轴有交点,求整数t的值.”甲答:t=4,乙答:t=5或6,则正确的是( )
A.只有甲答的对
B.只有乙答的对
C.两人答案合在一起才完整
D.两人答案合在一起也不完整
【考点】反比例函数图象上点的坐标特征;坐标与图形变化﹣对称;一次函数的性质;一次函数图象上点的坐标特征;反比例函数的图象;反比例函数的性质.
【专题】函数及其图象;推理能力.
【答案】D
【分析】先根据AB两点都在同一反比例函数图象上得到关于m的方程:m(m+1)=(m+3)(m﹣1),解方程求出m的值,通过作直线l1和l2求出线段AA′和BB′的中点坐标,再根据线段A′B′与y轴有交点时,xA′≤0≤xB′,或线段A′B′与x轴有交点时,yB′≤0≤yA′,即可确定t的取值范围.
【解答】解:根据题意作出点A和点B关于直线l的对称点:点A′和点B′.直线l交y轴于点P,交x轴于点Q,如图:
∵点A和点B在同一个反比例函数图象上,
∴xA yA=xB yB,即:m(m+1)=(m+3)(m﹣1).
解得:m=3.
∴点A坐标为(3,4),点B坐标为(6,2)
过点A作直线l2⊥l交l于点C,过点B作l3⊥l交l于点D,
根据点A的坐标可得,点A在直线l1:y=x+1上;根据点B的坐标可知点B在直线l2:y=x﹣4上.
由求解出点C的坐标为(,);
由求解出点D的坐标为(,).
根据轴对称的性质,点C是线段AA′的中点,点D是线段BB′的中点.
∵xC,yC.
则xA′=t﹣4,yA′=t﹣3.
同理可得:xB′=t﹣2,yB′=t﹣6.
当线段A′B′与y轴有交点时,xA′≤0≤xB′,即:t﹣4≤0≤t﹣2,解得:2≤t≤4.
当线段A′B′与x轴有交点时,yB′≤0≤yA′,即:t﹣6≤0≤t﹣3,解得:3≤t≤6.
∴2≤t≤6,整数t的值为2,3,4,5,6.
故答案为:D.
【点评】本题考查了反比例函数的图象和性质,一次函数的图象和性质,轴对称图形的性质,一元一次不等式组,求出AB两点关于直线l的对称点坐标是解答本题的难点.
二.填空题(共5小题)
11.(2025 武汉)在平面直角坐标系中,某反比例函数y的图象分别位于第一、第三象限.写出一个满足条件的k的值是 1(答案不唯一) .
【考点】反比例函数的性质;反比例函数的图象.
【专题】反比例函数及其应用;几何直观.
【答案】1(答案不唯一).
【分析】根据反比例函数图象分布确定k的取值范围,在k的取值范围内选取一个数即可.
【解答】解:∵反比例函数y的图象分别位于第一、第三象限,
∴k>0,
不妨令k=1.
故答案为:1(答案不唯一).
【点评】本题考查了反比例函数的图象与性质,熟练掌握反比例函数的性质是关键.
12.(2025 大同模拟)近视眼镜的度数y(度)与镜片焦距x(米)之间有如图所示的反比例函数关系,王老师计划配一副近视眼镜,测得镜片的焦距为0.16米,则王老师镜片的度数为 625 度.
【考点】反比例函数的应用.
【专题】反比例函数及其应用.
【答案】625.
【分析】首先求出反比例函数解析式,然后把x=0.16代入计算即可.
【解答】解:设反比例函数解析式为,
将(0.4,250)代入得,,
解得k=100,
∴反比例函数解析式为,
把x=0.16代入,得度,
故答案为:625.
【点评】本题考查了求反比例函数值,反比例函数的应用,掌握以上性质是解题的关键.
13.(2025 普兰店区一模)我们称关于x的二次函数y=px2+qx+k为一次函数y=px+q和反比例函数的“非对称韦达函数”,一次函数y=px+q和反比例函数的交点称为二次函数y=px2+qx+k的“韦达点”,若一次函数y=ax+2b和反比例函数的“非对称韦达函数”的两个“韦达点”的横坐标为s,t,其中实数a>b>c,a+b+c=0.则的取值范围为 .
【考点】反比例函数图象上点的坐标特征;二次函数的性质;二次函数图象上点的坐标特征;二次函数图象与几何变换;一次函数图象与几何变换;反比例函数的性质.
【专题】一次函数及其应用;反比例函数及其应用;二次函数图象及其性质;运算能力.
【答案】.
【分析】联立方程组,根据根与系数的故选求出的值,在根据a,b,c的取值求出的取值范围即可.
【解答】解:∵a>b>c,a+b+c=0,
∴a>0,c<0,a+a+c>0,a+c+c<0,
∴﹣2,
∵一次函数y=ax+2b和反比例函数的“非对称韦达函数”的两个“韦达点”的横坐标为s,t,
∴s,t是方程ax+2b,即ax2+2bx+c=0的两根,
∴s+tst,
∵
=2,
=2
=2
=2,
∵﹣2,
∴2,
即.
故答案为:.
【点评】本题主要考查了反比例函数图象上点的坐标特征一次函数图象与几何变换,二次函数的性质,二次函数图象与几何变换,根据题干所给定义结合根与系数的关系来求解是本题解题的关键.
14.(2025 武安市二模)对于反比例函数y(k>0),称M(,),N(,)为该反比例函数图象的两个“焦点”,且若P为反比例函数图象上的任意一点,则恒有|PM﹣PN|=2.如图,M,N为反比例函数y(k>0)的图象的两个焦点,A为该反比例函数在第三象限的图象上的一个动点,B为∠NAM的平分线上的一点,且AB⊥BM,OB=2,则k的值为 2 .
【考点】反比例函数图象上点的坐标特征;反比例函数的图象.
【专题】反比例函数及其应用;运算能力.
【答案】2.
【分析】依据题意,延长AN,MB相交于点H.由AB平分∠MAN,且BM⊥AB,可得AH=AM,再由利用“焦点”的结论,得|AM﹣AN|=2,结合点O,B分别为MN,MH的中点,可得2,进而可以判断得解.
【解答】解:如图,延长AN,MB相交于点H.∵AB平分∠MAN,且BM⊥AB,
∴AH=AM,点B为HM的中点.利用“焦点”的结论,得
|AM﹣AN|=2.
∵点O,B分别为MN,MH的中点,
∴2,
∴k=2.
故答案为:2.
【点评】本题主要考查了反比例函数的应用,解题时要熟练掌握并能灵活运用反比例函数的性质是关键.
15.(2025 齐齐哈尔四模)如图,将抛物线y=x2沿y=x向下平移,使平移后的抛物线经过原点,且平移后的抛物线的对称轴与原抛物线y=x2交于点A,则经过点A的反比例函数的解析式为 .
【考点】反比例函数图象上点的坐标特征;二次函数的性质;二次函数图象上点的坐标特征;二次函数图象与几何变换;一次函数图象上点的坐标特征.
【专题】反比例函数及其应用;二次函数图象及其性质;运算能力.
【答案】.
【分析】根据题意可设将抛物线y=x2向下平移t(t>0)个单位长度,向左平移t个长度可得到新抛物线,则新抛物线解析式为y=(x+t)2﹣t,利用待定系数法可求出平移后的抛物线解析式为y=(x+1)2﹣1,进而可求出点A的坐标,再利用待定系数法求出对应的反比例函数解析式即可.
【解答】解:可设将抛物线y=x2向下平移t(t>0)个单位长度,向左平移t个长度可得到新抛物线,
∴新抛物线解析式为y=(x+t)2﹣t,
∵平移后的抛物线经过原点,
∴0=(0+t)2﹣t,
解得t=1或t=0(舍去),
∴平移后的抛物线解析式为y=(x+1)2﹣1,
∴平移后的抛物线对称轴为直线x=﹣1,
在y=x2中,当x=﹣1时,y=1,
∴A(﹣1,1),
设经过点A的反比例函数解析式为,
∴,
∴k=﹣1,
∴经过点A的反比例函数解析式为,
故答案为:.
【点评】本题主要考查了二次函数图象的平移问题,求反比例函数解析式,熟练掌握以上知识点是关键.
三.解答题(共5小题)
16.(2025 樟树市校级三模)如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(4,7),反比例函数(x>0)的图象经过BC的中点D,且与AB交于点E.
(1)求反比例函数的解析式及点E的坐标;
(2)若点F是OC边上的一点,且△BCF为等腰三角形,求直线FB的解析式.
【考点】反比例函数综合题.
【专题】代数几何综合题;运算能力;推理能力.
【答案】(1)y(x>0).(4,);
(2)y=x+3.
【分析】(1)先根据点B的坐标为(4,7)求出D点坐标,代入反比例函数y(x>0)即可求出m的值,进而得出解析式,再把x=4代入求出y的值即可得出E点坐标;
(2)根据△BCF为等腰三角形得出CF的长,进而得出F点的坐标,利用待定系数法求出直线FB的解析式即可.
【解答】解:(1)∵点B的坐标为(4,7),点D是BC的中点,
∴D(2,7),
∵点D在反比例函数y(x>0)上,
∴7,
解得:m=14,
∴反比例函数的解析式为y(x>0).
∵四边形OABC是矩形,点B的坐标为(4,7),
∴点E的横坐标为4,
把x=4代入y得y,
∴点E的坐标为(4,);
(2)∵△BCF为等腰三角形,点B的坐标为(4,7),∠BCF=90°,
∴BC=CF=4,
∴F(0,3),
设直线BF的解析式为y=ax+b(a≠0),
∴将点B(4,7),F(0,3)代入,得,
解得,
∴直线FB的解析式为y=x+3.
【点评】本题考查的是反比例函数综合题,熟知反比例函数图象上点的坐标特点、矩形的性质、一次函数的性质等知识是解答此题的关键.
17.(2025 武侯区校级模拟)如图,在平面直角坐标系xOy 中,直线 y=ax+12 与y轴正半轴交于点A,与x轴正半轴交于点B,与双曲线y(x>0)的交点为C(4,m),D(C在D的左边),且C,D恰好是线段AB的三等分点.
(1)求a,k的值;
(2)P是线段OB上一点,连接CP.
①若CP将△AOB 的面积分成5:7两部分,求点P的坐标;
②将直线CP沿直线AB进行翻折,与双曲线交于另一点E,连接PE,若 CE=2CP,求点P的坐标.
【考点】反比例函数与一次函数的交点问题.
【专题】一次函数及其应用;反比例函数及其应用;三角形;图形的相似;几何直观;运算能力;推理能力.
【答案】(1)a=﹣1,k=32;
(2)①(1.5,0)或(4.5,0);②(7.2,0).
【分析】(1)过点C作CH⊥x轴于点H,则CH∥OA,依题意设AC=CD=DB=t,则AB=3t,BC=2t,再求出点A(0,12)得AO=12,证明△BCH和△BOA相似,由相似三角形性质得CH=8,进而得点C(4,8),将点C(4,8)代入y=ax+12,得a=﹣1,将点C(4,8)代入y得k=32;
(2)①求出点B(12,0)得S△AOBAO BO=72,设点P的坐标为(m,0),则BP=12﹣m,进而得S△BPCCH BP=48﹣4m,S四边形AOPC=S△AOB﹣S△BPC=24+4m,再分两种情况讨论如下:(ⅰ)当S四边形AOPC:S△BPC=5:7时,则(24+4m):(48﹣4m)=5:7,由此得m=1.5,则点P(1.5,0);(ⅱ)当S△BPC:S四边形AOPC=5:7时,则(48﹣4m):(24+4m)=5:7,由此得m=4.5,则点P(4.5,0),综上所述即可得出答案;
②直线CP沿直线AB进行翻折后点P的对应点为Q,连接BQ,过点E作EF⊥x轴于点F,证明△AOB是等腰直角三角形得∠OBA=45°,由翻折的性质得BC是线段PQ的垂直平分线得CP=CQ=EQ,进而得△BPQ是等腰三角形,则∠PBQ=90°,根据由此得CH∥BQ∥EF,根据平行线分线段成比例定理得BH=BF=8,则OF=20,从而得点E(20,1.6),则CE2=296.96,设点P(n,0)得CP2=(n﹣4)2+82,再根据CE=2CP得296.96=4[(n﹣4)2+82],据此解出n=7.2,继而可得点P的坐标.
【解答】解:(1)过点C作CH⊥x轴于点H,如图1所示:
∵∠CHB=∠AOB=90°,
∴CH∥OA,
∵C,D恰好是线段AB的三等分点,
∴设AC=CD=DB=t,
∴AB=3t,BC=2t,
对于直线y=ax+12,当x=0时,y=12,
∴点A的坐标为(0,12),
∴AO=12,
∵CH∥OA,
∴△BCH∽△BOA,
∴,
∴,
∴CH=8,
∴点C的坐标为(4,8),
将点C(4,8)代入y=ax+12,得:4a+12=8,
解得:a=﹣1,
将点C(4,8)代入y,得:k=4×8=32;
(2)①由(1)可知:直线AB的表达式为:y=﹣x+12,
∴当y=0时,x=12,
∴点B的坐标为(12,0),
∴BO=12,
∵点A(0,12),
∴AO=12,
∴S△AOBAO BO12×12=72,
∵点P在线段OB上,
∴设点P的坐标为(m,0),
∴OP=m,
∴BP=OB﹣OP=12﹣m,
∴S△BPCCH BP8(12﹣m)=48﹣4m,
∴S四边形AOPC=S△AOB﹣S△BPC=72﹣(48﹣4m)=24+4m,
当CP将△AOB的面积分成5:7两部分时,有以下两种情况:
(ⅰ)当S四边形AOPC:S△BPC=5:7时,
∴(24+4m):(48﹣4m)=5:7,
解得:m=1.5,
此时点P的坐标为(1.5,0);
(ⅱ)当S△BPC:S四边形AOPC=5:7时,
∴(48﹣4m):(24+4m)=5:7,
解得:m=4.5,
此时点P的坐标为(4.5,0),
综上所述:点P的坐标为(1.5,0)或(4.5,0);
②直线CP沿直线AB进行翻折后点P的对应点为Q,连接BQ,过点E作EF⊥x轴于点F,如图2所示:
∵BO=AO=12,
∴△AOB是等腰直角三角形,
∴∠OBA=45°,
由翻折的性质得:CP=AQ,PQ⊥AB,
∴BC是线段PQ的垂直平分线,
∴BP=BQ,
∴△BPQ是等腰三角形,
∵PQ⊥AB,
∴∠QBC=∠OBA=45°,
∴∠PBQ=∠QBC+∠OBA=90°,
∴BQ⊥x轴,
∵CE=AQ+EQ=CP+EQ,CE=2CP,
∴CP+EQ=2CP,
∴EQ=CP=CQ,
∵CH⊥x轴,BQ⊥x轴,EF⊥x轴,
∴CH∥BQ∥EF,
根据平行线分线段成比例定理得:BH=BF,
由(1)可知:反比例函数的表达式为:y(x>0),点C(4,8),
∴OH=4,
∵OB=12,
∴BH=OB﹣OH=8,
∴BH=BF=8,
即HF=16,
∴OF=OH+HF=20,
∴点E的横坐标为20,
∵点E在反比例y(x>0)的图象上,
∴点E的坐标为(20,1.6),
∴CE2=(4﹣20)2+(8﹣1.6)2=296.96,
设点P的坐标为(n,0),
∴CP2=(n﹣4)2+82,
∵CE=2CP,
∴CE2=4CP2,
∴296.96=4[(n﹣4)2+82],
整理得:(n﹣4)2=10.24,
∴n﹣4=±3.2,
由n﹣4=3.2,解得:n=7.2,
∴点P的坐标为(7.2,0);
由n﹣4=﹣3.2,解得:n=0.8,
∴点P的坐标为(0.8,0),此时CP沿AB翻折后与双曲线y(x>0)没有交点,故不合题意,舍去,
∴点P的坐标为(7.2,0).
【点评】此题主要考查了反比例函数与一次函数的交点,图形的翻折变换及其性质,三角形的面积,熟练掌握图形的翻折变换及其性质,相似三角形的判定和性质,三角形的面积公式是解决问题的关键,分类讨论是解决问题的易错点.
18.(2025 广州)如图,曲线G:y(x>0)经过点P(4,t).
(1)求t的值;
(2)直线l:y=﹣x+b也经过点P,求l与y轴交点的坐标,并在图中画出直线l;
(3)在(2)的条件下,若在l与两坐标轴围成的三角形内部(不包含边界)随机取一个格点(横、纵坐标都是整数的点),求该格点在曲线G上的概率.
【考点】反比例函数与一次函数的交点问题.
【专题】函数及其图象;一次函数及其应用;概率及其应用;模型思想.
【答案】(1);
(2)l与y轴交点的坐标为(0,4.5),图中画出直线l见解答;
(3).
【分析】(1)直接把(4,t)代入y进行计算,得t;
(2)先得出P(4,),再代入直线l:y=﹣x+4.5,即可求出t与y轴交点的坐标,再由两点确定一直线画出直线l的函数图象;
(3)先得出格点共有6个,分别是(1,3),(1,2),(1,1),(2,1),(2,2),(3,1),再分析所得格点(1,2),(2,1)在曲线G上,即有两个格点在曲线G上,最后由概率公式解答即可.
【解答】解:(1)曲线G:y过点P(4,t),
∴t;
(2)由(1)得t,
故P(4,),
∵直线l:y=﹣x+b也经过点P,
∴把(4,)代入y=﹣x+b,得,
解得b=4.5,
∴y=﹣x+4.5,
令x=0,则y=0+4.5=4.5,
∴l与y轴交点的坐标为(0,4.5),
直线的函数图象,如图所示:
(3)根据题意,在l与两坐标轴围成的三角形内部(不包括边界)的格点共有6个,分别是(1,3),(1,2),(1,1),(2,1),(2,2),(3,1),
∵曲线G:y(x>0),
则1×3=3≠2,1×2=2,1×1≠2,2×1=2,2×2=4≠2,3×1=3≠2,
∴格点(1,2),(2,1)在曲线G上,即有两个格点在曲线G上,
∴该格点在曲线G上的概率.
【点评】本题考查了概率公式,反比例函数的性质,一次函数的性质,画函数图象,掌握相关性质是解答本题的关键.
19.(2025 巴中模拟)如图,在平面直角坐标系xOy中,一次函数y=kx+b与反比例函数y(x>0)的图象交于点A(2,6),B(n,3),与x轴,y轴分别交于C,D两点.
(1)求一次函数和反比例函数的表达式;
(2)请根据图象直接写出关于x的不等式kx+b(x>0)的解集;
(3)在直线CD上有点P,△PCO的面积为12,求点P的坐标.
【考点】反比例函数与一次函数的交点问题.
【专题】一次函数及其应用;反比例函数及其应用;运算能力.
【答案】(1),;
(2)0<x<2或x>4;
(3)点P的坐标为或.
【分析】(1)先把A(2,6)代入得m=12,再把B(n,3)代入,求出B(4,3),运用待定系数法进行求一次函数的解析式,即可作答.
(2)认真观察图象,且结合A(2,6),B(4,3),运用数形结合思想得不等式的解集0<x<2或x>4,即可作答.
(3)先求出C(6,0),得OC=6,设,运用三角形面积公式列式计算,即可作答.
【解答】解:(1)由条件可得,
∴m=12,
∴,
把B(n,3)代入,得,
∴n=4,
则B(4,3),
把A(2,6)和B(4,3)分别代入y=kx+b,
得,
解得,
∴.
(2)由(1)得,B(4,3),,
∵一次函数与反比例函数的图象交于点A(2,6),B(4,3),
∴不等式的解集0<x<2或x>4;
(3)依题意,与x轴交于C点,
∴当y=0时,则,
解得x=6,
∴C(6,0),
∴OC=6,
∵直线CD上有点P,
设,
∵△PCO的面积为12,
∴,
则,
∴或,
解得或,
则或.
【点评】本题考查了反比例函数与一次函数的交点,求反比例函数的解析式,求一次函数的解析式,一次函数与几何综合,正确掌握相关性质内容是解题的关键.
20.(2025 浙江模拟)如图,在平面直角坐标系中,点C,D都在反比例函数的图象上,CE⊥x轴于点E,DB⊥x轴于点B,OC与BD的延长线相交于点A.
(1)若△OCE的面积为6.
①求反比例函数的表达式.
②当y≤4时,求自变量x的取值范围.
(2)已知CE=4,BD,求AB的长.
【考点】待定系数法求反比例函数解析式;反比例函数的性质;反比例函数系数k的几何意义;反比例函数图象上点的坐标特征.
【专题】反比例函数及其应用;运算能力;推理能力.
【答案】见试题解答内容
【分析】(1)①利用反比例函数系数k的几何意义即可求解;
②求得y=4时,自变量x的值,然后根据图象即可求解;
【解答】解:(1)①点C在反比例函数的图象上,CE⊥x轴于点E,
∴S△OCE|k|,
∵△OCE的面积为6,
∴|k|=6,
∵k>0,
∴k=12,
∴反比例函数的表达式为y;
②当y=4时,则4,解得x=3,
由图象可知,当y≤4时,x≥3.
(2)∵点C,D都在反比例函数的图象上,CE⊥x轴于点E,DB⊥x轴于点B,OC与BD的延长线相交于点A,
∴CE∥BD,,
∵CE=4,BD,
∴4OEOB,
∴,
∵CE∥AB,
∴,
∴AB=3CE=3×4=12.
【点评】本题考查了反比例函数系数k的几何意义,反比例函数图象上点的坐标特征,反比例函数的性质,平行线分线段成比例定理,数形结合是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
