期末评估测试卷(B) (含答案) 2025-2026学年数学人教版九年级上册
文档属性
| 名称 | 期末评估测试卷(B) (含答案) 2025-2026学年数学人教版九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 265.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-08 09:42:29 | ||
图片预览



文档简介
期末评估测试卷(B)
(总分:120分 时间:120分钟)
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.如图,射线OP绕端点O从一个位置旋转到另一个位置所形成的图形是( )
A.扇形 B.圆弧 C.角 D.三角形
2.若抛物线y=ax2+bx+c(a≠0)经过A(1,0),B(3,0)两点,则抛物线的对称轴为直线 ( )
A.x=1 B.x=2 C.x=3 D.x=4
3.如图,四边形ABCD是边长为5的正方形,E是DC上一点,DE=1,将△ADE绕着点A顺时针旋转到与△ABF重合,则EF的长度为 ( )
A. B.
C.5 D.2
4.不透明的袋子中有5个相同的小球,分别写有1,2,3,4,x五个数字,随机摸出一个小球,上面的数字是奇数的概率为,则x可以是 ( )
A.0 B.2 C.4 D.5
5.某数学兴趣小组四人以接龙的方式用配方法解一元二次方程,每人负责完成一个步骤,如图所示.老师看后,发现有一位同学所负责的步骤是错误的,则这位同学是 ( )
原方程 甲 乙 丙 丁
x2-2x-8=0→x2-2x=8→x2-2x+1=8+1→(x-1)2=9→x=4
A.甲 B.乙
C.丙 D.丁
6.如果点P(3-m,1-2m)关于原点O的对称点P1在第二象限,那么当m取偶数时,点P关于x轴对称的点P2的坐标为 ( )
A.(1,-3) B.(1,3)
C.(2,-1) D.(2,1)
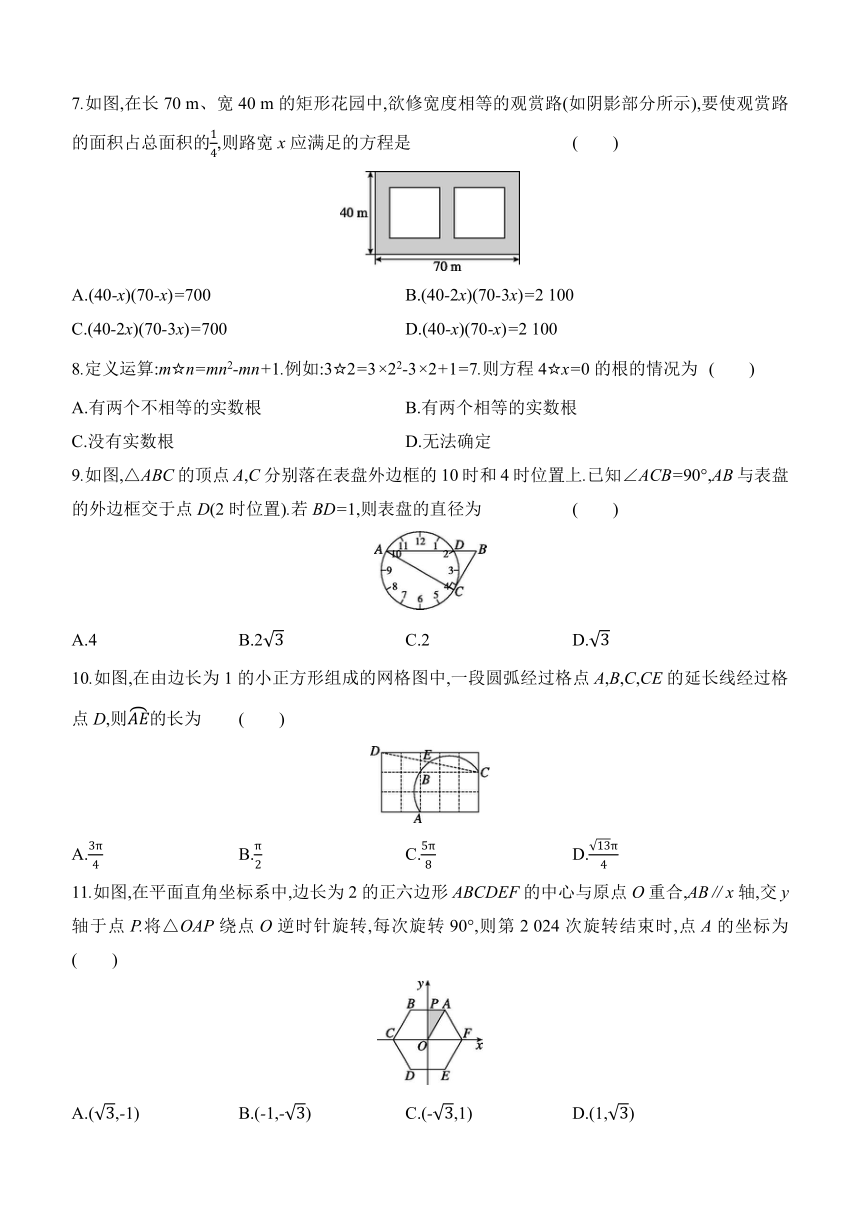
7.如图,在长70 m、宽40 m的矩形花园中,欲修宽度相等的观赏路(如阴影部分所示),要使观赏路的面积占总面积的,则路宽x应满足的方程是 ( )
A.(40-x)(70-x)=700 B.(40-2x)(70-3x)=2 100
C.(40-2x)(70-3x)=700 D.(40-x)(70-x)=2 100
8.定义运算:m☆n=mn2-mn+1.例如:3☆2=3×22-3×2+1=7.则方程4☆x=0的根的情况为 ( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法确定
9.如图,△ABC的顶点A,C分别落在表盘外边框的10时和4时位置上.已知∠ACB=90°,AB与表盘的外边框交于点D(2时位置).若BD=1,则表盘的直径为 ( )
A.4 B.2 C.2 D.
10.如图,在由边长为1的小正方形组成的网格图中,一段圆弧经过格点A,B,C,CE的延长线经过格点D,则的长为 ( )
A. B. C. D.
11.如图,在平面直角坐标系中,边长为2的正六边形ABCDEF的中心与原点O重合,AB∥x轴,交y轴于点P.将△OAP绕点O逆时针旋转,每次旋转90°,则第2 024次旋转结束时,点A的坐标为 ( )
A.(,-1) B.(-1,-) C.(-,1) D.(1,)
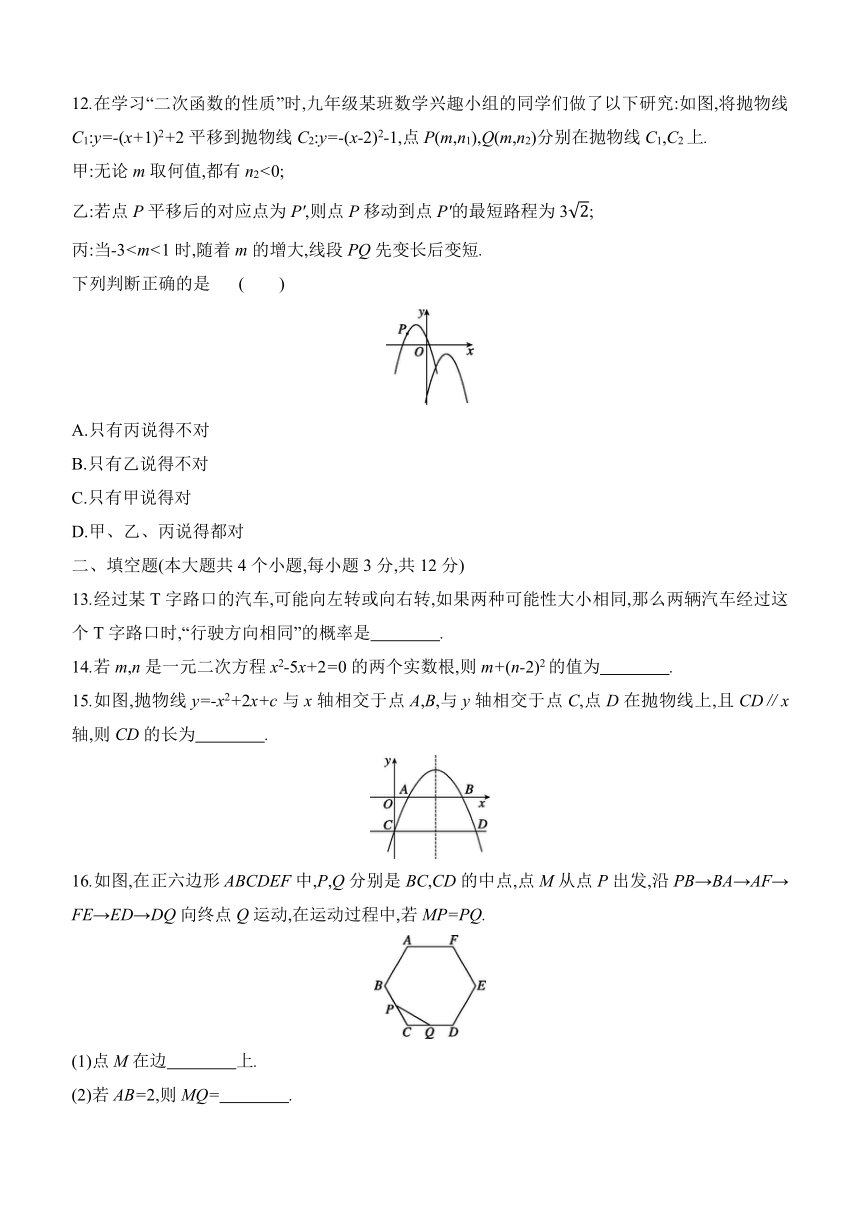
12.在学习“二次函数的性质”时,九年级某班数学兴趣小组的同学们做了以下研究:如图,将抛物线C1:y=-(x+1)2+2平移到抛物线C2:y=-(x-2)2-1,点P(m,n1),Q(m,n2)分别在抛物线C1,C2上.
甲:无论m取何值,都有n2<0;
乙:若点P平移后的对应点为P',则点P移动到点P'的最短路程为3;
丙:当-3下列判断正确的是 ( )
A.只有丙说得不对
B.只有乙说得不对
C.只有甲说得对
D.甲、乙、丙说得都对
二、填空题(本大题共4个小题,每小题3分,共12分)
13.经过某T字路口的汽车,可能向左转或向右转,如果两种可能性大小相同,那么两辆汽车经过这个T字路口时,“行驶方向相同”的概率是 .
14.若m,n是一元二次方程x2-5x+2=0的两个实数根,则m+(n-2)2的值为 .
15.如图,抛物线y=-x2+2x+c与x轴相交于点A,B,与y轴相交于点C,点D在抛物线上,且CD∥x轴,则CD的长为 .
16.如图,在正六边形ABCDEF中,P,Q分别是BC,CD的中点,点M从点P出发,沿PB→BA→AF→ FE→ED→DQ向终点Q运动,在运动过程中,若MP=PQ.
(1)点M在边 上.
(2)若AB=2,则MQ= .
三、解答题(本大题共8 个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(7分)已知关于x的方程x2+mx+m-2=0.
(1)若该方程的一个根为x=1,求m的值及该方程的另一个根.
(2)求证:不论m取何实数,该方程都有两个不相等的实数根.
18.(8分)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-4,-2),B(-2,0),C(0,-3),△A1B1C是△ABC绕点C顺时针旋转90°后得到的图形.
(1)在所给的平面直角坐标系中画出△A1B1C.
(2)若点B2与点B1关于原点对称,直接写出线段A1B2的长.
(3)求点B旋转形成的的长度.
19.(8分)(2024甘肃中考)在一只不透明的布袋中,装有质地、大小均相同的四个小球,小球上分别标有数字1,2,3,4.甲、乙两人玩摸球游戏,规则如下:两人同时从袋中随机各摸出1个小球,若两球上的数字之和为奇数,则甲胜;若两球上的数字之和为偶数,则乙胜.
(1)请用画树状图或列表的方法,求甲获胜的概率.
(2)这个游戏规则对甲、乙双方公平吗 请说明理由.
20.(8分)日晷是我国古代使用的一种计时仪器,某日晷底座的正面与晷面在同一平面上.如图,☉O表示日晷的晷面圆周,日晷底座的底边AB在水平线l上,△OAB为等边三角形,OA,OB与☉O分别交于P,Q两点.C,D是☉O上两点,CD∥AB,过点O作OE⊥AB于点E,交CD于点F,交☉O于点M.已知CD=60 cm,FM=30 cm,ME=20 cm.
(1)求☉O的半径.
(2)求图中阴影部分的面积.
21.(9分)(2024河南中考)从地面竖直向上发射的物体离地面的高度h(m)满足解析式h=-5t2+v0t,其中t(s)是物体运动的时间,v0(m/s)是物体被发射时的速度.社团活动时,科学小组在实验楼前从地面竖直向上发射小球.
(1)小球被发射后 s时离地面的高度最大(用含v0的式子表示).
(2)若小球离地面的最大高度为20 m,求小球被发射时的速度.
(3)按(2)中的速度发射小球,小球离地面的高度有两次与实验楼的高度相同.小明说:“这两次间隔的时间为3 s.”已知实验楼高15 m,请判断他的说法是否正确,并说明理由.
22.(9分)(2025保定期中)如图,在△ABC中,AB=AC,∠BAC=60°,在△ABC外有一点D,连接AD,BD,CD,将△ACD绕点A按顺时针方向旋转得到△ABE,AD与BE相交于点F,且∠BFD=97°,连接DE.
(1)求∠ADC的大小.
(2)若∠BDC=7°,BD=3,CD=5,求DE的长.
23.(11分)(2024浙江中考)如图,在圆内接四边形ABCD中,AD(1)若∠AFE=60°,CD为直径,求∠ABD的度数.
(2)求证:①EF∥BC.
②EF=BD.
24.(12分)如图,斜坡AC上种有若干树木,底部有一喷水管BC,某时刻从B处喷出的水流恰好落在A处,水流呈抛物线状.建立恰当的平面直角坐标系,得到点A(0,2),B(6,0.5).已知喷水管BC及所有树木都与OC垂直,抛物线对应的函数解析式为y=-x2+bx+c.
(1)求该抛物线对应的函数解析式并写出其顶点坐标.
(2)若抛物线恰好过小树MN的树顶N,点M在斜坡AC上,且点A到M,N两点的距离相等,求点M的坐标.
(3)若DE,MN为两棵等高的小树(MN在左侧,小树粗细忽略不计,点M,D均在斜坡上且与点 C不重合),抛物线恰好经过E,N两点.
①当MN=1.25时,求DM的长.
②直接写出点M的横坐标m的取值范围.
【详解答案】
1.C 解析:一条射线绕着端点从一个位置旋转到另一个位置所形成的图形是角.故选C.
2.B 解析:∵抛物线y=ax2+bx+c(a≠0)经过A(1,0),B(3,0)两点,∴抛物线的对称轴为直线x==2.故选B.
3.D 解析:由旋转的性质可知,△ADE≌△ABF.根据题意,得BC=CD=5,BF=DE=1,∠BCD=90°.∴FC=BC+BF=6,CE=CD-DE=4.∴EF===2.故选D.
4.D 解析:根据上面的数字是奇数的概率为可得,奇数的个数为5×=3(个),∵1,2,3,4中1,3为奇数,有两个,∴x为奇数.只有D选项符合.故选D.
5.D 解析:∵x2-2x-8=0,∴x2-2x=8.∴x2-2x+1=8+1.∴(x-1)2=9.∴x-1=±3.解得x1=4,x2=-2.综上所述,丁同学是错的.故选D.
6.B 解析:∵点P(3-m,1-2m)关于原点O的对称点P1在第二象限,∴点P在第四象限.∴由①,得m<3.由②,得m>.∴7.B 解析:根据题意,得(40-2x)(70-3x)=×40×70.整理,得(40-2x)(70-3x)=2 100.故选B.
8.B 解析:方程4☆x=0化为4x2-4x+1=0.∵Δ=(-4)2-4×4×1=0,∴方程有两个相等的实数根.故选B.
9.B 解析:如图,连接CD.∵线段AC恰好平分表盘,∴AC是表盘的直径.∴∠ADC=90°.∴∠BDC=90°.∵=2,∴∠ACD=2∠A.∵∠A+∠ACD=90°,∴3∠A=90°.∴∠A=30°.∴∠ACD=60°.∵∠ACB=90°,∴∠BCD=30°.在Rt△BCD中,∵BD=1,∴BC=2BD=2.∴CD===.在Rt△ACD中,∵∠A=30°,∴AC=2CD=2,即表盘的直径为2.故选B.
10.D 解析:如图,连接AC,AD,取AC的中点O,连接OE.
∵∠ABC=90°,∴AC为直径.∵AC2=AD2=32+22=13,CD2=12+52=26,∴AC2+AD2=CD2.∴△ACD为等腰直角三角形.∴∠ACD=45°.∴∠AOE=2∠ACD=90°.∵AO=AC=,∴的长为=.故选D.
11.D 解析:∵正六边形ABCDEF的边长为2,中心与原点O重合,AB∥x轴,∴AP=1,AO=2,∠OPA=90°.∴OP==.∵第1次旋转结束时,点A的坐标为(-,1);第2次旋转结束时,点A的坐标为(-1,-);第3次旋转结束时,点A的坐标为(,-1);第4次旋转结束时,点A的坐标为(1,),∴4次一个循环.∵2 024÷4=506,∴第2 024次旋转结束时,点A的坐标为(1,).故选D.
12.A 解析:∵抛物线C2:y=-(x-2)2-1开口向下,顶点为(2,-1),∴无论m取何值,都有n2<0.故甲说得对;∵抛物线C1:y=-(x+1)2+2的顶点为(-1,2),抛物线C2:y=-(x-2)2-1的顶点为(2,-1),∴将抛物线C1:y=-(x+1)2+2向右平移3个单位长度,向下平移3个单位长度得到抛物线C2:y=-(x-2)2-1.∴点P移动到点P'的最短路程为=3.故乙说得对;∵PQ=|-(m+1)2+2+(m-2)2+1|=|-6m+6|,∴当-313. 解析:画树状图如下:
由图可知,共有4种等可能的结果,其中行驶方向相同的有2种,∴“行驶方向相同”的概率是=.
14.7 解析:∵m,n是一元二次方程x2-5x+2=0的两个实数根,∴m2-5m+2=0,m+n=5.∴m2-5m=-2,n=5-m.∴m+(n-2)2=m+(3-m)2=m2-5m+9=-2+9=7.
15.2 解析:抛物线的对称轴为直线x=-=-=1,令x=0,则y=c,∴点C的坐标为(0,c).∵CD∥x轴,∴点D(2,c).∴CD的长为2.
16.(1)AB (2)3
解析:(1)由点M的移动的路线可知,当MP=PQ时,点M在边AB上,且M是AB的中点.
(2)如图,取六边形ABCDEF的中心O,连接AD,OF.由正六边形的性质可知,AD∥BC,AD过正六边形ABCDEF的中心O,∠AOF==60°.∵OA=OF,∴△AOF是等边三角形.∴OA=OF=AF=AB=2.∴AD=2OA=4.∵Q是CD的中点,M是AB的中点,∴MQ是梯形BCDA的中位线.∴MQ=(BC+AD)=×(2+4)=3.
17.解:(1)∵该方程的一个根为x=1,
∴1+m+m-2=0.
解得m=.
∴方程为x2+x-=0.
解得x1=1,x2=-.
∴该方程的另一个根为-.
(2)证明:∵Δ=m2-4(m-2)×1=(m-2)2+4>0,
∴不论m取何实数,该方程都有两个不相等的实数根.
18.解:(1)如图,△A1B1C即为所求作.
(2)A1B2=4.
解法提示:∵点B2与点B1关于原点对称,∴点B2(-3,1).
∴A1B2=1-(-3)=4.
(3)由勾股定理,得CB==.
∴的长度为=π.
19.解:(1)画树状图如下:
由图可知,共有12种等可能的结果,其中甲获胜的结果有8种,
∴甲获胜的概率为=.
(2)不公平.理由如下:
由(1)中树状图可知,乙获胜的结果有4种,
∴乙获胜的概率为=.
∵>,
∴这个游戏规则对甲、乙双方不公平.
20.解:(1)∵OE⊥AB,AB∥CD,∴OE⊥CD.
∵CD=60 cm,
∴DF=CD=30 cm.
如图,连接OD.设☉O的半径OD=r cm,则OF=OM-FM=(r-30)cm.
在Rt△ODF中,r2=(30)2+(r-30)2.
解得r=60,即☉O的半径为60 cm.
(2)∵△OAB为等边三角形,
∴∠OBE=∠AOB=60°.
在Rt△BOE中,OE=60+20=80(cm),
∠BOE=30°,
∴OB=2BE.
设BE=x cm,则OB=2x cm.
根据勾股定理,得x2+802=(2x)2.
解得x=.
∴OB=AB=cm.
∴S△OAB=AB·OE=××80=(cm2).
∵S扇形POQ==600π(cm2),
∴S阴影=-600π(cm2).
21.解:(1)
(2)当t=时,h=20.
∴-5×2+v0×=20.
解得v0=20(负值已舍去).
∴小球被发射时的速度是20 m/s.
(3)小明的说法不正确.理由如下:
由(2),得h=-5t2+20t.
当h=15时,15=-5t2+20t.
解得t1=1,t2=3.
∵3-1=2(s),
∴小明的说法不正确.
22.解:(1)∵将△ACD绕点A按顺时针方向旋转得到△ABE,
∴AB=AC,∠ADC=∠BEA,∠CAD=∠BAE,
∴∠CAD-∠BAD=∠BAE-∠BAD,
即∠BAC=∠EAD=60°.
∵∠BFD=97°=∠AFE,
∴∠BEA=180°-97°-60°=23°.
∴∠ADC=∠BEA=23°.
(2)∵将△ACD绕点A按顺时针方向旋转得到△ABE,
∴△ACD≌△ABE.
∴CD=BE=5,AD=AE.
∵AD=AE,∠EAD=60°,
∴△AED是等边三角形.
∴∠ADE=60°.
∵∠BDC=7°,∠ADC=23°,∠ADE=60°,
∴∠BDE=∠BDC+∠ADC+∠ADE=90°.
∴DE===4.
23.解:(1)∵CD为直径,
∴∠CAD=90°.
∵∠AFE=∠ADC=60°,
∴∠ACD=90°-60°=30°.
∴∠ABD=∠ACD=30°.
(2)证明:①如图,延长AB至点M.
∵四边形ABCD是圆内接四边形,
∴∠ADC+∠ABC=180°.
又∵∠ABC+∠CBM=180°,
∴∠CBM=∠ADC.
又∵∠AFE=∠ADC,
∴∠AFE=∠CBM.∴EF∥BC.
②如图,过点D作DG∥BC交☉O于点G,连接AG,CG.
∵DG∥BC,∴=.∴BD=CG.
∵四边形ACGD是圆内接四边形,
∴∠ADG+∠ACG=180°.
又∵∠ADG+∠GDE=180°,
∴∠GDE=∠ACG.
由(1)知,EF∥BC,∴EF∥DG.
∴∠DEF=∠GDE.
∴∠DEF=∠ACG,即∠AEF=∠ACG.
∵∠AFE=∠ADC,∠ADC=∠AGC,
∴∠AFE=∠AGC.
∵AE=AC,∴△AEF≌△ACG(AAS).
∴EF=CG.∴EF=BD.
24.解:(1)∵点A(0,2),B(6,0.5)在抛物线y=-x2+bx+c上,
∴解得
∴该抛物线对应的函数解析式为y=-x2+x+2=-(x-2)2+.
∴抛物线的顶点坐标为2,.
(2)∵点B(6,0.5),BC⊥OC,点C在x轴上,∴点C的坐标为(6,0).
∵点A(0,2),
∴直线AC的解析式为y=-x+2.
∵点M在直线AC上,
∴设点M的坐标为m,-m+2.
∵MA=NA,MN⊥x轴,点A(0,2),
∴点N的坐标可以表示为m,m+2.
∵点N在抛物线上,
∴m+2=-m2+m+2.
解得m1=,m2=0(不符合题意,舍去).
∴点M的坐标为,.
(3)①令d=-x2+x+2--x+2,化简,得d=-x2+x.
∵MN=DE=1.25,
∴当d=1.25时,-x2+x=1.25.
解得x1=,x2=.
∵MN在DE左侧,
∴xM=,xD=.
∴yM=,yD=.
根据勾股定理,得DM=.
②解法提示:设MN=DE=d0,则d=
-x2+x=d0,
在0即直线d=d0与抛物线d=-x2+x在0当x=6时,d=-×62+5=,
令-x2+x=,
得x=或x=6(舍去),
∴又d=-x2+x=-x-2+,
抛物线图象的对称轴为直线x=,
m为直线d=d0与抛物线d=-x2+x两交点中靠左一点的横坐标,故m<.
综上,
(总分:120分 时间:120分钟)
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.如图,射线OP绕端点O从一个位置旋转到另一个位置所形成的图形是( )
A.扇形 B.圆弧 C.角 D.三角形
2.若抛物线y=ax2+bx+c(a≠0)经过A(1,0),B(3,0)两点,则抛物线的对称轴为直线 ( )
A.x=1 B.x=2 C.x=3 D.x=4
3.如图,四边形ABCD是边长为5的正方形,E是DC上一点,DE=1,将△ADE绕着点A顺时针旋转到与△ABF重合,则EF的长度为 ( )
A. B.
C.5 D.2
4.不透明的袋子中有5个相同的小球,分别写有1,2,3,4,x五个数字,随机摸出一个小球,上面的数字是奇数的概率为,则x可以是 ( )
A.0 B.2 C.4 D.5
5.某数学兴趣小组四人以接龙的方式用配方法解一元二次方程,每人负责完成一个步骤,如图所示.老师看后,发现有一位同学所负责的步骤是错误的,则这位同学是 ( )
原方程 甲 乙 丙 丁
x2-2x-8=0→x2-2x=8→x2-2x+1=8+1→(x-1)2=9→x=4
A.甲 B.乙
C.丙 D.丁
6.如果点P(3-m,1-2m)关于原点O的对称点P1在第二象限,那么当m取偶数时,点P关于x轴对称的点P2的坐标为 ( )
A.(1,-3) B.(1,3)
C.(2,-1) D.(2,1)
7.如图,在长70 m、宽40 m的矩形花园中,欲修宽度相等的观赏路(如阴影部分所示),要使观赏路的面积占总面积的,则路宽x应满足的方程是 ( )
A.(40-x)(70-x)=700 B.(40-2x)(70-3x)=2 100
C.(40-2x)(70-3x)=700 D.(40-x)(70-x)=2 100
8.定义运算:m☆n=mn2-mn+1.例如:3☆2=3×22-3×2+1=7.则方程4☆x=0的根的情况为 ( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法确定
9.如图,△ABC的顶点A,C分别落在表盘外边框的10时和4时位置上.已知∠ACB=90°,AB与表盘的外边框交于点D(2时位置).若BD=1,则表盘的直径为 ( )
A.4 B.2 C.2 D.
10.如图,在由边长为1的小正方形组成的网格图中,一段圆弧经过格点A,B,C,CE的延长线经过格点D,则的长为 ( )
A. B. C. D.
11.如图,在平面直角坐标系中,边长为2的正六边形ABCDEF的中心与原点O重合,AB∥x轴,交y轴于点P.将△OAP绕点O逆时针旋转,每次旋转90°,则第2 024次旋转结束时,点A的坐标为 ( )
A.(,-1) B.(-1,-) C.(-,1) D.(1,)
12.在学习“二次函数的性质”时,九年级某班数学兴趣小组的同学们做了以下研究:如图,将抛物线C1:y=-(x+1)2+2平移到抛物线C2:y=-(x-2)2-1,点P(m,n1),Q(m,n2)分别在抛物线C1,C2上.
甲:无论m取何值,都有n2<0;
乙:若点P平移后的对应点为P',则点P移动到点P'的最短路程为3;
丙:当-3
A.只有丙说得不对
B.只有乙说得不对
C.只有甲说得对
D.甲、乙、丙说得都对
二、填空题(本大题共4个小题,每小题3分,共12分)
13.经过某T字路口的汽车,可能向左转或向右转,如果两种可能性大小相同,那么两辆汽车经过这个T字路口时,“行驶方向相同”的概率是 .
14.若m,n是一元二次方程x2-5x+2=0的两个实数根,则m+(n-2)2的值为 .
15.如图,抛物线y=-x2+2x+c与x轴相交于点A,B,与y轴相交于点C,点D在抛物线上,且CD∥x轴,则CD的长为 .
16.如图,在正六边形ABCDEF中,P,Q分别是BC,CD的中点,点M从点P出发,沿PB→BA→AF→ FE→ED→DQ向终点Q运动,在运动过程中,若MP=PQ.
(1)点M在边 上.
(2)若AB=2,则MQ= .
三、解答题(本大题共8 个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(7分)已知关于x的方程x2+mx+m-2=0.
(1)若该方程的一个根为x=1,求m的值及该方程的另一个根.
(2)求证:不论m取何实数,该方程都有两个不相等的实数根.
18.(8分)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-4,-2),B(-2,0),C(0,-3),△A1B1C是△ABC绕点C顺时针旋转90°后得到的图形.
(1)在所给的平面直角坐标系中画出△A1B1C.
(2)若点B2与点B1关于原点对称,直接写出线段A1B2的长.
(3)求点B旋转形成的的长度.
19.(8分)(2024甘肃中考)在一只不透明的布袋中,装有质地、大小均相同的四个小球,小球上分别标有数字1,2,3,4.甲、乙两人玩摸球游戏,规则如下:两人同时从袋中随机各摸出1个小球,若两球上的数字之和为奇数,则甲胜;若两球上的数字之和为偶数,则乙胜.
(1)请用画树状图或列表的方法,求甲获胜的概率.
(2)这个游戏规则对甲、乙双方公平吗 请说明理由.
20.(8分)日晷是我国古代使用的一种计时仪器,某日晷底座的正面与晷面在同一平面上.如图,☉O表示日晷的晷面圆周,日晷底座的底边AB在水平线l上,△OAB为等边三角形,OA,OB与☉O分别交于P,Q两点.C,D是☉O上两点,CD∥AB,过点O作OE⊥AB于点E,交CD于点F,交☉O于点M.已知CD=60 cm,FM=30 cm,ME=20 cm.
(1)求☉O的半径.
(2)求图中阴影部分的面积.
21.(9分)(2024河南中考)从地面竖直向上发射的物体离地面的高度h(m)满足解析式h=-5t2+v0t,其中t(s)是物体运动的时间,v0(m/s)是物体被发射时的速度.社团活动时,科学小组在实验楼前从地面竖直向上发射小球.
(1)小球被发射后 s时离地面的高度最大(用含v0的式子表示).
(2)若小球离地面的最大高度为20 m,求小球被发射时的速度.
(3)按(2)中的速度发射小球,小球离地面的高度有两次与实验楼的高度相同.小明说:“这两次间隔的时间为3 s.”已知实验楼高15 m,请判断他的说法是否正确,并说明理由.
22.(9分)(2025保定期中)如图,在△ABC中,AB=AC,∠BAC=60°,在△ABC外有一点D,连接AD,BD,CD,将△ACD绕点A按顺时针方向旋转得到△ABE,AD与BE相交于点F,且∠BFD=97°,连接DE.
(1)求∠ADC的大小.
(2)若∠BDC=7°,BD=3,CD=5,求DE的长.
23.(11分)(2024浙江中考)如图,在圆内接四边形ABCD中,AD
(2)求证:①EF∥BC.
②EF=BD.
24.(12分)如图,斜坡AC上种有若干树木,底部有一喷水管BC,某时刻从B处喷出的水流恰好落在A处,水流呈抛物线状.建立恰当的平面直角坐标系,得到点A(0,2),B(6,0.5).已知喷水管BC及所有树木都与OC垂直,抛物线对应的函数解析式为y=-x2+bx+c.
(1)求该抛物线对应的函数解析式并写出其顶点坐标.
(2)若抛物线恰好过小树MN的树顶N,点M在斜坡AC上,且点A到M,N两点的距离相等,求点M的坐标.
(3)若DE,MN为两棵等高的小树(MN在左侧,小树粗细忽略不计,点M,D均在斜坡上且与点 C不重合),抛物线恰好经过E,N两点.
①当MN=1.25时,求DM的长.
②直接写出点M的横坐标m的取值范围.
【详解答案】
1.C 解析:一条射线绕着端点从一个位置旋转到另一个位置所形成的图形是角.故选C.
2.B 解析:∵抛物线y=ax2+bx+c(a≠0)经过A(1,0),B(3,0)两点,∴抛物线的对称轴为直线x==2.故选B.
3.D 解析:由旋转的性质可知,△ADE≌△ABF.根据题意,得BC=CD=5,BF=DE=1,∠BCD=90°.∴FC=BC+BF=6,CE=CD-DE=4.∴EF===2.故选D.
4.D 解析:根据上面的数字是奇数的概率为可得,奇数的个数为5×=3(个),∵1,2,3,4中1,3为奇数,有两个,∴x为奇数.只有D选项符合.故选D.
5.D 解析:∵x2-2x-8=0,∴x2-2x=8.∴x2-2x+1=8+1.∴(x-1)2=9.∴x-1=±3.解得x1=4,x2=-2.综上所述,丁同学是错的.故选D.
6.B 解析:∵点P(3-m,1-2m)关于原点O的对称点P1在第二象限,∴点P在第四象限.∴由①,得m<3.由②,得m>.∴
8.B 解析:方程4☆x=0化为4x2-4x+1=0.∵Δ=(-4)2-4×4×1=0,∴方程有两个相等的实数根.故选B.
9.B 解析:如图,连接CD.∵线段AC恰好平分表盘,∴AC是表盘的直径.∴∠ADC=90°.∴∠BDC=90°.∵=2,∴∠ACD=2∠A.∵∠A+∠ACD=90°,∴3∠A=90°.∴∠A=30°.∴∠ACD=60°.∵∠ACB=90°,∴∠BCD=30°.在Rt△BCD中,∵BD=1,∴BC=2BD=2.∴CD===.在Rt△ACD中,∵∠A=30°,∴AC=2CD=2,即表盘的直径为2.故选B.
10.D 解析:如图,连接AC,AD,取AC的中点O,连接OE.
∵∠ABC=90°,∴AC为直径.∵AC2=AD2=32+22=13,CD2=12+52=26,∴AC2+AD2=CD2.∴△ACD为等腰直角三角形.∴∠ACD=45°.∴∠AOE=2∠ACD=90°.∵AO=AC=,∴的长为=.故选D.
11.D 解析:∵正六边形ABCDEF的边长为2,中心与原点O重合,AB∥x轴,∴AP=1,AO=2,∠OPA=90°.∴OP==.∵第1次旋转结束时,点A的坐标为(-,1);第2次旋转结束时,点A的坐标为(-1,-);第3次旋转结束时,点A的坐标为(,-1);第4次旋转结束时,点A的坐标为(1,),∴4次一个循环.∵2 024÷4=506,∴第2 024次旋转结束时,点A的坐标为(1,).故选D.
12.A 解析:∵抛物线C2:y=-(x-2)2-1开口向下,顶点为(2,-1),∴无论m取何值,都有n2<0.故甲说得对;∵抛物线C1:y=-(x+1)2+2的顶点为(-1,2),抛物线C2:y=-(x-2)2-1的顶点为(2,-1),∴将抛物线C1:y=-(x+1)2+2向右平移3个单位长度,向下平移3个单位长度得到抛物线C2:y=-(x-2)2-1.∴点P移动到点P'的最短路程为=3.故乙说得对;∵PQ=|-(m+1)2+2+(m-2)2+1|=|-6m+6|,∴当-3
由图可知,共有4种等可能的结果,其中行驶方向相同的有2种,∴“行驶方向相同”的概率是=.
14.7 解析:∵m,n是一元二次方程x2-5x+2=0的两个实数根,∴m2-5m+2=0,m+n=5.∴m2-5m=-2,n=5-m.∴m+(n-2)2=m+(3-m)2=m2-5m+9=-2+9=7.
15.2 解析:抛物线的对称轴为直线x=-=-=1,令x=0,则y=c,∴点C的坐标为(0,c).∵CD∥x轴,∴点D(2,c).∴CD的长为2.
16.(1)AB (2)3
解析:(1)由点M的移动的路线可知,当MP=PQ时,点M在边AB上,且M是AB的中点.
(2)如图,取六边形ABCDEF的中心O,连接AD,OF.由正六边形的性质可知,AD∥BC,AD过正六边形ABCDEF的中心O,∠AOF==60°.∵OA=OF,∴△AOF是等边三角形.∴OA=OF=AF=AB=2.∴AD=2OA=4.∵Q是CD的中点,M是AB的中点,∴MQ是梯形BCDA的中位线.∴MQ=(BC+AD)=×(2+4)=3.
17.解:(1)∵该方程的一个根为x=1,
∴1+m+m-2=0.
解得m=.
∴方程为x2+x-=0.
解得x1=1,x2=-.
∴该方程的另一个根为-.
(2)证明:∵Δ=m2-4(m-2)×1=(m-2)2+4>0,
∴不论m取何实数,该方程都有两个不相等的实数根.
18.解:(1)如图,△A1B1C即为所求作.
(2)A1B2=4.
解法提示:∵点B2与点B1关于原点对称,∴点B2(-3,1).
∴A1B2=1-(-3)=4.
(3)由勾股定理,得CB==.
∴的长度为=π.
19.解:(1)画树状图如下:
由图可知,共有12种等可能的结果,其中甲获胜的结果有8种,
∴甲获胜的概率为=.
(2)不公平.理由如下:
由(1)中树状图可知,乙获胜的结果有4种,
∴乙获胜的概率为=.
∵>,
∴这个游戏规则对甲、乙双方不公平.
20.解:(1)∵OE⊥AB,AB∥CD,∴OE⊥CD.
∵CD=60 cm,
∴DF=CD=30 cm.
如图,连接OD.设☉O的半径OD=r cm,则OF=OM-FM=(r-30)cm.
在Rt△ODF中,r2=(30)2+(r-30)2.
解得r=60,即☉O的半径为60 cm.
(2)∵△OAB为等边三角形,
∴∠OBE=∠AOB=60°.
在Rt△BOE中,OE=60+20=80(cm),
∠BOE=30°,
∴OB=2BE.
设BE=x cm,则OB=2x cm.
根据勾股定理,得x2+802=(2x)2.
解得x=.
∴OB=AB=cm.
∴S△OAB=AB·OE=××80=(cm2).
∵S扇形POQ==600π(cm2),
∴S阴影=-600π(cm2).
21.解:(1)
(2)当t=时,h=20.
∴-5×2+v0×=20.
解得v0=20(负值已舍去).
∴小球被发射时的速度是20 m/s.
(3)小明的说法不正确.理由如下:
由(2),得h=-5t2+20t.
当h=15时,15=-5t2+20t.
解得t1=1,t2=3.
∵3-1=2(s),
∴小明的说法不正确.
22.解:(1)∵将△ACD绕点A按顺时针方向旋转得到△ABE,
∴AB=AC,∠ADC=∠BEA,∠CAD=∠BAE,
∴∠CAD-∠BAD=∠BAE-∠BAD,
即∠BAC=∠EAD=60°.
∵∠BFD=97°=∠AFE,
∴∠BEA=180°-97°-60°=23°.
∴∠ADC=∠BEA=23°.
(2)∵将△ACD绕点A按顺时针方向旋转得到△ABE,
∴△ACD≌△ABE.
∴CD=BE=5,AD=AE.
∵AD=AE,∠EAD=60°,
∴△AED是等边三角形.
∴∠ADE=60°.
∵∠BDC=7°,∠ADC=23°,∠ADE=60°,
∴∠BDE=∠BDC+∠ADC+∠ADE=90°.
∴DE===4.
23.解:(1)∵CD为直径,
∴∠CAD=90°.
∵∠AFE=∠ADC=60°,
∴∠ACD=90°-60°=30°.
∴∠ABD=∠ACD=30°.
(2)证明:①如图,延长AB至点M.
∵四边形ABCD是圆内接四边形,
∴∠ADC+∠ABC=180°.
又∵∠ABC+∠CBM=180°,
∴∠CBM=∠ADC.
又∵∠AFE=∠ADC,
∴∠AFE=∠CBM.∴EF∥BC.
②如图,过点D作DG∥BC交☉O于点G,连接AG,CG.
∵DG∥BC,∴=.∴BD=CG.
∵四边形ACGD是圆内接四边形,
∴∠ADG+∠ACG=180°.
又∵∠ADG+∠GDE=180°,
∴∠GDE=∠ACG.
由(1)知,EF∥BC,∴EF∥DG.
∴∠DEF=∠GDE.
∴∠DEF=∠ACG,即∠AEF=∠ACG.
∵∠AFE=∠ADC,∠ADC=∠AGC,
∴∠AFE=∠AGC.
∵AE=AC,∴△AEF≌△ACG(AAS).
∴EF=CG.∴EF=BD.
24.解:(1)∵点A(0,2),B(6,0.5)在抛物线y=-x2+bx+c上,
∴解得
∴该抛物线对应的函数解析式为y=-x2+x+2=-(x-2)2+.
∴抛物线的顶点坐标为2,.
(2)∵点B(6,0.5),BC⊥OC,点C在x轴上,∴点C的坐标为(6,0).
∵点A(0,2),
∴直线AC的解析式为y=-x+2.
∵点M在直线AC上,
∴设点M的坐标为m,-m+2.
∵MA=NA,MN⊥x轴,点A(0,2),
∴点N的坐标可以表示为m,m+2.
∵点N在抛物线上,
∴m+2=-m2+m+2.
解得m1=,m2=0(不符合题意,舍去).
∴点M的坐标为,.
(3)①令d=-x2+x+2--x+2,化简,得d=-x2+x.
∵MN=DE=1.25,
∴当d=1.25时,-x2+x=1.25.
解得x1=,x2=.
∵MN在DE左侧,
∴xM=,xD=.
∴yM=,yD=.
根据勾股定理,得DM=.
②
-x2+x=d0,
在0
令-x2+x=,
得x=或x=6(舍去),
∴
抛物线图象的对称轴为直线x=,
m为直线d=d0与抛物线d=-x2+x两交点中靠左一点的横坐标,故m<.
综上,
同课章节目录
