第二十三章 旋转 评估测试卷(含答案) 2025-2026学年数学人教版九年级上册
文档属性
| 名称 | 第二十三章 旋转 评估测试卷(含答案) 2025-2026学年数学人教版九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 441.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-08 09:48:02 | ||
图片预览



文档简介
第二十三章评估测试卷
(总分:120分 时间:120分钟)
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
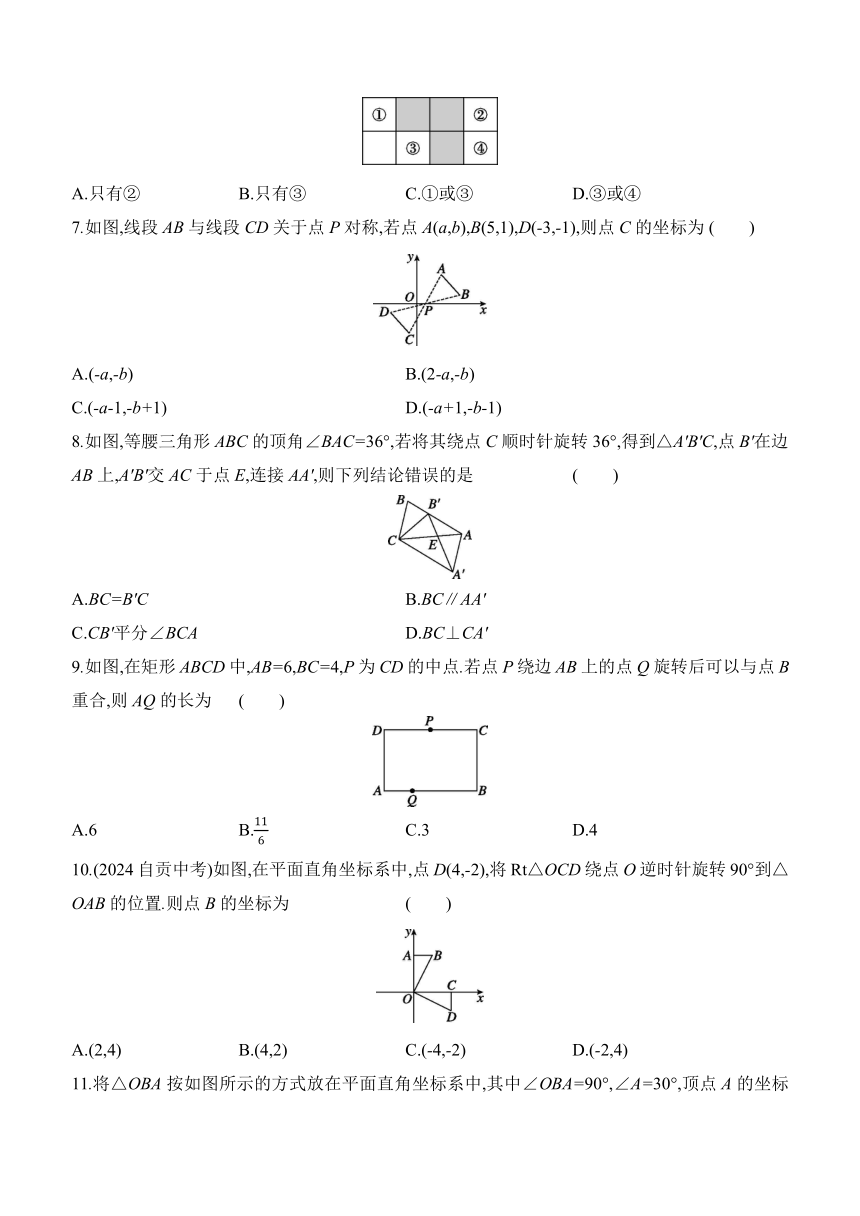
1.(2024潍坊中考)下列著名曲线中,既是轴对称图形,也是中心对称图形的是 ( )
A. B. C. D.
2.如图,教室内地面有个倾斜的畚箕,箕面AB与水平地面的夹角∠CAB为61°,小明将它扶起(将畚箕绕点A顺时针旋转)后平放在地面,箕面AB绕点A旋转的度数为 ( )
A.119° B.120° C.61° D.121°
3.已知点A(4-2m,5)关于原点对称的点在第三象限,则m的取值范围是 ( )
A.m<2 B.m<-2 C.m>2 D.m>-2
4.如图,三个完全相同的四边形组成的图案绕点O旋转可以和原图形重合,则旋转角可以是 ( )
A.60° B.90° C.120° D.150°
5.如图,在△ABC中,∠ACB=90°,∠B=30°,AB=4,将△ABC绕点A顺时针旋转得到△AB'C',当点C'落在边AB上时,线段CC'的长度为 ( )
A. B.1 C. D.2
6.如图是由8个正方形组成的网格.现在嘉嘉想再给一个正方形涂上阴影,使四个阴影正方形所组成的图形是中心对称图形,则嘉嘉应该涂的正方形是 ( )
A.只有② B.只有③ C.①或③ D.③或④
7.如图,线段AB与线段CD关于点P对称,若点A(a,b),B(5,1),D(-3,-1),则点C的坐标为 ( )
A.(-a,-b) B.(2-a,-b)
C.(-a-1,-b+1) D.(-a+1,-b-1)
8.如图,等腰三角形ABC的顶角∠BAC=36°,若将其绕点C顺时针旋转36°,得到△A'B'C,点B'在边AB上,A'B'交AC于点E,连接AA',则下列结论错误的是 ( )
A.BC=B'C B.BC∥AA'
C.CB'平分∠BCA D.BC⊥CA'
9.如图,在矩形ABCD中,AB=6,BC=4,P为CD的中点.若点P绕边AB上的点Q旋转后可以与点B重合,则AQ的长为 ( )
A.6 B. C.3 D.4
10.(2024自贡中考)如图,在平面直角坐标系中,点D(4,-2),将Rt△OCD绕点O逆时针旋转90°到△OAB的位置.则点B的坐标为 ( )
A.(2,4) B.(4,2) C.(-4,-2) D.(-2,4)
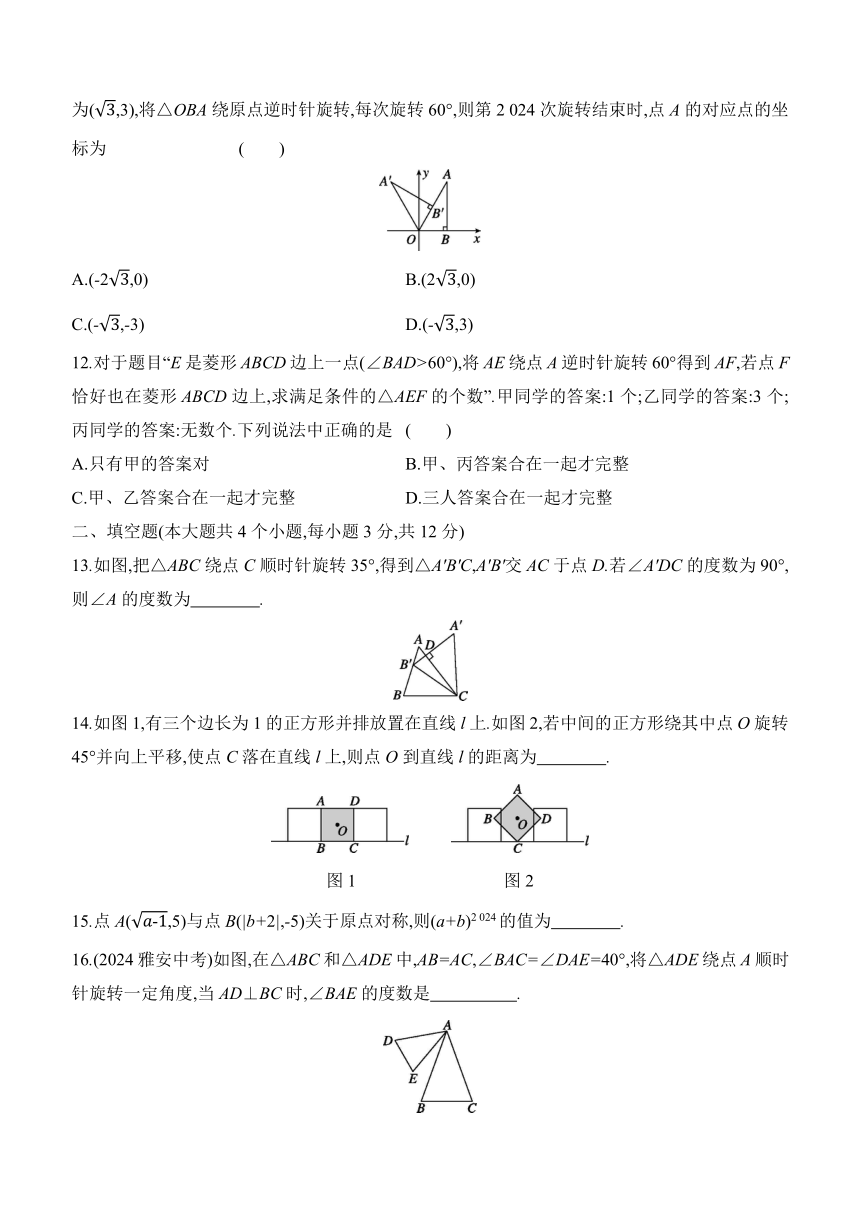
11.将△OBA按如图所示的方式放在平面直角坐标系中,其中∠OBA=90°,∠A=30°,顶点A的坐标为(,3),将△OBA绕原点逆时针旋转,每次旋转60°,则第2 024次旋转结束时,点A的对应点的坐标为 ( )
A.(-2,0) B.(2,0)
C.(-,-3) D.(-,3)
12.对于题目“E是菱形ABCD边上一点(∠BAD>60°),将AE绕点A逆时针旋转60°得到AF,若点F恰好也在菱形ABCD边上,求满足条件的△AEF的个数”.甲同学的答案:1个;乙同学的答案:3个;丙同学的答案:无数个.下列说法中正确的是 ( )
A.只有甲的答案对 B.甲、丙答案合在一起才完整
C.甲、乙答案合在一起才完整 D.三人答案合在一起才完整
二、填空题(本大题共4个小题,每小题3分,共12分)
13.如图,把△ABC绕点C顺时针旋转35°,得到△A'B'C,A'B'交AC于点D.若∠A'DC的度数为90°,则∠A的度数为 .
14.如图1,有三个边长为1的正方形并排放置在直线l上.如图2,若中间的正方形绕其中点O旋转45°并向上平移,使点C落在直线l上,则点O到直线l的距离为 .
图1 图2
15.点A(,5)与点B(|b+2|,-5)关于原点对称,则(a+b)2 024的值为 .
16.(2024雅安中考)如图,在△ABC和△ADE中,AB=AC,∠BAC=∠DAE=40°,将△ADE绕点A顺时针旋转一定角度,当AD⊥BC时,∠BAE的度数是 .
三、解答题(本大题共8 个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(7分)(2024安徽中考)如图,在由边长为1个单位长度的小正方形组成的网格中建立平面直角坐标系,格点(网格线的交点)A,B,C,D的坐标分别为(7,8),(2,8),(10,4),(5,4).
(1)以点D为旋转中心,将△ABC旋转180°得到△A1B1C1,画出△A1B1C1.
(2)直接写出以点B,C1,B1,C为顶点的四边形的面积.
(3)在所给的网格图中确定一个格点E,使得射线AE平分∠BAC,写出点E的坐标.
18.(8分)如图,在△ABC中,∠B=15°,∠ACB=25°,AB=6 cm,△ABC逆时针旋转一定角度后与△ADE重合,且C恰好是AD的中点.
(1)指出旋转中心,并求出旋转的度数.
(2)求∠BAE的度数和AE的长.
19.(8分)如图,△ABC是等边三角形,点E在边AC上,连接BE,将BE绕点B逆时针旋转60°得到BD,连接DE,AD.
(1)求证:AD=CE.
(2)若BC=8 cm,BE=7 cm,求△ADE的周长.
20.(8分)如图,将△ABC绕点A逆时针旋转一个角度α,得到△ADE,点B的对应点D恰好落在边BC上.且点A,B,E在同一条直线上.
(1)求证:DA平分∠BDE.
(2)若AC⊥DE,求旋转角α的度数.
21.(9分)如图,已知 ABCD的对称中心在原点O,且点A(-2,1),B(-3,-2).
(1)求点C及点D的坐标.
(2)求 ABCD的面积.
22.(9分)如图,点M,N分别在正方形ABCD的边BC,CD上,且∠MAN=45°,把△ADN绕点A顺时针旋转90°得到△ABE.
(1)求证:△AEM≌△ANM.
(2)若BM=3,DN=2,求正方形ABCD的边长.
23.(11分)如图,在△ABC和△CDE中,AB=AC=CE,BC=DC=DE,AB>BC,∠BAC=∠DCE=α,点B,C,D都在直线l上.
(1)按下列要求作图(不写作法,保留作图痕迹):
①画出点E关于直线l的对称点E',连接CE',DE'.
②以点C为旋转中心,将①中所得△CDE'按逆时针方向旋转,使得CE'与CA重合,得到△CD'E″(A),画出△CD'E″(A).
(2)解决下面的问题:
①线段AB和线段CD'的位置关系是 ,请说明理由.
②求α.
24.(12分)(1)操作发现:
如图1,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.现将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B',点C的对应点为C',连接BB',如图所示,则∠AB'B的度数为 .
(2)解决问题:
如图2,在等边三角形ABC内有一点P,且PA=2,PB=,PC=1,如果将△BPC绕点B逆时针旋转60°得到△BP'A,求∠BPC的度数和PP'的长.
图1 图2
【详解答案】
1.C 解析:A选项是轴对称图形,不是中心对称图形,故选项A不符合题意;B选项不是轴对称图形,是中心对称图形,故选项B不符合题意;C选项既是轴对称图形,也是中心对称图形,故选项C符合题意;D选项是轴对称图形,不是中心对称图形,故选项D不符合题意.故选C.
2.A 解析:∵箕面AB与水平地面的夹角∠CAB为61°,∴∠BAB'=180°-∠CAB=180°-61°=119°,即旋转角为119°.∴箕面AB绕点A旋转的度数为119°.故选A.
3.A 解析:∵点A(4-2m,5)关于原点对称的点在第三象限,∴点A(4-2m,5)在第一象限.∴4-2m>0.解得m<2.故选A.
4.C 解析:∵360°÷3=120°,∴旋转角的度数是120°的整数倍.故选C.
5.D 解析:∵∠ACB=90°,∠B=30°,AB=4,∴AC=2,∠CAC'=60°.∵将△ABC绕点A顺时针旋转得到△AB'C',∴AC'=AC=2.∴△CAC'为等边三角形.∴CC'=AC=2.故选D.
6.D 解析:由题图可知,将正方形③或④涂上阴影,能使四个阴影正方形所组成的图形是中心对称图形.故选D.
7.B 解析:设点C(m,n),∵线段AB与线段CD关于点P对称,∴P为线段AC,BD的中点.∴=,=.∴m=2-a,n=-b.∴点C(2-a,-b).故选B.
8.D 解析:∵等腰三角形ABC的顶角∠BAC=36°,∴∠B=∠BCA=72°.∵将其绕点C顺时针旋转36°,得到△A'B'C,点B'在边AB上,∴CB=CB',CA=CA',∠ACA'=∠BCB'=36°.∴∠CAA'=∠CA'A=72°,∠B'CA=∠BCA-∠BCB'=36°.∴∠BCB'=∠B'CA.∴CB'平分∠BCA.∴∠B+∠BAA'=72°+36°+72°=180°.∴BC∥AA',∠BCA'=72°+36°=108°.∴ABC选项结论正确,D选项结论错误.故选D.
9.B 解析:如图,连接PQ,过点Q作QE⊥CD于点E.
则AQ=DE,AD=EQ.∵点P绕边AB上的点Q旋转后可以与点B重合,∴PQ=BQ.∵四边形ABCD为矩形,∴CD=AB=6,EQ=AD=BC=4.∵P为CD的中点,∴DP=3.设AQ=DE=x,则PE=3-x,BQ=PQ=6-x,在Rt△EPQ中,由勾股定理,得PQ2=EQ2+EP2,即(6-x)2=42+(3-x)2,解得x=.∴AQ的长为.故选B.
10.A 解析:∵点D(4,-2),∴OC=4,CD=2.由旋转的性质,得OA=OC=4,AB=CD=2,∴点B的坐标为(2,4).故选A.
11.A 解析:由题意可知,6次旋转为1个循环,第1次旋转时,过点A'作x轴的垂线,垂足为C,如图1所示.
图1
由顶点A的坐标为(,3)可知,OB=,AB=3.∵∠A=30°,∴∠AOB=90°-∠A=60°.∴OA=2OB=2.由旋转的性质可知,△AOB≌△A'OB'.∴∠A'OB'=∠AOB=60°,OA'=OA.∴∠A'OC=180°-∠A'OB'-∠AOB=60°.
在△A'OC和△AOB中,
∴△A'OC≌△AOB(AAS).∴OC=OB=,A'C=AB=3.∴此时点A'的坐标为(-,3).当第2次旋转时,如图2所示.
图2
此时点A'的对应点A″的坐标为(-2,0).当第3次旋转时,第3次的点A的对应点与点A中心对称,故坐标为(-,-3).当第4次旋转时,第4次的点A的对应点与点A'中心对称,故坐标为(,-3).当第5次旋转时,第5次的点A的对应点与点A″中心对称,故坐标为(2,0).第6次旋转时,与点A重合.故在前6次旋转中,点A的对应点的坐标分别为(-,3),(-2,0),(-,-3),(,-3),(2,0),(,3).由于2 024÷6=337……2,故第2 024次旋转结束时,点A的对应点的坐标为(-2,0).故选A.
12.D 解析:①如图1,当60°<∠BAD<120°时,只有一种情况.
图1
②如图2,当∠BAD=120°时,有无数个满足条件的△AEF,此时△ABE≌△ACF.
图2
③如图3,当∠BAD>120°时,有3个满足条件的△AEF.
图3
综上所述,甲、乙、丙三人答案合在一起才完整.故选D.
13.55° 解析:∵△ABC绕点C顺时针旋转35°,得到△A'B'C,∴∠ACA'=35°.∵∠A'DC=90°,∴∠A'=55°.∵∠A的对应角是∠A',即∠A=∠A',∴∠A=55°.
14. 解析:如图,连接OB,OC.
由题意,得OC⊥直线l.∵BC=1,△OBC是等腰直角三角形,∴OB2+OC2=BC2.∴OB=OC=.
15.1 解析:∵点A(,5)与点B(|b+2|,-5)关于原点对称,∴=-|b+2|.∵≥0,|b+2|≥0,∴a-1=0,b+2=0.解得a=1,b=-2.∴(a+b)2 024=(-1)2 024=1.
16.60°或120° 解析:
图1
如图1,当AD⊥BC时,延长AD交BC于点J.∵AB=AC,∠BAC=∠DAE=40°,∴∠BAJ=∠CAJ=20°.∴∠BAE=20°+40°=60°.如图2,当AD⊥BC时,延长DA交BC于点H.
图2
∵AB=AC,∠BAC=∠DAE=40°,∴∠BAH=∠CAH=20°.∴∠BAE=180°-20°-40°=120°.综上所述,∠BAE的度数是60°或120°.
17.解:(1)如图,△A1B1C1即为所求作.
(2)以点B,C1,B1,C为顶点的四边形的面积为40.
(3)如图,点E即为所求作,点E的坐标为(6,6).(答案不唯一)
18.解:(1)∵△ABC逆时针旋转一定角度后与△ADE重合,A为公共顶点,
∴旋转中心是点A.
根据旋转的性质可知,∠CAE=∠BAD=180°-∠B-∠ACB=140°.
∴旋转的度数是140°.
∴旋转中心是点A,旋转的度数是140°.
(2)由(1)可知,∠CAE=∠BAD=140°,
∴∠BAE=360°-∠CAE-∠BAD=80°.
由旋转的性质可知,AB=AD,AC=AE.
又∵C恰好是AD的中点,
∴AC=AD=AB=3 cm.
∴AE=3 cm.
19.解:(1)证明:∵△ABC是等边三角形,
∴BA=BC,∠ABC=60°.
∵BD是由BE绕点B逆时针旋转60°得到的,
∴BD=BE,∠EBD=60°.
∴△BDE是等边三角形.
∴∠EBD=∠ABC.
∴∠EBD-∠ABE=∠ABC-∠ABE,即∠ABD=∠CBE.
∴△ABD≌△CBE(SAS).
∴AD=CE.
(2)∵△ABC和△BDE都是等边三角形,
∴AC=BC=8 cm,DE=BE=7 cm.
∴AE+AD=AE+CE=AC=8 cm.
∴△ADE的周长为AD+AE+DE=8+7=15(cm).
20.解:(1)证明:由旋转的性质,得∠ADE=∠B,AD=AB,
∴∠ADB=∠B.
∴∠ADE=∠ADB.
∴DA平分∠BDE.
(2)如图,设AC与DE交于点O,标注各角.
由旋转的性质,得AB=AD,∠3=∠4=α,∠C=∠E.
∵AC⊥DE,
∴∠AOE=90°.
∴∠C=∠E=90°-∠3=90°-α.
∵AB=AD,
∴∠2=∠B===90°-α.
∵∠3=∠B+∠C,
∴α=90°-α+90°-α.
解得α=72°.
∴旋转角α的度数为72°.
21.解:(1)∵平行四边形ABCD关于点O中心对称,点A(-2,1),B(-3,-2),
∴点C(2,-1),D(3,2).
(2)设直线AB的解析式为y=kx+b(k≠0).
把点A,B代入,得
解得
∴直线AB的解析式为y=3x+7.
当y=0时,x=-.
由(1)可知,点A到x轴的距离为1,点B到x轴的距离为2,
∴S ABCD=4×××(1+2)=14.
22.解:(1)证明:由旋转的性质,得AE=AN,∠BAE=∠DAN.
∵四边形ABCD是正方形,
∴∠BAD=90°,即∠BAN+∠DAN=90°.
∴∠BAN+∠BAE=90°,即∠EAN=90°.
∵∠MAN=45°,
∴∠MAE=∠EAN-∠MAN=90°-45°=45°.
在△AEM和△ANM中,
∴△AEM≌△ANM(SAS).
(2)设正方形ABCD的边长为x,则BC=CD=x.
∵BM=3,DN=2,
∴CM=BC-BM=x-3,CN=CD-DN=x-2.
由旋转的性质,得BE=DN=2.
∴ME=BE+BM=2+3=5.
由(1)可知,△AEM≌△ANM,
∴ME=MN=5.
又∵四边形ABCD是正方形,
∴∠C=90°.
在Rt△CMN中,CM2+CN2=MN2,
即(x-3)2+(x-2)2=52,
解得x=6或-1(不符合题意,舍去).
∴正方形ABCD的边长为6.
23.解:(1)①②如图所示:
(2)①平行 理由如下:
由题意,得∠DCE=∠DCE'=∠D'CA=α.
∴∠BAC=∠D'CA=α.
∴AB∥CD'.
②由旋转的性质,得DE'=D'A,CE'=CA,D'C=DC,∠D'AC=∠CE'D.
∵AB∥CD',AB>BC=DC=D'C,
∴四边形ABCD'是梯形.
∵BC=DE=DE'=D'A,
∴四边形ABCD'是等腰梯形.
∵DC=DE,∠CED=∠CE'D,
∴∠CED=∠DCE=∠CE'D=α.
∴∠D'AC=∠CE'D=α.
∴∠ABC=∠D'AB=α+α=2α.
∵AB=AC,
∴∠ACB=∠ABC=2α.
在△ABC中,
∵∠BAC+∠ABC+∠ACB=180°,
∴α+2α+2α=180°.解得α=36°.
24.解:(1)45°
(2)∵△ABC为等边三角形,
∴BA=BC,∠ABC=60°.
∵△BPC绕点B逆时针旋转60°得到△BP'A,
∴P'A=PC=1,P'B=PB=,
∠PBP'=60°,△BPC≌△BP'A.
∴△BPP'为等边三角形.
∴∠BP'P=60°,PP'=PB=.
在△APP'中,∵P'A=1,PP'=,PA=2,
∴P'A2+PP'2=PA2.
∴△APP'为直角三角形,∠AP'P=90°.
∴∠BP'A=∠AP'P+∠BP'P=90°+60°=150°.
∵△BPC≌△BP'A,
∴∠BPC=∠BP'A=150°.
∴∠BPC的度数为150°,PP'的长为.
(总分:120分 时间:120分钟)
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2024潍坊中考)下列著名曲线中,既是轴对称图形,也是中心对称图形的是 ( )
A. B. C. D.
2.如图,教室内地面有个倾斜的畚箕,箕面AB与水平地面的夹角∠CAB为61°,小明将它扶起(将畚箕绕点A顺时针旋转)后平放在地面,箕面AB绕点A旋转的度数为 ( )
A.119° B.120° C.61° D.121°
3.已知点A(4-2m,5)关于原点对称的点在第三象限,则m的取值范围是 ( )
A.m<2 B.m<-2 C.m>2 D.m>-2
4.如图,三个完全相同的四边形组成的图案绕点O旋转可以和原图形重合,则旋转角可以是 ( )
A.60° B.90° C.120° D.150°
5.如图,在△ABC中,∠ACB=90°,∠B=30°,AB=4,将△ABC绕点A顺时针旋转得到△AB'C',当点C'落在边AB上时,线段CC'的长度为 ( )
A. B.1 C. D.2
6.如图是由8个正方形组成的网格.现在嘉嘉想再给一个正方形涂上阴影,使四个阴影正方形所组成的图形是中心对称图形,则嘉嘉应该涂的正方形是 ( )
A.只有② B.只有③ C.①或③ D.③或④
7.如图,线段AB与线段CD关于点P对称,若点A(a,b),B(5,1),D(-3,-1),则点C的坐标为 ( )
A.(-a,-b) B.(2-a,-b)
C.(-a-1,-b+1) D.(-a+1,-b-1)
8.如图,等腰三角形ABC的顶角∠BAC=36°,若将其绕点C顺时针旋转36°,得到△A'B'C,点B'在边AB上,A'B'交AC于点E,连接AA',则下列结论错误的是 ( )
A.BC=B'C B.BC∥AA'
C.CB'平分∠BCA D.BC⊥CA'
9.如图,在矩形ABCD中,AB=6,BC=4,P为CD的中点.若点P绕边AB上的点Q旋转后可以与点B重合,则AQ的长为 ( )
A.6 B. C.3 D.4
10.(2024自贡中考)如图,在平面直角坐标系中,点D(4,-2),将Rt△OCD绕点O逆时针旋转90°到△OAB的位置.则点B的坐标为 ( )
A.(2,4) B.(4,2) C.(-4,-2) D.(-2,4)
11.将△OBA按如图所示的方式放在平面直角坐标系中,其中∠OBA=90°,∠A=30°,顶点A的坐标为(,3),将△OBA绕原点逆时针旋转,每次旋转60°,则第2 024次旋转结束时,点A的对应点的坐标为 ( )
A.(-2,0) B.(2,0)
C.(-,-3) D.(-,3)
12.对于题目“E是菱形ABCD边上一点(∠BAD>60°),将AE绕点A逆时针旋转60°得到AF,若点F恰好也在菱形ABCD边上,求满足条件的△AEF的个数”.甲同学的答案:1个;乙同学的答案:3个;丙同学的答案:无数个.下列说法中正确的是 ( )
A.只有甲的答案对 B.甲、丙答案合在一起才完整
C.甲、乙答案合在一起才完整 D.三人答案合在一起才完整
二、填空题(本大题共4个小题,每小题3分,共12分)
13.如图,把△ABC绕点C顺时针旋转35°,得到△A'B'C,A'B'交AC于点D.若∠A'DC的度数为90°,则∠A的度数为 .
14.如图1,有三个边长为1的正方形并排放置在直线l上.如图2,若中间的正方形绕其中点O旋转45°并向上平移,使点C落在直线l上,则点O到直线l的距离为 .
图1 图2
15.点A(,5)与点B(|b+2|,-5)关于原点对称,则(a+b)2 024的值为 .
16.(2024雅安中考)如图,在△ABC和△ADE中,AB=AC,∠BAC=∠DAE=40°,将△ADE绕点A顺时针旋转一定角度,当AD⊥BC时,∠BAE的度数是 .
三、解答题(本大题共8 个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(7分)(2024安徽中考)如图,在由边长为1个单位长度的小正方形组成的网格中建立平面直角坐标系,格点(网格线的交点)A,B,C,D的坐标分别为(7,8),(2,8),(10,4),(5,4).
(1)以点D为旋转中心,将△ABC旋转180°得到△A1B1C1,画出△A1B1C1.
(2)直接写出以点B,C1,B1,C为顶点的四边形的面积.
(3)在所给的网格图中确定一个格点E,使得射线AE平分∠BAC,写出点E的坐标.
18.(8分)如图,在△ABC中,∠B=15°,∠ACB=25°,AB=6 cm,△ABC逆时针旋转一定角度后与△ADE重合,且C恰好是AD的中点.
(1)指出旋转中心,并求出旋转的度数.
(2)求∠BAE的度数和AE的长.
19.(8分)如图,△ABC是等边三角形,点E在边AC上,连接BE,将BE绕点B逆时针旋转60°得到BD,连接DE,AD.
(1)求证:AD=CE.
(2)若BC=8 cm,BE=7 cm,求△ADE的周长.
20.(8分)如图,将△ABC绕点A逆时针旋转一个角度α,得到△ADE,点B的对应点D恰好落在边BC上.且点A,B,E在同一条直线上.
(1)求证:DA平分∠BDE.
(2)若AC⊥DE,求旋转角α的度数.
21.(9分)如图,已知 ABCD的对称中心在原点O,且点A(-2,1),B(-3,-2).
(1)求点C及点D的坐标.
(2)求 ABCD的面积.
22.(9分)如图,点M,N分别在正方形ABCD的边BC,CD上,且∠MAN=45°,把△ADN绕点A顺时针旋转90°得到△ABE.
(1)求证:△AEM≌△ANM.
(2)若BM=3,DN=2,求正方形ABCD的边长.
23.(11分)如图,在△ABC和△CDE中,AB=AC=CE,BC=DC=DE,AB>BC,∠BAC=∠DCE=α,点B,C,D都在直线l上.
(1)按下列要求作图(不写作法,保留作图痕迹):
①画出点E关于直线l的对称点E',连接CE',DE'.
②以点C为旋转中心,将①中所得△CDE'按逆时针方向旋转,使得CE'与CA重合,得到△CD'E″(A),画出△CD'E″(A).
(2)解决下面的问题:
①线段AB和线段CD'的位置关系是 ,请说明理由.
②求α.
24.(12分)(1)操作发现:
如图1,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.现将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B',点C的对应点为C',连接BB',如图所示,则∠AB'B的度数为 .
(2)解决问题:
如图2,在等边三角形ABC内有一点P,且PA=2,PB=,PC=1,如果将△BPC绕点B逆时针旋转60°得到△BP'A,求∠BPC的度数和PP'的长.
图1 图2
【详解答案】
1.C 解析:A选项是轴对称图形,不是中心对称图形,故选项A不符合题意;B选项不是轴对称图形,是中心对称图形,故选项B不符合题意;C选项既是轴对称图形,也是中心对称图形,故选项C符合题意;D选项是轴对称图形,不是中心对称图形,故选项D不符合题意.故选C.
2.A 解析:∵箕面AB与水平地面的夹角∠CAB为61°,∴∠BAB'=180°-∠CAB=180°-61°=119°,即旋转角为119°.∴箕面AB绕点A旋转的度数为119°.故选A.
3.A 解析:∵点A(4-2m,5)关于原点对称的点在第三象限,∴点A(4-2m,5)在第一象限.∴4-2m>0.解得m<2.故选A.
4.C 解析:∵360°÷3=120°,∴旋转角的度数是120°的整数倍.故选C.
5.D 解析:∵∠ACB=90°,∠B=30°,AB=4,∴AC=2,∠CAC'=60°.∵将△ABC绕点A顺时针旋转得到△AB'C',∴AC'=AC=2.∴△CAC'为等边三角形.∴CC'=AC=2.故选D.
6.D 解析:由题图可知,将正方形③或④涂上阴影,能使四个阴影正方形所组成的图形是中心对称图形.故选D.
7.B 解析:设点C(m,n),∵线段AB与线段CD关于点P对称,∴P为线段AC,BD的中点.∴=,=.∴m=2-a,n=-b.∴点C(2-a,-b).故选B.
8.D 解析:∵等腰三角形ABC的顶角∠BAC=36°,∴∠B=∠BCA=72°.∵将其绕点C顺时针旋转36°,得到△A'B'C,点B'在边AB上,∴CB=CB',CA=CA',∠ACA'=∠BCB'=36°.∴∠CAA'=∠CA'A=72°,∠B'CA=∠BCA-∠BCB'=36°.∴∠BCB'=∠B'CA.∴CB'平分∠BCA.∴∠B+∠BAA'=72°+36°+72°=180°.∴BC∥AA',∠BCA'=72°+36°=108°.∴ABC选项结论正确,D选项结论错误.故选D.
9.B 解析:如图,连接PQ,过点Q作QE⊥CD于点E.
则AQ=DE,AD=EQ.∵点P绕边AB上的点Q旋转后可以与点B重合,∴PQ=BQ.∵四边形ABCD为矩形,∴CD=AB=6,EQ=AD=BC=4.∵P为CD的中点,∴DP=3.设AQ=DE=x,则PE=3-x,BQ=PQ=6-x,在Rt△EPQ中,由勾股定理,得PQ2=EQ2+EP2,即(6-x)2=42+(3-x)2,解得x=.∴AQ的长为.故选B.
10.A 解析:∵点D(4,-2),∴OC=4,CD=2.由旋转的性质,得OA=OC=4,AB=CD=2,∴点B的坐标为(2,4).故选A.
11.A 解析:由题意可知,6次旋转为1个循环,第1次旋转时,过点A'作x轴的垂线,垂足为C,如图1所示.
图1
由顶点A的坐标为(,3)可知,OB=,AB=3.∵∠A=30°,∴∠AOB=90°-∠A=60°.∴OA=2OB=2.由旋转的性质可知,△AOB≌△A'OB'.∴∠A'OB'=∠AOB=60°,OA'=OA.∴∠A'OC=180°-∠A'OB'-∠AOB=60°.
在△A'OC和△AOB中,
∴△A'OC≌△AOB(AAS).∴OC=OB=,A'C=AB=3.∴此时点A'的坐标为(-,3).当第2次旋转时,如图2所示.
图2
此时点A'的对应点A″的坐标为(-2,0).当第3次旋转时,第3次的点A的对应点与点A中心对称,故坐标为(-,-3).当第4次旋转时,第4次的点A的对应点与点A'中心对称,故坐标为(,-3).当第5次旋转时,第5次的点A的对应点与点A″中心对称,故坐标为(2,0).第6次旋转时,与点A重合.故在前6次旋转中,点A的对应点的坐标分别为(-,3),(-2,0),(-,-3),(,-3),(2,0),(,3).由于2 024÷6=337……2,故第2 024次旋转结束时,点A的对应点的坐标为(-2,0).故选A.
12.D 解析:①如图1,当60°<∠BAD<120°时,只有一种情况.
图1
②如图2,当∠BAD=120°时,有无数个满足条件的△AEF,此时△ABE≌△ACF.
图2
③如图3,当∠BAD>120°时,有3个满足条件的△AEF.
图3
综上所述,甲、乙、丙三人答案合在一起才完整.故选D.
13.55° 解析:∵△ABC绕点C顺时针旋转35°,得到△A'B'C,∴∠ACA'=35°.∵∠A'DC=90°,∴∠A'=55°.∵∠A的对应角是∠A',即∠A=∠A',∴∠A=55°.
14. 解析:如图,连接OB,OC.
由题意,得OC⊥直线l.∵BC=1,△OBC是等腰直角三角形,∴OB2+OC2=BC2.∴OB=OC=.
15.1 解析:∵点A(,5)与点B(|b+2|,-5)关于原点对称,∴=-|b+2|.∵≥0,|b+2|≥0,∴a-1=0,b+2=0.解得a=1,b=-2.∴(a+b)2 024=(-1)2 024=1.
16.60°或120° 解析:
图1
如图1,当AD⊥BC时,延长AD交BC于点J.∵AB=AC,∠BAC=∠DAE=40°,∴∠BAJ=∠CAJ=20°.∴∠BAE=20°+40°=60°.如图2,当AD⊥BC时,延长DA交BC于点H.
图2
∵AB=AC,∠BAC=∠DAE=40°,∴∠BAH=∠CAH=20°.∴∠BAE=180°-20°-40°=120°.综上所述,∠BAE的度数是60°或120°.
17.解:(1)如图,△A1B1C1即为所求作.
(2)以点B,C1,B1,C为顶点的四边形的面积为40.
(3)如图,点E即为所求作,点E的坐标为(6,6).(答案不唯一)
18.解:(1)∵△ABC逆时针旋转一定角度后与△ADE重合,A为公共顶点,
∴旋转中心是点A.
根据旋转的性质可知,∠CAE=∠BAD=180°-∠B-∠ACB=140°.
∴旋转的度数是140°.
∴旋转中心是点A,旋转的度数是140°.
(2)由(1)可知,∠CAE=∠BAD=140°,
∴∠BAE=360°-∠CAE-∠BAD=80°.
由旋转的性质可知,AB=AD,AC=AE.
又∵C恰好是AD的中点,
∴AC=AD=AB=3 cm.
∴AE=3 cm.
19.解:(1)证明:∵△ABC是等边三角形,
∴BA=BC,∠ABC=60°.
∵BD是由BE绕点B逆时针旋转60°得到的,
∴BD=BE,∠EBD=60°.
∴△BDE是等边三角形.
∴∠EBD=∠ABC.
∴∠EBD-∠ABE=∠ABC-∠ABE,即∠ABD=∠CBE.
∴△ABD≌△CBE(SAS).
∴AD=CE.
(2)∵△ABC和△BDE都是等边三角形,
∴AC=BC=8 cm,DE=BE=7 cm.
∴AE+AD=AE+CE=AC=8 cm.
∴△ADE的周长为AD+AE+DE=8+7=15(cm).
20.解:(1)证明:由旋转的性质,得∠ADE=∠B,AD=AB,
∴∠ADB=∠B.
∴∠ADE=∠ADB.
∴DA平分∠BDE.
(2)如图,设AC与DE交于点O,标注各角.
由旋转的性质,得AB=AD,∠3=∠4=α,∠C=∠E.
∵AC⊥DE,
∴∠AOE=90°.
∴∠C=∠E=90°-∠3=90°-α.
∵AB=AD,
∴∠2=∠B===90°-α.
∵∠3=∠B+∠C,
∴α=90°-α+90°-α.
解得α=72°.
∴旋转角α的度数为72°.
21.解:(1)∵平行四边形ABCD关于点O中心对称,点A(-2,1),B(-3,-2),
∴点C(2,-1),D(3,2).
(2)设直线AB的解析式为y=kx+b(k≠0).
把点A,B代入,得
解得
∴直线AB的解析式为y=3x+7.
当y=0时,x=-.
由(1)可知,点A到x轴的距离为1,点B到x轴的距离为2,
∴S ABCD=4×××(1+2)=14.
22.解:(1)证明:由旋转的性质,得AE=AN,∠BAE=∠DAN.
∵四边形ABCD是正方形,
∴∠BAD=90°,即∠BAN+∠DAN=90°.
∴∠BAN+∠BAE=90°,即∠EAN=90°.
∵∠MAN=45°,
∴∠MAE=∠EAN-∠MAN=90°-45°=45°.
在△AEM和△ANM中,
∴△AEM≌△ANM(SAS).
(2)设正方形ABCD的边长为x,则BC=CD=x.
∵BM=3,DN=2,
∴CM=BC-BM=x-3,CN=CD-DN=x-2.
由旋转的性质,得BE=DN=2.
∴ME=BE+BM=2+3=5.
由(1)可知,△AEM≌△ANM,
∴ME=MN=5.
又∵四边形ABCD是正方形,
∴∠C=90°.
在Rt△CMN中,CM2+CN2=MN2,
即(x-3)2+(x-2)2=52,
解得x=6或-1(不符合题意,舍去).
∴正方形ABCD的边长为6.
23.解:(1)①②如图所示:
(2)①平行 理由如下:
由题意,得∠DCE=∠DCE'=∠D'CA=α.
∴∠BAC=∠D'CA=α.
∴AB∥CD'.
②由旋转的性质,得DE'=D'A,CE'=CA,D'C=DC,∠D'AC=∠CE'D.
∵AB∥CD',AB>BC=DC=D'C,
∴四边形ABCD'是梯形.
∵BC=DE=DE'=D'A,
∴四边形ABCD'是等腰梯形.
∵DC=DE,∠CED=∠CE'D,
∴∠CED=∠DCE=∠CE'D=α.
∴∠D'AC=∠CE'D=α.
∴∠ABC=∠D'AB=α+α=2α.
∵AB=AC,
∴∠ACB=∠ABC=2α.
在△ABC中,
∵∠BAC+∠ABC+∠ACB=180°,
∴α+2α+2α=180°.解得α=36°.
24.解:(1)45°
(2)∵△ABC为等边三角形,
∴BA=BC,∠ABC=60°.
∵△BPC绕点B逆时针旋转60°得到△BP'A,
∴P'A=PC=1,P'B=PB=,
∠PBP'=60°,△BPC≌△BP'A.
∴△BPP'为等边三角形.
∴∠BP'P=60°,PP'=PB=.
在△APP'中,∵P'A=1,PP'=,PA=2,
∴P'A2+PP'2=PA2.
∴△APP'为直角三角形,∠AP'P=90°.
∴∠BP'A=∠AP'P+∠BP'P=90°+60°=150°.
∵△BPC≌△BP'A,
∴∠BPC=∠BP'A=150°.
∴∠BPC的度数为150°,PP'的长为.
同课章节目录
