第二十四章 圆 评估测试卷 (含答案) 2025-2026学年数学人教版九年级上册
文档属性
| 名称 | 第二十四章 圆 评估测试卷 (含答案) 2025-2026学年数学人教版九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 393.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-08 09:49:20 | ||
图片预览



文档简介
第二十四章 圆 评估测试卷
(总分:120分 时间:120分钟)
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
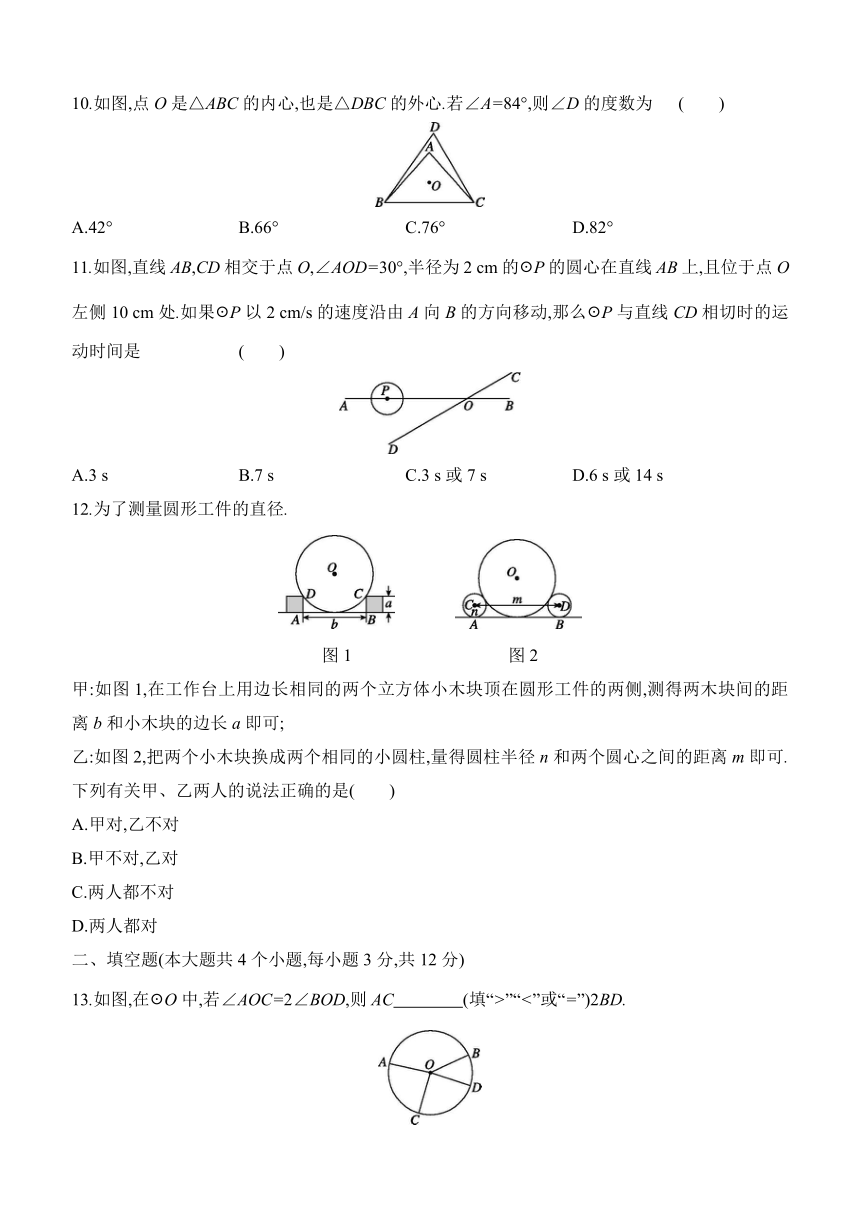
1.已知AB是半径为5的圆的一条弦,则AB的长不可能是 ( )
A.4 B.8 C.10 D.12
2.已知☉O的直径为10 cm,点P到圆心O的距离为8 cm,则点P和圆的位置关系是 ( )
A.点在圆内 B.点在圆外 C.点在圆上 D.无法判断
3.如图,在△ABC中,∠ACB=90°,AC=4,点D在边AB上,且AD=5,以AC为直径作☉O,设线段CD的中点为P,则点P与☉O的位置关系是 ( )
A.点P在☉O内 B.点P在☉O上
C.点P在☉O外 D.无法确定
4.(2024长沙中考)如图,在☉O中,弦AB的长为8,圆心O到AB的距离OE=4,则☉O的半径长为 ( )
A.4 B.4 C.5 D.5
5.如图,将正六边形纸片的空白部分剪下,得到三部分图形,记Ⅰ,Ⅱ,Ⅲ部分的面积分别为SⅠ,SⅡ,SⅢ.给出以下结论:①Ⅰ和Ⅱ合在一起能拼成一个菱形;②Ⅲ中最大的内角是150°;③SⅢ=2(SⅠ+SⅡ).其中正确的结论是 ( )
→
A.①② B.①③
C.②③ D.①②③
6.如图,CD是☉O的直径,点A,B在☉O上.若=,∠AOC=40°,则∠D的大小为 ( )
A.10° B.20°
C.40° D.45°
7.如图,四边形ABCD的边AB,BC,CD,DA和☉O分别相切于点L,M,N,P.若四边形ABCD的周长为20,则AB+CD的值为 ( )
A.5 B.8
C.10 D.12
8.(2024河北中考)扇文化是中华优秀传统文化的组成部分,在我国有着深厚的底蕴.如图,某折扇张开的角度为120°时,扇面面积为S,该折扇张开的角度为n°时,扇面面积为Sn.若m=,则m与n关系的图象大致是 ( )
A B C D
9.(2024泸州中考)如图,EA,ED是☉O的切线,切点为A,D,点B,C在☉O上.若∠BAE+∠BCD=236°,则∠E的度数为 ( )
A.56° B.60°
C.68° D.70°
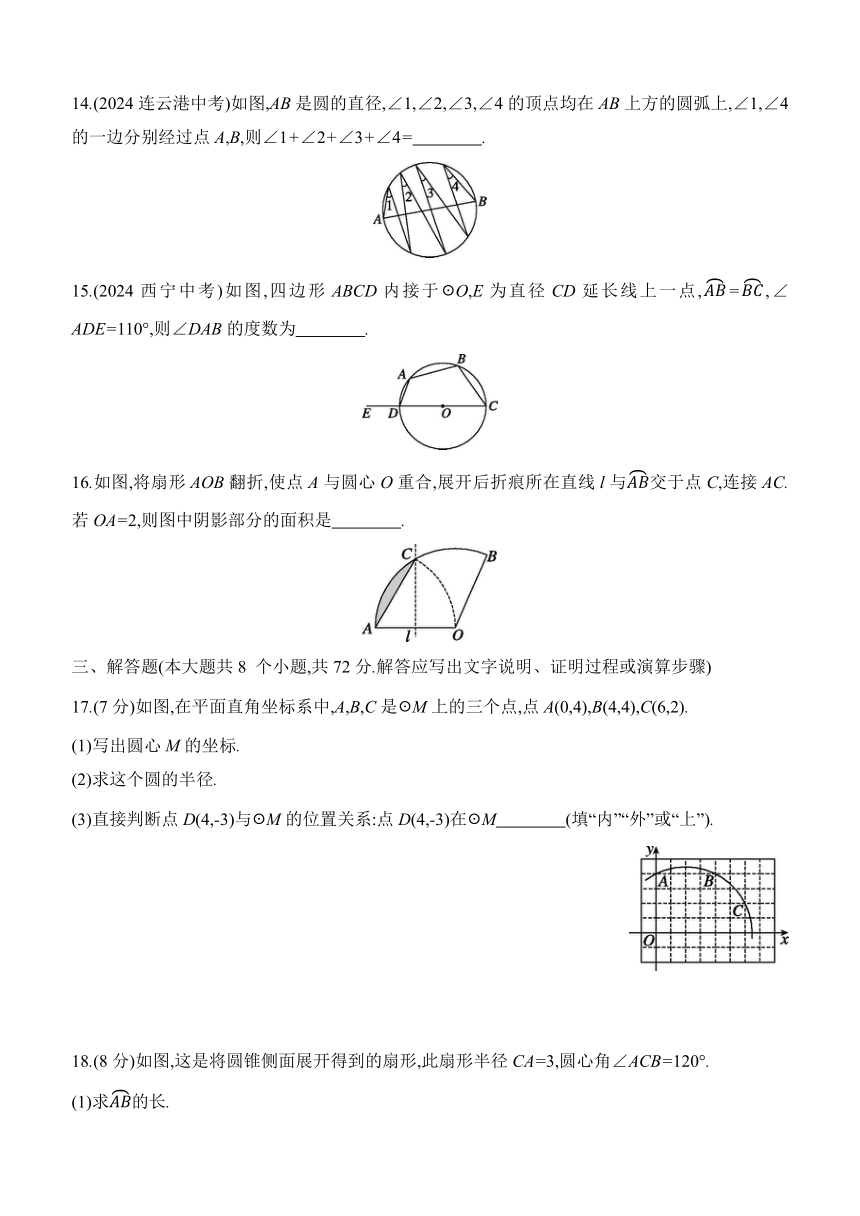
10.如图,点O是△ABC的内心,也是△DBC的外心.若∠A=84°,则∠D的度数为 ( )
A.42° B.66° C.76° D.82°
11.如图,直线AB,CD相交于点O,∠AOD=30°,半径为2 cm的☉P的圆心在直线AB上,且位于点O左侧10 cm处.如果☉P以2 cm/s的速度沿由A向B的方向移动,那么☉P与直线CD相切时的运动时间是 ( )
A.3 s B.7 s C.3 s或7 s D.6 s或14 s
12.为了测量圆形工件的直径.
图1 图2
甲:如图1,在工作台上用边长相同的两个立方体小木块顶在圆形工件的两侧,测得两木块间的距离b和小木块的边长a即可;
乙:如图2,把两个小木块换成两个相同的小圆柱,量得圆柱半径n和两个圆心之间的距离m即可.下列有关甲、乙两人的说法正确的是( )
A.甲对,乙不对
B.甲不对,乙对
C.两人都不对
D.两人都对
二、填空题(本大题共4个小题,每小题3分,共12分)
13.如图,在☉O中,若∠AOC=2∠BOD,则AC (填“>”“<”或“=”)2BD.
14.(2024连云港中考)如图,AB是圆的直径,∠1,∠2,∠3,∠4的顶点均在AB上方的圆弧上,∠1,∠4的一边分别经过点A,B,则∠1+∠2+∠3+∠4= .
15.(2024西宁中考)如图,四边形ABCD内接于☉O,E为直径CD延长线上一点,=,∠ADE=110°,则∠DAB的度数为 .
16.如图,将扇形AOB翻折,使点A与圆心O重合,展开后折痕所在直线l与交于点C,连接AC.若OA=2,则图中阴影部分的面积是 .
三、解答题(本大题共8 个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(7分)如图,在平面直角坐标系中,A,B,C是☉M上的三个点,点A(0,4),B(4,4),C(6,2).
(1)写出圆心M的坐标.
(2)求这个圆的半径.
(3)直接判断点D(4,-3)与☉M的位置关系:点D(4,-3)在☉M (填“内”“外”或“上”).
18.(8分)如图,这是将圆锥侧面展开得到的扇形,此扇形半径CA=3,圆心角∠ACB=120°.
(1)求的长.
(2)求此圆锥的高OC的长.
19.(8分)如图,在☉O中,AB=CD,AB与CD相交于点M.
求证:(1)=.
(2)AM=DM.
20.(8分)如图是正在修建的某大门上半部分的截面,其为圆弧形,跨度CD(弧所对的弦)的长为3.2 m,拱高AB(弧的中点到弦的距离)为0.8 m.
(1)求该圆弧所在圆的半径.
(2)在修建中,在距大门边框的一端(点D)0.4 m处将竖立支撑杆HG,求支撑杆HG的高度.
21.(9分)司南是我国古代辨别方向用的一种仪器(图1),其早在战国时期就已被发明,是现在所用指南针的始祖.如图2,司南中心为一圆形,圆心为点O,直径为20,根据八个方位将圆形八等分(图2中点A~H),过点E作☉O的切线与AG的延长线交于点M,连接EG.
(1)相邻两个方位间所夹的圆心角的度数为 .
(2)求AG的长.
(3)求线段ME与EG的长,并比较大小.
图1 图2
22.(9分)(2024自贡中考)在Rt△ABC中,∠C=90°,☉O是△ABC的内切圆,切点分别为D,E,F.
(1)图1中三组相等的线段分别是CE=CF,AF= ,BD= ;若AC=3,BC=4,则☉O的半径长为 .
(2)如图2,延长AC到点M,使AM=AB,过点M作MN⊥AB于点N.求证:MN是☉O的切线.
图1 图2
23.(11分)如图,☉O的直径AB=16,半径OC⊥AB,D为上一动点(不包括B,C两点),DE⊥OC,DF⊥AB,垂足分别为E,F.
(1)求EF的长.
(2)若E为OC的中点,
①求劣弧CD的长度.
②若P为直径AB上一动点,直接写出PC+PD的最小值.
24.(12分)如图1,矩形ABCD与以EF为直径的半圆O在直线l的上方,线段AB与点E,F都在直线l上,且AB=7,EF=10,BC>5.点B以1个单位长度/s的速度从点E处出发,沿射线EF的方向运动,矩形ABCD随之运动,运动时间为t s.
(1)如图2,当t=2.5 s时,求半圆O在矩形ABCD内的弧的长度.
(2)在点B运动的过程中,当AD,BC都与半圆O相交时,设这两个交点为G,H.连接OG,OH.若∠GOH为直角,求此时t的值.
图1 图2 备用图
【详解答案】
1.D 解析:∵圆中最长的弦为直径,∴弦长AB≤10.故选D.
2.B 解析:∵☉O的直径为10 cm,∴☉O的半径为5 cm.∵点P到圆心O的距离为8 cm>5 cm,∴点P在圆外.故选B.
3.C 解析:如图,连接OP.∵以AC为直径作☉O,线段CD的中点为P,∴OP是△CAD的中位线.∴OP=AD=2.5.∵AO=CO=AC=2<2.5,∴点P与☉O的位置关系是点P在☉O外.故选C.
4.B 解析:∵OE⊥AB,∴AE=EB=4.∴OA===4.故选B.
5.B 解析:如图所示的正六边形可以分割成6个全等的三角形,于是Ⅰ部分、Ⅱ部分相当于其中的1个三角形,Ⅲ部分相当于4个这样的三角形,故①Ⅰ和Ⅱ合在一起能拼成一个菱形是正确的;③SⅢ=2(SⅠ+SⅡ)是正确的;②Ⅲ中最大的内角是=120°,因此②是不正确的.综上所述,正确的有①③.故选B.
6.B 解析:如图,连接OB.
∵=,∠AOC=40°,∴∠BOC=40°.∵=,∴∠D=∠BOC=20°.故选B.
7.C 解析:由切线长定理,得AL=AP,DP=DN,CN=CM,BM=BL.∴四边形ABCD的周长为AB+BC+CD+DA=AL+BL+BM+CM+CN+DN+DP+AP=2AB+2CD=20.∴AB+CD=10.故选C.
8.C 解析:设该扇子所在圆的半径为R,S==.∴πR2=3S.∵该折扇张开的角度为n°时,扇面面积为Sn,∴Sn==×3S=.∴m====n.∴m是n的正比例函数.故选C.
9.C 解析:如图,连接AD.∵四边形ABCD是☉O的内接四边形,∴∠BAD+∠BCD=180°.∵∠BAE+∠BCD=236°,∴∠EAD+∠BAD+∠BCD=∠EAD+180°=236°.∴∠EAD=56°.∵EA,ED是☉O的切线,切点为A,D,∴EA=ED.∴∠EDA=∠EAD=56°.∴∠E=180°-∠EDA-∠EAD=180°-56°-56°=68°.故选C.
10.B 解析:如图,连接OB,OC.∵点O是△ABC的内心,∠A=84°,∴OB,OC是∠ABC,∠ACB的平分线.∴∠OBC=∠ABC,∠OCB=∠ACB.∴∠BOC=180°-∠OBC-∠OCB=180°-(∠ABC+∠ACB)=180°-(180°-∠A)=90°+∠A=132°.∵点O也是△DBC的外心,∴∠D=∠BOC=66°.∴∠D的度数为66°.故选B.
11.C 解析:①当圆心P在直线CD的左侧时,设此时圆心为P1,CD与☉P1相切于点E(图略),∴P1E⊥CD.∵☉P的半径为2 cm,∴P1E=2 cm.∵∠AOD=30°,P1E⊥CD,∴P1O=4 cm.∴PP1=PO-P1O=10-4=6(cm).∴t=6÷2=3(s).②当圆心P在直线CD的右侧时,设此时圆心为P2,同理可得PP2=PO+P2O=10+4=14(cm),∴t=14÷2=7(s).综上所述,☉P与直线CD相切时经过的运动时间是3 s或7 s,故选C.
12.D 解析:如图1,设圆的半径为r,圆形工件与工作台相切于点M,连接DC,OD,连接OM交DC于点P.∴OM⊥AB.∵DC∥AB,∴OM⊥DC.∴PD=PC=CD=AB=b.∵PM=BC=a,∴OP=OM-PM=r-a.∵OD2=OP2+PD2,∴r2=(r-a)2+b2.∴r=.∴甲对.如图2,设圆的半径为R,圆形工件与工作台相切于点H,连接OH交CD于点K,连接OC,OD,CA,DB.∴OH⊥AB.∵CD∥AB,∴OH⊥CD.∵OC=R+n,OD=R+n,∴OC=OD.∴KC=KD=m.∵KH=CA=DB=n,∴OK=OH-KH=R-n.∵OC2=OK2+CK2,∴(R+n)2=(R-n)2+m2.∴R=.∴乙对.∴甲、乙两人都对.故选D.
图1 图2
13.< 解析:如图,以OD为边作∠DOE=∠BOD,OE与☉O交于点E,连接AC,BE,BD,ED,则∠BOE=2∠BOD,BD=DE.∵∠AOC=2∠BOD,∴∠AOC=∠BOE.∴AC=BE.在△BDE中,BE14.90° 解析:∵AB是圆的直径,∴AB所对的弧是半圆,所对圆心角的度数为180°.∵∠1,∠2,∠3,∠4所对的弧的和为半圆,∴∠1+∠2+∠3+∠4=×180°=90°.
15.125° 解析:如图,连接OA,OB.∵∠ADE=110°,∠ADE+∠ADO=180°,∴∠ADO=70°.∵OA=OD,∴∠OAD=∠ODA=70°.∴∠AOD=40°.∴∠AOC=140°.∵=,∴∠AOB=∠BOC=70°.∵OB=OC,∴∠OCB=∠OBC=55°.∵四边形ABCD为☉O的内接四边形,∴∠DAB+∠OCB=180°.∴∠DAB=125°.
16.- 解析:如图,连接CO.设直线l与AO交于点D.∵在扇形AOB中,OA=2,∴OC=OA=2.∵点A与圆心O重合,∴AD=OD=1,CD⊥AO.∴OC=AC.∴OA=OC=AC=2.∴△OAC是等边三角形.∴∠COD=60°.∵CD⊥OA,∴CD==.∴阴影部分的面积为-×2×=-.
17.解:(1)如图,圆心M的坐标为(2,0).
(2)如图,连接MA.∵点A(0,4),M(2,0),
∴MA==2.
∴这个圆的半径为2.
(3)内
18.解:(1)的长==2π.
(2)设OA的长为r,则2πr=2π.
解得r=1.
在Rt△AOC中,∠AOC=90°,
由勾股定理,得
OC===2.
19.证明:(1)∵在☉O中,AB=CD,
∴=.
∴-=-.
∴=.
(2)如图,连接AC,BD.
∵=,
∴AC=BD.
在△ACM和△DBM中,
∴△ACM≌△DBM(ASA).
∴AM=DM.
20.解:(1)由题可知,AB垂直平分CD,
∴圆心O在BA的延长线上.
如图,连接OC.
设☉O的半径为r m,则OA=(r-0.8)m.
∵OB⊥CD,
∴CA=DA=CD=×3.2=1.6(m).
在Rt△OAC中,AC2+OA2=OC2,
即1.62+(r-0.8)2=r2.
解得r=2,即该圆弧所在圆的半径为2 m.
(2)如图,连接OG,过点G作GE⊥AB于点E.
∵DH=0.4 m,
∴AH=AD-DH=1.2 m.
∵∠GEA=∠EAH=∠GHA=90°,
∴四边形AHGE为矩形.
∴AE=GH,GE=AH=1.2 m.
在Rt△OEG中,
OE===1.6(m).
∵OA=OB-AB=2-0.8=1.2(m),
∴AE=OE-OA=1.6-1.2=0.4(m).
∴HG=0.4 m,即支撑杆HG的高度为0.4 m.
21.解:(1)45°
(2)∵AE为☉O的直径,
∴∠AGE=90°.
∵=,∴AG=EG,∠GAE=∠AEG=45°.
∵AE=20,
∴根据勾股定理,得AG2+EG2=AE2.
∴AG=EG=10.
(3)∵ME为☉O的切线,∴∠AEM=90°.
由(2)知,∠GAE=45°,∴∠M=45°.∴ME=AE=20.
由(2)知,EG=10.
∵20>10,∴ME>EG.
22.解:(1)AD BE 1
解析:如图1,连接OE,OF.
图1
由切线长定理可知,AF=AD,BD=BE.
∵∠C=90°,☉O是△ABC的内切圆,
∴∠C=∠OEC=∠OFC=90°,OE=OF.
∴四边形OECF是正方形.
设OE=OF=CF=CE=x,则BE=BC-CE=4-x=BD,AF=AC-CF=3-x=AD.
∵AB===5,∴BD+AD=AB=4-x+3-x=5.解得x=1.∴OE=1,即☉O的半径长为1.
(2)证明:如图2,过点O作OH⊥MN于点H,连接OD,OE,OF.
图2
∵∠ANM=90°=∠ACB,∠A=∠A,AM=AB,
∴△AMN≌△ABC(AAS).
∴AN=AC.
∵AD=AF,
∴AN-AD=AC-AF,
即DN=CF.
由(1)可知,CF=OE,∴DN=OE.
∵∠ANM=90°=∠ODN=∠OHN,
∴四边形OHND是矩形.∴OH=DN.
∴OH=OE,即OH是☉O的半径.
∵OH⊥MN,∴MN是☉O的切线.
23.解:(1)如图,连接OD.
∵☉O的直径AB=16,
∴☉O的半径为8.
∵OC⊥AB,DE⊥OC,DF⊥AB,
∴∠EOB=∠OED=∠OFD=90°.
∴四边形OFDE是矩形.
∴EF=OD=8.
(2)①∵E为OC的中点,
∴OE=OC=OD.
∵DE⊥OC,
∴∠EDO=30°.
∴∠DOE=60°.
∴劣弧CD的长度为=.
②PC+PD的最小值为8.
解法提示:如图,延长CO交☉O于点G,连接DG交AB于点P,则PC+PD的最小值为DG.
设DE=x.
∵∠G=∠COD=30°,DE⊥OC,
∴DG=2DE=2x.
∵OE=OC=4,
∴EG=OE+OG=4+8=12.
在△EDG中,DE2+EG2=DG2,
即x2+(12)2=(2x)2.
解得x=4.
∴DG=8.
∴PC+PD的最小值为8.
24.解:(1)如图,设BC与半圆O交于点M,连接OM,ME.
当t=2.5 s时,BE=2.5.
∵EF=10,∴OE=EF=5.
∴OB=OE-BE=2.5.∴EB=OB.
在矩形ABCD中,∠ABC=90°,
∴ME=MO.
又∵MO=EO,∴ME=EO=MO.
∴△MOE是等边三角形.
∴∠EOM=60°.
∴的长度==,
即半圆O在矩形ABCD内的弧的长度为.
(2)如图,连接OG,OH.
∵∠GOH=90°,
∴∠AOG+∠BOH=90°.
∵∠AGO+∠AOG=90°,
∴∠AGO=∠BOH.
在△AGO和△BOH中,
∴△AGO≌△BOH(AAS).
∴AG=BO=BE-OE=t-5.
∵AB=7,∴AE=BE-AB=t-7.
∴AO=OE-AE=5-(t-7)=12-t.
在Rt△AGO中,AG2+AO2=OG2,
∴(t-5)2+(12-t)2=52.
解得t1=8,t2=9,即此时t的值为8或9.
(总分:120分 时间:120分钟)
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知AB是半径为5的圆的一条弦,则AB的长不可能是 ( )
A.4 B.8 C.10 D.12
2.已知☉O的直径为10 cm,点P到圆心O的距离为8 cm,则点P和圆的位置关系是 ( )
A.点在圆内 B.点在圆外 C.点在圆上 D.无法判断
3.如图,在△ABC中,∠ACB=90°,AC=4,点D在边AB上,且AD=5,以AC为直径作☉O,设线段CD的中点为P,则点P与☉O的位置关系是 ( )
A.点P在☉O内 B.点P在☉O上
C.点P在☉O外 D.无法确定
4.(2024长沙中考)如图,在☉O中,弦AB的长为8,圆心O到AB的距离OE=4,则☉O的半径长为 ( )
A.4 B.4 C.5 D.5
5.如图,将正六边形纸片的空白部分剪下,得到三部分图形,记Ⅰ,Ⅱ,Ⅲ部分的面积分别为SⅠ,SⅡ,SⅢ.给出以下结论:①Ⅰ和Ⅱ合在一起能拼成一个菱形;②Ⅲ中最大的内角是150°;③SⅢ=2(SⅠ+SⅡ).其中正确的结论是 ( )
→
A.①② B.①③
C.②③ D.①②③
6.如图,CD是☉O的直径,点A,B在☉O上.若=,∠AOC=40°,则∠D的大小为 ( )
A.10° B.20°
C.40° D.45°
7.如图,四边形ABCD的边AB,BC,CD,DA和☉O分别相切于点L,M,N,P.若四边形ABCD的周长为20,则AB+CD的值为 ( )
A.5 B.8
C.10 D.12
8.(2024河北中考)扇文化是中华优秀传统文化的组成部分,在我国有着深厚的底蕴.如图,某折扇张开的角度为120°时,扇面面积为S,该折扇张开的角度为n°时,扇面面积为Sn.若m=,则m与n关系的图象大致是 ( )
A B C D
9.(2024泸州中考)如图,EA,ED是☉O的切线,切点为A,D,点B,C在☉O上.若∠BAE+∠BCD=236°,则∠E的度数为 ( )
A.56° B.60°
C.68° D.70°
10.如图,点O是△ABC的内心,也是△DBC的外心.若∠A=84°,则∠D的度数为 ( )
A.42° B.66° C.76° D.82°
11.如图,直线AB,CD相交于点O,∠AOD=30°,半径为2 cm的☉P的圆心在直线AB上,且位于点O左侧10 cm处.如果☉P以2 cm/s的速度沿由A向B的方向移动,那么☉P与直线CD相切时的运动时间是 ( )
A.3 s B.7 s C.3 s或7 s D.6 s或14 s
12.为了测量圆形工件的直径.
图1 图2
甲:如图1,在工作台上用边长相同的两个立方体小木块顶在圆形工件的两侧,测得两木块间的距离b和小木块的边长a即可;
乙:如图2,把两个小木块换成两个相同的小圆柱,量得圆柱半径n和两个圆心之间的距离m即可.下列有关甲、乙两人的说法正确的是( )
A.甲对,乙不对
B.甲不对,乙对
C.两人都不对
D.两人都对
二、填空题(本大题共4个小题,每小题3分,共12分)
13.如图,在☉O中,若∠AOC=2∠BOD,则AC (填“>”“<”或“=”)2BD.
14.(2024连云港中考)如图,AB是圆的直径,∠1,∠2,∠3,∠4的顶点均在AB上方的圆弧上,∠1,∠4的一边分别经过点A,B,则∠1+∠2+∠3+∠4= .
15.(2024西宁中考)如图,四边形ABCD内接于☉O,E为直径CD延长线上一点,=,∠ADE=110°,则∠DAB的度数为 .
16.如图,将扇形AOB翻折,使点A与圆心O重合,展开后折痕所在直线l与交于点C,连接AC.若OA=2,则图中阴影部分的面积是 .
三、解答题(本大题共8 个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(7分)如图,在平面直角坐标系中,A,B,C是☉M上的三个点,点A(0,4),B(4,4),C(6,2).
(1)写出圆心M的坐标.
(2)求这个圆的半径.
(3)直接判断点D(4,-3)与☉M的位置关系:点D(4,-3)在☉M (填“内”“外”或“上”).
18.(8分)如图,这是将圆锥侧面展开得到的扇形,此扇形半径CA=3,圆心角∠ACB=120°.
(1)求的长.
(2)求此圆锥的高OC的长.
19.(8分)如图,在☉O中,AB=CD,AB与CD相交于点M.
求证:(1)=.
(2)AM=DM.
20.(8分)如图是正在修建的某大门上半部分的截面,其为圆弧形,跨度CD(弧所对的弦)的长为3.2 m,拱高AB(弧的中点到弦的距离)为0.8 m.
(1)求该圆弧所在圆的半径.
(2)在修建中,在距大门边框的一端(点D)0.4 m处将竖立支撑杆HG,求支撑杆HG的高度.
21.(9分)司南是我国古代辨别方向用的一种仪器(图1),其早在战国时期就已被发明,是现在所用指南针的始祖.如图2,司南中心为一圆形,圆心为点O,直径为20,根据八个方位将圆形八等分(图2中点A~H),过点E作☉O的切线与AG的延长线交于点M,连接EG.
(1)相邻两个方位间所夹的圆心角的度数为 .
(2)求AG的长.
(3)求线段ME与EG的长,并比较大小.
图1 图2
22.(9分)(2024自贡中考)在Rt△ABC中,∠C=90°,☉O是△ABC的内切圆,切点分别为D,E,F.
(1)图1中三组相等的线段分别是CE=CF,AF= ,BD= ;若AC=3,BC=4,则☉O的半径长为 .
(2)如图2,延长AC到点M,使AM=AB,过点M作MN⊥AB于点N.求证:MN是☉O的切线.
图1 图2
23.(11分)如图,☉O的直径AB=16,半径OC⊥AB,D为上一动点(不包括B,C两点),DE⊥OC,DF⊥AB,垂足分别为E,F.
(1)求EF的长.
(2)若E为OC的中点,
①求劣弧CD的长度.
②若P为直径AB上一动点,直接写出PC+PD的最小值.
24.(12分)如图1,矩形ABCD与以EF为直径的半圆O在直线l的上方,线段AB与点E,F都在直线l上,且AB=7,EF=10,BC>5.点B以1个单位长度/s的速度从点E处出发,沿射线EF的方向运动,矩形ABCD随之运动,运动时间为t s.
(1)如图2,当t=2.5 s时,求半圆O在矩形ABCD内的弧的长度.
(2)在点B运动的过程中,当AD,BC都与半圆O相交时,设这两个交点为G,H.连接OG,OH.若∠GOH为直角,求此时t的值.
图1 图2 备用图
【详解答案】
1.D 解析:∵圆中最长的弦为直径,∴弦长AB≤10.故选D.
2.B 解析:∵☉O的直径为10 cm,∴☉O的半径为5 cm.∵点P到圆心O的距离为8 cm>5 cm,∴点P在圆外.故选B.
3.C 解析:如图,连接OP.∵以AC为直径作☉O,线段CD的中点为P,∴OP是△CAD的中位线.∴OP=AD=2.5.∵AO=CO=AC=2<2.5,∴点P与☉O的位置关系是点P在☉O外.故选C.
4.B 解析:∵OE⊥AB,∴AE=EB=4.∴OA===4.故选B.
5.B 解析:如图所示的正六边形可以分割成6个全等的三角形,于是Ⅰ部分、Ⅱ部分相当于其中的1个三角形,Ⅲ部分相当于4个这样的三角形,故①Ⅰ和Ⅱ合在一起能拼成一个菱形是正确的;③SⅢ=2(SⅠ+SⅡ)是正确的;②Ⅲ中最大的内角是=120°,因此②是不正确的.综上所述,正确的有①③.故选B.
6.B 解析:如图,连接OB.
∵=,∠AOC=40°,∴∠BOC=40°.∵=,∴∠D=∠BOC=20°.故选B.
7.C 解析:由切线长定理,得AL=AP,DP=DN,CN=CM,BM=BL.∴四边形ABCD的周长为AB+BC+CD+DA=AL+BL+BM+CM+CN+DN+DP+AP=2AB+2CD=20.∴AB+CD=10.故选C.
8.C 解析:设该扇子所在圆的半径为R,S==.∴πR2=3S.∵该折扇张开的角度为n°时,扇面面积为Sn,∴Sn==×3S=.∴m====n.∴m是n的正比例函数.故选C.
9.C 解析:如图,连接AD.∵四边形ABCD是☉O的内接四边形,∴∠BAD+∠BCD=180°.∵∠BAE+∠BCD=236°,∴∠EAD+∠BAD+∠BCD=∠EAD+180°=236°.∴∠EAD=56°.∵EA,ED是☉O的切线,切点为A,D,∴EA=ED.∴∠EDA=∠EAD=56°.∴∠E=180°-∠EDA-∠EAD=180°-56°-56°=68°.故选C.
10.B 解析:如图,连接OB,OC.∵点O是△ABC的内心,∠A=84°,∴OB,OC是∠ABC,∠ACB的平分线.∴∠OBC=∠ABC,∠OCB=∠ACB.∴∠BOC=180°-∠OBC-∠OCB=180°-(∠ABC+∠ACB)=180°-(180°-∠A)=90°+∠A=132°.∵点O也是△DBC的外心,∴∠D=∠BOC=66°.∴∠D的度数为66°.故选B.
11.C 解析:①当圆心P在直线CD的左侧时,设此时圆心为P1,CD与☉P1相切于点E(图略),∴P1E⊥CD.∵☉P的半径为2 cm,∴P1E=2 cm.∵∠AOD=30°,P1E⊥CD,∴P1O=4 cm.∴PP1=PO-P1O=10-4=6(cm).∴t=6÷2=3(s).②当圆心P在直线CD的右侧时,设此时圆心为P2,同理可得PP2=PO+P2O=10+4=14(cm),∴t=14÷2=7(s).综上所述,☉P与直线CD相切时经过的运动时间是3 s或7 s,故选C.
12.D 解析:如图1,设圆的半径为r,圆形工件与工作台相切于点M,连接DC,OD,连接OM交DC于点P.∴OM⊥AB.∵DC∥AB,∴OM⊥DC.∴PD=PC=CD=AB=b.∵PM=BC=a,∴OP=OM-PM=r-a.∵OD2=OP2+PD2,∴r2=(r-a)2+b2.∴r=.∴甲对.如图2,设圆的半径为R,圆形工件与工作台相切于点H,连接OH交CD于点K,连接OC,OD,CA,DB.∴OH⊥AB.∵CD∥AB,∴OH⊥CD.∵OC=R+n,OD=R+n,∴OC=OD.∴KC=KD=m.∵KH=CA=DB=n,∴OK=OH-KH=R-n.∵OC2=OK2+CK2,∴(R+n)2=(R-n)2+m2.∴R=.∴乙对.∴甲、乙两人都对.故选D.
图1 图2
13.< 解析:如图,以OD为边作∠DOE=∠BOD,OE与☉O交于点E,连接AC,BE,BD,ED,则∠BOE=2∠BOD,BD=DE.∵∠AOC=2∠BOD,∴∠AOC=∠BOE.∴AC=BE.在△BDE中,BE
15.125° 解析:如图,连接OA,OB.∵∠ADE=110°,∠ADE+∠ADO=180°,∴∠ADO=70°.∵OA=OD,∴∠OAD=∠ODA=70°.∴∠AOD=40°.∴∠AOC=140°.∵=,∴∠AOB=∠BOC=70°.∵OB=OC,∴∠OCB=∠OBC=55°.∵四边形ABCD为☉O的内接四边形,∴∠DAB+∠OCB=180°.∴∠DAB=125°.
16.- 解析:如图,连接CO.设直线l与AO交于点D.∵在扇形AOB中,OA=2,∴OC=OA=2.∵点A与圆心O重合,∴AD=OD=1,CD⊥AO.∴OC=AC.∴OA=OC=AC=2.∴△OAC是等边三角形.∴∠COD=60°.∵CD⊥OA,∴CD==.∴阴影部分的面积为-×2×=-.
17.解:(1)如图,圆心M的坐标为(2,0).
(2)如图,连接MA.∵点A(0,4),M(2,0),
∴MA==2.
∴这个圆的半径为2.
(3)内
18.解:(1)的长==2π.
(2)设OA的长为r,则2πr=2π.
解得r=1.
在Rt△AOC中,∠AOC=90°,
由勾股定理,得
OC===2.
19.证明:(1)∵在☉O中,AB=CD,
∴=.
∴-=-.
∴=.
(2)如图,连接AC,BD.
∵=,
∴AC=BD.
在△ACM和△DBM中,
∴△ACM≌△DBM(ASA).
∴AM=DM.
20.解:(1)由题可知,AB垂直平分CD,
∴圆心O在BA的延长线上.
如图,连接OC.
设☉O的半径为r m,则OA=(r-0.8)m.
∵OB⊥CD,
∴CA=DA=CD=×3.2=1.6(m).
在Rt△OAC中,AC2+OA2=OC2,
即1.62+(r-0.8)2=r2.
解得r=2,即该圆弧所在圆的半径为2 m.
(2)如图,连接OG,过点G作GE⊥AB于点E.
∵DH=0.4 m,
∴AH=AD-DH=1.2 m.
∵∠GEA=∠EAH=∠GHA=90°,
∴四边形AHGE为矩形.
∴AE=GH,GE=AH=1.2 m.
在Rt△OEG中,
OE===1.6(m).
∵OA=OB-AB=2-0.8=1.2(m),
∴AE=OE-OA=1.6-1.2=0.4(m).
∴HG=0.4 m,即支撑杆HG的高度为0.4 m.
21.解:(1)45°
(2)∵AE为☉O的直径,
∴∠AGE=90°.
∵=,∴AG=EG,∠GAE=∠AEG=45°.
∵AE=20,
∴根据勾股定理,得AG2+EG2=AE2.
∴AG=EG=10.
(3)∵ME为☉O的切线,∴∠AEM=90°.
由(2)知,∠GAE=45°,∴∠M=45°.∴ME=AE=20.
由(2)知,EG=10.
∵20>10,∴ME>EG.
22.解:(1)AD BE 1
解析:如图1,连接OE,OF.
图1
由切线长定理可知,AF=AD,BD=BE.
∵∠C=90°,☉O是△ABC的内切圆,
∴∠C=∠OEC=∠OFC=90°,OE=OF.
∴四边形OECF是正方形.
设OE=OF=CF=CE=x,则BE=BC-CE=4-x=BD,AF=AC-CF=3-x=AD.
∵AB===5,∴BD+AD=AB=4-x+3-x=5.解得x=1.∴OE=1,即☉O的半径长为1.
(2)证明:如图2,过点O作OH⊥MN于点H,连接OD,OE,OF.
图2
∵∠ANM=90°=∠ACB,∠A=∠A,AM=AB,
∴△AMN≌△ABC(AAS).
∴AN=AC.
∵AD=AF,
∴AN-AD=AC-AF,
即DN=CF.
由(1)可知,CF=OE,∴DN=OE.
∵∠ANM=90°=∠ODN=∠OHN,
∴四边形OHND是矩形.∴OH=DN.
∴OH=OE,即OH是☉O的半径.
∵OH⊥MN,∴MN是☉O的切线.
23.解:(1)如图,连接OD.
∵☉O的直径AB=16,
∴☉O的半径为8.
∵OC⊥AB,DE⊥OC,DF⊥AB,
∴∠EOB=∠OED=∠OFD=90°.
∴四边形OFDE是矩形.
∴EF=OD=8.
(2)①∵E为OC的中点,
∴OE=OC=OD.
∵DE⊥OC,
∴∠EDO=30°.
∴∠DOE=60°.
∴劣弧CD的长度为=.
②PC+PD的最小值为8.
解法提示:如图,延长CO交☉O于点G,连接DG交AB于点P,则PC+PD的最小值为DG.
设DE=x.
∵∠G=∠COD=30°,DE⊥OC,
∴DG=2DE=2x.
∵OE=OC=4,
∴EG=OE+OG=4+8=12.
在△EDG中,DE2+EG2=DG2,
即x2+(12)2=(2x)2.
解得x=4.
∴DG=8.
∴PC+PD的最小值为8.
24.解:(1)如图,设BC与半圆O交于点M,连接OM,ME.
当t=2.5 s时,BE=2.5.
∵EF=10,∴OE=EF=5.
∴OB=OE-BE=2.5.∴EB=OB.
在矩形ABCD中,∠ABC=90°,
∴ME=MO.
又∵MO=EO,∴ME=EO=MO.
∴△MOE是等边三角形.
∴∠EOM=60°.
∴的长度==,
即半圆O在矩形ABCD内的弧的长度为.
(2)如图,连接OG,OH.
∵∠GOH=90°,
∴∠AOG+∠BOH=90°.
∵∠AGO+∠AOG=90°,
∴∠AGO=∠BOH.
在△AGO和△BOH中,
∴△AGO≌△BOH(AAS).
∴AG=BO=BE-OE=t-5.
∵AB=7,∴AE=BE-AB=t-7.
∴AO=OE-AE=5-(t-7)=12-t.
在Rt△AGO中,AG2+AO2=OG2,
∴(t-5)2+(12-t)2=52.
解得t1=8,t2=9,即此时t的值为8或9.
同课章节目录
