第二十五章 概率初步 评估测试卷(含答案) 2025-2026学年数学人教版九年级上册
文档属性
| 名称 | 第二十五章 概率初步 评估测试卷(含答案) 2025-2026学年数学人教版九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 281.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-08 09:49:52 | ||
图片预览



文档简介
第二十五章 概率初步 评估测试卷
(总分:120分 时间:120分钟)
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2024湖北中考)在下列事件中,必然事件是 ( )
A.掷一次骰子,向上一面的点数是3
B.篮球队员在罚球线上投篮一次,未投中
C.经过有交通信号灯的路口,遇到红灯
D.任意画一个三角形,其内角和是180°
2.(2024贵州中考)小星同学通过大量重复的定点投篮练习,用频率估计他投中的概率为0.4.下列说法正确的是 ( )
A.小星定点投篮1次,不一定能投中 B.小星定点投篮1次,一定可以投中
C.小星定点投篮10次,一定投中4次 D.小星定点投篮4次,一定投中1次
3.(2024济南中考)3月14日是国际数学节.某学校在今年国际数学节策划了“竞速华容道”“玩转幻方”和“巧解鲁班锁”三个挑战活动.如果小红和小丽每人随机选择参加其中一个活动,那么她们恰好选到同一个活动的概率是 ( )
A. B. C. D.
4.从分别写有“大”“美”“江”“汉”汉字的四张卡片(除汉字外无其他差别)中,随机抽出两张,抽出的卡片上的汉字能组成“江汉”的概率是( )
A. B. C. D.
5.(2024辽宁中考)一个不透明的袋子中装有4个白球、3个红球、2个绿球、1个黑球,每个球除颜色外都相同.从中随机摸出一个球,则下列事件发生的概率为的是 ( )
A.摸出白球 B.摸出红球 C.摸出绿球 D.摸出黑球
6.如图,一飞镖游戏板由大小相等的小正方形格子构成,向游戏板随机投掷一枚飞镖,击中阴影区域的概率是 ( )
A. B.
C. D.
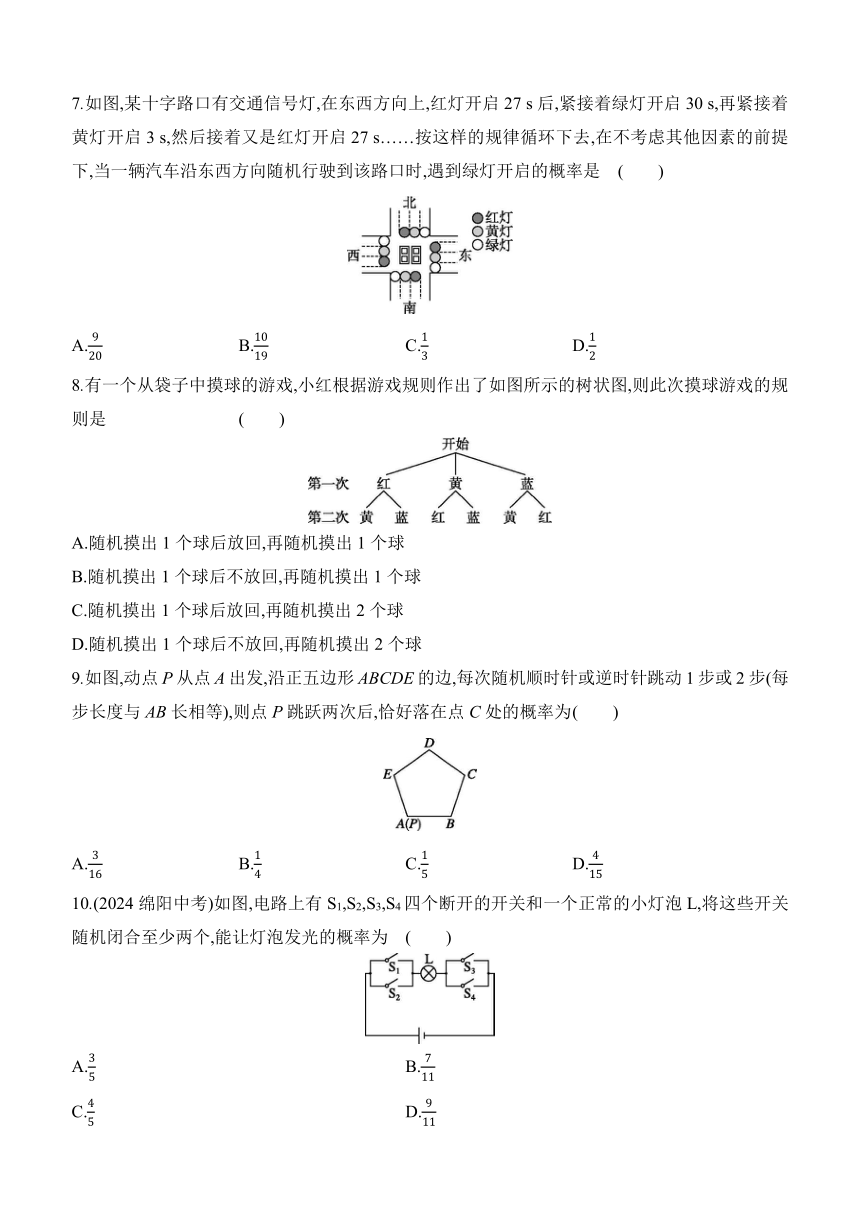
7.如图,某十字路口有交通信号灯,在东西方向上,红灯开启27 s后,紧接着绿灯开启30 s,再紧接着黄灯开启3 s,然后接着又是红灯开启27 s……按这样的规律循环下去,在不考虑其他因素的前提下,当一辆汽车沿东西方向随机行驶到该路口时,遇到绿灯开启的概率是 ( )
A. B. C. D.
8.有一个从袋子中摸球的游戏,小红根据游戏规则作出了如图所示的树状图,则此次摸球游戏的规则是 ( )
A.随机摸出1个球后放回,再随机摸出1个球
B.随机摸出1个球后不放回,再随机摸出1个球
C.随机摸出1个球后放回,再随机摸出2个球
D.随机摸出1个球后不放回,再随机摸出2个球
9.如图,动点P从点A出发,沿正五边形ABCDE的边,每次随机顺时针或逆时针跳动1步或2步(每步长度与AB长相等),则点P跳跃两次后,恰好落在点C处的概率为 ( )
A. B. C. D.
10.(2024绵阳中考)如图,电路上有S1,S2,S3,S4四个断开的开关和一个正常的小灯泡L,将这些开关随机闭合至少两个,能让灯泡发光的概率为 ( )
A. B.
C. D.
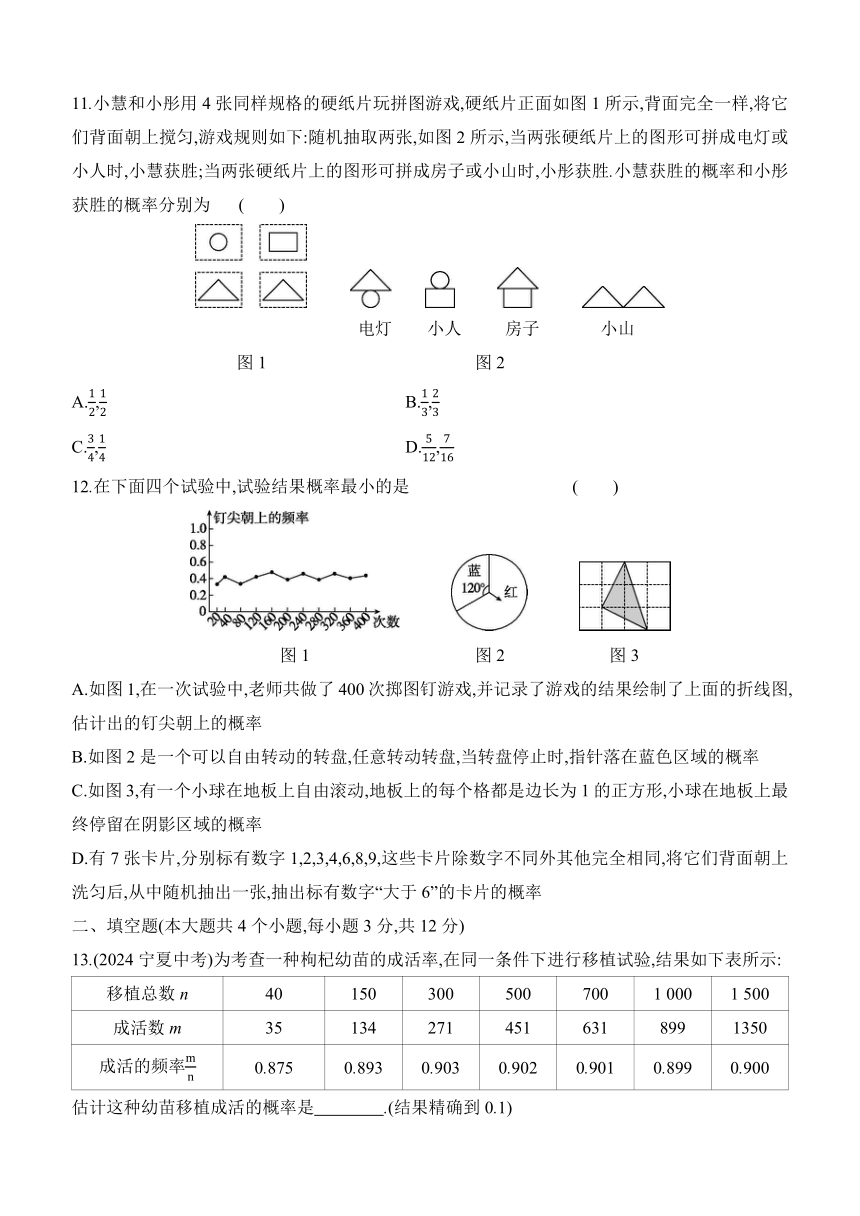
11.小慧和小彤用4张同样规格的硬纸片玩拼图游戏,硬纸片正面如图1所示,背面完全一样,将它们背面朝上搅匀,游戏规则如下:随机抽取两张,如图2所示,当两张硬纸片上的图形可拼成电灯或小人时,小慧获胜;当两张硬纸片上的图形可拼成房子或小山时,小彤获胜.小慧获胜的概率和小彤获胜的概率分别为 ( )
电灯 小人 房子 小山
图1 图2
A., B.,
C., D.,
12.在下面四个试验中,试验结果概率最小的是 ( )
图1 图2 图3
A.如图1,在一次试验中,老师共做了400次掷图钉游戏,并记录了游戏的结果绘制了上面的折线图,估计出的钉尖朝上的概率
B.如图2是一个可以自由转动的转盘,任意转动转盘,当转盘停止时,指针落在蓝色区域的概率
C.如图3,有一个小球在地板上自由滚动,地板上的每个格都是边长为1的正方形,小球在地板上最终停留在阴影区域的概率
D.有7张卡片,分别标有数字1,2,3,4,6,8,9,这些卡片除数字不同外其他完全相同,将它们背面朝上洗匀后,从中随机抽出一张,抽出标有数字“大于6”的卡片的概率
二、填空题(本大题共4个小题,每小题3分,共12分)
13.(2024宁夏中考)为考查一种枸杞幼苗的成活率,在同一条件下进行移植试验,结果如下表所示:
移植总数n 40 150 300 500 700 1 000 1 500
成活数m 35 134 271 451 631 899 1350
成活的频率 0.875 0.893 0.903 0.902 0.901 0.899 0.900
估计这种幼苗移植成活的概率是 .(结果精确到0.1)
14.(2024成都中考)盒中有x枚黑棋和y枚白棋,这些棋除颜色外无其他差别.从盒中随机取出一枚棋子,如果它是黑棋的概率是,那么的值为 .
15.某市准备为青少年举行一次网球知识讲座,小明和妹妹都是网球球迷,要求爸爸去买门票,但爸爸只买回一张门票,为了确定谁去听讲座,小明想了一个办法:他拿出一个装有质地、大小均相同的2x个红球与3x个白球的袋子,让爸爸从中摸出一个球,如果摸出的是红球,那么妹妹去听讲座;如果摸出的是白球,那么小明去听讲座.则该办法 .(填“公平”或“不公平”)
16.体育课上,小强、小东、小智三人练习踢足球,足球从一人传到另一人就记为踢一次.若踢了三次后,要使踢到小强处的概率最小,应该从 开始踢.
三、解答题(本大题共8 个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(7分)(2024西宁中考)2024年4月23日是第29个世界读书日,我市某社区开展了以“最美人间四月天,不负韶华读书时”为主题的系列读书活动.
(1)为了解西宁市初中生每周的累计读书时长,应采用的调查方式是 (填“全面调查”或“抽样调查”).
(2)该社区某校准备从A,B,C,D四名同学中选择两人作为“好书推荐官”,参加社区的好书推荐活动.请用画树状图或列表的方法列出所有等可能的结果,并求出A,B两名同学恰好同时被选中的概率.
18.(8分)在一个不透明的袋子中装有9个红球和6个黄球,这些球除颜色外其他都相同,将袋子中的球充分摇匀后,随机摸出一个球.
(1)摸出的球是红球的概率是多少 摸出的球是黄球的概率是多少
(2)为了使摸出红球和黄球的概率相同,再放进去5个球,那么这5个球中红球和黄球的数量分别是多少
19.(8分)下表是某厂质检部门对该厂生产的一批排球质量检测的情况.
抽取的排球数 500 1 000 1 500 2 000 3 000
合格品数 471 946 1 425 b 2 853
抽到合格品的频率 a 0.946 0.950 0.949 0.951
(1)a的值为 ,b的值为 .
(2)从这批排球中任意抽取一个,是合格品的概率约是 (精确到0.01).
(3)如果要生产23 750个合格的排球,那么该厂估计要生产多少个排球
20.(8分)人体的许多特征都是由基因控制的.如人的单眼皮或双眼皮,这是由一对人体基因控制的,控制单眼皮的基因f是隐性的,控制双眼皮的基因F是显性的,这样控制眼皮的一对基因可能是ff,FF或者Ff.基因是ff的人是单眼皮,基因是FF或Ff的人是双眼皮.在遗传时,父母分别将他们所携带的一对基因中的一个遗传给子女,而且是等可能的.例如,父母都是双眼皮而且他们的基因都是Ff,那么他们的子女的基因只有ff,FF或者Ff三种可能,具体情况可用下表表示:
父亲基因Ff 母亲基因Ff F f
F FF Ff
f Ff ff
(1)根据表格,请你计算出他们的子女是双眼皮的概率.
(2)如果父亲的基因是ff,母亲的基因是Ff,请用画树状图法表示他们子女的基因,并求他们的子女是双眼皮的概率.
(3)你觉得父母双方只要一方基因是 时,他们的子女一定是双眼皮.
21.(9分)(2024青岛中考)学校拟举办庆祝“新中国成立75周年”文艺汇演,每班选派一名志愿者.九年级(1)班的小明和小红都想参加,于是两人决定一起做“摸牌”游戏,获胜者参加.规则如下:将牌面数字分别为1,2,3的三张纸牌(除牌面数字外,其余都相同)背面朝上,洗匀后放在桌面上,小明先从中随机摸出一张,记下数字后放回并洗匀,小红再从中随机摸出一张.若两次摸到的数字之和大于4,则小明胜;若和小于4,则小红胜;若和等于4,则重复上述过程.
(1)小明从三张纸牌中随机摸出一张,摸到“1”的概率是 .
(2)请用列表或画树状图的方法,说明这个游戏对双方是否公平.
22.(9分)某渔民准备将自家的鱼塘转让出去,现在需要通过估计鱼塘中鱼的数量来估算鱼塘的价值,他从鱼塘中打捞了200条鱼,在每一条鱼身上做好标记后,把这些鱼放归鱼塘,经过一段时间后,再从鱼塘中打捞鱼,通过多次试验得到数据如下表所示:
每次打捞鱼数 50 100 200 300 500
每次打捞鱼中带标记的鱼数 4 11 19 31 n
打捞到带标记的鱼的频率 0.080 m 0.095 0.103 0.100
根据表中数据,回答下列问题:
(1)表中m的值为 ,n的值为 .
(2)随机从鱼塘中打捞一条鱼,根据表中数据估计打捞到带标记的鱼的概率为 (精确到0.1).
(3)若每条鱼大约40元,则这片鱼塘的价值大约是多少
23.(11分)小明正在参加全国“数学竞赛”,只要他再答对最后两道单选题就能顺利过关,其中第一道题有3个选项,第二道题有4个选项,而这两道题小明都不会,不过小明还有一次“求助”没有使用(使用“求助”可让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,随机选择一个选项,那么小明答对第一道题的概率是多少
(2)如果小明将“求助”留在第二题使用,请用画树状图或列表的方法求小明能顺利过关的概率.
(3)请你从概率的角度分析,建议小明在第几题使用“求助”,才能使他过关的概率较大.
24.(12分)(2024淄博中考)希望中学做了如下表的调查报告(不完整):
调查目的 了解本校学生:(1)周家务劳动的时间;(2)最喜欢的劳动课程
调查方式 随机问卷调查
调查对象 部分七年级学生(该校所有学生周家务劳动时间都在1~3.5 h范围内)
调查内容 (1)你的周家务劳动时间(单位:h)是 ( ) ①1~1.5 ②1.5~2 ③2~2.5 ④2.5~3 ⑤3~3.5 (2)你最喜欢的劳动课程是(必选且只选一门) ( ) A.家政 B.烹饪 C.剪纸 D.园艺 E.陶艺
调查 结果 周家务劳动时间频数分布直方图 周家务劳动时间扇形图 劳动课程条形图
结合调查信息,回答下列问题:
(1)参与本次问卷调查的学生有 名;在扇形图中,第④组所对应扇形的圆心角的度数为 .
(2)补全周家务劳动时间的频数分布直方图.
(3)若该校七年级学生共有800名,请估计最喜欢“烹饪”课程的学生人数.
(4)小红和小颖分别从“家政”等五门最喜欢的劳动课程中任选一门学习,请用列表或画树状图的方法,求两人恰好选到同一门课程的概率.
【详解答案】
1.D 解析:A.掷一次骰子,向上一面的点数是3,是随机事件,不符合题意;B.篮球队员在罚球线上投篮一次,未投中,是随机事件,不符合题意;C.经过有交通信号灯的路口,遇到红灯,是随机事件,不符合题意;D.任意画一个三角形,其内角和是180°,是必然事件,符合题意.故选D.
2.A 解析:A,B.小星定点投篮1次,不一定能投中,故A符合题意,B不符合题意;C.小星定点投篮10次,不一定能投中4次,故不符合题意;D.小星定点投篮4次,不一定能投中1次,故不符合题意.故选A.
3.C 解析:把“竞速华容道”“玩转幻方”和“巧解鲁班锁”三个活动分别记为A,B,C,画树状图如下:
∵共有9种等可能的结果,小红和小丽恰好选到同一个活动的结果有3种,∴小红和小丽恰好选到同一个活动的概率为=.故选C.
4.B 解析:列表如下:
第1张 第2张 大 美 江 汉
大 (美,大) (江,大) (汉,大)
美 (大,美) (江,美) (汉,美)
江 (大,江) (美,江) (汉,江)
汉 (大,汉) (美,汉) (江,汉)
∵共有12种等可能的结果,其中抽出的卡片上的汉字能组成“江汉”的结果有2种,
∴抽出的卡片上的汉字能组成“江汉”的概率为=.故选B.
5.B 解析:∵一个不透明的袋子中装有4个白球、3个红球、2个绿球、1个黑球,共有10个球,∴从中随机摸出一个球,摸出白球的概率为=,摸出红球的概率为,摸出绿球的概率为=,摸出黑球的概率为.故选B.
6.A 解析:设小正方形的边长为1,则阴影区域的面积为3×3-×3×1-×2×1-×3×2=,游戏板的面积为3×3=9,∴击中阴影区域的概率是=.故选A.
7.D 解析:由题意,得当一辆汽车沿东西方向随机行驶到该路口时,遇到绿灯开启的概率是=.故选D.
8.B 解析:观察题中树状图可知,袋子中共有红、黄、蓝三个小球,所以此次摸球游戏的规则是随机摸出1个球后不放回,再随机摸出1个球.故选B.
9.A 解析:画树状图如下:
共有16种等可能的结果,点P跳跃两次后,恰好落在点C处的结果有3种,∴点P跳跃两次后,恰好落在点C处的概率为.故选A.
10.D 解析:将这些开关随机闭合至少两个,所有等可能的结果有(S1,S2),(S1,S3),(S1,S4),(S2,S3),(S2,S4),(S3,S4), (S1,S2,S3),(S1,S2,S4),(S1,S3,S4),(S2,S3,S4),(S1,S2,S3,S4),共11种,其中能让灯泡发光的结果有(S1,S3),(S1,S4),(S2,S3), (S2,S4),(S1,S2,S3),(S1,S2,S4),(S1,S3,S4),(S2,S3,S4),(S1,S2,S3,S4),共9种,∴将这些开关随机闭合至少两个,能让灯泡发光的概率为.故选D.
11.A 解析:用A,B分别表示图案为圆和长方形的硬纸片,C,D表示图案为三角形的两张硬纸片,列表如下:
A B C D
A (A,B) (A,C) (A,D)
B (B,A) (B,C) (B,D)
C (C,A) (C,B) (C,D)
D (D,A) (D,B) (D,C)
∵共有12种等可能的结果,其中可拼成电灯或小人的结果有6种,可拼成房子或小山的结果有6种,∴P(小慧获胜)==,P(小彤获胜)==.故选A.
12.C 解析:A.如题图1,在一次试验中,老师共做了400次掷图钉游戏,并记录了游戏的结果绘制了折线图,估计出的钉尖朝上的概率为0.4;B.如题图2是一个可以自由转动的转盘,任意转动转盘,当转盘停止时,指针落在蓝色区域的概率为≈0.33;C.如题图3,有一个小球在地板上自由滚动,地板上的每个格都是边长为1的正方形,则小球在地板上最终停留在阴影区域的概率为=≈0.21;D.有7张卡片,分别标有数字1,2,3,4,6,8,9,这些卡片除数字不同外其他完全相同,将它们背面朝上洗匀后,从中随机抽出一张,抽出标有数字“大于6”的卡片的概率为≈0.29.∴0.21最小.故选C.
13.0.9 解析:∵根据题表中数据,成活的频率逐渐稳定在0.9左右,∴估计这种枸杞幼苗在此条件下移植成活的概率是0.9.
14. 解析:∵盒中有x枚黑棋和y枚白棋,∴共有(x+y)枚棋.∵从盒中随机取出一枚棋子,它是黑棋的概率是,∴可得关系式=.∴8x=3x+3y,即5x=3y.∴=.
15.不公平 解析:∵红球有2x个,白球有3x个,∴摸出红球的概率为=,摸出白球的概率为=.∵<,∴该办法不公平.
16.小强 解析:若从小强开始踢,画树状图如下:
从小强开始踢,P(踢到小强处)==;同理可得,若从小东开始踢,P(踢到小强处)=;若从小智开始踢,P(踢到小强处)=.所以应从小强开始踢.
17.解:(1)抽样调查
(2)画树状图如下:
∵共有12种等可能的结果,其中A,B两名同学恰好同时被选中的结果有2种,
∴A,B两名同学恰好同时被选中的概率为=.
18.解:(1)由题意可知,摸出每一球的可能性相同,
∴摸出红球的概率是=,
摸出黄球的概率是=.
(2)设放入红球x个,则放入黄球(5-x)个.
由题意,得=.
解得x=1.∴5-x=4.
∴放进去的这5个球中红球有1个,黄球有4个.
19.解:(1)0.942 1 898 (2)0.95
(3)23 750÷0.95=25 000(个).
∴该厂估计要生产25 000个排球.
20.解:(1)由题中表格可知,一共有4种等可能的结果,其中他们的子女是双眼皮的结果有3种,
∴他们的子女是双眼皮的概率为.
(2)画树状图如下:
由树状图可知,一共有4种等可能的结果,其中他们的子女是双眼皮的结果有2种,
∴他们的子女是双眼皮的概率为=.
(3)FF
21.解:(1)
(2)游戏公平.理由如下:
根据题意,列表如下:
小明 小红 1 2 3
1 2 3 4
2 3 4 5
3 4 5 6
由表可知,共有9种等可能的结果,其中两次摸到的数字之和大于4的有3种,两次摸到的数字之和小于4的有3种,
∴小明获胜的概率是=,小红获胜的概率为=.
∴两人获胜的概率相等.
∴这个游戏对双方公平.
22.解:(1)0.110 50
(2)0.1
(3)∵这个鱼塘中的鱼约有200÷0.1=2 000(条),
2 000×40=80 000(元),
∴这片鱼塘的价值大约是80 000元.
23.解:(1)∵第一道单选题有3个选项,
∴如果小明第一题不使用“求助”,那么小明答对第一道题的概率是.
(2)分别用A,B,C表示第一道单选题的3个选项,a,b,c表示第二道单选题剩下的3个选项,画树状图如下:
由图可知,共有9种等可能的结果,小明顺利通关的结果只有1种,
∴小明能顺利通关的概率为.
(3)如果小明在第一题使用“求助”,分别用A,B表示第一道单选题剩下的2个选项,a,b,c,d表示第二道单选题的4个选项,画树状图如下:
由图可知,共有8种等可能的结果,小明顺利过关的结果有1种,∴小明能顺利过关的概率为.∵>,
∴建议小明在第一题使用“求助”.
24.解:(1)100 126°
(2)周家务劳动时间是③2~2.5的学生有100-10-20-35-10=25(名).
补全周家务劳动时间的频数分布直方图如图所示:
周家务劳动时间频数分布直方图
(3)800×=176(名).
∴估计最喜欢“烹饪”课程的学生有176名.
(4)根据题意,列表如下:
A B C D E
A (A,A) (A,B) (A,C) (A,D) (A,E)
B (B,A) (B,B) (B,C) (B,D) (B,E)
C (C,A) (C,B) (C,C) (C,D) (C,E)
D (D,A) (D,B) (D,C) (D,D) (D,E)
E (E,A) (E,B) (E,C) (E,D) (E,E)
由表可知,共有25种等可能的结果,其中两人恰好选到同一门课程的结果有5种,
∴两人恰好选到同一门课程的概率为=.
(总分:120分 时间:120分钟)
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2024湖北中考)在下列事件中,必然事件是 ( )
A.掷一次骰子,向上一面的点数是3
B.篮球队员在罚球线上投篮一次,未投中
C.经过有交通信号灯的路口,遇到红灯
D.任意画一个三角形,其内角和是180°
2.(2024贵州中考)小星同学通过大量重复的定点投篮练习,用频率估计他投中的概率为0.4.下列说法正确的是 ( )
A.小星定点投篮1次,不一定能投中 B.小星定点投篮1次,一定可以投中
C.小星定点投篮10次,一定投中4次 D.小星定点投篮4次,一定投中1次
3.(2024济南中考)3月14日是国际数学节.某学校在今年国际数学节策划了“竞速华容道”“玩转幻方”和“巧解鲁班锁”三个挑战活动.如果小红和小丽每人随机选择参加其中一个活动,那么她们恰好选到同一个活动的概率是 ( )
A. B. C. D.
4.从分别写有“大”“美”“江”“汉”汉字的四张卡片(除汉字外无其他差别)中,随机抽出两张,抽出的卡片上的汉字能组成“江汉”的概率是( )
A. B. C. D.
5.(2024辽宁中考)一个不透明的袋子中装有4个白球、3个红球、2个绿球、1个黑球,每个球除颜色外都相同.从中随机摸出一个球,则下列事件发生的概率为的是 ( )
A.摸出白球 B.摸出红球 C.摸出绿球 D.摸出黑球
6.如图,一飞镖游戏板由大小相等的小正方形格子构成,向游戏板随机投掷一枚飞镖,击中阴影区域的概率是 ( )
A. B.
C. D.
7.如图,某十字路口有交通信号灯,在东西方向上,红灯开启27 s后,紧接着绿灯开启30 s,再紧接着黄灯开启3 s,然后接着又是红灯开启27 s……按这样的规律循环下去,在不考虑其他因素的前提下,当一辆汽车沿东西方向随机行驶到该路口时,遇到绿灯开启的概率是 ( )
A. B. C. D.
8.有一个从袋子中摸球的游戏,小红根据游戏规则作出了如图所示的树状图,则此次摸球游戏的规则是 ( )
A.随机摸出1个球后放回,再随机摸出1个球
B.随机摸出1个球后不放回,再随机摸出1个球
C.随机摸出1个球后放回,再随机摸出2个球
D.随机摸出1个球后不放回,再随机摸出2个球
9.如图,动点P从点A出发,沿正五边形ABCDE的边,每次随机顺时针或逆时针跳动1步或2步(每步长度与AB长相等),则点P跳跃两次后,恰好落在点C处的概率为 ( )
A. B. C. D.
10.(2024绵阳中考)如图,电路上有S1,S2,S3,S4四个断开的开关和一个正常的小灯泡L,将这些开关随机闭合至少两个,能让灯泡发光的概率为 ( )
A. B.
C. D.
11.小慧和小彤用4张同样规格的硬纸片玩拼图游戏,硬纸片正面如图1所示,背面完全一样,将它们背面朝上搅匀,游戏规则如下:随机抽取两张,如图2所示,当两张硬纸片上的图形可拼成电灯或小人时,小慧获胜;当两张硬纸片上的图形可拼成房子或小山时,小彤获胜.小慧获胜的概率和小彤获胜的概率分别为 ( )
电灯 小人 房子 小山
图1 图2
A., B.,
C., D.,
12.在下面四个试验中,试验结果概率最小的是 ( )
图1 图2 图3
A.如图1,在一次试验中,老师共做了400次掷图钉游戏,并记录了游戏的结果绘制了上面的折线图,估计出的钉尖朝上的概率
B.如图2是一个可以自由转动的转盘,任意转动转盘,当转盘停止时,指针落在蓝色区域的概率
C.如图3,有一个小球在地板上自由滚动,地板上的每个格都是边长为1的正方形,小球在地板上最终停留在阴影区域的概率
D.有7张卡片,分别标有数字1,2,3,4,6,8,9,这些卡片除数字不同外其他完全相同,将它们背面朝上洗匀后,从中随机抽出一张,抽出标有数字“大于6”的卡片的概率
二、填空题(本大题共4个小题,每小题3分,共12分)
13.(2024宁夏中考)为考查一种枸杞幼苗的成活率,在同一条件下进行移植试验,结果如下表所示:
移植总数n 40 150 300 500 700 1 000 1 500
成活数m 35 134 271 451 631 899 1350
成活的频率 0.875 0.893 0.903 0.902 0.901 0.899 0.900
估计这种幼苗移植成活的概率是 .(结果精确到0.1)
14.(2024成都中考)盒中有x枚黑棋和y枚白棋,这些棋除颜色外无其他差别.从盒中随机取出一枚棋子,如果它是黑棋的概率是,那么的值为 .
15.某市准备为青少年举行一次网球知识讲座,小明和妹妹都是网球球迷,要求爸爸去买门票,但爸爸只买回一张门票,为了确定谁去听讲座,小明想了一个办法:他拿出一个装有质地、大小均相同的2x个红球与3x个白球的袋子,让爸爸从中摸出一个球,如果摸出的是红球,那么妹妹去听讲座;如果摸出的是白球,那么小明去听讲座.则该办法 .(填“公平”或“不公平”)
16.体育课上,小强、小东、小智三人练习踢足球,足球从一人传到另一人就记为踢一次.若踢了三次后,要使踢到小强处的概率最小,应该从 开始踢.
三、解答题(本大题共8 个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(7分)(2024西宁中考)2024年4月23日是第29个世界读书日,我市某社区开展了以“最美人间四月天,不负韶华读书时”为主题的系列读书活动.
(1)为了解西宁市初中生每周的累计读书时长,应采用的调查方式是 (填“全面调查”或“抽样调查”).
(2)该社区某校准备从A,B,C,D四名同学中选择两人作为“好书推荐官”,参加社区的好书推荐活动.请用画树状图或列表的方法列出所有等可能的结果,并求出A,B两名同学恰好同时被选中的概率.
18.(8分)在一个不透明的袋子中装有9个红球和6个黄球,这些球除颜色外其他都相同,将袋子中的球充分摇匀后,随机摸出一个球.
(1)摸出的球是红球的概率是多少 摸出的球是黄球的概率是多少
(2)为了使摸出红球和黄球的概率相同,再放进去5个球,那么这5个球中红球和黄球的数量分别是多少
19.(8分)下表是某厂质检部门对该厂生产的一批排球质量检测的情况.
抽取的排球数 500 1 000 1 500 2 000 3 000
合格品数 471 946 1 425 b 2 853
抽到合格品的频率 a 0.946 0.950 0.949 0.951
(1)a的值为 ,b的值为 .
(2)从这批排球中任意抽取一个,是合格品的概率约是 (精确到0.01).
(3)如果要生产23 750个合格的排球,那么该厂估计要生产多少个排球
20.(8分)人体的许多特征都是由基因控制的.如人的单眼皮或双眼皮,这是由一对人体基因控制的,控制单眼皮的基因f是隐性的,控制双眼皮的基因F是显性的,这样控制眼皮的一对基因可能是ff,FF或者Ff.基因是ff的人是单眼皮,基因是FF或Ff的人是双眼皮.在遗传时,父母分别将他们所携带的一对基因中的一个遗传给子女,而且是等可能的.例如,父母都是双眼皮而且他们的基因都是Ff,那么他们的子女的基因只有ff,FF或者Ff三种可能,具体情况可用下表表示:
父亲基因Ff 母亲基因Ff F f
F FF Ff
f Ff ff
(1)根据表格,请你计算出他们的子女是双眼皮的概率.
(2)如果父亲的基因是ff,母亲的基因是Ff,请用画树状图法表示他们子女的基因,并求他们的子女是双眼皮的概率.
(3)你觉得父母双方只要一方基因是 时,他们的子女一定是双眼皮.
21.(9分)(2024青岛中考)学校拟举办庆祝“新中国成立75周年”文艺汇演,每班选派一名志愿者.九年级(1)班的小明和小红都想参加,于是两人决定一起做“摸牌”游戏,获胜者参加.规则如下:将牌面数字分别为1,2,3的三张纸牌(除牌面数字外,其余都相同)背面朝上,洗匀后放在桌面上,小明先从中随机摸出一张,记下数字后放回并洗匀,小红再从中随机摸出一张.若两次摸到的数字之和大于4,则小明胜;若和小于4,则小红胜;若和等于4,则重复上述过程.
(1)小明从三张纸牌中随机摸出一张,摸到“1”的概率是 .
(2)请用列表或画树状图的方法,说明这个游戏对双方是否公平.
22.(9分)某渔民准备将自家的鱼塘转让出去,现在需要通过估计鱼塘中鱼的数量来估算鱼塘的价值,他从鱼塘中打捞了200条鱼,在每一条鱼身上做好标记后,把这些鱼放归鱼塘,经过一段时间后,再从鱼塘中打捞鱼,通过多次试验得到数据如下表所示:
每次打捞鱼数 50 100 200 300 500
每次打捞鱼中带标记的鱼数 4 11 19 31 n
打捞到带标记的鱼的频率 0.080 m 0.095 0.103 0.100
根据表中数据,回答下列问题:
(1)表中m的值为 ,n的值为 .
(2)随机从鱼塘中打捞一条鱼,根据表中数据估计打捞到带标记的鱼的概率为 (精确到0.1).
(3)若每条鱼大约40元,则这片鱼塘的价值大约是多少
23.(11分)小明正在参加全国“数学竞赛”,只要他再答对最后两道单选题就能顺利过关,其中第一道题有3个选项,第二道题有4个选项,而这两道题小明都不会,不过小明还有一次“求助”没有使用(使用“求助”可让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,随机选择一个选项,那么小明答对第一道题的概率是多少
(2)如果小明将“求助”留在第二题使用,请用画树状图或列表的方法求小明能顺利过关的概率.
(3)请你从概率的角度分析,建议小明在第几题使用“求助”,才能使他过关的概率较大.
24.(12分)(2024淄博中考)希望中学做了如下表的调查报告(不完整):
调查目的 了解本校学生:(1)周家务劳动的时间;(2)最喜欢的劳动课程
调查方式 随机问卷调查
调查对象 部分七年级学生(该校所有学生周家务劳动时间都在1~3.5 h范围内)
调查内容 (1)你的周家务劳动时间(单位:h)是 ( ) ①1~1.5 ②1.5~2 ③2~2.5 ④2.5~3 ⑤3~3.5 (2)你最喜欢的劳动课程是(必选且只选一门) ( ) A.家政 B.烹饪 C.剪纸 D.园艺 E.陶艺
调查 结果 周家务劳动时间频数分布直方图 周家务劳动时间扇形图 劳动课程条形图
结合调查信息,回答下列问题:
(1)参与本次问卷调查的学生有 名;在扇形图中,第④组所对应扇形的圆心角的度数为 .
(2)补全周家务劳动时间的频数分布直方图.
(3)若该校七年级学生共有800名,请估计最喜欢“烹饪”课程的学生人数.
(4)小红和小颖分别从“家政”等五门最喜欢的劳动课程中任选一门学习,请用列表或画树状图的方法,求两人恰好选到同一门课程的概率.
【详解答案】
1.D 解析:A.掷一次骰子,向上一面的点数是3,是随机事件,不符合题意;B.篮球队员在罚球线上投篮一次,未投中,是随机事件,不符合题意;C.经过有交通信号灯的路口,遇到红灯,是随机事件,不符合题意;D.任意画一个三角形,其内角和是180°,是必然事件,符合题意.故选D.
2.A 解析:A,B.小星定点投篮1次,不一定能投中,故A符合题意,B不符合题意;C.小星定点投篮10次,不一定能投中4次,故不符合题意;D.小星定点投篮4次,不一定能投中1次,故不符合题意.故选A.
3.C 解析:把“竞速华容道”“玩转幻方”和“巧解鲁班锁”三个活动分别记为A,B,C,画树状图如下:
∵共有9种等可能的结果,小红和小丽恰好选到同一个活动的结果有3种,∴小红和小丽恰好选到同一个活动的概率为=.故选C.
4.B 解析:列表如下:
第1张 第2张 大 美 江 汉
大 (美,大) (江,大) (汉,大)
美 (大,美) (江,美) (汉,美)
江 (大,江) (美,江) (汉,江)
汉 (大,汉) (美,汉) (江,汉)
∵共有12种等可能的结果,其中抽出的卡片上的汉字能组成“江汉”的结果有2种,
∴抽出的卡片上的汉字能组成“江汉”的概率为=.故选B.
5.B 解析:∵一个不透明的袋子中装有4个白球、3个红球、2个绿球、1个黑球,共有10个球,∴从中随机摸出一个球,摸出白球的概率为=,摸出红球的概率为,摸出绿球的概率为=,摸出黑球的概率为.故选B.
6.A 解析:设小正方形的边长为1,则阴影区域的面积为3×3-×3×1-×2×1-×3×2=,游戏板的面积为3×3=9,∴击中阴影区域的概率是=.故选A.
7.D 解析:由题意,得当一辆汽车沿东西方向随机行驶到该路口时,遇到绿灯开启的概率是=.故选D.
8.B 解析:观察题中树状图可知,袋子中共有红、黄、蓝三个小球,所以此次摸球游戏的规则是随机摸出1个球后不放回,再随机摸出1个球.故选B.
9.A 解析:画树状图如下:
共有16种等可能的结果,点P跳跃两次后,恰好落在点C处的结果有3种,∴点P跳跃两次后,恰好落在点C处的概率为.故选A.
10.D 解析:将这些开关随机闭合至少两个,所有等可能的结果有(S1,S2),(S1,S3),(S1,S4),(S2,S3),(S2,S4),(S3,S4), (S1,S2,S3),(S1,S2,S4),(S1,S3,S4),(S2,S3,S4),(S1,S2,S3,S4),共11种,其中能让灯泡发光的结果有(S1,S3),(S1,S4),(S2,S3), (S2,S4),(S1,S2,S3),(S1,S2,S4),(S1,S3,S4),(S2,S3,S4),(S1,S2,S3,S4),共9种,∴将这些开关随机闭合至少两个,能让灯泡发光的概率为.故选D.
11.A 解析:用A,B分别表示图案为圆和长方形的硬纸片,C,D表示图案为三角形的两张硬纸片,列表如下:
A B C D
A (A,B) (A,C) (A,D)
B (B,A) (B,C) (B,D)
C (C,A) (C,B) (C,D)
D (D,A) (D,B) (D,C)
∵共有12种等可能的结果,其中可拼成电灯或小人的结果有6种,可拼成房子或小山的结果有6种,∴P(小慧获胜)==,P(小彤获胜)==.故选A.
12.C 解析:A.如题图1,在一次试验中,老师共做了400次掷图钉游戏,并记录了游戏的结果绘制了折线图,估计出的钉尖朝上的概率为0.4;B.如题图2是一个可以自由转动的转盘,任意转动转盘,当转盘停止时,指针落在蓝色区域的概率为≈0.33;C.如题图3,有一个小球在地板上自由滚动,地板上的每个格都是边长为1的正方形,则小球在地板上最终停留在阴影区域的概率为=≈0.21;D.有7张卡片,分别标有数字1,2,3,4,6,8,9,这些卡片除数字不同外其他完全相同,将它们背面朝上洗匀后,从中随机抽出一张,抽出标有数字“大于6”的卡片的概率为≈0.29.∴0.21最小.故选C.
13.0.9 解析:∵根据题表中数据,成活的频率逐渐稳定在0.9左右,∴估计这种枸杞幼苗在此条件下移植成活的概率是0.9.
14. 解析:∵盒中有x枚黑棋和y枚白棋,∴共有(x+y)枚棋.∵从盒中随机取出一枚棋子,它是黑棋的概率是,∴可得关系式=.∴8x=3x+3y,即5x=3y.∴=.
15.不公平 解析:∵红球有2x个,白球有3x个,∴摸出红球的概率为=,摸出白球的概率为=.∵<,∴该办法不公平.
16.小强 解析:若从小强开始踢,画树状图如下:
从小强开始踢,P(踢到小强处)==;同理可得,若从小东开始踢,P(踢到小强处)=;若从小智开始踢,P(踢到小强处)=.所以应从小强开始踢.
17.解:(1)抽样调查
(2)画树状图如下:
∵共有12种等可能的结果,其中A,B两名同学恰好同时被选中的结果有2种,
∴A,B两名同学恰好同时被选中的概率为=.
18.解:(1)由题意可知,摸出每一球的可能性相同,
∴摸出红球的概率是=,
摸出黄球的概率是=.
(2)设放入红球x个,则放入黄球(5-x)个.
由题意,得=.
解得x=1.∴5-x=4.
∴放进去的这5个球中红球有1个,黄球有4个.
19.解:(1)0.942 1 898 (2)0.95
(3)23 750÷0.95=25 000(个).
∴该厂估计要生产25 000个排球.
20.解:(1)由题中表格可知,一共有4种等可能的结果,其中他们的子女是双眼皮的结果有3种,
∴他们的子女是双眼皮的概率为.
(2)画树状图如下:
由树状图可知,一共有4种等可能的结果,其中他们的子女是双眼皮的结果有2种,
∴他们的子女是双眼皮的概率为=.
(3)FF
21.解:(1)
(2)游戏公平.理由如下:
根据题意,列表如下:
小明 小红 1 2 3
1 2 3 4
2 3 4 5
3 4 5 6
由表可知,共有9种等可能的结果,其中两次摸到的数字之和大于4的有3种,两次摸到的数字之和小于4的有3种,
∴小明获胜的概率是=,小红获胜的概率为=.
∴两人获胜的概率相等.
∴这个游戏对双方公平.
22.解:(1)0.110 50
(2)0.1
(3)∵这个鱼塘中的鱼约有200÷0.1=2 000(条),
2 000×40=80 000(元),
∴这片鱼塘的价值大约是80 000元.
23.解:(1)∵第一道单选题有3个选项,
∴如果小明第一题不使用“求助”,那么小明答对第一道题的概率是.
(2)分别用A,B,C表示第一道单选题的3个选项,a,b,c表示第二道单选题剩下的3个选项,画树状图如下:
由图可知,共有9种等可能的结果,小明顺利通关的结果只有1种,
∴小明能顺利通关的概率为.
(3)如果小明在第一题使用“求助”,分别用A,B表示第一道单选题剩下的2个选项,a,b,c,d表示第二道单选题的4个选项,画树状图如下:
由图可知,共有8种等可能的结果,小明顺利过关的结果有1种,∴小明能顺利过关的概率为.∵>,
∴建议小明在第一题使用“求助”.
24.解:(1)100 126°
(2)周家务劳动时间是③2~2.5的学生有100-10-20-35-10=25(名).
补全周家务劳动时间的频数分布直方图如图所示:
周家务劳动时间频数分布直方图
(3)800×=176(名).
∴估计最喜欢“烹饪”课程的学生有176名.
(4)根据题意,列表如下:
A B C D E
A (A,A) (A,B) (A,C) (A,D) (A,E)
B (B,A) (B,B) (B,C) (B,D) (B,E)
C (C,A) (C,B) (C,C) (C,D) (C,E)
D (D,A) (D,B) (D,C) (D,D) (D,E)
E (E,A) (E,B) (E,C) (E,D) (E,E)
由表可知,共有25种等可能的结果,其中两人恰好选到同一门课程的结果有5种,
∴两人恰好选到同一门课程的概率为=.
同课章节目录
