数学:《立体几何第9课时》教案(苏教版必修2)
文档属性
| 名称 | 数学:《立体几何第9课时》教案(苏教版必修2) |
|
|
| 格式 | rar | ||
| 文件大小 | 20.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-02-26 00:00:00 | ||
图片预览


文档简介
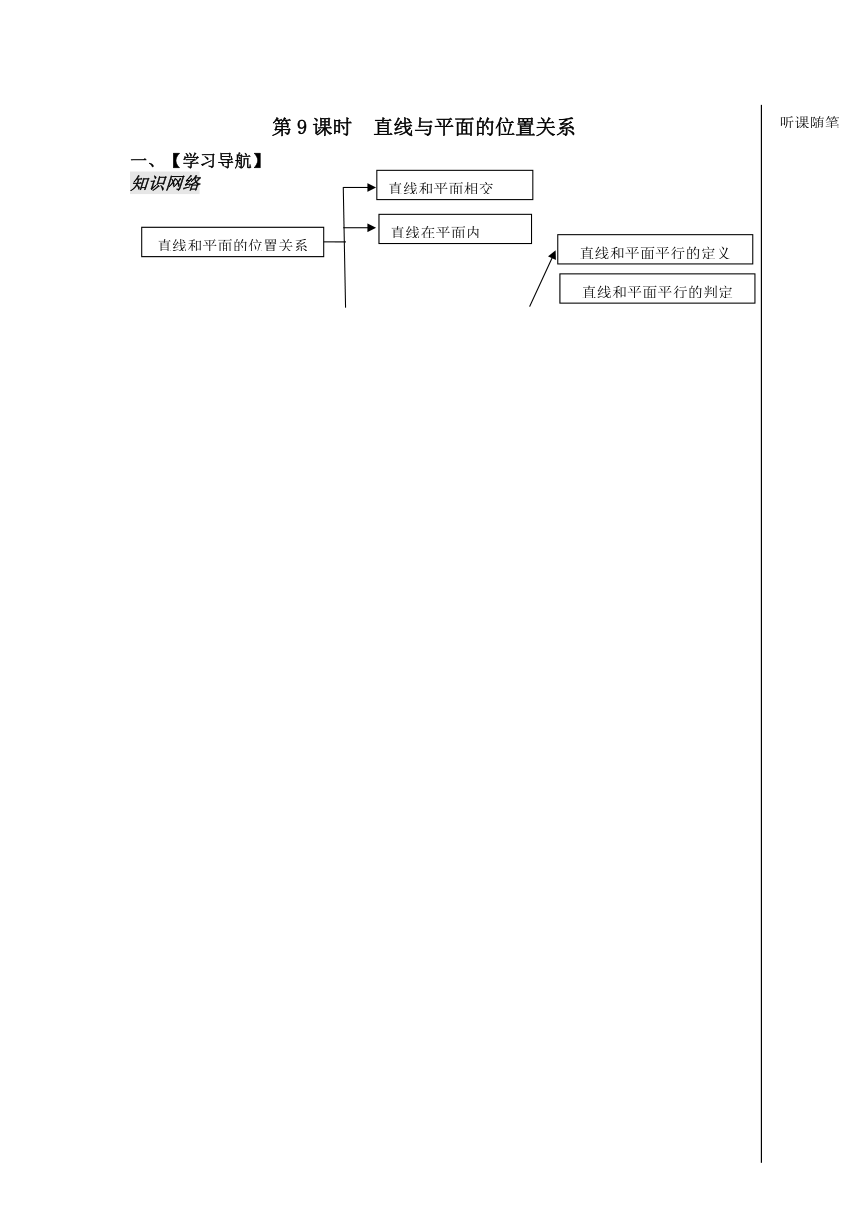
第9课时 直线与平面的位置关系
一、【学习导航】
知识网络
学习要求
1.掌握直线与平面的位置关系.
2.掌握直线和平面平行的判定与性质定理.
.3.应用直线和平面平行的判定和性质定理证明两条直线平行等有关问题.
【课堂互动】
自学评价
1. 直线和平面位置关系
位置关系 符号表示 图形表示
直线a在平面α内
直线a在平面α相交
直线a在平面α相交
2.直线在平面内是指:
3.直线和平面平行的判定定理
符号表示
说明:本章中出现的判定定理的证明不作要求
4.直线和平面平行的性质定理
已知:
求证:
见书31页
证明:
【精典范例】
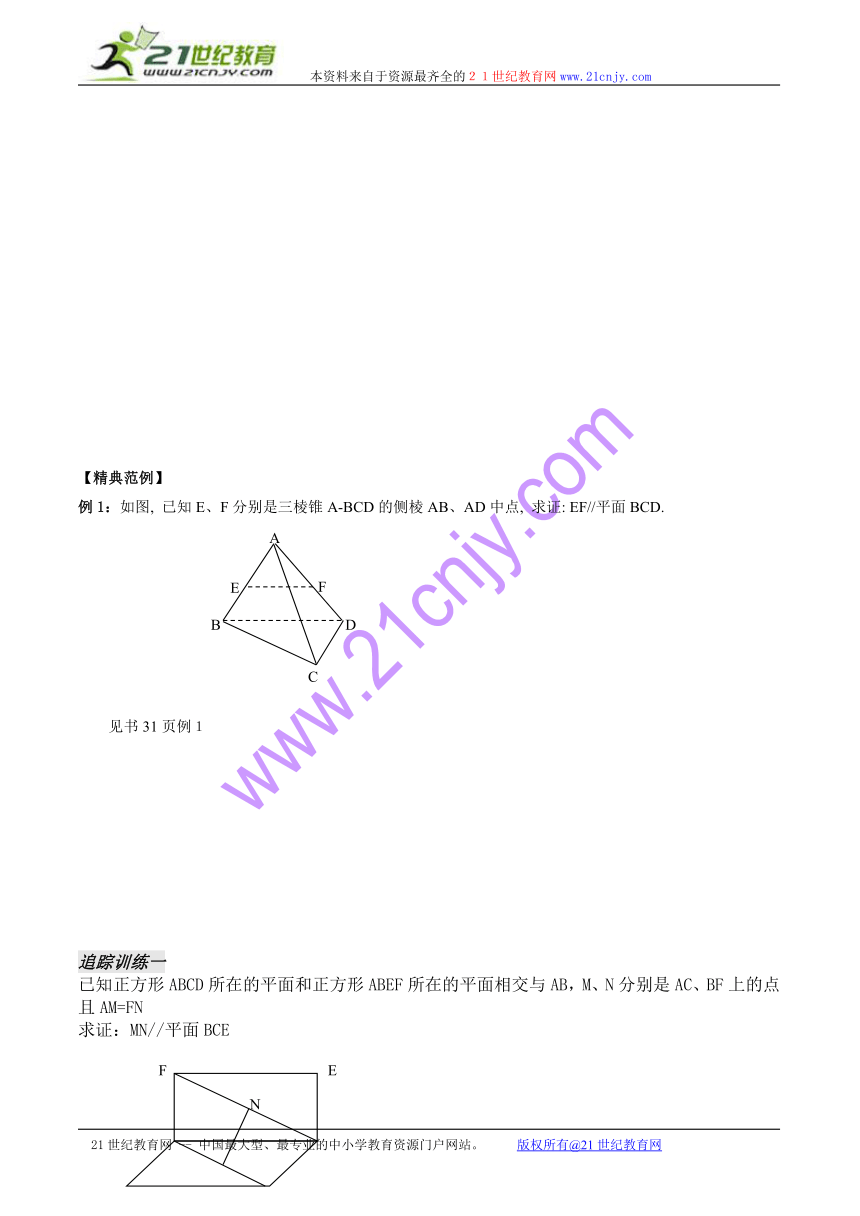
例1:如图, 已知E、F分别是三棱锥A-BCD的侧棱AB、AD中点, 求证: EF//平面BCD.
见书31页例1
追踪训练一
已知正方形ABCD所在的平面和正方形ABEF所在的平面相交与AB,M、N分别是AC、BF上的点且AM=FN
求证:MN//平面BCE
证明:作NP//AB交BE于点P
作NQ//AB交BC于点Q
而AC=BF,AM=FN,
∴MC=NB,有AB=EF
∴MQ//NP,有MQ=NP
∴四边形MQNP是平行四边形.
∴MN//PQ,而PQ平面BCE
∴MN//平面BCE
例2.一个长方体木块如图所示, 要经过平面A1C1内一点P和棱BC将木块锯开, 应怎样画线
见书31页例2
例3.求证: 如果三个平面两两相交于直线, 并且其中两条直线平行, 那么第三条直线也和它们平行.
已知:
求证:
见书31页例3
[思考]: 如果三个平面两两相交于三条直线, 并且其中的两条直线相交, 那么第三条直线和这两条直线有怎样的位置关系
追踪训练二
1.指出下列命题是否正确,并说明理由:
(1).如果一条直线不在平面内,那么这条直线就与这个平面平行;错
(2).过直线外一点有无数个平面与这条直线平行;正确
(3).过平面外一点有无数个直线与这条平面平行。正确
2.已知直线a,b和平面α,下列命题正确的是 (D )
A.若a//α,bα则a//b
B. 若a//α,b//α则a//b
C. 若a//b,bα则a//α
D. 若a//b,bα则a//α或bα
3.在长方体ABCD-A1B1C1D1的面中:
(1)与直线AB平行的平面是:面A1C1, 面DC1
(2)与直线A A1平行的平面是:面BC1, 面DC1
(3)与直线AD平行的平面是:面BC1, 面A1C1
学生质疑
教师释疑
听课随笔
直线和平面相交
直线在平面内
直线和平面平行的定义
直线和平面的位置关系
直线和平面平行的判定
直线和平面平行
直线和平面平行的判定
与性质定理的应用
直线和平面平行的性质
A
E
F
B
C
D
F
E
N
B
A
M
D
C
A
B
C
D
A1
D1
C1
B1
P
·
听课随笔
听课随笔
C1
D1
B1
A1
D
C
B
A
一、【学习导航】
知识网络
学习要求
1.掌握直线与平面的位置关系.
2.掌握直线和平面平行的判定与性质定理.
.3.应用直线和平面平行的判定和性质定理证明两条直线平行等有关问题.
【课堂互动】
自学评价
1. 直线和平面位置关系
位置关系 符号表示 图形表示
直线a在平面α内
直线a在平面α相交
直线a在平面α相交
2.直线在平面内是指:
3.直线和平面平行的判定定理
符号表示
说明:本章中出现的判定定理的证明不作要求
4.直线和平面平行的性质定理
已知:
求证:
见书31页
证明:
【精典范例】
例1:如图, 已知E、F分别是三棱锥A-BCD的侧棱AB、AD中点, 求证: EF//平面BCD.
见书31页例1
追踪训练一
已知正方形ABCD所在的平面和正方形ABEF所在的平面相交与AB,M、N分别是AC、BF上的点且AM=FN
求证:MN//平面BCE
证明:作NP//AB交BE于点P
作NQ//AB交BC于点Q
而AC=BF,AM=FN,
∴MC=NB,有AB=EF
∴MQ//NP,有MQ=NP
∴四边形MQNP是平行四边形.
∴MN//PQ,而PQ平面BCE
∴MN//平面BCE
例2.一个长方体木块如图所示, 要经过平面A1C1内一点P和棱BC将木块锯开, 应怎样画线
见书31页例2
例3.求证: 如果三个平面两两相交于直线, 并且其中两条直线平行, 那么第三条直线也和它们平行.
已知:
求证:
见书31页例3
[思考]: 如果三个平面两两相交于三条直线, 并且其中的两条直线相交, 那么第三条直线和这两条直线有怎样的位置关系
追踪训练二
1.指出下列命题是否正确,并说明理由:
(1).如果一条直线不在平面内,那么这条直线就与这个平面平行;错
(2).过直线外一点有无数个平面与这条直线平行;正确
(3).过平面外一点有无数个直线与这条平面平行。正确
2.已知直线a,b和平面α,下列命题正确的是 (D )
A.若a//α,bα则a//b
B. 若a//α,b//α则a//b
C. 若a//b,bα则a//α
D. 若a//b,bα则a//α或bα
3.在长方体ABCD-A1B1C1D1的面中:
(1)与直线AB平行的平面是:面A1C1, 面DC1
(2)与直线A A1平行的平面是:面BC1, 面DC1
(3)与直线AD平行的平面是:面BC1, 面A1C1
学生质疑
教师释疑
听课随笔
直线和平面相交
直线在平面内
直线和平面平行的定义
直线和平面的位置关系
直线和平面平行的判定
直线和平面平行
直线和平面平行的判定
与性质定理的应用
直线和平面平行的性质
A
E
F
B
C
D
F
E
N
B
A
M
D
C
A
B
C
D
A1
D1
C1
B1
P
·
听课随笔
听课随笔
C1
D1
B1
A1
D
C
B
A
