第一章 集合与常用逻辑用语 章末小结(含答案) 2024~2025学年高一数学人教A版(2019)必修第一册
文档属性
| 名称 | 第一章 集合与常用逻辑用语 章末小结(含答案) 2024~2025学年高一数学人教A版(2019)必修第一册 |
|
|
| 格式 | docx | ||
| 文件大小 | 133.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-06 20:55:58 | ||
图片预览



文档简介
第一章 集合与常用逻辑用语 章末小结
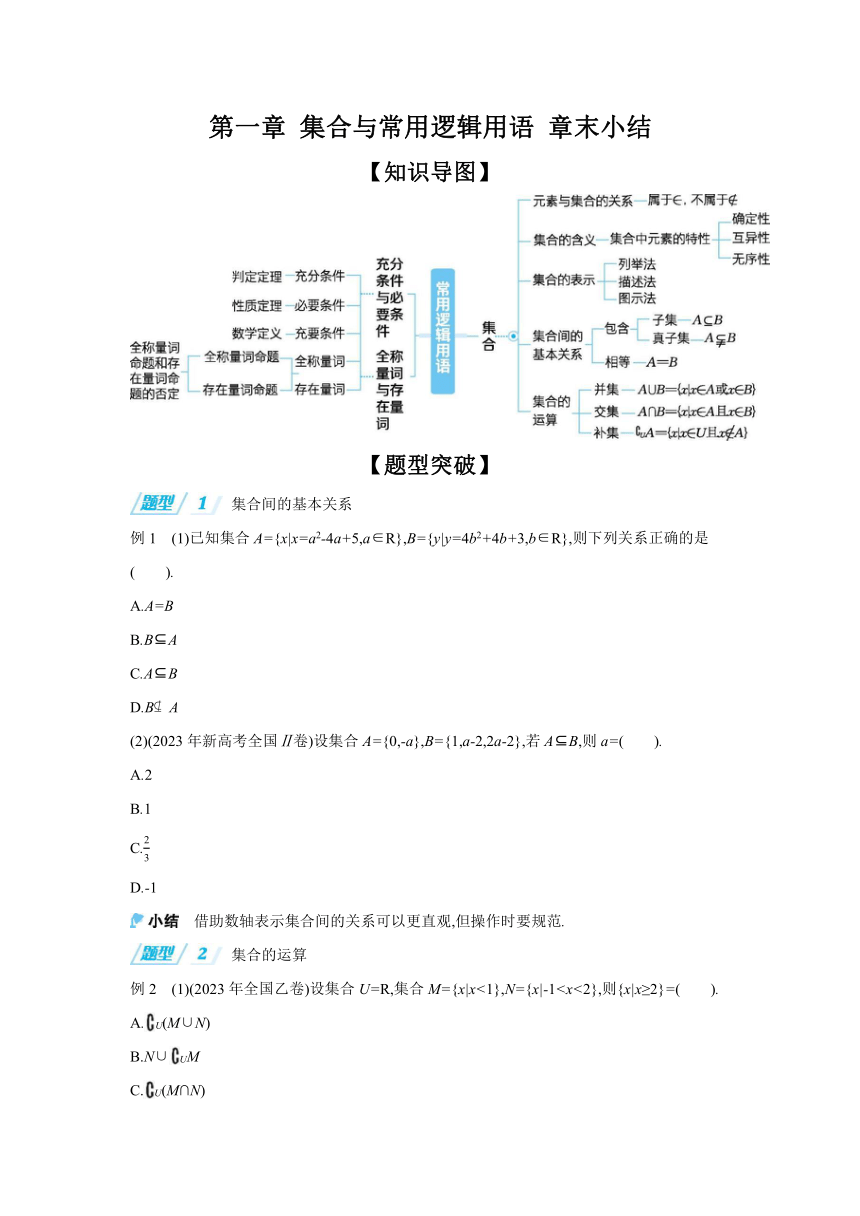
【知识导图】
【题型突破】
集合间的基本关系
例1 (1)已知集合A={x|x=a2-4a+5,a∈R},B={y|y=4b2+4b+3,b∈R},则下列关系正确的是( ).
A.A=B
B.B A
C.A B
D.B A
(2)(2023年新高考全国Ⅱ卷)设集合A={0,-a},B={1,a-2,2a-2},若A B,则a=( ).
A.2
B.1
C.
D.-1
借助数轴表示集合间的关系可以更直观,但操作时要规范.
集合的运算
例2 (1)(2023年全国乙卷)设集合U=R,集合M={x|x<1},N={x|-1A.U(M∪N)
B.N∪UM
C.U(M∩N)
D.M∪UN
(2)(2023年全国甲卷)设全集U=Z,集合M={x|x=3k+1,k∈Z},N={x|x=3k+2,k∈Z},则U(M∪N)=( ).
A.{x|x=3k,k∈Z}
B.{x|x=3k-1,k∈Z}
C.{x|x=3k-2,k∈Z}
D.
集合有交、并、补这三种常见的运算,它是集合中的核心内容.在进行集合的运算时,往往由于运算能力弱或考虑不全面而出错,此时,数轴(或Venn图)是个好帮手,能将复杂问题直观化.在具体应用时要注意检验端点值是否符合题意,以免增解或漏解.
充分条件与必要条件的判定
例3 (1)(2023年北京卷)若xy≠0,则“x+y=0”是“+=-2”的( ).
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
(2)已知集合A={x|-4≤x≤4},B={x|x5”是“A B”的( ).
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
例4 若a,b都是实数,试从①ab=0;②a+b=0;③a·(a2+b2)=0;④ab>0中选出满足下列条件的式子,用序号填空:
(1)使a,b都为0的必要条件是 ;
(2)使a,b都不为0的充分条件是 ;
(3)使a,b至少有一个为0的充要条件是 .
在判定充分条件、必要条件时,要注意既要看由p能否推出q,又要看由q能否推出p,不能顾此失彼.
充分条件与必要条件的应用
例5 已知集合A={x∈R|2x+m<0},B={x∈R|x<-1或x>3}.
(1)是否存在实数m,使得x∈A是x∈B成立的充分条件
(2)是否存在实数m,使得x∈A是x∈B成立的必要条件
充分条件与必要条件的应用技巧
(1)应用:可利用充分性与必要性进行相关问题的求解,特别是求参数的值或取值范围.
(2)求解步骤:先把p,q等价转化,再利用充分条件、必要条件与集合间的包含关系,建立关于参数的不等式(组)进行求解.
全称量词命题与存在量词命题
例6 (1) 命题“ x∈R,x2-2x+1≥0”的否定是( ).
A. x∈R,x2-2x+1≤0
B. x∈R,x2-2x+1≥0
C. x∈R,x2-2x+1<0
D. x∈R,x2-2x+1<0
(2)若命题p: x∈R,x2-2x+m≠0是真命题,则实数m的取值范围是( ).
A.{m|m≥1} B.{m|m>1}
C.{m|m<1} D.{m|m≤1}
1.全称量词命题的否定一定是存在量词命题,存在量词命题的否定一定是全称量词命题.首先改变量词,把全称量词改为存在量词,把存在量词改为全称量词,然后把判断词加以否定.
2.通过写含有量词的命题的否定及利用命题的真假求参数范围等,培养逻辑推理和数学运算素养.
集合的实际应用
例7 某班有36名同学参加数学、物理、化学课外探究小组,每名同学至多参加两个小组,已知参加数学、物理、化学小组的人数分别为26,15,13,同时参加数学和物理小组的有6人,同时参加物理和化学小组的有4人,则同时参加数学和化学小组的有 人.
数学建模是对现实问题进行数学抽象,用数学语言表达问题、用数学方法构建模型解决问题的素养,主要表现在:发现和提出问题,建立和求解模型,检验和完善模型,分析和解决问题.本章中数学建模思想主要体现在集合的实际应用问题中.
【拓展延伸】
集合论的背景
(一)集合论的诞生
集合论是德国著名数学家格奥尔格·康托尔(Cantor, 1845-1918)于19世纪末创立的.他对集合所下的定义是:把若干确定的有区别的(不论是具体的或抽象的)事物合并起来,看作一个整体,就称为一个集合,其中各事物称为该集合的元素.
(二)集合论的发展
到20世纪初,集合论已得到数学家们的认可,他们乐观地认为,从算术公理系统出发,借助集合论的概念,便可以建造起整个数学大厦,但罗素悖论的提出指出了集合论的漏洞.
罗素(B.Russell,1872-1970)构造了一个所有不属于自身(不包含自身作为元素)的集合D,现在问D是否属于D 如果D属于D,那么D满足D的定义,因此D不应属于自身,即D不属于D;另一方面,如果D不属于D,那么D不满足D的定义,因此D应属于自身,即D属于D.这样不论何种情况都存在着矛盾.
这个仅涉及集合和属于两个最基本概念的悖论,如此简单明了,以致根本留不下为集合论漏洞辩解的余地,绝对严密的数学陷入了自相矛盾之中,这就是数学史上的第三次数学危机.危机产生后,众多数学家投入到解决问题的工作中去.1908年,恩斯特·策梅洛(E.Zermelo,1871-1953)提出了公理化集合论,后经改进,形成无矛盾的集合论公理系统,简称ZF公理系统.原本直观的集合概念被建立在严格的公理基础之上,从而避免了悖论的出现,这就是集合论发展的第二个阶段:公理化集合论.
参考答案
第一章章末小结
题型突破·知方法
例1 (1)B (2)B 【解析】(1)A={x|x=(a-2)2+1,a∈R},即A中的元素x≥1;B={y|y=(2b+1)2+2,b∈R},即B中的元素y≥2.故B A.
(2)依题意,有a-2=0或2a-2=0.当a-2=0,即a=2时,A={0,-2},B={1,0,2},不满足A B;当2a-2=0,即a=1时,A={0,-1},B={-1,0,1},满足A B.所以a=1.
例2 (1)A (2)A 【解析】(1)M∪N={x|x<2},所以U(M∪N)={x|x≥2}.故选A.
(2)集合M∪N表示被3除余1或2的整数集,则它在整数集中的补集是恰好被3整除的整数集.故选A.
例3 (1)C (2)A 【解析】(1)(法一)因为xy≠0,且+=-2,
所以x2+y2=-2xy,即x2+y2+2xy=0,即(x+y)2=0,所以x+y=0.
所以“x+y=0”是“+=-2”的充要条件.
(法二)充分性:因为xy≠0,且x+y=0,所以x=-y,
所以+=+=-1-1=-2,所以充分性成立.
必要性:因为xy≠0,且+=-2,
所以x2+y2=-2xy,即x2+y2+2xy=0,即(x+y)2=0,所以x+y=0,所以必要性成立.
所以“x+y=0”是“+=-2”的充要条件.
(2)因为A B a>4,而a>5 a>4,且a>4 a>5,所以“a>5”是“A B”的充分不必要条件.
例4 (1)①②③ (2)④ (3)① 【解析】①ab=0 a=0或b=0,即a,b至少有一个为0;
②a+b=0 a,b互为相反数,则a,b可能均为0,也可能一个为正数一个为负数;
③a(a2+b2)=0 a=0,b为任意实数;
④ab>0 或即a,b同为正数或同为负数.
综上可知,(1)使a,b都为0的必要条件是①②③;
(2)使a,b都不为0的充分条件是④;
(3)使a,b至少有一个为0的充要条件是①.
例5 【解析】由2x+m<0,得x<-.
(1)欲使x∈A是x∈B成立的充分条件,
则只要 {x|x<-1或x>3},则只要-≤-1,即m≥2,
故存在实数m≥2,使x∈A是x∈B成立的充分条件.
(2)欲使x∈A是x∈B成立的必要条件,
则只要 {x|x<-1或x>3},这是不可能的,
故不存在实数m,使x∈A是x∈B成立的必要条件.
例6 (1)C (2)B 【解析】(1)∵命题“ x∈R,x2-2x+1≥0”为全称量词命题,
∴命题的否定为: x∈R,x2-2x+1<0,故选C.
(2)命题p: x∈R,x2-2x+m≠0是真命题,则m≠-(x2-2x),
∵-(x2-2x)=-(x-1)2+1≤1,
∴m>1,
∴实数m的取值范围是{m|m>1}.故选B.
例7 8 【解析】设参加数学、物理、化学小组的人数构成的集合分别为A,B,C,同时参加数学和化学小组的有x人,由题意可得如图所示的Venn图.
由全班共36名同学可得(26-6-x)+6+(15-4-6)+4+(13-4-x)+x=36,解得x=8,即同时参加数学和化学小组的有8人.
【知识导图】
【题型突破】
集合间的基本关系
例1 (1)已知集合A={x|x=a2-4a+5,a∈R},B={y|y=4b2+4b+3,b∈R},则下列关系正确的是( ).
A.A=B
B.B A
C.A B
D.B A
(2)(2023年新高考全国Ⅱ卷)设集合A={0,-a},B={1,a-2,2a-2},若A B,则a=( ).
A.2
B.1
C.
D.-1
借助数轴表示集合间的关系可以更直观,但操作时要规范.
集合的运算
例2 (1)(2023年全国乙卷)设集合U=R,集合M={x|x<1},N={x|-1
B.N∪UM
C.U(M∩N)
D.M∪UN
(2)(2023年全国甲卷)设全集U=Z,集合M={x|x=3k+1,k∈Z},N={x|x=3k+2,k∈Z},则U(M∪N)=( ).
A.{x|x=3k,k∈Z}
B.{x|x=3k-1,k∈Z}
C.{x|x=3k-2,k∈Z}
D.
集合有交、并、补这三种常见的运算,它是集合中的核心内容.在进行集合的运算时,往往由于运算能力弱或考虑不全面而出错,此时,数轴(或Venn图)是个好帮手,能将复杂问题直观化.在具体应用时要注意检验端点值是否符合题意,以免增解或漏解.
充分条件与必要条件的判定
例3 (1)(2023年北京卷)若xy≠0,则“x+y=0”是“+=-2”的( ).
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
(2)已知集合A={x|-4≤x≤4},B={x|x
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
例4 若a,b都是实数,试从①ab=0;②a+b=0;③a·(a2+b2)=0;④ab>0中选出满足下列条件的式子,用序号填空:
(1)使a,b都为0的必要条件是 ;
(2)使a,b都不为0的充分条件是 ;
(3)使a,b至少有一个为0的充要条件是 .
在判定充分条件、必要条件时,要注意既要看由p能否推出q,又要看由q能否推出p,不能顾此失彼.
充分条件与必要条件的应用
例5 已知集合A={x∈R|2x+m<0},B={x∈R|x<-1或x>3}.
(1)是否存在实数m,使得x∈A是x∈B成立的充分条件
(2)是否存在实数m,使得x∈A是x∈B成立的必要条件
充分条件与必要条件的应用技巧
(1)应用:可利用充分性与必要性进行相关问题的求解,特别是求参数的值或取值范围.
(2)求解步骤:先把p,q等价转化,再利用充分条件、必要条件与集合间的包含关系,建立关于参数的不等式(组)进行求解.
全称量词命题与存在量词命题
例6 (1) 命题“ x∈R,x2-2x+1≥0”的否定是( ).
A. x∈R,x2-2x+1≤0
B. x∈R,x2-2x+1≥0
C. x∈R,x2-2x+1<0
D. x∈R,x2-2x+1<0
(2)若命题p: x∈R,x2-2x+m≠0是真命题,则实数m的取值范围是( ).
A.{m|m≥1} B.{m|m>1}
C.{m|m<1} D.{m|m≤1}
1.全称量词命题的否定一定是存在量词命题,存在量词命题的否定一定是全称量词命题.首先改变量词,把全称量词改为存在量词,把存在量词改为全称量词,然后把判断词加以否定.
2.通过写含有量词的命题的否定及利用命题的真假求参数范围等,培养逻辑推理和数学运算素养.
集合的实际应用
例7 某班有36名同学参加数学、物理、化学课外探究小组,每名同学至多参加两个小组,已知参加数学、物理、化学小组的人数分别为26,15,13,同时参加数学和物理小组的有6人,同时参加物理和化学小组的有4人,则同时参加数学和化学小组的有 人.
数学建模是对现实问题进行数学抽象,用数学语言表达问题、用数学方法构建模型解决问题的素养,主要表现在:发现和提出问题,建立和求解模型,检验和完善模型,分析和解决问题.本章中数学建模思想主要体现在集合的实际应用问题中.
【拓展延伸】
集合论的背景
(一)集合论的诞生
集合论是德国著名数学家格奥尔格·康托尔(Cantor, 1845-1918)于19世纪末创立的.他对集合所下的定义是:把若干确定的有区别的(不论是具体的或抽象的)事物合并起来,看作一个整体,就称为一个集合,其中各事物称为该集合的元素.
(二)集合论的发展
到20世纪初,集合论已得到数学家们的认可,他们乐观地认为,从算术公理系统出发,借助集合论的概念,便可以建造起整个数学大厦,但罗素悖论的提出指出了集合论的漏洞.
罗素(B.Russell,1872-1970)构造了一个所有不属于自身(不包含自身作为元素)的集合D,现在问D是否属于D 如果D属于D,那么D满足D的定义,因此D不应属于自身,即D不属于D;另一方面,如果D不属于D,那么D不满足D的定义,因此D应属于自身,即D属于D.这样不论何种情况都存在着矛盾.
这个仅涉及集合和属于两个最基本概念的悖论,如此简单明了,以致根本留不下为集合论漏洞辩解的余地,绝对严密的数学陷入了自相矛盾之中,这就是数学史上的第三次数学危机.危机产生后,众多数学家投入到解决问题的工作中去.1908年,恩斯特·策梅洛(E.Zermelo,1871-1953)提出了公理化集合论,后经改进,形成无矛盾的集合论公理系统,简称ZF公理系统.原本直观的集合概念被建立在严格的公理基础之上,从而避免了悖论的出现,这就是集合论发展的第二个阶段:公理化集合论.
参考答案
第一章章末小结
题型突破·知方法
例1 (1)B (2)B 【解析】(1)A={x|x=(a-2)2+1,a∈R},即A中的元素x≥1;B={y|y=(2b+1)2+2,b∈R},即B中的元素y≥2.故B A.
(2)依题意,有a-2=0或2a-2=0.当a-2=0,即a=2时,A={0,-2},B={1,0,2},不满足A B;当2a-2=0,即a=1时,A={0,-1},B={-1,0,1},满足A B.所以a=1.
例2 (1)A (2)A 【解析】(1)M∪N={x|x<2},所以U(M∪N)={x|x≥2}.故选A.
(2)集合M∪N表示被3除余1或2的整数集,则它在整数集中的补集是恰好被3整除的整数集.故选A.
例3 (1)C (2)A 【解析】(1)(法一)因为xy≠0,且+=-2,
所以x2+y2=-2xy,即x2+y2+2xy=0,即(x+y)2=0,所以x+y=0.
所以“x+y=0”是“+=-2”的充要条件.
(法二)充分性:因为xy≠0,且x+y=0,所以x=-y,
所以+=+=-1-1=-2,所以充分性成立.
必要性:因为xy≠0,且+=-2,
所以x2+y2=-2xy,即x2+y2+2xy=0,即(x+y)2=0,所以x+y=0,所以必要性成立.
所以“x+y=0”是“+=-2”的充要条件.
(2)因为A B a>4,而a>5 a>4,且a>4 a>5,所以“a>5”是“A B”的充分不必要条件.
例4 (1)①②③ (2)④ (3)① 【解析】①ab=0 a=0或b=0,即a,b至少有一个为0;
②a+b=0 a,b互为相反数,则a,b可能均为0,也可能一个为正数一个为负数;
③a(a2+b2)=0 a=0,b为任意实数;
④ab>0 或即a,b同为正数或同为负数.
综上可知,(1)使a,b都为0的必要条件是①②③;
(2)使a,b都不为0的充分条件是④;
(3)使a,b至少有一个为0的充要条件是①.
例5 【解析】由2x+m<0,得x<-.
(1)欲使x∈A是x∈B成立的充分条件,
则只要 {x|x<-1或x>3},则只要-≤-1,即m≥2,
故存在实数m≥2,使x∈A是x∈B成立的充分条件.
(2)欲使x∈A是x∈B成立的必要条件,
则只要 {x|x<-1或x>3},这是不可能的,
故不存在实数m,使x∈A是x∈B成立的必要条件.
例6 (1)C (2)B 【解析】(1)∵命题“ x∈R,x2-2x+1≥0”为全称量词命题,
∴命题的否定为: x∈R,x2-2x+1<0,故选C.
(2)命题p: x∈R,x2-2x+m≠0是真命题,则m≠-(x2-2x),
∵-(x2-2x)=-(x-1)2+1≤1,
∴m>1,
∴实数m的取值范围是{m|m>1}.故选B.
例7 8 【解析】设参加数学、物理、化学小组的人数构成的集合分别为A,B,C,同时参加数学和化学小组的有x人,由题意可得如图所示的Venn图.
由全班共36名同学可得(26-6-x)+6+(15-4-6)+4+(13-4-x)+x=36,解得x=8,即同时参加数学和化学小组的有8人.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
