专题2 有理数及其运算(含答案) 2025-2026学年数学北师大版(2024)七年级上册
文档属性
| 名称 | 专题2 有理数及其运算(含答案) 2025-2026学年数学北师大版(2024)七年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 223.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-08 09:45:03 | ||
图片预览

文档简介
期末复习
专题2 有理数及其运算
考点一 有理数的认识与分类
在0,2.1,-4,-3.2这四个数中,是负分数的是( )
A.0 B.2.1
C.-4 D.-3.2
考点二 数轴的应用
有理数a,b在数轴上对应点的位置如图所示,下列判断正确的是( )
A.|a|<1 B.ab>0
C.a+b>0 D.1-a>1
考点三 相反数与绝对值
[2024·铁西区期末]如图,数轴上点A,B,C,D表示的数分别为a,b,c,d,相邻两点间的距离均为2个单位长度。
(1)若a与c互为相反数,则d=______;
(2)若这四个数中最小数与最大数的和等于10,求a的值。
考点四 有理数的混合运算
计算:
(1)-(-3+5)+32×(1-3);
(2)6×-22+|-3|;
(3)(-1)100×5+(-2)4÷;
(4)÷(-5)。
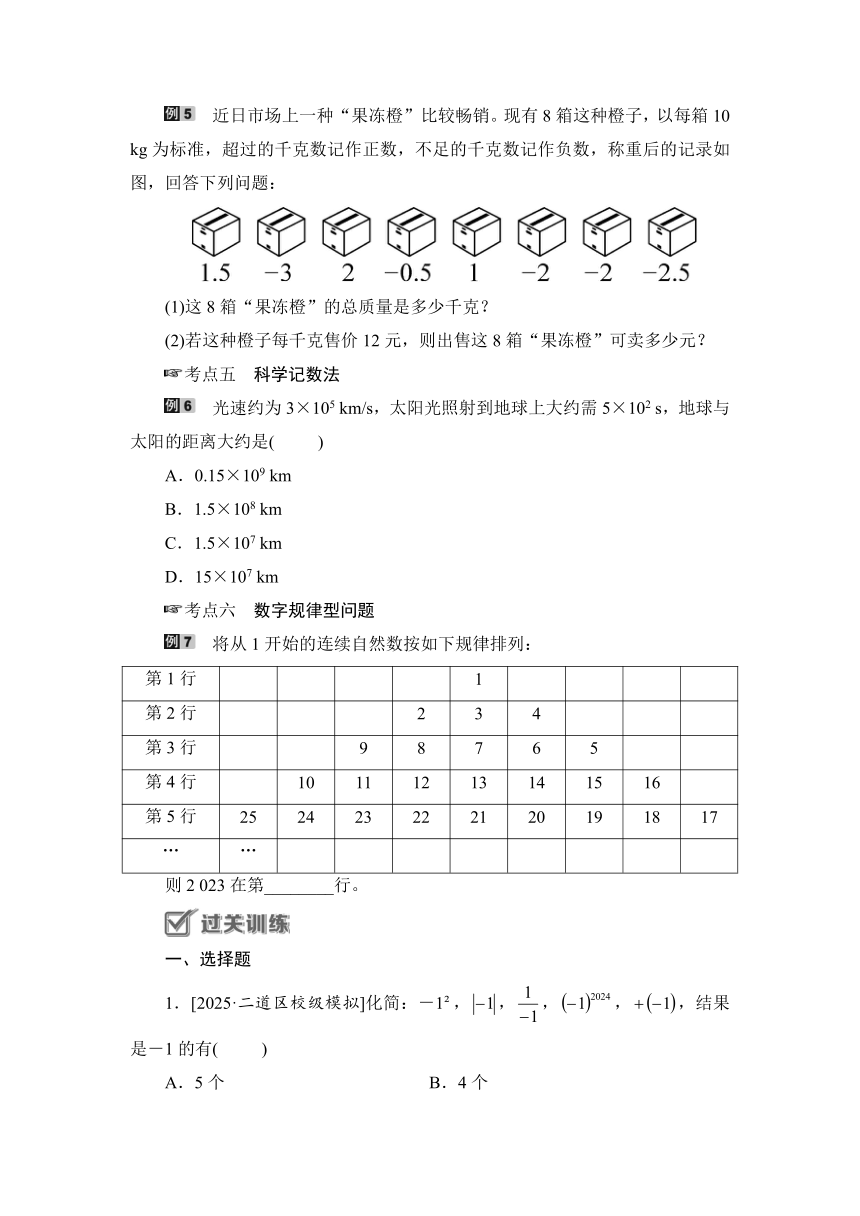
近日市场上一种“果冻橙”比较畅销。现有8箱这种橙子,以每箱10 kg为标准,超过的千克数记作正数,不足的千克数记作负数,称重后的记录如图,回答下列问题:
(1)这8箱“果冻橙”的总质量是多少千克?
(2)若这种橙子每千克售价12元,则出售这8箱“果冻橙”可卖多少元?
考点五 科学记数法
光速约为3×105 km/s,太阳光照射到地球上大约需5×102 s,地球与太阳的距离大约是( )
A.0.15×109 km
B.1.5×108 km
C.1.5×107 km
D.15×107 km
考点六 数字规律型问题
将从1开始的连续自然数按如下规律排列:
第1行 1
第2行 2 3 4
第3行 9 8 7 6 5
第4行 10 11 12 13 14 15 16
第5行 25 24 23 22 21 20 19 18 17
… …
则2 023在第________行。
一、选择题
1.[2025·二道区校级模拟]化简:-1 ,,,,,结果是-1的有( )
A.5个 B.4个
C.3个 D.2个
2.数轴上表示数m和m+2的点到原点的距离相等,则m的值为( )
A.-2 B.2
C.1 D.-1
3.点A在数轴上,点A所对应的数用2a+1表示,且点A到原点的距离等于3,则a的值为( )
A.-2或1 B.-2或2
C.-2 D.1
4.如图,乐乐将-3,-2,-1,0,1,2,3,4,5分别填入九个空格内,使每行、每列、每条对角线上的三个数之和相等,则a-b+c的值为( )
A.-1 B.0
C.1 D.3
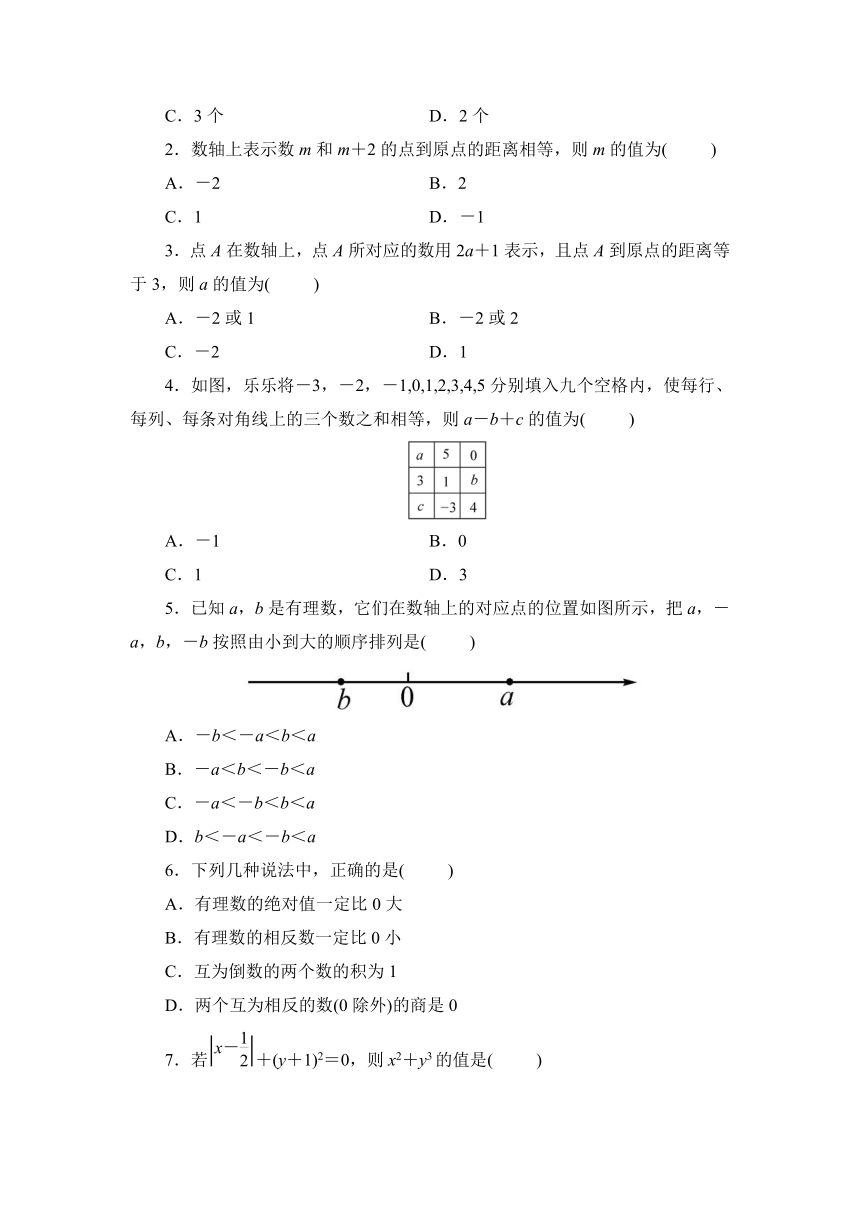
5.已知a,b是有理数,它们在数轴上的对应点的位置如图所示,把a,-a,b,-b按照由小到大的顺序排列是( )
A.-b<-a<b<a
B.-a<b<-b<a
C.-a<-b<b<a
D.b<-a<-b<a
6.下列几种说法中,正确的是( )
A.有理数的绝对值一定比0大
B.有理数的相反数一定比0小
C.互为倒数的两个数的积为1
D.两个互为相反的数(0除外)的商是0
7.若+(y+1)2=0,则x2+y3的值是( )
A. B.
C.- D.-
8.观察下列树枝分杈的规律图,若第n个图树枝数用Yn表示,则Y9-Y4=( )
A.240 B.496
C.528 D.1 008
9.[2024·山东青岛期中]数学符号是数学学科中用来表示数量关系和空间形式的符号系统,它们具有高度的抽象性和简洁性。在数学中,记,,,,…,。则的值为( )
A.-1 B.0
C.1 D.2
二、填空题
10.若有理数a,b,c在数轴上的位置如图所示,则|a-c|-|b+c|可化简为____________。
11.“转化”是一种解决问题的常用策略,有时画图可以帮助我们找到解决问题的方法。例如,借助图1,可以把算式1+3+5+7+9+11转化为62=36。请你观察图2,可以把算式++++转化为___________=_______.
图1 图2
12.如图所示的是一组有规律的图案,第1个图案由4个菱形组成,第2个图案由7个菱形组成……则第5个图案由________个菱形组成。
13.阅读下列运算程序,探究其运算规律:m△n=a,且m△(n+x)=a-x,(m+x)△n=a+3x。若1△1=-2,则1△2=________,2△1=______,20△23=________。
三、解答题
14.计算:
(1)1.25×(-4)-32×;
(2)-14-×[2-(-3)2]。
15.计算:
(1)-÷;
(2)100÷52-14-×12。
16.李师傅在某玩具厂工作,厂里规定每名工人每周要生产某种玩具210个,平均每天生产30个,但由于各种原因,实际每天生产量与计划量相比有出入。下表是李师傅某周的生产情况(超产记为正、不足记为负):
星期 一 二 三 四 五 六 日
生产量/个 +9 -10 -4 +8 -3 +6 0
(1)根据记录的数据可知,李师傅星期三生产玩具________个;本周实际生产玩具________个。
(2)该厂实行“每日计件工资制”:每生产一个玩具可得工资5元,若超额完成每日任务,则超过部分每个另奖励2元;若未完成每日任务,则每少生产一个倒扣3元。问李师傅这一周的工资总额是多少元?
(3)现有“每周计件工资制”:每生产一个玩具可得工资5元,若超额完成每周任务,则超过部分每个另奖2元;若未完成每周任务,则每少生产一个倒扣3元。与(2)中的“每日计件工资制”相比,实行“每_____计件工资制”李师傅的工资更多(填“日”或“周”),多______元。
17.结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示4和1的两点之间的距离是______;表示-3和2的两点之间的距离是______;一般地,数轴上表示数m和数n的两点之间的距离等于|m-n|。如果表示数a和-1的两点之间的距离是3,那么a的值为____________。
(2)若数轴上表示数a的点位于-4与2之间,则|a+4|+|a-2|的值为______。
(3)利用数轴找出所有符合条件的整数点x,使得|x+2|+|x-5|=7,这些点表示的数的和是________。
(4)当a取何值时,|a+3|+|a-1|+|a-4|的值最小?最小值是多少?
扫码看视频
18.【概念学习】
现规定:求若干个相同的有理数(均不等于0)的商的运算叫作除方,比如2÷2÷2,(-3)÷(-3)÷(-3)÷(-3)等,类比有理数的乘方,我们把2÷2÷2写作2③,读作“2的圈3次方”,(-3)÷(-3)÷(-3)÷(-3)写作(-3)④,读作“(-3)的圈4次方”,一般地把____________ (a≠0)写作a,读作“a的圈n次方”。
【初步探究】
(1)直接写出计算结果:3②=______,③=________。
(2)下列关于除方的说法中,错误的有______(在横线上填写序号即可)。
A.任何非零数的圈2次方都等于1
B.任何非零数的圈3次方都等于它的倒数
C.负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数
D.圈n次方等于它本身的数是1或-1
【深入思考】
我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,那么有理数的除方运算如何转化为乘方运算呢?
(3)归纳:请把有理数a(a≠0)的圈n(n≥3)次方写成幂的形式为:a=______。
(4)比较:(-2)⑩______(-4)⑩(填“>”“<”或“=”)。
(5)计算:-1③+142÷①×(-7)⑥-(-48)÷④。
参考答案
【考点归类】
【例1】D 【例2】D
【例3】(1)4 (2)a=2
【例4】(1)-20 (2)-2 (3)-59 (4)-
【例5】(1)74.5 kg。
(2)出售这8箱“果冻橙”可卖894元。
【例6】B 【例7】45
【过关训练】
1.C 2.D 3.A 4.C 5.B 6.C 7.D 8.B 9.B 10.-a-b 11.1- 12.16
13.-3 1 33 14.(1)21 (2)
15.(1) (2)2
16.(1)26 216 (2)李师傅这一周的工资总额是1075元。 (3)周 17
17.(1)3 5 -4或2 (2)6 (3)12 (4)a=1时有最小值,最小值为7。
18.(1)1 -3 (2)D (3) (4)> (5)-
。
专题2 有理数及其运算
考点一 有理数的认识与分类
在0,2.1,-4,-3.2这四个数中,是负分数的是( )
A.0 B.2.1
C.-4 D.-3.2
考点二 数轴的应用
有理数a,b在数轴上对应点的位置如图所示,下列判断正确的是( )
A.|a|<1 B.ab>0
C.a+b>0 D.1-a>1
考点三 相反数与绝对值
[2024·铁西区期末]如图,数轴上点A,B,C,D表示的数分别为a,b,c,d,相邻两点间的距离均为2个单位长度。
(1)若a与c互为相反数,则d=______;
(2)若这四个数中最小数与最大数的和等于10,求a的值。
考点四 有理数的混合运算
计算:
(1)-(-3+5)+32×(1-3);
(2)6×-22+|-3|;
(3)(-1)100×5+(-2)4÷;
(4)÷(-5)。
近日市场上一种“果冻橙”比较畅销。现有8箱这种橙子,以每箱10 kg为标准,超过的千克数记作正数,不足的千克数记作负数,称重后的记录如图,回答下列问题:
(1)这8箱“果冻橙”的总质量是多少千克?
(2)若这种橙子每千克售价12元,则出售这8箱“果冻橙”可卖多少元?
考点五 科学记数法
光速约为3×105 km/s,太阳光照射到地球上大约需5×102 s,地球与太阳的距离大约是( )
A.0.15×109 km
B.1.5×108 km
C.1.5×107 km
D.15×107 km
考点六 数字规律型问题
将从1开始的连续自然数按如下规律排列:
第1行 1
第2行 2 3 4
第3行 9 8 7 6 5
第4行 10 11 12 13 14 15 16
第5行 25 24 23 22 21 20 19 18 17
… …
则2 023在第________行。
一、选择题
1.[2025·二道区校级模拟]化简:-1 ,,,,,结果是-1的有( )
A.5个 B.4个
C.3个 D.2个
2.数轴上表示数m和m+2的点到原点的距离相等,则m的值为( )
A.-2 B.2
C.1 D.-1
3.点A在数轴上,点A所对应的数用2a+1表示,且点A到原点的距离等于3,则a的值为( )
A.-2或1 B.-2或2
C.-2 D.1
4.如图,乐乐将-3,-2,-1,0,1,2,3,4,5分别填入九个空格内,使每行、每列、每条对角线上的三个数之和相等,则a-b+c的值为( )
A.-1 B.0
C.1 D.3
5.已知a,b是有理数,它们在数轴上的对应点的位置如图所示,把a,-a,b,-b按照由小到大的顺序排列是( )
A.-b<-a<b<a
B.-a<b<-b<a
C.-a<-b<b<a
D.b<-a<-b<a
6.下列几种说法中,正确的是( )
A.有理数的绝对值一定比0大
B.有理数的相反数一定比0小
C.互为倒数的两个数的积为1
D.两个互为相反的数(0除外)的商是0
7.若+(y+1)2=0,则x2+y3的值是( )
A. B.
C.- D.-
8.观察下列树枝分杈的规律图,若第n个图树枝数用Yn表示,则Y9-Y4=( )
A.240 B.496
C.528 D.1 008
9.[2024·山东青岛期中]数学符号是数学学科中用来表示数量关系和空间形式的符号系统,它们具有高度的抽象性和简洁性。在数学中,记,,,,…,。则的值为( )
A.-1 B.0
C.1 D.2
二、填空题
10.若有理数a,b,c在数轴上的位置如图所示,则|a-c|-|b+c|可化简为____________。
11.“转化”是一种解决问题的常用策略,有时画图可以帮助我们找到解决问题的方法。例如,借助图1,可以把算式1+3+5+7+9+11转化为62=36。请你观察图2,可以把算式++++转化为___________=_______.
图1 图2
12.如图所示的是一组有规律的图案,第1个图案由4个菱形组成,第2个图案由7个菱形组成……则第5个图案由________个菱形组成。
13.阅读下列运算程序,探究其运算规律:m△n=a,且m△(n+x)=a-x,(m+x)△n=a+3x。若1△1=-2,则1△2=________,2△1=______,20△23=________。
三、解答题
14.计算:
(1)1.25×(-4)-32×;
(2)-14-×[2-(-3)2]。
15.计算:
(1)-÷;
(2)100÷52-14-×12。
16.李师傅在某玩具厂工作,厂里规定每名工人每周要生产某种玩具210个,平均每天生产30个,但由于各种原因,实际每天生产量与计划量相比有出入。下表是李师傅某周的生产情况(超产记为正、不足记为负):
星期 一 二 三 四 五 六 日
生产量/个 +9 -10 -4 +8 -3 +6 0
(1)根据记录的数据可知,李师傅星期三生产玩具________个;本周实际生产玩具________个。
(2)该厂实行“每日计件工资制”:每生产一个玩具可得工资5元,若超额完成每日任务,则超过部分每个另奖励2元;若未完成每日任务,则每少生产一个倒扣3元。问李师傅这一周的工资总额是多少元?
(3)现有“每周计件工资制”:每生产一个玩具可得工资5元,若超额完成每周任务,则超过部分每个另奖2元;若未完成每周任务,则每少生产一个倒扣3元。与(2)中的“每日计件工资制”相比,实行“每_____计件工资制”李师傅的工资更多(填“日”或“周”),多______元。
17.结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示4和1的两点之间的距离是______;表示-3和2的两点之间的距离是______;一般地,数轴上表示数m和数n的两点之间的距离等于|m-n|。如果表示数a和-1的两点之间的距离是3,那么a的值为____________。
(2)若数轴上表示数a的点位于-4与2之间,则|a+4|+|a-2|的值为______。
(3)利用数轴找出所有符合条件的整数点x,使得|x+2|+|x-5|=7,这些点表示的数的和是________。
(4)当a取何值时,|a+3|+|a-1|+|a-4|的值最小?最小值是多少?
扫码看视频
18.【概念学习】
现规定:求若干个相同的有理数(均不等于0)的商的运算叫作除方,比如2÷2÷2,(-3)÷(-3)÷(-3)÷(-3)等,类比有理数的乘方,我们把2÷2÷2写作2③,读作“2的圈3次方”,(-3)÷(-3)÷(-3)÷(-3)写作(-3)④,读作“(-3)的圈4次方”,一般地把____________ (a≠0)写作a,读作“a的圈n次方”。
【初步探究】
(1)直接写出计算结果:3②=______,③=________。
(2)下列关于除方的说法中,错误的有______(在横线上填写序号即可)。
A.任何非零数的圈2次方都等于1
B.任何非零数的圈3次方都等于它的倒数
C.负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数
D.圈n次方等于它本身的数是1或-1
【深入思考】
我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,那么有理数的除方运算如何转化为乘方运算呢?
(3)归纳:请把有理数a(a≠0)的圈n(n≥3)次方写成幂的形式为:a=______。
(4)比较:(-2)⑩______(-4)⑩(填“>”“<”或“=”)。
(5)计算:-1③+142÷①×(-7)⑥-(-48)÷④。
参考答案
【考点归类】
【例1】D 【例2】D
【例3】(1)4 (2)a=2
【例4】(1)-20 (2)-2 (3)-59 (4)-
【例5】(1)74.5 kg。
(2)出售这8箱“果冻橙”可卖894元。
【例6】B 【例7】45
【过关训练】
1.C 2.D 3.A 4.C 5.B 6.C 7.D 8.B 9.B 10.-a-b 11.1- 12.16
13.-3 1 33 14.(1)21 (2)
15.(1) (2)2
16.(1)26 216 (2)李师傅这一周的工资总额是1075元。 (3)周 17
17.(1)3 5 -4或2 (2)6 (3)12 (4)a=1时有最小值,最小值为7。
18.(1)1 -3 (2)D (3) (4)> (5)-
。
同课章节目录
