专题4 基本平面图形(含答案) 2025-2026学年数学北师大版(2024)七年级上册
文档属性
| 名称 | 专题4 基本平面图形(含答案) 2025-2026学年数学北师大版(2024)七年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 245.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-08 09:45:57 | ||
图片预览



文档简介
期末复习
专题4 基本平面图形
考点一 线段、射线、直线的概念
已知线段AB,点P是直线AB上一点,直线上共有3条线段:AB,PA和PB。若其中有一条线段的长度是另一条线段长度的两倍,则称点P是线段AB的“巧分点”,线段AB的“巧分点”的个数是( )
A.3 B.6
C.8 D.9
考点二 线段的计算
如图,直线l上有A,B两点,AB=12 cm,O是线段AB上的一点,OA=2OB。
(1)OA=______cm,OB=______cm。
(2)若C是线段AB上一点(点C不与点A,B重合),且满足AC=CO+CB,求CO的长。
(3)若动点P,Q分别从A,B同时出发,向右运动,点P的速度为2 cm/s,点Q的速度为1 cm/s。设运动时间为t s,当点P与点Q重合时,P,Q两点停止运动。当t为何值时,2OP-OQ=4
考点三 角的计算
计算:
(1)56°18′+72°48′=__________________;
(2)131°28′-51°32′15″=____________________;
(3)12°30′20″×2=_________________;
(4)12°31′21″÷3=___________________。
已知∠AOB=120°,从∠AOB的顶点O引出一条射线OC,射线OC在∠AOB的内部,将射线OC绕点O逆时针旋转60°形成∠COD。
(1)如图1,若∠AOD=90°,比较∠AOC和∠BOD的大小,并说明理由。
(2)作射线OE,射线OE为∠AOD的平分线,设∠AOC=α。
①如图2,当0°<α<60°时,若射线OC恰好平分∠AOE,求∠BOD的度数;
②当α≠60°时,请探究∠COE与∠BOD之间的数量关系。
图1 图2
考点四 与角有关的探究型问题
已知∠AOB=90°,∠COD=80°,OE是∠AOC的平分线。
(1)如图1,当∠AOD=∠AOB时,求∠DOE的度数;
(2)如图2,若OD在∠AOB内部运动,且OF是∠AOD的平分线时,求∠AOE-∠DOF的值;
(3)在(1)的条件下,若射线OP从OE出发绕点O以每秒10°的速度逆时针旋转,射线OQ从OD出发绕点O以每秒6°的速度顺时针旋转,若射线OP,OQ同时开始旋转t s(0<t<23.5)后得到∠COP=∠AOQ,求t的值。
图1 图2
一、选择题
1.下列各式中,角度互化正确的是( )
A.63.5°=63°50′
B.23°12′36″=23.48°
C.18°18′18″=18.33°
D.22.25°=22°15′
2.α,β都是钝角,甲、乙、丙、丁四位同学计算(α+β)的结果依次为50°,26°,72°和90°,其中有正确的结果,则正确的是( )
A.甲 B.乙
C.丙 D.丁
3.若∠C=90°,∠A=25°30′,则∠C-∠A的结果是( )
A.75°30′ B.74°30′
C.65°30′ D.64°30′
4.如图,∠AOD=60°,∠AOB∶∠BOC=1∶4,OD平分∠BOC,则∠AOC的度数为( )
A.20° B.80°
C.100° D.120°
5.时钟的时间是3时30分,时钟面上的时针与分针的夹角是( )
A.90° B.100°
C.75° D.105°
6.如图,在长方形纸片ABCD中,M为边AD的中点,将纸片沿BM,CM折叠,使点A落在点A1处,点D落在点D1处。若∠1=30°,则∠BMC的度数为( )
A.135° B.120°
C.105° D.100°
7.将一个圆分割成三个扇形,它们的圆心角的度数之比为1∶2∶3,则三个扇形中圆心角度数最大的是( )
A.30° B.60°
C.120° D.180°
8.如果线段AB=5 cm,BC=3 cm,且点A,B,C在同一条直线上,那么A,C两点的距离是( )
A.2 cm
B.8 cm
C.2 cm或8 cm
D.以上答案都不正确
二、填空题
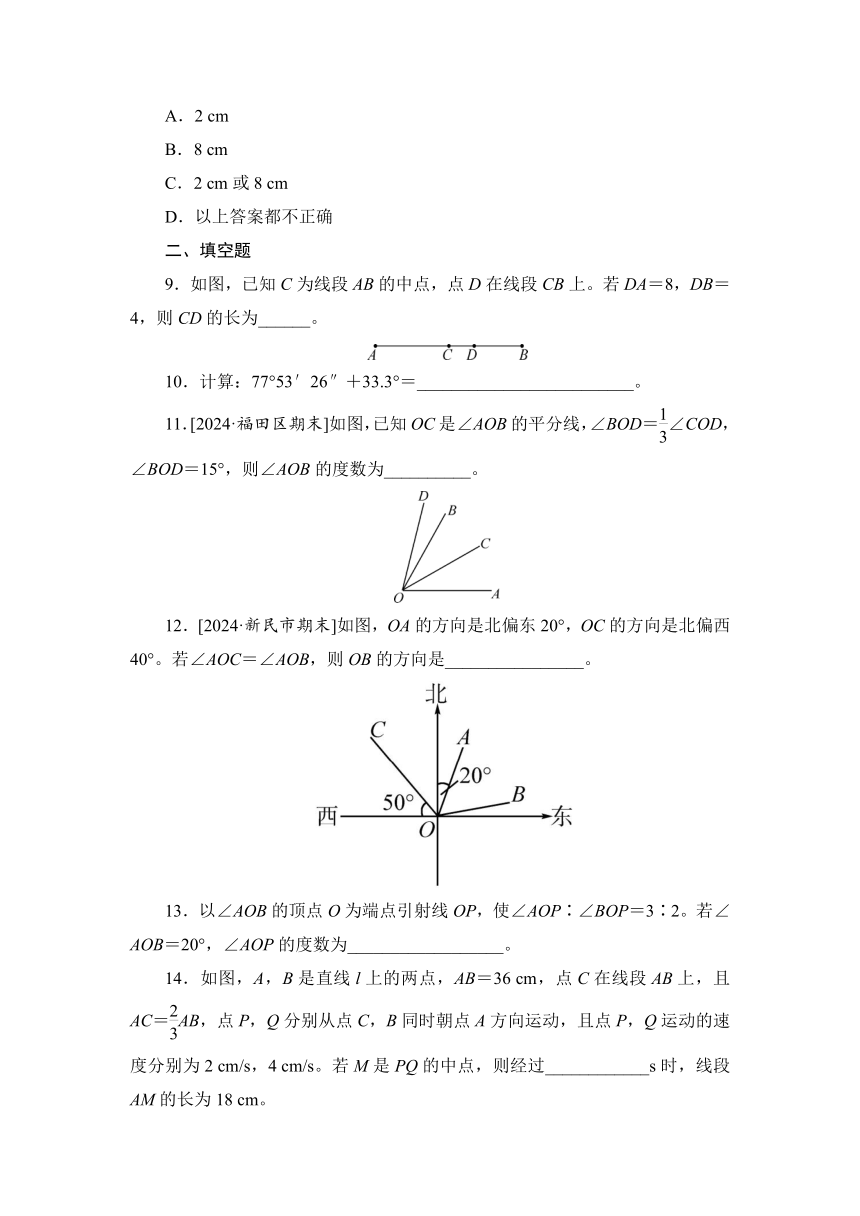
9.如图,已知C为线段AB的中点,点D在线段CB上。若DA=8,DB=4,则CD的长为______。
10.计算:77°53′26″+33.3°=_________________________。
11.[2024·福田区期末]如图,已知OC是∠AOB的平分线,∠BOD=∠COD,∠BOD=15°,则∠AOB的度数为__________。
12.[2024·新民市期末]如图,OA的方向是北偏东20°,OC的方向是北偏西40°。若∠AOC=∠AOB,则OB的方向是________________。
13.以∠AOB的顶点O为端点引射线OP,使∠AOP∶∠BOP=3∶2。若∠AOB=20°,∠AOP的度数为__________________。
14.如图,A,B是直线l上的两点,AB=36 cm,点C在线段AB上,且AC=AB,点P,Q分别从点C,B同时朝点A方向运动,且点P,Q运动的速度分别为2 cm/s,4 cm/s。若M是PQ的中点,则经过____________s时,线段AM的长为18 cm。
三、解答题
15.阅读材料:用尺规作图要求作线段AB等于线段a时,小明的具体作法如下:
已知:线段a,如图1。
求作:线段AB,使得线段AB=a。
解:作图步骤如下:
①作射线AM;
②用圆规在射线AM上截取AB=a,如图2。
∴线段AB为所求作的线段。
解决下列问题:
已知:线段b,如图3。
(1)请你依照小明的作法,在图2中的射线AB上作线段BD,使BD=b;(不要求写作法和结论,保留作图痕迹)
(2)在(1)的条件下,取AD的中点E,若AB=3,BD=2,求线段BE的长。
图1 图2 图3
16.将直角三角板MON(∠MON=90°)的直角顶点O放在直线AB上,过点O作射线OC,使∠BOC=62°。
(1)如图1,当三角板MON的一边ON与射线OB重合时,∠MOC的度数为__________。
(2)将三角板MON绕点O逆时针转动,
①如图2,当OC平分∠MOB时,求∠BON的度数;
②如图3,当∠NOC=∠AOM时,求∠NOC的度数。
图1 图2 图3
17.已知O为直线AB上一点,过点O向直线AB上方引两条射线OC,OD,且OC平分∠AOD。
(1)请在图1中∠BOD的内部画一条射线OE,使得OE平分∠BOD,并求此时∠COE的度数。
(2)如图2,若在∠BOD内部画的射线OE,恰好使得∠BOE=3∠DOE,且∠COE=70°,求此时∠BOE的度数。
图1 图2
18.如图,已知直线l上有两条可以左右移动的线段:AB=m,CD=n,且m,n满足|m-4|+(n-8)2=0,M,N分别为AB,CD的中点。
(1)求线段AB,CD的长。
(2)线段AB以每秒4个单位长度的速度向右运动,同时线段CD以每秒1个单位长度的速度向右运动。若运动6 s后,MN=4,求此时线段BC的长。
(3)若BC=24,将线段CD固定不动,线段AB以每秒4个单位长度的速度向右运动,在线段AB向右运动的某一个时间段t内,始终有MN+AD为定值。求出这个定值,并直接写出t在哪一个时间段内。
19.[2024秋·沈阳期中]如果有两个点在由两条有公共端点的线段组成的一条折线上,且把这条折线分成长度相等的三部分,那么这两个点依次叫作这条折线的“折点”和“折点”。如图,点M和N 分别是折线A-B-C的“折点”和“折点”。
(1)当AB=BC时,点M与点 重合;
(2)当AB>BC时,若点D为线段AB的中点,BD=8,CN=6,求BN的长;
(3)若点D在线段BC上,且CD=BC,BD=a,CN =b,求BM
的长(用含a,b的代数式表示)。
20.(1)如图1,已知C,D为线段AB上两点,且AB=4AD=5BC,M,N分别是线段AC和BD的中点。若线段AB=20 cm,则线段AD=______cm,BC=______cm,MN=__________cm。
(2)已知OC,OD为从∠AOB顶点发出的两条射线,∠AOB=5∠BOC且∠AOB=120°,射线OM和射线ON分别平分∠AOC,∠BOD。
①如图2,若OC,OD均为∠AOB内的两条射线,且∠AOB=4∠AOD,求∠MON的度数;
②如图3,若OC为∠AOB外的一条射线,且∠MON=20°,则∠AOD的度数为__________________。
图1 图2 图3
21.已知O为直线AD上的一点,以O为顶点作∠COE=90°,射线OF平分∠AOE。
(1)如图1,若∠DOE=54°,则∠AOC=__________,∠COF=__________;
(2)若将∠COE绕点O旋转至图2的位置,射线OF仍然平分∠AOE,请写出∠COF与∠DOE之间的数量关系,并说明理由;
(3)若将∠COE绕点O旋转至图3的位置,射线OF仍然平分∠AOE,求2∠COF+∠DOE的度数。
图1 图2 图3
参考答案
【考点归类】
【例1】D
【例2】(1)8 4 (2)CO的长是 cm。
(3)当t的值为1.6或8时,2OP-OQ=4。
【例3】(1)129°6′ (2)79°55′45″ (3)25°40″ (4)4°10′27″
【例4】(1)∠AOC=∠BOD。理由略。
(2)①∠BOD=40°
②∠COE=∠BOD
【例5】(1)∠DOE=25°
(2)∠AOE-∠DOF=40°
(3)t的值为或。
【过关训练】
1.D 2.B 3.D 4.C 5.C 6.C 7.D 8.C 9.2 10.111°11′26″ 11.60° 12.北偏东80° 13.12°或60° 14.4或16
15.(1)略
(2)BE的长为0.5或2.5。
16.(1)28° (2)①∠BON=34° ②∠NOC=7°
17.(1)画图略,∠COE=90°
(2)∠BOE=60°
18.(1)AB=4,CD=8。
(2)BC的长为16或8。
(3)当7.5≤t≤9时,MN+AD为定值6。
19.(1)B (2)4 (3)或
20.(1)5 4 4.5 (2)①∠MON=27° ②16°或64°
21.(1)36° 27° (2)∠COF=∠DOE。理由略。 (3)360°
。
专题4 基本平面图形
考点一 线段、射线、直线的概念
已知线段AB,点P是直线AB上一点,直线上共有3条线段:AB,PA和PB。若其中有一条线段的长度是另一条线段长度的两倍,则称点P是线段AB的“巧分点”,线段AB的“巧分点”的个数是( )
A.3 B.6
C.8 D.9
考点二 线段的计算
如图,直线l上有A,B两点,AB=12 cm,O是线段AB上的一点,OA=2OB。
(1)OA=______cm,OB=______cm。
(2)若C是线段AB上一点(点C不与点A,B重合),且满足AC=CO+CB,求CO的长。
(3)若动点P,Q分别从A,B同时出发,向右运动,点P的速度为2 cm/s,点Q的速度为1 cm/s。设运动时间为t s,当点P与点Q重合时,P,Q两点停止运动。当t为何值时,2OP-OQ=4
考点三 角的计算
计算:
(1)56°18′+72°48′=__________________;
(2)131°28′-51°32′15″=____________________;
(3)12°30′20″×2=_________________;
(4)12°31′21″÷3=___________________。
已知∠AOB=120°,从∠AOB的顶点O引出一条射线OC,射线OC在∠AOB的内部,将射线OC绕点O逆时针旋转60°形成∠COD。
(1)如图1,若∠AOD=90°,比较∠AOC和∠BOD的大小,并说明理由。
(2)作射线OE,射线OE为∠AOD的平分线,设∠AOC=α。
①如图2,当0°<α<60°时,若射线OC恰好平分∠AOE,求∠BOD的度数;
②当α≠60°时,请探究∠COE与∠BOD之间的数量关系。
图1 图2
考点四 与角有关的探究型问题
已知∠AOB=90°,∠COD=80°,OE是∠AOC的平分线。
(1)如图1,当∠AOD=∠AOB时,求∠DOE的度数;
(2)如图2,若OD在∠AOB内部运动,且OF是∠AOD的平分线时,求∠AOE-∠DOF的值;
(3)在(1)的条件下,若射线OP从OE出发绕点O以每秒10°的速度逆时针旋转,射线OQ从OD出发绕点O以每秒6°的速度顺时针旋转,若射线OP,OQ同时开始旋转t s(0<t<23.5)后得到∠COP=∠AOQ,求t的值。
图1 图2
一、选择题
1.下列各式中,角度互化正确的是( )
A.63.5°=63°50′
B.23°12′36″=23.48°
C.18°18′18″=18.33°
D.22.25°=22°15′
2.α,β都是钝角,甲、乙、丙、丁四位同学计算(α+β)的结果依次为50°,26°,72°和90°,其中有正确的结果,则正确的是( )
A.甲 B.乙
C.丙 D.丁
3.若∠C=90°,∠A=25°30′,则∠C-∠A的结果是( )
A.75°30′ B.74°30′
C.65°30′ D.64°30′
4.如图,∠AOD=60°,∠AOB∶∠BOC=1∶4,OD平分∠BOC,则∠AOC的度数为( )
A.20° B.80°
C.100° D.120°
5.时钟的时间是3时30分,时钟面上的时针与分针的夹角是( )
A.90° B.100°
C.75° D.105°
6.如图,在长方形纸片ABCD中,M为边AD的中点,将纸片沿BM,CM折叠,使点A落在点A1处,点D落在点D1处。若∠1=30°,则∠BMC的度数为( )
A.135° B.120°
C.105° D.100°
7.将一个圆分割成三个扇形,它们的圆心角的度数之比为1∶2∶3,则三个扇形中圆心角度数最大的是( )
A.30° B.60°
C.120° D.180°
8.如果线段AB=5 cm,BC=3 cm,且点A,B,C在同一条直线上,那么A,C两点的距离是( )
A.2 cm
B.8 cm
C.2 cm或8 cm
D.以上答案都不正确
二、填空题
9.如图,已知C为线段AB的中点,点D在线段CB上。若DA=8,DB=4,则CD的长为______。
10.计算:77°53′26″+33.3°=_________________________。
11.[2024·福田区期末]如图,已知OC是∠AOB的平分线,∠BOD=∠COD,∠BOD=15°,则∠AOB的度数为__________。
12.[2024·新民市期末]如图,OA的方向是北偏东20°,OC的方向是北偏西40°。若∠AOC=∠AOB,则OB的方向是________________。
13.以∠AOB的顶点O为端点引射线OP,使∠AOP∶∠BOP=3∶2。若∠AOB=20°,∠AOP的度数为__________________。
14.如图,A,B是直线l上的两点,AB=36 cm,点C在线段AB上,且AC=AB,点P,Q分别从点C,B同时朝点A方向运动,且点P,Q运动的速度分别为2 cm/s,4 cm/s。若M是PQ的中点,则经过____________s时,线段AM的长为18 cm。
三、解答题
15.阅读材料:用尺规作图要求作线段AB等于线段a时,小明的具体作法如下:
已知:线段a,如图1。
求作:线段AB,使得线段AB=a。
解:作图步骤如下:
①作射线AM;
②用圆规在射线AM上截取AB=a,如图2。
∴线段AB为所求作的线段。
解决下列问题:
已知:线段b,如图3。
(1)请你依照小明的作法,在图2中的射线AB上作线段BD,使BD=b;(不要求写作法和结论,保留作图痕迹)
(2)在(1)的条件下,取AD的中点E,若AB=3,BD=2,求线段BE的长。
图1 图2 图3
16.将直角三角板MON(∠MON=90°)的直角顶点O放在直线AB上,过点O作射线OC,使∠BOC=62°。
(1)如图1,当三角板MON的一边ON与射线OB重合时,∠MOC的度数为__________。
(2)将三角板MON绕点O逆时针转动,
①如图2,当OC平分∠MOB时,求∠BON的度数;
②如图3,当∠NOC=∠AOM时,求∠NOC的度数。
图1 图2 图3
17.已知O为直线AB上一点,过点O向直线AB上方引两条射线OC,OD,且OC平分∠AOD。
(1)请在图1中∠BOD的内部画一条射线OE,使得OE平分∠BOD,并求此时∠COE的度数。
(2)如图2,若在∠BOD内部画的射线OE,恰好使得∠BOE=3∠DOE,且∠COE=70°,求此时∠BOE的度数。
图1 图2
18.如图,已知直线l上有两条可以左右移动的线段:AB=m,CD=n,且m,n满足|m-4|+(n-8)2=0,M,N分别为AB,CD的中点。
(1)求线段AB,CD的长。
(2)线段AB以每秒4个单位长度的速度向右运动,同时线段CD以每秒1个单位长度的速度向右运动。若运动6 s后,MN=4,求此时线段BC的长。
(3)若BC=24,将线段CD固定不动,线段AB以每秒4个单位长度的速度向右运动,在线段AB向右运动的某一个时间段t内,始终有MN+AD为定值。求出这个定值,并直接写出t在哪一个时间段内。
19.[2024秋·沈阳期中]如果有两个点在由两条有公共端点的线段组成的一条折线上,且把这条折线分成长度相等的三部分,那么这两个点依次叫作这条折线的“折点”和“折点”。如图,点M和N 分别是折线A-B-C的“折点”和“折点”。
(1)当AB=BC时,点M与点 重合;
(2)当AB>BC时,若点D为线段AB的中点,BD=8,CN=6,求BN的长;
(3)若点D在线段BC上,且CD=BC,BD=a,CN =b,求BM
的长(用含a,b的代数式表示)。
20.(1)如图1,已知C,D为线段AB上两点,且AB=4AD=5BC,M,N分别是线段AC和BD的中点。若线段AB=20 cm,则线段AD=______cm,BC=______cm,MN=__________cm。
(2)已知OC,OD为从∠AOB顶点发出的两条射线,∠AOB=5∠BOC且∠AOB=120°,射线OM和射线ON分别平分∠AOC,∠BOD。
①如图2,若OC,OD均为∠AOB内的两条射线,且∠AOB=4∠AOD,求∠MON的度数;
②如图3,若OC为∠AOB外的一条射线,且∠MON=20°,则∠AOD的度数为__________________。
图1 图2 图3
21.已知O为直线AD上的一点,以O为顶点作∠COE=90°,射线OF平分∠AOE。
(1)如图1,若∠DOE=54°,则∠AOC=__________,∠COF=__________;
(2)若将∠COE绕点O旋转至图2的位置,射线OF仍然平分∠AOE,请写出∠COF与∠DOE之间的数量关系,并说明理由;
(3)若将∠COE绕点O旋转至图3的位置,射线OF仍然平分∠AOE,求2∠COF+∠DOE的度数。
图1 图2 图3
参考答案
【考点归类】
【例1】D
【例2】(1)8 4 (2)CO的长是 cm。
(3)当t的值为1.6或8时,2OP-OQ=4。
【例3】(1)129°6′ (2)79°55′45″ (3)25°40″ (4)4°10′27″
【例4】(1)∠AOC=∠BOD。理由略。
(2)①∠BOD=40°
②∠COE=∠BOD
【例5】(1)∠DOE=25°
(2)∠AOE-∠DOF=40°
(3)t的值为或。
【过关训练】
1.D 2.B 3.D 4.C 5.C 6.C 7.D 8.C 9.2 10.111°11′26″ 11.60° 12.北偏东80° 13.12°或60° 14.4或16
15.(1)略
(2)BE的长为0.5或2.5。
16.(1)28° (2)①∠BON=34° ②∠NOC=7°
17.(1)画图略,∠COE=90°
(2)∠BOE=60°
18.(1)AB=4,CD=8。
(2)BC的长为16或8。
(3)当7.5≤t≤9时,MN+AD为定值6。
19.(1)B (2)4 (3)或
20.(1)5 4 4.5 (2)①∠MON=27° ②16°或64°
21.(1)36° 27° (2)∠COF=∠DOE。理由略。 (3)360°
。
同课章节目录
