2.位置 (含答案)(同步练习)人教版五年级上册
文档属性
| 名称 | 2.位置 (含答案)(同步练习)人教版五年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 559.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 08:56:24 | ||
图片预览


文档简介
2.位置 练习(含答案)
一、单选题
1.同一间教室,聪聪坐在教室的第2列、第5排,用数对(2,5)表示,如果用数对(a,3)表示明明在教室里的座位,那么下列说法正确的是( )。
A.明明的位置不可能在第3列 B.明明的位置不可能在第3排
C.明明的位置一定在第3排 D.明明的位置一定在第3列
2.大新坐在第3排第4列,可以用(4,3)表示.小刚坐在第5排第1列,表示为( )。
A.(4,5) B.(5,1) C.(1,5)
3.如下图所示, 长方形ABCD的顶点 D用数对表示是 (10, 5),顶点B用数对表示是(2,1),那么顶点C 可以用数对表示为( )。
A.(10, 1) B.(1, 10) C.(5, 2) D.(2, 5)
4. 小丽参加团体操比赛,她的位置用数对表示是(3,8),如果这时的方队是一个正方形,参加团体操比赛的至少有( )人。
A.9 B.24 C.64 D.36
5.下列数对中,( )所表示的位置与数对(3,4)所表示的位置距离最近。
A.(4,1) B.(5,5) C.(2,3) D.(1,4)
6. 在一幅图上,如果A 点用数对表示为(1,5),B点用数对表示为(1,1),C点用数对表示为(3,1),那么三角形ABC一定是( )三角形。
A.锐角 B.钝角 C.直角 D.等腰
7. 在平面图上,点A和点B(6,2)在同一行,与点C(2,7)在同一列,点A 的位置用数对表示是( )。
A.(2,7) B.(2,2) C.(6,2) D.(6,7)
8.如图,有一张方格纸,每个小方格的边长是1 cm,上面堆叠着若干个相同的小正方体。如果小正方体甲的位置用(1,1,1)表示,小正方体乙的位置用(5,2,2)表示,那么小正方体丙的位置可以用( )表示。
A.(2,3,6) B.(2,3,5) C.(3,2,5) D.(3,2,6)
9. 下面的说法中,正确的是 ( )。
A.一个数对只能确定一个位置
B.循环小数都是无限小数,无限小数都是循环小数
C.一个数除以0.1相当于把这个数缩小到原来的
D.两个小数相除,商一定比1小
10. 新情境·传统文化中国象棋是中国棋文化,也是中华民族的文化瑰宝。 “马行日,象飞田”是人们熟知的象棋口诀,如图是中国象棋的一部分。 “马”下一步可能走到的位置是 ( )。
A.(2, 3) B.(3,3) C.(4, 1) D.(4,3)
二、填空题
11.五(1)班教室的座位共有8列,每列座位同样多,且全部坐满。第8列倒数第二位同学的位置用数对表示是(8,5),五(1)班共有学生 人。
12. 张亮坐在教室的第3列第5行,用数对(3,5)表示;赵雪坐在教室的第6列第1行,用数对( , )表示;李明的座位号用数对(5,3)表示,他坐在教室的第 列第 行。
13.数对(x,8)和数对(y,8)在同一 中;数对(6,m)和数对(6,n)在同一 中。(填“列”或“行”)
14.刘兵的位置用数对表示是(3,6),他正后方第一个同学的位置是( , )。
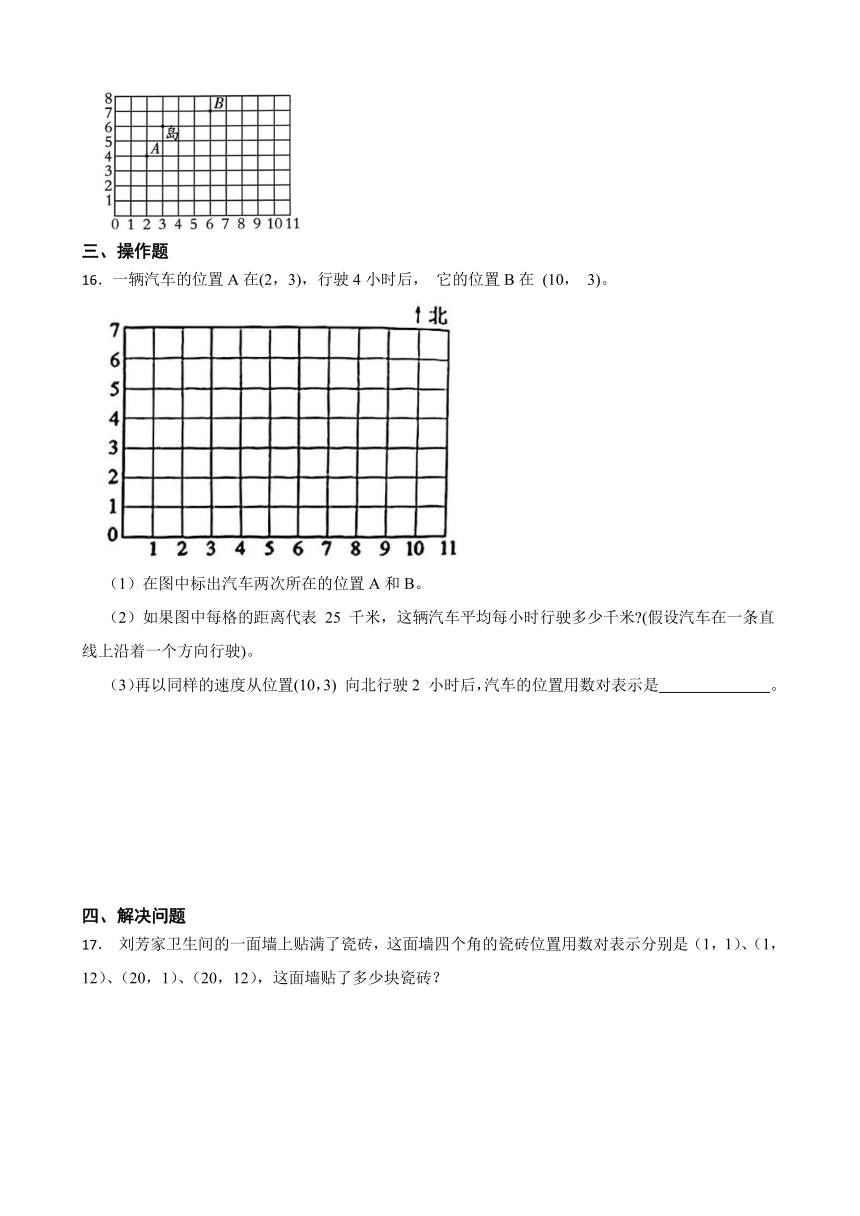
15.如图,A、B两艘海监船正在某岛附近巡逻,如果这个岛的位置用(3,6)表示,那么海监船A 的位置可表示为( , ),海监船B的位置可表示为( , )。
三、操作题
16.一辆汽车的位置A在(2,3),行驶4小时后, 它的位置B在 (10, 3)。
(1)在图中标出汽车两次所在的位置A和B。
(2)如果图中每格的距离代表 25 千米,这辆汽车平均每小时行驶多少千米 (假设汽车在一条直线上沿着一个方向行驶)。
(3)再以同样的速度从位置(10,3) 向北行驶2 小时后,汽车的位置用数对表示是 。
四、解决问题
17. 刘芳家卫生间的一面墙上贴满了瓷砖,这面墙四个角的瓷砖位置用数对表示分别是(1,1)、(1,12)、(20,1)、(20,12),这面墙贴了多少块瓷砖?
18.北京时间 2024 年1月 17 日 22时27 分,搭载天舟七号货运飞船的长征七号遥八运载火箭,在中国文昌航天发射场点火发射,发射取得圆满成功。某科技实验小学的同学们排成一个方阵观看现场直播,刘亚宁在正中间,她的位置可以用数对(8,8)表示,整个方阵一共有多少名同学在观看现场直播?
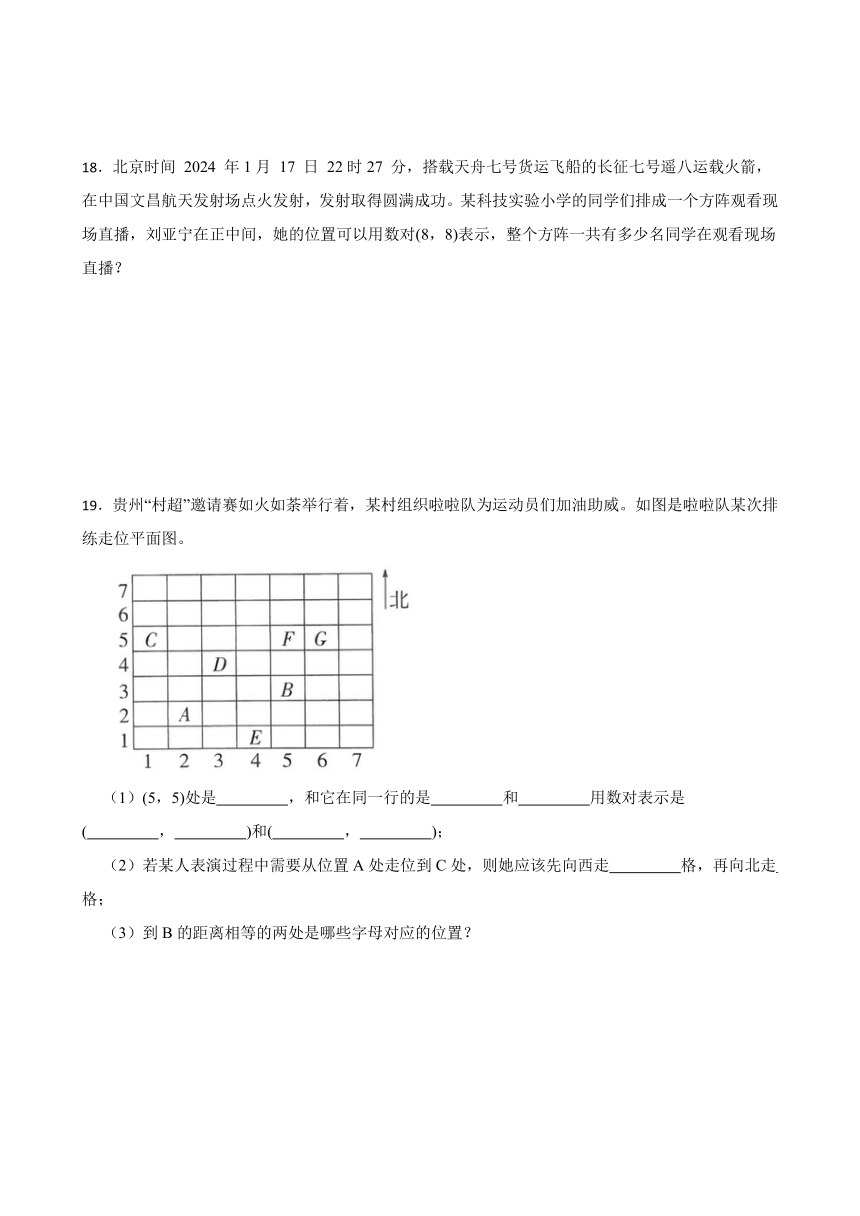
19.贵州“村超”邀请赛如火如荼举行着,某村组织啦啦队为运动员们加油助威。如图是啦啦队某次排练走位平面图。
(1)(5,5)处是 ,和它在同一行的是 和 用数对表示是( , )和( , );
(2)若某人表演过程中需要从位置A处走位到C处,则她应该先向西走 格,再向北走 格;
(3)到B的距离相等的两处是哪些字母对应的位置?
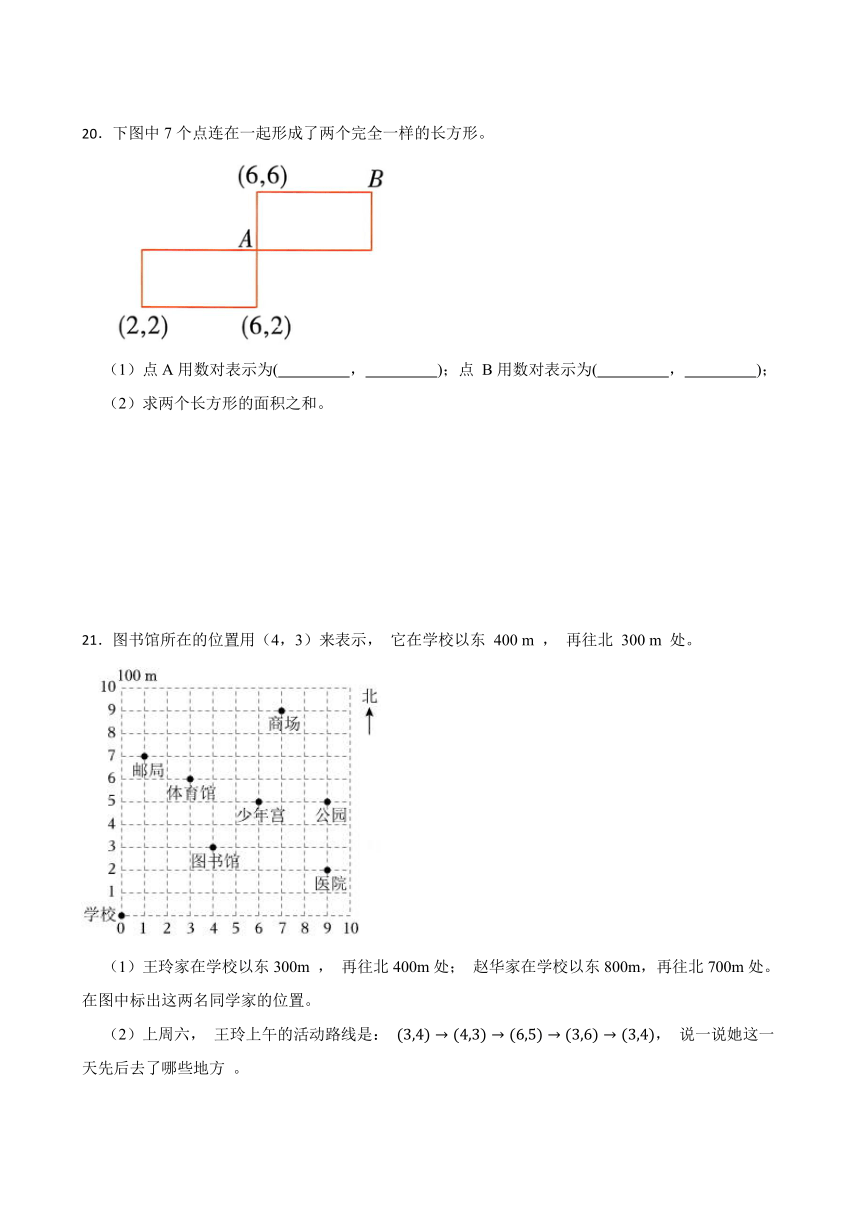
20.下图中7个点连在一起形成了两个完全一样的长方形。
(1)点A用数对表示为( , );点 B用数对表示为( , );
(2)求两个长方形的面积之和。
21.图书馆所在的位置用(4,3)来表示, 它在学校以东 400 m , 再往北 300 m 处。
(1)王玲家在学校以东300m , 再往北400m处; 赵华家在学校以东800m,再往北700m处。在图中标出这两名同学家的位置。
(2)上周六, 王玲上午的活动路线是: , 说一说她这一天先后去了哪些地方 。
答案解析部分
1.C
解:第2列、第5排,用数对(2,5)表示,则数对(a,3)表示第a列,第3排。
故答案为:C。
用数对表示位置的方法是:第一个数字表示列,第二个数字表示行,中间用“,”隔开。
2.C
解:小刚坐在第5排第1列,表示为(1,5) 。
故答案为:C。
小刚坐在第5排第1列,要把列放在前面,排数放在后面,表示为(1,5) 。
3.A
解:顶点C与D同列,与B同行,点C表示为(10,1)。
故答案为:A。
数对中第一个数表示列,第二个数表示行。根据C与D同列判断C在10列,根据C与B同行判断C在1行。
4.C
解:根据题目给出的数对(3,8),可以确定小丽在第3列第8行。
由于方队是一个正方形,所以行数和列数应该相等。
根据小丽位置的信息方队至少有8行8列。
由于方队有8行8列,所以总人数为8×8=64人。
故答案为:64
首先,根据题目给出的小丽的位置数对(3,8),可以确定她在第3列第8行。由于方队是一个正方形,行数和列数应该相等。因此,方队至少有8行8列。最后,通过计算8行8列的方队总人数,可以得到参加团体操表演的至少人数。
5.C
解:A.(4,1)与数对(3,4)所表示的位置有3列的距离,有4行的距离,所以不是最近的位置。
B.(5,5)与数对(3,4)所表示的位置有2列的距离,有1行的距离,所以不是最近的位置。
C.(2,3)与数对(3,4)所表示的位置有1列的距离,有1行的距离,所以是最近的位置。
D.(1,4)与数对(3,4)所表示的位置有2列的距离,有0行的距离,所以不是最近的位置。
故答案为:C
根据数对表示物体位置的方法,数对(3,4)表示的位置在第3列第4行,与它在同一行的是(1,4),然后计算与数对(3,4)所表示的位置距离的远近,进而判断即可。本题考查用数对表示位置,解答本题的关键是掌握用数对表示位置的方法。
6.C
解:点A和点B在同一列,点B和点C在同一行,所以三角形ABC一定是直角三角形。
故答案为:C
用数对表示位置时,前一个数表示第几列,后一个数表示第几行。当两个数对第一个数相同时,说明在同一列;当两个数对第二个数相同时,说明在同一行。本题考查用数对表示位置,解答本题的关键是掌握用数对表示位置的方法。
7.B
解:点A和点B(6,2)在同一行,所以点A是在第2行;点A与点C(2,7)在同一列,所以点A是在第2列;所以A的位置是(2,2)。
故答案为:B
数对表示位置的方法是:第一个数字表示列,第二个数字表示行,由此即可解答。此题考查了数对表示位置的方法的灵活应用
8.B
解:观察小正方体甲和乙的表示方法,可知第1 个数表示小正方体所在的列数,第2个数表示小正方体所在的行数,第3个数表示小正方体所在的层数。小正方体丙在第2列,第3行,第5层,因此表示为(2,3,5)。
故答案为:B
本题考查的是空间坐标系中的位置确定问题。类似于三维坐标系的定位方法,题目要求确定小正方体丙的位置。给定的坐标系统以小方格的边长为单位,每个坐标表示在方格纸上的x(水平)、y(垂直)和z(高)方向上的位置。题目给出了甲、乙两小正方体的位置,要求根据相同的方法确定丙的位置。
9.A
解:A项:一个数对确定了列数和行数,则只能确定一个位置,原题干说法正确;
B项:循环小数都是无限小数,无限小数可能是循环小数,也可能是无限不循环小数,原题干说法错误;
C项:一个数除以0.1相当于把这个数扩大到原来的 10(0除外),原题干说法错误;
D项:两个小数相除,商可能大于、小于或者等于1,原题干说法错误。
故答案为:A。
A项:用数对表示位置时,前面一个数表示第几列,后面一个数表示第几行;列数一般从左往右数,行数一般从前往后数;
B项:循环小数的位数是无限的,所以一定是无限小数;但无限小数可能是循环小数,也可能是无限不循环小数,所以无限小数不一定都是循环小数;
C项:一个数除以0.1相当于把这个数扩大到原来的 10(0除外);
D项:一个数(0和负数除外)除以小于1的数,所得的商大于原来的数;反之,商小于原来的数;一个数(0和负数除外)乘小于1的数,所得的积小于原来的数,反之,积大于原来的数。一个数乘1还得原数。
10.B
解:“马”下一步可能走到的位置是(1,3)或者(3,3)。
故答案为:B。
用数对表示位置时,前面一个数表示第几列,后面一个数表示第几行;列数一般从左往右数,行数一般从前往后数。
11.48
解:第8列倒数第二位同学的位置用数对表示是(8,5),说明第8列最后一位同学的位置用数对表示是(8,6),即五(1)班教室的座位共有8列6行,8×6=48(人),五(1)班共有学生48人。
故答案为:48。
用数对表示位置时,前面一个数表示第几列,后面一个数表示第几行;列数一般从左往右数,行数一般从前往后数,总人数=列数×行数。
12.6;1;5;3
解:根据题意,可得
张亮的座位用数对(3,5)表示,这说明张亮坐在教室的第3列第5行。
赵雪坐在教室的第6列第1行,因此赵雪的座位数对为(6,1)。
对于李明的座位,数对是(5,3),则表明李明坐在教室的第5列第3行。
故答案为:6;1;5;3
数对中左边的数为列,右边的数为行。
13.行;列
解:(x,8)和数对(y,8) 中,8=8,即在同一行; 数对(6,m)和数对(6,n) 中,6=6,即在同一列。
故答案为:行,列。
用数对表示位置,先写列,后写行,即(列,行), 很明显数对(x,8)和数对(y,8)在同一列中, 数对(6,m)和数对(6,n)在同一 行中。
14.3;7
解:(3,6+1)=(3,7)。
故答案为:3,7。
根据数对表示位置的方法:第一个数字表示列,第二个数字表示行;刘兵的位置表示在第3列,第6行;他正后方第一个同学应该与刘兵在同一列,即在第3列,在他后面一行,即第6+1=7行,由此即可解答。
15.2;4;6;7
解:根据题意,可知
岛的位置是:(3,6)
再根据平面图中坐标的表示方法,可得
A的位置为:(2,4)
B的位置为:(6,7)
故答案为:2;4;6;7
先理解岛位置的表示方法,即横向从左到右表示横坐标,纵坐标从下到上表示纵坐标,然后再根据岛的位置确定A和B两艘船的位置。
16.(1)解:
(2)解:25×(10-2)
=25×8
=200(千米)
200÷4=50(千米/小时)
答:这辆汽车平均每小时行驶50千米/小时。
(3)(10,7)
解:(3)解:50×2÷25+3
=100÷25+3
=4+3
=7
故答案为:(3)(10,7)。
(1)A(2,3)、B(10,3),每个数对的前一个数表示行,后一个数表示列,据此标出位置A和B;
(2)图中A和B之间距离10-2=8(个)格子,已知每格的距离代表25千米,乘以8个格子即为这辆汽车4个小时行驶的路程,然后根据“速度=路程÷时间”即可得出这辆汽车的速度;
(3)汽车行驶2小时,驶过的路程为50×2=100(千米),在图中表现为100÷25=4(个)格子,故汽车此时的位置应为(10,3+4),即(10,7)。
17.解:20×12=240(块)
由这面墙四个角的瓷砖位置可知,这面墙一共有20列,12行,根据瓷砖的块数=列数×行数,据此进行计算即可。
18.解:根据题目,刘亚宁的位置是(8,8),这表示她是在方阵的中心位置。
因此,可推断出方阵的总行数和总列数都应该是:2×8-1=15(人)
所以,这个方阵的总人数就是行数乘以列数,即15×15=225(人)
答:整个方阵一共有225名同学在观看现场直播
首先,我们要理解题目的意思,数对(8,8)表示刘亚宁在方阵的第8行第8列,这意味着她是在方阵的中心位置。因此,我们可以推断出方阵的总行数和总列数。
19.(1)F;C;G;1;5;6;5
(2)1;3
(3)根据题图可知位置G与B的列数相差1,行数相差2,位置E 与 B 的距离也是列数相差1,行数相差2,E和G到B的距离相等。
解:(1)数对(5,5)表示的是第5列第5行,对应的是位置F;和F在同一行的是C和G,C在第1列第5行,G在第6列第5行,用数对表示为(1,5)和(6,5);
(2)根据题图可知,A在第2列第2行,C的位置在第1列第5行,则由(2,2)向(1,5)移动时,需要先向西移动1格,再向北移动3格。
故答案为:(1)F,C,G,1,5,6
(2)1,3
(1)根据题目描述和解析示例,我们可以得知(5,5)处的位置是F,与F在同一行的是C和G。用数对表示C和G的位置分别是(1,5)和(6,5)。这说明了坐标系中,相同的行意味着y坐标相同,而列的不同则由x坐标的变化来区分。
(2)对于从A移动到C的过程,首先需要识别A和C的具体位置。由图可推断,A在第2列第2行,而C在第1列第5行。要从A移动到C,首先要向西(左)移动1格,以从第2列移动到第1列,再向北(上)移动3格,从第2行移动到第5行。因此,移动过程为先向西1格,再向北3格。
(3)要找出与B距离相等的两个位置,关键在于理解“距离相等”的含义。在坐标系中,距离相等可以通过比较点之间的列数和行数差值来判断。通过分析,我们发现G和E到B的距离相等,它们的列数与B的差值相同,行数与B的差值也相同,但方向相反,即G在B的右下方,而E在B的左上方。这说明,对于给定的点,通过列数和行数的相同差值,可以找到与其距离相等的点。
20.(1)6;4;10;6
(2)解:一个长方形的面积为(6-2)×(4-2)=8
两个长方形的面积之和为8×2=16,
答:两个长方形的面积之和为16。
解:(1)(6-2)÷2+2=4
点A:(6,4)
(6-2)+6=10
点B:(10,6)
故答案为:6,4,10,6
(1)根据题干和题图中已知点的位置可知,点A所在的行数是(6-2)÷2+2=4,点A所在的列数是6,所以点A用数对表示为(6,4),点B所在的行数是6,点B所在的列数是(6-2)+6=10,所以点B用数对表示为(10,6)。
(2)根据题目所给的数对信息以及两个长方形的位置可以知道长方形的长是4,宽是2,所以一个长方形的面积是8,两个长方形的面积是16
21.(1)解:如图:
(2)解:她从家先到图书馆,再到少年宫,然后去体育馆,最后回家。
(1)从学校开始往东数3格,再往北数4格即为王玲家,从学校开始往东数8格,再往北数7格即为赵华家;
(2)(3,4)为王玲家,(4,3)为图书馆,(6,5)为少年宫,(3,6)为体育馆,据此解答。
一、单选题
1.同一间教室,聪聪坐在教室的第2列、第5排,用数对(2,5)表示,如果用数对(a,3)表示明明在教室里的座位,那么下列说法正确的是( )。
A.明明的位置不可能在第3列 B.明明的位置不可能在第3排
C.明明的位置一定在第3排 D.明明的位置一定在第3列
2.大新坐在第3排第4列,可以用(4,3)表示.小刚坐在第5排第1列,表示为( )。
A.(4,5) B.(5,1) C.(1,5)
3.如下图所示, 长方形ABCD的顶点 D用数对表示是 (10, 5),顶点B用数对表示是(2,1),那么顶点C 可以用数对表示为( )。
A.(10, 1) B.(1, 10) C.(5, 2) D.(2, 5)
4. 小丽参加团体操比赛,她的位置用数对表示是(3,8),如果这时的方队是一个正方形,参加团体操比赛的至少有( )人。
A.9 B.24 C.64 D.36
5.下列数对中,( )所表示的位置与数对(3,4)所表示的位置距离最近。
A.(4,1) B.(5,5) C.(2,3) D.(1,4)
6. 在一幅图上,如果A 点用数对表示为(1,5),B点用数对表示为(1,1),C点用数对表示为(3,1),那么三角形ABC一定是( )三角形。
A.锐角 B.钝角 C.直角 D.等腰
7. 在平面图上,点A和点B(6,2)在同一行,与点C(2,7)在同一列,点A 的位置用数对表示是( )。
A.(2,7) B.(2,2) C.(6,2) D.(6,7)
8.如图,有一张方格纸,每个小方格的边长是1 cm,上面堆叠着若干个相同的小正方体。如果小正方体甲的位置用(1,1,1)表示,小正方体乙的位置用(5,2,2)表示,那么小正方体丙的位置可以用( )表示。
A.(2,3,6) B.(2,3,5) C.(3,2,5) D.(3,2,6)
9. 下面的说法中,正确的是 ( )。
A.一个数对只能确定一个位置
B.循环小数都是无限小数,无限小数都是循环小数
C.一个数除以0.1相当于把这个数缩小到原来的
D.两个小数相除,商一定比1小
10. 新情境·传统文化中国象棋是中国棋文化,也是中华民族的文化瑰宝。 “马行日,象飞田”是人们熟知的象棋口诀,如图是中国象棋的一部分。 “马”下一步可能走到的位置是 ( )。
A.(2, 3) B.(3,3) C.(4, 1) D.(4,3)
二、填空题
11.五(1)班教室的座位共有8列,每列座位同样多,且全部坐满。第8列倒数第二位同学的位置用数对表示是(8,5),五(1)班共有学生 人。
12. 张亮坐在教室的第3列第5行,用数对(3,5)表示;赵雪坐在教室的第6列第1行,用数对( , )表示;李明的座位号用数对(5,3)表示,他坐在教室的第 列第 行。
13.数对(x,8)和数对(y,8)在同一 中;数对(6,m)和数对(6,n)在同一 中。(填“列”或“行”)
14.刘兵的位置用数对表示是(3,6),他正后方第一个同学的位置是( , )。
15.如图,A、B两艘海监船正在某岛附近巡逻,如果这个岛的位置用(3,6)表示,那么海监船A 的位置可表示为( , ),海监船B的位置可表示为( , )。
三、操作题
16.一辆汽车的位置A在(2,3),行驶4小时后, 它的位置B在 (10, 3)。
(1)在图中标出汽车两次所在的位置A和B。
(2)如果图中每格的距离代表 25 千米,这辆汽车平均每小时行驶多少千米 (假设汽车在一条直线上沿着一个方向行驶)。
(3)再以同样的速度从位置(10,3) 向北行驶2 小时后,汽车的位置用数对表示是 。
四、解决问题
17. 刘芳家卫生间的一面墙上贴满了瓷砖,这面墙四个角的瓷砖位置用数对表示分别是(1,1)、(1,12)、(20,1)、(20,12),这面墙贴了多少块瓷砖?
18.北京时间 2024 年1月 17 日 22时27 分,搭载天舟七号货运飞船的长征七号遥八运载火箭,在中国文昌航天发射场点火发射,发射取得圆满成功。某科技实验小学的同学们排成一个方阵观看现场直播,刘亚宁在正中间,她的位置可以用数对(8,8)表示,整个方阵一共有多少名同学在观看现场直播?
19.贵州“村超”邀请赛如火如荼举行着,某村组织啦啦队为运动员们加油助威。如图是啦啦队某次排练走位平面图。
(1)(5,5)处是 ,和它在同一行的是 和 用数对表示是( , )和( , );
(2)若某人表演过程中需要从位置A处走位到C处,则她应该先向西走 格,再向北走 格;
(3)到B的距离相等的两处是哪些字母对应的位置?
20.下图中7个点连在一起形成了两个完全一样的长方形。
(1)点A用数对表示为( , );点 B用数对表示为( , );
(2)求两个长方形的面积之和。
21.图书馆所在的位置用(4,3)来表示, 它在学校以东 400 m , 再往北 300 m 处。
(1)王玲家在学校以东300m , 再往北400m处; 赵华家在学校以东800m,再往北700m处。在图中标出这两名同学家的位置。
(2)上周六, 王玲上午的活动路线是: , 说一说她这一天先后去了哪些地方 。
答案解析部分
1.C
解:第2列、第5排,用数对(2,5)表示,则数对(a,3)表示第a列,第3排。
故答案为:C。
用数对表示位置的方法是:第一个数字表示列,第二个数字表示行,中间用“,”隔开。
2.C
解:小刚坐在第5排第1列,表示为(1,5) 。
故答案为:C。
小刚坐在第5排第1列,要把列放在前面,排数放在后面,表示为(1,5) 。
3.A
解:顶点C与D同列,与B同行,点C表示为(10,1)。
故答案为:A。
数对中第一个数表示列,第二个数表示行。根据C与D同列判断C在10列,根据C与B同行判断C在1行。
4.C
解:根据题目给出的数对(3,8),可以确定小丽在第3列第8行。
由于方队是一个正方形,所以行数和列数应该相等。
根据小丽位置的信息方队至少有8行8列。
由于方队有8行8列,所以总人数为8×8=64人。
故答案为:64
首先,根据题目给出的小丽的位置数对(3,8),可以确定她在第3列第8行。由于方队是一个正方形,行数和列数应该相等。因此,方队至少有8行8列。最后,通过计算8行8列的方队总人数,可以得到参加团体操表演的至少人数。
5.C
解:A.(4,1)与数对(3,4)所表示的位置有3列的距离,有4行的距离,所以不是最近的位置。
B.(5,5)与数对(3,4)所表示的位置有2列的距离,有1行的距离,所以不是最近的位置。
C.(2,3)与数对(3,4)所表示的位置有1列的距离,有1行的距离,所以是最近的位置。
D.(1,4)与数对(3,4)所表示的位置有2列的距离,有0行的距离,所以不是最近的位置。
故答案为:C
根据数对表示物体位置的方法,数对(3,4)表示的位置在第3列第4行,与它在同一行的是(1,4),然后计算与数对(3,4)所表示的位置距离的远近,进而判断即可。本题考查用数对表示位置,解答本题的关键是掌握用数对表示位置的方法。
6.C
解:点A和点B在同一列,点B和点C在同一行,所以三角形ABC一定是直角三角形。
故答案为:C
用数对表示位置时,前一个数表示第几列,后一个数表示第几行。当两个数对第一个数相同时,说明在同一列;当两个数对第二个数相同时,说明在同一行。本题考查用数对表示位置,解答本题的关键是掌握用数对表示位置的方法。
7.B
解:点A和点B(6,2)在同一行,所以点A是在第2行;点A与点C(2,7)在同一列,所以点A是在第2列;所以A的位置是(2,2)。
故答案为:B
数对表示位置的方法是:第一个数字表示列,第二个数字表示行,由此即可解答。此题考查了数对表示位置的方法的灵活应用
8.B
解:观察小正方体甲和乙的表示方法,可知第1 个数表示小正方体所在的列数,第2个数表示小正方体所在的行数,第3个数表示小正方体所在的层数。小正方体丙在第2列,第3行,第5层,因此表示为(2,3,5)。
故答案为:B
本题考查的是空间坐标系中的位置确定问题。类似于三维坐标系的定位方法,题目要求确定小正方体丙的位置。给定的坐标系统以小方格的边长为单位,每个坐标表示在方格纸上的x(水平)、y(垂直)和z(高)方向上的位置。题目给出了甲、乙两小正方体的位置,要求根据相同的方法确定丙的位置。
9.A
解:A项:一个数对确定了列数和行数,则只能确定一个位置,原题干说法正确;
B项:循环小数都是无限小数,无限小数可能是循环小数,也可能是无限不循环小数,原题干说法错误;
C项:一个数除以0.1相当于把这个数扩大到原来的 10(0除外),原题干说法错误;
D项:两个小数相除,商可能大于、小于或者等于1,原题干说法错误。
故答案为:A。
A项:用数对表示位置时,前面一个数表示第几列,后面一个数表示第几行;列数一般从左往右数,行数一般从前往后数;
B项:循环小数的位数是无限的,所以一定是无限小数;但无限小数可能是循环小数,也可能是无限不循环小数,所以无限小数不一定都是循环小数;
C项:一个数除以0.1相当于把这个数扩大到原来的 10(0除外);
D项:一个数(0和负数除外)除以小于1的数,所得的商大于原来的数;反之,商小于原来的数;一个数(0和负数除外)乘小于1的数,所得的积小于原来的数,反之,积大于原来的数。一个数乘1还得原数。
10.B
解:“马”下一步可能走到的位置是(1,3)或者(3,3)。
故答案为:B。
用数对表示位置时,前面一个数表示第几列,后面一个数表示第几行;列数一般从左往右数,行数一般从前往后数。
11.48
解:第8列倒数第二位同学的位置用数对表示是(8,5),说明第8列最后一位同学的位置用数对表示是(8,6),即五(1)班教室的座位共有8列6行,8×6=48(人),五(1)班共有学生48人。
故答案为:48。
用数对表示位置时,前面一个数表示第几列,后面一个数表示第几行;列数一般从左往右数,行数一般从前往后数,总人数=列数×行数。
12.6;1;5;3
解:根据题意,可得
张亮的座位用数对(3,5)表示,这说明张亮坐在教室的第3列第5行。
赵雪坐在教室的第6列第1行,因此赵雪的座位数对为(6,1)。
对于李明的座位,数对是(5,3),则表明李明坐在教室的第5列第3行。
故答案为:6;1;5;3
数对中左边的数为列,右边的数为行。
13.行;列
解:(x,8)和数对(y,8) 中,8=8,即在同一行; 数对(6,m)和数对(6,n) 中,6=6,即在同一列。
故答案为:行,列。
用数对表示位置,先写列,后写行,即(列,行), 很明显数对(x,8)和数对(y,8)在同一列中, 数对(6,m)和数对(6,n)在同一 行中。
14.3;7
解:(3,6+1)=(3,7)。
故答案为:3,7。
根据数对表示位置的方法:第一个数字表示列,第二个数字表示行;刘兵的位置表示在第3列,第6行;他正后方第一个同学应该与刘兵在同一列,即在第3列,在他后面一行,即第6+1=7行,由此即可解答。
15.2;4;6;7
解:根据题意,可知
岛的位置是:(3,6)
再根据平面图中坐标的表示方法,可得
A的位置为:(2,4)
B的位置为:(6,7)
故答案为:2;4;6;7
先理解岛位置的表示方法,即横向从左到右表示横坐标,纵坐标从下到上表示纵坐标,然后再根据岛的位置确定A和B两艘船的位置。
16.(1)解:
(2)解:25×(10-2)
=25×8
=200(千米)
200÷4=50(千米/小时)
答:这辆汽车平均每小时行驶50千米/小时。
(3)(10,7)
解:(3)解:50×2÷25+3
=100÷25+3
=4+3
=7
故答案为:(3)(10,7)。
(1)A(2,3)、B(10,3),每个数对的前一个数表示行,后一个数表示列,据此标出位置A和B;
(2)图中A和B之间距离10-2=8(个)格子,已知每格的距离代表25千米,乘以8个格子即为这辆汽车4个小时行驶的路程,然后根据“速度=路程÷时间”即可得出这辆汽车的速度;
(3)汽车行驶2小时,驶过的路程为50×2=100(千米),在图中表现为100÷25=4(个)格子,故汽车此时的位置应为(10,3+4),即(10,7)。
17.解:20×12=240(块)
由这面墙四个角的瓷砖位置可知,这面墙一共有20列,12行,根据瓷砖的块数=列数×行数,据此进行计算即可。
18.解:根据题目,刘亚宁的位置是(8,8),这表示她是在方阵的中心位置。
因此,可推断出方阵的总行数和总列数都应该是:2×8-1=15(人)
所以,这个方阵的总人数就是行数乘以列数,即15×15=225(人)
答:整个方阵一共有225名同学在观看现场直播
首先,我们要理解题目的意思,数对(8,8)表示刘亚宁在方阵的第8行第8列,这意味着她是在方阵的中心位置。因此,我们可以推断出方阵的总行数和总列数。
19.(1)F;C;G;1;5;6;5
(2)1;3
(3)根据题图可知位置G与B的列数相差1,行数相差2,位置E 与 B 的距离也是列数相差1,行数相差2,E和G到B的距离相等。
解:(1)数对(5,5)表示的是第5列第5行,对应的是位置F;和F在同一行的是C和G,C在第1列第5行,G在第6列第5行,用数对表示为(1,5)和(6,5);
(2)根据题图可知,A在第2列第2行,C的位置在第1列第5行,则由(2,2)向(1,5)移动时,需要先向西移动1格,再向北移动3格。
故答案为:(1)F,C,G,1,5,6
(2)1,3
(1)根据题目描述和解析示例,我们可以得知(5,5)处的位置是F,与F在同一行的是C和G。用数对表示C和G的位置分别是(1,5)和(6,5)。这说明了坐标系中,相同的行意味着y坐标相同,而列的不同则由x坐标的变化来区分。
(2)对于从A移动到C的过程,首先需要识别A和C的具体位置。由图可推断,A在第2列第2行,而C在第1列第5行。要从A移动到C,首先要向西(左)移动1格,以从第2列移动到第1列,再向北(上)移动3格,从第2行移动到第5行。因此,移动过程为先向西1格,再向北3格。
(3)要找出与B距离相等的两个位置,关键在于理解“距离相等”的含义。在坐标系中,距离相等可以通过比较点之间的列数和行数差值来判断。通过分析,我们发现G和E到B的距离相等,它们的列数与B的差值相同,行数与B的差值也相同,但方向相反,即G在B的右下方,而E在B的左上方。这说明,对于给定的点,通过列数和行数的相同差值,可以找到与其距离相等的点。
20.(1)6;4;10;6
(2)解:一个长方形的面积为(6-2)×(4-2)=8
两个长方形的面积之和为8×2=16,
答:两个长方形的面积之和为16。
解:(1)(6-2)÷2+2=4
点A:(6,4)
(6-2)+6=10
点B:(10,6)
故答案为:6,4,10,6
(1)根据题干和题图中已知点的位置可知,点A所在的行数是(6-2)÷2+2=4,点A所在的列数是6,所以点A用数对表示为(6,4),点B所在的行数是6,点B所在的列数是(6-2)+6=10,所以点B用数对表示为(10,6)。
(2)根据题目所给的数对信息以及两个长方形的位置可以知道长方形的长是4,宽是2,所以一个长方形的面积是8,两个长方形的面积是16
21.(1)解:如图:
(2)解:她从家先到图书馆,再到少年宫,然后去体育馆,最后回家。
(1)从学校开始往东数3格,再往北数4格即为王玲家,从学校开始往东数8格,再往北数7格即为赵华家;
(2)(3,4)为王玲家,(4,3)为图书馆,(6,5)为少年宫,(3,6)为体育馆,据此解答。
