苏教版六年级上册 长方体与正方体 单元整体教学课件(共27张PPT)
文档属性
| 名称 | 苏教版六年级上册 长方体与正方体 单元整体教学课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 10:18:23 | ||
图片预览





文档简介
(共27张PPT)
《长方体和正方体》
苏教版六年级上册第一单元
高标引航 精准施教
单元整体教学设计
目录
Contents
1
2
3
单元目标设计
4
5
达成策略
单元整体规划
单元整体教学分析
课标引领
课标引领
01
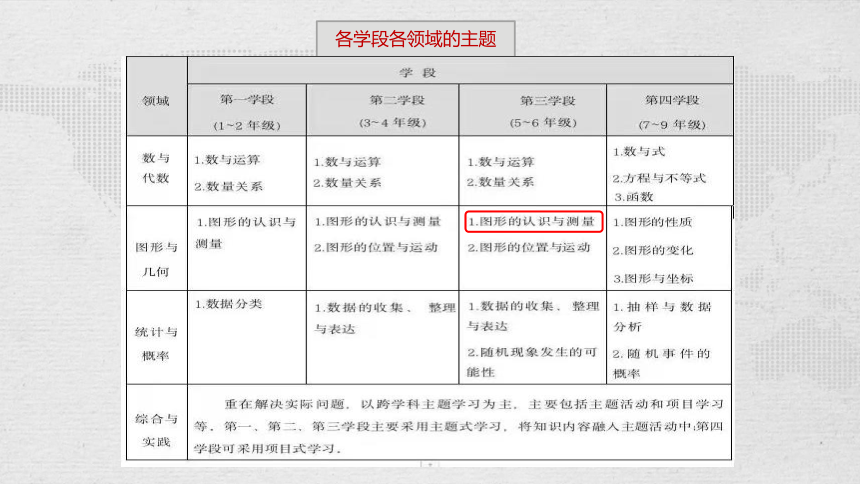
各学段各领域的主题
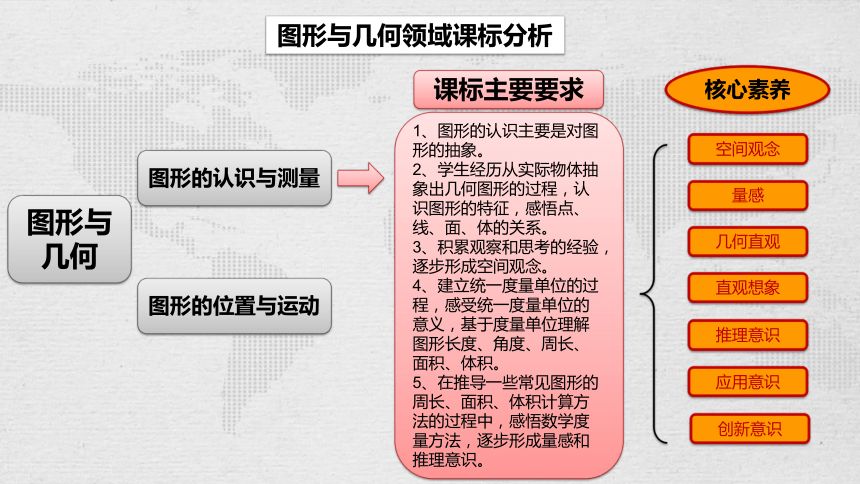
图形与几何领域课标分析
图形与几何
图形的认识与测量
图形的位置与运动
1、图形的认识主要是对图形的抽象。
2、学生经历从实际物体抽象出几何图形的过程,认识图形的特征,感悟点、线、面、体的关系。
3、积累观察和思考的经验,逐步形成空间观念。
4、建立统一度量单位的过程,感受统一度量单位的意义,基于度量单位理解图形长度、角度、周长、面积、体积。
5、在推导一些常见图形的周长、面积、体积计算方法的过程中,感悟数学度量方法,逐步形成量感和推理意识。
课标主要要求
核心素养
空间观念
量感
几何直观
推理意识
直观想象
应用意识
创新意识
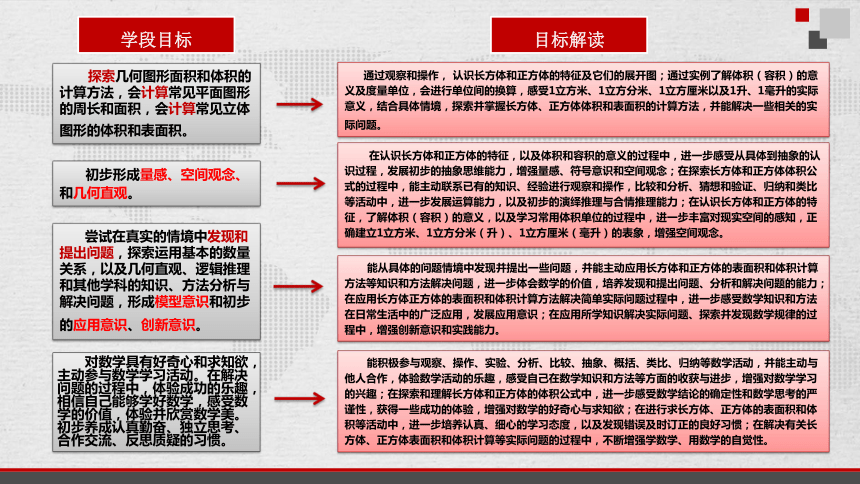
学段目标
探索几何图形面积和体积的计算方法,会计算常见平面图形的周长和面积,会计算常见立体图形的体积和表面积。
初步形成量感、空间观念、和几何直观。
尝试在真实的情境中发现和提出问题,探索运用基本的数量关系,以及几何直观、逻辑推理和其他学科的知识、方法分析与解决问题,形成模型意识和初步的应用意识、创新意识。
对数学具有好奇心和求知欲,主动参与数学学习活动。在解决问题的过程中,体验成功的乐趣,相信自己能够学好数学,感受数学的价值,体验并欣赏数学美。初步养成认真勤奋、独立思考、合作交流、反思质疑的习惯。
目标解读
通过观察和操作, 认识长方体和正方体的特征及它们的展开图;通过实例了解体积(容积)的意义及度量单位,会进行单位间的换算,感受1立方米、1立方分米、1立方厘米以及1升、1毫升的实际意义,结合具体情境,探索并掌握长方体、正方体体积和表面积的计算方法,并能解决一些相关的实际问题。
在认识长方体和正方体的特征,以及体积和容积的意义的过程中,进一步感受从具体到抽象的认识过程,发展初步的抽象思维能力,增强量感、符号意识和空间观念;在探索长方体和正方体体积公式的过程中,能主动联系已有的知识、经验进行观察和操作,比较和分析、猜想和验证、归纳和类比等活动中,进一步发展运算能力,以及初步的演绎推理与合情推理能力;在认识长方体和正方体的特征,了解体积(容积)的意义,以及学习常用体积单位的过程中,进一步丰富对现实空间的感知,正确建立1立方米、1立方分米(升)、1立方厘米(毫升)的表象,增强空间观念。
能从具体的问题情境中发现并提出一些问题,并能主动应用长方体和正方体的表面积和体积计算方法等知识和方法解决问题,进一步体会数学的价值,培养发现和提出问题、分析和解决问题的能力;在应用长方体正方体的表面积和体积计算方法解决简单实际问题过程中,进一步感受数学知识和方法在日常生活中的广泛应用,发展应用意识;在应用所学知识解决实际问题、探索并发现数学规律的过程中,增强创新意识和实践能力。
能积极参与观察、操作、实验、分析、比较、抽象、概括、类比、归纳等数学活动,并能主动与他人合作,体验数学活动的乐趣,感受自己在数学知识和方法等方面的收获与进步,增强对数学学习的兴趣;在探索和理解长方体和正方体的体积公式中,进一步感受数学结论的确定性和数学思考的严谨性,获得一些成功的体验,增强对数学的好奇心与求知欲;在进行求长方体、正方体的表面积和体积等活动中,进一步培养认真、细心的学习态度,以及发现错误及时订正的良好习惯;在解决有关长方体、正方体表面积和体积计算等实际问题的过程中,不断增强学数学、用数学的自觉性。
单元整体教学分析
02
单元整体教学分析
单元整体教学设计分析
学生为本
依托教材
课标导向
教材分析
本单元分析
学情分析
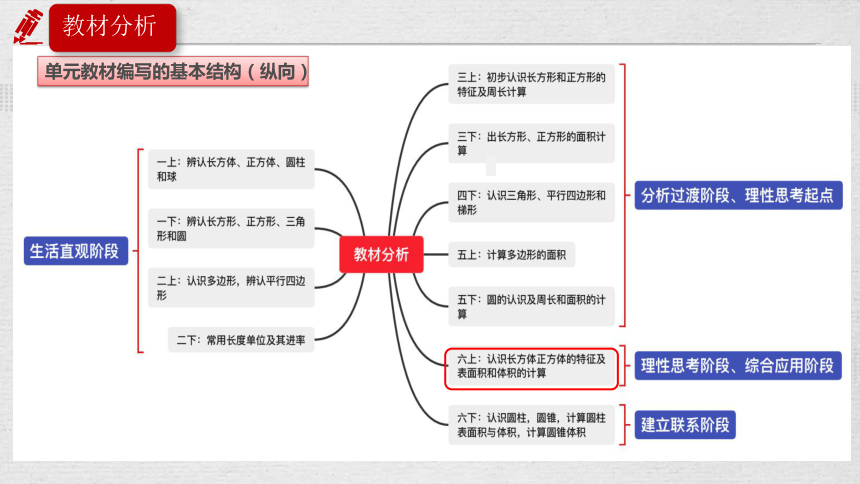
单元教材编写的基本结构(纵向)
教材分析
单元教材编写的基本结构(横向)
教材分析
另附有:整理与练习、表面涂色的正方体(探索规律)
苏教版 青岛版 人教版 北师版
知识编排年级不同,但本单元的结构和内容大致相同。
不同版本教材对比整合
教材分析
体积是体积单位的累积
依据给出的数据,想象出图形的样子
依据实物,
建立立体模型
随着学生知识的不断累积,对建立空间观念的要求也是梯度上升的。
单元核心概念
建立空间观念
本单元分析
课程总目标
学段目标
课程内容
思想方法
课程总目标
学段目标
课程内容
单元思想方法
实验
类推
转化
探究长方体迁移类推到探究正方体。
面积是面积单位的累积迁移类推到
体积是体积单位的累积。
将求三维图形的表面积转化为求
二维图形的面积
通过实验法发现物体是占有一定空间的,
所占空间是有大小的,理解体积的含义。
通过实验法发现容器容纳物体的体积也有
大小,进而理解容积。
本单元分析
学生初步认识了长方体和正方体
会求各种基本平面图形的周长和面积
知道从哪些方面研究平面图形
会用转化法推导图形的面积
长方体正方体的特征、表面积和体积
知道从哪些方面研究立体图形
01
02
03
已有知识基础
已有活动经验
潜在知识
水平
学情分析
单元目标设计
03
教学目标
课标导向
依托教材
学生为本
借助具体的实物,认识长方体和正方体的特征,理解长方体和正方体的表面积和体积(容积)的含义。建立常用的体积(容积)单位(难点),会进行单位间的换算,会计算长方体和正方体的表面积和体积(重点)。
知识技能
方法素养
表面积是几何体所有面的面积之和。
体积是物体所占空间的大小。
体积单位的数量就是几何体的体积。
基本理解
在观察、比较、实验和动手操作等活动中,能进行有条理的思考,发展空间观念、几何直观能力、推理能力和应用意识,体会转化、数形结合和模型思想。体验学习数学的乐趣。
单元教学目标的确立
单元整体规划
04
单元整体规划
单元内容 基本理解 评价任务 达成策略
例1、例2、例3 长方体正方体的特征与其展开图(2课时) 长方体和正方体有6个面、8个顶点、12条;相对的面相同,相对的棱相等。 判断一个几何体是不是长方体和正方体。 求一个长方体、正方体的棱长和。 借助长方体和正方体模型通过观察、对比,引导学生有序思考,认识面、棱、顶点的概念,发现面、棱的特点。
例4、例5 长方体正方体的表面积(3课时) 表面积是长方体(或正方体)6个面的总面积。 计算长方体与正方体纸盒、无盖鱼缸的面积。 借助展开图,探究表面积意义和计算方法,体现数形结合思想。
例6、例7、例8 体积(容积)和体积(容积)单位(3课时) 体积是物体所占空间的大小; 容积是所能容纳物体的体积; 1立方分米=1升,1立方厘米=1毫升。 一个水桶的体积和容积分别表示什么?估测橡皮、铅笔盒、教室的体积是多少?三者之间有什么大小关系? 借助实验操作,认识体积和容积的意义,通过切割,认识体积单位和它们间的关系。
例9、例10、例11、例12 长方体正方体的体积及体积单位换算(4课时) 长方体正方体的体积大小就是求所含体积单位的个数。计算的本质是一行几个体积单位×可以摆几行×可以摆几层。 计算给定长宽高(棱长)的长方体(正方体)体积,并与体积单位个数结合,说出计算意义。 认识体积单位作用的基础上,通过拼摆,理解长方体正方体的体积大小就是求所含体积单位的个数,进而发现长宽高与体积单位个数的关系,形成数学模型。
整理与练习(2课时) 加深对以上知识的理解,完善长方体和正方体的结构认识。 应用长方体、正方体,体积及体积单位知识解决问题 通过小组讨论回顾知识,独立练习、个别检查、组织交流、作业批改等形式,反馈掌握情况,分析错误原因,提高解决问题的能力。
表面涂色的正方体(1课时) 每种小正方体的个数与大正方体的棱平分的份数有关。 探索1面涂色、2面涂色、3面涂色正 方体位置及个数的规律。 通过观察、想象,再对大正方体切割,获得并分析数据,探索规律。
单元整体规划
类推
转化
实验
学习方
法
数学思
想
关键能
力
数形结合
模型思想
空间想象能力
推理能力
问题解决能力
新知探究课
单元起始课
单元总结课
拓展练习课
首尾呼应
形成闭环
直观观察
初步感知
实验操作
自主归纳
交流辨析
内化提升
总结概括
实践应用
迁移类推
发展素养
单元知识学习的基本规律
体现知识的建构过程
符合学生的认知特点
达成策略
05
课标
课程内容
达成策略
教材呈现
课程内容
达成策略
教材呈现
认识长方体、正方体及展开图
课标
借助实物和模型,通过看、量、比等操作活动,逐步概括长方体和正方体的特征,揭示长方体长、宽、高的概念;通过折、剪、拼等操作活动,经历实物到展开图的转换。掌握分析几何体的一般方法,提高推理能力,发展空间观念。
达成策略
课程内容
达成策略
教材呈现
计算长方体、正方体的表面积
课标
经历长方体和正方体表面积的推理过程,会计算表面积,掌握由特殊到一般的推理方法。加强空间观念、几何直观、推理能力和应用能力。
达成策略
课程内容
达成策略
教材呈现
体积(容积)和体积(容积)单位
课标
经历观察、实验、比较、抽象、概括的活动过程,体会体积和容积概念;从测量的实际需要出发,认识体积单位,感受每个体积单位的实际大小,初步建立空间观念。
达成策略
课程内容
达成策略
教材呈现
长方体和正方体的体积以及体积单位间的换算
课标
观察摆成的长方体体积与长宽高的关系,知道体积公式的由来,理解测量的本质就是求所含单位的个数,并能应用。渗透不完全归纳法和猜想验证等数学方法。通过观察、比较、计算、推理等活动,发现相邻体积单位间的进率,发展演绎推理能力。
达成策略
感谢倾听!
《长方体和正方体》
苏教版六年级上册第一单元
高标引航 精准施教
单元整体教学设计
目录
Contents
1
2
3
单元目标设计
4
5
达成策略
单元整体规划
单元整体教学分析
课标引领
课标引领
01
各学段各领域的主题
图形与几何领域课标分析
图形与几何
图形的认识与测量
图形的位置与运动
1、图形的认识主要是对图形的抽象。
2、学生经历从实际物体抽象出几何图形的过程,认识图形的特征,感悟点、线、面、体的关系。
3、积累观察和思考的经验,逐步形成空间观念。
4、建立统一度量单位的过程,感受统一度量单位的意义,基于度量单位理解图形长度、角度、周长、面积、体积。
5、在推导一些常见图形的周长、面积、体积计算方法的过程中,感悟数学度量方法,逐步形成量感和推理意识。
课标主要要求
核心素养
空间观念
量感
几何直观
推理意识
直观想象
应用意识
创新意识
学段目标
探索几何图形面积和体积的计算方法,会计算常见平面图形的周长和面积,会计算常见立体图形的体积和表面积。
初步形成量感、空间观念、和几何直观。
尝试在真实的情境中发现和提出问题,探索运用基本的数量关系,以及几何直观、逻辑推理和其他学科的知识、方法分析与解决问题,形成模型意识和初步的应用意识、创新意识。
对数学具有好奇心和求知欲,主动参与数学学习活动。在解决问题的过程中,体验成功的乐趣,相信自己能够学好数学,感受数学的价值,体验并欣赏数学美。初步养成认真勤奋、独立思考、合作交流、反思质疑的习惯。
目标解读
通过观察和操作, 认识长方体和正方体的特征及它们的展开图;通过实例了解体积(容积)的意义及度量单位,会进行单位间的换算,感受1立方米、1立方分米、1立方厘米以及1升、1毫升的实际意义,结合具体情境,探索并掌握长方体、正方体体积和表面积的计算方法,并能解决一些相关的实际问题。
在认识长方体和正方体的特征,以及体积和容积的意义的过程中,进一步感受从具体到抽象的认识过程,发展初步的抽象思维能力,增强量感、符号意识和空间观念;在探索长方体和正方体体积公式的过程中,能主动联系已有的知识、经验进行观察和操作,比较和分析、猜想和验证、归纳和类比等活动中,进一步发展运算能力,以及初步的演绎推理与合情推理能力;在认识长方体和正方体的特征,了解体积(容积)的意义,以及学习常用体积单位的过程中,进一步丰富对现实空间的感知,正确建立1立方米、1立方分米(升)、1立方厘米(毫升)的表象,增强空间观念。
能从具体的问题情境中发现并提出一些问题,并能主动应用长方体和正方体的表面积和体积计算方法等知识和方法解决问题,进一步体会数学的价值,培养发现和提出问题、分析和解决问题的能力;在应用长方体正方体的表面积和体积计算方法解决简单实际问题过程中,进一步感受数学知识和方法在日常生活中的广泛应用,发展应用意识;在应用所学知识解决实际问题、探索并发现数学规律的过程中,增强创新意识和实践能力。
能积极参与观察、操作、实验、分析、比较、抽象、概括、类比、归纳等数学活动,并能主动与他人合作,体验数学活动的乐趣,感受自己在数学知识和方法等方面的收获与进步,增强对数学学习的兴趣;在探索和理解长方体和正方体的体积公式中,进一步感受数学结论的确定性和数学思考的严谨性,获得一些成功的体验,增强对数学的好奇心与求知欲;在进行求长方体、正方体的表面积和体积等活动中,进一步培养认真、细心的学习态度,以及发现错误及时订正的良好习惯;在解决有关长方体、正方体表面积和体积计算等实际问题的过程中,不断增强学数学、用数学的自觉性。
单元整体教学分析
02
单元整体教学分析
单元整体教学设计分析
学生为本
依托教材
课标导向
教材分析
本单元分析
学情分析
单元教材编写的基本结构(纵向)
教材分析
单元教材编写的基本结构(横向)
教材分析
另附有:整理与练习、表面涂色的正方体(探索规律)
苏教版 青岛版 人教版 北师版
知识编排年级不同,但本单元的结构和内容大致相同。
不同版本教材对比整合
教材分析
体积是体积单位的累积
依据给出的数据,想象出图形的样子
依据实物,
建立立体模型
随着学生知识的不断累积,对建立空间观念的要求也是梯度上升的。
单元核心概念
建立空间观念
本单元分析
课程总目标
学段目标
课程内容
思想方法
课程总目标
学段目标
课程内容
单元思想方法
实验
类推
转化
探究长方体迁移类推到探究正方体。
面积是面积单位的累积迁移类推到
体积是体积单位的累积。
将求三维图形的表面积转化为求
二维图形的面积
通过实验法发现物体是占有一定空间的,
所占空间是有大小的,理解体积的含义。
通过实验法发现容器容纳物体的体积也有
大小,进而理解容积。
本单元分析
学生初步认识了长方体和正方体
会求各种基本平面图形的周长和面积
知道从哪些方面研究平面图形
会用转化法推导图形的面积
长方体正方体的特征、表面积和体积
知道从哪些方面研究立体图形
01
02
03
已有知识基础
已有活动经验
潜在知识
水平
学情分析
单元目标设计
03
教学目标
课标导向
依托教材
学生为本
借助具体的实物,认识长方体和正方体的特征,理解长方体和正方体的表面积和体积(容积)的含义。建立常用的体积(容积)单位(难点),会进行单位间的换算,会计算长方体和正方体的表面积和体积(重点)。
知识技能
方法素养
表面积是几何体所有面的面积之和。
体积是物体所占空间的大小。
体积单位的数量就是几何体的体积。
基本理解
在观察、比较、实验和动手操作等活动中,能进行有条理的思考,发展空间观念、几何直观能力、推理能力和应用意识,体会转化、数形结合和模型思想。体验学习数学的乐趣。
单元教学目标的确立
单元整体规划
04
单元整体规划
单元内容 基本理解 评价任务 达成策略
例1、例2、例3 长方体正方体的特征与其展开图(2课时) 长方体和正方体有6个面、8个顶点、12条;相对的面相同,相对的棱相等。 判断一个几何体是不是长方体和正方体。 求一个长方体、正方体的棱长和。 借助长方体和正方体模型通过观察、对比,引导学生有序思考,认识面、棱、顶点的概念,发现面、棱的特点。
例4、例5 长方体正方体的表面积(3课时) 表面积是长方体(或正方体)6个面的总面积。 计算长方体与正方体纸盒、无盖鱼缸的面积。 借助展开图,探究表面积意义和计算方法,体现数形结合思想。
例6、例7、例8 体积(容积)和体积(容积)单位(3课时) 体积是物体所占空间的大小; 容积是所能容纳物体的体积; 1立方分米=1升,1立方厘米=1毫升。 一个水桶的体积和容积分别表示什么?估测橡皮、铅笔盒、教室的体积是多少?三者之间有什么大小关系? 借助实验操作,认识体积和容积的意义,通过切割,认识体积单位和它们间的关系。
例9、例10、例11、例12 长方体正方体的体积及体积单位换算(4课时) 长方体正方体的体积大小就是求所含体积单位的个数。计算的本质是一行几个体积单位×可以摆几行×可以摆几层。 计算给定长宽高(棱长)的长方体(正方体)体积,并与体积单位个数结合,说出计算意义。 认识体积单位作用的基础上,通过拼摆,理解长方体正方体的体积大小就是求所含体积单位的个数,进而发现长宽高与体积单位个数的关系,形成数学模型。
整理与练习(2课时) 加深对以上知识的理解,完善长方体和正方体的结构认识。 应用长方体、正方体,体积及体积单位知识解决问题 通过小组讨论回顾知识,独立练习、个别检查、组织交流、作业批改等形式,反馈掌握情况,分析错误原因,提高解决问题的能力。
表面涂色的正方体(1课时) 每种小正方体的个数与大正方体的棱平分的份数有关。 探索1面涂色、2面涂色、3面涂色正 方体位置及个数的规律。 通过观察、想象,再对大正方体切割,获得并分析数据,探索规律。
单元整体规划
类推
转化
实验
学习方
法
数学思
想
关键能
力
数形结合
模型思想
空间想象能力
推理能力
问题解决能力
新知探究课
单元起始课
单元总结课
拓展练习课
首尾呼应
形成闭环
直观观察
初步感知
实验操作
自主归纳
交流辨析
内化提升
总结概括
实践应用
迁移类推
发展素养
单元知识学习的基本规律
体现知识的建构过程
符合学生的认知特点
达成策略
05
课标
课程内容
达成策略
教材呈现
课程内容
达成策略
教材呈现
认识长方体、正方体及展开图
课标
借助实物和模型,通过看、量、比等操作活动,逐步概括长方体和正方体的特征,揭示长方体长、宽、高的概念;通过折、剪、拼等操作活动,经历实物到展开图的转换。掌握分析几何体的一般方法,提高推理能力,发展空间观念。
达成策略
课程内容
达成策略
教材呈现
计算长方体、正方体的表面积
课标
经历长方体和正方体表面积的推理过程,会计算表面积,掌握由特殊到一般的推理方法。加强空间观念、几何直观、推理能力和应用能力。
达成策略
课程内容
达成策略
教材呈现
体积(容积)和体积(容积)单位
课标
经历观察、实验、比较、抽象、概括的活动过程,体会体积和容积概念;从测量的实际需要出发,认识体积单位,感受每个体积单位的实际大小,初步建立空间观念。
达成策略
课程内容
达成策略
教材呈现
长方体和正方体的体积以及体积单位间的换算
课标
观察摆成的长方体体积与长宽高的关系,知道体积公式的由来,理解测量的本质就是求所含单位的个数,并能应用。渗透不完全归纳法和猜想验证等数学方法。通过观察、比较、计算、推理等活动,发现相邻体积单位间的进率,发展演绎推理能力。
达成策略
感谢倾听!
