4.6圆与圆的位置关系

课件66张PPT。5.6圆与圆的位置关系 1、点与圆的位置关系d < r
d = r
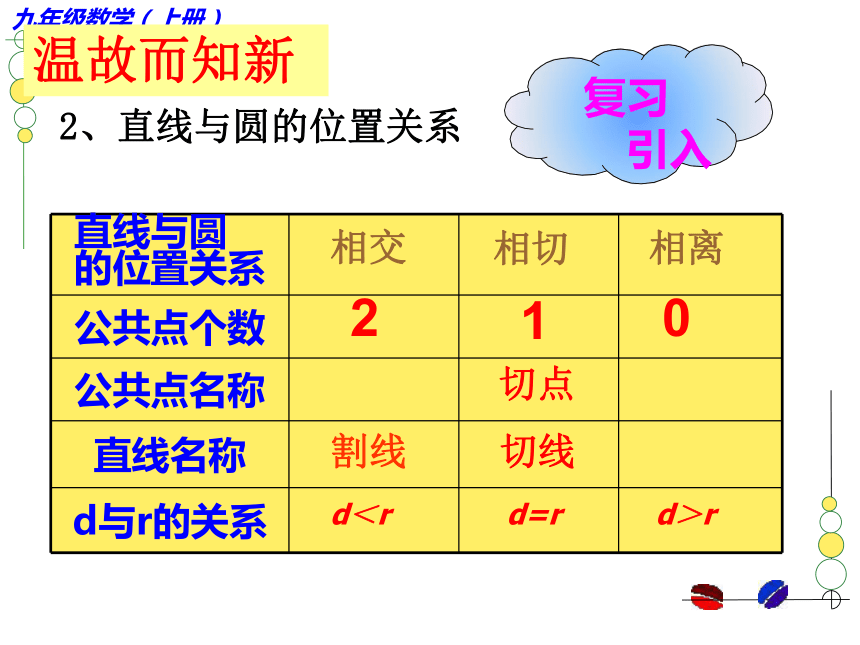
d > r温故而知新相交相切d＞rd＜rd=r相离210切点温故而知新2、直线与圆的位置关系哇！天怎么突然黑了？原来是发生日食了！走进生活生活中的数学新 北 京 新 奥 运 2 0 0 8生活情境再现 观察硬币的运动过程,思考两圆公共点的个数在如何变化？ 在纸上画一个半径为3cm的⊙O1，把一枚硬币平放在纸上作为另一个圆，将这枚硬币向圆不断移动：看一看瞧一瞧在这一过程中两圆出现了哪几种位置关系？ 在纸上画一个半径为3cm的⊙O1，把一枚硬币平放在纸上作为另一个圆，将这枚硬币向圆不断移动看一看瞧一瞧 两个圆没有公共点，并且每个圆上的点都在另一个圆的外部时，叫做这两个圆外离 两个圆有唯一的公共点，并且除了这个公共点以外，每个圆上的点都在另一个圆的外部时，叫做这两个圆 这个唯一的公共点叫做 外切切点 两个圆有两个公共点时，叫做这两个圆相交 两个圆有唯一的公共点，并且除了这个公共点以外，一个圆上的点都在另一个圆的内部时，叫做这两个圆 内切这个唯一公共点叫做切点内切和外切统称为相切 两个圆没有公共点，并且一个圆上的点都在另一个圆的内部时，叫做这两个圆内含 两圆同心是两圆内含的一种特例圆
和
圆
的
位
置
关
系外 离内 切相 交外 切内 含没有公共点相 离一个公共点相切两个公共点相交思考1、如何区分两圆外离、内含？答案：相同点——两圆都没有公共点。
不同点——外离是每一圆上的点都在另一圆的外部。
内含是其中一圆上的点都在另一圆的内部。2、如何区分两圆外切、内切？答案：相同点——两圆都有唯一公共点。
不同点——外切是除公共点外，每一圆上的点都在另一圆的外部。
内切是除公共点外，一圆上的点都在另一圆的内部。连心线：过两圆心的直线圆心距：两圆心之间的距离想一想：两个圆组成的图形是轴对称图形吗？是中心对称图形吗？两圆组成的图形是轴对称图形，它们的对称轴是连心线。如果两个圆相切，那么切点一定在连心线上。o1o2Rrdd>R+r精彩源于发现外离Rrdo1o2d=R+rT外切o1o2rRdd=R-r (R>r)T内切R-rr)dRro1o2相交dr)o1rRdo20≤内含： 两圆的位置关系0≤两圆位置关系的性质与判定:性质判定0R―rR+r同心圆内含外离 外切相交内切位 置 关 系 数 字 化d
比一比,赛一赛,看谁答得快. 1、若两圆只有一个交点,则这两圆外切. （ ）×2、如果两圆没有交点，则这两圆的位置关系是外离. （ ）
× 3、当O 1 O 2=0时,两圆位置关系是同心圆. （ ）√4、若O1O2=1.5,r=1,R=3,则O1 O2×5、若O1O2=4，且r=7,R=3,
则O1O2× 设圆O和圆P的半径分别为R、r，圆心距为d。在下列情况下，两圆的位置关系怎样？①R=6 r=3 d=4②R=6 r=3 d=0③R=3 r=7 d=4④R=5 r=3 d=8小组竞答⑤R=6 r=3 d=10⑥R=5 r=3 d=1相交内切外离内含外切内含例1、已知：⊙O1、⊙O2的半径为r1、 r2 ， 圆心距d=5， r1=2 （1）若⊙O1与⊙O2外切，求r2 .（2）若r2 =7,⊙O1与⊙O2 有怎样的位置关系？（3）若r2 =4,⊙O1与⊙O2有怎样的位置关系？大家来计算∵ ⊙O1 与⊙O2外切,
∴ r1+ r2=d
由r1=2,d=5,得 r2=3相交内切解：设⊙B的半径为R
(1)若⊙A与⊙B外切，
则 OB=4+R =10
∴R=6 cm(2)若⊙A与⊙B内切，
则 OB=R-4=10
∴R=14 cm
所以⊙B的半径为6cm或14cm..BA例2.如图⊙A的半径为4cm，点B是⊙A外一点，AB=10cm。若以B为圆心作⊙B与⊙A相切，求⊙B的半径？实例研讨·P例3：如图， ⊙O的半径为5cm，点P是⊙O内一点， OP=2cm. ⊙P与⊙O内切，则⊙P的半径是多少？ 口答题填写表格(其中R、r表示两圆的半径,d表示圆心距)d＞130≤d＜3相交内含17或391．⊙O1和⊙O2的半径分别为3 cm和4cm，若两圆外切，则d＝ .若两圆内切，则d＝____．当堂检测:3．半径为5cm的⊙O外一点P，则以点P为圆心且与⊙O相切的⊙P能画______个．2.两圆半径分别为10 cm和R,圆心距为13cm，
若这两圆相切，则R的值是___ .如果点P在⊙O内呢？4.两圆半径之比为3：5，当两圆内切时，
圆心距为4 cm，则两圆外切时圆心距的
长为____．6．两圆内切，圆心距为3，一个圆的半径为5，另一个圆的半径为 .5．两圆内切时圆心距是2，这两圆外切时圆心距是5，两圆半径分别为 、 __.外离内含外切相离相 交内切相切021d＞R+r0≤d＜R-rR-r ＜d＜R+rd=R+rd=R-r圆与圆的位置关系相切两圆的性质如果两个圆相切，那么切点一定在连心线上. 小 结1、若两圆有唯一公共点，且两圆半径分别为5和2，则两圆圆心距为 。相信自己2、 已知，两圆相外切，半径分别是1㎝和2㎝ ，要作和这两个已知圆都相切且半径等于3㎝的圆，可作_____个。7或353、两个圆的半径的比为2 : 3 ,内切时圆心距等于 8cm,那么这两圆相交时,圆心距d的取值范围是 。8cm圆的半径是4cm，则两圆的圆心距 。7、已知两圆的半径分别为3和2，如果两圆没
有公共点，则圆心距的取值范围为 。相交相切14cm或6cmd＞5或0≤d＜1
8、如图，王大伯家房屋后有一块长12m,宽8m的
矩形空地，他在以长边BC为直径的半圆内种菜.
他家养的一只羊平时拴在A处的一棵树上，拴羊
的绳长为3m.
问羊是否能吃到菜？为什么？
相交两圆的性质定理相交两圆的连心线垂直平分公共弦已知：⊙O1和⊙O2相交于A、B（如图）
求证：O1O2是AB的垂直平分线∵ O1A=O1B
∴ O1点在AB的垂直平分线上
∵ O2A=O2B
∴ O2点在AB的垂直平分线上
∴ O1O2是AB的垂直平分线证明：连结O1A、O1B、O2A、O2B如图， ⊙O的半径为5cm，点P是⊙O外（1）以P为圆心作⊙P与⊙O外切，小圆⊙P的半径是多少？（2）以P为圆心作⊙P与⊙O内切，大圆⊙P的半径是多少？A一点， OP=8cm.例题1以P为圆心作⊙P与⊙O相切，则⊙P的半径是多少？ 点P在⊙O 内，则⊙P的半径是多少？练习题·P 且OP=2cm ，⊙P与⊙O内切.例2、已知⊙O1和⊙O2内切于点A，⊙O1的弦AB交⊙O2于C，⊙O1与⊙O2的半径之比为3：2，AB=12，求BC 变1、变为外切变2、得出AC与AB的比为定值 解 ∵两圆相交 ∴R- r △ =b2-4ac=[-2(d-R)]2-4r2
=4(d-R)2-4r2
=4(d-R+r)(d-R-r)
=4[d-(R-r)][d-(R+r)]
∵d-(R-r)>0 d-(R+r)<0
∴ 4[d-(R-r)][d-(R+r)]<0
∴ 方程没有实数根 例3、已知⊙01和⊙02的半径分别为R和r(R>r),
圆心距为d,若两圆相交,试判定关于x的方
程x2-2(d-R)x+r2=0的根的情况。
例4、已知⊙O的半径为R，⊙P的半径为r（r＜R） 且⊙P的圆心P在⊙O上，设C是⊙P上一点，过点C与⊙P相切的直线交⊙O于A、B两点
（1）若点C在线段OP上，求证：PA·PB=2Rr
（2）若点C不在线段OP上，但在⊙O的内部，此时（1）中的结论是否成立？若成立，请给予证明；若不成立，请说明理由cDDDE8、这是一块铁板，上面有A、B、C三个点，经测量AB=9cm,BC=13cm,CA=
14cm,以各顶点为圆心的三个圆两两外切。求各圆的半径。xxyyzzx+y=9
y+z=13
z+x=14 一个内径3cm的圆钢管在内径为10cm的钢管内沿管壁滚动。（1）小钢管的圆心与大钢管的圆心的距离是多少？ 你一定能行（2）小钢管的圆心经过的路线是什么？(3) 若在钢管外沿管壁滚动情况又如何? 今有一圆形硬币，在这硬币的周围排列几枚同样大小的硬币，使所有的硬币都与这枚硬币相切，并彼此外切，则需硬币多少枚？试一试 1、如图1所示，在矩形ABCD中，AB=20cm，BC=4cm，点P从A开始沿折线A—B—C—D以4cm/s的速度移动，点Q从C开始沿CD边以1cm/s的速度移动，如果点P和Q分别从A和C同时出发，当其中一点到达D时，另一点也随之停止运动，设运动时间为t（s）
（1）t为何值时，四边形APQD为矩形？
（2）如图2所示，如果⊙P和⊙Q的半径都是2cm，那么t为何值时，⊙P和⊙Q外切？
?
?4t20-t20-t=4t0＜t≤5 5＜t≤6 6＜t≤11课后思考题2、如图所示，形如量角器的半圆O的直径DE＝12cm，形如三角形的△ABC中，∠ACB＝900，∠ABC＝300，BC＝12cm，半圆O以2cm/s的速度从左向右运动，在运动过程中，点D、E始终在直线BC上，设运动时间为t(s)，当t=0s时，半圆O在△ABC的左侧，OC＝8cm。
（1）当t为何值时，△ABC的一边所在直线与半圆O所在的圆直切？ACBAACBAB(C)AB(C)(C)(B)A
（2）当△ABC的一边所在直线与半圆O所在的圆相切时，如果半圆O与直线DE围成的区域与△ABC三边围成的区域有重叠部分，求重叠部分的面积。 B(C)(C)(B)AAF课后思考（2008威海市）如图，点A，B在直线MN上，AB＝11厘米，⊙A，⊙B的半径均为1厘米．⊙A以每秒2厘米的速度自左向右运动，与此同时，⊙B的半径也不断增大，其半径r（厘米）与时间t（秒）之间的关系式为r＝1+t（t≥0）．
（1）试写出点A，B之间的距离d（厘米）与时间t
（秒）之间的函数表达式；
（2）问点A出发后多少秒两圆相切？ 三、定圆⊙ O半径为4cm， 动圆⊙ P半径为1cm
（1）当两圆外切时OP为 cm？点P在什么样的圆上运动？即P点的轨迹是 。
（2）当两圆内切时OP为 cm？点P在什么样的圆上运动？即P点的轨迹是 。O 2、 ⊙Ｏ１与⊙Ｏ２的圆心O1、
O2的坐标分别是O1(3，0)、
O2(0，4)，两圆的半径分别
是R=8,r=2,则⊙Ｏ１与⊙Ｏ２
的位置关系是 .XYOO1O2 d内含··=5 例题分析