直线与圆的位置关系（1）

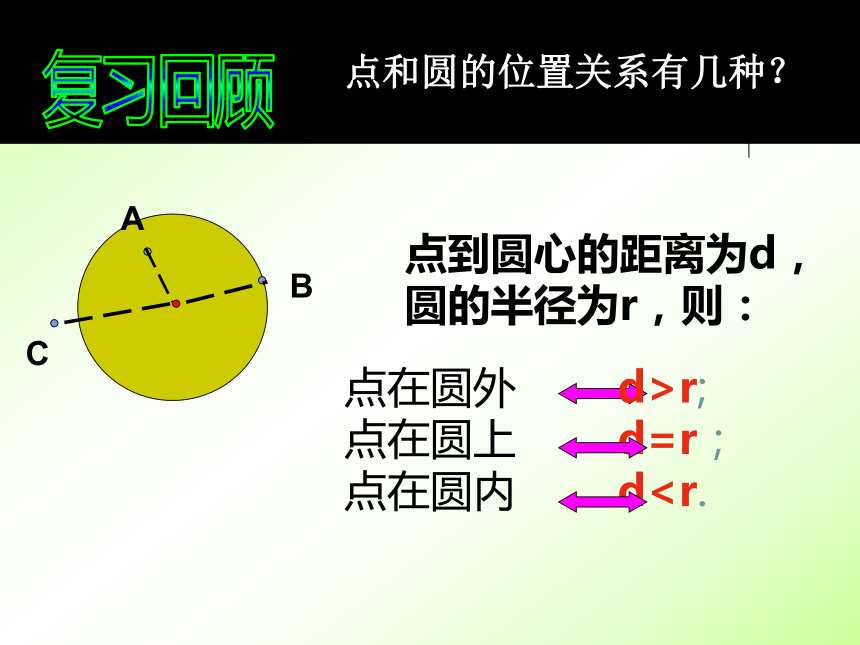
课件29张PPT。直线与圆的位置关系(1)点和圆的位置关系有几种？ 点到圆心的距离为d，圆的半径为r，则：复习回顾点在圆外 d>r;
点在圆上 d=r；
点在圆内 dABC思考：如果把点换成一条直线，直
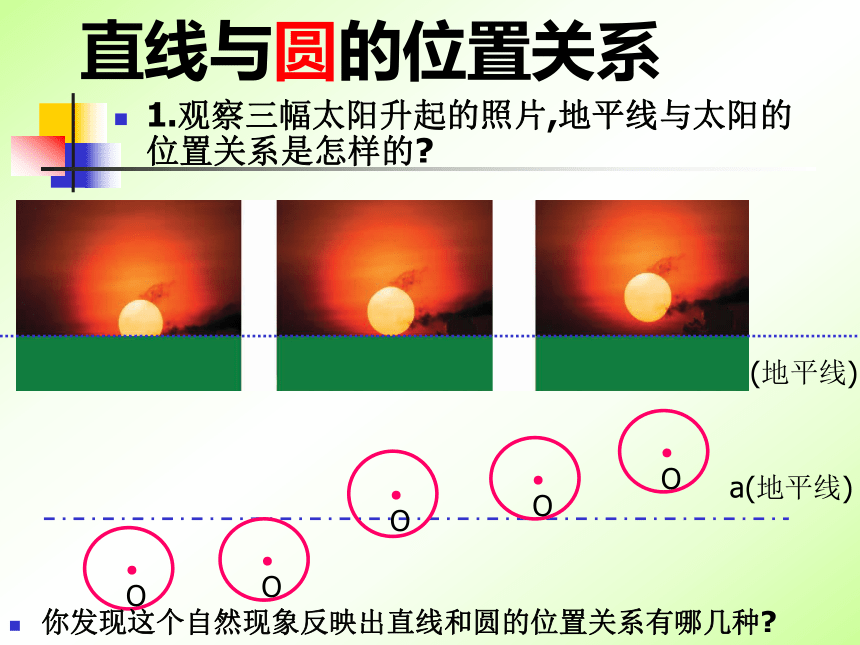
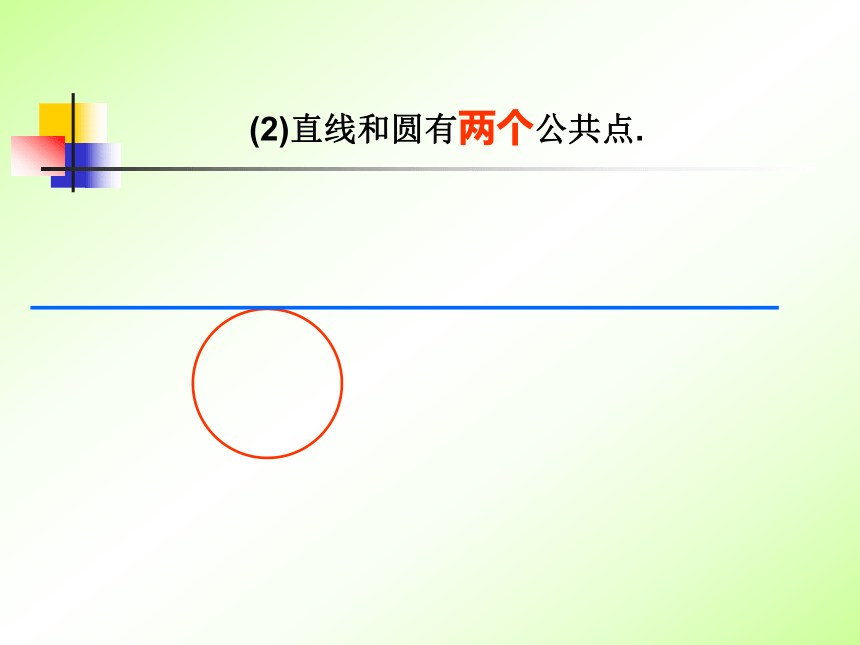
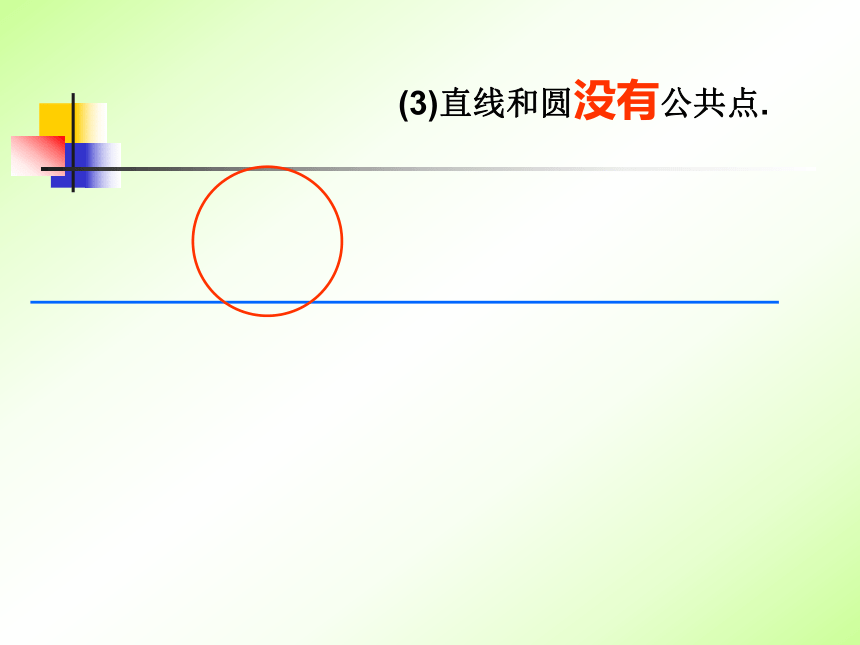
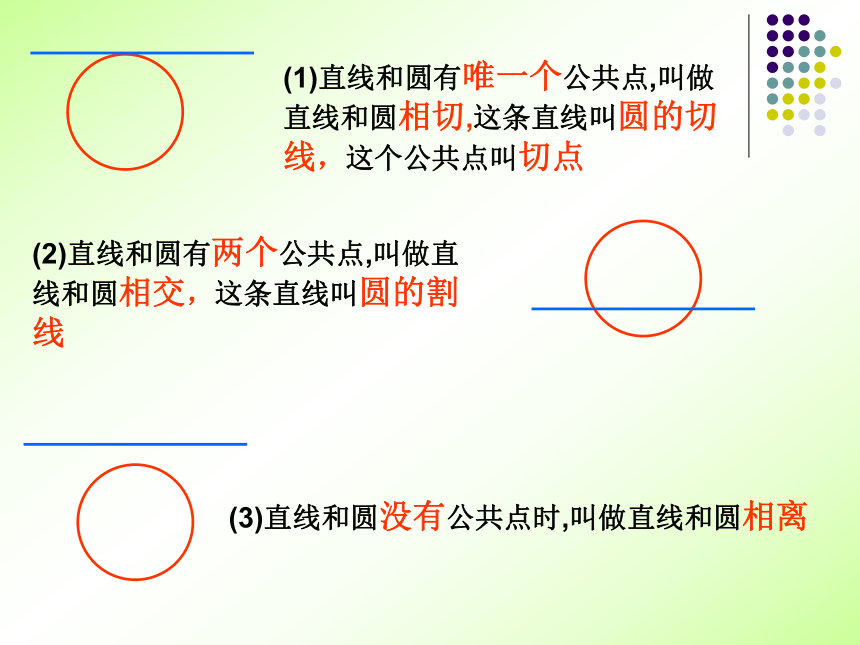
线和圆又有哪几种位置关系？新课引入直线与圆的位置关系(地平线)a(地平线)你发现这个自然现象反映出直线和圆的位置关系有哪几种?1.观察三幅太阳升起的照片,地平线与太阳的位置关系是怎样的?总体看来应该有下列三种情况:(1)直线和圆有一个公共点(2)直线和圆有两个公共点.(3)直线和圆没有公共点.(1)直线和圆有唯一个公共点,叫做直线和圆相切,这条直线叫圆的切线，这个公共点叫切点(2)直线和圆有两个公共点,叫做直线和圆相交，这条直线叫圆的割线(3)直线和圆没有公共点时,叫做直线和圆相离观察太阳落山的照片,在太阳落山的过程中,太阳与地平线(直线a)经历了哪些位置关系的变化?
a(地平线)

看图判断直线l与 ⊙O的位置关系（1）（3）（2）相离lll·O·O·O相交 小小应用注意：直线是可以无限延伸的．相切 前面复习知道:点和圆的位置关系可以用圆心到点之间的距离,这一数量关系来刻画他们的位置关系;那么直线和圆的位置关系是否也可以用数量关系来刻画他们三种位置关系呢?下面我们一起来研究一下!
利用圆心到直线的距离d与圆的半径r之间的大小关系ddd.O.O.Orrr相离相切相交1、直线与圆相离 => d>r2、直线与圆相切 => d=r3、直线与圆相交 => d<
<
想一想当直线与圆
相离、相切、
相交时，d与
r有何关系？l23.A.B.
C.D.E.F. NH.Q.你能根据d与r的大小关系确定直线与圆的位置关系吗?相交相切相离 课堂练习：210
d > 5cmd = 5cmd < 5cm 课堂练习：
例：在Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，以C为圆心，r为半径的圆与AB有怎样的位置关系？为什么？
（1）r=2cm；（2）r=2.4cm (3)r=3cm．分析：要了解AB与⊙C的位置
关系，只要知道圆心C到AB的
距离d与r的关系．已知r，只需求
出C到AB的距离d。怎样求？图上
有没有？ 例题欣赏如何作出？解：过C作CD⊥AB，垂足为D在△ABC中，AB=5根据三角形的面积公式有∴即圆心C到AB的距离d=2.4cm所以 (1)当r=2cm时,有d>r,因此⊙C和AB相离。（2）当r=2.4cm时,有d=r,因此⊙C和AB相切。（3）当r=3cm时，有d1)与圆有公共点的直线是圆的切线 ( )
2)过圆外一点画一条直线,则直线与圆相离( )
3)过圆内一点画一条直线,则直线与圆相交( )
××√2. 设⊙O的半径为3，直线a上一点到圆心的距离为3，则直线a与⊙O的位置关系是（ ）
（A）相交 （B）相切
（C）相离 （D）相切或相交D3、如图，已知∠AOB=30度，M为OB上一点，且OM=5cm，以M为圆心、r为半径的圆与直线OA有怎样的位置关系？为什么？(1) r=2cm(2) r=4cm(3) r=2.5cm答案： (1)相离(2)相交(3)相切．自我检验4.如图,在△ABC中,∠A=450,AC=4,以C为圆心,r为半径的圆与直线AB有怎样的位置关系?为什么?
(1) r=2 (2) r=2 (3) r=32相离相切相交小结：1、直线与圆的位置关系：0d>r1d=r切点切线2d以C为圆心，r为半径作圆。
①当r满足　　　　　 时， 直线ＡＢ与⊙Ｃ相离。
②当r满足　　　　　 时，直线ＡＢ与⊙Ｃ相切。
③当r满足　　　　　 时，直线ＡＢ与⊙Ｃ相交。
130﹤r﹤r=r﹥④当r满足 时,
线段ＡＢ与⊙Ｃ只有一个公共点。
5CD= cm(1)当r= 时,⊙O上有且只有1个点到直线l的距离为3;探索归纳在同一平面内,已知点O到直线l的距离为5.以点O为圆心,r为半径画圆.问题:(2)当r= 时, ⊙O上有且只有3个点到直线l的距离为3;(3)随着r的变化, ⊙O上到直线l的距离等于3的点的个数有那些变化?结束寄语具有丰富知识和经验的人，比只须一种知识和经验更容易产生新的联想和独到的见解。再见