直线与圆的位置关系（2）

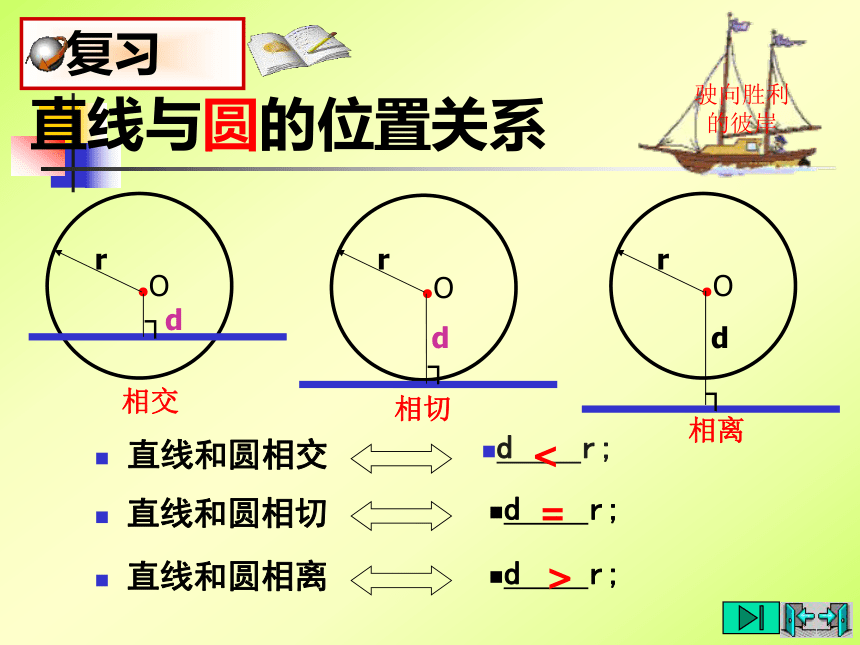
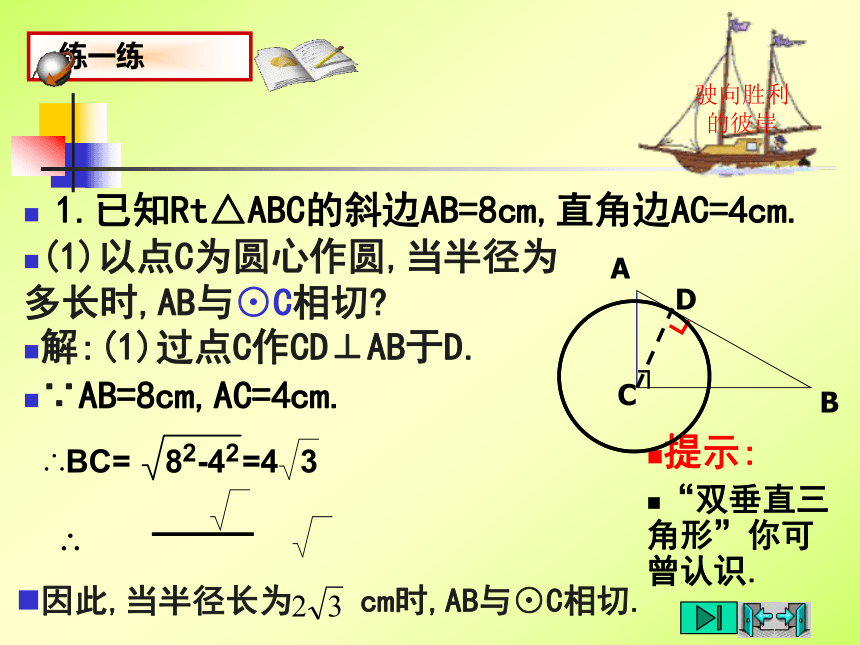
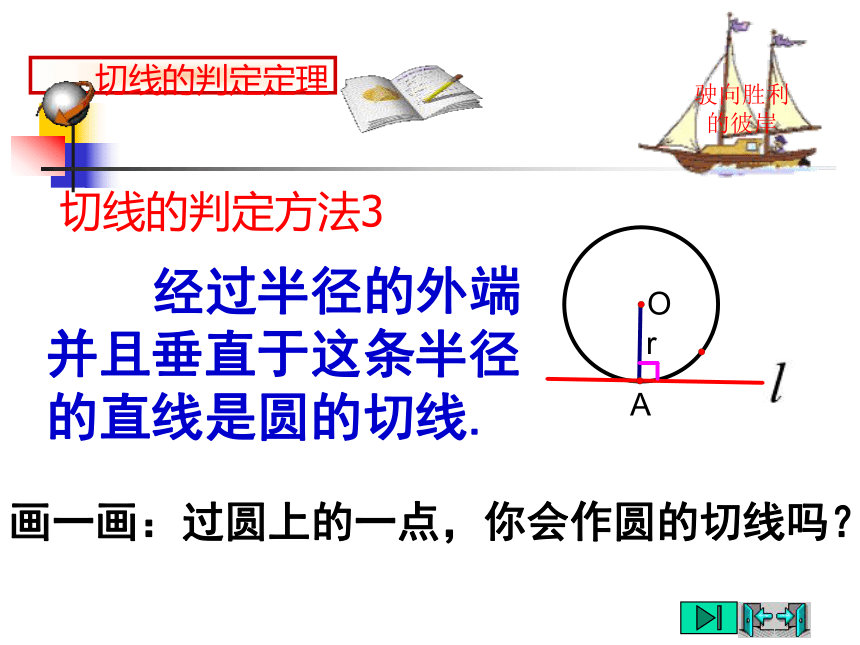
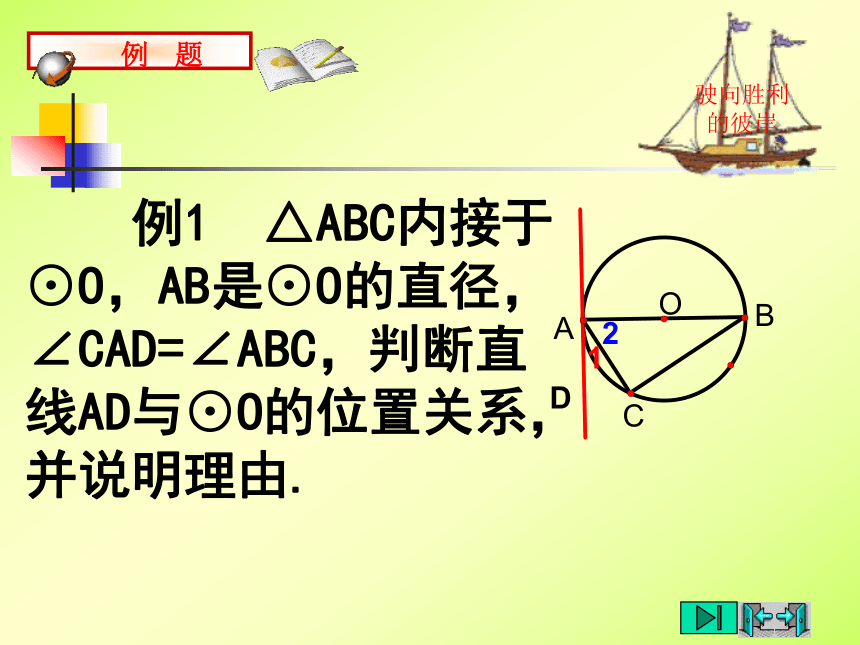
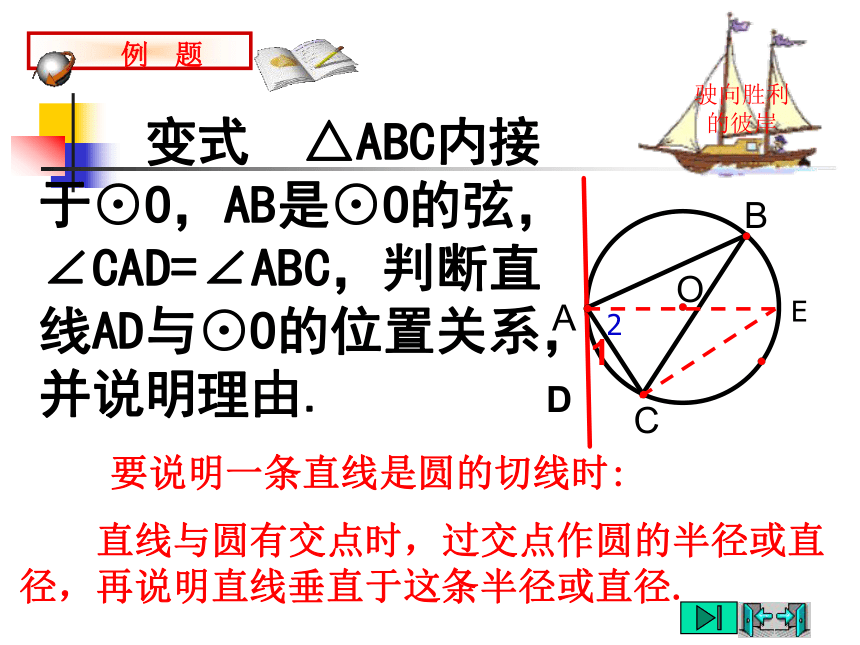
课件20张PPT。直线与圆的位置关系(2)直线和圆相交驶向胜利的彼岸d r;d r; 直线和圆相切 直线和圆相离d r;直线与圆的位置关系<=>驶向胜利的彼岸1.已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.(1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切?提示:
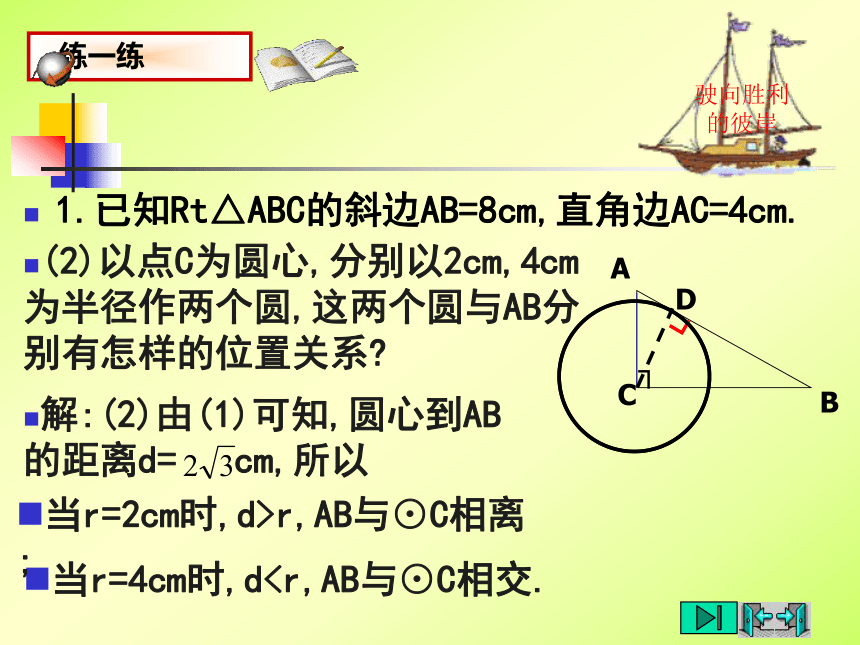
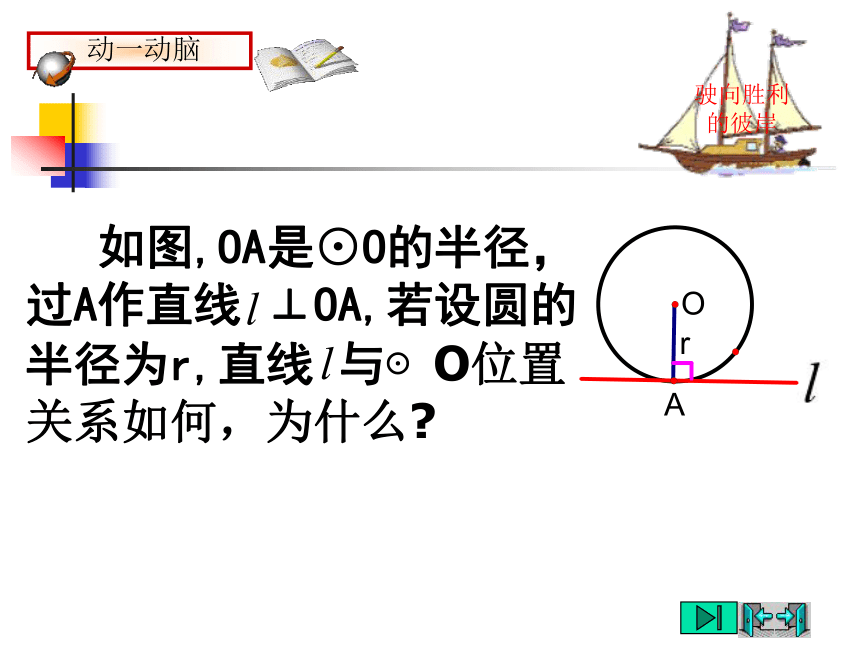
“双垂直三角形”你可曾认识.解:(1)过点C作CD⊥AB于D.∵AB=8cm,AC=4cm.因此,当半径长为 cm时,AB与⊙C相切.驶向胜利的彼岸1.已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.(2)以点C为圆心,分别以2cm,4cm为半径作两个圆,这两个圆与AB分别有怎样的位置关系?当r=4cm时,dr,AB与⊙C相离;解:(2)由(1)可知,圆心到AB的距离d= cm,所以议一议：请你说说如何判断一条直线是圆的切线？1.与圆有惟一公共点的直线是圆的切线2.与圆心距离等于半径的直线是圆的切线驶向胜利的彼岸动一动脑 如图,OA是⊙O的半径，过A作直线 ⊥OA,若设圆的半径为r,直线 与⊙O位置关系如何，为什么?驶向胜利的彼岸切线的判定定理 经过半径的外端并且垂直于这条半径的直线是圆的切线.切线的判定方法3画一画：过圆上的一点，你会作圆的切线吗？驶向胜利的彼岸例 题　　例1 △ABC内接于⊙O，AB是⊙O的直径，∠CAD=∠ABC，判断直线AD与⊙O的位置关系，并说明理由.驶向胜利的彼岸例 题　　变式 △ABC内接于⊙O，AB是⊙O的弦，∠CAD=∠ABC，判断直线AD与⊙O的位置关系，并说明理由. 要说明一条直线是圆的切线时:
直线与圆有交点时，过交点作圆的半径或直径，再说明直线垂直于这条半径或直径.如图：P是∠BAC的平分线上一点，PD⊥AC,垂足为D。AB与以P为圆心、PD为半径的圆相切吗？为什么？ 要说明一条直线是圆的切线时:
当直线与圆公共点没有确定时，则应过圆心作直线的垂线段，再说明这条垂线段等于半径.探索切线性质如图,直线CD与⊙O相切于点A,直径AB与直线CD有怎样的位置关系?说说你的理由.直径AB垂直于直线CD.驶向胜利的彼岸探索切线性质小亮的理由是:直径AB与直线CD要么垂直,要么不垂直.假设AB与CD不垂直,过点O作OM⊥CD,垂足为M,驶向胜利的彼岸则OM∵CD是⊙O的切线,A是切点, ∴CD⊥OA.已知直线和圆相切时：常
连接切点与圆心。-----辅助线驶向胜利的彼岸切线的性质定理的应用1.直线BC与半径为r的⊙O相交,且点O到直线BC的距离为5,求r的取值范围..2.一枚直径为d的硬币沿直线滚动一圈.圆心经过的距离是多少?.提示:硬币滚动一圈,圆心经过的路经是与直线平行的一条线段,其长度等于圆的周长.驶向胜利的彼岸例 题　　例2 PA、PB是⊙O的切线，切点分别为A、B，C是⊙O上一点，若∠APB=40°，
求∠ACB的度数.已知直线和圆相切时：常
连接切点与圆心。-----辅助线驶向胜利的彼岸例 题　　例3 点O是∠DPC的角平分线上的一点，⊙O与PD相切于A，
说明：PC与⊙O相切.驶向胜利的彼岸小结3.经过半径的外端并且垂直于这条半径的直线是圆的切线.切线的判定方法切线的性质3.圆的切线垂直于过切点的半径.1.与圆有惟一公共点的直线是圆的切线2.与圆心距离等于半径的直线是圆的切线1.切线与圆有惟一的公共点2.圆心到切线的距离等于半径要说明一条直线是圆的切线时 （1）直线与圆有交点时，连接交点与圆心，证垂直；
（2）直线与圆“无”交点时，过圆心作直线的垂线，证明垂线段的长等于半径.挑战自我 P136:习题5.5 5、6、7祝你成功!驶向胜利的彼岸结束寄语具有丰富知识和经验的人，比只须一种知识和经验更容易产生新的联想和独到的见解。再见