圆的对称性（2）

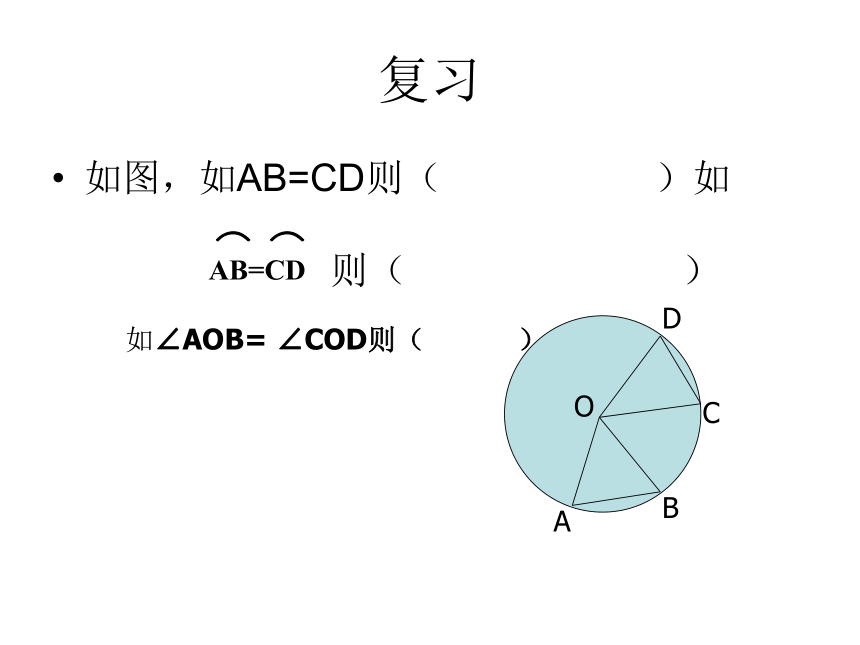
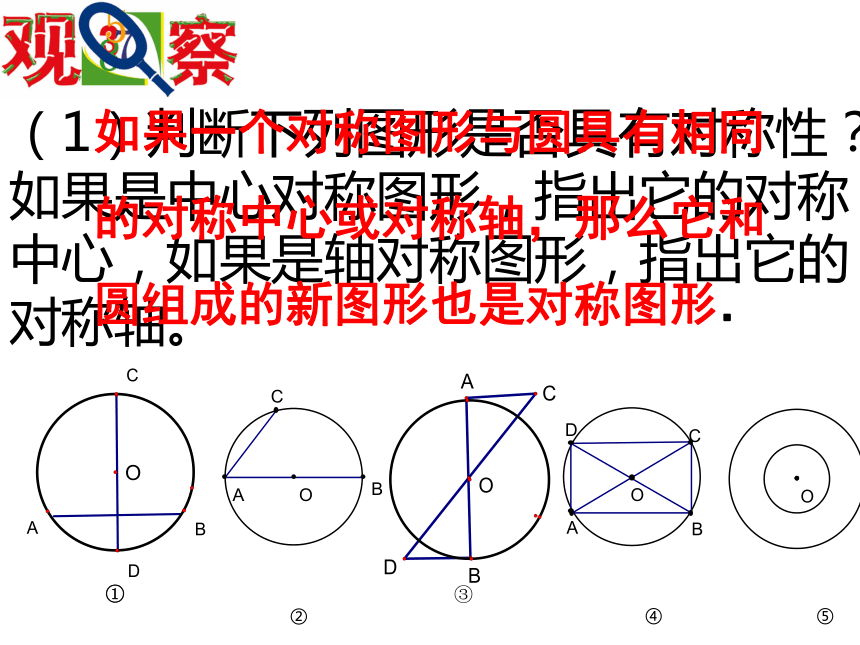
课件29张PPT。圆的对称性(2)复习如图，如AB=CD则（ ）如 OABCD如∠AOB= ∠COD则（ ）则（ ）圆的对称性圆是轴对称图形吗？它的对称轴是什么?你能找到多少条对称轴？你是用什么方法解决上述问题的?圆的对称性圆是轴对称图形.圆的对称轴是任意一条经过圆心的直线(直径所在的直线）,它有无数条对称轴.可利用折叠的方法即可解决上述问题. 如何确定圆形纸片的圆心？说说你的想法。 将圆纸片对折,确定出圆的一条直径;用同样的方法,再确定出圆的另一条直径.两条直径的交点即为圆形纸片的圆心.（1）判断下列图形是否具有对称性？如果是中心对称图形，指出它的对称中心，如果是轴对称图形，指出它的对称轴。①③如果一个对称图形与圆具有相同
的对称中心或对称轴，那么它和
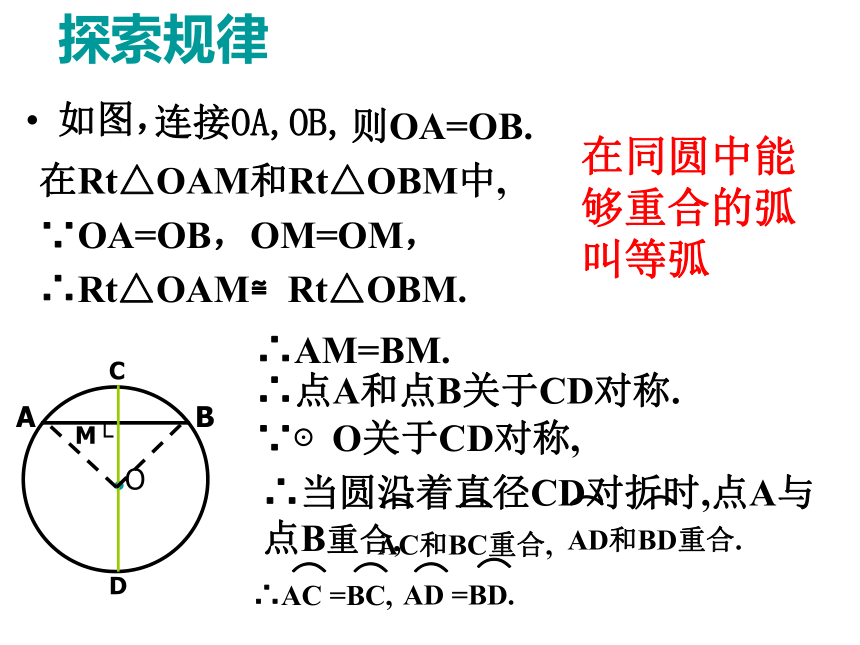
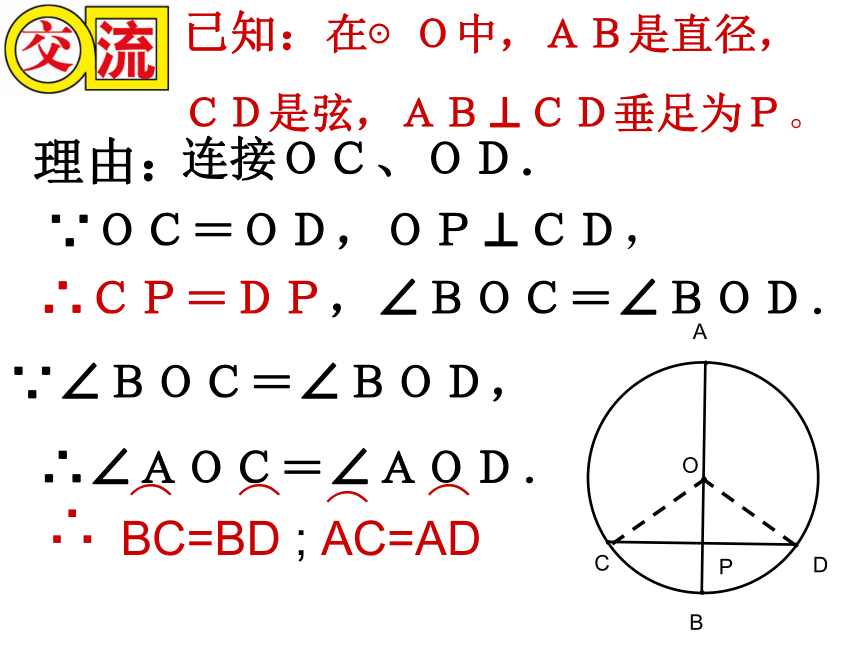
圆组成的新图形也是对称图形．③AM=BM,探索规律AB是⊙O的一条弦.你能发现图中有哪些等量关系?与同伴说说你的想法和理由.作直径CD,使CD⊥AB,垂足为M.下图是轴对称图形吗?如果是,其对称轴是什么?由 ① CD是直径② CD⊥AB如图，连接OA,OB,则OA=OB.在Rt△OAM和Rt△OBM中,∵OA=OB，OM=OM，∴Rt△OAM≌Rt△OBM.∴AM=BM.∴点A和点B关于CD对称.∵⊙O关于CD对称,∴当圆沿着直径CD对折时,点A与点B重合,探索规律在同圆中能够重合的弧叫等弧理由：连接ＯＣ、ＯＤ．∵ＯＣ＝ＯＤ，ＯＰ⊥ＣＤ，∴ＣＰ＝ＤＰ，∠ＢＯＣ＝∠ＢＯＤ．∵∠ＢＯＣ＝∠ＢＯＤ，∴∠ＡＯＣ＝∠ＡＯＤ．已知：在⊙Ｏ中，ＡＢ是直径，
ＣＤ是弦，ＡＢ⊥ＣＤ垂足为Ｐ。垂径定理 垂直于弦的直径平分弦,并且平分
弦所对的两 条弧.CD⊥弦AB,如图∵ CD是⊙O的直径（ ⊙O中，CD经过点O）,∴AM=BM,AM=BM探索规律判断下列图形是否符合垂径定理的条件例题解析例1：如图，已知在圆O中，弦AB的长为8㎝，
圆心O到AB的距离为3 ㎝，求圆O的半径。变式1:在半径为5 ㎝的圆O中，有长8 ㎝的
　　弦AB，求点O与AB的距离。
　　2：在半径为5 ㎝的圆O中，圆心O到弦AB的距离为3 ㎝，求AB的长。例2 已知：如图，在以O为圆心的两个同心圆中，大圆的弦AB交小圆于C，D两点，AC与BD相等吗？为什么？
P练习2:在圆O中，直径CE⊥AB于D，OD=4 ㎝，弦AC= ㎝ ，求圆O的半径。
　　练习1 ：如图，圆O的弦AB＝8 ㎝ ，DC＝2㎝，直径CE⊥AB于D，求半径OC的长。挑战自我画一画如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.并且AM=BM.AB拓展1.如图，AB,CD是⊙O的两条平行弦，AC与BD相等吗？为什么？⌒⌒2.在半径为5cm的⊙ O中，弦AB∥CD,且AB=6cm,CD=8cm,求AB,CD之间的距离3.如图，∠C=90°，⊙C与AB交于点D，AC=5,CB=12,求AD的长
四、圆的问题可以化归为直线型问题解决。这是
一种研究数学的重要思想 二、垂径定理：一、圆是轴对称图形，其对称轴是　　　　垂直于弦的直径平分这条弦，并且平分弦所对的弧．
三、垂径定理和勾股定理相结合，构造　　　　　　　　　　
　　直角三角形，可解决计算弦长、半　　　　　
　　径、圆心到弦的距离等问题．
　　　　　　　　　　　　　任意一
条过圆心的直线（或直径所在直线．）例2．某居民区一处圆形下水管道破裂，修理人员准备更换一段新管道．如图所示，污水水面宽度为60cm，水面至管道顶部距离为10cm，问修理人员应准备半径多大的管道？OＥＦ解：过Ｏ点作ＯＥ⊥ＡＢ，
并延长ＯＥ交⊙Ｏ于Ｆ，连接ＯＡ　垂径定理和勾股定理相结合，构
造直角三角形，把圆的问题化归
为直线形问题解决。
O思考: 在例2中,我们已计算出⊙Ｏ的半径Ｒ＝５０cm,如果水面宽度由60cm变为80cm,那么污水面下降了多少cm?O两弦在圆心同旁两弦在圆心两旁Ｒ＝５０cm；
ＣＤ＝８０cm作垂径，连半径，构造
直角三角形注意圆的对称性 如图，⊙O的直径是10，弦 AB的长为8，P是AB上的一个动点，
①则OP的求值范围是 。
②使线段OP的长度为整数值的P点
位置有 个。
p1p2C注意圆的轴对称性3≤OP≤55１．以矩形ABCD的边ＡＢ为直径
的⊙Ｏ交ＣＤ于E、F，DE=1cm,
EF=3cm,则AB=___练习：2．如图，过⊙O内一点P，作⊙O的弦AB，使它以点P为中点。
　　如上图，⊙O的直径是10，
　　线段OP的长为3，则过点P
的所有弦中，①最大弦长为 ，
②最短弦长为 ，③弦长为整数
的有 条？ 连半径，构造
直角三角形3.CD为⊙O的直径,弦AB⊥CD于点E,CE=1,AB=10,求CD的长.CD4.如图，OA=OB，AB交⊙O与点C、D，AC与BD是否相等？为什么？
５.在直径为650mm的圆柱形油罐内装进一些油后，其横截面如图，若油面宽AB=600mm，求油的最大深度。
思考题:如图，CD为圆O的直径，弦
　　AB交CD于E， ∠ CEB=30°，
　　DE=9㎝，CE=3㎝，求弦AB的长。谢谢光临!