圆的复习课

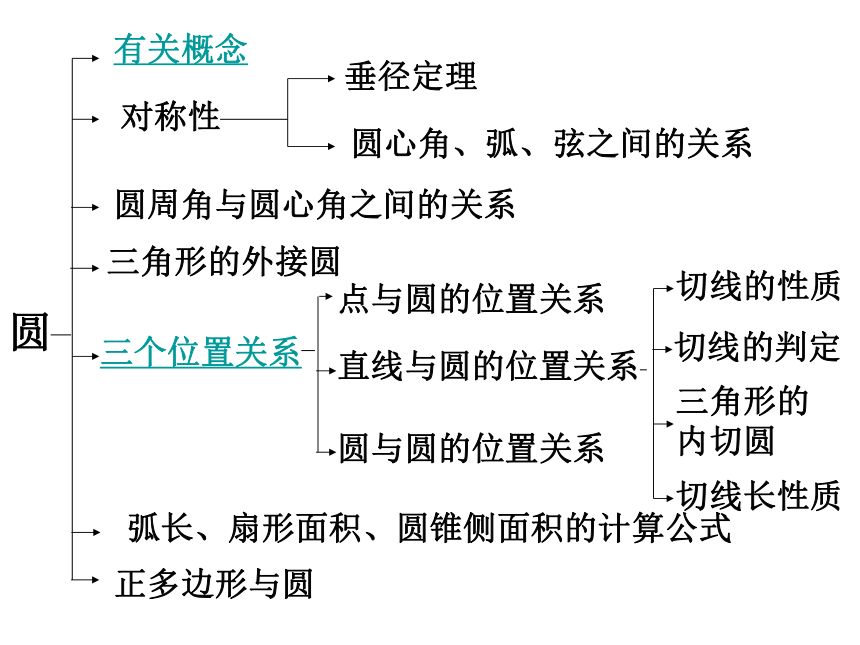
课件52张PPT。圆复习课圆有关概念对称性圆周角与圆心角之间的关系三角形的外接圆弧长、扇形面积、圆锥侧面积的计算公式垂径定理圆心角、弧、弦之间的关系三个位置关系点与圆的位置关系直线与圆的位置关系圆与圆的位置关系正多边形与圆切线的性质切线的判定三角形的内切圆切线长性质即时考你：.OADQCBPHGFE如图(1)直径是_______;

(2)弦是_____________;

(3) PQ是直径吗?______;

(4)线段EF、GH
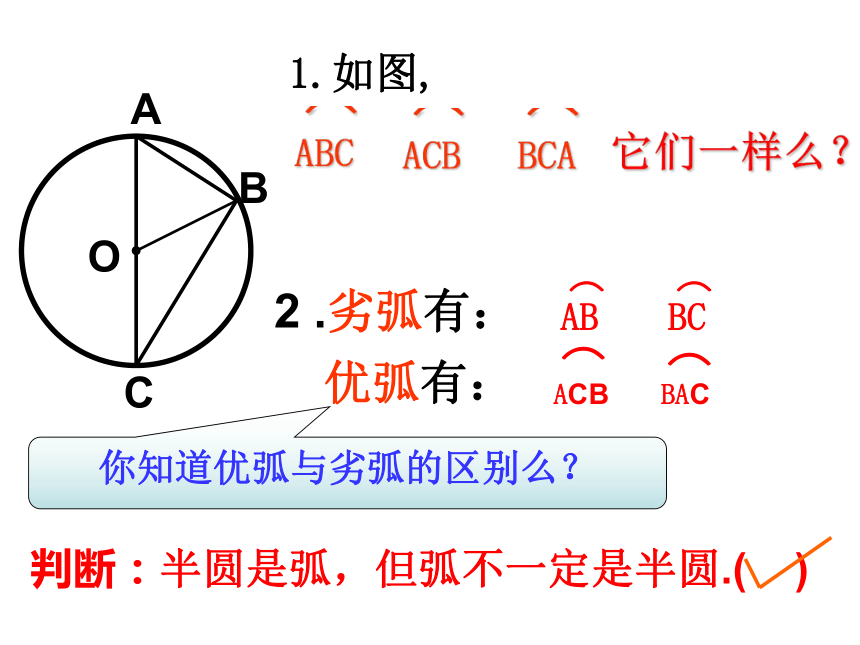
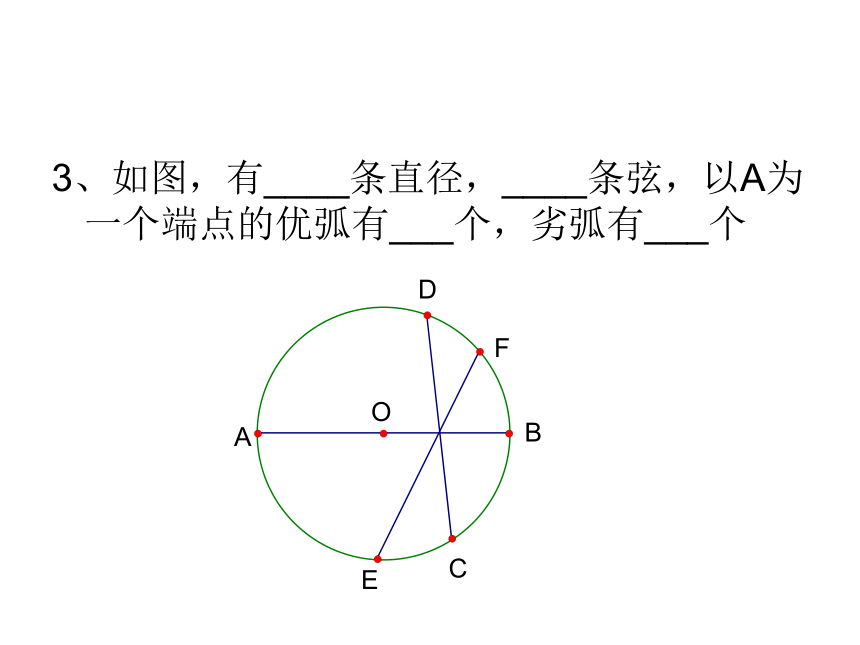
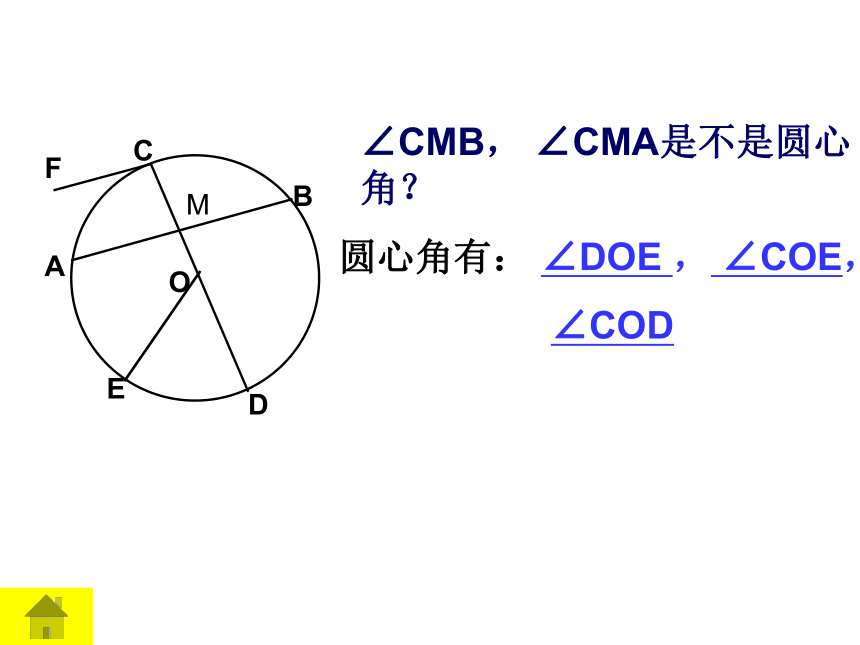
是弦吗？_______.KABCD、DK、AB不是不是在圆中有长度不等的弦，一个圆中相同长度的弦有多少条？直径是圆中最长的弦。●OBCA 1.如图,2 .劣弧有：优弧有：你知道优弧与劣弧的区别么？判断：半圆是弧，但弧不一定是半圆.( ) 3、如图，有____条直径，____条弦，以A为一个端点的优弧有___个，劣弧有___个弦与弧1、请写出图中所有的弦；2、请任选一条弦，写出这条弦所对的弧；一条弦对的弧有两条∠CMB， ∠CMA是不是圆心角？圆心角有： ∠DOE ， ∠COE，
∠COD火眼真睛判断
（1）圆是一条封闭曲线，它上面的任何一点到某个定点的距离都等于定长。
（2）圆的任何一条弦的两端点，把圆分成两条弧，所以一条弦对两条弧。
（3）到圆心的距离小于半径的点在圆上。
（4）直径是弦，且圆内最长的弦是直径。
（5）半圆是弧，弧小于半圆。1、下列说法错误的是（ ）A、圆上的点到圆心的距离相等
B、过圆心的线段是直径
C、直径是圆中最长的弦
D、半径相等的圆是等圆
2.下列说法：①直径是弦 ②弦是直径 ③半圆是弧，但弧不一定是半圆 ④长度相等的两条弧是等弧⑤完全重合的两条弧是等弧。
正确的命题有（ ）
A、1个 B、2个 C、3个 D、4个火眼真睛练习1.过圆上一点可以作圆的最长弦有( )条.
A. 1 B. 2 C. 3 D.无数条
2. M是⊙O内一点，已知过点M的⊙O最长的弦为10 cm，
最短的弦长为8 cm，则OM=?_____ cm.?
3.图中有____条直径,____条非直径的弦,圆中以A为一个
端点的优弧有____条,劣弧有____条.
4.如图, ⊙O中,点A、O、D以及点B、O、C分别在一直线
上，图中弦的条数为_____。
5.CD为⊙O的直径,∠EOD=72°,AE交⊙O于B,
且AB=OC,则∠A=_______.A12442第5题24°3如图，E是⊙O上一点，AB是⊙O的弦，OE的延长线交AB的延长线于C。如果BC=OE， ∠C=40°，求∠ EOA的度数。如图，已知AB、AC是⊙O的两条弦，且AB=AC，若∠BOC=110 °，求∠BAO的度数。返回垂径定理③AM=BM,重视：模型“垂径定理直角三角形” 若 ① CD是直径② CD⊥AB　　1.定理 垂直于弦的直径平分弦,并且平分弦所的两条弧. 在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦中,有一组量相等,那么它们所对应的其余各组量都分别相等.如由条件:③AB=A′B′①∠AOB=∠A′O′B′圆心角、弧、弦、弦心距的关系圆周角有关性质 90°的圆周角所对的弦是直径.性质: 同弧或等弧所对的圆周角相等,都等于这弧
所对的圆心角的一半. 直径所对的圆周角是直角.判断: (1) 相等的圆心角所对的弧相等.
(2)相等的圆周角所对的弧相等.
(3) 等弧所对的圆周角相等.(×)(×)(√)1．如图，已知ＡＢ、ＣＤ是⊙Ｏ的两条平行弦，⊙Ｏ的半径是５ｃｍ，ＡＢ＝８ｃｍ，ＣＤ＝６ｃｍ。求ＡＢ、ＣＤ的距离2．如图4，⊙M与x 轴相交于点A（2，0），B（8，0），
与y轴相切于点C，则圆心M的坐标是 .练习3.矩形ABCD与圆O交于A,B,E,F，DE=1cm,EF=3cm,则AB=___5.圆内接四边形ABCD中，∠A∶∠B∶∠C∶∠D可以是（ ）
　　A、1∶2∶3∶4 B、1∶3∶2∶4
　　C、4∶2∶3∶1 D、4∶2∶1∶37.如图,则∠1+∠2=__6. 在⊙O中，弦AB所对的圆心角∠AOB=100°，则弦AB所对的圆周角为____________.在⊙O中,AB、CD是直径.AD与BC平行吗?说说你的理由.四边形ACBD是什么形?为什么?
已知:如图,点O是∠EPF的平分线的一点,以O为圆心的圆和EPF的两边分别交于点A、B和C、D.
求证: ∠OBA=∠OCD返回d < r
d = r
d > r点和圆的位置关系1、⊙O的半径为R，圆心到点A的距离为d，且R、d分别是方程x2－6x＋8＝0的两根，则点A与⊙O的位置关系是（ ）
A．点A在⊙O内部 B．点A在⊙O上
C．点A在⊙O外部 D．点A不在⊙O上2、(1)如图，P是O外的一点，直线PA分别交O于点A,B,则PA是点P到O上的点的最短距离，PB是点P到O上的点的最长距离。说明理由
（2）一点和⊙O上的最近点距离为
4cm,最远距离为10cm, 则这个圆的
半径是______cm.
相交相切d＞rd＜rd=r相离210切点直线与圆的位置关系讨论　在Rt△ABC中，∠C=90°，AC=5cm,BC=12cm，以C为圆心，r为半径作圆。
①当r满足　　　　　 时， 直线ＡＢ与⊙Ｃ相离。
②当r满足　　　　　 时，直线ＡＢ与⊙Ｃ相切。
③当r满足　　　　　 时，直线ＡＢ与⊙Ｃ相交。
130﹤r﹤r=r﹥④当r满足 时,
线段ＡＢ与⊙Ｃ只有一个公共点。
5CD= cm(1)当r= 时,⊙O上有且只有1个点到直线l的距离为3;探索归纳在同一平面内,已知点O到直线l的距离为5.以点O为圆心,r为半径画圆.问题:(2)当r= 时, ⊙O上有且只有3个点到直线l的距离为3;(3)随着r的变化, ⊙O上到直线l的距离等于3的点的个数有那些变化?外离内含外切相离相 交内切相切021d＞R+r0≤d＜R-rR-r ＜d＜R+rd=R+rd=R-r圆与圆的位置关系1、若两圆有唯一公共点，且两圆半径分别为5和2，则两圆圆心距为 。3、两圆内切时圆心距是2，这两圆外切时圆心距是5，两圆半径分别为 、 __.4、两圆内切，圆心距为3，一个圆的半径为5，另一个圆的半径为 .2、已知两圆的半径分别为3和2，如果两圆没有公共点，则圆心距的取值范围为 。7、 已知，两圆相外切，半径分别是1㎝和2㎝ ，要作和这两个已知圆都相切且半径等于3㎝的圆，可作_____个。5、两圆半径为R和r（R＞r）圆心距为d且有 d2+R2=2Rd+r2则两圆位置关系为 。6、半径为5cm的⊙O外一点P，则以点P为圆心且与⊙O相切的⊙P能画______个．如果点P在⊙O内呢？（１）定义（２）圆心到直线的距离d＝圆的半径r（３）经过半径的外端,并且垂直于这条半径的直线是圆的切线.
切线的判定和性质一、切线的判定方法　如图
∵OA是⊙O的半径, 且CD⊥OA,
∴ CD是⊙O的切线.切线的判定方法3的两种应用　1、如果已知直线与圆有交点，往往要作出过这一点的半径，再证明直线垂直于这条半径即可；
　　2、如果不明确直线与圆的交点，往往要作出圆心到直线的垂线段，再证明这条垂线段等于半径即可．切线的性质3、圆的切线垂直于过切点的半径.
∵CD切⊙O于Ａ, OA是⊙O的半径∴CD⊥OA.1、与圆只有一个公共点2、到圆心的距离等于圆的半径（常用的辅助线是连接圆心和切点） 例.如图,在Rt△ABC中,∠BCA =90°,以BC为直径的⊙O交AB于点P,Q是AC的中点．判断直线PQ与⊙O的位置关系,并说明理由．解法一：猜想直线PQ与⊙O相切，理由如下：连结OP，CP∵BC为⊙O的直径∴∠BPC= 90°在Rt△ACP中,Q为斜边AC的中点∴PQ=CQ∴∠1=∠2∵OP=OC∴∠3=∠4而∠BCA=90°∴∠1+∠3=90°∴∠2+∠4= 90°即OP⊥PQ又∵OP为⊙O的半径
∴ PQ为⊙O的切线返回∴∠APC=90°例.如图，△ABC中，AB=AC，O是BC的中点，以O为圆心的圆与AB相切于点D，说明：AC是圆的切线ABCO三角形的外接圆和内切圆：ABCI三角形内切圆的圆心叫三角形的内心。三角形外接圆的圆心叫三角形的外心三角形三边垂直平分线的交点三角形三内角角平分线的交点到三角形各边的距离相等到三角形各顶点的距离相等从圆外一点向圆所引的两条切线长相等;并且这一点和圆心的连线平分两条切线的夹角.切线长性质∵PA,PB切⊙O于A,B
∴PA=PB ∠1=∠21、直角三角形的两条直角边分别是5cm和12cm，则它的外接圆半径　　，内切圆半径　　；2、一个三角形,它的周长为30cm,这个三角形的面积为30cm2 ,则它的内切圆半径为______．直角三角形的内切圆半径与三边关系.三角形的内切圆半径与圆面积.已知⊙O内切于四边形ABCD，AB=AD，连结AC、BD，由这些条件你能推出哪些结论？（不添加辅助线）(1) ∠ABD=∠ADB
(2)AC平分∠BAD
(3)AC过圆心
(4)AC垂直平分BD
(5)AB+CD=AD+BC
(6) CA平分∠BCD
(7)BC=CD
(8)S四边形ABCD=AC·BD/2
(9)△ABC≌△ADC
(10)AB2+CD2=BC2+DA2扇形的面积公式为：
S=因此扇形面积的计算公式为
S= 或 S= r弧长和扇形的面积圆锥的侧面积和全面积1、 扇形AOB的半径为12cm,
∠AOB=120°,求AB的长和扇形
的面积及周长.2 、如图,当半径为30cm的转动轮
转过120°时,传送带上的物体A平移
的距离为______.A3、小红准备自己动手用纸板制作圆锥形的生日礼帽,如图,圆锥帽底面积半径为9cm,母线长为36cm,请你帮助他们计算制作一个这样的生日礼帽需要纸板
的面积为_________.|--36cm---|9cm.4、如图有一圆锥形粮堆,其正视图为边长是6m的正三角形ABC,粮堆的母线AC的中点P处有一老鼠正在偷吃粮食此时,小猫正在B处,它要沿圆锥侧面到达P,
处捕捉老鼠,则小猫
所经过的最短路程
是_____.(保留 ).5.圆的半径为R,则弦长L的取值范
围是___________.6.在正方形铁皮上剪下一个圆形和
扇形,使之恰好围成一个圆锥模型,
设圆的半径为r,扇形半径为R,则r,
R间的关系是
________.|--R---|r对于平面图形A,如果存在一个圆,使图形A上的任意一点到圆心的距离不大于这个圆的半径,那么称图形A被这个圆所覆盖.例如,图中的三角形被一个圆所覆盖.
回答问题:1、边长为1cm的正方形被一个半径为r的圆所覆盖, r的最小值是多少?
2、边长为1cm的正三角形被一个半径为r的圆所覆盖, r的最小值是多少?
3、半径为1cm 的圆被边长为a的正方形所覆盖, a的最小值是多少?
4、半径为1cm的圆被边长为a的正三角形所覆盖, a的最小值是多少? 如图，AB是⊙O的直径，CD是∠ACB的平分线交⊙O于点D 问题（1）：你能找出图中相等的圆周角和相等的线段吗?步步高升 如图，AB是⊙O的直径，CD是∠ACB的平分线交⊙O于点D 问题（2）：图中有哪些相似的三角形？步步高升问题（3）：根据以上两个问题所得的结果，你还能得到其他结论吗？ 如图，AB是⊙O的直径，CD是∠ACB的平分线交⊙O于点D 步步高升问题（4）：若点C在半圆上运动（不和A，B重合），在此运动过程中，哪些线段是不变的，哪些线段发生了改变？ 如图，AB是⊙O的直径，CD是∠ACB的平分线交⊙O于点D 步步高升 如图，AB是⊙O的直径，CD是∠ACB的平分线交⊙O于点D 问题（5）：若点C在半圆上运动（不和A，B重合），你能求出 的值？步步高升 若将直径AB改为非直径AB，CD仍为∠ACB的
平分线， 仍为定值 吗？ 若设∠ACB=α,你能求出这个定值吗?共创佳绩3.如图，在矩形ABCD中，AB=20cm，BC=4cm，点p从A开始折线A——B——C——D以4cm/秒的 速度 移动，点Q从C开始沿CD边以1cm/秒的速度移动，如果点P、Q分别从A、C同时出发，当其中一点到达D时，另一点也随之停止运动，设运动的时间t（秒）
（1）t为何值时，四边形APQD为矩形/
（2）如图（2），如果⊙P和⊙Q的半径都是2cm，那么t为何值时， ⊙P和⊙Q外切？