第二章 有理数及其运算 单元复习(含答案)2025-2026学年数学北师大版(2024)七年级上册
文档属性
| 名称 | 第二章 有理数及其运算 单元复习(含答案)2025-2026学年数学北师大版(2024)七年级上册 | 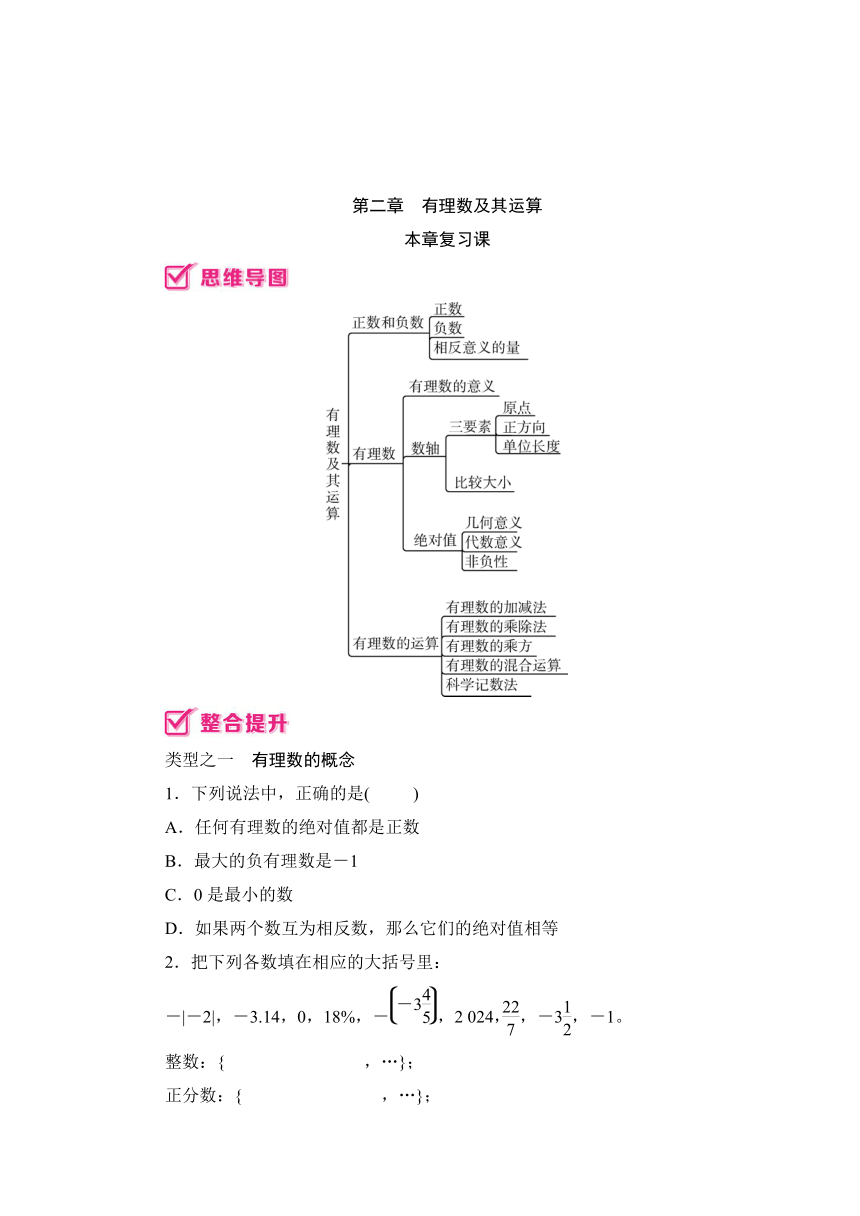 | |
| 格式 | docx | ||
| 文件大小 | 211.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-08 22:25:18 | ||
图片预览



文档简介
第二章 有理数及其运算
本章复习课
类型之一 有理数的概念
1.下列说法中,正确的是( )
A.任何有理数的绝对值都是正数
B.最大的负有理数是-1
C.0是最小的数
D.如果两个数互为相反数,那么它们的绝对值相等
2.把下列各数填在相应的大括号里:
-|-2|,-3.14,0,18%,-,2 024,,-3,-1。
整数:{ ,…};
正分数:{ ,…};
非负有理数:{ ,…}。
类型之二 相反数、倒数、绝对值等概念
3.[2024·沈阳月考]下列说法正确的是( )
A.-|-a|一定是负数
B.只有两个数相等时,它们的绝对值才相等
C.若|a|=|b|,则a与b互为相反数
D.若|a|=-a,则a是非正数
4.下列说法中,正确的是( )
A.2与-2互为倒数
B.2与互为相反数
C.0的相反数是0
D.2的绝对值是-2
类型之三 数轴与有理数
5.如图,将数轴上-6与6两点间的线段六等分,这五个等分点所对应的数依次为a1,a2,a3,a4,a5,则下列结论正确的是( )
A.a3>0
B.|a1|=|a4|
C.a1+a2+a3+a4+a5=0
D.a2+a5<0
6.在数轴上画出表示下列各数的点:-1.8,0,-|-3.5|,,-,(-1)2。再将这些数重新排成一行,并用“<”号把它们连接起来。
类型之四 科学记数法
7.“国家中小学智慧云平台”上线的某天,全国大约有5 450 000人在平台上学习,将5 450 000这个数据用科学记数法表示为( )
A.545×10 B.0.545×10
C.5.45×106 D.54.5×105
类型之五 有理数的运算
8.计算:
(1)×52-(-52)×+52÷(-4);
(2)(-1)5-×[2-(-3)3];
(3)-0.52+-|-22-4|-3×。
类型之六 有理数的混合运算的应用
9.[2024·沈阳月考]网约车司机老张某天上午8:00~9:15沿着金桥北路在高桥和东吴公园之间营运,这条路近似看成南北走向。如果规定向北为正,向南为负,他这天上午行车里程(单位:km)如下:
+3,-2,+3,-4,+3,-2,-5.5,+3。
(1)将第几名乘客送到目的地时,老张刚好回到上午出发点?
(2)将最后一名乘客送到目的地时,老张距上午出发点多远?在出发点的南面还是北面?
(3)若该网约车的收费标准为:起步价11元(不超过3 km),超过3 km,超过部分每千米2元(不足1 km按1 km算)。则老张在这天上午8:00~9:15一共收入多少元?
10.[2024·沈阳月考]如图,A,B分别为数轴上的两点,点A对应的数为-20,点B对应的数为100。
(1)请写出与A,B两点距离相等的点M所对应的数;
(2)现有一只电子蚂蚁P从点B出发,以6个单位长度/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从点A出发,以4个单位长度/秒的速度向右运动,设两只电子蚂蚁在数轴上的点C相遇,你知道点C对应的数是多少吗?
(3)若一只电子蚂蚁P从点B出发,以6个单位长度/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从点A出发,以4个单位长度/秒的速度也向左运动,请问:当它们运动多少时间时,两只蚂蚁间的距离为20个单位长度?
类型之七 数轴上的动点问题
11.[2025·沈阳市皇姑期末]如图,数轴上点A,B,C,D所表示的数分别为-4,-2,3,10,O为坐标原点。某学习小组经过验证后得到一个正确的结论:若数轴上一条线段两个端点表示的数分别为a和b,则这条线段的中点表示的数为。在此基础上,该小组给出“平均距离”的定义:在同一条直线上,两条线段的中点之间的距离称为这两条线段的“平均距离”。例如,线段AB的中点所表示的数是,线段CD的中点所表示的数是,线段AB和线段CD的“平均距离”为。
接下来同学们提出下列问题,请你解答:
(1)线段AB和线段OD的“平均距离”为 。
(2)若线段AB以每秒1个单位长度的速度向左运动,同时点C以每秒v个单位长度的速度向左运动,点O和点D静止不动,设运动时间为秒。若线段AB和线段CD的“平均距离”保持不变,求v的值。
(3)若线段AB以每秒1个单位长度的速度向右运动,点O,C,D静止不动,设运动时间为秒。当AB和CD的“平均距离”是线段BC的一半时,求t的值。
12.[2025·沈阳市浑南新区期末]我们规定将数轴上某一点P表示的数记为。对于数轴上不同的三个点A,B,C,若有,其中k为有理数,则称点B是点A关于点C的“k倍友好点”。如图,已知在数轴上,原点为O,点M,N表示的数分别为。
(1)若点N是点M关于原点O的“倍友好点”,求的值。
(2)若点T是点M关于点N的“3倍友好点”,求的值。
(3)点Q在数轴上运动(点Q不与M,N两点重合),点是点M关于点Q的“3倍友好点”,点是点N关于点Q的“倍友好点”。当点Q运动时,点Q表示的数为。
①若,求的长;(若的长是定值,请求出这个定值;若的长不是定值,请用含的代数式表示)
②若,在点Q在数轴上运动的过程中,当时,请直接写出的值。
13.[2025·丹东市期末]【基础定义】定义:在数轴上,若点到点的距离恰好是3,则称点为点的“幸运点”。若点到点的距离之和为6,则称点为点的“幸运中心”。
【基础应用】
(1)若点表示的数是-2,则点的“幸运点”点表示的数是 。
(2)已知点表示的数是,点表示的数是,且。若点为点 的“幸运中心”,则点表示的数可以是 。(填一个满足要求的数即可)
【提升应用】
(3)如图,若点表示的数是-1,点表示的数是4,点表示的数是8,一只电子蚂蚁从点出发,以每秒3个单位长度的速度沿数轴向左运动。若经过秒时,电子蚂蚁是点的“幸运中心”,求的值。
14.[2024·沈阳市皇姑期末]如图,在数轴上依次有,,三点,点,,对应的数字分别为,0,。已知,。
(1)求,的值;
(2)一动点从点出发,以每秒1个单位长度的速度向终点运动,1秒后,另一动点从点出发,以每秒2个单位长度的速度向终点运动,点,到达终点后停止运动。设点运动的时间为秒。
①当点与点相遇时,求此时的值;
②当时,请直接写出的值。
参考答案
【整合提升】
1.D 2.略 3.D 4.C 5.C
6.-|-3.5|<-1.8<0<(-1)2<<-。
7.C 8.(1)52 (2)-5 (3)-6
9.(1)将第4名乘客送到目的地时,老张刚好回到上午出发点。
(2)将最后一名乘客送到目的地时,老张距上午出发点1.5 km,在出发点的南面。
(3)老张在这天上午8:00~9:15一共收入96元。
10.(1)点M对应的数是40。
(2)点C对应的数是28。
(3)当它们运动50秒或70秒时,两只蚂蚁间的距离为20个单位长度。
11.(1)8 (2) (3)t=8或t=14
12.(1)k=-2 (2) (3)①18 ②或
13.(1)1或-5 (2)0(答案不唯一) (3)或
14.(1)a=-6,b=4 (2)①t=4 ②t的值为2或或或10。
。
本章复习课
类型之一 有理数的概念
1.下列说法中,正确的是( )
A.任何有理数的绝对值都是正数
B.最大的负有理数是-1
C.0是最小的数
D.如果两个数互为相反数,那么它们的绝对值相等
2.把下列各数填在相应的大括号里:
-|-2|,-3.14,0,18%,-,2 024,,-3,-1。
整数:{ ,…};
正分数:{ ,…};
非负有理数:{ ,…}。
类型之二 相反数、倒数、绝对值等概念
3.[2024·沈阳月考]下列说法正确的是( )
A.-|-a|一定是负数
B.只有两个数相等时,它们的绝对值才相等
C.若|a|=|b|,则a与b互为相反数
D.若|a|=-a,则a是非正数
4.下列说法中,正确的是( )
A.2与-2互为倒数
B.2与互为相反数
C.0的相反数是0
D.2的绝对值是-2
类型之三 数轴与有理数
5.如图,将数轴上-6与6两点间的线段六等分,这五个等分点所对应的数依次为a1,a2,a3,a4,a5,则下列结论正确的是( )
A.a3>0
B.|a1|=|a4|
C.a1+a2+a3+a4+a5=0
D.a2+a5<0
6.在数轴上画出表示下列各数的点:-1.8,0,-|-3.5|,,-,(-1)2。再将这些数重新排成一行,并用“<”号把它们连接起来。
类型之四 科学记数法
7.“国家中小学智慧云平台”上线的某天,全国大约有5 450 000人在平台上学习,将5 450 000这个数据用科学记数法表示为( )
A.545×10 B.0.545×10
C.5.45×106 D.54.5×105
类型之五 有理数的运算
8.计算:
(1)×52-(-52)×+52÷(-4);
(2)(-1)5-×[2-(-3)3];
(3)-0.52+-|-22-4|-3×。
类型之六 有理数的混合运算的应用
9.[2024·沈阳月考]网约车司机老张某天上午8:00~9:15沿着金桥北路在高桥和东吴公园之间营运,这条路近似看成南北走向。如果规定向北为正,向南为负,他这天上午行车里程(单位:km)如下:
+3,-2,+3,-4,+3,-2,-5.5,+3。
(1)将第几名乘客送到目的地时,老张刚好回到上午出发点?
(2)将最后一名乘客送到目的地时,老张距上午出发点多远?在出发点的南面还是北面?
(3)若该网约车的收费标准为:起步价11元(不超过3 km),超过3 km,超过部分每千米2元(不足1 km按1 km算)。则老张在这天上午8:00~9:15一共收入多少元?
10.[2024·沈阳月考]如图,A,B分别为数轴上的两点,点A对应的数为-20,点B对应的数为100。
(1)请写出与A,B两点距离相等的点M所对应的数;
(2)现有一只电子蚂蚁P从点B出发,以6个单位长度/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从点A出发,以4个单位长度/秒的速度向右运动,设两只电子蚂蚁在数轴上的点C相遇,你知道点C对应的数是多少吗?
(3)若一只电子蚂蚁P从点B出发,以6个单位长度/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从点A出发,以4个单位长度/秒的速度也向左运动,请问:当它们运动多少时间时,两只蚂蚁间的距离为20个单位长度?
类型之七 数轴上的动点问题
11.[2025·沈阳市皇姑期末]如图,数轴上点A,B,C,D所表示的数分别为-4,-2,3,10,O为坐标原点。某学习小组经过验证后得到一个正确的结论:若数轴上一条线段两个端点表示的数分别为a和b,则这条线段的中点表示的数为。在此基础上,该小组给出“平均距离”的定义:在同一条直线上,两条线段的中点之间的距离称为这两条线段的“平均距离”。例如,线段AB的中点所表示的数是,线段CD的中点所表示的数是,线段AB和线段CD的“平均距离”为。
接下来同学们提出下列问题,请你解答:
(1)线段AB和线段OD的“平均距离”为 。
(2)若线段AB以每秒1个单位长度的速度向左运动,同时点C以每秒v个单位长度的速度向左运动,点O和点D静止不动,设运动时间为秒。若线段AB和线段CD的“平均距离”保持不变,求v的值。
(3)若线段AB以每秒1个单位长度的速度向右运动,点O,C,D静止不动,设运动时间为秒。当AB和CD的“平均距离”是线段BC的一半时,求t的值。
12.[2025·沈阳市浑南新区期末]我们规定将数轴上某一点P表示的数记为。对于数轴上不同的三个点A,B,C,若有,其中k为有理数,则称点B是点A关于点C的“k倍友好点”。如图,已知在数轴上,原点为O,点M,N表示的数分别为。
(1)若点N是点M关于原点O的“倍友好点”,求的值。
(2)若点T是点M关于点N的“3倍友好点”,求的值。
(3)点Q在数轴上运动(点Q不与M,N两点重合),点是点M关于点Q的“3倍友好点”,点是点N关于点Q的“倍友好点”。当点Q运动时,点Q表示的数为。
①若,求的长;(若的长是定值,请求出这个定值;若的长不是定值,请用含的代数式表示)
②若,在点Q在数轴上运动的过程中,当时,请直接写出的值。
13.[2025·丹东市期末]【基础定义】定义:在数轴上,若点到点的距离恰好是3,则称点为点的“幸运点”。若点到点的距离之和为6,则称点为点的“幸运中心”。
【基础应用】
(1)若点表示的数是-2,则点的“幸运点”点表示的数是 。
(2)已知点表示的数是,点表示的数是,且。若点为点 的“幸运中心”,则点表示的数可以是 。(填一个满足要求的数即可)
【提升应用】
(3)如图,若点表示的数是-1,点表示的数是4,点表示的数是8,一只电子蚂蚁从点出发,以每秒3个单位长度的速度沿数轴向左运动。若经过秒时,电子蚂蚁是点的“幸运中心”,求的值。
14.[2024·沈阳市皇姑期末]如图,在数轴上依次有,,三点,点,,对应的数字分别为,0,。已知,。
(1)求,的值;
(2)一动点从点出发,以每秒1个单位长度的速度向终点运动,1秒后,另一动点从点出发,以每秒2个单位长度的速度向终点运动,点,到达终点后停止运动。设点运动的时间为秒。
①当点与点相遇时,求此时的值;
②当时,请直接写出的值。
参考答案
【整合提升】
1.D 2.略 3.D 4.C 5.C
6.-|-3.5|<-1.8<0<(-1)2<<-。
7.C 8.(1)52 (2)-5 (3)-6
9.(1)将第4名乘客送到目的地时,老张刚好回到上午出发点。
(2)将最后一名乘客送到目的地时,老张距上午出发点1.5 km,在出发点的南面。
(3)老张在这天上午8:00~9:15一共收入96元。
10.(1)点M对应的数是40。
(2)点C对应的数是28。
(3)当它们运动50秒或70秒时,两只蚂蚁间的距离为20个单位长度。
11.(1)8 (2) (3)t=8或t=14
12.(1)k=-2 (2) (3)①18 ②或
13.(1)1或-5 (2)0(答案不唯一) (3)或
14.(1)a=-6,b=4 (2)①t=4 ②t的值为2或或或10。
。
同课章节目录
