2026中考数学二次根式三年真题汇总(含解析)
文档属性
| 名称 | 2026中考数学二次根式三年真题汇总(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-09 05:08:24 | ||
图片预览




文档简介
2026中考数学二次根式三年真题汇总
考点01 有意义
1.(2025·北京·中考真题)若在实数范围内有意义,则实数x的取值范围是 .
2.(2025·黑龙江齐齐哈尔·中考真题)若代数式有意义,则实数的取值范围是 .
3.(2025·四川凉山·中考真题)若式子在实数范围内有意义,则m的取值范围是 .
4.(2024·黑龙江齐齐哈尔·中考真题)在函数中,自变量的取值范围是 .
5.(2024·上海·中考真题)已知,则 .
6.(2023·四川绵阳·中考真题)使代数式有意义的整数有( )
A.个 B.个 C.个 D.个
7.(2023·湖南永州·中考真题)已知x为正整数,写出一个使在实数的范围内没有意义的x值是 .
8.(2023·湖南·中考真题)对于二次根式的乘法运算,一般地,有.该运算法则成立的条件是( )
A. B. C. D.
考点02 二次根式的相关运算
1.(2025·安徽·中考真题)下列计算正确的是( )
A. B.
C. D.
2.(2025·四川凉山·中考真题)若,则的平方根是( )
A.8 B. C. D.
3.(2025·湖南·中考真题)化简 .
4.(2024·甘肃兰州·中考真题)计算:.
5.(2024·内蒙古呼伦贝尔·中考真题)实数在数轴上的对应位置如图所示,则的化简结果是( )
A.2 B. C. D.-2
6.(2024·内蒙古包头·中考真题)计算所得结果是( )
A.3 B. C. D.
7.(2024·青海西宁·中考真题)在一个不透明的袋中装有5个相同的小球,分别写有,,,,,随机摸出一个小球,上面的二次根式是最简二次根式的概率是 .
8.(2025·天津·中考真题)计算的结果为 .
9.(2024·江苏南京·中考真题)计算 .
10.(2024·重庆·中考真题)已知,则实数的范围是( )
A. B. C. D.
11.(2023·湖北恩施·中考真题)先化简,再求值:,其中.
12.(2025·吉林长春·中考真题)先化简.再求值:,其中.
13.(2023·湖南湘西·中考真题)先化简,再求值:,其中.
考点03 二次根式中的规律问题
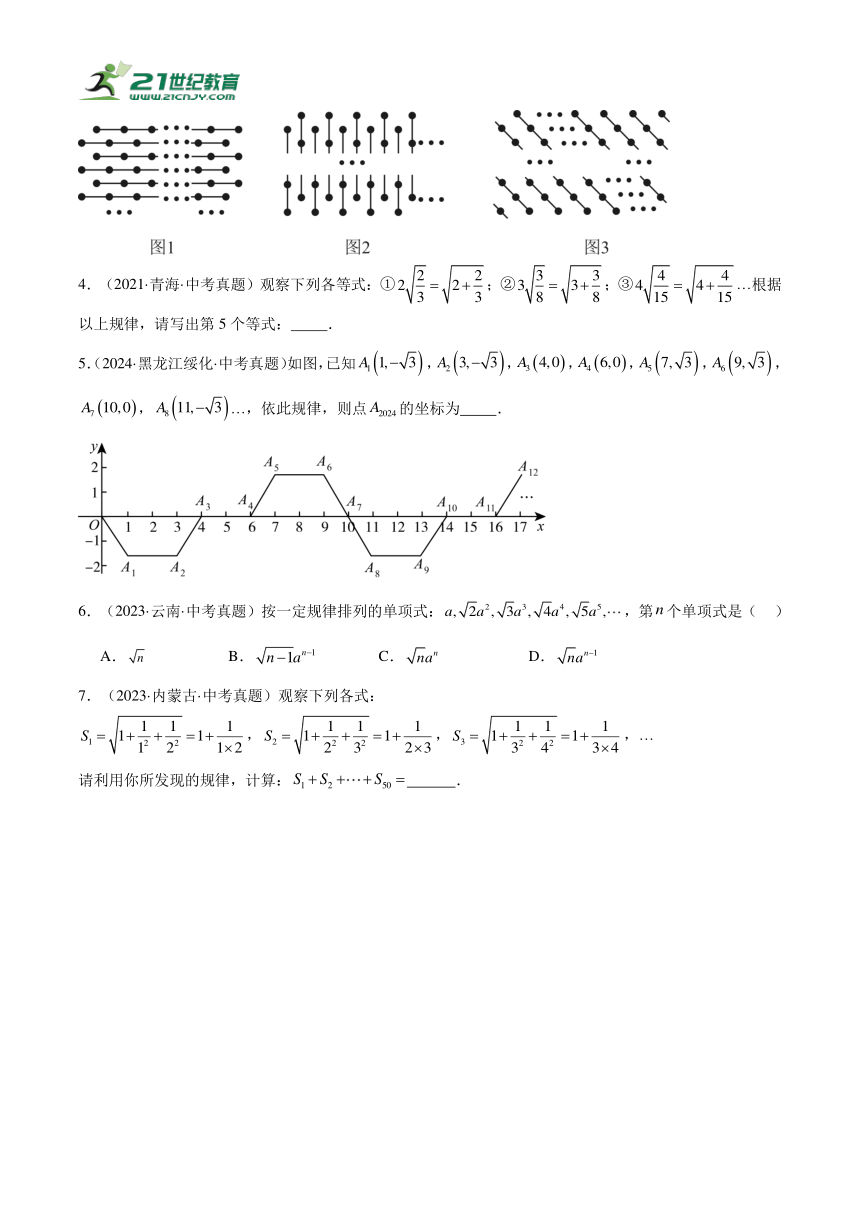
1.(2024·四川德阳·中考真题)将一组数,按以下方式进行排列:
则第八行左起第1个数是( )
A. B. C. D.
2.(2025·安徽·中考真题)综合与实践
【项目主题】
某劳动实践小组拟用正三角形和正六边形两种环保组件改善小区幼儿园室内活动场地.
【项目准备】
(1)密铺知识学习:用形状、大小完全相同的一种或几种平面图形进行拼接,使图形之间既没有空隙也没有重叠地铺成一片,叫做图形的密铺.
(2)密铺方式构建:运用密铺知识得到图1、图2所示的两种拼接方式,其中正六边形和正三角形组件的边长均为.
(3)密铺规律探究:为方便研究,称图3、图4分别为图1、图2的“拼接单元”.
观察发现:自左向右拼接图1时,每增加一个图3所示的拼接单元,则增加1个正六边形和2个正三角形,长度增加,从而x个这样的拼接单元拼成一行的长度为.
自左向右拼接图2时,每增加一个图4所示的拼接单元,则增加① 个正六边形和② 个正三角形,长度增加③ cm,从而y个这样的拼接单元拼成一行的长度为④ cm.
【项目分析】
(1)项目条件:场地为长、宽的矩形;正三角形和正六边形组件的单价分别为1元和5元.
(2)基本约定:项目成本仅计算所需组件的费用.
(3)方式确定:
(i)考虑成本因素,采用图1方式进行密铺;
(ii)每行用正六边形组件顶着左墙开始,从左向右用一个正六边形与两个正三角形组件按图1所示方式依次交替拼接,当不能继续拼接时,该行拼接结束;
(iii)第一行紧靠墙边,从前往后按相同方式逐行密铺,直至不能拼接为止.
(4)方案论证:按上述确定的方式进行密铺,有以下两种方案.
方案一:第一行沿着长度为6 m的墙自左向右拼接(如图5).
根据规律,令,解得,所以每行可以先拼块拼接单元,即共用去个正六边形和个正三角形组件,由知,所拼长度为,剩余恰好还可以摆放一个正六边形组件(如图5所示的阴影正六边形).最终需用个正六边形和个正三角形组件,由知,方案一每行的成本为元.
由于每行宽度为(按计算),设拼成s行,则,解得,故需铺行.由知,方案一所需的总成本为元.
方案二:第一行沿着长度为的墙自左向右拼接.
类似于方案一的成本计算,令
方案二每行的成本为⑤ 元,总成本为⑥ 元.
【项目实施】
根据以上分析,选用总成本较少的方案完成实践活动(略).
请将上述材料中横线上所缺内容补充完整:
________;②________;③________;④________;⑤________;⑥________.
3.(2024·江苏盐城·中考真题)发现问题
小明买菠萝时发现,通常情况下,销售员都是先削去菠萝的皮,再斜着铲去菠萝的籽.
提出问题
销售员斜着铲去菠萝的籽,除了方便操作,是否还蕴含着什么数学道理呢?
分析问题
某菠萝可以近似看成圆柱体,若忽略籽的体积和铲去果肉的厚度与宽度,那么籽在侧面展开图上可以看成点,每个点表示不同的籽.该菠萝的籽在侧面展开图上呈交错规律排列,每行有n个籽,每列有k个籽,行上相邻两籽、列上相邻两籽的间距都为d(n,k均为正整数,,),如图1所示.
小明设计了如下三种铲籽方案.
方案1:图1是横向铲籽示意图,每行铲的路径长为________,共铲________行,则铲除全部籽的路径总长为________;
方案2:图2是纵向铲籽示意图,则铲除全部籽的路径总长为________;
方案3:图3是销售员斜着铲籽示意图,写出该方案铲除全部籽的路径总长.
解决问题
在三个方案中,哪种方案铲籽路径总长最短?请写出比较过程,并对销售员的操作方法进行评价.
4.(2021·青海·中考真题)观察下列各等式:①;②;③…根据以上规律,请写出第5个等式: .
5.(2024·黑龙江绥化·中考真题)如图,已知,,,,,,,…,依此规律,则点的坐标为 .
6.(2023·云南·中考真题)按一定规律排列的单项式:,第个单项式是( )
A. B. C. D.
7.(2023·内蒙古·中考真题)观察下列各式:
,,,…
请利用你所发现的规律,计算: .
答案解析
考点01 有意义
1.(2025·北京·中考真题)若在实数范围内有意义,则实数x的取值范围是 .
【答案】
【分析】本题主要考查二次根式有意义的条件以及解一元一次不等式,熟练掌握二次根式有意义的条件是解题的关键.
此题可根据二次根式有意义的条件“被开方数要为非负数”得到不等式求解.
【详解】解:∵在实数范围内有意义,
∴,
解得:,
故答案为:.
2.(2025·黑龙江齐齐哈尔·中考真题)若代数式有意义,则实数的取值范围是 .
【答案】且
【分析】本题主要考查代数式有意义的条件,由二次根式及分式、零指数幂有意义的条件可得:且,求解即可得到答案.
【详解】解:∵代数式有意义,
∴且,
∴且.
故答案为:且.
3.(2025·四川凉山·中考真题)若式子在实数范围内有意义,则m的取值范围是 .
【答案】
【分析】本题考查了二次根式有意义的条件,分式有意义的条件,掌握二次根式有意义则被开方数非负,分式有意义则分母不为0是解题的关键.
根据二次根式有意义的条件,分式有意义的条件得到,再求解即可.
【详解】解:∵式子在实数范围内有意义,
∴,
解得:,
∴m的取值范围是,
故答案为:.
4.(2024·黑龙江齐齐哈尔·中考真题)在函数中,自变量的取值范围是 .
【答案】且
【分析】本题考查了求自变量的取值范围,根据二次根式有意义的条件和分式有意义的条件列出不等式组解答即可求解,掌握二次根式有意义的条件和分式有意义的条件是解题的关键.
【详解】解:由题意可得,,
解得且,
故答案为:且.
5.(2024·上海·中考真题)已知,则 .
【答案】1
【分析】本题主要考查了二次根式有意义的条件,掌握二次根式中的被开方数是非负数是解题的关键.由二次根式被开方数大于0可知,则可得出,求出x即可.
【详解】解:根据题意可知:,
∴,
解得:,
故答案为:1.
6.(2023·四川绵阳·中考真题)使代数式有意义的整数有( )
A.个 B.个 C.个 D.个
【答案】B
【分析】根据组合代数式有意义的条件,分别根据分式有意义的条件和二次根式有意义的条件,列不等式求解即可.
【详解】解:根据题意可得:
,
解得,
∴使代数式有意义的整数有,,0,1.
共有4个.
故选:B.
【点睛】此题主要考查了代数式有意义的条件,关键是利用分式的分母不为零和二次根式的被开方数为非负数,列不等式(组)求解,是常考题型,比较简单.
7.(2023·湖南永州·中考真题)已知x为正整数,写出一个使在实数的范围内没有意义的x值是 .
【答案】1(答案不唯一)
【分析】根据二次根式有意义的条件,可得当时,没有意义,解不等式,即可解答.
【详解】解:当时,没有意义,
解得,
为正整数,
可取1,2,
故答案为:1.
【点睛】本题考查了二次根式有意义的条件,熟知根号下的式子小于零时,二次根式无意义,是解题的关键.
8.(2023·湖南·中考真题)对于二次根式的乘法运算,一般地,有.该运算法则成立的条件是( )
A. B. C. D.
【答案】D
【分析】根据二次根式有意义的条件得出不等式组,再解不等式组即可得出结果.
【详解】解:根据二次根式有意义的条件,得,
,
故选:D.
【点睛】二次根式有意义的条件,及解不等式组,掌握二次根式有意义的条件是被开方数为非负数是本题的关键.
考点02 二次根式的相关运算
1.(2025·安徽·中考真题)下列计算正确的是( )
A. B.
C. D.
【答案】B
【分析】本题主要考查二次根式的性质,求一个数的立方根,幂的乘方,同底数幂乘法,熟练掌握相关运算法则是解题的关键;根据相关计算法则求出对应选项中式子的结果即可得到答案.
【详解】解;A、,原式计算错误,不符合题意;
B、,原式计算正确,符合题意;
C、,原式计算错误,不符合题意;
D、,原式计算错误,不符合题意;
故选;B.
2.(2025·四川凉山·中考真题)若,则的平方根是( )
A.8 B. C. D.
【答案】C
【分析】本题考查非负性,解二元一次方程组,求一个数的平方根,利用二次根式的性质进行化简,先根据非负性,得到关于的二元一次方程组,两个方程相减后求出的值,再根据平方根的定义,进行求解即可.熟练掌握非负性,平方根的定义,是解题的关键.
【详解】解:∵,
∴,
,得:,
∴的平方根是;
故选:C.
3.(2025·湖南·中考真题)化简 .
【答案】
【分析】本题主要考查了化简二次根式,利用二次根式性质化简即可.
【详解】解:,
故答案为:.
4.(2024·甘肃兰州·中考真题)计算:.
【答案】
【分析】本题考查二次根式的运算,先根据二次根式的性质化简,进行乘法运算,再合并同类二次根式即可.
【详解】解:原式
.
5.(2024·内蒙古呼伦贝尔·中考真题)实数在数轴上的对应位置如图所示,则的化简结果是( )
A.2 B. C. D.-2
【答案】A
【分析】本题考查了实数与数轴的关系,二次根式的性质和绝对值的化简法则,根据数轴可得,,,再利用二次根式的性质和绝对值的化简法则,化简计算即可.
【详解】解∶由数轴知∶,,
∴,
∴
,
故选:A.
6.(2024·内蒙古包头·中考真题)计算所得结果是( )
A.3 B. C. D.
【答案】C
【分析】本题考查化简二次根式,根据二次根式的性质,化简即可.
【详解】解:;
故选C.
7.(2024·青海西宁·中考真题)在一个不透明的袋中装有5个相同的小球,分别写有,,,,,随机摸出一个小球,上面的二次根式是最简二次根式的概率是 .
【答案】/0.4
【分析】此题考查了简单概率的计算.熟练掌握概率的意义和计算方法是解题的关键.概率是随机事件发生可能性大小的数值,计算方法是在n次等可能结果的一次试验中事件A包含其中的m种结果,A事件发生的概率为.
在5个二次根式中,,是最简二次根式,再由概率公式求解即可.
【详解】解:在,,,,这5个二次根式中,,是最简二次根式,有2个,
∴随机摸出一个小球,上面的二次根式是最简二次根式的概率是,
故答案为:.
8.(2025·天津·中考真题)计算的结果为 .
【答案】60
【分析】本题主要考查了利用平方差公式进行二次根式的运算,解题的关键是熟练掌握平方差公式.
利用平方差公式进行计算即可.
【详解】解:
,
故答案为:60.
9.(2024·江苏南京·中考真题)计算 .
【答案】
【分析】本题考查了二次根式的乘除,根据二次根式的乘除运算法则计算即可得解,熟练掌握运算法则是解此题的关键.
【详解】解:,
故答案为:.
10.(2024·重庆·中考真题)已知,则实数的范围是( )
A. B. C. D.
【答案】B
【分析】此题考查的是求无理数的取值范围,二次根式的加减运算,掌握求算术平方根的取值范围的方法是解决此题的关键.先求出,即可求出m的范围.
【详解】解:∵,
∵,
∴,
故选:B.
11.(2023·湖北恩施·中考真题)先化简,再求值:,其中.
【答案】,
【分析】先把括号内的分式进行通分,再将除法变为乘法化简,最后代入x的值计算即可.
【详解】解:原式
当时,
原式.
【点睛】本题考查了分式的化简求值和二次根式的混合运算,正确化简分式是解题的关键.
12.(2025·吉林长春·中考真题)先化简.再求值:,其中.
【答案】,4
【分析】本题主要考查整式的混合运算,根据完全平方公式将括号展开后合并得最简结果,再把代入计算即可.
【详解】解:
,
当时,原式.
13.(2023·湖南湘西·中考真题)先化简,再求值:,其中.
【答案】,
【分析】原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,最后把的值代入计算即可.
【详解】解:
当时,原式
【点睛】本题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.
考点03 二次根式中的规律问题
1.(2024·四川德阳·中考真题)将一组数,按以下方式进行排列:
则第八行左起第1个数是( )
A. B. C. D.
【答案】C
【分析】本题考查了数字类规律探索,正确归纳类推出一般规律是解题关键.求出第七行共有28个数,从而可得第八行左起第1个数是第29个数,据此求解即可得.
【详解】解:由图可知,第一行共有1个数,第二行共有2个数,第三行共有3个数,
归纳类推得:第七行共有个数,
则第八行左起第1个数是,
故选:C.
2.(2025·安徽·中考真题)综合与实践
【项目主题】
某劳动实践小组拟用正三角形和正六边形两种环保组件改善小区幼儿园室内活动场地.
【项目准备】
(1)密铺知识学习:用形状、大小完全相同的一种或几种平面图形进行拼接,使图形之间既没有空隙也没有重叠地铺成一片,叫做图形的密铺.
(2)密铺方式构建:运用密铺知识得到图1、图2所示的两种拼接方式,其中正六边形和正三角形组件的边长均为.
(3)密铺规律探究:为方便研究,称图3、图4分别为图1、图2的“拼接单元”.
观察发现:自左向右拼接图1时,每增加一个图3所示的拼接单元,则增加1个正六边形和2个正三角形,长度增加,从而x个这样的拼接单元拼成一行的长度为.
自左向右拼接图2时,每增加一个图4所示的拼接单元,则增加① 个正六边形和② 个正三角形,长度增加③ cm,从而y个这样的拼接单元拼成一行的长度为④ cm.
【项目分析】
(1)项目条件:场地为长、宽的矩形;正三角形和正六边形组件的单价分别为1元和5元.
(2)基本约定:项目成本仅计算所需组件的费用.
(3)方式确定:
(i)考虑成本因素,采用图1方式进行密铺;
(ii)每行用正六边形组件顶着左墙开始,从左向右用一个正六边形与两个正三角形组件按图1所示方式依次交替拼接,当不能继续拼接时,该行拼接结束;
(iii)第一行紧靠墙边,从前往后按相同方式逐行密铺,直至不能拼接为止.
(4)方案论证:按上述确定的方式进行密铺,有以下两种方案.
方案一:第一行沿着长度为6 m的墙自左向右拼接(如图5).
根据规律,令,解得,所以每行可以先拼块拼接单元,即共用去个正六边形和个正三角形组件,由知,所拼长度为,剩余恰好还可以摆放一个正六边形组件(如图5所示的阴影正六边形).最终需用个正六边形和个正三角形组件,由知,方案一每行的成本为元.
由于每行宽度为(按计算),设拼成s行,则,解得,故需铺行.由知,方案一所需的总成本为元.
方案二:第一行沿着长度为的墙自左向右拼接.
类似于方案一的成本计算,令
方案二每行的成本为⑤ 元,总成本为⑥ 元.
【项目实施】
根据以上分析,选用总成本较少的方案完成实践活动(略).
请将上述材料中横线上所缺内容补充完整:
________;②________;③________;④________;⑤________;⑥________.
【答案】;;;;;
【分析】本题主要考查了平面镶嵌,通过观察图4所示的拼接单元,数出增加的正六边形和正三角形的数量,再根据边长计算出长度的增加量,进而得出y个拼接单元拼成一行的长度.涉及根据给定的拼接条件进行不等式计算,以确定拼接单元数量、组件数量,
进而计算每行成本和总成本.方案二的计算方法与方案一类似.
【详解】解:项目主题:
观察图4可知,每增加一个图4所示的拼接单元,增加1个正六边形和6个正三角
形;
由正六边形和正三角形组件的边长均为,观察图4可得
增加的长度为3个边长,即
计算 y个拼接单元拼成一行的长度第一个拼接单元有一个正六边形左边的,每增加一个拼接单元长度增加,所以y个这样的拼接单元拼成一行的长度为
项目分析:
计算方案二每行可拼接的单元数量令,
移项可得,即,
两边同时除以,解得,
每行可以先拼块拼接单元.
计算方案二每行所需的正六边形和正三角形组件数量
拼块拼接单元,
共用去个正六边形和个正三角形组件.
由知,所拼长度为,
剩余,无法再摆放组件.
由知,方案二每行的成本为元.
由于每行宽度为(按计算),设拼成s行,
则,
两边同时除以,,
故需铺17行.
计算方案二的总成本.
方案二所需的总成本为元.
项目实施:
两种方案比较可知:.
选方案二完成实践活动.
故答案为:;;;;;.
3.(2024·江苏盐城·中考真题)发现问题
小明买菠萝时发现,通常情况下,销售员都是先削去菠萝的皮,再斜着铲去菠萝的籽.
提出问题
销售员斜着铲去菠萝的籽,除了方便操作,是否还蕴含着什么数学道理呢?
分析问题
某菠萝可以近似看成圆柱体,若忽略籽的体积和铲去果肉的厚度与宽度,那么籽在侧面展开图上可以看成点,每个点表示不同的籽.该菠萝的籽在侧面展开图上呈交错规律排列,每行有n个籽,每列有k个籽,行上相邻两籽、列上相邻两籽的间距都为d(n,k均为正整数,,),如图1所示.
小明设计了如下三种铲籽方案.
方案1:图1是横向铲籽示意图,每行铲的路径长为________,共铲________行,则铲除全部籽的路径总长为________;
方案2:图2是纵向铲籽示意图,则铲除全部籽的路径总长为________;
方案3:图3是销售员斜着铲籽示意图,写出该方案铲除全部籽的路径总长.
解决问题
在三个方案中,哪种方案铲籽路径总长最短?请写出比较过程,并对销售员的操作方法进行评价.
【答案】分析问题:方案1:;;;方案2:;方案3:;解决问题:方案3路径最短,理由见解析
【分析】分析问题:方案1:根据题意列出代数式即可求解;方案2:根据题意列出代数式即可求解;方案3:根据图得出斜着铲每两个点之间的距离为,根据题意得一共有列,行,斜着铲相当于有n条线段长,同时有个,即可得出总路径长;
解决问题:利用作差法比较三种方案即可.
题目主要考查列代数式,整式的加减运算,二次根式的应用,理解题意是解题关键.
【详解】解:方案1:根据题意每行有n个籽,行上相邻两籽的间距为d,
∴每行铲的路径长为,
∵每列有k个籽,呈交错规律排列,
∴相当于有行,
∴铲除全部籽的路径总长为,
故答案为:;;;
方案2:根据题意每列有k个籽,列上相邻两籽的间距为d,
∴每列铲的路径长为,
∵每行有n个籽,呈交错规律排列,,
∴相当于有列,
∴铲除全部籽的路径总长为,
故答案为:;
方案3:由图得斜着铲每两个点之间的距离为,
根据题意得一共有列,行,
斜着铲相当于有n条线段长,同时有个,
∴铲除全部籽的路径总长为:;
解决问题
由上得:,
∴方案1的路径总长大于方案2的路径总长;
,
∵,
当时,
,
,
∴方案3铲籽路径总长最短,销售员的操作方法是选择最短的路径,减少对菠萝的损耗.
4.(2021·青海·中考真题)观察下列各等式:①;②;③…根据以上规律,请写出第5个等式: .
【答案】
【分析】根据左边根号外的因数与根号内的分子相同,根号内的分母为分子平方与1的差,右边根号内为左边根号外与根号内两数之和,即可找到其中规律,从而写出第n个等式,再将n=6代入即可求出答案.
【详解】解:猜想第n个为:
(n为大于等于2的自然数);
理由如下:
∵n≥2,
∴
添项得:
,
提取公因式得:
分解分子得:
;
即:
;
第5个式子,即n=6,代入得:
,
故填:.
【点睛】本题考查二次根式的计算,需要通过观察分析和寻求规律、归纳和论证的抽象思维能力,得出一般性的结论;解答此题的关键是仔细观察、细致分析,局部找规律,整体找关系.
5.(2024·黑龙江绥化·中考真题)如图,已知,,,,,,,…,依此规律,则点的坐标为 .
【答案】
【分析】本题考查了点坐标的规律探究.解题的关键在于根据题意推导出一般性规律.根据题意可知个点坐标的纵坐标为一个循环,的坐标为,据此可求得的坐标.
【详解】解:∵,,,,,,,…,,
∴可知个点坐标的纵坐标为一个循环,的坐标为,
∵,
∴的坐标为.
∴的坐标为
故答案为:.
6.(2023·云南·中考真题)按一定规律排列的单项式:,第个单项式是( )
A. B. C. D.
【答案】C
【分析】根据单项式的规律可得,系数为,字母为,指数为1开始的自然数,据此即可求解.
【详解】解:按一定规律排列的单项式:,第个单项式是,
故选:C.
【点睛】本题考查了单项式规律题,找到单项式的变化规律是解题的关键.
7.(2023·内蒙古·中考真题)观察下列各式:
,,,…
请利用你所发现的规律,计算: .
【答案】/
【分析】直接根据已知数据变化规律进而将原式变形求出答案.
【详解】
,
故答案为:.
【点睛】本题考查数字变化规律,正确将原式变形是解题的关键.
考点01 有意义
1.(2025·北京·中考真题)若在实数范围内有意义,则实数x的取值范围是 .
2.(2025·黑龙江齐齐哈尔·中考真题)若代数式有意义,则实数的取值范围是 .
3.(2025·四川凉山·中考真题)若式子在实数范围内有意义,则m的取值范围是 .
4.(2024·黑龙江齐齐哈尔·中考真题)在函数中,自变量的取值范围是 .
5.(2024·上海·中考真题)已知,则 .
6.(2023·四川绵阳·中考真题)使代数式有意义的整数有( )
A.个 B.个 C.个 D.个
7.(2023·湖南永州·中考真题)已知x为正整数,写出一个使在实数的范围内没有意义的x值是 .
8.(2023·湖南·中考真题)对于二次根式的乘法运算,一般地,有.该运算法则成立的条件是( )
A. B. C. D.
考点02 二次根式的相关运算
1.(2025·安徽·中考真题)下列计算正确的是( )
A. B.
C. D.
2.(2025·四川凉山·中考真题)若,则的平方根是( )
A.8 B. C. D.
3.(2025·湖南·中考真题)化简 .
4.(2024·甘肃兰州·中考真题)计算:.
5.(2024·内蒙古呼伦贝尔·中考真题)实数在数轴上的对应位置如图所示,则的化简结果是( )
A.2 B. C. D.-2
6.(2024·内蒙古包头·中考真题)计算所得结果是( )
A.3 B. C. D.
7.(2024·青海西宁·中考真题)在一个不透明的袋中装有5个相同的小球,分别写有,,,,,随机摸出一个小球,上面的二次根式是最简二次根式的概率是 .
8.(2025·天津·中考真题)计算的结果为 .
9.(2024·江苏南京·中考真题)计算 .
10.(2024·重庆·中考真题)已知,则实数的范围是( )
A. B. C. D.
11.(2023·湖北恩施·中考真题)先化简,再求值:,其中.
12.(2025·吉林长春·中考真题)先化简.再求值:,其中.
13.(2023·湖南湘西·中考真题)先化简,再求值:,其中.
考点03 二次根式中的规律问题
1.(2024·四川德阳·中考真题)将一组数,按以下方式进行排列:
则第八行左起第1个数是( )
A. B. C. D.
2.(2025·安徽·中考真题)综合与实践
【项目主题】
某劳动实践小组拟用正三角形和正六边形两种环保组件改善小区幼儿园室内活动场地.
【项目准备】
(1)密铺知识学习:用形状、大小完全相同的一种或几种平面图形进行拼接,使图形之间既没有空隙也没有重叠地铺成一片,叫做图形的密铺.
(2)密铺方式构建:运用密铺知识得到图1、图2所示的两种拼接方式,其中正六边形和正三角形组件的边长均为.
(3)密铺规律探究:为方便研究,称图3、图4分别为图1、图2的“拼接单元”.
观察发现:自左向右拼接图1时,每增加一个图3所示的拼接单元,则增加1个正六边形和2个正三角形,长度增加,从而x个这样的拼接单元拼成一行的长度为.
自左向右拼接图2时,每增加一个图4所示的拼接单元,则增加① 个正六边形和② 个正三角形,长度增加③ cm,从而y个这样的拼接单元拼成一行的长度为④ cm.
【项目分析】
(1)项目条件:场地为长、宽的矩形;正三角形和正六边形组件的单价分别为1元和5元.
(2)基本约定:项目成本仅计算所需组件的费用.
(3)方式确定:
(i)考虑成本因素,采用图1方式进行密铺;
(ii)每行用正六边形组件顶着左墙开始,从左向右用一个正六边形与两个正三角形组件按图1所示方式依次交替拼接,当不能继续拼接时,该行拼接结束;
(iii)第一行紧靠墙边,从前往后按相同方式逐行密铺,直至不能拼接为止.
(4)方案论证:按上述确定的方式进行密铺,有以下两种方案.
方案一:第一行沿着长度为6 m的墙自左向右拼接(如图5).
根据规律,令,解得,所以每行可以先拼块拼接单元,即共用去个正六边形和个正三角形组件,由知,所拼长度为,剩余恰好还可以摆放一个正六边形组件(如图5所示的阴影正六边形).最终需用个正六边形和个正三角形组件,由知,方案一每行的成本为元.
由于每行宽度为(按计算),设拼成s行,则,解得,故需铺行.由知,方案一所需的总成本为元.
方案二:第一行沿着长度为的墙自左向右拼接.
类似于方案一的成本计算,令
方案二每行的成本为⑤ 元,总成本为⑥ 元.
【项目实施】
根据以上分析,选用总成本较少的方案完成实践活动(略).
请将上述材料中横线上所缺内容补充完整:
________;②________;③________;④________;⑤________;⑥________.
3.(2024·江苏盐城·中考真题)发现问题
小明买菠萝时发现,通常情况下,销售员都是先削去菠萝的皮,再斜着铲去菠萝的籽.
提出问题
销售员斜着铲去菠萝的籽,除了方便操作,是否还蕴含着什么数学道理呢?
分析问题
某菠萝可以近似看成圆柱体,若忽略籽的体积和铲去果肉的厚度与宽度,那么籽在侧面展开图上可以看成点,每个点表示不同的籽.该菠萝的籽在侧面展开图上呈交错规律排列,每行有n个籽,每列有k个籽,行上相邻两籽、列上相邻两籽的间距都为d(n,k均为正整数,,),如图1所示.
小明设计了如下三种铲籽方案.
方案1:图1是横向铲籽示意图,每行铲的路径长为________,共铲________行,则铲除全部籽的路径总长为________;
方案2:图2是纵向铲籽示意图,则铲除全部籽的路径总长为________;
方案3:图3是销售员斜着铲籽示意图,写出该方案铲除全部籽的路径总长.
解决问题
在三个方案中,哪种方案铲籽路径总长最短?请写出比较过程,并对销售员的操作方法进行评价.
4.(2021·青海·中考真题)观察下列各等式:①;②;③…根据以上规律,请写出第5个等式: .
5.(2024·黑龙江绥化·中考真题)如图,已知,,,,,,,…,依此规律,则点的坐标为 .
6.(2023·云南·中考真题)按一定规律排列的单项式:,第个单项式是( )
A. B. C. D.
7.(2023·内蒙古·中考真题)观察下列各式:
,,,…
请利用你所发现的规律,计算: .
答案解析
考点01 有意义
1.(2025·北京·中考真题)若在实数范围内有意义,则实数x的取值范围是 .
【答案】
【分析】本题主要考查二次根式有意义的条件以及解一元一次不等式,熟练掌握二次根式有意义的条件是解题的关键.
此题可根据二次根式有意义的条件“被开方数要为非负数”得到不等式求解.
【详解】解:∵在实数范围内有意义,
∴,
解得:,
故答案为:.
2.(2025·黑龙江齐齐哈尔·中考真题)若代数式有意义,则实数的取值范围是 .
【答案】且
【分析】本题主要考查代数式有意义的条件,由二次根式及分式、零指数幂有意义的条件可得:且,求解即可得到答案.
【详解】解:∵代数式有意义,
∴且,
∴且.
故答案为:且.
3.(2025·四川凉山·中考真题)若式子在实数范围内有意义,则m的取值范围是 .
【答案】
【分析】本题考查了二次根式有意义的条件,分式有意义的条件,掌握二次根式有意义则被开方数非负,分式有意义则分母不为0是解题的关键.
根据二次根式有意义的条件,分式有意义的条件得到,再求解即可.
【详解】解:∵式子在实数范围内有意义,
∴,
解得:,
∴m的取值范围是,
故答案为:.
4.(2024·黑龙江齐齐哈尔·中考真题)在函数中,自变量的取值范围是 .
【答案】且
【分析】本题考查了求自变量的取值范围,根据二次根式有意义的条件和分式有意义的条件列出不等式组解答即可求解,掌握二次根式有意义的条件和分式有意义的条件是解题的关键.
【详解】解:由题意可得,,
解得且,
故答案为:且.
5.(2024·上海·中考真题)已知,则 .
【答案】1
【分析】本题主要考查了二次根式有意义的条件,掌握二次根式中的被开方数是非负数是解题的关键.由二次根式被开方数大于0可知,则可得出,求出x即可.
【详解】解:根据题意可知:,
∴,
解得:,
故答案为:1.
6.(2023·四川绵阳·中考真题)使代数式有意义的整数有( )
A.个 B.个 C.个 D.个
【答案】B
【分析】根据组合代数式有意义的条件,分别根据分式有意义的条件和二次根式有意义的条件,列不等式求解即可.
【详解】解:根据题意可得:
,
解得,
∴使代数式有意义的整数有,,0,1.
共有4个.
故选:B.
【点睛】此题主要考查了代数式有意义的条件,关键是利用分式的分母不为零和二次根式的被开方数为非负数,列不等式(组)求解,是常考题型,比较简单.
7.(2023·湖南永州·中考真题)已知x为正整数,写出一个使在实数的范围内没有意义的x值是 .
【答案】1(答案不唯一)
【分析】根据二次根式有意义的条件,可得当时,没有意义,解不等式,即可解答.
【详解】解:当时,没有意义,
解得,
为正整数,
可取1,2,
故答案为:1.
【点睛】本题考查了二次根式有意义的条件,熟知根号下的式子小于零时,二次根式无意义,是解题的关键.
8.(2023·湖南·中考真题)对于二次根式的乘法运算,一般地,有.该运算法则成立的条件是( )
A. B. C. D.
【答案】D
【分析】根据二次根式有意义的条件得出不等式组,再解不等式组即可得出结果.
【详解】解:根据二次根式有意义的条件,得,
,
故选:D.
【点睛】二次根式有意义的条件,及解不等式组,掌握二次根式有意义的条件是被开方数为非负数是本题的关键.
考点02 二次根式的相关运算
1.(2025·安徽·中考真题)下列计算正确的是( )
A. B.
C. D.
【答案】B
【分析】本题主要考查二次根式的性质,求一个数的立方根,幂的乘方,同底数幂乘法,熟练掌握相关运算法则是解题的关键;根据相关计算法则求出对应选项中式子的结果即可得到答案.
【详解】解;A、,原式计算错误,不符合题意;
B、,原式计算正确,符合题意;
C、,原式计算错误,不符合题意;
D、,原式计算错误,不符合题意;
故选;B.
2.(2025·四川凉山·中考真题)若,则的平方根是( )
A.8 B. C. D.
【答案】C
【分析】本题考查非负性,解二元一次方程组,求一个数的平方根,利用二次根式的性质进行化简,先根据非负性,得到关于的二元一次方程组,两个方程相减后求出的值,再根据平方根的定义,进行求解即可.熟练掌握非负性,平方根的定义,是解题的关键.
【详解】解:∵,
∴,
,得:,
∴的平方根是;
故选:C.
3.(2025·湖南·中考真题)化简 .
【答案】
【分析】本题主要考查了化简二次根式,利用二次根式性质化简即可.
【详解】解:,
故答案为:.
4.(2024·甘肃兰州·中考真题)计算:.
【答案】
【分析】本题考查二次根式的运算,先根据二次根式的性质化简,进行乘法运算,再合并同类二次根式即可.
【详解】解:原式
.
5.(2024·内蒙古呼伦贝尔·中考真题)实数在数轴上的对应位置如图所示,则的化简结果是( )
A.2 B. C. D.-2
【答案】A
【分析】本题考查了实数与数轴的关系,二次根式的性质和绝对值的化简法则,根据数轴可得,,,再利用二次根式的性质和绝对值的化简法则,化简计算即可.
【详解】解∶由数轴知∶,,
∴,
∴
,
故选:A.
6.(2024·内蒙古包头·中考真题)计算所得结果是( )
A.3 B. C. D.
【答案】C
【分析】本题考查化简二次根式,根据二次根式的性质,化简即可.
【详解】解:;
故选C.
7.(2024·青海西宁·中考真题)在一个不透明的袋中装有5个相同的小球,分别写有,,,,,随机摸出一个小球,上面的二次根式是最简二次根式的概率是 .
【答案】/0.4
【分析】此题考查了简单概率的计算.熟练掌握概率的意义和计算方法是解题的关键.概率是随机事件发生可能性大小的数值,计算方法是在n次等可能结果的一次试验中事件A包含其中的m种结果,A事件发生的概率为.
在5个二次根式中,,是最简二次根式,再由概率公式求解即可.
【详解】解:在,,,,这5个二次根式中,,是最简二次根式,有2个,
∴随机摸出一个小球,上面的二次根式是最简二次根式的概率是,
故答案为:.
8.(2025·天津·中考真题)计算的结果为 .
【答案】60
【分析】本题主要考查了利用平方差公式进行二次根式的运算,解题的关键是熟练掌握平方差公式.
利用平方差公式进行计算即可.
【详解】解:
,
故答案为:60.
9.(2024·江苏南京·中考真题)计算 .
【答案】
【分析】本题考查了二次根式的乘除,根据二次根式的乘除运算法则计算即可得解,熟练掌握运算法则是解此题的关键.
【详解】解:,
故答案为:.
10.(2024·重庆·中考真题)已知,则实数的范围是( )
A. B. C. D.
【答案】B
【分析】此题考查的是求无理数的取值范围,二次根式的加减运算,掌握求算术平方根的取值范围的方法是解决此题的关键.先求出,即可求出m的范围.
【详解】解:∵,
∵,
∴,
故选:B.
11.(2023·湖北恩施·中考真题)先化简,再求值:,其中.
【答案】,
【分析】先把括号内的分式进行通分,再将除法变为乘法化简,最后代入x的值计算即可.
【详解】解:原式
当时,
原式.
【点睛】本题考查了分式的化简求值和二次根式的混合运算,正确化简分式是解题的关键.
12.(2025·吉林长春·中考真题)先化简.再求值:,其中.
【答案】,4
【分析】本题主要考查整式的混合运算,根据完全平方公式将括号展开后合并得最简结果,再把代入计算即可.
【详解】解:
,
当时,原式.
13.(2023·湖南湘西·中考真题)先化简,再求值:,其中.
【答案】,
【分析】原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,最后把的值代入计算即可.
【详解】解:
当时,原式
【点睛】本题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.
考点03 二次根式中的规律问题
1.(2024·四川德阳·中考真题)将一组数,按以下方式进行排列:
则第八行左起第1个数是( )
A. B. C. D.
【答案】C
【分析】本题考查了数字类规律探索,正确归纳类推出一般规律是解题关键.求出第七行共有28个数,从而可得第八行左起第1个数是第29个数,据此求解即可得.
【详解】解:由图可知,第一行共有1个数,第二行共有2个数,第三行共有3个数,
归纳类推得:第七行共有个数,
则第八行左起第1个数是,
故选:C.
2.(2025·安徽·中考真题)综合与实践
【项目主题】
某劳动实践小组拟用正三角形和正六边形两种环保组件改善小区幼儿园室内活动场地.
【项目准备】
(1)密铺知识学习:用形状、大小完全相同的一种或几种平面图形进行拼接,使图形之间既没有空隙也没有重叠地铺成一片,叫做图形的密铺.
(2)密铺方式构建:运用密铺知识得到图1、图2所示的两种拼接方式,其中正六边形和正三角形组件的边长均为.
(3)密铺规律探究:为方便研究,称图3、图4分别为图1、图2的“拼接单元”.
观察发现:自左向右拼接图1时,每增加一个图3所示的拼接单元,则增加1个正六边形和2个正三角形,长度增加,从而x个这样的拼接单元拼成一行的长度为.
自左向右拼接图2时,每增加一个图4所示的拼接单元,则增加① 个正六边形和② 个正三角形,长度增加③ cm,从而y个这样的拼接单元拼成一行的长度为④ cm.
【项目分析】
(1)项目条件:场地为长、宽的矩形;正三角形和正六边形组件的单价分别为1元和5元.
(2)基本约定:项目成本仅计算所需组件的费用.
(3)方式确定:
(i)考虑成本因素,采用图1方式进行密铺;
(ii)每行用正六边形组件顶着左墙开始,从左向右用一个正六边形与两个正三角形组件按图1所示方式依次交替拼接,当不能继续拼接时,该行拼接结束;
(iii)第一行紧靠墙边,从前往后按相同方式逐行密铺,直至不能拼接为止.
(4)方案论证:按上述确定的方式进行密铺,有以下两种方案.
方案一:第一行沿着长度为6 m的墙自左向右拼接(如图5).
根据规律,令,解得,所以每行可以先拼块拼接单元,即共用去个正六边形和个正三角形组件,由知,所拼长度为,剩余恰好还可以摆放一个正六边形组件(如图5所示的阴影正六边形).最终需用个正六边形和个正三角形组件,由知,方案一每行的成本为元.
由于每行宽度为(按计算),设拼成s行,则,解得,故需铺行.由知,方案一所需的总成本为元.
方案二:第一行沿着长度为的墙自左向右拼接.
类似于方案一的成本计算,令
方案二每行的成本为⑤ 元,总成本为⑥ 元.
【项目实施】
根据以上分析,选用总成本较少的方案完成实践活动(略).
请将上述材料中横线上所缺内容补充完整:
________;②________;③________;④________;⑤________;⑥________.
【答案】;;;;;
【分析】本题主要考查了平面镶嵌,通过观察图4所示的拼接单元,数出增加的正六边形和正三角形的数量,再根据边长计算出长度的增加量,进而得出y个拼接单元拼成一行的长度.涉及根据给定的拼接条件进行不等式计算,以确定拼接单元数量、组件数量,
进而计算每行成本和总成本.方案二的计算方法与方案一类似.
【详解】解:项目主题:
观察图4可知,每增加一个图4所示的拼接单元,增加1个正六边形和6个正三角
形;
由正六边形和正三角形组件的边长均为,观察图4可得
增加的长度为3个边长,即
计算 y个拼接单元拼成一行的长度第一个拼接单元有一个正六边形左边的,每增加一个拼接单元长度增加,所以y个这样的拼接单元拼成一行的长度为
项目分析:
计算方案二每行可拼接的单元数量令,
移项可得,即,
两边同时除以,解得,
每行可以先拼块拼接单元.
计算方案二每行所需的正六边形和正三角形组件数量
拼块拼接单元,
共用去个正六边形和个正三角形组件.
由知,所拼长度为,
剩余,无法再摆放组件.
由知,方案二每行的成本为元.
由于每行宽度为(按计算),设拼成s行,
则,
两边同时除以,,
故需铺17行.
计算方案二的总成本.
方案二所需的总成本为元.
项目实施:
两种方案比较可知:.
选方案二完成实践活动.
故答案为:;;;;;.
3.(2024·江苏盐城·中考真题)发现问题
小明买菠萝时发现,通常情况下,销售员都是先削去菠萝的皮,再斜着铲去菠萝的籽.
提出问题
销售员斜着铲去菠萝的籽,除了方便操作,是否还蕴含着什么数学道理呢?
分析问题
某菠萝可以近似看成圆柱体,若忽略籽的体积和铲去果肉的厚度与宽度,那么籽在侧面展开图上可以看成点,每个点表示不同的籽.该菠萝的籽在侧面展开图上呈交错规律排列,每行有n个籽,每列有k个籽,行上相邻两籽、列上相邻两籽的间距都为d(n,k均为正整数,,),如图1所示.
小明设计了如下三种铲籽方案.
方案1:图1是横向铲籽示意图,每行铲的路径长为________,共铲________行,则铲除全部籽的路径总长为________;
方案2:图2是纵向铲籽示意图,则铲除全部籽的路径总长为________;
方案3:图3是销售员斜着铲籽示意图,写出该方案铲除全部籽的路径总长.
解决问题
在三个方案中,哪种方案铲籽路径总长最短?请写出比较过程,并对销售员的操作方法进行评价.
【答案】分析问题:方案1:;;;方案2:;方案3:;解决问题:方案3路径最短,理由见解析
【分析】分析问题:方案1:根据题意列出代数式即可求解;方案2:根据题意列出代数式即可求解;方案3:根据图得出斜着铲每两个点之间的距离为,根据题意得一共有列,行,斜着铲相当于有n条线段长,同时有个,即可得出总路径长;
解决问题:利用作差法比较三种方案即可.
题目主要考查列代数式,整式的加减运算,二次根式的应用,理解题意是解题关键.
【详解】解:方案1:根据题意每行有n个籽,行上相邻两籽的间距为d,
∴每行铲的路径长为,
∵每列有k个籽,呈交错规律排列,
∴相当于有行,
∴铲除全部籽的路径总长为,
故答案为:;;;
方案2:根据题意每列有k个籽,列上相邻两籽的间距为d,
∴每列铲的路径长为,
∵每行有n个籽,呈交错规律排列,,
∴相当于有列,
∴铲除全部籽的路径总长为,
故答案为:;
方案3:由图得斜着铲每两个点之间的距离为,
根据题意得一共有列,行,
斜着铲相当于有n条线段长,同时有个,
∴铲除全部籽的路径总长为:;
解决问题
由上得:,
∴方案1的路径总长大于方案2的路径总长;
,
∵,
当时,
,
,
∴方案3铲籽路径总长最短,销售员的操作方法是选择最短的路径,减少对菠萝的损耗.
4.(2021·青海·中考真题)观察下列各等式:①;②;③…根据以上规律,请写出第5个等式: .
【答案】
【分析】根据左边根号外的因数与根号内的分子相同,根号内的分母为分子平方与1的差,右边根号内为左边根号外与根号内两数之和,即可找到其中规律,从而写出第n个等式,再将n=6代入即可求出答案.
【详解】解:猜想第n个为:
(n为大于等于2的自然数);
理由如下:
∵n≥2,
∴
添项得:
,
提取公因式得:
分解分子得:
;
即:
;
第5个式子,即n=6,代入得:
,
故填:.
【点睛】本题考查二次根式的计算,需要通过观察分析和寻求规律、归纳和论证的抽象思维能力,得出一般性的结论;解答此题的关键是仔细观察、细致分析,局部找规律,整体找关系.
5.(2024·黑龙江绥化·中考真题)如图,已知,,,,,,,…,依此规律,则点的坐标为 .
【答案】
【分析】本题考查了点坐标的规律探究.解题的关键在于根据题意推导出一般性规律.根据题意可知个点坐标的纵坐标为一个循环,的坐标为,据此可求得的坐标.
【详解】解:∵,,,,,,,…,,
∴可知个点坐标的纵坐标为一个循环,的坐标为,
∵,
∴的坐标为.
∴的坐标为
故答案为:.
6.(2023·云南·中考真题)按一定规律排列的单项式:,第个单项式是( )
A. B. C. D.
【答案】C
【分析】根据单项式的规律可得,系数为,字母为,指数为1开始的自然数,据此即可求解.
【详解】解:按一定规律排列的单项式:,第个单项式是,
故选:C.
【点睛】本题考查了单项式规律题,找到单项式的变化规律是解题的关键.
7.(2023·内蒙古·中考真题)观察下列各式:
,,,…
请利用你所发现的规律,计算: .
【答案】/
【分析】直接根据已知数据变化规律进而将原式变形求出答案.
【详解】
,
故答案为:.
【点睛】本题考查数字变化规律,正确将原式变形是解题的关键.
同课章节目录
