2026中考数学专题复习锐角三角函数三年真题汇总(含解析)
文档属性
| 名称 | 2026中考数学专题复习锐角三角函数三年真题汇总(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 15.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-09 00:00:00 | ||
图片预览


文档简介
2026中考数学专题复习锐角三角函数三年真题汇总
考点01 三角函数的定义
1.(2023·四川乐山·中考真题)我国汉代数学家赵爽在注解《周髀算经》时给出“赵爽弦图”,如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形面积为25,小正方形面积为1,则( )
A. B. C. D.
2.(2024·广西·中考真题)如图,在中,,.
(1)尺规作图:作线段的垂直平分线l,分别交,于点D,E:(要求:保留作图痕迹,不写作法,标明字母)
(2)在(1)所作的图中,连接,若,求的长.
3.(2025·山东东营·中考真题)《九章算术》是我国古代数学成就的杰出代表,其中《方田》章给出计算弧田面积所用公式为:弧田面积(弦矢+矢),弧田(如图)是由圆弧和其所对的弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.在如图所示的弧田中,“弦”为8,“矢”为2,则的值为 .
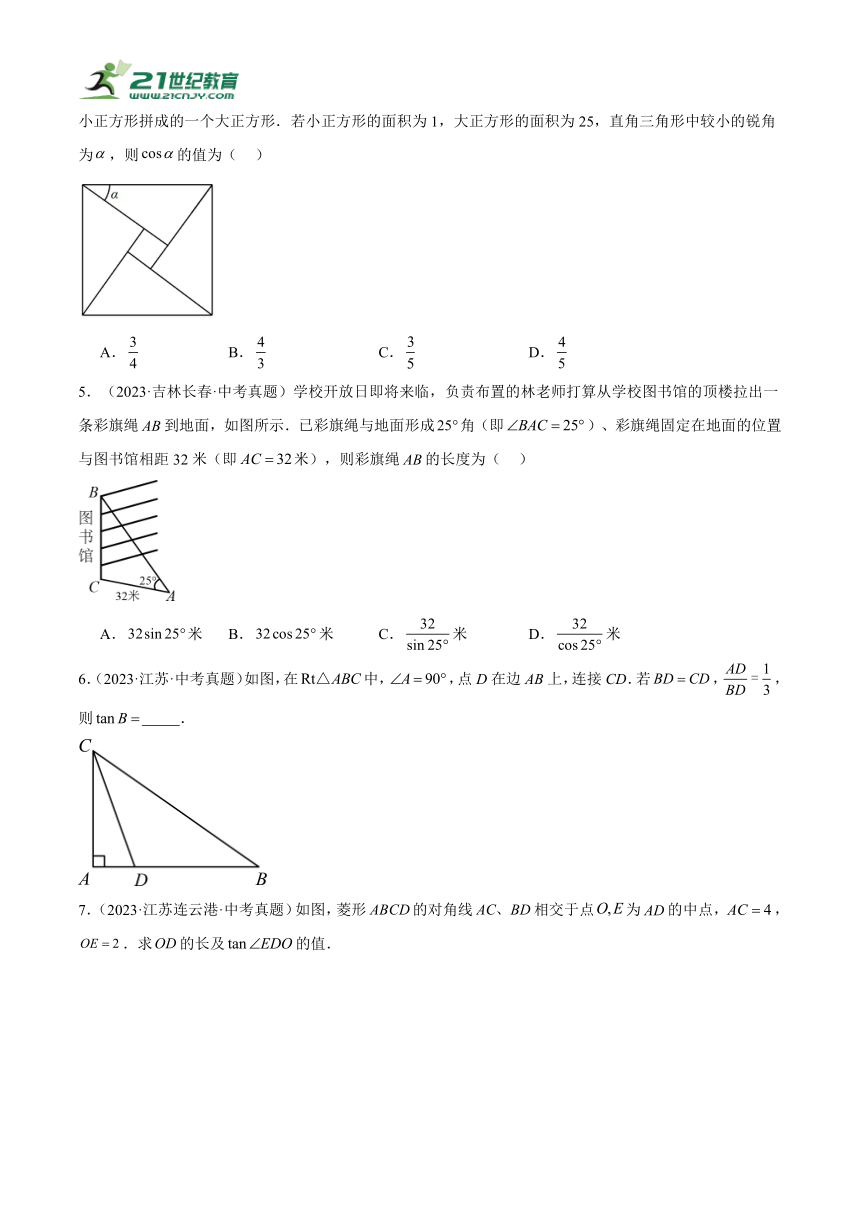
4.(2023·内蒙古·中考真题)如图是源于我国汉代数学家赵爽的弦图,它是由四个全等直角三角形与一个小正方形拼成的一个大正方形.若小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为,则的值为( )
A. B. C. D.
5.(2023·吉林长春·中考真题)学校开放日即将来临,负责布置的林老师打算从学校图书馆的顶楼拉出一条彩旗绳到地面,如图所示.已彩旗绳与地面形成角(即)、彩旗绳固定在地面的位置与图书馆相距32米(即米),则彩旗绳的长度为( )
A.米 B.米 C.米 D.米
6.(2023·江苏·中考真题)如图,在中,,点D在边AB上,连接CD.若,,则 .
7.(2023·江苏连云港·中考真题)如图,菱形的对角线相交于点为的中点,,.求的长及的值.
8.(2024·山东淄博·中考真题)如图,在综合与实践活动课上,小强先测得教学楼在水平地面上的影长为.又在点处测得该楼的顶端的仰角是.则用科学计算器计算教学楼高度的按键顺序正确的是( )
A. B.
C. D.
考点02 解直角三角形的实际应用——俯仰角
1.(2025·四川达州·中考真题)为了让莲花湖湿地公园的天更蓝,水更清,莲花湖管委会定期利用无人机指引工作人员清理湖中垃圾.已知无人机悬停在湖面上的处,工作人员所乘小船在处测得无人机的仰角为,当工作人员沿正前方向划行米到达处,测得无人机的仰角为,求无人机离湖面的高度(结果不取近似值)
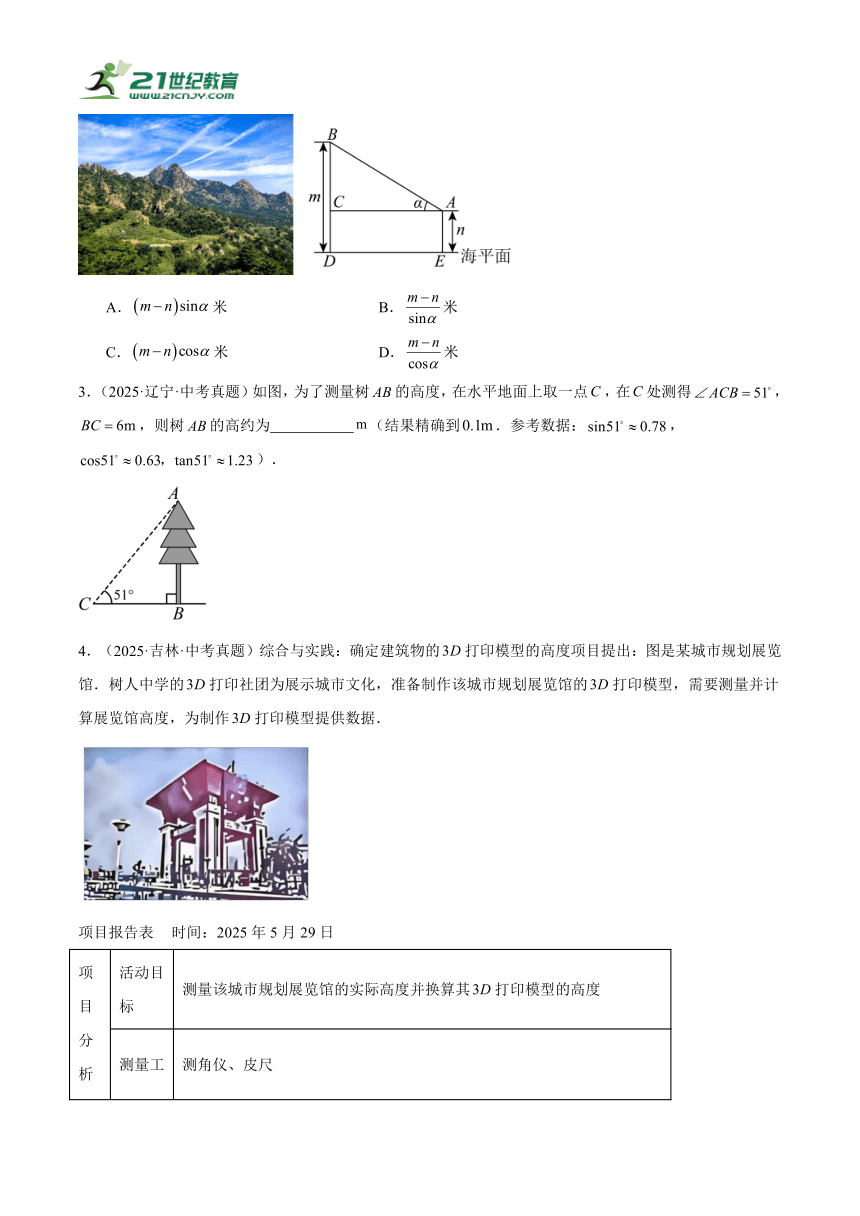
2.(2025·吉林长春·中考真题)如图,已知某山峰的海拔高度为米,一位登山者到达海拔高度为米的点处.测得山峰顶端的仰角为.则、两点之间的距离为( )
A.米 B.米
C.米 D.米
3.(2025·辽宁·中考真题)如图,为了测量树的高度,在水平地面上取一点,在处测得,,则树的高约为 (结果精确到.参考数据:,).
4.(2025·吉林·中考真题)综合与实践:确定建筑物的打印模型的高度项目提出:图是某城市规划展览馆.树人中学的打印社团为展示城市文化,准备制作该城市规划展览馆的打印模型,需要测量并计算展览馆高度,为制作打印模型提供数据.
项目报告表 时间:2025年5月29日
项目分析 活动目标 测量该城市规划展览馆的实际高度并换算其打印模型的高度
测量工具 测角仪、皮尺
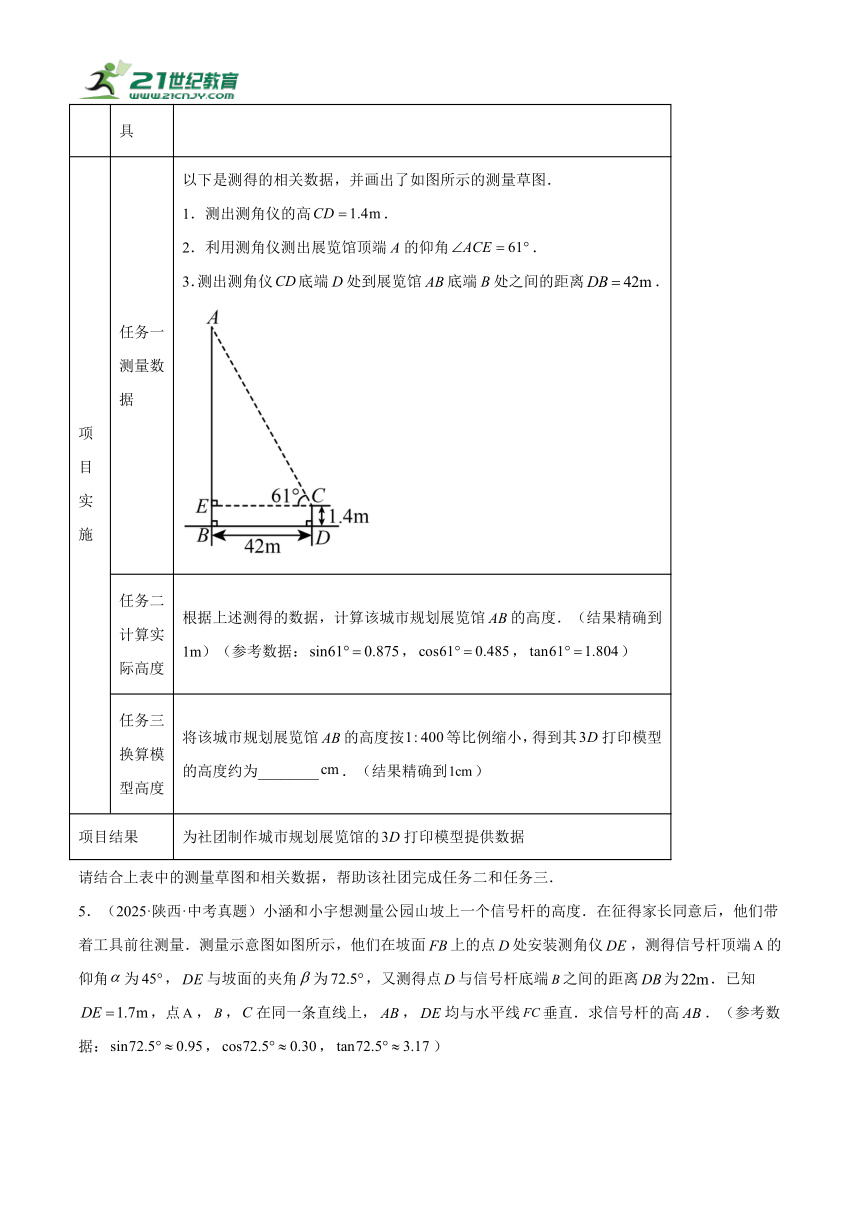
项目实施 任务一测量数据 以下是测得的相关数据,并画出了如图所示的测量草图. 1.测出测角仪的高. 2.利用测角仪测出展览馆顶端A的仰角. 3.测出测角仪底端D处到展览馆底端B处之间的距离.
任务二计算实际高度 根据上述测得的数据,计算该城市规划展览馆的高度.(结果精确到1m)(参考数据:,,)
任务三换算模型高度 将该城市规划展览馆的高度按等比例缩小,得到其打印模型的高度约为________.(结果精确到)
项目结果 为社团制作城市规划展览馆的打印模型提供数据
请结合上表中的测量草图和相关数据,帮助该社团完成任务二和任务三.
5.(2025·陕西·中考真题)小涵和小宇想测量公园山坡上一个信号杆的高度.在征得家长同意后,他们带着工具前往测量.测量示意图如图所示,他们在坡面上的点处安装测角仪,测得信号杆顶端的仰角为,与坡面的夹角为,又测得点与信号杆底端之间的距离为.已知,点,,在同一条直线上,,均与水平线垂直.求信号杆的高.(参考数据:,,)
6.(2025·安徽·中考真题)某公司为庆祝新产品上市,在甲楼与乙楼的楼顶之间悬挂彩带营造喜庆气氛.如图所示,甲楼和乙楼分别用与水平地面垂直的线段和表示,彩带用线段表示.工作人员在点A处测得点C的俯角为,测得点D的仰角为.已知,求的长(精确到).参考数据:,,,,,.
7.(2024·四川雅安·中考真题)在数学课外实践活动中,某小组测量一栋楼房的高度(如图),他们在A处仰望楼顶,测得仰角为,再往楼的方向前进50米至B处,测得仰角为,那么这栋楼的高度为(人的身高忽略不计)( )
A.米 B.25米 C.米 D.50米
8.(2024·黑龙江牡丹江·中考真题)如图,某数学活动小组用高度为米的测角仪,对垂直于地面的建筑物的高度进行测量,于点C.在B处测得A的仰角,然后将测角仪向建筑物方向水平移动6米至处,于点G,测得A的仰角,的延长线交于点E,求建筑物的高度(结果保留小数点后一位).(参考数据:)
考点03 解直角三角形的实际应用——坡度、坡角
1.(2025·四川资阳·中考真题)如图,已知水平地面上方有一个水平的平台,该平台上有一个竖直的建筑物.在处测得建筑物顶端的仰角为,在处测得的仰角为,斜坡的坡度米,.(点在同一竖直平面内).
(1)求平台的高度;
(2)求建筑物的高度(即的长).
2.(2024·四川巴中·中考真题)某兴趣小组开展了测量电线塔高度的实践活动.如图所示,斜坡的坡度,,在处测得电线塔顶部的仰角为,在处测得电线塔顶部的仰角为.
(1)求点离水平地面的高度.
(2)求电线塔的高度(结果保留根号).
3.(2024·四川眉山·中考真题)如图,斜坡的坡度,在斜坡上有一棵垂直于水平面的大树,当太阳光与水平面的夹角为时,大树在斜坡上的影子长为10米,则大树的高为 米.
4.(2024·四川广安·中考真题)风电项目对于调整能源结构和转变经济发展方式具有重要意义.某电力部门在某地安装了一批风力发电机,如图(1)某校实践活动小组对其中一架风力发电机的塔杆高度进行了测量,图(2)为测量示意图(点,,,均在同一平面内,).已知斜坡长为20米,斜坡的坡角为,在斜坡顶部处测得风力发电机塔杆顶端点的仰角为,坡底与塔杆底的距离米,求该风力发电机塔杆的高度.
(结果精确到个位;参考数据:,,,)
5.(2023·江苏泰州·中考真题)如图,堤坝长为,坡度i为,底端A在地面上,堤坝与对面的山之间有一深沟,山顶D处立有高的铁塔.小明欲测量山高,他在A处看到铁塔顶端C刚好在视线上,又在坝顶B处测得塔底D的仰角为.求堤坝高及山高.(,,,小明身高忽略不计,结果精确到)
6.(2023·湖北·中考真题)为了防洪需要,某地决定新建一座拦水坝,如图,拦水坝的横断面为梯形,斜面坡度是指坡面的铅直高度与水平宽度的比.已知斜坡长度为20米,,求斜坡的长.(结果精确到米)(参考数据:)
7.(2023·四川自贡·中考真题)为测量学校后山高度,数学兴趣小组活动过程如下:
(1)测量坡角
如图1,后山一侧有三段相对平直的山坡,山的高度即为三段坡面的铅直高度之和,坡面的长度可以直接测量得到,要求山坡高度还需要知道坡角大小.
如图2,同学们将两根直杆的一端放在坡面起始端A处,直杆沿坡面方向放置,在直杆另一端N用细线系小重物G,当直杆与铅垂线重合时,测得两杆夹角的度数,由此可得山坡AB坡角的度数.请直接写出之间的数量关系.
(2)测量山高
同学们测得山坡的坡长依次为40米,50米,40米,坡角依次为;为求,小熠同学在作业本上画了一个含角的(如图3),量得.求山高.(,结果精确到1米)
(3)测量改进
由于测量工作量较大,同学们围绕如何优化测量进行了深入探究,有了以下新的测量方法.
如图4,5,在学校操场上,将直杆NP置于的顶端,当与铅垂线重合时,转动直杆,使点N,P,D共线,测得的度数,从而得到山顶仰角,向后山方向前进40米,采用相同方式,测得山顶仰角;画一个含的直角三角形,量得该角对边和另一直角边分别为厘米,厘米,再画一个含的直角三角形,量得该角对边和另一直角边分别为厘米,厘米.已知杆高MN为米,求山高.(结果用不含的字母表示)
考点04 解直角三角形的实际应用——方位角
1.(2025·重庆·中考真题)为加强森林防火,某林场采用人工瞭望与无人机巡视两种方式监测森林情况.如图,A,B,C,D在同一平面内.A是瞭望台,某一时刻,观测到甲无人机位于A的正东方向10千米的B处,乙无人机位于A的南偏西方向20千米的D处.两无人机同时飞往C处巡视,D位于C的正西方向上,B位于C的北偏西方向上.(参考数据:,,,)
(1)求的长度(结果保留小数点后一位);
(2)甲、乙两无人机同时分别从B,D出发沿往C处进行巡视,乙无人机速度为甲无人机速度的2倍.当两无人机相距20千米时,它们可以开始相互接收到信号.请问甲无人机飞离B处多少千米时,两无人机可以开始相互接收到信号(结果保留小数点后一位)?
2.(2025·山东烟台·中考真题)【综合与实践】
烟台山灯塔被誉为“黄海夜明珠”,它坐落在烟台山上,为过往船只提供导航服务.为了解渔船海上作业情况,某日,数学兴趣小组开展了实践探究活动.
如图,一艘渔船自东向西以每小时海里的速度向码头航行,小组同学收集到以下信息:
位置信息 码头A在灯塔B北偏西方向
14:30时,渔船航行至灯塔北偏东方向的处
15:00时,渔船航行至灯塔东北方向的处
天气预警 受暖湿气流影响,今天17:30到夜间,码头附近海域将出现浓雾天气.请注意防范.
请根据以上信息,解答下列问题:
(1)求渔船在航行过程中到灯塔的最短距离;
(2)若不改变航行速度,请通过计算说明渔船能否在浓雾到来前到达码头(参考数据:,,,,,).
3.(2024·海南·中考真题)木兰灯塔是亚洲最高、世界第二高的航标灯塔,位于海南岛的最北端,是海南岛东北部最重要的航标.某天,一艘渔船自西向东(沿方向)以每小时10海里的速度在琼州海峡航行,如图所示.
航行记录记录一:上午8时,渔船到达木兰灯塔P北偏西方向上的A处. 记录二:上午8时30分,渔船到达木兰灯塔P北偏西方向上的B处. 记录三:根据气象观测,当天凌晨4时到上午9时,受天文大潮和天气影响,琼州海峡C点周围5海里内,会出现异常海况,点C位于木兰灯塔P北偏东方向.
请你根据以上信息解决下列问题:
(1)填空:________,________, ________海里;
(2)若该渔船不改变航线与速度,是否会进入“海况异常”区,请计算说明.
(参考数据:)
4.(2024·四川资阳·中考真题)如图,某海域有两灯塔A,B,其中灯塔B在灯塔A的南偏东方向,且A,B相距海里.一渔船在C处捕鱼,测得C处在灯塔A的北偏东方向、灯塔B的正北方向.
(1)求B,C两处的距离;
(2)该渔船从C处沿北偏东方向航行一段时间后,突发故障滞留于D处,并发出求救信号.此时,在灯塔B处的渔政船测得D处在北偏东方向,便立即以18海里/小时的速度沿方向航行至D处救援,求渔政船的航行时间.
(注:点A,B,C,D在同一水平面内;参考数据:,)
5.(2024·江苏连云港·中考真题)图1是古代数学家杨辉在《详解九章算法》中对“邑的计算”的相关研究.数学兴趣小组也类比进行了如下探究:如图2,正八边形游乐城的边长为,南门设立在边的正中央,游乐城南侧有一条东西走向的道路,在上(门宽及门与道路间距离忽略不计),东侧有一条南北走向的道路,C处有一座雕塑.在处测得雕塑在北偏东方向上,在处测得雕塑在北偏东方向上.
(1)__________,__________;
(2)求点到道路的距离;
(3)若该小组成员小李出南门O后沿道路向东行走,求她离处不超过多少千米,才能确保观察雕塑不会受到游乐城的影响?(结果精确到,参考数据:,,,,)
6.(2023·山东临沂·中考真题)如图,灯塔A周围9海里内有暗礁.一渔船由东向西航行至B处,测得灯塔A在北偏西58°方向上,继续航行6海里后到达C处,测得灯塔A在西北方向上.如果渔船不改变航线继续向西航行,有没有触礁的危险?
(参考数据:)
考点05 解直角三角形的实际应用——其他
1.(2025·贵州·中考真题)某小区在设计时,计划在如图①的住宅楼正前方建一栋文体活动中心.设计示意图如图②所示,已知,该地冬至正午太阳高度角为.如果你是建筑设计师,请结合示意图和已知条件完成下列任务.
任务一:计算冬至正午太阳照到住宅楼的位置与地面之间的距离的长;
任务二:为符合建筑规范对日照的要求,让整栋住宅楼在冬至正午太阳高度角下恰好都能照射到阳光,需将活动中心沿方向移动一定的距离(活动中心高度不变),求该活动中心移动了多少米?
(参考数据:.结果保留小数点后一位)
2.(2025·青海·中考真题)数学实践
【问题背景】
中国传统农业智慧遇上现代数学模型.“豇豆不上架,产量少一半”的农谚流传至今,现代科学揭示了其秘密:当支架与地面形成夹角时,既能在早春聚热防冻害,又能在盛夏分散强光,就像给豇豆装了智能遮阳篷.
【问题呈现】
用两根竹竿交叉,斜插入地面,交叉点在何处会使支架与地面形成夹角?
【模型建立】
环节一:数据收集
两根竹竿长度均为1.8米,插入地下的部分为0.3米,竹竿与地面接触点间距为0.6米且与地面所形成的夹角均为.
环节二:数学抽象
如图:已知线段与交于点,,与直线分别交于点,,,,,,求的长度.(结果精确到0.1,参考数据:,,)
【模型求解】
【问题总结】
交叉点距顶端的长度即为______时,支架与地面形成夹角,这样更贴合作物的生长规律.
3.(2025·湖南·中考真题)如图,某处有一个晾衣装置,固定立柱和分别垂直地面水平线于点,,分米,.在点,之间的晾衣绳上有固定挂钩,分米,一件连衣裙挂在点处(点与点重合),且直线.
(1)如图1,当该连衣裙下端点刚好接触到地面水平线时,点到直线的距离等于12分米,求该连衣裙的长度;
(2)如图2,为避免该连衣裙接触到地面,在另一端固定挂钩处再挂一条长裤(点在点的右侧),若,求此时该连衣裙下端点到地面水平线的距离约为多少分米?(结果保留整数,参考数据:,,)
4.(2025·四川宜宾·中考真题)如图,扇形为某运动场内的投掷区,所在圆的圆心为O、A、B、N、O在同一直线上.直线与所在相切于点.此时测得;从点处沿方向前进8.0米到达B处.直线与所在相切于点,此时测得.(参考数据:)
(1)求圆心角的度数;
(2)求的弧长(结果精确到米).
5.(2024·内蒙古·中考真题)实验是培养学生创新能力的重要途径.如图是小亮同学安装的化学实验装置,安装要求为试管口略向下倾斜,铁夹应固定在距试管口的三分之一处.现将左侧的实验装置图抽象成右侧示意图,已知试管,试管倾斜角为.
(1)求试管口B与铁杆的水平距离的长度;(结果用含非特殊角的三角函数表示)
(2)实验时,导气管紧靠水槽壁,延长交的延长线于点F,且于点N(点C,D,N,F在一条直线上),经测得:,求线段的长度.(结果用含非特殊角的三角函数表示)
6.(2024·甘肃兰州·中考真题)单摆是一种能够产生往复摆动的装置,某兴趣小组利用摆球和摆线进行与单摆相关的实验探究,并撰写实验报告如下.
实验主题 探究摆球运动过程中高度的变化
实验用具 摆球,摆线,支架,摄像机等
实验说明 如图1,在支架的横杆点O处用摆线悬挂一个摆球,将摆球拉高后松手,摆球开始往复运动.(摆线的长度变化忽略不计) 如图2,摆球静止时的位置为点A,拉紧摆线将摆球拉至点B处,,,;当摆球运动至点C时,,.(点O,A,B,C,D,E在同一平面内)
实验图示
解决问题:根据以上信息,求的长.(结果精确到)
参考数据:,.
7.(2024·四川广元·中考真题)小明从科普读物中了解到,光从真空射入介质发生折射时,入射角的正弦值与折射角的正弦值的比值叫做介质的“绝对折射率”,简称“折射率”.它表示光在介质中传播时,介质对光作用的一种特征.
(1)若光从真空射入某介质,入射角为,折射角为,且,,求该介质的折射率;
(2)现有一块与(1)中折射率相同的长方体介质,如图①所示,点A,B,C,D分别是长方体棱的中点,若光线经真空从矩形对角线交点O处射入,其折射光线恰好从点C处射出.如图②,已知,,求截面的面积.
8.(2024·江苏苏州·中考真题)图①是某种可调节支撑架,为水平固定杆,竖直固定杆,活动杆可绕点A旋转,为液压可伸缩支撑杆,已知,,.
(1)如图②,当活动杆处于水平状态时,求可伸缩支撑杆的长度(结果保留根号);
(2)如图③,当活动杆绕点A由水平状态按逆时针方向旋转角度,且(为锐角),求此时可伸缩支撑杆的长度(结果保留根号).
9.(2023·山东济南·中考真题)图1是某越野车的侧面示意图,折线段表示车后盖,已知,,,该车的高度.如图2,打开后备箱,车后盖落在处,与水平面的夹角.
(1)求打开后备箱后,车后盖最高点到地面的距离;
(2)若小琳爸爸的身高为,他从打开的车后盖处经过,有没有碰头的危险 请说明理由.
(结果精确到,参考数据:,,,)
考点06 三角函数与四边形的综合
1.(2025·四川资阳·中考真题)在四边形中,是边上的一点,是对角线的中点.
(1)如图1,四边形是正方形,连接,作交于点,求证:;
(2)如图2,四边形是平行四边形,,连接,作交于点,连接,求的值;
(3)如图3,四边形是菱形,,连接交于点是边上的一点,,若,求的长.
2.(2025·北京·中考真题)如图,在中,D,E分别为的中点,,垂足为F,点G在的延长线上,.
(1)求证:四边形是矩形;
(2)若,,,求和的长.
3.(2025·黑龙江·中考真题)如图,在正方形中,点在边上(不与点B、C重合),点E在的延长线上,且,连接、、,过点作于点,分别交、、于点、、.则下列结论:①;②;③;④若,则;⑤图中共有5个等腰三角形.其中正确的结论是( )
A.①②③⑤ B.①②④⑤ C.①②③④ D.①③④⑤
4.(2025·甘肃兰州·中考真题)如图,在菱形中,,垂足为E,交于点F,.若,则 .
5.(2025·贵州·中考真题)如图,在矩形中,点E,F,M分别在,,边上,分别交对角线、线段于点G,H,且是的中点.若,则的长为 .
6.(2024·江苏南通·中考真题)若菱形的周长为,且有一个内角为,则该菱形的高为 .
7.(2024·四川巴中·中考真题)如图,矩形的对角线与交于点,于点,延长与交于点.若,,则点到的距离为 .
8.(2023·辽宁丹东·中考真题)如图,在矩形中,对角线与相交于点O,,,垂足为点E,F是的中点,连接,若,则矩形的周长是( )
A. B. C. D.
考点07 三角函数与圆的综合
1.(2025·广东深圳·中考真题)如图1,在中,是的中点,,.
(1)求证:四边形为菱形;
(2)如图2,若点为上一点,,且,,三点均在上,连接,与相切于点,
①求__________;
②求的半径;
(3)利用圆规和无刻度直尺在图2中作射线,交于点,保留作图痕迹,不用写出作法和理由.
2.(2025·江苏苏州·中考真题)如图,在四边形中,.以为直径的经过点D,且与边交于点E,连接.
(1)求证:为的切线;
(2)若,求的长.
3.(2025·陕西·中考真题)如图,点在的边上,以为半径的⊙与相切于点,与相交于点,为⊙的直径,与相交于点,.
(1)求证:;
(2)若,,求的长.
4.(2025·四川成都·中考真题)如图,点C在以为直径的半圆O上,连接,过点C作半圆O的切线,交的延长线于点D,在上取点E,使,连接,交于点F.
(1)求证:;
(2)若,,求半圆O的半径及的长.
5.(2025·福建·中考真题)如图,四边形ABCD内接于,AD,BC的延长线相交于点E,AC,BD相交于点F.G是AB上一点,GD交AC于点H,且.
(1)求证:;
(2)求证:;
(3)若,求的周长.
6.(2025·新疆·中考真题)如图,为的直径,C为上一点,于点F,,交于点G,交于点D.
(1)求证:是的切线;
(2)若,,求的长.
7.(2025·黑龙江齐齐哈尔·中考真题)如图,内接于,为的直径,点D在的延长线上,连接,,过点B作,交于点E.
(1)求证:是的切线;
(2)若点B是的中点,且,求的半径.
答案解析
考点01 三角函数的定义
1.(2023·四川乐山·中考真题)我国汉代数学家赵爽在注解《周髀算经》时给出“赵爽弦图”,如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形面积为25,小正方形面积为1,则( )
A. B. C. D.
【答案】A
【分析】先由两个正方形的面积分别得出其边长,由赵爽弦图的特征可得,则,在中,利用勾股定理求出,最后按照正弦函数的定义计算求解即可.
【详解】解:∵大正方形的面积是25,小正方形面积是1,
∴大正方形的边长,小正方形的边长,
∵,
∴,
在中,,
∴,
解得(负值舍去)
∴.
故选A.
【点睛】本题考查了勾股定理、弦图及正弦函数的计算,明确相关性质及定理是解题的关键.
2.(2024·广西·中考真题)如图,在中,,.
(1)尺规作图:作线段的垂直平分线l,分别交,于点D,E:(要求:保留作图痕迹,不写作法,标明字母)
(2)在(1)所作的图中,连接,若,求的长.
【答案】(1)见详解
(2)
【分析】(1)分别以A、B为圆心,大于为半径画弧,分别交,于点D,E,作直线,则直线l即为所求.
(2)连接,由线段垂直平分线的性质可得出,由等边对等角可得出,由三角形内角和得出,则得出为等腰直角三角形,再根据正弦的定义即可求出的长.
【详解】(1)解:如下直线l即为所求.
(2)连接如下图:
∵为线段的垂直平分线,
∴,
∴,
∴,
∴为等腰直角三角形,
∴,
∴
【点睛】本题主要考查了作线段的垂线平分线,线段的垂线平分线的性质,等腰三角形的性质,三角形内角和定理以及正弦的定义.掌握线段的垂直平分线的性质是解题的关键.
3.(2025·山东东营·中考真题)《九章算术》是我国古代数学成就的杰出代表,其中《方田》章给出计算弧田面积所用公式为:弧田面积(弦矢+矢),弧田(如图)是由圆弧和其所对的弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.在如图所示的弧田中,“弦”为8,“矢”为2,则的值为 .
【答案】/
【分析】本题主要考查垂径定理、勾股定理、三角函数的定义等知识点.如图,作交于,交圆弧于,利用垂径定理和勾股定理构建方程组求出,,利用余弦函数定义即可解决问题.
【详解】解:如图,作交于,交圆弧于,
由题意:,
设,由,
∴,
∵,为半径,
∴,
在中,
由勾股定理得,
∴,
解得,
∴,
∴.
故答案为:.
4.(2023·内蒙古·中考真题)如图是源于我国汉代数学家赵爽的弦图,它是由四个全等直角三角形与一个小正方形拼成的一个大正方形.若小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为,则的值为( )
A. B. C. D.
【答案】D
【分析】首先根据两个正方形的面积分别求出两个正方形的边长,然后结合题意进一步设直角三角形短的直角边为,则较长的直角边为,再接着利用勾股定理得到关于的方程,据此进一步求出直角三角形各个直角边的边长,最后求出的值即可.
【详解】∵小正方形的面积为,大正方形的面积为25,
∴小正方形的边长为1,大正方形的边长为5,
设直角三角形短的直角边为,则较长的直角边为,其中,
∴,其中,
解得:,,
∴,
故选:D.
【点睛】本题主要考查了勾股定理与一元二次方程及三角函数的综合运用,熟练掌握相关概念是解题关键.
5.(2023·吉林长春·中考真题)学校开放日即将来临,负责布置的林老师打算从学校图书馆的顶楼拉出一条彩旗绳到地面,如图所示.已彩旗绳与地面形成角(即)、彩旗绳固定在地面的位置与图书馆相距32米(即米),则彩旗绳的长度为( )
A.米 B.米 C.米 D.米
【答案】D
【分析】根据余弦值的概念即邻边与斜边之比,即可求出答案.
【详解】解:表示的是地面,表示是图书馆,
,
为直角三角形,
(米).
故选:D.
【点睛】本题考查的是解直角三角形的应用,涉及到余弦值,解题的关键在于熟练掌握余弦值的概念.
6.(2023·江苏·中考真题)如图,在中,,点D在边AB上,连接CD.若,,则 .
【答案】/
【分析】由题意可设,则,,在中求得,在中求出答案即可.
【详解】解: ,,
设,则,,
在中,由勾股定理得:,
在中,.
【点睛】本题考查的是求锐角三角函数,解题关键是根据比值设未知数,表示出边长从而求出锐角三角函数值.
7.(2023·江苏连云港·中考真题)如图,菱形的对角线相交于点为的中点,,.求的长及的值.
【答案】,
【分析】根据菱形的性质得出,中,勾股定理求得的长,根据正切的定义即可求解.
【详解】在菱形中,.
∵,∴.
在中,∵为中点,
∴.
∵.
∴.
∴.
∴.
【点睛】本题考查了菱形的性质,勾股定理,求正切,熟练掌握以上知识是解题的关键.
8.(2024·山东淄博·中考真题)如图,在综合与实践活动课上,小强先测得教学楼在水平地面上的影长为.又在点处测得该楼的顶端的仰角是.则用科学计算器计算教学楼高度的按键顺序正确的是( )
A. B.
C. D.
【答案】A
【分析】本题考查解直角三角形的应用,用计算器计算三角函数值,根据题意,得到,进行判断即可.
【详解】解:由题意,得:在中,,,
∴;
计算器的按键为 ;
故选A.
考点02 解直角三角形的实际应用——俯仰角
1.(2025·四川达州·中考真题)为了让莲花湖湿地公园的天更蓝,水更清,莲花湖管委会定期利用无人机指引工作人员清理湖中垃圾.已知无人机悬停在湖面上的处,工作人员所乘小船在处测得无人机的仰角为,当工作人员沿正前方向划行米到达处,测得无人机的仰角为,求无人机离湖面的高度(结果不取近似值)
【答案】无人机离湖面的高度为米
【分析】本题考查了解直角三角形的应用,构造直角三角形是解题的关键;过点作于点,设,根据题意得出,,在中,根据,列出方程,解方程,即可求解.
【详解】解:如图,过点作于点,
依题意
设,
在中,
∴,
∵
∴,
在中,
∴
解得:
答:无人机离湖面的高度为米
2.(2025·吉林长春·中考真题)如图,已知某山峰的海拔高度为米,一位登山者到达海拔高度为米的点处.测得山峰顶端的仰角为.则、两点之间的距离为( )
A.米 B.米
C.米 D.米
【答案】B
【分析】本题主要考查了解直角三角形的实际应用,掌握三角函数的定义是解题的关键.
由题意得四边形是矩形,则,那么,再解即可.
【详解】解:由题意得,四边形是矩形,
∴,
∴,
由题意得,,
∴,
∴,
故选:B.
3.(2025·辽宁·中考真题)如图,为了测量树的高度,在水平地面上取一点,在处测得,,则树的高约为 (结果精确到.参考数据:,).
【答案】
【分析】本题考查了解直角三角形的实际应用,正确使用三角函数是解题的关键.
在中,由即可求解.
【详解】解:由题意得,
∴在中,,
故答案为:.
4.(2025·吉林·中考真题)综合与实践:确定建筑物的打印模型的高度项目提出:图是某城市规划展览馆.树人中学的打印社团为展示城市文化,准备制作该城市规划展览馆的打印模型,需要测量并计算展览馆高度,为制作打印模型提供数据.
项目报告表 时间:2025年5月29日
项目分析 活动目标 测量该城市规划展览馆的实际高度并换算其打印模型的高度
测量工具 测角仪、皮尺
项目实施 任务一测量数据 以下是测得的相关数据,并画出了如图所示的测量草图. 1.测出测角仪的高. 2.利用测角仪测出展览馆顶端A的仰角. 3.测出测角仪底端D处到展览馆底端B处之间的距离.
任务二计算实际高度 根据上述测得的数据,计算该城市规划展览馆的高度.(结果精确到1m)(参考数据:,,)
任务三换算模型高度 将该城市规划展览馆的高度按等比例缩小,得到其打印模型的高度约为________.(结果精确到)
项目结果 为社团制作城市规划展览馆的打印模型提供数据
请结合上表中的测量草图和相关数据,帮助该社团完成任务二和任务三.
【答案】该城市规划展览馆的高度为;打印模型的高度约为
【分析】本题考查了解直角三角形的实际应用,比例的基本性质,正确理解题意是解题的关键.
任务二:先由矩形得到,,然后解即可;
任务三:由比例尺等于图上距离比上实际距离求解即可.
【详解】解:任务二:由题意得为矩形,
∴,,
∵在中,
∴,
∴,
答:该城市规划展览馆的高度为;
任务三:设打印模型的高度约为,
则由题意得:,
解得:,
答:打印模型的高度约为.
5.(2025·陕西·中考真题)小涵和小宇想测量公园山坡上一个信号杆的高度.在征得家长同意后,他们带着工具前往测量.测量示意图如图所示,他们在坡面上的点处安装测角仪,测得信号杆顶端的仰角为,与坡面的夹角为,又测得点与信号杆底端之间的距离为.已知,点,,在同一条直线上,,均与水平线垂直.求信号杆的高.(参考数据:,,)
【答案】信号杆的高为
【分析】本题考查了解直角三角形的应用,三角形内角和性质,矩形的判定与性质,等角对等边,正确掌握相关性质内容是解题的关键.先理解题意,得出,再在中,运用,,代入数值进行计算,得出的值,然后证明四边形是矩形,故,根据,,得,,把数值代入进行计算,即可作答.
【详解】解:过点E作于点,过点D作于点,如图所示:
∵,均与水平线垂直.
∴
∴,
∵
∴
在中,,
则,
在中,,
则,
∵过点E作于点,过点D作于点,
∴,
∴四边形是矩形
∴,
∵,,
∴,
∴,
∴,
信号杆的高为.
6.(2025·安徽·中考真题)某公司为庆祝新产品上市,在甲楼与乙楼的楼顶之间悬挂彩带营造喜庆气氛.如图所示,甲楼和乙楼分别用与水平地面垂直的线段和表示,彩带用线段表示.工作人员在点A处测得点C的俯角为,测得点D的仰角为.已知,求的长(精确到).参考数据:,,,,,.
【答案】
【分析】本题主要考查了解直角三角形的实际应用,过点A作,垂足为点E,则四边形为矩形,可得,解求出的长,再解求出的长即可得到答案.
【详解】解:过点A作,垂足为点E.
∵线段和都与地面垂直,
∴四边形为矩形,
∴.
在中,,
∴.
在中,,
.
答:的长为.
7.(2024·四川雅安·中考真题)在数学课外实践活动中,某小组测量一栋楼房的高度(如图),他们在A处仰望楼顶,测得仰角为,再往楼的方向前进50米至B处,测得仰角为,那么这栋楼的高度为(人的身高忽略不计)( )
A.米 B.25米 C.米 D.50米
【答案】A
【分析】此题考查了解直角三角形的应用-仰角俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形.
设米,在中,利用锐角三角函数定义表示出,在中,利用锐角三角函数定义表示出,再由列出关于的方程,求出方程的解得到的值即可.
【详解】解:设米,
在中,,
,即,
整理得:米,
在中,,
,即,
整理得:米,
∵米,
∴,即,
解得:,
侧这栋楼的高度为米.
故选:A.
8.(2024·黑龙江牡丹江·中考真题)如图,某数学活动小组用高度为米的测角仪,对垂直于地面的建筑物的高度进行测量,于点C.在B处测得A的仰角,然后将测角仪向建筑物方向水平移动6米至处,于点G,测得A的仰角,的延长线交于点E,求建筑物的高度(结果保留小数点后一位).(参考数据:)
【答案】17.5米
【分析】本题主要考查了矩形的性质与判定,解直角三角形的实际应用,由题意可得四边形是矩形,则.解直角三角形得到,进而得到,据此求出即可得到答案.
【详解】解:根据题意可知四边形是矩形,
.
如图,.
,
.
,
.
(米)
答:建筑物的高度约为米.
考点03 解直角三角形的实际应用——坡度、坡角
1.(2025·四川资阳·中考真题)如图,已知水平地面上方有一个水平的平台,该平台上有一个竖直的建筑物.在处测得建筑物顶端的仰角为,在处测得的仰角为,斜坡的坡度米,.(点在同一竖直平面内).
(1)求平台的高度;
(2)求建筑物的高度(即的长).
【答案】(1)10米
(2)米
【分析】本题考查解直角三角形的实际应用,矩形的判定及性质.
(1)过点B作于点E,则,根据斜坡的坡度,得到,从而在中,根据勾股定理构造方程,求解即可;
(2)延长交于点F,得到四边形是矩形,因此米,,设米,则(米),通过解直角三角形在中,求得(米),在中,求得∴(米),进而根据列出方程,求解即可.
【详解】(1)解:过点B作于点E,则
∵斜坡的坡度,
∴,
∵在中,,
即,
∴米,
∴平台的高度是10米.
(2)解:延长交于点F,
∵,,
∴,
∴四边形是矩形,
∴米,,
设米,则(米),
∵在中,,
∴(米),
∵在中,,
∴(米),
∴米,
由(1)有(米),
∵,
∴,
解得,
∴(米),
即建筑物的高度(即的长)为米.
2.(2024·四川巴中·中考真题)某兴趣小组开展了测量电线塔高度的实践活动.如图所示,斜坡的坡度,,在处测得电线塔顶部的仰角为,在处测得电线塔顶部的仰角为.
(1)求点离水平地面的高度.
(2)求电线塔的高度(结果保留根号).
【答案】(1);
(2)电线塔的高度.
【分析】本题主要考查了解直角三角形的实际应用.
(1)由斜坡的坡度,求得,利用正切函数的定义得到,据此求解即可;
(2)作于点,设,先解得到,解得到米,进而得到方程,解方程即可得到答案.
【详解】(1)解:∵斜坡的坡度,
∴,
∵,
∴,
∵,
∴;
(2)解:作于点,则四边形是矩形,,,
设,
在中,,
∴,
在中,,
在中,,,
∴,
∴,
∴,
∴,
∴
答:电线塔的高度.
3.(2024·四川眉山·中考真题)如图,斜坡的坡度,在斜坡上有一棵垂直于水平面的大树,当太阳光与水平面的夹角为时,大树在斜坡上的影子长为10米,则大树的高为 米.
【答案】/
【分析】此题考查了解直角三角形的应用,勾股定理,解题的关键是正确构造直角三角形.
如图,过点作水平地面的平行线,交的延长线于点,设米,米,勾股定理求出,解直角三角形求出,进而求解即可.
【详解】解:如图,过点作水平地面的平行线,交的延长线于点,
则,
在中,,
设米,米,
,
,
米,米,
,
(米),
(米),
答:大树的高度为米.
故答案为:.
4.(2024·四川广安·中考真题)风电项目对于调整能源结构和转变经济发展方式具有重要意义.某电力部门在某地安装了一批风力发电机,如图(1)某校实践活动小组对其中一架风力发电机的塔杆高度进行了测量,图(2)为测量示意图(点,,,均在同一平面内,).已知斜坡长为20米,斜坡的坡角为,在斜坡顶部处测得风力发电机塔杆顶端点的仰角为,坡底与塔杆底的距离米,求该风力发电机塔杆的高度.
(结果精确到个位;参考数据:,,,)
【答案】32m
【分析】本题考查的是矩形的判定与性质,解直角三角形的实际应用,过点作于点,作于点,先求解,,再证明,再利用锐角的正切可得,从而可得答案.
【详解】解:过点作于点,作于点
由题意得:,
在中,
,
,
,
四边形为矩形,
,,
,
在中.
,
答:该风力发电机塔杆的高度为.
5.(2023·江苏泰州·中考真题)如图,堤坝长为,坡度i为,底端A在地面上,堤坝与对面的山之间有一深沟,山顶D处立有高的铁塔.小明欲测量山高,他在A处看到铁塔顶端C刚好在视线上,又在坝顶B处测得塔底D的仰角为.求堤坝高及山高.(,,,小明身高忽略不计,结果精确到)
【答案】堤坝高为8米,山高为20米.
【分析】过B作于H,设,,根据勾股定理得到,求得,过B作于F,则,设,解直角三角形即可得到结论.
【详解】解:过B作于H,
∵坡度i为,
∴设,,
∴,
∴,
∴,
过B作于F,
则,
设,
∵.
∴,
∴,
∵坡度i为,
∴,
∴,
∴(米),
∴(米),
答:堤坝高为8米,山高为20米.
【点睛】本题考查了解直角三角形的应用-俯角仰角,解直角三角形的应用-坡角坡度,正确地作出辅助线是解题的关键.
6.(2023·湖北·中考真题)为了防洪需要,某地决定新建一座拦水坝,如图,拦水坝的横断面为梯形,斜面坡度是指坡面的铅直高度与水平宽度的比.已知斜坡长度为20米,,求斜坡的长.(结果精确到米)(参考数据:)
【答案】斜坡的长约为10米
【分析】过点作于点,在中,利用正弦函数求得,在中,利用勾股定理即可求解.
【详解】解:过点作于点,则四边形是矩形,
在中,,
.
∴.
∵,
∴在中,(米).
答:斜坡的长约为10米.
【点睛】此题考查的是解直角三角形的应用-坡度坡角问题,掌握坡度坡角的概念、熟记锐角三角函数的定义是解题的关键.
7.(2023·四川自贡·中考真题)为测量学校后山高度,数学兴趣小组活动过程如下:
(1)测量坡角
如图1,后山一侧有三段相对平直的山坡,山的高度即为三段坡面的铅直高度之和,坡面的长度可以直接测量得到,要求山坡高度还需要知道坡角大小.
如图2,同学们将两根直杆的一端放在坡面起始端A处,直杆沿坡面方向放置,在直杆另一端N用细线系小重物G,当直杆与铅垂线重合时,测得两杆夹角的度数,由此可得山坡AB坡角的度数.请直接写出之间的数量关系.
(2)测量山高
同学们测得山坡的坡长依次为40米,50米,40米,坡角依次为;为求,小熠同学在作业本上画了一个含角的(如图3),量得.求山高.(,结果精确到1米)
(3)测量改进
由于测量工作量较大,同学们围绕如何优化测量进行了深入探究,有了以下新的测量方法.
如图4,5,在学校操场上,将直杆NP置于的顶端,当与铅垂线重合时,转动直杆,使点N,P,D共线,测得的度数,从而得到山顶仰角,向后山方向前进40米,采用相同方式,测得山顶仰角;画一个含的直角三角形,量得该角对边和另一直角边分别为厘米,厘米,再画一个含的直角三角形,量得该角对边和另一直角边分别为厘米,厘米.已知杆高MN为米,求山高.(结果用不含的字母表示)
【答案】(1);
(2)山高为69米;
(3)山高的高为米..
【分析】(1)利用互余的性质即可求解;
(2)先求得,再分别在、、中,解直角三角形即可求解;
(3)先求得,,在和中,分别求得和的长,得到方程,据此即可求解.
【详解】(1)解:由题意得,
∴;
(2)解:在中,.
∴,
在中,,米,
∴(米),
在中,,米,
∴(米),
在中,,米,
∴(米),
∴山高(米),
答:山高为69米;
(3)解:如图,由题意得,,
设山高,则,
在中,,,
∴,
∴,
在中,,,
∴,
∴,
∵,
∴,即,
解得,山高
答:山高的高为米.
【点睛】本题考查了解直角三角形的应用,能够正确地构建出直角三角形,将实际问题化归为解直角三角形的问题是解答此类题的关键.
考点04 解直角三角形的实际应用——方位角
1.(2025·重庆·中考真题)为加强森林防火,某林场采用人工瞭望与无人机巡视两种方式监测森林情况.如图,A,B,C,D在同一平面内.A是瞭望台,某一时刻,观测到甲无人机位于A的正东方向10千米的B处,乙无人机位于A的南偏西方向20千米的D处.两无人机同时飞往C处巡视,D位于C的正西方向上,B位于C的北偏西方向上.(参考数据:,,,)
(1)求的长度(结果保留小数点后一位);
(2)甲、乙两无人机同时分别从B,D出发沿往C处进行巡视,乙无人机速度为甲无人机速度的2倍.当两无人机相距20千米时,它们可以开始相互接收到信号.请问甲无人机飞离B处多少千米时,两无人机可以开始相互接收到信号(结果保留小数点后一位)?
【答案】(1)千米
(2)千米
【分析】本题主要考查了解直角三角形的实际应用,矩形的性质与判定, 正确作出辅助线构造直角三角形是解题的关键。
(1)过点A作于E,过点B作于F,由题意得,,解得到千米,千米,证明四边形是矩形, 得到千米,千米,得到千米,再利用勾股定理即可求出的长;
(2)当甲无人机运动到M,乙无人机运动到N时,此时满足千米.过点M作于T,由题意得,,解得到千米,千米,则千米,设千米,则千米,千米,解得到千米,千米,则千米,由勾股定理得,解方程即可得到答案。
【详解】(1)解:如图所示,过点A作于E,过点B作于F,
∴,
由题意得,,
在中,千米,
千米,
∵无人机位于A的正东方向10千米的B处,D位于C的正西方向上,
∴,
∴,
∴四边形是矩形,
∴千米,千米,
∴千米,
∴千米,
答:的长度约为千米;
(2)解:如图所示,当甲无人机运动到M,乙无人机运动到N时,此时满足千米.过点M作于T,
由题意得,,
在中,千米,
千米,
∴千米,
设千米,则千米,千米,
在中,千米,
千米,
∴千米,
在中,由勾股定理得,
∴,
∴或(此时大于的长,舍去),
∴千米,
答:甲无人机飞离B处千米时,两无人机可以开始相互接收到信号.
2.(2025·山东烟台·中考真题)【综合与实践】
烟台山灯塔被誉为“黄海夜明珠”,它坐落在烟台山上,为过往船只提供导航服务.为了解渔船海上作业情况,某日,数学兴趣小组开展了实践探究活动.
如图,一艘渔船自东向西以每小时海里的速度向码头航行,小组同学收集到以下信息:
位置信息 码头A在灯塔B北偏西方向
14:30时,渔船航行至灯塔北偏东方向的处
15:00时,渔船航行至灯塔东北方向的处
天气预警 受暖湿气流影响,今天17:30到夜间,码头附近海域将出现浓雾天气.请注意防范.
请根据以上信息,解答下列问题:
(1)求渔船在航行过程中到灯塔的最短距离;
(2)若不改变航行速度,请通过计算说明渔船能否在浓雾到来前到达码头(参考数据:,,,,,).
【答案】(1)渔船在航行过程中到灯塔的最短距离为海里
(2)不改变航行速度,渔船能在浓雾到来前到达码头
【分析】本题考查了解直角三角形的应用,构造直角三角形是解题的关键;
(1)过点作于点,设,根据题意得出,解,得出,建立方程,即可求解;
(2)求得的距离,计算的距离,根据路程除以速度得到航行时间,结合题意,即可求解.
【详解】(1)解:如图,过点作于点,
设,
依题意,,,,
∴,,
∴,
在中,,
∴,
解得:,
∴渔船在航行过程中到灯塔的最短距离为海里;
(2)解:在中,,,
∴,
∴,
小时分钟,
从14:30,经过分钟是,在之前到达,
∴不改变航行速度,渔船能在浓雾到来前到达码头.
3.(2024·海南·中考真题)木兰灯塔是亚洲最高、世界第二高的航标灯塔,位于海南岛的最北端,是海南岛东北部最重要的航标.某天,一艘渔船自西向东(沿方向)以每小时10海里的速度在琼州海峡航行,如图所示.
航行记录记录一:上午8时,渔船到达木兰灯塔P北偏西方向上的A处. 记录二:上午8时30分,渔船到达木兰灯塔P北偏西方向上的B处. 记录三:根据气象观测,当天凌晨4时到上午9时,受天文大潮和天气影响,琼州海峡C点周围5海里内,会出现异常海况,点C位于木兰灯塔P北偏东方向.
请你根据以上信息解决下列问题:
(1)填空:________,________, ________海里;
(2)若该渔船不改变航线与速度,是否会进入“海况异常”区,请计算说明.
(参考数据:)
【答案】(1)30;75;5
(2)该渔船不改变航线与速度,会进入“海况异常”区
【分析】本题主要考查了方位角的计算,解直角三角形的实际应用,三角形内角和定理:
(1)根据方位角的描述和三角形内角和定理可求出两个角的度数,根据路程等于速度乘以时间可以计算出对应线段的长度;
(2)设海里,先解得到,再解得到海里,海里,据此可得,解得海里;证明,则海里;再求出上午9时时船与C点的距离即可得到结论.
【详解】(1)解:如图所示,过点P作于D,
由题意得, ,
∴;
∵一艘渔船自西向东(沿方向)以每小时10海里的速度在琼州海峡航行,上午8时从A出发到上午8时30分到达B,
∴海里.
(2)解:设海里,
在中,海里,
在中,海里,海里,
∵,
∴,
解得,
∴海里,
∵,
∴,
∴海里;
上午9时时,船距离A的距离为海里,
∵,
∴该渔船不改变航线与速度,会进入“海况异常”区.
4.(2024·四川资阳·中考真题)如图,某海域有两灯塔A,B,其中灯塔B在灯塔A的南偏东方向,且A,B相距海里.一渔船在C处捕鱼,测得C处在灯塔A的北偏东方向、灯塔B的正北方向.
(1)求B,C两处的距离;
(2)该渔船从C处沿北偏东方向航行一段时间后,突发故障滞留于D处,并发出求救信号.此时,在灯塔B处的渔政船测得D处在北偏东方向,便立即以18海里/小时的速度沿方向航行至D处救援,求渔政船的航行时间.
(注:点A,B,C,D在同一水平面内;参考数据:,)
【答案】(1)B,C两处的距离为16海里
(2)渔政船的航行时间为小时
【分析】本题考查了解直角三角形的实际应用,解题的关键是正确画出辅助线,构造直角三角形.
(1)根据题意易得,则,再求出(海里),即可解答;
(2)过点D作于点F,设海里,则,,则,求出,进而得出海里,海里,根据勾股定理可得:(海里),即可解答.
【详解】(1)解:过点A作于点E,
∵灯塔B在灯塔A的南偏东方向,C处在灯塔A的北偏东方向、灯塔B的正北方向.
∴,
∴,
∵,
∴,
∵海里,
∴(海里),
∴(海里),
∴B,C两处的距离为16海里.
(2)解:过点D作于点F,
设海里,
∵,
∴,
由(1)可知,海里,
∴海里,
∵,
∴,
∴,
解得:,
∴海里,海里,
根据勾股定理可得:(海里),
∴渔政船的航行时间为(小时),
答:渔政船的航行时间为小时.
5.(2024·江苏连云港·中考真题)图1是古代数学家杨辉在《详解九章算法》中对“邑的计算”的相关研究.数学兴趣小组也类比进行了如下探究:如图2,正八边形游乐城的边长为,南门设立在边的正中央,游乐城南侧有一条东西走向的道路,在上(门宽及门与道路间距离忽略不计),东侧有一条南北走向的道路,C处有一座雕塑.在处测得雕塑在北偏东方向上,在处测得雕塑在北偏东方向上.
(1)__________,__________;
(2)求点到道路的距离;
(3)若该小组成员小李出南门O后沿道路向东行走,求她离处不超过多少千米,才能确保观察雕塑不会受到游乐城的影响?(结果精确到,参考数据:,,,,)
【答案】(1),
(2)2.0千米
(3)
【分析】本题考查正多边形的外角,解直角三角形,相似三角形的判定和性质:
(1)求出正八边形的一个外角的度数,再根据角的和差关系进行求解即可;
(2)过点作,垂足为,解,求出,解,求出,即可;
(3)连接并延长交于点,延长交于点,过点作,垂足为,解,求出,证明,列出比例式进行求解即可.
【详解】(1)解:∵正八边形的一个外角的度数为:,
∴,;
故答案为:;
(2)过点作,垂足为.
在中,,,
.
在中,,
.
答:点到道路的距离为2.0千米.
(3)连接并延长交于点,延长交于点,过点作,垂足为.
正八边形的外角均为,
在中,.
.
又,,
.
∵,
∴,
,即,
,
.
答:小李离点不超过2.4km,才能确保观察雕塑不会受到游乐城的影响.
6.(2023·山东临沂·中考真题)如图,灯塔A周围9海里内有暗礁.一渔船由东向西航行至B处,测得灯塔A在北偏西58°方向上,继续航行6海里后到达C处,测得灯塔A在西北方向上.如果渔船不改变航线继续向西航行,有没有触礁的危险?
(参考数据:)
【答案】渔船没有触礁的危险
【分析】过点作,分别解和,求出的长,即可得出结论.
【详解】解:过点作,由题意,得:,,,
设,
在中,,
∴,
∴,
在中,,
∴,
∴,
∵,
∴渔船没有触礁的危险.
【点睛】本题考查解直角三角形的应用—方向角问题.解题的关键是添加辅助线,构造直角三角形.
考点05 解直角三角形的实际应用——其他
1.(2025·贵州·中考真题)某小区在设计时,计划在如图①的住宅楼正前方建一栋文体活动中心.设计示意图如图②所示,已知,该地冬至正午太阳高度角为.如果你是建筑设计师,请结合示意图和已知条件完成下列任务.
任务一:计算冬至正午太阳照到住宅楼的位置与地面之间的距离的长;
任务二:为符合建筑规范对日照的要求,让整栋住宅楼在冬至正午太阳高度角下恰好都能照射到阳光,需将活动中心沿方向移动一定的距离(活动中心高度不变),求该活动中心移动了多少米?
(参考数据:.结果保留小数点后一位)
【答案】任务一:,任务二:该活动中心移动了2米;
【分析】本题考查的是矩形的判定与性质,解直角三角形的实际应用;
任务一:如图,过作于,结合题意可得:四边形为矩形,,可得,,求解,进一步可得答案;
任务二:如图,过作的平行线,过作的平行线,两线交于点,交于点,过作于,可得,四边形为矩形,,求解,进一步可得答案.
【详解】解:任务一:如图,过作于,
结合题意可得:四边形为矩形,,
∵,
∴,,
∵,
∴,
∴;
任务二:如图,过作的平行线,过作的平行线,两线交于点,交于点,过作于,
∴,四边形为矩形,
∴,
∴,
∴;
∴该活动中心移动了2米.
2.(2025·青海·中考真题)数学实践
【问题背景】
中国传统农业智慧遇上现代数学模型.“豇豆不上架,产量少一半”的农谚流传至今,现代科学揭示了其秘密:当支架与地面形成夹角时,既能在早春聚热防冻害,又能在盛夏分散强光,就像给豇豆装了智能遮阳篷.
【问题呈现】
用两根竹竿交叉,斜插入地面,交叉点在何处会使支架与地面形成夹角?
【模型建立】
环节一:数据收集
两根竹竿长度均为1.8米,插入地下的部分为0.3米,竹竿与地面接触点间距为0.6米且与地面所形成的夹角均为.
环节二:数学抽象
如图:已知线段与交于点,,与直线分别交于点,,,,,,求的长度.(结果精确到0.1,参考数据:,,)
【模型求解】
【问题总结】
交叉点距顶端的长度即为______时,支架与地面形成夹角,这样更贴合作物的生长规律.
【答案】,
【分析】本题考查的是解直角三角形的应用,如图,过作于,根据等腰三角形的性质可得,结合可得答案;最后由即可得到答案.
【详解】解:数学抽象:如图,过作于,
∵,
∴,
∵,
∴,
∴,
∴,
问题总结:∵,,
∴.
3.(2025·湖南·中考真题)如图,某处有一个晾衣装置,固定立柱和分别垂直地面水平线于点,,分米,.在点,之间的晾衣绳上有固定挂钩,分米,一件连衣裙挂在点处(点与点重合),且直线.
(1)如图1,当该连衣裙下端点刚好接触到地面水平线时,点到直线的距离等于12分米,求该连衣裙的长度;
(2)如图2,为避免该连衣裙接触到地面,在另一端固定挂钩处再挂一条长裤(点在点的右侧),若,求此时该连衣裙下端点到地面水平线的距离约为多少分米?(结果保留整数,参考数据:,,)
【答案】(1)14分米
(2)2分米
【分析】本题主要考查了解直角三角形的实际应用,勾股定理,矩形的性质与判定,正确作出辅助线构造直角三角形是解题的关键.
(1)可证明四边形是矩形,得到;在中,利用勾股定理求出的长,进而求出的长即可得到答案;
(2)过点E作于H,延长交于T,则四边形是矩形,可得;解求出的长,进而求出的长,据此求出的长即可得到答案.
【详解】(1)解:∵,
∴四边形是矩形,
∴;
在中,分米,分米,
∴分米,
∴分米,
∴分米,
答:该连衣裙的长度为14分米;
(2)如图所示,过点E作于H,延长交于T,
∵,
∴四边形是矩形,
∴;
在中,分米,,,
∴分米,
分米,
∴分米,
∴分米,
分米,
∴分米;
答:此时该连衣裙下端点到地面水平线的距离约为2分米.
4.(2025·四川宜宾·中考真题)如图,扇形为某运动场内的投掷区,所在圆的圆心为O、A、B、N、O在同一直线上.直线与所在相切于点.此时测得;从点处沿方向前进8.0米到达B处.直线与所在相切于点,此时测得.(参考数据:)
(1)求圆心角的度数;
(2)求的弧长(结果精确到米).
【答案】(1)
(2)
【分析】本题考查了解直角三角形的应用,圆的切线的性质,弧长公式,熟练掌握各知识点并灵活运用是解题的关键.
(1)由圆的切线的性质得到,再由直角三角形锐角互余即可求解;
(2)先解,设,,再解得到,求出,求出半径,再由弧长公式即可求解.
【详解】(1)解:∵直线与所在相切于点,
∴,
∵,
∴;
(2)解:∵直线与所在相切于点,
∴,
∵,
∴,
设,
∴,
∵,
∴,
∵在中,,
∴,
∴,
解得:,
∴,
∴的弧长为:,
答:的弧长为.
5.(2024·内蒙古·中考真题)实验是培养学生创新能力的重要途径.如图是小亮同学安装的化学实验装置,安装要求为试管口略向下倾斜,铁夹应固定在距试管口的三分之一处.现将左侧的实验装置图抽象成右侧示意图,已知试管,试管倾斜角为.
(1)求试管口B与铁杆的水平距离的长度;(结果用含非特殊角的三角函数表示)
(2)实验时,导气管紧靠水槽壁,延长交的延长线于点F,且于点N(点C,D,N,F在一条直线上),经测得:,求线段的长度.(结果用含非特殊角的三角函数表示)
【答案】(1)
(2)
【分析】本题主要考查了解直角三角形的应用,通过作辅助线构造直角三角形,掌握直角三角形中的边角关系是解题关键.
(1)先求出,再在中,利用余弦的定义求解即可得;
(2)过点作于点,过点作于点,先解直角三角形可得的长,从而可得的长,再判断出是等腰直角三角形,从而可得的长,最后根据求解即可得.
【详解】(1)解:∵,
∴,
由题意可知,,
在中,,
∴,
答:试管口与铁杆的水平距离的长度.
(2)解:如图,过点作于点,过点作于点,
则四边形和四边形都是矩形,
∴,
在中,,,
∴,
∵,
∴,
∴,
∵,,,
∴,
∴是等腰直角三角形,
∴,
∴,
答:线段的长度为.
6.(2024·甘肃兰州·中考真题)单摆是一种能够产生往复摆动的装置,某兴趣小组利用摆球和摆线进行与单摆相关的实验探究,并撰写实验报告如下.
实验主题 探究摆球运动过程中高度的变化
实验用具 摆球,摆线,支架,摄像机等
实验说明 如图1,在支架的横杆点O处用摆线悬挂一个摆球,将摆球拉高后松手,摆球开始往复运动.(摆线的长度变化忽略不计) 如图2,摆球静止时的位置为点A,拉紧摆线将摆球拉至点B处,,,;当摆球运动至点C时,,.(点O,A,B,C,D,E在同一平面内)
实验图示
解决问题:根据以上信息,求的长.(结果精确到)
参考数据:,.
【答案】的长为
【分析】本题考查的是解直角三角形的实际应用,先求解,再求解,从而可得答案;
【详解】解:∵,,;
∴,
,
∴,
∵,,
∴,
∴;
∴的长为;
7.(2024·四川广元·中考真题)小明从科普读物中了解到,光从真空射入介质发生折射时,入射角的正弦值与折射角的正弦值的比值叫做介质的“绝对折射率”,简称“折射率”.它表示光在介质中传播时,介质对光作用的一种特征.
(1)若光从真空射入某介质,入射角为,折射角为,且,,求该介质的折射率;
(2)现有一块与(1)中折射率相同的长方体介质,如图①所示,点A,B,C,D分别是长方体棱的中点,若光线经真空从矩形对角线交点O处射入,其折射光线恰好从点C处射出.如图②,已知,,求截面的面积.
【答案】(1);
(2).
【分析】本题主要考查了解直角三角形的应用,勾股定理等知识,
(1)根据,设,则,利用勾股定理求出,进而可得,问题即可得解;
(2)根据折射率与(1)的材料相同,可得折射率为,根据,可得,则有,在中,设,,问题随之得解.
【详解】(1)∵,
∴如图,
设,则,由勾股定理得,,
∴,
又∵,
∴,
∴折射率为:.
(2)根据折射率与(1)的材料相同,可得折射率为,
∵,
∴,
∴.
∵四边形是矩形,点O是中点,
∴,,
又∵,
∴,
在中,设,,
由勾股定理得,,
∴.
又∵,
∴,
∴,
∴,
∴截面的面积为:.
8.(2024·江苏苏州·中考真题)图①是某种可调节支撑架,为水平固定杆,竖直固定杆,活动杆可绕点A旋转,为液压可伸缩支撑杆,已知,,.
(1)如图②,当活动杆处于水平状态时,求可伸缩支撑杆的长度(结果保留根号);
(2)如图③,当活动杆绕点A由水平状态按逆时针方向旋转角度,且(为锐角),求此时可伸缩支撑杆的长度(结果保留根号).
【答案】(1)
(2)
【分析】本题考查了解直角三角形的应用,解题的关键是:
(1)过点C作,垂足为E,判断四边形为矩形,可求出,,然后在中,根据勾股定理求出即可;
(2)过点D作,交的延长线于点F,交于点G.判断四边形为矩形,得出.在中,利用正切定义求出.利用勾股定理求出,由,可求出,,,.在中,根据勾股定理求出即可.
【详解】(1)解:如图,过点C作,垂足为E,
由题意可知,,
又,
四边形为矩形.
,,
,.
,
.
在中,.
即可伸缩支撑杆的长度为;
(2)解:过点D作,交的延长线于点F,交于点G.
由题意可知,四边形为矩形,
.
在中,,
.
,
,
,.
,,
,.
在中,.
即可伸缩支撑杆的长度为.
9.(2023·山东济南·中考真题)图1是某越野车的侧面示意图,折线段表示车后盖,已知,,,该车的高度.如图2,打开后备箱,车后盖落在处,与水平面的夹角.
(1)求打开后备箱后,车后盖最高点到地面的距离;
(2)若小琳爸爸的身高为,他从打开的车后盖处经过,有没有碰头的危险 请说明理由.
(结果精确到,参考数据:,,,)
【答案】(1)车后盖最高点到地面的距离为
(2)没有危险,详见解析
【分析】(1)作,垂足为点,先求出的长,再求出的长即可;
(2)过作,垂足为点,先求得,再得到,再求得,从而得出到地面的距离为,最后比较即可.
【详解】(1)如图,作,垂足为点
在中
∵,
∴
∴
∵平行线间的距离处处相等
∴
答:车后盖最高点到地面的距离为.
(2)没有危险,理由如下:
过作,垂足为点
∵,
∴
∵
∴
在中,
∴.
∵平行线间的距离处处相等
∴到地面的距离为.
∵
∴没有危险.
【点睛】本题主要考查了解直角三角形的应用,掌握直角三角形的边角关系是解题的关键.
考点06 三角函数与四边形的综合
1.(2025·四川资阳·中考真题)在四边形中,是边上的一点,是对角线的中点.
(1)如图1,四边形是正方形,连接,作交于点,求证:;
(2)如图2,四边形是平行四边形,,连接,作交于点,连接,求的值;
(3)如图3,四边形是菱形,,连接交于点是边上的一点,,若,求的长.
【答案】(1)见解析
(2)
(3)
【分析】(1)连接,根据正方形的性质,利用得到,即可证明结论;
(2)过点A作于点G,过点F作于点,根据勾股定理求出长,然后根据平行四边形的面积公式求出长,根据正切得到长,然后设,则,求出长,再根据正切得到求出a的值,解答即可;
(3)过点D作于点P,作于点Q,设,求出,,然后表示,,在射线上截取,在射线上截取,根据全等得到,,,然后根据勾股定理求出x值,再根据相似三角形的对应边成比例解答即可.
【详解】(1)证明:连接,
∵是正方形,,
∴,,,
∴,
∴,
∴;
(2)解:过点A作于点G,过点F作于点,
(3)∵,,
∴,
∴,
∵,
∴,
又∵,
∴,
又∵,
∴,
∴,
∴,
∵是平行四边形,
∴,
∴,
∴,
∴,
∴,即,
设,则,
∴,
同理可得,即,
解得,
∴,
又∵O是的中点,
∴,
∴,
∴;
过点D作于点P,作于点Q,设,
∵是菱形,
∴,,
∴,
∴,
∴,,
∵,
∴,
∴,
∴,,
在射线上截取,在射线上截取,
∵是菱形,
∴,,
∴,,
又∵,
∴,
∴,,
同理:,,
∴,
∴,
∴,即,
∴,
解得,
又∵,
∴,,
∴,
∴,即,
解得:,
又∵O是的中点,
∴,
∴.
【点睛】本题考查四边形的综合,解直角三角形,相似三角形的判定和性质,勾股定理,全等三角形的判定和性质,作辅助线构造全等三角形是解题的关键.
2.(2025·北京·中考真题)如图,在中,D,E分别为的中点,,垂足为F,点G在的延长线上,.
(1)求证:四边形是矩形;
(2)若,,,求和的长.
【答案】(1)见解析
(2)
【分析】本题主要考查了矩形的判定,三角形中位线定理,勾股定理,解直角三角形,熟知相关知识是解题的关键.
(1)由三角形中位线定理可得,即,则可证明四边形是平行四边形,再由,即可证明平行四边形是矩形;
(2)求出,解得到,则;由线段中点的定义可得;过点A作于H,解得到,则,再利用勾股定即可求出的长.
【详解】(1)证明:∵D,E分别为的中点,
∴是的中位线,
∴,即,
∵,
∴四边形是平行四边形,
又∵,
∴平行四边形是矩形;
(2)解:∵,
∴;
∵,
∴,
在中,,,
∴,
∴;
∵点D为的中点,
∴;
如图所示,过点A作于H,
在中,,
∴,
在中,由勾股定理得.
3.(2025·黑龙江·中考真题)如图,在正方形中,点在边上(不与点B、C重合),点E在的延长线上,且,连接、、,过点作于点,分别交、、于点、、.则下列结论:①;②;③;④若,则;⑤图中共有5个等腰三角形.其中正确的结论是( )
A.①②③⑤ B.①②④⑤ C.①②③④ D.①③④⑤
【答案】C
【分析】本题考查了正方形性质、等腰三角形的判定和性质、相似三角形的判定和性质、解三角形等,解题关键是利用垂直证明角的关系,从而证明三角形全等或相似.
容易证明,从而可得,进而可得,从而可得②正确,过点作,交于点,构造,结合四边形是平行四边形可得,可得①正确,再利用角关系证明,,可得,从而得出结论③正确,过点作,设,由可得,解三角形求出,,从而求出,故结论④正确,再判定不一定是等腰三角形,得出等腰三角形有、、、,共四个,故结论⑤错误.
【详解】解:如图1,过点作,交于点,
∵在正方形中,
∴,,,,
∴、是等腰三角形,
又∵,,
∴,
∴,,,
∴是等腰三角形,
∵,
∴,
又∵,
∴,
∵,
∴,,
∴,
设,
∵,,
∴,故结论②正确;
∴,即是等腰三角形,
∵在和中,
,
∴,
∴,
∵,,
∴四边形是平行四边形,
∴,
∴,故结论①正确,
∵,,
∴,
∴,
∴,
∵,,
∴,
∴
∴,
∵,
∴,
∴,故结论③正确,
过点作,如图2;
设,由可得,,
∴,
∵,
∴,
∴,故结论④正确,
∵,,
∴不一定等于,,
∴ 不一定是等腰三角形,
故等腰三角形有、、、,共四个,故结论⑤错误,
综上所述:正确结论有①②③④.
故选C.
4.(2025·甘肃兰州·中考真题)如图,在菱形中,,垂足为E,交于点F,.若,则 .
【答案】4
【分析】根据菱形的性质,得,又结合,,得出是等边三角形,就可以得知和都是含的直角三角形,解出三角形,即可求出的长.
【详解】解:连接,,
,,
垂直平分,
,
菱形,
,
是等边三角形,
,
,
,
,,
.
故答案为:4.
【点睛】本题考查了菱形的性质、垂直平分线的性质、等边三角形的判定与性质以及解直角三角形,熟练掌握这些性质定理是关键.
5.(2025·贵州·中考真题)如图,在矩形中,点E,F,M分别在,,边上,分别交对角线、线段于点G,H,且是的中点.若,则的长为 .
【答案】
【分析】如图,连接,交于,过作于,求解,证明是的中位线,可得,,,证明四边形是平行四边形,可得,而,,求解,再进一步求解即可.
【详解】解:如图,连接,交于,过作于,
∵,,
∴,
∵矩形,
∴,,
∴,,
∵是的中点,
∴是的中位线,
∴,,
∴,
∴,
∵,,
∴,
∵,
∴四边形是平行四边形,
∴,而,,
∴,
∴,
∴,
∴;
故答案为:
【点睛】本题考查的是平行四边形的判定与性质,矩形的性质,三角形的中位线的性质,锐角三角函数的应用,作出合适的辅助线是解本题的关键.
6.(2024·江苏南通·中考真题)若菱形的周长为,且有一个内角为,则该菱形的高为 .
【答案】
【分析】本题考查的是菱形的性质,锐角的正弦的含义,先画图,求解,过作于,结合可得答案.
【详解】解:如图,菱形的周长为,
∴,
过作于,而,
∴,
故答案为:
7.(2024·四川巴中·中考真题)如图,矩形的对角线与交于点,于点,延长与交于点.若,,则点到的距离为 .
【答案】
【分析】本题考查了矩形的性质,勾股定理,解直角三角形的相关知识,过点F作,垂足为H,利用勾股定理求出的长,利用角的余弦值求出的长,再利用勾股定理求出,从而得出,利用三角形面积求出即可.
【详解】解:如图,过点F作,垂足为H,
四边形为矩形,
,,
,,
,
,即,
解得:,
,即,
解得:,
,
,
,即,
解得:,
故答案为:.
8.(2023·辽宁丹东·中考真题)如图,在矩形中,对角线与相交于点O,,,垂足为点E,F是的中点,连接,若,则矩形的周长是( )
A. B. C. D.
【答案】D
【分析】根据矩形的性质得出,即可求证为等边三角形,进而得出点E为中点,根据中位线定理得出,易得,求出,即可得出矩形的周长.
【详解】解:∵四边形是矩形,
∴,
∵,
∴为等边三角形,
∵,
∴点E为中点,
∵F是的中点,若,
∴,
∵,
∴,
∴,
∴矩形的周长,
故选:D.
【点睛】矩形主要考查了矩形的性质,等边三角形的判定和性质,中位线定理,解直角三角形,解题的关键是掌握矩形的对角线相等,等边三角形三线合一,三角形的中位线平行于第三边且等于第三边的一半,以及解直角三角形的方法和步骤.
考点07 三角函数与圆的综合
1.(2025·广东深圳·中考真题)如图1,在中,是的中点,,.
(1)求证:四边形为菱形;
(2)如图2,若点为上一点,,且,,三点均在上,连接,与相切于点,
①求__________;
②求的半径;
(3)利用圆规和无刻度直尺在图2中作射线,交于点,保留作图痕迹,不用写出作法和理由.
【答案】(1)见解析
(2)①30°;②
(3)见解析
【分析】(1)先证明四边形为平行四边形,斜边上的中线得到,即可得证;
(2)①根据菱形的性质,得到,等角对等边得到,三角形的外角得到,切线得到,再根据角的和差关系进行求解即可;②解直角三角形,进行求解即可;
(3)利用尺规作图作,即可.
【详解】(1)解:,
四边形为平行四边形,
又,且为中点
,
平行四边形为菱形.
(2)①四边形为菱形.
,
,
又,
,
,
切于,
,
;
;
②设半径为,
,
,
,,
;
解得:;
(3)由题意,作图如下:
【点睛】本题考查菱形的判定和性质,斜边上的中线,切线的性质,解直角三角形,尺规作平行线,熟练掌握相关知识点,是解题的关键.
2.(2025·江苏苏州·中考真题)如图,在四边形中,.以为直径的经过点D,且与边交于点E,连接.
(1)求证:为的切线;
(2)若,求的长.
【答案】(1)详见解析
(2).
【分析】(1)只要证明,即可证明为的切线;
(2)过点D作,垂足为F,在中,,,,求得,,在中,,,,求得,再根据圆内接四边形的性质结合等边对等角求得,据此求解即可.
【详解】(1)证明:∵,
∴,
又∵,
∴,
∵为的直径,
∴,
∴,
∴,即,
∴,
∴为的切线;
(2)解:如图,过点D作,垂足为F,
∵,
∴,
∴,
∵中,,,,
∴,
∴,
∵,,
∴,
∴,
∴,
∵中,,,,
∴,
∵,,
∴,
∵四边形内接于,
∴,
∵,
∴,
∴.
【点睛】本题考查了圆周角定理,圆内接四边形的性质,切线的判定,解直角三角形的应用.正确引出辅助线解决问题是解题的关键.
3.(2025·陕西·中考真题)如图,点在的边上,以为半径的⊙与相切于点,与相交于点,为⊙的直径,与相交于点,.
(1)求证:;
(2)若,,求的长.
【答案】(1)证明见解析
(2)
【分析】(1)如图,连接,证明,,即,可得,进一步证明,可得;
(2)求解,设的半径为,结合,可得,可得:,,求解,证明,可得,进一步可得答案.
【详解】(1)解:如图,连接,
∵以为半径的⊙与相切于点,
∴,
∵,
∴,即,
∴,
∴,
∵,
∴,
∴,
∴;
(2)解:∵,,
∴,
设的半径为,
∴,,而,,
∴,
解得:,
∴,,,
∵,则,
∴,
∵,
∴,
∴,
∴.
【点睛】本题考查的是等腰三角形的判定与性质,平行线的性质,勾股定理的应用,相似三角形的判定与性质,圆周角定理的应用,切线的性质,锐角三角函数的应用,作出合适的辅助线是解本题的关键.
4.(2025·四川成都·中考真题)如图,点C在以为直径的半圆O上,连接,过点C作半圆O的切线,交的延长线于点D,在上取点E,使,连接,交于点F.
(1)求证:;
(2)若,,求半圆O的半径及的长.
【答案】(1)见解析
(2)半圆O的半径为2,
【分析】(1)连接,切线得到,等边对等角得到,圆周角定理得到,同角的余角得到,等量代换得到,即可得证;
(2)连接,设半圆O的半径为,解直角三角形,求出半径的长,进行求出的长,平行得到,解直角三角形,求出,的长,角平分线的性质,以及同高三角形的面积比等于底边比,得到,进行求解即可.
【详解】(1)解:连接,则:,
∴,
∵过点C作半圆O的切线,交的延长线于点D,
∴,
∴,
∵为直径,
∴,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∴;
(2)设半圆O的半径为,则,
∵,
∴,
∵,
∴,
∴,即:半圆O的半径为2;
∴,
连接,则:,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴平分,
∴到的距离相等,都等于的长,
∴,
∴,
∴,
∴.
【点睛】本题考查切线的性质,圆周角定理,解直角三角形,角平分线的性质等知识点,熟练掌握相关知识点,是解题的关键.
5.(2025·福建·中考真题)如图,四边形ABCD内接于,AD,BC的延长线相交于点E,AC,BD相交于点F.G是AB上一点,GD交AC于点H,且.
(1)求证:;
(2)求证:;
(3)若,求的周长.
【答案】(1)见解析
(2)见解析
(3)
【分析】(1)利用得,结合同弧所对圆周角,再根据三角形外角性质,完成证明 .
(2)先证得,再通过角的等量代换证,推出,从而得 .
(3)利用(2)结论将周长转化为,通过相似三角形及三角函数、勾股定理求出的长,即周长为 .
【详解】(1)证明:,
.
,
,
.
,
.
(2)证明:,
.
,
,
又,
,
,
.
由(1)知,,
又,
,
.
,
.
∵,
,
,
,
.
(3)解:由(2)知,,
的周长为.
设,则.
由(2)可知,.
又,
,
,
,
.
又,
,
.
过点C作,垂足为P,则.
四边形是圆内接四边形,
,
又,
,
.
在中,,即.
,
,
,
.
在中,,
,
解得,或(舍去).
.
的周长为.
【点睛】本题考查圆的性质、等腰三角形、相似三角形、解直角三角形等知识,通过角与边的转化、相似三角形判定与性质解题,关键是利用圆的性质和三角形知识进行边角关系推导.
6.(2025·新疆·中考真题)如图,为的直径,C为上一点,于点F,,交于点G,交于点D.
(1)求证:是的切线;
(2)若,,求的长.
【答案】(1)见解析
(2)
【分析】(1)连接,证明,得到,即可证明结论;
(2)证明,求出,得到,即可求出的长.
【详解】(1)证明:连接,
∵于点F,
∴,
∵
∴,
∵
∴,
∴,
即
∵是的半径,
∴是的切线;
(2)∵为的直径,
∴
∵,
∴,
∴
∵,
∴
∵
∴,
∵,,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
设,则,
∵,
∴
∴,
∵,
∴,
∴
解得,
∵
∴
解得,
∴
∴,
∴
【点睛】此题考查了解直角三角形、切线的判定、勾股定理、圆周角定理、相似三角形的判定和性质、平行线分线段成比例定理等知识,熟练掌握切线的判定、相似三角形的判定和性质是关键.
7.(2025·黑龙江齐齐哈尔·中考真题)如图,内接于,为的直径,点D在的延长线上,连接,,过点B作,交于点E.
(1)求证:是的切线;
(2)若点B是的中点,且,求的半径.
【答案】(1)见解析
(2)
【分析】本题考查圆周角定理,切线的判定,解直角三角形,熟练掌握相关定理和切线的判定方法,是解题的关键:
(1)连接,圆周角定理,得到,进而得到,等边对等角,得到,结合,推出,即可得证;
(2)根据线段之间的数量关系求出,进而求出的长,勾股定理求出的长,即可得出结果.
【详解】(1)证明:连接,
是的直径,
,
,
,
,即,
.
为的半径,
是的切线.
(2)解:点B是的中点,
.
,
.
,
.
又,
.
.
在中.
.
即半径为.
考点01 三角函数的定义
1.(2023·四川乐山·中考真题)我国汉代数学家赵爽在注解《周髀算经》时给出“赵爽弦图”,如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形面积为25,小正方形面积为1,则( )
A. B. C. D.
2.(2024·广西·中考真题)如图,在中,,.
(1)尺规作图:作线段的垂直平分线l,分别交,于点D,E:(要求:保留作图痕迹,不写作法,标明字母)
(2)在(1)所作的图中,连接,若,求的长.
3.(2025·山东东营·中考真题)《九章算术》是我国古代数学成就的杰出代表,其中《方田》章给出计算弧田面积所用公式为:弧田面积(弦矢+矢),弧田(如图)是由圆弧和其所对的弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.在如图所示的弧田中,“弦”为8,“矢”为2,则的值为 .
4.(2023·内蒙古·中考真题)如图是源于我国汉代数学家赵爽的弦图,它是由四个全等直角三角形与一个小正方形拼成的一个大正方形.若小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为,则的值为( )
A. B. C. D.
5.(2023·吉林长春·中考真题)学校开放日即将来临,负责布置的林老师打算从学校图书馆的顶楼拉出一条彩旗绳到地面,如图所示.已彩旗绳与地面形成角(即)、彩旗绳固定在地面的位置与图书馆相距32米(即米),则彩旗绳的长度为( )
A.米 B.米 C.米 D.米
6.(2023·江苏·中考真题)如图,在中,,点D在边AB上,连接CD.若,,则 .
7.(2023·江苏连云港·中考真题)如图,菱形的对角线相交于点为的中点,,.求的长及的值.
8.(2024·山东淄博·中考真题)如图,在综合与实践活动课上,小强先测得教学楼在水平地面上的影长为.又在点处测得该楼的顶端的仰角是.则用科学计算器计算教学楼高度的按键顺序正确的是( )
A. B.
C. D.
考点02 解直角三角形的实际应用——俯仰角
1.(2025·四川达州·中考真题)为了让莲花湖湿地公园的天更蓝,水更清,莲花湖管委会定期利用无人机指引工作人员清理湖中垃圾.已知无人机悬停在湖面上的处,工作人员所乘小船在处测得无人机的仰角为,当工作人员沿正前方向划行米到达处,测得无人机的仰角为,求无人机离湖面的高度(结果不取近似值)
2.(2025·吉林长春·中考真题)如图,已知某山峰的海拔高度为米,一位登山者到达海拔高度为米的点处.测得山峰顶端的仰角为.则、两点之间的距离为( )
A.米 B.米
C.米 D.米
3.(2025·辽宁·中考真题)如图,为了测量树的高度,在水平地面上取一点,在处测得,,则树的高约为 (结果精确到.参考数据:,).
4.(2025·吉林·中考真题)综合与实践:确定建筑物的打印模型的高度项目提出:图是某城市规划展览馆.树人中学的打印社团为展示城市文化,准备制作该城市规划展览馆的打印模型,需要测量并计算展览馆高度,为制作打印模型提供数据.
项目报告表 时间:2025年5月29日
项目分析 活动目标 测量该城市规划展览馆的实际高度并换算其打印模型的高度
测量工具 测角仪、皮尺
项目实施 任务一测量数据 以下是测得的相关数据,并画出了如图所示的测量草图. 1.测出测角仪的高. 2.利用测角仪测出展览馆顶端A的仰角. 3.测出测角仪底端D处到展览馆底端B处之间的距离.
任务二计算实际高度 根据上述测得的数据,计算该城市规划展览馆的高度.(结果精确到1m)(参考数据:,,)
任务三换算模型高度 将该城市规划展览馆的高度按等比例缩小,得到其打印模型的高度约为________.(结果精确到)
项目结果 为社团制作城市规划展览馆的打印模型提供数据
请结合上表中的测量草图和相关数据,帮助该社团完成任务二和任务三.
5.(2025·陕西·中考真题)小涵和小宇想测量公园山坡上一个信号杆的高度.在征得家长同意后,他们带着工具前往测量.测量示意图如图所示,他们在坡面上的点处安装测角仪,测得信号杆顶端的仰角为,与坡面的夹角为,又测得点与信号杆底端之间的距离为.已知,点,,在同一条直线上,,均与水平线垂直.求信号杆的高.(参考数据:,,)
6.(2025·安徽·中考真题)某公司为庆祝新产品上市,在甲楼与乙楼的楼顶之间悬挂彩带营造喜庆气氛.如图所示,甲楼和乙楼分别用与水平地面垂直的线段和表示,彩带用线段表示.工作人员在点A处测得点C的俯角为,测得点D的仰角为.已知,求的长(精确到).参考数据:,,,,,.
7.(2024·四川雅安·中考真题)在数学课外实践活动中,某小组测量一栋楼房的高度(如图),他们在A处仰望楼顶,测得仰角为,再往楼的方向前进50米至B处,测得仰角为,那么这栋楼的高度为(人的身高忽略不计)( )
A.米 B.25米 C.米 D.50米
8.(2024·黑龙江牡丹江·中考真题)如图,某数学活动小组用高度为米的测角仪,对垂直于地面的建筑物的高度进行测量,于点C.在B处测得A的仰角,然后将测角仪向建筑物方向水平移动6米至处,于点G,测得A的仰角,的延长线交于点E,求建筑物的高度(结果保留小数点后一位).(参考数据:)
考点03 解直角三角形的实际应用——坡度、坡角
1.(2025·四川资阳·中考真题)如图,已知水平地面上方有一个水平的平台,该平台上有一个竖直的建筑物.在处测得建筑物顶端的仰角为,在处测得的仰角为,斜坡的坡度米,.(点在同一竖直平面内).
(1)求平台的高度;
(2)求建筑物的高度(即的长).
2.(2024·四川巴中·中考真题)某兴趣小组开展了测量电线塔高度的实践活动.如图所示,斜坡的坡度,,在处测得电线塔顶部的仰角为,在处测得电线塔顶部的仰角为.
(1)求点离水平地面的高度.
(2)求电线塔的高度(结果保留根号).
3.(2024·四川眉山·中考真题)如图,斜坡的坡度,在斜坡上有一棵垂直于水平面的大树,当太阳光与水平面的夹角为时,大树在斜坡上的影子长为10米,则大树的高为 米.
4.(2024·四川广安·中考真题)风电项目对于调整能源结构和转变经济发展方式具有重要意义.某电力部门在某地安装了一批风力发电机,如图(1)某校实践活动小组对其中一架风力发电机的塔杆高度进行了测量,图(2)为测量示意图(点,,,均在同一平面内,).已知斜坡长为20米,斜坡的坡角为,在斜坡顶部处测得风力发电机塔杆顶端点的仰角为,坡底与塔杆底的距离米,求该风力发电机塔杆的高度.
(结果精确到个位;参考数据:,,,)
5.(2023·江苏泰州·中考真题)如图,堤坝长为,坡度i为,底端A在地面上,堤坝与对面的山之间有一深沟,山顶D处立有高的铁塔.小明欲测量山高,他在A处看到铁塔顶端C刚好在视线上,又在坝顶B处测得塔底D的仰角为.求堤坝高及山高.(,,,小明身高忽略不计,结果精确到)
6.(2023·湖北·中考真题)为了防洪需要,某地决定新建一座拦水坝,如图,拦水坝的横断面为梯形,斜面坡度是指坡面的铅直高度与水平宽度的比.已知斜坡长度为20米,,求斜坡的长.(结果精确到米)(参考数据:)
7.(2023·四川自贡·中考真题)为测量学校后山高度,数学兴趣小组活动过程如下:
(1)测量坡角
如图1,后山一侧有三段相对平直的山坡,山的高度即为三段坡面的铅直高度之和,坡面的长度可以直接测量得到,要求山坡高度还需要知道坡角大小.
如图2,同学们将两根直杆的一端放在坡面起始端A处,直杆沿坡面方向放置,在直杆另一端N用细线系小重物G,当直杆与铅垂线重合时,测得两杆夹角的度数,由此可得山坡AB坡角的度数.请直接写出之间的数量关系.
(2)测量山高
同学们测得山坡的坡长依次为40米,50米,40米,坡角依次为;为求,小熠同学在作业本上画了一个含角的(如图3),量得.求山高.(,结果精确到1米)
(3)测量改进
由于测量工作量较大,同学们围绕如何优化测量进行了深入探究,有了以下新的测量方法.
如图4,5,在学校操场上,将直杆NP置于的顶端,当与铅垂线重合时,转动直杆,使点N,P,D共线,测得的度数,从而得到山顶仰角,向后山方向前进40米,采用相同方式,测得山顶仰角;画一个含的直角三角形,量得该角对边和另一直角边分别为厘米,厘米,再画一个含的直角三角形,量得该角对边和另一直角边分别为厘米,厘米.已知杆高MN为米,求山高.(结果用不含的字母表示)
考点04 解直角三角形的实际应用——方位角
1.(2025·重庆·中考真题)为加强森林防火,某林场采用人工瞭望与无人机巡视两种方式监测森林情况.如图,A,B,C,D在同一平面内.A是瞭望台,某一时刻,观测到甲无人机位于A的正东方向10千米的B处,乙无人机位于A的南偏西方向20千米的D处.两无人机同时飞往C处巡视,D位于C的正西方向上,B位于C的北偏西方向上.(参考数据:,,,)
(1)求的长度(结果保留小数点后一位);
(2)甲、乙两无人机同时分别从B,D出发沿往C处进行巡视,乙无人机速度为甲无人机速度的2倍.当两无人机相距20千米时,它们可以开始相互接收到信号.请问甲无人机飞离B处多少千米时,两无人机可以开始相互接收到信号(结果保留小数点后一位)?
2.(2025·山东烟台·中考真题)【综合与实践】
烟台山灯塔被誉为“黄海夜明珠”,它坐落在烟台山上,为过往船只提供导航服务.为了解渔船海上作业情况,某日,数学兴趣小组开展了实践探究活动.
如图,一艘渔船自东向西以每小时海里的速度向码头航行,小组同学收集到以下信息:
位置信息 码头A在灯塔B北偏西方向
14:30时,渔船航行至灯塔北偏东方向的处
15:00时,渔船航行至灯塔东北方向的处
天气预警 受暖湿气流影响,今天17:30到夜间,码头附近海域将出现浓雾天气.请注意防范.
请根据以上信息,解答下列问题:
(1)求渔船在航行过程中到灯塔的最短距离;
(2)若不改变航行速度,请通过计算说明渔船能否在浓雾到来前到达码头(参考数据:,,,,,).
3.(2024·海南·中考真题)木兰灯塔是亚洲最高、世界第二高的航标灯塔,位于海南岛的最北端,是海南岛东北部最重要的航标.某天,一艘渔船自西向东(沿方向)以每小时10海里的速度在琼州海峡航行,如图所示.
航行记录记录一:上午8时,渔船到达木兰灯塔P北偏西方向上的A处. 记录二:上午8时30分,渔船到达木兰灯塔P北偏西方向上的B处. 记录三:根据气象观测,当天凌晨4时到上午9时,受天文大潮和天气影响,琼州海峡C点周围5海里内,会出现异常海况,点C位于木兰灯塔P北偏东方向.
请你根据以上信息解决下列问题:
(1)填空:________,________, ________海里;
(2)若该渔船不改变航线与速度,是否会进入“海况异常”区,请计算说明.
(参考数据:)
4.(2024·四川资阳·中考真题)如图,某海域有两灯塔A,B,其中灯塔B在灯塔A的南偏东方向,且A,B相距海里.一渔船在C处捕鱼,测得C处在灯塔A的北偏东方向、灯塔B的正北方向.
(1)求B,C两处的距离;
(2)该渔船从C处沿北偏东方向航行一段时间后,突发故障滞留于D处,并发出求救信号.此时,在灯塔B处的渔政船测得D处在北偏东方向,便立即以18海里/小时的速度沿方向航行至D处救援,求渔政船的航行时间.
(注:点A,B,C,D在同一水平面内;参考数据:,)
5.(2024·江苏连云港·中考真题)图1是古代数学家杨辉在《详解九章算法》中对“邑的计算”的相关研究.数学兴趣小组也类比进行了如下探究:如图2,正八边形游乐城的边长为,南门设立在边的正中央,游乐城南侧有一条东西走向的道路,在上(门宽及门与道路间距离忽略不计),东侧有一条南北走向的道路,C处有一座雕塑.在处测得雕塑在北偏东方向上,在处测得雕塑在北偏东方向上.
(1)__________,__________;
(2)求点到道路的距离;
(3)若该小组成员小李出南门O后沿道路向东行走,求她离处不超过多少千米,才能确保观察雕塑不会受到游乐城的影响?(结果精确到,参考数据:,,,,)
6.(2023·山东临沂·中考真题)如图,灯塔A周围9海里内有暗礁.一渔船由东向西航行至B处,测得灯塔A在北偏西58°方向上,继续航行6海里后到达C处,测得灯塔A在西北方向上.如果渔船不改变航线继续向西航行,有没有触礁的危险?
(参考数据:)
考点05 解直角三角形的实际应用——其他
1.(2025·贵州·中考真题)某小区在设计时,计划在如图①的住宅楼正前方建一栋文体活动中心.设计示意图如图②所示,已知,该地冬至正午太阳高度角为.如果你是建筑设计师,请结合示意图和已知条件完成下列任务.
任务一:计算冬至正午太阳照到住宅楼的位置与地面之间的距离的长;
任务二:为符合建筑规范对日照的要求,让整栋住宅楼在冬至正午太阳高度角下恰好都能照射到阳光,需将活动中心沿方向移动一定的距离(活动中心高度不变),求该活动中心移动了多少米?
(参考数据:.结果保留小数点后一位)
2.(2025·青海·中考真题)数学实践
【问题背景】
中国传统农业智慧遇上现代数学模型.“豇豆不上架,产量少一半”的农谚流传至今,现代科学揭示了其秘密:当支架与地面形成夹角时,既能在早春聚热防冻害,又能在盛夏分散强光,就像给豇豆装了智能遮阳篷.
【问题呈现】
用两根竹竿交叉,斜插入地面,交叉点在何处会使支架与地面形成夹角?
【模型建立】
环节一:数据收集
两根竹竿长度均为1.8米,插入地下的部分为0.3米,竹竿与地面接触点间距为0.6米且与地面所形成的夹角均为.
环节二:数学抽象
如图:已知线段与交于点,,与直线分别交于点,,,,,,求的长度.(结果精确到0.1,参考数据:,,)
【模型求解】
【问题总结】
交叉点距顶端的长度即为______时,支架与地面形成夹角,这样更贴合作物的生长规律.
3.(2025·湖南·中考真题)如图,某处有一个晾衣装置,固定立柱和分别垂直地面水平线于点,,分米,.在点,之间的晾衣绳上有固定挂钩,分米,一件连衣裙挂在点处(点与点重合),且直线.
(1)如图1,当该连衣裙下端点刚好接触到地面水平线时,点到直线的距离等于12分米,求该连衣裙的长度;
(2)如图2,为避免该连衣裙接触到地面,在另一端固定挂钩处再挂一条长裤(点在点的右侧),若,求此时该连衣裙下端点到地面水平线的距离约为多少分米?(结果保留整数,参考数据:,,)
4.(2025·四川宜宾·中考真题)如图,扇形为某运动场内的投掷区,所在圆的圆心为O、A、B、N、O在同一直线上.直线与所在相切于点.此时测得;从点处沿方向前进8.0米到达B处.直线与所在相切于点,此时测得.(参考数据:)
(1)求圆心角的度数;
(2)求的弧长(结果精确到米).
5.(2024·内蒙古·中考真题)实验是培养学生创新能力的重要途径.如图是小亮同学安装的化学实验装置,安装要求为试管口略向下倾斜,铁夹应固定在距试管口的三分之一处.现将左侧的实验装置图抽象成右侧示意图,已知试管,试管倾斜角为.
(1)求试管口B与铁杆的水平距离的长度;(结果用含非特殊角的三角函数表示)
(2)实验时,导气管紧靠水槽壁,延长交的延长线于点F,且于点N(点C,D,N,F在一条直线上),经测得:,求线段的长度.(结果用含非特殊角的三角函数表示)
6.(2024·甘肃兰州·中考真题)单摆是一种能够产生往复摆动的装置,某兴趣小组利用摆球和摆线进行与单摆相关的实验探究,并撰写实验报告如下.
实验主题 探究摆球运动过程中高度的变化
实验用具 摆球,摆线,支架,摄像机等
实验说明 如图1,在支架的横杆点O处用摆线悬挂一个摆球,将摆球拉高后松手,摆球开始往复运动.(摆线的长度变化忽略不计) 如图2,摆球静止时的位置为点A,拉紧摆线将摆球拉至点B处,,,;当摆球运动至点C时,,.(点O,A,B,C,D,E在同一平面内)
实验图示
解决问题:根据以上信息,求的长.(结果精确到)
参考数据:,.
7.(2024·四川广元·中考真题)小明从科普读物中了解到,光从真空射入介质发生折射时,入射角的正弦值与折射角的正弦值的比值叫做介质的“绝对折射率”,简称“折射率”.它表示光在介质中传播时,介质对光作用的一种特征.
(1)若光从真空射入某介质,入射角为,折射角为,且,,求该介质的折射率;
(2)现有一块与(1)中折射率相同的长方体介质,如图①所示,点A,B,C,D分别是长方体棱的中点,若光线经真空从矩形对角线交点O处射入,其折射光线恰好从点C处射出.如图②,已知,,求截面的面积.
8.(2024·江苏苏州·中考真题)图①是某种可调节支撑架,为水平固定杆,竖直固定杆,活动杆可绕点A旋转,为液压可伸缩支撑杆,已知,,.
(1)如图②,当活动杆处于水平状态时,求可伸缩支撑杆的长度(结果保留根号);
(2)如图③,当活动杆绕点A由水平状态按逆时针方向旋转角度,且(为锐角),求此时可伸缩支撑杆的长度(结果保留根号).
9.(2023·山东济南·中考真题)图1是某越野车的侧面示意图,折线段表示车后盖,已知,,,该车的高度.如图2,打开后备箱,车后盖落在处,与水平面的夹角.
(1)求打开后备箱后,车后盖最高点到地面的距离;
(2)若小琳爸爸的身高为,他从打开的车后盖处经过,有没有碰头的危险 请说明理由.
(结果精确到,参考数据:,,,)
考点06 三角函数与四边形的综合
1.(2025·四川资阳·中考真题)在四边形中,是边上的一点,是对角线的中点.
(1)如图1,四边形是正方形,连接,作交于点,求证:;
(2)如图2,四边形是平行四边形,,连接,作交于点,连接,求的值;
(3)如图3,四边形是菱形,,连接交于点是边上的一点,,若,求的长.
2.(2025·北京·中考真题)如图,在中,D,E分别为的中点,,垂足为F,点G在的延长线上,.
(1)求证:四边形是矩形;
(2)若,,,求和的长.
3.(2025·黑龙江·中考真题)如图,在正方形中,点在边上(不与点B、C重合),点E在的延长线上,且,连接、、,过点作于点,分别交、、于点、、.则下列结论:①;②;③;④若,则;⑤图中共有5个等腰三角形.其中正确的结论是( )
A.①②③⑤ B.①②④⑤ C.①②③④ D.①③④⑤
4.(2025·甘肃兰州·中考真题)如图,在菱形中,,垂足为E,交于点F,.若,则 .
5.(2025·贵州·中考真题)如图,在矩形中,点E,F,M分别在,,边上,分别交对角线、线段于点G,H,且是的中点.若,则的长为 .
6.(2024·江苏南通·中考真题)若菱形的周长为,且有一个内角为,则该菱形的高为 .
7.(2024·四川巴中·中考真题)如图,矩形的对角线与交于点,于点,延长与交于点.若,,则点到的距离为 .
8.(2023·辽宁丹东·中考真题)如图,在矩形中,对角线与相交于点O,,,垂足为点E,F是的中点,连接,若,则矩形的周长是( )
A. B. C. D.
考点07 三角函数与圆的综合
1.(2025·广东深圳·中考真题)如图1,在中,是的中点,,.
(1)求证:四边形为菱形;
(2)如图2,若点为上一点,,且,,三点均在上,连接,与相切于点,
①求__________;
②求的半径;
(3)利用圆规和无刻度直尺在图2中作射线,交于点,保留作图痕迹,不用写出作法和理由.
2.(2025·江苏苏州·中考真题)如图,在四边形中,.以为直径的经过点D,且与边交于点E,连接.
(1)求证:为的切线;
(2)若,求的长.
3.(2025·陕西·中考真题)如图,点在的边上,以为半径的⊙与相切于点,与相交于点,为⊙的直径,与相交于点,.
(1)求证:;
(2)若,,求的长.
4.(2025·四川成都·中考真题)如图,点C在以为直径的半圆O上,连接,过点C作半圆O的切线,交的延长线于点D,在上取点E,使,连接,交于点F.
(1)求证:;
(2)若,,求半圆O的半径及的长.
5.(2025·福建·中考真题)如图,四边形ABCD内接于,AD,BC的延长线相交于点E,AC,BD相交于点F.G是AB上一点,GD交AC于点H,且.
(1)求证:;
(2)求证:;
(3)若,求的周长.
6.(2025·新疆·中考真题)如图,为的直径,C为上一点,于点F,,交于点G,交于点D.
(1)求证:是的切线;
(2)若,,求的长.
7.(2025·黑龙江齐齐哈尔·中考真题)如图,内接于,为的直径,点D在的延长线上,连接,,过点B作,交于点E.
(1)求证:是的切线;
(2)若点B是的中点,且,求的半径.
答案解析
考点01 三角函数的定义
1.(2023·四川乐山·中考真题)我国汉代数学家赵爽在注解《周髀算经》时给出“赵爽弦图”,如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形面积为25,小正方形面积为1,则( )
A. B. C. D.
【答案】A
【分析】先由两个正方形的面积分别得出其边长,由赵爽弦图的特征可得,则,在中,利用勾股定理求出,最后按照正弦函数的定义计算求解即可.
【详解】解:∵大正方形的面积是25,小正方形面积是1,
∴大正方形的边长,小正方形的边长,
∵,
∴,
在中,,
∴,
解得(负值舍去)
∴.
故选A.
【点睛】本题考查了勾股定理、弦图及正弦函数的计算,明确相关性质及定理是解题的关键.
2.(2024·广西·中考真题)如图,在中,,.
(1)尺规作图:作线段的垂直平分线l,分别交,于点D,E:(要求:保留作图痕迹,不写作法,标明字母)
(2)在(1)所作的图中,连接,若,求的长.
【答案】(1)见详解
(2)
【分析】(1)分别以A、B为圆心,大于为半径画弧,分别交,于点D,E,作直线,则直线l即为所求.
(2)连接,由线段垂直平分线的性质可得出,由等边对等角可得出,由三角形内角和得出,则得出为等腰直角三角形,再根据正弦的定义即可求出的长.
【详解】(1)解:如下直线l即为所求.
(2)连接如下图:
∵为线段的垂直平分线,
∴,
∴,
∴,
∴为等腰直角三角形,
∴,
∴
【点睛】本题主要考查了作线段的垂线平分线,线段的垂线平分线的性质,等腰三角形的性质,三角形内角和定理以及正弦的定义.掌握线段的垂直平分线的性质是解题的关键.
3.(2025·山东东营·中考真题)《九章算术》是我国古代数学成就的杰出代表,其中《方田》章给出计算弧田面积所用公式为:弧田面积(弦矢+矢),弧田(如图)是由圆弧和其所对的弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.在如图所示的弧田中,“弦”为8,“矢”为2,则的值为 .
【答案】/
【分析】本题主要考查垂径定理、勾股定理、三角函数的定义等知识点.如图,作交于,交圆弧于,利用垂径定理和勾股定理构建方程组求出,,利用余弦函数定义即可解决问题.
【详解】解:如图,作交于,交圆弧于,
由题意:,
设,由,
∴,
∵,为半径,
∴,
在中,
由勾股定理得,
∴,
解得,
∴,
∴.
故答案为:.
4.(2023·内蒙古·中考真题)如图是源于我国汉代数学家赵爽的弦图,它是由四个全等直角三角形与一个小正方形拼成的一个大正方形.若小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为,则的值为( )
A. B. C. D.
【答案】D
【分析】首先根据两个正方形的面积分别求出两个正方形的边长,然后结合题意进一步设直角三角形短的直角边为,则较长的直角边为,再接着利用勾股定理得到关于的方程,据此进一步求出直角三角形各个直角边的边长,最后求出的值即可.
【详解】∵小正方形的面积为,大正方形的面积为25,
∴小正方形的边长为1,大正方形的边长为5,
设直角三角形短的直角边为,则较长的直角边为,其中,
∴,其中,
解得:,,
∴,
故选:D.
【点睛】本题主要考查了勾股定理与一元二次方程及三角函数的综合运用,熟练掌握相关概念是解题关键.
5.(2023·吉林长春·中考真题)学校开放日即将来临,负责布置的林老师打算从学校图书馆的顶楼拉出一条彩旗绳到地面,如图所示.已彩旗绳与地面形成角(即)、彩旗绳固定在地面的位置与图书馆相距32米(即米),则彩旗绳的长度为( )
A.米 B.米 C.米 D.米
【答案】D
【分析】根据余弦值的概念即邻边与斜边之比,即可求出答案.
【详解】解:表示的是地面,表示是图书馆,
,
为直角三角形,
(米).
故选:D.
【点睛】本题考查的是解直角三角形的应用,涉及到余弦值,解题的关键在于熟练掌握余弦值的概念.
6.(2023·江苏·中考真题)如图,在中,,点D在边AB上,连接CD.若,,则 .
【答案】/
【分析】由题意可设,则,,在中求得,在中求出答案即可.
【详解】解: ,,
设,则,,
在中,由勾股定理得:,
在中,.
【点睛】本题考查的是求锐角三角函数,解题关键是根据比值设未知数,表示出边长从而求出锐角三角函数值.
7.(2023·江苏连云港·中考真题)如图,菱形的对角线相交于点为的中点,,.求的长及的值.
【答案】,
【分析】根据菱形的性质得出,中,勾股定理求得的长,根据正切的定义即可求解.
【详解】在菱形中,.
∵,∴.
在中,∵为中点,
∴.
∵.
∴.
∴.
∴.
【点睛】本题考查了菱形的性质,勾股定理,求正切,熟练掌握以上知识是解题的关键.
8.(2024·山东淄博·中考真题)如图,在综合与实践活动课上,小强先测得教学楼在水平地面上的影长为.又在点处测得该楼的顶端的仰角是.则用科学计算器计算教学楼高度的按键顺序正确的是( )
A. B.
C. D.
【答案】A
【分析】本题考查解直角三角形的应用,用计算器计算三角函数值,根据题意,得到,进行判断即可.
【详解】解:由题意,得:在中,,,
∴;
计算器的按键为 ;
故选A.
考点02 解直角三角形的实际应用——俯仰角
1.(2025·四川达州·中考真题)为了让莲花湖湿地公园的天更蓝,水更清,莲花湖管委会定期利用无人机指引工作人员清理湖中垃圾.已知无人机悬停在湖面上的处,工作人员所乘小船在处测得无人机的仰角为,当工作人员沿正前方向划行米到达处,测得无人机的仰角为,求无人机离湖面的高度(结果不取近似值)
【答案】无人机离湖面的高度为米
【分析】本题考查了解直角三角形的应用,构造直角三角形是解题的关键;过点作于点,设,根据题意得出,,在中,根据,列出方程,解方程,即可求解.
【详解】解:如图,过点作于点,
依题意
设,
在中,
∴,
∵
∴,
在中,
∴
解得:
答:无人机离湖面的高度为米
2.(2025·吉林长春·中考真题)如图,已知某山峰的海拔高度为米,一位登山者到达海拔高度为米的点处.测得山峰顶端的仰角为.则、两点之间的距离为( )
A.米 B.米
C.米 D.米
【答案】B
【分析】本题主要考查了解直角三角形的实际应用,掌握三角函数的定义是解题的关键.
由题意得四边形是矩形,则,那么,再解即可.
【详解】解:由题意得,四边形是矩形,
∴,
∴,
由题意得,,
∴,
∴,
故选:B.
3.(2025·辽宁·中考真题)如图,为了测量树的高度,在水平地面上取一点,在处测得,,则树的高约为 (结果精确到.参考数据:,).
【答案】
【分析】本题考查了解直角三角形的实际应用,正确使用三角函数是解题的关键.
在中,由即可求解.
【详解】解:由题意得,
∴在中,,
故答案为:.
4.(2025·吉林·中考真题)综合与实践:确定建筑物的打印模型的高度项目提出:图是某城市规划展览馆.树人中学的打印社团为展示城市文化,准备制作该城市规划展览馆的打印模型,需要测量并计算展览馆高度,为制作打印模型提供数据.
项目报告表 时间:2025年5月29日
项目分析 活动目标 测量该城市规划展览馆的实际高度并换算其打印模型的高度
测量工具 测角仪、皮尺
项目实施 任务一测量数据 以下是测得的相关数据,并画出了如图所示的测量草图. 1.测出测角仪的高. 2.利用测角仪测出展览馆顶端A的仰角. 3.测出测角仪底端D处到展览馆底端B处之间的距离.
任务二计算实际高度 根据上述测得的数据,计算该城市规划展览馆的高度.(结果精确到1m)(参考数据:,,)
任务三换算模型高度 将该城市规划展览馆的高度按等比例缩小,得到其打印模型的高度约为________.(结果精确到)
项目结果 为社团制作城市规划展览馆的打印模型提供数据
请结合上表中的测量草图和相关数据,帮助该社团完成任务二和任务三.
【答案】该城市规划展览馆的高度为;打印模型的高度约为
【分析】本题考查了解直角三角形的实际应用,比例的基本性质,正确理解题意是解题的关键.
任务二:先由矩形得到,,然后解即可;
任务三:由比例尺等于图上距离比上实际距离求解即可.
【详解】解:任务二:由题意得为矩形,
∴,,
∵在中,
∴,
∴,
答:该城市规划展览馆的高度为;
任务三:设打印模型的高度约为,
则由题意得:,
解得:,
答:打印模型的高度约为.
5.(2025·陕西·中考真题)小涵和小宇想测量公园山坡上一个信号杆的高度.在征得家长同意后,他们带着工具前往测量.测量示意图如图所示,他们在坡面上的点处安装测角仪,测得信号杆顶端的仰角为,与坡面的夹角为,又测得点与信号杆底端之间的距离为.已知,点,,在同一条直线上,,均与水平线垂直.求信号杆的高.(参考数据:,,)
【答案】信号杆的高为
【分析】本题考查了解直角三角形的应用,三角形内角和性质,矩形的判定与性质,等角对等边,正确掌握相关性质内容是解题的关键.先理解题意,得出,再在中,运用,,代入数值进行计算,得出的值,然后证明四边形是矩形,故,根据,,得,,把数值代入进行计算,即可作答.
【详解】解:过点E作于点,过点D作于点,如图所示:
∵,均与水平线垂直.
∴
∴,
∵
∴
在中,,
则,
在中,,
则,
∵过点E作于点,过点D作于点,
∴,
∴四边形是矩形
∴,
∵,,
∴,
∴,
∴,
信号杆的高为.
6.(2025·安徽·中考真题)某公司为庆祝新产品上市,在甲楼与乙楼的楼顶之间悬挂彩带营造喜庆气氛.如图所示,甲楼和乙楼分别用与水平地面垂直的线段和表示,彩带用线段表示.工作人员在点A处测得点C的俯角为,测得点D的仰角为.已知,求的长(精确到).参考数据:,,,,,.
【答案】
【分析】本题主要考查了解直角三角形的实际应用,过点A作,垂足为点E,则四边形为矩形,可得,解求出的长,再解求出的长即可得到答案.
【详解】解:过点A作,垂足为点E.
∵线段和都与地面垂直,
∴四边形为矩形,
∴.
在中,,
∴.
在中,,
.
答:的长为.
7.(2024·四川雅安·中考真题)在数学课外实践活动中,某小组测量一栋楼房的高度(如图),他们在A处仰望楼顶,测得仰角为,再往楼的方向前进50米至B处,测得仰角为,那么这栋楼的高度为(人的身高忽略不计)( )
A.米 B.25米 C.米 D.50米
【答案】A
【分析】此题考查了解直角三角形的应用-仰角俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形.
设米,在中,利用锐角三角函数定义表示出,在中,利用锐角三角函数定义表示出,再由列出关于的方程,求出方程的解得到的值即可.
【详解】解:设米,
在中,,
,即,
整理得:米,
在中,,
,即,
整理得:米,
∵米,
∴,即,
解得:,
侧这栋楼的高度为米.
故选:A.
8.(2024·黑龙江牡丹江·中考真题)如图,某数学活动小组用高度为米的测角仪,对垂直于地面的建筑物的高度进行测量,于点C.在B处测得A的仰角,然后将测角仪向建筑物方向水平移动6米至处,于点G,测得A的仰角,的延长线交于点E,求建筑物的高度(结果保留小数点后一位).(参考数据:)
【答案】17.5米
【分析】本题主要考查了矩形的性质与判定,解直角三角形的实际应用,由题意可得四边形是矩形,则.解直角三角形得到,进而得到,据此求出即可得到答案.
【详解】解:根据题意可知四边形是矩形,
.
如图,.
,
.
,
.
(米)
答:建筑物的高度约为米.
考点03 解直角三角形的实际应用——坡度、坡角
1.(2025·四川资阳·中考真题)如图,已知水平地面上方有一个水平的平台,该平台上有一个竖直的建筑物.在处测得建筑物顶端的仰角为,在处测得的仰角为,斜坡的坡度米,.(点在同一竖直平面内).
(1)求平台的高度;
(2)求建筑物的高度(即的长).
【答案】(1)10米
(2)米
【分析】本题考查解直角三角形的实际应用,矩形的判定及性质.
(1)过点B作于点E,则,根据斜坡的坡度,得到,从而在中,根据勾股定理构造方程,求解即可;
(2)延长交于点F,得到四边形是矩形,因此米,,设米,则(米),通过解直角三角形在中,求得(米),在中,求得∴(米),进而根据列出方程,求解即可.
【详解】(1)解:过点B作于点E,则
∵斜坡的坡度,
∴,
∵在中,,
即,
∴米,
∴平台的高度是10米.
(2)解:延长交于点F,
∵,,
∴,
∴四边形是矩形,
∴米,,
设米,则(米),
∵在中,,
∴(米),
∵在中,,
∴(米),
∴米,
由(1)有(米),
∵,
∴,
解得,
∴(米),
即建筑物的高度(即的长)为米.
2.(2024·四川巴中·中考真题)某兴趣小组开展了测量电线塔高度的实践活动.如图所示,斜坡的坡度,,在处测得电线塔顶部的仰角为,在处测得电线塔顶部的仰角为.
(1)求点离水平地面的高度.
(2)求电线塔的高度(结果保留根号).
【答案】(1);
(2)电线塔的高度.
【分析】本题主要考查了解直角三角形的实际应用.
(1)由斜坡的坡度,求得,利用正切函数的定义得到,据此求解即可;
(2)作于点,设,先解得到,解得到米,进而得到方程,解方程即可得到答案.
【详解】(1)解:∵斜坡的坡度,
∴,
∵,
∴,
∵,
∴;
(2)解:作于点,则四边形是矩形,,,
设,
在中,,
∴,
在中,,
在中,,,
∴,
∴,
∴,
∴,
∴
答:电线塔的高度.
3.(2024·四川眉山·中考真题)如图,斜坡的坡度,在斜坡上有一棵垂直于水平面的大树,当太阳光与水平面的夹角为时,大树在斜坡上的影子长为10米,则大树的高为 米.
【答案】/
【分析】此题考查了解直角三角形的应用,勾股定理,解题的关键是正确构造直角三角形.
如图,过点作水平地面的平行线,交的延长线于点,设米,米,勾股定理求出,解直角三角形求出,进而求解即可.
【详解】解:如图,过点作水平地面的平行线,交的延长线于点,
则,
在中,,
设米,米,
,
,
米,米,
,
(米),
(米),
答:大树的高度为米.
故答案为:.
4.(2024·四川广安·中考真题)风电项目对于调整能源结构和转变经济发展方式具有重要意义.某电力部门在某地安装了一批风力发电机,如图(1)某校实践活动小组对其中一架风力发电机的塔杆高度进行了测量,图(2)为测量示意图(点,,,均在同一平面内,).已知斜坡长为20米,斜坡的坡角为,在斜坡顶部处测得风力发电机塔杆顶端点的仰角为,坡底与塔杆底的距离米,求该风力发电机塔杆的高度.
(结果精确到个位;参考数据:,,,)
【答案】32m
【分析】本题考查的是矩形的判定与性质,解直角三角形的实际应用,过点作于点,作于点,先求解,,再证明,再利用锐角的正切可得,从而可得答案.
【详解】解:过点作于点,作于点
由题意得:,
在中,
,
,
,
四边形为矩形,
,,
,
在中.
,
答:该风力发电机塔杆的高度为.
5.(2023·江苏泰州·中考真题)如图,堤坝长为,坡度i为,底端A在地面上,堤坝与对面的山之间有一深沟,山顶D处立有高的铁塔.小明欲测量山高,他在A处看到铁塔顶端C刚好在视线上,又在坝顶B处测得塔底D的仰角为.求堤坝高及山高.(,,,小明身高忽略不计,结果精确到)
【答案】堤坝高为8米,山高为20米.
【分析】过B作于H,设,,根据勾股定理得到,求得,过B作于F,则,设,解直角三角形即可得到结论.
【详解】解:过B作于H,
∵坡度i为,
∴设,,
∴,
∴,
∴,
过B作于F,
则,
设,
∵.
∴,
∴,
∵坡度i为,
∴,
∴,
∴(米),
∴(米),
答:堤坝高为8米,山高为20米.
【点睛】本题考查了解直角三角形的应用-俯角仰角,解直角三角形的应用-坡角坡度,正确地作出辅助线是解题的关键.
6.(2023·湖北·中考真题)为了防洪需要,某地决定新建一座拦水坝,如图,拦水坝的横断面为梯形,斜面坡度是指坡面的铅直高度与水平宽度的比.已知斜坡长度为20米,,求斜坡的长.(结果精确到米)(参考数据:)
【答案】斜坡的长约为10米
【分析】过点作于点,在中,利用正弦函数求得,在中,利用勾股定理即可求解.
【详解】解:过点作于点,则四边形是矩形,
在中,,
.
∴.
∵,
∴在中,(米).
答:斜坡的长约为10米.
【点睛】此题考查的是解直角三角形的应用-坡度坡角问题,掌握坡度坡角的概念、熟记锐角三角函数的定义是解题的关键.
7.(2023·四川自贡·中考真题)为测量学校后山高度,数学兴趣小组活动过程如下:
(1)测量坡角
如图1,后山一侧有三段相对平直的山坡,山的高度即为三段坡面的铅直高度之和,坡面的长度可以直接测量得到,要求山坡高度还需要知道坡角大小.
如图2,同学们将两根直杆的一端放在坡面起始端A处,直杆沿坡面方向放置,在直杆另一端N用细线系小重物G,当直杆与铅垂线重合时,测得两杆夹角的度数,由此可得山坡AB坡角的度数.请直接写出之间的数量关系.
(2)测量山高
同学们测得山坡的坡长依次为40米,50米,40米,坡角依次为;为求,小熠同学在作业本上画了一个含角的(如图3),量得.求山高.(,结果精确到1米)
(3)测量改进
由于测量工作量较大,同学们围绕如何优化测量进行了深入探究,有了以下新的测量方法.
如图4,5,在学校操场上,将直杆NP置于的顶端,当与铅垂线重合时,转动直杆,使点N,P,D共线,测得的度数,从而得到山顶仰角,向后山方向前进40米,采用相同方式,测得山顶仰角;画一个含的直角三角形,量得该角对边和另一直角边分别为厘米,厘米,再画一个含的直角三角形,量得该角对边和另一直角边分别为厘米,厘米.已知杆高MN为米,求山高.(结果用不含的字母表示)
【答案】(1);
(2)山高为69米;
(3)山高的高为米..
【分析】(1)利用互余的性质即可求解;
(2)先求得,再分别在、、中,解直角三角形即可求解;
(3)先求得,,在和中,分别求得和的长,得到方程,据此即可求解.
【详解】(1)解:由题意得,
∴;
(2)解:在中,.
∴,
在中,,米,
∴(米),
在中,,米,
∴(米),
在中,,米,
∴(米),
∴山高(米),
答:山高为69米;
(3)解:如图,由题意得,,
设山高,则,
在中,,,
∴,
∴,
在中,,,
∴,
∴,
∵,
∴,即,
解得,山高
答:山高的高为米.
【点睛】本题考查了解直角三角形的应用,能够正确地构建出直角三角形,将实际问题化归为解直角三角形的问题是解答此类题的关键.
考点04 解直角三角形的实际应用——方位角
1.(2025·重庆·中考真题)为加强森林防火,某林场采用人工瞭望与无人机巡视两种方式监测森林情况.如图,A,B,C,D在同一平面内.A是瞭望台,某一时刻,观测到甲无人机位于A的正东方向10千米的B处,乙无人机位于A的南偏西方向20千米的D处.两无人机同时飞往C处巡视,D位于C的正西方向上,B位于C的北偏西方向上.(参考数据:,,,)
(1)求的长度(结果保留小数点后一位);
(2)甲、乙两无人机同时分别从B,D出发沿往C处进行巡视,乙无人机速度为甲无人机速度的2倍.当两无人机相距20千米时,它们可以开始相互接收到信号.请问甲无人机飞离B处多少千米时,两无人机可以开始相互接收到信号(结果保留小数点后一位)?
【答案】(1)千米
(2)千米
【分析】本题主要考查了解直角三角形的实际应用,矩形的性质与判定, 正确作出辅助线构造直角三角形是解题的关键。
(1)过点A作于E,过点B作于F,由题意得,,解得到千米,千米,证明四边形是矩形, 得到千米,千米,得到千米,再利用勾股定理即可求出的长;
(2)当甲无人机运动到M,乙无人机运动到N时,此时满足千米.过点M作于T,由题意得,,解得到千米,千米,则千米,设千米,则千米,千米,解得到千米,千米,则千米,由勾股定理得,解方程即可得到答案。
【详解】(1)解:如图所示,过点A作于E,过点B作于F,
∴,
由题意得,,
在中,千米,
千米,
∵无人机位于A的正东方向10千米的B处,D位于C的正西方向上,
∴,
∴,
∴四边形是矩形,
∴千米,千米,
∴千米,
∴千米,
答:的长度约为千米;
(2)解:如图所示,当甲无人机运动到M,乙无人机运动到N时,此时满足千米.过点M作于T,
由题意得,,
在中,千米,
千米,
∴千米,
设千米,则千米,千米,
在中,千米,
千米,
∴千米,
在中,由勾股定理得,
∴,
∴或(此时大于的长,舍去),
∴千米,
答:甲无人机飞离B处千米时,两无人机可以开始相互接收到信号.
2.(2025·山东烟台·中考真题)【综合与实践】
烟台山灯塔被誉为“黄海夜明珠”,它坐落在烟台山上,为过往船只提供导航服务.为了解渔船海上作业情况,某日,数学兴趣小组开展了实践探究活动.
如图,一艘渔船自东向西以每小时海里的速度向码头航行,小组同学收集到以下信息:
位置信息 码头A在灯塔B北偏西方向
14:30时,渔船航行至灯塔北偏东方向的处
15:00时,渔船航行至灯塔东北方向的处
天气预警 受暖湿气流影响,今天17:30到夜间,码头附近海域将出现浓雾天气.请注意防范.
请根据以上信息,解答下列问题:
(1)求渔船在航行过程中到灯塔的最短距离;
(2)若不改变航行速度,请通过计算说明渔船能否在浓雾到来前到达码头(参考数据:,,,,,).
【答案】(1)渔船在航行过程中到灯塔的最短距离为海里
(2)不改变航行速度,渔船能在浓雾到来前到达码头
【分析】本题考查了解直角三角形的应用,构造直角三角形是解题的关键;
(1)过点作于点,设,根据题意得出,解,得出,建立方程,即可求解;
(2)求得的距离,计算的距离,根据路程除以速度得到航行时间,结合题意,即可求解.
【详解】(1)解:如图,过点作于点,
设,
依题意,,,,
∴,,
∴,
在中,,
∴,
解得:,
∴渔船在航行过程中到灯塔的最短距离为海里;
(2)解:在中,,,
∴,
∴,
小时分钟,
从14:30,经过分钟是,在之前到达,
∴不改变航行速度,渔船能在浓雾到来前到达码头.
3.(2024·海南·中考真题)木兰灯塔是亚洲最高、世界第二高的航标灯塔,位于海南岛的最北端,是海南岛东北部最重要的航标.某天,一艘渔船自西向东(沿方向)以每小时10海里的速度在琼州海峡航行,如图所示.
航行记录记录一:上午8时,渔船到达木兰灯塔P北偏西方向上的A处. 记录二:上午8时30分,渔船到达木兰灯塔P北偏西方向上的B处. 记录三:根据气象观测,当天凌晨4时到上午9时,受天文大潮和天气影响,琼州海峡C点周围5海里内,会出现异常海况,点C位于木兰灯塔P北偏东方向.
请你根据以上信息解决下列问题:
(1)填空:________,________, ________海里;
(2)若该渔船不改变航线与速度,是否会进入“海况异常”区,请计算说明.
(参考数据:)
【答案】(1)30;75;5
(2)该渔船不改变航线与速度,会进入“海况异常”区
【分析】本题主要考查了方位角的计算,解直角三角形的实际应用,三角形内角和定理:
(1)根据方位角的描述和三角形内角和定理可求出两个角的度数,根据路程等于速度乘以时间可以计算出对应线段的长度;
(2)设海里,先解得到,再解得到海里,海里,据此可得,解得海里;证明,则海里;再求出上午9时时船与C点的距离即可得到结论.
【详解】(1)解:如图所示,过点P作于D,
由题意得, ,
∴;
∵一艘渔船自西向东(沿方向)以每小时10海里的速度在琼州海峡航行,上午8时从A出发到上午8时30分到达B,
∴海里.
(2)解:设海里,
在中,海里,
在中,海里,海里,
∵,
∴,
解得,
∴海里,
∵,
∴,
∴海里;
上午9时时,船距离A的距离为海里,
∵,
∴该渔船不改变航线与速度,会进入“海况异常”区.
4.(2024·四川资阳·中考真题)如图,某海域有两灯塔A,B,其中灯塔B在灯塔A的南偏东方向,且A,B相距海里.一渔船在C处捕鱼,测得C处在灯塔A的北偏东方向、灯塔B的正北方向.
(1)求B,C两处的距离;
(2)该渔船从C处沿北偏东方向航行一段时间后,突发故障滞留于D处,并发出求救信号.此时,在灯塔B处的渔政船测得D处在北偏东方向,便立即以18海里/小时的速度沿方向航行至D处救援,求渔政船的航行时间.
(注:点A,B,C,D在同一水平面内;参考数据:,)
【答案】(1)B,C两处的距离为16海里
(2)渔政船的航行时间为小时
【分析】本题考查了解直角三角形的实际应用,解题的关键是正确画出辅助线,构造直角三角形.
(1)根据题意易得,则,再求出(海里),即可解答;
(2)过点D作于点F,设海里,则,,则,求出,进而得出海里,海里,根据勾股定理可得:(海里),即可解答.
【详解】(1)解:过点A作于点E,
∵灯塔B在灯塔A的南偏东方向,C处在灯塔A的北偏东方向、灯塔B的正北方向.
∴,
∴,
∵,
∴,
∵海里,
∴(海里),
∴(海里),
∴B,C两处的距离为16海里.
(2)解:过点D作于点F,
设海里,
∵,
∴,
由(1)可知,海里,
∴海里,
∵,
∴,
∴,
解得:,
∴海里,海里,
根据勾股定理可得:(海里),
∴渔政船的航行时间为(小时),
答:渔政船的航行时间为小时.
5.(2024·江苏连云港·中考真题)图1是古代数学家杨辉在《详解九章算法》中对“邑的计算”的相关研究.数学兴趣小组也类比进行了如下探究:如图2,正八边形游乐城的边长为,南门设立在边的正中央,游乐城南侧有一条东西走向的道路,在上(门宽及门与道路间距离忽略不计),东侧有一条南北走向的道路,C处有一座雕塑.在处测得雕塑在北偏东方向上,在处测得雕塑在北偏东方向上.
(1)__________,__________;
(2)求点到道路的距离;
(3)若该小组成员小李出南门O后沿道路向东行走,求她离处不超过多少千米,才能确保观察雕塑不会受到游乐城的影响?(结果精确到,参考数据:,,,,)
【答案】(1),
(2)2.0千米
(3)
【分析】本题考查正多边形的外角,解直角三角形,相似三角形的判定和性质:
(1)求出正八边形的一个外角的度数,再根据角的和差关系进行求解即可;
(2)过点作,垂足为,解,求出,解,求出,即可;
(3)连接并延长交于点,延长交于点,过点作,垂足为,解,求出,证明,列出比例式进行求解即可.
【详解】(1)解:∵正八边形的一个外角的度数为:,
∴,;
故答案为:;
(2)过点作,垂足为.
在中,,,
.
在中,,
.
答:点到道路的距离为2.0千米.
(3)连接并延长交于点,延长交于点,过点作,垂足为.
正八边形的外角均为,
在中,.
.
又,,
.
∵,
∴,
,即,
,
.
答:小李离点不超过2.4km,才能确保观察雕塑不会受到游乐城的影响.
6.(2023·山东临沂·中考真题)如图,灯塔A周围9海里内有暗礁.一渔船由东向西航行至B处,测得灯塔A在北偏西58°方向上,继续航行6海里后到达C处,测得灯塔A在西北方向上.如果渔船不改变航线继续向西航行,有没有触礁的危险?
(参考数据:)
【答案】渔船没有触礁的危险
【分析】过点作,分别解和,求出的长,即可得出结论.
【详解】解:过点作,由题意,得:,,,
设,
在中,,
∴,
∴,
在中,,
∴,
∴,
∵,
∴渔船没有触礁的危险.
【点睛】本题考查解直角三角形的应用—方向角问题.解题的关键是添加辅助线,构造直角三角形.
考点05 解直角三角形的实际应用——其他
1.(2025·贵州·中考真题)某小区在设计时,计划在如图①的住宅楼正前方建一栋文体活动中心.设计示意图如图②所示,已知,该地冬至正午太阳高度角为.如果你是建筑设计师,请结合示意图和已知条件完成下列任务.
任务一:计算冬至正午太阳照到住宅楼的位置与地面之间的距离的长;
任务二:为符合建筑规范对日照的要求,让整栋住宅楼在冬至正午太阳高度角下恰好都能照射到阳光,需将活动中心沿方向移动一定的距离(活动中心高度不变),求该活动中心移动了多少米?
(参考数据:.结果保留小数点后一位)
【答案】任务一:,任务二:该活动中心移动了2米;
【分析】本题考查的是矩形的判定与性质,解直角三角形的实际应用;
任务一:如图,过作于,结合题意可得:四边形为矩形,,可得,,求解,进一步可得答案;
任务二:如图,过作的平行线,过作的平行线,两线交于点,交于点,过作于,可得,四边形为矩形,,求解,进一步可得答案.
【详解】解:任务一:如图,过作于,
结合题意可得:四边形为矩形,,
∵,
∴,,
∵,
∴,
∴;
任务二:如图,过作的平行线,过作的平行线,两线交于点,交于点,过作于,
∴,四边形为矩形,
∴,
∴,
∴;
∴该活动中心移动了2米.
2.(2025·青海·中考真题)数学实践
【问题背景】
中国传统农业智慧遇上现代数学模型.“豇豆不上架,产量少一半”的农谚流传至今,现代科学揭示了其秘密:当支架与地面形成夹角时,既能在早春聚热防冻害,又能在盛夏分散强光,就像给豇豆装了智能遮阳篷.
【问题呈现】
用两根竹竿交叉,斜插入地面,交叉点在何处会使支架与地面形成夹角?
【模型建立】
环节一:数据收集
两根竹竿长度均为1.8米,插入地下的部分为0.3米,竹竿与地面接触点间距为0.6米且与地面所形成的夹角均为.
环节二:数学抽象
如图:已知线段与交于点,,与直线分别交于点,,,,,,求的长度.(结果精确到0.1,参考数据:,,)
【模型求解】
【问题总结】
交叉点距顶端的长度即为______时,支架与地面形成夹角,这样更贴合作物的生长规律.
【答案】,
【分析】本题考查的是解直角三角形的应用,如图,过作于,根据等腰三角形的性质可得,结合可得答案;最后由即可得到答案.
【详解】解:数学抽象:如图,过作于,
∵,
∴,
∵,
∴,
∴,
∴,
问题总结:∵,,
∴.
3.(2025·湖南·中考真题)如图,某处有一个晾衣装置,固定立柱和分别垂直地面水平线于点,,分米,.在点,之间的晾衣绳上有固定挂钩,分米,一件连衣裙挂在点处(点与点重合),且直线.
(1)如图1,当该连衣裙下端点刚好接触到地面水平线时,点到直线的距离等于12分米,求该连衣裙的长度;
(2)如图2,为避免该连衣裙接触到地面,在另一端固定挂钩处再挂一条长裤(点在点的右侧),若,求此时该连衣裙下端点到地面水平线的距离约为多少分米?(结果保留整数,参考数据:,,)
【答案】(1)14分米
(2)2分米
【分析】本题主要考查了解直角三角形的实际应用,勾股定理,矩形的性质与判定,正确作出辅助线构造直角三角形是解题的关键.
(1)可证明四边形是矩形,得到;在中,利用勾股定理求出的长,进而求出的长即可得到答案;
(2)过点E作于H,延长交于T,则四边形是矩形,可得;解求出的长,进而求出的长,据此求出的长即可得到答案.
【详解】(1)解:∵,
∴四边形是矩形,
∴;
在中,分米,分米,
∴分米,
∴分米,
∴分米,
答:该连衣裙的长度为14分米;
(2)如图所示,过点E作于H,延长交于T,
∵,
∴四边形是矩形,
∴;
在中,分米,,,
∴分米,
分米,
∴分米,
∴分米,
分米,
∴分米;
答:此时该连衣裙下端点到地面水平线的距离约为2分米.
4.(2025·四川宜宾·中考真题)如图,扇形为某运动场内的投掷区,所在圆的圆心为O、A、B、N、O在同一直线上.直线与所在相切于点.此时测得;从点处沿方向前进8.0米到达B处.直线与所在相切于点,此时测得.(参考数据:)
(1)求圆心角的度数;
(2)求的弧长(结果精确到米).
【答案】(1)
(2)
【分析】本题考查了解直角三角形的应用,圆的切线的性质,弧长公式,熟练掌握各知识点并灵活运用是解题的关键.
(1)由圆的切线的性质得到,再由直角三角形锐角互余即可求解;
(2)先解,设,,再解得到,求出,求出半径,再由弧长公式即可求解.
【详解】(1)解:∵直线与所在相切于点,
∴,
∵,
∴;
(2)解:∵直线与所在相切于点,
∴,
∵,
∴,
设,
∴,
∵,
∴,
∵在中,,
∴,
∴,
解得:,
∴,
∴的弧长为:,
答:的弧长为.
5.(2024·内蒙古·中考真题)实验是培养学生创新能力的重要途径.如图是小亮同学安装的化学实验装置,安装要求为试管口略向下倾斜,铁夹应固定在距试管口的三分之一处.现将左侧的实验装置图抽象成右侧示意图,已知试管,试管倾斜角为.
(1)求试管口B与铁杆的水平距离的长度;(结果用含非特殊角的三角函数表示)
(2)实验时,导气管紧靠水槽壁,延长交的延长线于点F,且于点N(点C,D,N,F在一条直线上),经测得:,求线段的长度.(结果用含非特殊角的三角函数表示)
【答案】(1)
(2)
【分析】本题主要考查了解直角三角形的应用,通过作辅助线构造直角三角形,掌握直角三角形中的边角关系是解题关键.
(1)先求出,再在中,利用余弦的定义求解即可得;
(2)过点作于点,过点作于点,先解直角三角形可得的长,从而可得的长,再判断出是等腰直角三角形,从而可得的长,最后根据求解即可得.
【详解】(1)解:∵,
∴,
由题意可知,,
在中,,
∴,
答:试管口与铁杆的水平距离的长度.
(2)解:如图,过点作于点,过点作于点,
则四边形和四边形都是矩形,
∴,
在中,,,
∴,
∵,
∴,
∴,
∵,,,
∴,
∴是等腰直角三角形,
∴,
∴,
答:线段的长度为.
6.(2024·甘肃兰州·中考真题)单摆是一种能够产生往复摆动的装置,某兴趣小组利用摆球和摆线进行与单摆相关的实验探究,并撰写实验报告如下.
实验主题 探究摆球运动过程中高度的变化
实验用具 摆球,摆线,支架,摄像机等
实验说明 如图1,在支架的横杆点O处用摆线悬挂一个摆球,将摆球拉高后松手,摆球开始往复运动.(摆线的长度变化忽略不计) 如图2,摆球静止时的位置为点A,拉紧摆线将摆球拉至点B处,,,;当摆球运动至点C时,,.(点O,A,B,C,D,E在同一平面内)
实验图示
解决问题:根据以上信息,求的长.(结果精确到)
参考数据:,.
【答案】的长为
【分析】本题考查的是解直角三角形的实际应用,先求解,再求解,从而可得答案;
【详解】解:∵,,;
∴,
,
∴,
∵,,
∴,
∴;
∴的长为;
7.(2024·四川广元·中考真题)小明从科普读物中了解到,光从真空射入介质发生折射时,入射角的正弦值与折射角的正弦值的比值叫做介质的“绝对折射率”,简称“折射率”.它表示光在介质中传播时,介质对光作用的一种特征.
(1)若光从真空射入某介质,入射角为,折射角为,且,,求该介质的折射率;
(2)现有一块与(1)中折射率相同的长方体介质,如图①所示,点A,B,C,D分别是长方体棱的中点,若光线经真空从矩形对角线交点O处射入,其折射光线恰好从点C处射出.如图②,已知,,求截面的面积.
【答案】(1);
(2).
【分析】本题主要考查了解直角三角形的应用,勾股定理等知识,
(1)根据,设,则,利用勾股定理求出,进而可得,问题即可得解;
(2)根据折射率与(1)的材料相同,可得折射率为,根据,可得,则有,在中,设,,问题随之得解.
【详解】(1)∵,
∴如图,
设,则,由勾股定理得,,
∴,
又∵,
∴,
∴折射率为:.
(2)根据折射率与(1)的材料相同,可得折射率为,
∵,
∴,
∴.
∵四边形是矩形,点O是中点,
∴,,
又∵,
∴,
在中,设,,
由勾股定理得,,
∴.
又∵,
∴,
∴,
∴,
∴截面的面积为:.
8.(2024·江苏苏州·中考真题)图①是某种可调节支撑架,为水平固定杆,竖直固定杆,活动杆可绕点A旋转,为液压可伸缩支撑杆,已知,,.
(1)如图②,当活动杆处于水平状态时,求可伸缩支撑杆的长度(结果保留根号);
(2)如图③,当活动杆绕点A由水平状态按逆时针方向旋转角度,且(为锐角),求此时可伸缩支撑杆的长度(结果保留根号).
【答案】(1)
(2)
【分析】本题考查了解直角三角形的应用,解题的关键是:
(1)过点C作,垂足为E,判断四边形为矩形,可求出,,然后在中,根据勾股定理求出即可;
(2)过点D作,交的延长线于点F,交于点G.判断四边形为矩形,得出.在中,利用正切定义求出.利用勾股定理求出,由,可求出,,,.在中,根据勾股定理求出即可.
【详解】(1)解:如图,过点C作,垂足为E,
由题意可知,,
又,
四边形为矩形.
,,
,.
,
.
在中,.
即可伸缩支撑杆的长度为;
(2)解:过点D作,交的延长线于点F,交于点G.
由题意可知,四边形为矩形,
.
在中,,
.
,
,
,.
,,
,.
在中,.
即可伸缩支撑杆的长度为.
9.(2023·山东济南·中考真题)图1是某越野车的侧面示意图,折线段表示车后盖,已知,,,该车的高度.如图2,打开后备箱,车后盖落在处,与水平面的夹角.
(1)求打开后备箱后,车后盖最高点到地面的距离;
(2)若小琳爸爸的身高为,他从打开的车后盖处经过,有没有碰头的危险 请说明理由.
(结果精确到,参考数据:,,,)
【答案】(1)车后盖最高点到地面的距离为
(2)没有危险,详见解析
【分析】(1)作,垂足为点,先求出的长,再求出的长即可;
(2)过作,垂足为点,先求得,再得到,再求得,从而得出到地面的距离为,最后比较即可.
【详解】(1)如图,作,垂足为点
在中
∵,
∴
∴
∵平行线间的距离处处相等
∴
答:车后盖最高点到地面的距离为.
(2)没有危险,理由如下:
过作,垂足为点
∵,
∴
∵
∴
在中,
∴.
∵平行线间的距离处处相等
∴到地面的距离为.
∵
∴没有危险.
【点睛】本题主要考查了解直角三角形的应用,掌握直角三角形的边角关系是解题的关键.
考点06 三角函数与四边形的综合
1.(2025·四川资阳·中考真题)在四边形中,是边上的一点,是对角线的中点.
(1)如图1,四边形是正方形,连接,作交于点,求证:;
(2)如图2,四边形是平行四边形,,连接,作交于点,连接,求的值;
(3)如图3,四边形是菱形,,连接交于点是边上的一点,,若,求的长.
【答案】(1)见解析
(2)
(3)
【分析】(1)连接,根据正方形的性质,利用得到,即可证明结论;
(2)过点A作于点G,过点F作于点,根据勾股定理求出长,然后根据平行四边形的面积公式求出长,根据正切得到长,然后设,则,求出长,再根据正切得到求出a的值,解答即可;
(3)过点D作于点P,作于点Q,设,求出,,然后表示,,在射线上截取,在射线上截取,根据全等得到,,,然后根据勾股定理求出x值,再根据相似三角形的对应边成比例解答即可.
【详解】(1)证明:连接,
∵是正方形,,
∴,,,
∴,
∴,
∴;
(2)解:过点A作于点G,过点F作于点,
(3)∵,,
∴,
∴,
∵,
∴,
又∵,
∴,
又∵,
∴,
∴,
∴,
∵是平行四边形,
∴,
∴,
∴,
∴,
∴,即,
设,则,
∴,
同理可得,即,
解得,
∴,
又∵O是的中点,
∴,
∴,
∴;
过点D作于点P,作于点Q,设,
∵是菱形,
∴,,
∴,
∴,
∴,,
∵,
∴,
∴,
∴,,
在射线上截取,在射线上截取,
∵是菱形,
∴,,
∴,,
又∵,
∴,
∴,,
同理:,,
∴,
∴,
∴,即,
∴,
解得,
又∵,
∴,,
∴,
∴,即,
解得:,
又∵O是的中点,
∴,
∴.
【点睛】本题考查四边形的综合,解直角三角形,相似三角形的判定和性质,勾股定理,全等三角形的判定和性质,作辅助线构造全等三角形是解题的关键.
2.(2025·北京·中考真题)如图,在中,D,E分别为的中点,,垂足为F,点G在的延长线上,.
(1)求证:四边形是矩形;
(2)若,,,求和的长.
【答案】(1)见解析
(2)
【分析】本题主要考查了矩形的判定,三角形中位线定理,勾股定理,解直角三角形,熟知相关知识是解题的关键.
(1)由三角形中位线定理可得,即,则可证明四边形是平行四边形,再由,即可证明平行四边形是矩形;
(2)求出,解得到,则;由线段中点的定义可得;过点A作于H,解得到,则,再利用勾股定即可求出的长.
【详解】(1)证明:∵D,E分别为的中点,
∴是的中位线,
∴,即,
∵,
∴四边形是平行四边形,
又∵,
∴平行四边形是矩形;
(2)解:∵,
∴;
∵,
∴,
在中,,,
∴,
∴;
∵点D为的中点,
∴;
如图所示,过点A作于H,
在中,,
∴,
在中,由勾股定理得.
3.(2025·黑龙江·中考真题)如图,在正方形中,点在边上(不与点B、C重合),点E在的延长线上,且,连接、、,过点作于点,分别交、、于点、、.则下列结论:①;②;③;④若,则;⑤图中共有5个等腰三角形.其中正确的结论是( )
A.①②③⑤ B.①②④⑤ C.①②③④ D.①③④⑤
【答案】C
【分析】本题考查了正方形性质、等腰三角形的判定和性质、相似三角形的判定和性质、解三角形等,解题关键是利用垂直证明角的关系,从而证明三角形全等或相似.
容易证明,从而可得,进而可得,从而可得②正确,过点作,交于点,构造,结合四边形是平行四边形可得,可得①正确,再利用角关系证明,,可得,从而得出结论③正确,过点作,设,由可得,解三角形求出,,从而求出,故结论④正确,再判定不一定是等腰三角形,得出等腰三角形有、、、,共四个,故结论⑤错误.
【详解】解:如图1,过点作,交于点,
∵在正方形中,
∴,,,,
∴、是等腰三角形,
又∵,,
∴,
∴,,,
∴是等腰三角形,
∵,
∴,
又∵,
∴,
∵,
∴,,
∴,
设,
∵,,
∴,故结论②正确;
∴,即是等腰三角形,
∵在和中,
,
∴,
∴,
∵,,
∴四边形是平行四边形,
∴,
∴,故结论①正确,
∵,,
∴,
∴,
∴,
∵,,
∴,
∴
∴,
∵,
∴,
∴,故结论③正确,
过点作,如图2;
设,由可得,,
∴,
∵,
∴,
∴,故结论④正确,
∵,,
∴不一定等于,,
∴ 不一定是等腰三角形,
故等腰三角形有、、、,共四个,故结论⑤错误,
综上所述:正确结论有①②③④.
故选C.
4.(2025·甘肃兰州·中考真题)如图,在菱形中,,垂足为E,交于点F,.若,则 .
【答案】4
【分析】根据菱形的性质,得,又结合,,得出是等边三角形,就可以得知和都是含的直角三角形,解出三角形,即可求出的长.
【详解】解:连接,,
,,
垂直平分,
,
菱形,
,
是等边三角形,
,
,
,
,,
.
故答案为:4.
【点睛】本题考查了菱形的性质、垂直平分线的性质、等边三角形的判定与性质以及解直角三角形,熟练掌握这些性质定理是关键.
5.(2025·贵州·中考真题)如图,在矩形中,点E,F,M分别在,,边上,分别交对角线、线段于点G,H,且是的中点.若,则的长为 .
【答案】
【分析】如图,连接,交于,过作于,求解,证明是的中位线,可得,,,证明四边形是平行四边形,可得,而,,求解,再进一步求解即可.
【详解】解:如图,连接,交于,过作于,
∵,,
∴,
∵矩形,
∴,,
∴,,
∵是的中点,
∴是的中位线,
∴,,
∴,
∴,
∵,,
∴,
∵,
∴四边形是平行四边形,
∴,而,,
∴,
∴,
∴,
∴;
故答案为:
【点睛】本题考查的是平行四边形的判定与性质,矩形的性质,三角形的中位线的性质,锐角三角函数的应用,作出合适的辅助线是解本题的关键.
6.(2024·江苏南通·中考真题)若菱形的周长为,且有一个内角为,则该菱形的高为 .
【答案】
【分析】本题考查的是菱形的性质,锐角的正弦的含义,先画图,求解,过作于,结合可得答案.
【详解】解:如图,菱形的周长为,
∴,
过作于,而,
∴,
故答案为:
7.(2024·四川巴中·中考真题)如图,矩形的对角线与交于点,于点,延长与交于点.若,,则点到的距离为 .
【答案】
【分析】本题考查了矩形的性质,勾股定理,解直角三角形的相关知识,过点F作,垂足为H,利用勾股定理求出的长,利用角的余弦值求出的长,再利用勾股定理求出,从而得出,利用三角形面积求出即可.
【详解】解:如图,过点F作,垂足为H,
四边形为矩形,
,,
,,
,
,即,
解得:,
,即,
解得:,
,
,
,即,
解得:,
故答案为:.
8.(2023·辽宁丹东·中考真题)如图,在矩形中,对角线与相交于点O,,,垂足为点E,F是的中点,连接,若,则矩形的周长是( )
A. B. C. D.
【答案】D
【分析】根据矩形的性质得出,即可求证为等边三角形,进而得出点E为中点,根据中位线定理得出,易得,求出,即可得出矩形的周长.
【详解】解:∵四边形是矩形,
∴,
∵,
∴为等边三角形,
∵,
∴点E为中点,
∵F是的中点,若,
∴,
∵,
∴,
∴,
∴矩形的周长,
故选:D.
【点睛】矩形主要考查了矩形的性质,等边三角形的判定和性质,中位线定理,解直角三角形,解题的关键是掌握矩形的对角线相等,等边三角形三线合一,三角形的中位线平行于第三边且等于第三边的一半,以及解直角三角形的方法和步骤.
考点07 三角函数与圆的综合
1.(2025·广东深圳·中考真题)如图1,在中,是的中点,,.
(1)求证:四边形为菱形;
(2)如图2,若点为上一点,,且,,三点均在上,连接,与相切于点,
①求__________;
②求的半径;
(3)利用圆规和无刻度直尺在图2中作射线,交于点,保留作图痕迹,不用写出作法和理由.
【答案】(1)见解析
(2)①30°;②
(3)见解析
【分析】(1)先证明四边形为平行四边形,斜边上的中线得到,即可得证;
(2)①根据菱形的性质,得到,等角对等边得到,三角形的外角得到,切线得到,再根据角的和差关系进行求解即可;②解直角三角形,进行求解即可;
(3)利用尺规作图作,即可.
【详解】(1)解:,
四边形为平行四边形,
又,且为中点
,
平行四边形为菱形.
(2)①四边形为菱形.
,
,
又,
,
,
切于,
,
;
;
②设半径为,
,
,
,,
;
解得:;
(3)由题意,作图如下:
【点睛】本题考查菱形的判定和性质,斜边上的中线,切线的性质,解直角三角形,尺规作平行线,熟练掌握相关知识点,是解题的关键.
2.(2025·江苏苏州·中考真题)如图,在四边形中,.以为直径的经过点D,且与边交于点E,连接.
(1)求证:为的切线;
(2)若,求的长.
【答案】(1)详见解析
(2).
【分析】(1)只要证明,即可证明为的切线;
(2)过点D作,垂足为F,在中,,,,求得,,在中,,,,求得,再根据圆内接四边形的性质结合等边对等角求得,据此求解即可.
【详解】(1)证明:∵,
∴,
又∵,
∴,
∵为的直径,
∴,
∴,
∴,即,
∴,
∴为的切线;
(2)解:如图,过点D作,垂足为F,
∵,
∴,
∴,
∵中,,,,
∴,
∴,
∵,,
∴,
∴,
∴,
∵中,,,,
∴,
∵,,
∴,
∵四边形内接于,
∴,
∵,
∴,
∴.
【点睛】本题考查了圆周角定理,圆内接四边形的性质,切线的判定,解直角三角形的应用.正确引出辅助线解决问题是解题的关键.
3.(2025·陕西·中考真题)如图,点在的边上,以为半径的⊙与相切于点,与相交于点,为⊙的直径,与相交于点,.
(1)求证:;
(2)若,,求的长.
【答案】(1)证明见解析
(2)
【分析】(1)如图,连接,证明,,即,可得,进一步证明,可得;
(2)求解,设的半径为,结合,可得,可得:,,求解,证明,可得,进一步可得答案.
【详解】(1)解:如图,连接,
∵以为半径的⊙与相切于点,
∴,
∵,
∴,即,
∴,
∴,
∵,
∴,
∴,
∴;
(2)解:∵,,
∴,
设的半径为,
∴,,而,,
∴,
解得:,
∴,,,
∵,则,
∴,
∵,
∴,
∴,
∴.
【点睛】本题考查的是等腰三角形的判定与性质,平行线的性质,勾股定理的应用,相似三角形的判定与性质,圆周角定理的应用,切线的性质,锐角三角函数的应用,作出合适的辅助线是解本题的关键.
4.(2025·四川成都·中考真题)如图,点C在以为直径的半圆O上,连接,过点C作半圆O的切线,交的延长线于点D,在上取点E,使,连接,交于点F.
(1)求证:;
(2)若,,求半圆O的半径及的长.
【答案】(1)见解析
(2)半圆O的半径为2,
【分析】(1)连接,切线得到,等边对等角得到,圆周角定理得到,同角的余角得到,等量代换得到,即可得证;
(2)连接,设半圆O的半径为,解直角三角形,求出半径的长,进行求出的长,平行得到,解直角三角形,求出,的长,角平分线的性质,以及同高三角形的面积比等于底边比,得到,进行求解即可.
【详解】(1)解:连接,则:,
∴,
∵过点C作半圆O的切线,交的延长线于点D,
∴,
∴,
∵为直径,
∴,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∴;
(2)设半圆O的半径为,则,
∵,
∴,
∵,
∴,
∴,即:半圆O的半径为2;
∴,
连接,则:,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴平分,
∴到的距离相等,都等于的长,
∴,
∴,
∴,
∴.
【点睛】本题考查切线的性质,圆周角定理,解直角三角形,角平分线的性质等知识点,熟练掌握相关知识点,是解题的关键.
5.(2025·福建·中考真题)如图,四边形ABCD内接于,AD,BC的延长线相交于点E,AC,BD相交于点F.G是AB上一点,GD交AC于点H,且.
(1)求证:;
(2)求证:;
(3)若,求的周长.
【答案】(1)见解析
(2)见解析
(3)
【分析】(1)利用得,结合同弧所对圆周角,再根据三角形外角性质,完成证明 .
(2)先证得,再通过角的等量代换证,推出,从而得 .
(3)利用(2)结论将周长转化为,通过相似三角形及三角函数、勾股定理求出的长,即周长为 .
【详解】(1)证明:,
.
,
,
.
,
.
(2)证明:,
.
,
,
又,
,
,
.
由(1)知,,
又,
,
.
,
.
∵,
,
,
,
.
(3)解:由(2)知,,
的周长为.
设,则.
由(2)可知,.
又,
,
,
,
.
又,
,
.
过点C作,垂足为P,则.
四边形是圆内接四边形,
,
又,
,
.
在中,,即.
,
,
,
.
在中,,
,
解得,或(舍去).
.
的周长为.
【点睛】本题考查圆的性质、等腰三角形、相似三角形、解直角三角形等知识,通过角与边的转化、相似三角形判定与性质解题,关键是利用圆的性质和三角形知识进行边角关系推导.
6.(2025·新疆·中考真题)如图,为的直径,C为上一点,于点F,,交于点G,交于点D.
(1)求证:是的切线;
(2)若,,求的长.
【答案】(1)见解析
(2)
【分析】(1)连接,证明,得到,即可证明结论;
(2)证明,求出,得到,即可求出的长.
【详解】(1)证明:连接,
∵于点F,
∴,
∵
∴,
∵
∴,
∴,
即
∵是的半径,
∴是的切线;
(2)∵为的直径,
∴
∵,
∴,
∴
∵,
∴
∵
∴,
∵,,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
设,则,
∵,
∴
∴,
∵,
∴,
∴
解得,
∵
∴
解得,
∴
∴,
∴
【点睛】此题考查了解直角三角形、切线的判定、勾股定理、圆周角定理、相似三角形的判定和性质、平行线分线段成比例定理等知识,熟练掌握切线的判定、相似三角形的判定和性质是关键.
7.(2025·黑龙江齐齐哈尔·中考真题)如图,内接于,为的直径,点D在的延长线上,连接,,过点B作,交于点E.
(1)求证:是的切线;
(2)若点B是的中点,且,求的半径.
【答案】(1)见解析
(2)
【分析】本题考查圆周角定理,切线的判定,解直角三角形,熟练掌握相关定理和切线的判定方法,是解题的关键:
(1)连接,圆周角定理,得到,进而得到,等边对等角,得到,结合,推出,即可得证;
(2)根据线段之间的数量关系求出,进而求出的长,勾股定理求出的长,即可得出结果.
【详解】(1)证明:连接,
是的直径,
,
,
,
,即,
.
为的半径,
是的切线.
(2)解:点B是的中点,
.
,
.
,
.
又,
.
.
在中.
.
即半径为.
同课章节目录
