11.2 图形在坐标系中的平移 学案 (含3课时)2025-2026学年数学沪科版(2024)八年级上册
文档属性
| 名称 | 11.2 图形在坐标系中的平移 学案 (含3课时)2025-2026学年数学沪科版(2024)八年级上册 |

|
|
| 格式 | DOCX | ||
| 文件大小 | 964.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-09 00:00:00 | ||
图片预览


文档简介
11.2 图形在坐标系中的平移
课时1 平面直角坐标系中的图形
【学习目标】
1.充分应用平面上点的坐标的有关知识,进一步认识平面直角坐标系中的图形;
2.经历由坐标描点,绘制图形,让学生体会数学之生动美感.
【学习重点】
理解在平面直角坐标系中形成的图形.
【学习难点】
对平面上点的坐标的理解.
旧知回顾:
1.什么是平面直角坐标系?
答:先在平面内画两条互相垂直(通常一条水平,一条竖直)并且原点重合的数轴,水平的数轴叫作x轴或横轴,取向右为正方向;竖直的数轴叫作y轴或纵轴,取向上为正方向;两轴交点O为原点.这样就建立了平面直角坐标系,记作平面直角坐标系xOy,这个平面叫作坐标平面.
2.如图,在平面直角坐标系中,点C的坐标为 (B)
A.(-3,-2) B.(3,-2)
C.(-2,-3) D.(2,-3)
知识模块一 平面直角坐标系中点的坐标特点
阅读教材P6的内容,回答下列问题:
平面直角坐标系中各象限内,x轴及y轴上点的坐标的符号特征是什么?
答:第一象限、第二象限、第三象限、第四象限,这四个象限内的点的坐标符号分别为(+,+)、(-,+)、(-,-)、(+,-).坐标轴上的点(即x轴、y轴上的点)不属于任何一个象限.x轴上的点的纵坐标为0,表示为(x,0);y轴上的点的横坐标为0,表示为(0,y);原点坐标为(0,0).
典例1:点A(-3,2)在第__二__象限,点B(-3,-2)在第__三__象限,点C(3,2)在第__一__象限,点D(-3,-2)在第__三__象限,点E(0,2)在__y__轴上,点F(2,0)在__x__轴上.
典例2:若点M的坐标是(a,b),且a>0,b<0,则点M在 (D)
A.第一象限 B.第二象限 C.第三象限 D.第四象限
仿例:已知点P的坐标为(2a+3,a-4).
(1)若点P在x轴上,则a=__4__;
(2)若点P在y轴上,则a=__-__;
(3)若点P在第三象限内,则a的取值范围是__a<-__;
(4)若点P在第四象限内,且点P到x轴的距离为2,则a的值为__2__.
变例:在平面直角坐标系中,若点P(a-3,a+1)在第二象限,则a的取值范围为 (A)
A.-1<a<3 B.a>3 C.a<-1 D.a>1
知识模块二 建立平面直角坐标系求图形中点的坐标
阅读教材P7的内容,回答下列问题:
如何建立平面直角坐标系,不同的平面直角坐标系中图形顶点坐标会变化吗?
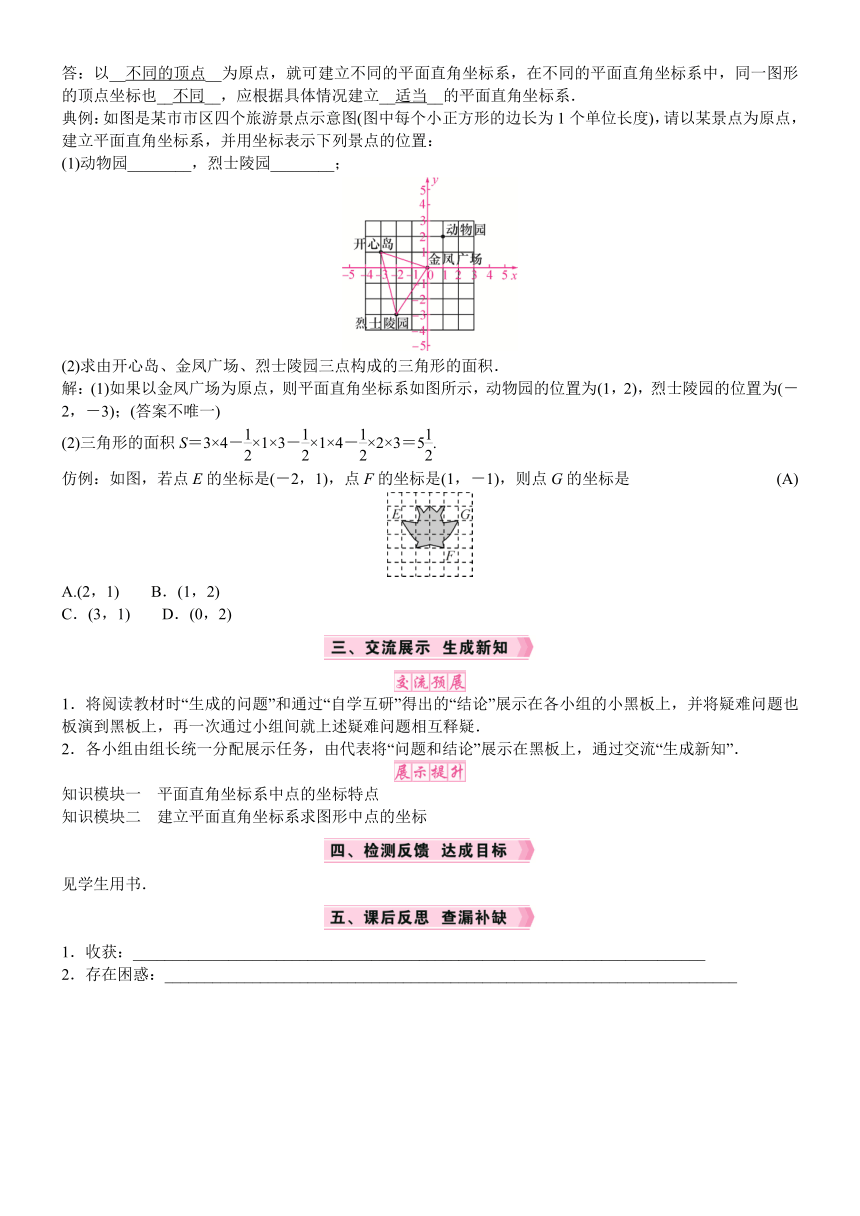
答:以__不同的顶点__为原点,就可建立不同的平面直角坐标系,在不同的平面直角坐标系中,同一图形的顶点坐标也__不同__,应根据具体情况建立__适当__的平面直角坐标系.
典例:如图是某市市区四个旅游景点示意图(图中每个小正方形的边长为1个单位长度),请以某景点为原点,建立平面直角坐标系,并用坐标表示下列景点的位置:
(1)动物园________,烈士陵园________;
(2)求由开心岛、金凤广场、烈士陵园三点构成的三角形的面积.
解:(1)如果以金凤广场为原点,则平面直角坐标系如图所示,动物园的位置为(1,2),烈士陵园的位置为(-2,-3);(答案不唯一)
(2)三角形的面积S=3×4-×1×3-×1×4-×2×3=5.
仿例:如图,若点E的坐标是(-2,1),点F的坐标是(1,-1),则点G的坐标是 (A)
A.(2,1) B.(1,2)
C.(3,1) D.(0,2)
1.将阅读教材时“生成的问题”和通过“自学互研”得出的“结论”展示在各小组的小黑板上,并将疑难问题也板演到黑板上,再一次通过小组间就上述疑难问题相互释疑.
2.各小组由组长统一分配展示任务,由代表将“问题和结论”展示在黑板上,通过交流“生成新知”.
知识模块一 平面直角坐标系中点的坐标特点
知识模块二 建立平面直角坐标系求图形中点的坐标
见学生用书.
1.收获:________________________________________________________________________
2.存在困惑:________________________________________________________________________
课时2 用方位角和距离确定物体的位置
【学习目标】
1.利用方位角和距离确定物体的位置;
2.借助图形思考问题,建立几何直观感,进一步体会确定物体位置的方法.
【学习重点】
会利用方位角和距离确定两个物体的相对位置.
【学习难点】
掌握方位角与距离定位法.
旧知回顾:
1.建立平面直角坐标系,必须满足三个条件:①__两__条数轴;②互相__垂直__;③公共__原点__.
2.在平面直角坐标系中,坐标平面就被两条坐标轴分成了四部分,这四个部分分别叫作第__一__象限、第__二__象限、第__三__象限、第__四__象限,这四个象限内的点的坐标符号分别为(+,+)、(-,+)、(-,-)、(+,-).坐标轴上的点(即x轴、y轴上的点)不属于任何一个象限.
3.在平面直角坐标系中,确定物体的位置需要__两__个数据.
4.已知点M(1,-2),N(-3,-2),则直线MN与x轴、y轴的位置关系分别为__平行、垂直__.
知识模块一 用方位角与距离确定物体的相对位置
阅读教材P9~P10内容,回答下列问题:
1.什么叫作方位角?怎样描述方位角?
答:表示一个物体相对于另一个物体的方向的角,叫作方位角.方位角一般是以观测者的位置为中心,将正北或正南方向线作为起始方向旋转到目标的方向所成的角(一般指锐角)来描述.
2.确定两个物体之间的相对位置包含__方位角__和__距离__两个要素.
范例:甲打电话给乙:“你在哪儿啊?”在下面乙的回话中,甲能确定乙位置的是 (B)
A.我和你相距300 m B.我在你北偏东30°的方向300 m处
C.我在你北偏东30°的方向 D.你向北走420 m,然后转90°再走200 m
仿例:如图,用方向和距离描述学校相对于小明家的位置,正确的是 (D)
A.北偏东55°,2 km
B.东北方向
C.东偏北35°,2 km
D.北偏东35°,2 km
变例:若小明家在公园的北偏东30°方向,距离公园5 000 m处,则公园在小明家的__南偏西30°__方向,距离小明家__5_000__m处.
解析:观测点与被观测点交换位置,方位变,距离不变.
知识模块二 用方位角与距离定位法描述物体的位置
阅读教材P10例4
如何用方位角与距离定位法描述物体的位置?
答:(1)确定观测点;
(2)测量方位角和图上距离,计算出实际距离;
(3)利用方位角与距离定位物体的位置.
典例:如图,三个圆的半径分别为10 km,20 km,30 km,点A在北偏东30°方向上,OB与正北方向的夹角为35°,点C在正南方向上,点A,B,C是分别位于三环、二环、一环上的三所学校,请用方位角和距离表示这三所学校的位置.
解:根据已知条件可得点A在北偏东30°方向,到点O的距离为30 km,点B在北偏西35°方向,到点O的距离为20 km,点C在正南方向,到点O的距离为10 km.
仿例:如图是小明家和学校所在地的简单地图,已知OA=2 cm,OB=2.5 cm,OP=4 cm,点C为OP的中点,回答下列问题:
(1)图中距小明家距离相同的是哪些地方?
(2)商场、学校、公园、停车场分别在小明家的什么方位?哪两个地方的方位是相同的?
(3)若学校距离小明家400 m,那么商场和停车场分别距离小明家多少米?
解:(1)学校和公园;
(2)商场在北偏西30°方向上,学校在北偏东45°方向上,公园与停车场在南偏东60°方向上,停车场与公园方位相同;
(3)商场500 m,停车场800 m.
说明:利用方位角和距离描述物体的位置,两者缺一不可.
1.将阅读教材时“生成的问题”和通过“自学互研”得出的“结论”展示在各小组的小黑板上,并将疑难问题也板演到黑板上,再一次通过小组间就上述疑难问题相互释疑.
2.各小组由组长统一分配展示任务,由代表将“问题和结论”展示在黑板上,通过交流“生成新知”.
知识模块一 用方位角与距离确定物体的相对位置
知识模块二 用方位角与距离定位法描述物体的位置
见学生用书.
1.收获:________________________________________________________________________
2.存在困惑:________________________________________________________________________
课时3 图形在坐标系中的平移
【学习目标】
1.能在直角坐标系中用坐标的方法研究图形的变换,掌握图形在平移过程中各点坐标的变化规律,理解图形在平面直角坐标系上的平移实质上就是点坐标的对应变换;
2.运用图形在平面直角坐标系中平移的点坐标的变化规律进行简单的平移作图.
【学习重点】
掌握用平面直角坐标系的变化规律来描述平移的过程.
【学习难点】
根据图形的平移过程,探索、归纳出坐标的变化规律.
情景导入:
如图:
1.将吉普车从点A(-2,-3)向右平移5个单位长度,得到点A1的坐标是__(3,-3)__.将吉普车从点A向上平移4个单位长度得到点A2的坐标是__(-2,1)__.将吉普车从点A1(3,-3)先向__左__平移__5__个单位长度、再向__上__平移__4__个单位长度得到点A2的坐标.
2.你认为点(-2,-3)在向上、向下平移及向左、向右平移的变化规律是什么?
答:向上、下平移纵坐标加上、减去一个数,横坐标不变,向左、右平移横坐标减去、加上一个数,纵坐标不变.
知识模块一 平面直角坐标系中点的平移
阅读教材P15~P16的内容,回答下列问题:
你认为平面直角坐标系中点的平移规律是什么?
答:平面直角坐标系中点的平移规律是:将点向左(向右)平移a个单位长度,则其横坐标减去(加上)a,将点向上(向下)平移b个单位长度,则其纵坐标加上(减去)b.
范例:在平面直角坐标系中,点P(2,3)先向左平移3个单位长度,再向下平移4个单位长度,得到点的坐标为 (B)
A.(5,7) B.(-1,-1) C.(-1,1) D.(5,-1)
仿例:若将点P(1,-m)向右平移2个单位长度后,再向上平移1个单位长度得到点Q(n,3),则点(m,n)的坐标为 (D)
A.(3,-2) B.(2,-3) C.(3,2) D.(-2,3)
分析:根据平移中点的变化规律:横坐标右移加,纵坐标上移加,可得Q点的坐标,从而列出有关m和n的方程,即可求出m、n的值.
变例:若将点P先向左平移3个单位长度,再向下平移2个单位长度后的对应点为Q(-1,3),则P点的坐标为 (C)
A.(-1,3) B.(-4,1) C.(2,5) D.(1,0)
解析:求点P的坐标即把点Q向右平移3个单位长度,再向上平移2个单位长度,则对应点P的横坐标为-1+3=2,纵坐标为3+2=5.∴点P的坐标为(2,5).故选C.
知识模块二 平面直角坐标系中图形的平移
阅读教材P16的内容,回答下列问题:
平面直角坐标系中图形的平移与其上面点的平移是否相同?
答:相同.在平面直角坐标系内,一个图形怎样移动,那么这个图形上的各个点就怎么移动.
典例:如图,将△ABC先向右平移6个单位长度,再向下平移2个单位长度,得到△A1B1C1,写出各顶点变动前后的坐标.
解:得到结论有:
A(-2,6)→A1(4,4);
B(-4,4)→B1(2,2);
C(1,1)→C1(7,-1).
仿例:说出下列由点A到点B是怎样平移的?
(1)A(x,y)―→B(x-1,y+2);
(2)A(x,y)―→B(x+3,y-2);
(3)A(x+3,y-2)―→B(x,y).
解:(1)点A向左平移1个单位长度,再向上平移2个单位长度,得到点B;
(2)点A向右平移3个单位长度,再向下平移2个单位长度,得到点B;
(3)点A向左平移3个单位长度,再向上平移2个单位长度,得到点B.
1.将阅读教材时“生成的问题”和通过“自学互研”得出的“结论”展示在各小组的小黑板上,并将疑难问题也板演到黑板上,再一次通过小组间就上述疑难问题相互释疑.
2.各小组由组长统一分配展示任务,由代表将“问题和结论”展示在黑板上,通过交流“生成新知”.
知识模块一 平面直角坐标系中点的平移
知识模块二 平面直角坐标系中图形的平移
见学生用书.
1.收获:________________________________________________________________________
2.存在困惑:________________________________________________________________________
课时1 平面直角坐标系中的图形
【学习目标】
1.充分应用平面上点的坐标的有关知识,进一步认识平面直角坐标系中的图形;
2.经历由坐标描点,绘制图形,让学生体会数学之生动美感.
【学习重点】
理解在平面直角坐标系中形成的图形.
【学习难点】
对平面上点的坐标的理解.
旧知回顾:
1.什么是平面直角坐标系?
答:先在平面内画两条互相垂直(通常一条水平,一条竖直)并且原点重合的数轴,水平的数轴叫作x轴或横轴,取向右为正方向;竖直的数轴叫作y轴或纵轴,取向上为正方向;两轴交点O为原点.这样就建立了平面直角坐标系,记作平面直角坐标系xOy,这个平面叫作坐标平面.
2.如图,在平面直角坐标系中,点C的坐标为 (B)
A.(-3,-2) B.(3,-2)
C.(-2,-3) D.(2,-3)
知识模块一 平面直角坐标系中点的坐标特点
阅读教材P6的内容,回答下列问题:
平面直角坐标系中各象限内,x轴及y轴上点的坐标的符号特征是什么?
答:第一象限、第二象限、第三象限、第四象限,这四个象限内的点的坐标符号分别为(+,+)、(-,+)、(-,-)、(+,-).坐标轴上的点(即x轴、y轴上的点)不属于任何一个象限.x轴上的点的纵坐标为0,表示为(x,0);y轴上的点的横坐标为0,表示为(0,y);原点坐标为(0,0).
典例1:点A(-3,2)在第__二__象限,点B(-3,-2)在第__三__象限,点C(3,2)在第__一__象限,点D(-3,-2)在第__三__象限,点E(0,2)在__y__轴上,点F(2,0)在__x__轴上.
典例2:若点M的坐标是(a,b),且a>0,b<0,则点M在 (D)
A.第一象限 B.第二象限 C.第三象限 D.第四象限
仿例:已知点P的坐标为(2a+3,a-4).
(1)若点P在x轴上,则a=__4__;
(2)若点P在y轴上,则a=__-__;
(3)若点P在第三象限内,则a的取值范围是__a<-__;
(4)若点P在第四象限内,且点P到x轴的距离为2,则a的值为__2__.
变例:在平面直角坐标系中,若点P(a-3,a+1)在第二象限,则a的取值范围为 (A)
A.-1<a<3 B.a>3 C.a<-1 D.a>1
知识模块二 建立平面直角坐标系求图形中点的坐标
阅读教材P7的内容,回答下列问题:
如何建立平面直角坐标系,不同的平面直角坐标系中图形顶点坐标会变化吗?
答:以__不同的顶点__为原点,就可建立不同的平面直角坐标系,在不同的平面直角坐标系中,同一图形的顶点坐标也__不同__,应根据具体情况建立__适当__的平面直角坐标系.
典例:如图是某市市区四个旅游景点示意图(图中每个小正方形的边长为1个单位长度),请以某景点为原点,建立平面直角坐标系,并用坐标表示下列景点的位置:
(1)动物园________,烈士陵园________;
(2)求由开心岛、金凤广场、烈士陵园三点构成的三角形的面积.
解:(1)如果以金凤广场为原点,则平面直角坐标系如图所示,动物园的位置为(1,2),烈士陵园的位置为(-2,-3);(答案不唯一)
(2)三角形的面积S=3×4-×1×3-×1×4-×2×3=5.
仿例:如图,若点E的坐标是(-2,1),点F的坐标是(1,-1),则点G的坐标是 (A)
A.(2,1) B.(1,2)
C.(3,1) D.(0,2)
1.将阅读教材时“生成的问题”和通过“自学互研”得出的“结论”展示在各小组的小黑板上,并将疑难问题也板演到黑板上,再一次通过小组间就上述疑难问题相互释疑.
2.各小组由组长统一分配展示任务,由代表将“问题和结论”展示在黑板上,通过交流“生成新知”.
知识模块一 平面直角坐标系中点的坐标特点
知识模块二 建立平面直角坐标系求图形中点的坐标
见学生用书.
1.收获:________________________________________________________________________
2.存在困惑:________________________________________________________________________
课时2 用方位角和距离确定物体的位置
【学习目标】
1.利用方位角和距离确定物体的位置;
2.借助图形思考问题,建立几何直观感,进一步体会确定物体位置的方法.
【学习重点】
会利用方位角和距离确定两个物体的相对位置.
【学习难点】
掌握方位角与距离定位法.
旧知回顾:
1.建立平面直角坐标系,必须满足三个条件:①__两__条数轴;②互相__垂直__;③公共__原点__.
2.在平面直角坐标系中,坐标平面就被两条坐标轴分成了四部分,这四个部分分别叫作第__一__象限、第__二__象限、第__三__象限、第__四__象限,这四个象限内的点的坐标符号分别为(+,+)、(-,+)、(-,-)、(+,-).坐标轴上的点(即x轴、y轴上的点)不属于任何一个象限.
3.在平面直角坐标系中,确定物体的位置需要__两__个数据.
4.已知点M(1,-2),N(-3,-2),则直线MN与x轴、y轴的位置关系分别为__平行、垂直__.
知识模块一 用方位角与距离确定物体的相对位置
阅读教材P9~P10内容,回答下列问题:
1.什么叫作方位角?怎样描述方位角?
答:表示一个物体相对于另一个物体的方向的角,叫作方位角.方位角一般是以观测者的位置为中心,将正北或正南方向线作为起始方向旋转到目标的方向所成的角(一般指锐角)来描述.
2.确定两个物体之间的相对位置包含__方位角__和__距离__两个要素.
范例:甲打电话给乙:“你在哪儿啊?”在下面乙的回话中,甲能确定乙位置的是 (B)
A.我和你相距300 m B.我在你北偏东30°的方向300 m处
C.我在你北偏东30°的方向 D.你向北走420 m,然后转90°再走200 m
仿例:如图,用方向和距离描述学校相对于小明家的位置,正确的是 (D)
A.北偏东55°,2 km
B.东北方向
C.东偏北35°,2 km
D.北偏东35°,2 km
变例:若小明家在公园的北偏东30°方向,距离公园5 000 m处,则公园在小明家的__南偏西30°__方向,距离小明家__5_000__m处.
解析:观测点与被观测点交换位置,方位变,距离不变.
知识模块二 用方位角与距离定位法描述物体的位置
阅读教材P10例4
如何用方位角与距离定位法描述物体的位置?
答:(1)确定观测点;
(2)测量方位角和图上距离,计算出实际距离;
(3)利用方位角与距离定位物体的位置.
典例:如图,三个圆的半径分别为10 km,20 km,30 km,点A在北偏东30°方向上,OB与正北方向的夹角为35°,点C在正南方向上,点A,B,C是分别位于三环、二环、一环上的三所学校,请用方位角和距离表示这三所学校的位置.
解:根据已知条件可得点A在北偏东30°方向,到点O的距离为30 km,点B在北偏西35°方向,到点O的距离为20 km,点C在正南方向,到点O的距离为10 km.
仿例:如图是小明家和学校所在地的简单地图,已知OA=2 cm,OB=2.5 cm,OP=4 cm,点C为OP的中点,回答下列问题:
(1)图中距小明家距离相同的是哪些地方?
(2)商场、学校、公园、停车场分别在小明家的什么方位?哪两个地方的方位是相同的?
(3)若学校距离小明家400 m,那么商场和停车场分别距离小明家多少米?
解:(1)学校和公园;
(2)商场在北偏西30°方向上,学校在北偏东45°方向上,公园与停车场在南偏东60°方向上,停车场与公园方位相同;
(3)商场500 m,停车场800 m.
说明:利用方位角和距离描述物体的位置,两者缺一不可.
1.将阅读教材时“生成的问题”和通过“自学互研”得出的“结论”展示在各小组的小黑板上,并将疑难问题也板演到黑板上,再一次通过小组间就上述疑难问题相互释疑.
2.各小组由组长统一分配展示任务,由代表将“问题和结论”展示在黑板上,通过交流“生成新知”.
知识模块一 用方位角与距离确定物体的相对位置
知识模块二 用方位角与距离定位法描述物体的位置
见学生用书.
1.收获:________________________________________________________________________
2.存在困惑:________________________________________________________________________
课时3 图形在坐标系中的平移
【学习目标】
1.能在直角坐标系中用坐标的方法研究图形的变换,掌握图形在平移过程中各点坐标的变化规律,理解图形在平面直角坐标系上的平移实质上就是点坐标的对应变换;
2.运用图形在平面直角坐标系中平移的点坐标的变化规律进行简单的平移作图.
【学习重点】
掌握用平面直角坐标系的变化规律来描述平移的过程.
【学习难点】
根据图形的平移过程,探索、归纳出坐标的变化规律.
情景导入:
如图:
1.将吉普车从点A(-2,-3)向右平移5个单位长度,得到点A1的坐标是__(3,-3)__.将吉普车从点A向上平移4个单位长度得到点A2的坐标是__(-2,1)__.将吉普车从点A1(3,-3)先向__左__平移__5__个单位长度、再向__上__平移__4__个单位长度得到点A2的坐标.
2.你认为点(-2,-3)在向上、向下平移及向左、向右平移的变化规律是什么?
答:向上、下平移纵坐标加上、减去一个数,横坐标不变,向左、右平移横坐标减去、加上一个数,纵坐标不变.
知识模块一 平面直角坐标系中点的平移
阅读教材P15~P16的内容,回答下列问题:
你认为平面直角坐标系中点的平移规律是什么?
答:平面直角坐标系中点的平移规律是:将点向左(向右)平移a个单位长度,则其横坐标减去(加上)a,将点向上(向下)平移b个单位长度,则其纵坐标加上(减去)b.
范例:在平面直角坐标系中,点P(2,3)先向左平移3个单位长度,再向下平移4个单位长度,得到点的坐标为 (B)
A.(5,7) B.(-1,-1) C.(-1,1) D.(5,-1)
仿例:若将点P(1,-m)向右平移2个单位长度后,再向上平移1个单位长度得到点Q(n,3),则点(m,n)的坐标为 (D)
A.(3,-2) B.(2,-3) C.(3,2) D.(-2,3)
分析:根据平移中点的变化规律:横坐标右移加,纵坐标上移加,可得Q点的坐标,从而列出有关m和n的方程,即可求出m、n的值.
变例:若将点P先向左平移3个单位长度,再向下平移2个单位长度后的对应点为Q(-1,3),则P点的坐标为 (C)
A.(-1,3) B.(-4,1) C.(2,5) D.(1,0)
解析:求点P的坐标即把点Q向右平移3个单位长度,再向上平移2个单位长度,则对应点P的横坐标为-1+3=2,纵坐标为3+2=5.∴点P的坐标为(2,5).故选C.
知识模块二 平面直角坐标系中图形的平移
阅读教材P16的内容,回答下列问题:
平面直角坐标系中图形的平移与其上面点的平移是否相同?
答:相同.在平面直角坐标系内,一个图形怎样移动,那么这个图形上的各个点就怎么移动.
典例:如图,将△ABC先向右平移6个单位长度,再向下平移2个单位长度,得到△A1B1C1,写出各顶点变动前后的坐标.
解:得到结论有:
A(-2,6)→A1(4,4);
B(-4,4)→B1(2,2);
C(1,1)→C1(7,-1).
仿例:说出下列由点A到点B是怎样平移的?
(1)A(x,y)―→B(x-1,y+2);
(2)A(x,y)―→B(x+3,y-2);
(3)A(x+3,y-2)―→B(x,y).
解:(1)点A向左平移1个单位长度,再向上平移2个单位长度,得到点B;
(2)点A向右平移3个单位长度,再向下平移2个单位长度,得到点B;
(3)点A向左平移3个单位长度,再向上平移2个单位长度,得到点B.
1.将阅读教材时“生成的问题”和通过“自学互研”得出的“结论”展示在各小组的小黑板上,并将疑难问题也板演到黑板上,再一次通过小组间就上述疑难问题相互释疑.
2.各小组由组长统一分配展示任务,由代表将“问题和结论”展示在黑板上,通过交流“生成新知”.
知识模块一 平面直角坐标系中点的平移
知识模块二 平面直角坐标系中图形的平移
见学生用书.
1.收获:________________________________________________________________________
2.存在困惑:________________________________________________________________________
