第13章 三角形中的边角关系、命题与证明 小结与复习 学案 2025-2026学年数学沪科版(2024)八年级上册
文档属性
| 名称 | 第13章 三角形中的边角关系、命题与证明 小结与复习 学案 2025-2026学年数学沪科版(2024)八年级上册 |
|
|
| 格式 | DOCX | ||
| 文件大小 | 882.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-09 00:00:00 | ||
图片预览

文档简介
第13章 三角形中的边角关系、命题与证明 小结与复习
【学习目标】
1.理解并掌握三角形及三角形的重要线段的概念;
2.掌握三角形的三边间的关系;会利用三角形的内角和定理及外角公式计算角度.
【学习重点】
会灵活运用内角和定理及外角公式计算角度.
【学习难点】
证明命题推理分析的过程.
知识结构我能建
三角形中的边角关系
命题-
知识模块一 三角形的边角关系
典例1:一个三角形的两边长分别为2和9,第三边为奇数,则此三角形的周长是多少?
解:设第三边长为x,∵9-2∵x为奇数,∴x=9,∴三角形周长为2+9+9=20.
仿例1:若一个等腰三角形的周长为17 cm,一边长为3 cm,则它的另一边长是__7__cm.
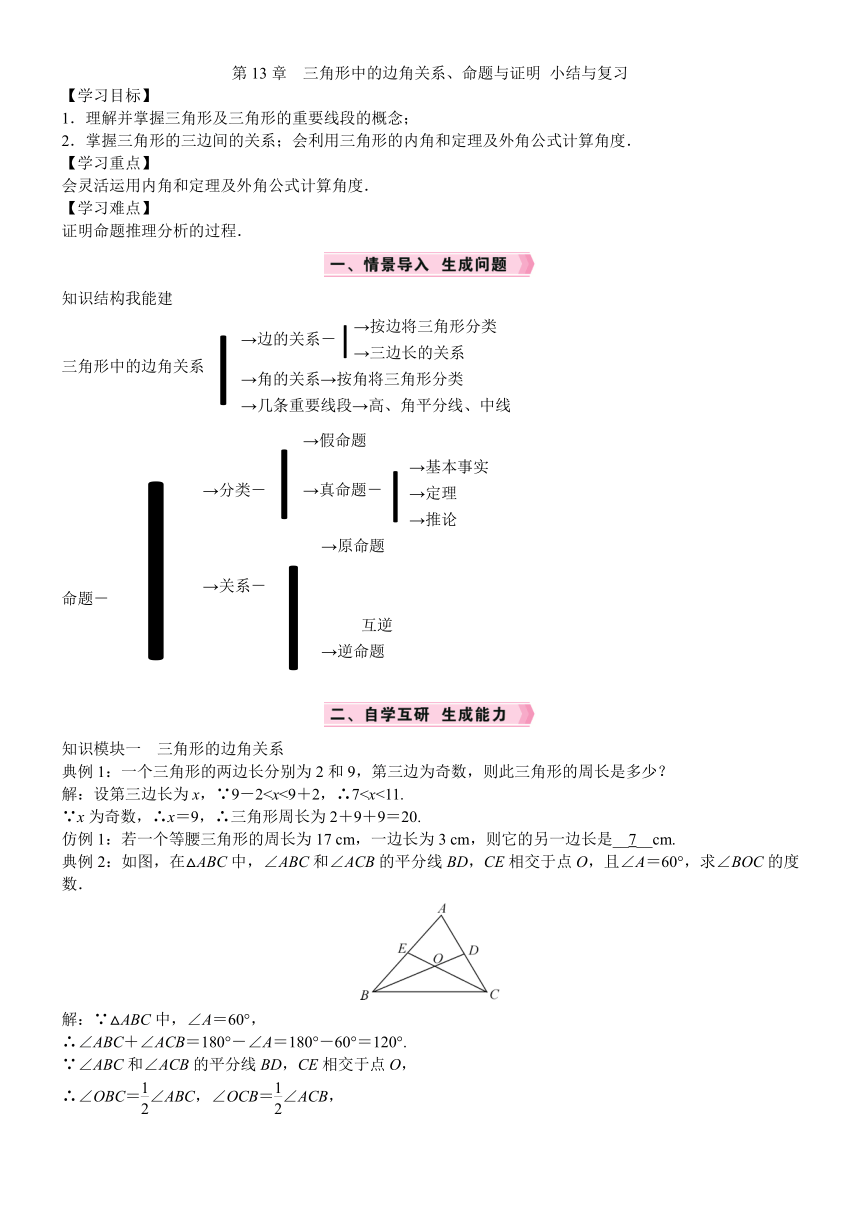
典例2:如图,在△ABC中,∠ABC和∠ACB的平分线BD,CE相交于点O,且∠A=60°,求∠BOC的度数.
解:∵△ABC中,∠A=60°,
∴∠ABC+∠ACB=180°-∠A=180°-60°=120°.
∵∠ABC和∠ACB的平分线BD,CE相交于点O,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=×120°=60°.
故∠BOC=180°-(∠OBC+∠OCB)=180°-60°=120°.
思考:若∠A=n°,则∠BOC的度数为多少?
仿例2:如图,已知AB∥CD,若∠A=20°,∠E=35°,求∠C的度数.
解:∵∠EFB是△AEF的一个外角,
∴∠EFB=∠A+∠E=20°+35°=55°,
∵AB∥CD,∴∠C=∠EFB=55°.
仿例3:
如图,AE,AD分别是△ABC的高和角平分线,且∠B=36°,∠C=76°,则∠DAE的度数为 (B)
A.40° B.20° C.18° D.38°
知识模块二 命题与证明
范例:下列命题错误的是 (C)
A.所有的实数都可用数轴上的点表示
B.等角的补角相等
C.无理数包括正无理数,0,负无理数
D.两点之间,线段最短
仿例1:请写出一个证明命题“若a>b,则|a|>|b|”是假命题的反例:__a=2,b=-3(答案不唯一)__.
仿例2:如图,点D,E分别在AB,AC上,DE∥BC,F是AD上一点,FE的延长线交BC的延长线于点G.
求证:(1)∠EGH>∠ADE;
(2)∠EGH=∠ADE+∠A+∠AEF.
证明:(1)∵∠EGH是△FBG的外角,∴∠EGH>∠B.
又∵DE∥BC,∴∠B=∠ADE,∴∠EGH>∠ADE;
(2)∵∠BFE是△AFE的外角,∴∠BFE=∠A+∠AEF.
∵∠EGH是△BFG的外角,
∴∠EGH=∠B+∠BFE,∴∠EGH=∠B+∠A+∠AEF.
又∵DE∥BC,∴∠B=∠ADE,∴∠EGH=∠ADE+∠A+∠AEF.
1.将阅读教材时“生成的问题”和通过“自学互研”得出的“结论”展示在各小组的小黑板上,并将疑难问题也板演到黑板上,再一次通过小组间就上述疑难问题相互释疑.
2.各小组由组长统一分配展示任务,由代表将“问题和结论”展示在黑板上,通过交流“生成新知”.
知识模块一 三角形的边角关系
知识模块二 命题与证明
见学生用书.
1.收获:________________________________________________________________________
2.存在困惑:________________________________________________________________________
【学习目标】
1.理解并掌握三角形及三角形的重要线段的概念;
2.掌握三角形的三边间的关系;会利用三角形的内角和定理及外角公式计算角度.
【学习重点】
会灵活运用内角和定理及外角公式计算角度.
【学习难点】
证明命题推理分析的过程.
知识结构我能建
三角形中的边角关系
命题-
知识模块一 三角形的边角关系
典例1:一个三角形的两边长分别为2和9,第三边为奇数,则此三角形的周长是多少?
解:设第三边长为x,∵9-2
仿例1:若一个等腰三角形的周长为17 cm,一边长为3 cm,则它的另一边长是__7__cm.
典例2:如图,在△ABC中,∠ABC和∠ACB的平分线BD,CE相交于点O,且∠A=60°,求∠BOC的度数.
解:∵△ABC中,∠A=60°,
∴∠ABC+∠ACB=180°-∠A=180°-60°=120°.
∵∠ABC和∠ACB的平分线BD,CE相交于点O,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=×120°=60°.
故∠BOC=180°-(∠OBC+∠OCB)=180°-60°=120°.
思考:若∠A=n°,则∠BOC的度数为多少?
仿例2:如图,已知AB∥CD,若∠A=20°,∠E=35°,求∠C的度数.
解:∵∠EFB是△AEF的一个外角,
∴∠EFB=∠A+∠E=20°+35°=55°,
∵AB∥CD,∴∠C=∠EFB=55°.
仿例3:
如图,AE,AD分别是△ABC的高和角平分线,且∠B=36°,∠C=76°,则∠DAE的度数为 (B)
A.40° B.20° C.18° D.38°
知识模块二 命题与证明
范例:下列命题错误的是 (C)
A.所有的实数都可用数轴上的点表示
B.等角的补角相等
C.无理数包括正无理数,0,负无理数
D.两点之间,线段最短
仿例1:请写出一个证明命题“若a>b,则|a|>|b|”是假命题的反例:__a=2,b=-3(答案不唯一)__.
仿例2:如图,点D,E分别在AB,AC上,DE∥BC,F是AD上一点,FE的延长线交BC的延长线于点G.
求证:(1)∠EGH>∠ADE;
(2)∠EGH=∠ADE+∠A+∠AEF.
证明:(1)∵∠EGH是△FBG的外角,∴∠EGH>∠B.
又∵DE∥BC,∴∠B=∠ADE,∴∠EGH>∠ADE;
(2)∵∠BFE是△AFE的外角,∴∠BFE=∠A+∠AEF.
∵∠EGH是△BFG的外角,
∴∠EGH=∠B+∠BFE,∴∠EGH=∠B+∠A+∠AEF.
又∵DE∥BC,∴∠B=∠ADE,∴∠EGH=∠ADE+∠A+∠AEF.
1.将阅读教材时“生成的问题”和通过“自学互研”得出的“结论”展示在各小组的小黑板上,并将疑难问题也板演到黑板上,再一次通过小组间就上述疑难问题相互释疑.
2.各小组由组长统一分配展示任务,由代表将“问题和结论”展示在黑板上,通过交流“生成新知”.
知识模块一 三角形的边角关系
知识模块二 命题与证明
见学生用书.
1.收获:________________________________________________________________________
2.存在困惑:________________________________________________________________________
