1.2 课时3 棱柱、圆柱、圆锥的表面展开图 课件(共17张PPT) 2025-2026学年数学鲁科版(五四学制)(2024)六年级上册
文档属性
| 名称 | 1.2 课时3 棱柱、圆柱、圆锥的表面展开图 课件(共17张PPT) 2025-2026学年数学鲁科版(五四学制)(2024)六年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 831.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-08 17:02:13 | ||
图片预览



文档简介
第一章 丰富的图形世界
1.2 从立体图形到平面图形
课时3 棱柱、圆柱、圆锥的表面展开图
1.了解棱柱、圆柱、圆锥的表面展开图.
2.能判断一个图形是不是一个几何体表面的展开图.
3.能根据展开图还原几何体或制作几何体模型.
复习导入
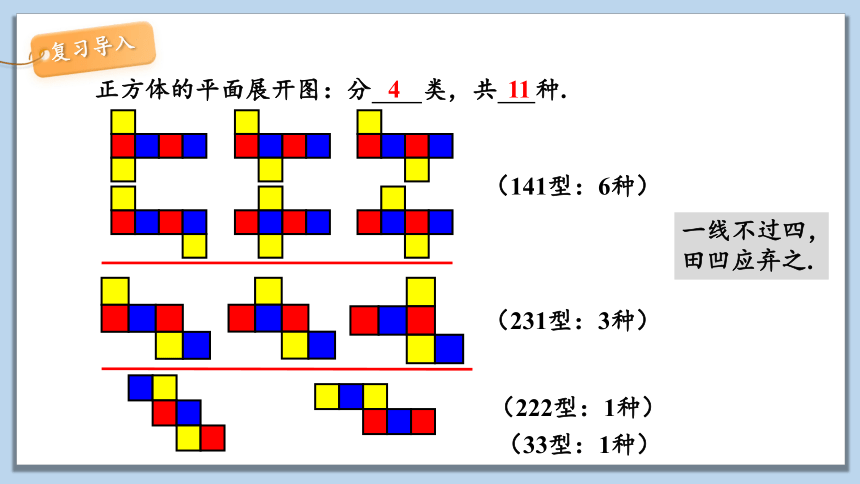
正方体的平面展开图:分 类,共 种.
(141型:6种)
(231型:3种)
(222型:1种)
(33型:1种)
一线不过四,田凹应弃之.
4 11
我们知道,正方体是四棱柱的一种特例,那么其他的棱柱展开图是怎样的呢?圆柱和圆锥呢?
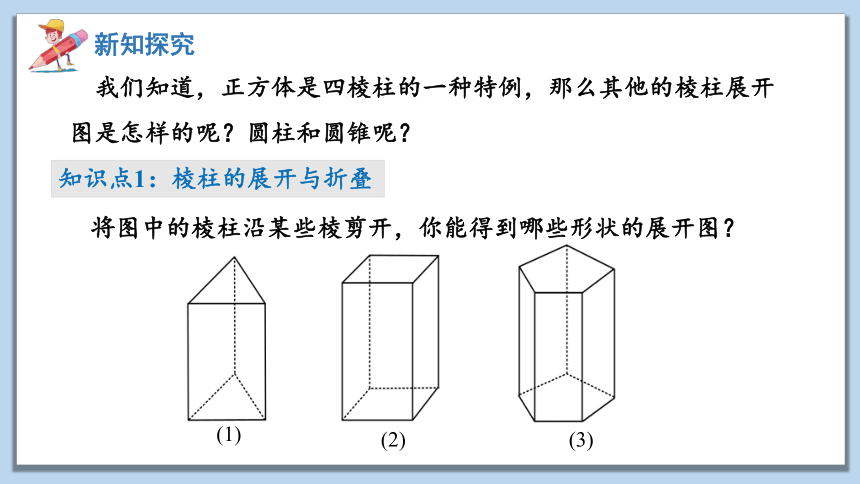
知识点1:棱柱的展开与折叠
将图中的棱柱沿某些棱剪开,你能得到哪些形状的展开图?
(1)
(2)
(3)
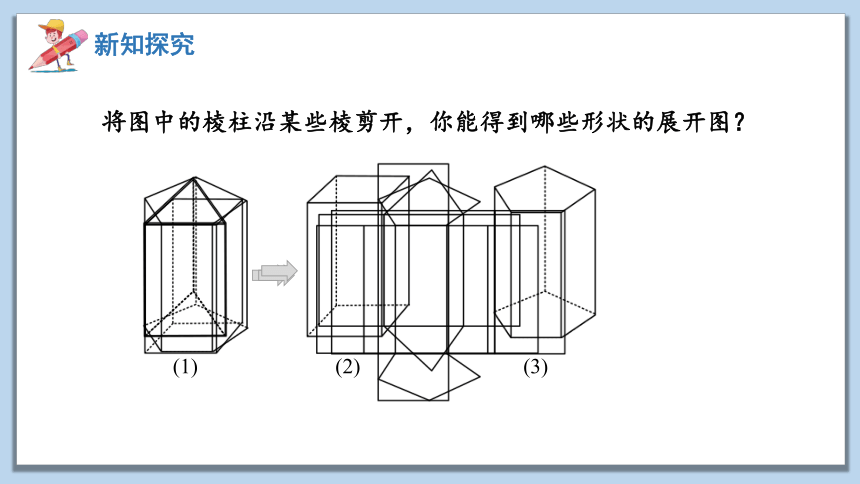
(1)
(2)
(3)
将图中的棱柱沿某些棱剪开,你能得到哪些形状的展开图?
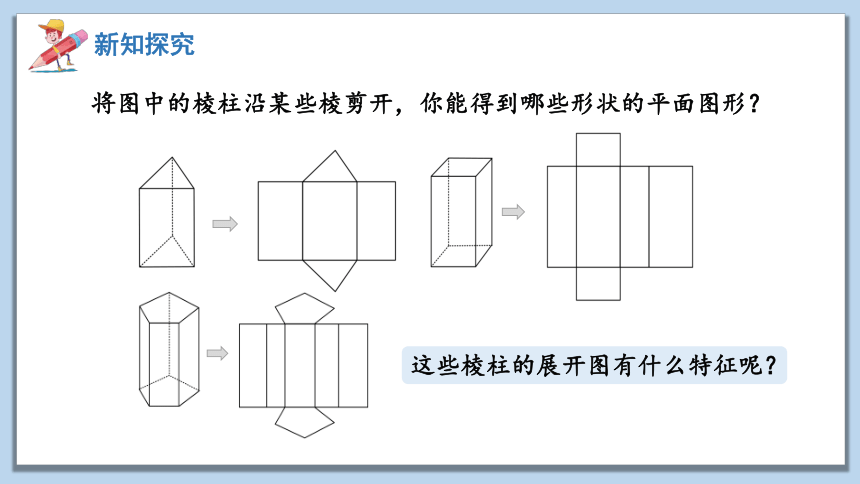
将图中的棱柱沿某些棱剪开,你能得到哪些形状的平面图形?
这些棱柱的展开图有什么特征呢?
归纳总结
棱柱展开图特征
1)棱柱有上下两个底面,它们的形状相同,且不在同侧.
2)棱柱侧面的形状都是长方形.
3) 棱柱侧面的个数和底面图形的边数相等.
4) 棱柱所有侧棱长度都相等.
观察·思考
下图中,哪些图形经过折叠可以围成一个棱柱?
(1)
(2)
(3)
(4)
如何修改一下就能围成一个棱柱了呢?
操作·思考
知识点2:圆柱、圆锥的展开与折叠
按照如图所示的方法把无底面的圆柱、圆锥的侧面展开,会得到什么图形呢?先想一想,再做一做.
如图,圆柱的侧面展开图是长方形,圆锥的侧面展开图是扇形.
归纳总结
圆柱的表面展开图是由一个长方形和两个圆组成.
圆锥的表面展开图是由一个扇形和一个圆组成.
典例分析
例1 如图是立体图形的展开图,你能说出这些立体图形的名称吗?
四棱柱
五棱柱
(1)
(2)
典例分析
例2 图中的两个图形经过折叠以后能否围成棱柱?先想一想,再折一折.
能围成三棱柱
不能围成棱柱
1.下面图形经过折叠不能围成棱柱的是( ? ??)
D
2.一个几何体的表面展开图如图所示,则这个几何体是( ??)
D
A B C D
3.如图是某个几何体的展开图,该几何体是( )
A.圆柱 B.三棱锥 C.三棱柱 D.圆锥
D
4.如图是一个四棱柱的表面展开图,根据图中的尺寸(单位:cm)求这个四棱柱的表面积和体积.
解:????=????(????????×????????+????×????????+????????×????)
=????????????????(cm2)
????=????????×????????×????=????????????????(cm3)
答:四棱柱的表面积为1752cm2,体积为3780cm3.
?
棱柱、圆柱、圆锥的
表面展开图
棱柱
圆柱
圆锥
平面图形
长方形
扇形
侧面都是一个曲的面
展开
折叠
侧面展开
侧面展开
1.2 从立体图形到平面图形
课时3 棱柱、圆柱、圆锥的表面展开图
1.了解棱柱、圆柱、圆锥的表面展开图.
2.能判断一个图形是不是一个几何体表面的展开图.
3.能根据展开图还原几何体或制作几何体模型.
复习导入
正方体的平面展开图:分 类,共 种.
(141型:6种)
(231型:3种)
(222型:1种)
(33型:1种)
一线不过四,田凹应弃之.
4 11
我们知道,正方体是四棱柱的一种特例,那么其他的棱柱展开图是怎样的呢?圆柱和圆锥呢?
知识点1:棱柱的展开与折叠
将图中的棱柱沿某些棱剪开,你能得到哪些形状的展开图?
(1)
(2)
(3)
(1)
(2)
(3)
将图中的棱柱沿某些棱剪开,你能得到哪些形状的展开图?
将图中的棱柱沿某些棱剪开,你能得到哪些形状的平面图形?
这些棱柱的展开图有什么特征呢?
归纳总结
棱柱展开图特征
1)棱柱有上下两个底面,它们的形状相同,且不在同侧.
2)棱柱侧面的形状都是长方形.
3) 棱柱侧面的个数和底面图形的边数相等.
4) 棱柱所有侧棱长度都相等.
观察·思考
下图中,哪些图形经过折叠可以围成一个棱柱?
(1)
(2)
(3)
(4)
如何修改一下就能围成一个棱柱了呢?
操作·思考
知识点2:圆柱、圆锥的展开与折叠
按照如图所示的方法把无底面的圆柱、圆锥的侧面展开,会得到什么图形呢?先想一想,再做一做.
如图,圆柱的侧面展开图是长方形,圆锥的侧面展开图是扇形.
归纳总结
圆柱的表面展开图是由一个长方形和两个圆组成.
圆锥的表面展开图是由一个扇形和一个圆组成.
典例分析
例1 如图是立体图形的展开图,你能说出这些立体图形的名称吗?
四棱柱
五棱柱
(1)
(2)
典例分析
例2 图中的两个图形经过折叠以后能否围成棱柱?先想一想,再折一折.
能围成三棱柱
不能围成棱柱
1.下面图形经过折叠不能围成棱柱的是( ? ??)
D
2.一个几何体的表面展开图如图所示,则这个几何体是( ??)
D
A B C D
3.如图是某个几何体的展开图,该几何体是( )
A.圆柱 B.三棱锥 C.三棱柱 D.圆锥
D
4.如图是一个四棱柱的表面展开图,根据图中的尺寸(单位:cm)求这个四棱柱的表面积和体积.
解:????=????(????????×????????+????×????????+????????×????)
=????????????????(cm2)
????=????????×????????×????=????????????????(cm3)
答:四棱柱的表面积为1752cm2,体积为3780cm3.
?
棱柱、圆柱、圆锥的
表面展开图
棱柱
圆柱
圆锥
平面图形
长方形
扇形
侧面都是一个曲的面
展开
折叠
侧面展开
侧面展开
同课章节目录
