16.1轴对称 同步练(含答案)2025-2026学年数学冀教版(2024)八年级上册
文档属性
| 名称 | 16.1轴对称 同步练(含答案)2025-2026学年数学冀教版(2024)八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 267.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-08 23:20:28 | ||
图片预览

文档简介
16.1轴对称
轴对称图形与轴对称
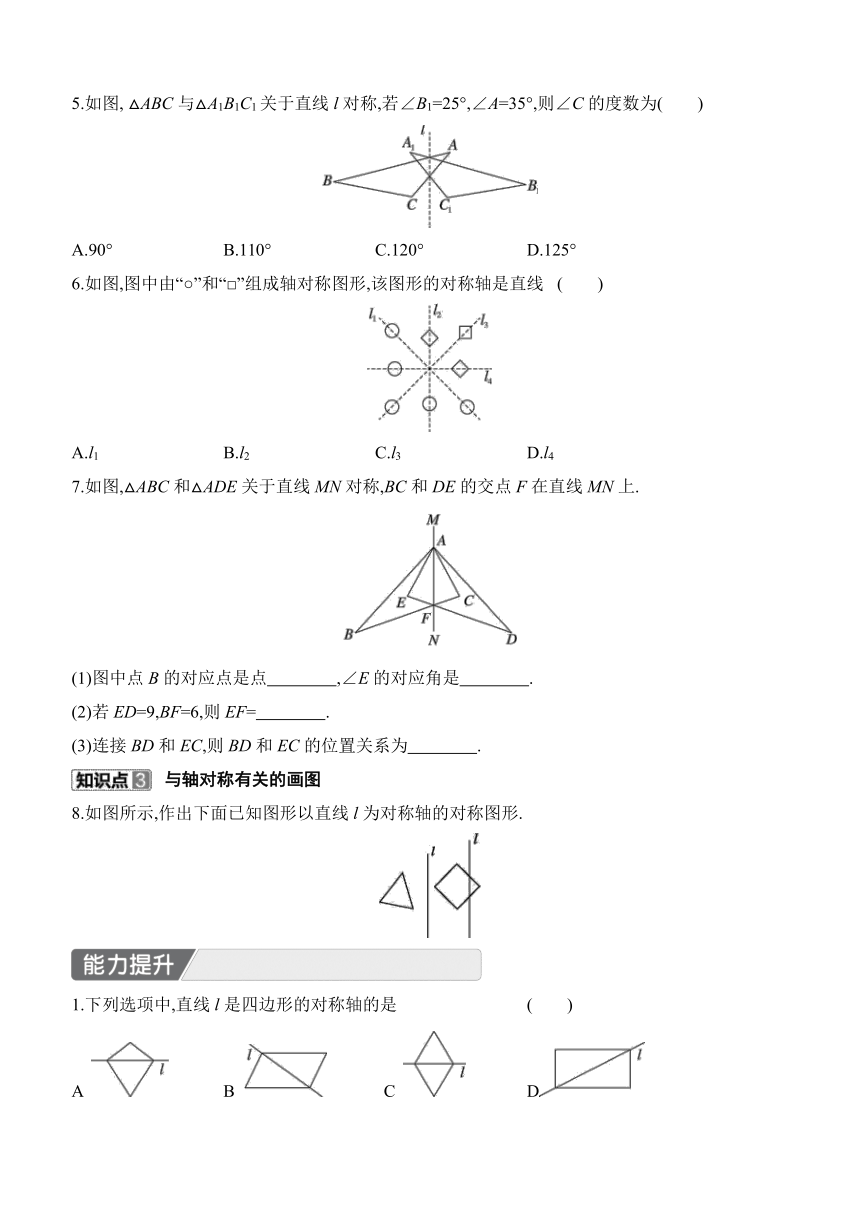
1.下列图形中是轴对称图形的是 ( )
A B C D
2.下图各组图形中成轴对称的图形有 ( )
A.1组 B.2组
C.3组 D.4组
3.(名师原创)如图所示的图形由四个全等的直角三角形组成,则图中有阴影的三角形与三角形 (填数字)或三角形 (填数字)成轴对称;如果把这四个直角三角形看做一个整体,则这个图形 (填“是”或“不是”)轴对称图形.
轴对称的性质
4.如图,△ABC和△A'B'C'关于直线l对称,则图中一定与AB相等的是 ( )
A.A'B' B.B'C'
C.A'C' D.CC'
5.如图, △ABC与△A1B1C1关于直线l对称,若∠B1=25°,∠A=35°,则∠C的度数为( )
A.90° B.110° C.120° D.125°
6.如图,图中由“○”和“□”组成轴对称图形,该图形的对称轴是直线 ( )
A.l1 B.l2 C.l3 D.l4
7.如图,△ABC和△ADE关于直线MN对称,BC和DE的交点F在直线MN上.
(1)图中点B的对应点是点 ,∠E的对应角是 .
(2)若ED=9,BF=6,则EF= .
(3)连接BD和EC,则BD和EC的位置关系为 .
与轴对称有关的画图
8.如图所示,作出下面已知图形以直线l为对称轴的对称图形.
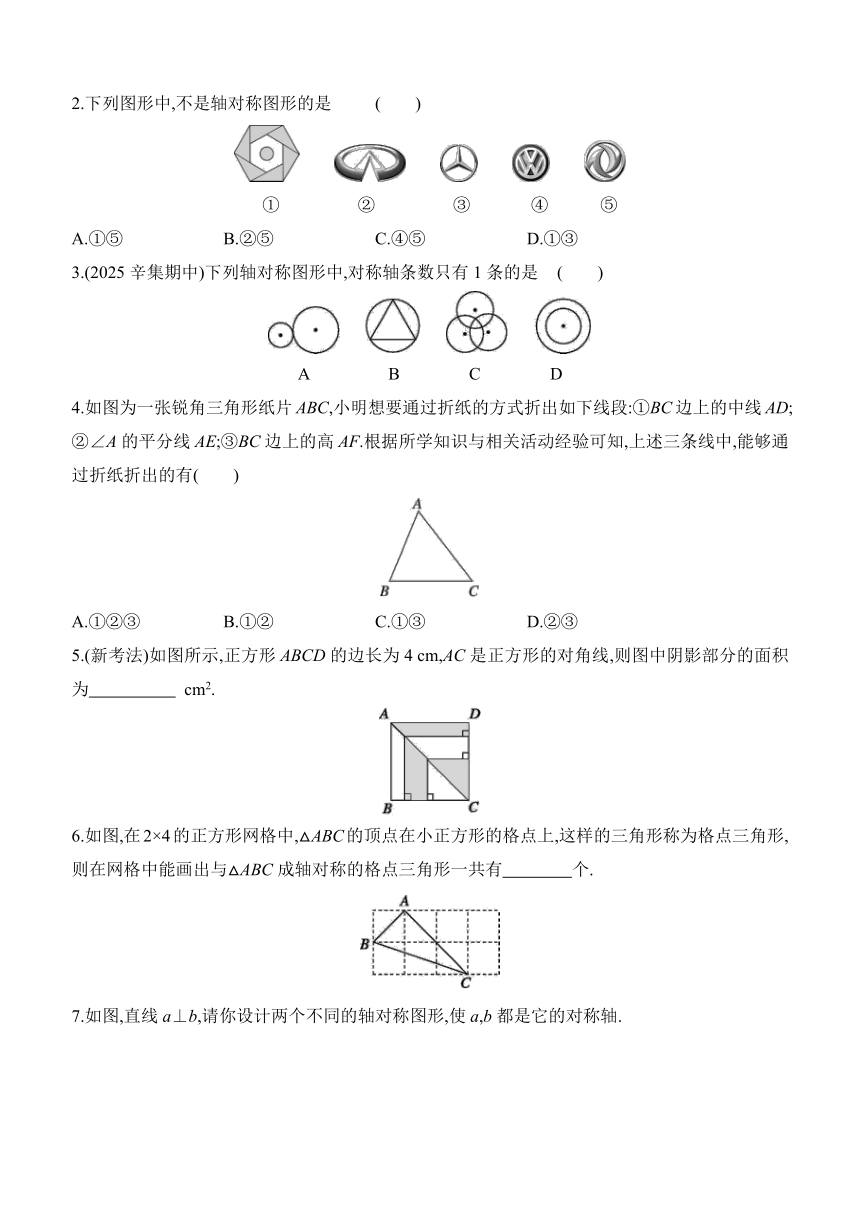
1.下列选项中,直线l是四边形的对称轴的是 ( )
A B C D
2.下列图形中,不是轴对称图形的是 ( )
① ② ③ ④ ⑤
A.①⑤ B.②⑤ C.④⑤ D.①③
3.(2025辛集期中)下列轴对称图形中,对称轴条数只有1条的是 ( )
A B C D
4.如图为一张锐角三角形纸片ABC,小明想要通过折纸的方式折出如下线段:①BC边上的中线AD;②∠A的平分线AE;③BC边上的高AF.根据所学知识与相关活动经验可知,上述三条线中,能够通过折纸折出的有( )
A.①②③ B.①② C.①③ D.②③
5.(新考法)如图所示,正方形ABCD的边长为4 cm,AC是正方形的对角线,则图中阴影部分的面积为 cm2.
6.如图,在2×4的正方形网格中,△ABC的顶点在小正方形的格点上,这样的三角形称为格点三角形,则在网格中能画出与△ABC成轴对称的格点三角形一共有 个.
7.如图,直线a⊥b,请你设计两个不同的轴对称图形,使a,b都是它的对称轴.
微专题5 镜面对称与水面对称问题
镜面对称
已知镜面中的影像求实际影像时,可以将镜面中的影像写到纸上,将纸向左(或向右)翻折,从背面看到的影像即为实际影像.
1.小明从镜子中看到对面电子钟如图所示,这时的时刻应是 .
水面对称
已知水面中的影像求实际影像时,可以将水面中的影像写到纸上,将纸向上(或向下)翻折,从背面看到的影像即为实际影像.
2.路面上有水,小红看到一个汽车车牌在水中的倒影为,它的实际车牌号是 .
【详解答案】
基础达标
1.C 2.C
3.1 3 是 4.A 5.C 6.C
7.(1)D ∠C (2)3 (3)平行
8.解:如图所示.
能力提升
1.C 解析:利用对称轴是任何一对对应点所连线段的垂直平分线,可对各选项进行判断.故选C.
2.A 解析:根据题意可知,①⑤不是轴对称图形,②③④是轴对称图形.故选A.
3.A 解析:A.图中只有1条对称轴,如图1,符合题意;B.图中有3条对称轴,如图2,不符合题意;C.图中有3条对称轴,如图3,不符合题意;D.图中有无数条对称轴,不符合题意.故选A.
4.A 解析:①如图1,使点B,C重合,中点为点D,连接AD,此时AD即为BC边上的中线;②如图2,折叠三角形纸片ABC,使AB与AC重叠,此时AE即为∠A的平分线;③如图3,沿直线AF折叠,使BF与CF重合,此时AF即为BC边上的高.综上所述,能够通过折纸折出的有①②③.故选A.
图1 图2 图3
5.8 解析:因为正方形是轴对称图形,其对角线所在的直线是它的一条对称轴,因此阴影部分的面积等于正方形ABCD的面积的一半,即阴影部分的面积=×4×4=8(cm2).
6.3 解析:与△ABC成轴对称的所有格点三角形如图所示.
7.解:如图所示.(答案不唯一)
微专题5
1.10:51 解析:∵是从镜子中看,∴对称轴为竖直方向的直线,∵2的对称数字是5,镜子中数字的顺序与实际数字顺序相反,∴这时的时刻应是10:51.
2.K62897 解析:将水中的倒影写到纸上,将纸向上(或向下)翻折,由此得到实际车牌号是K62897.
轴对称图形与轴对称
1.下列图形中是轴对称图形的是 ( )
A B C D
2.下图各组图形中成轴对称的图形有 ( )
A.1组 B.2组
C.3组 D.4组
3.(名师原创)如图所示的图形由四个全等的直角三角形组成,则图中有阴影的三角形与三角形 (填数字)或三角形 (填数字)成轴对称;如果把这四个直角三角形看做一个整体,则这个图形 (填“是”或“不是”)轴对称图形.
轴对称的性质
4.如图,△ABC和△A'B'C'关于直线l对称,则图中一定与AB相等的是 ( )
A.A'B' B.B'C'
C.A'C' D.CC'
5.如图, △ABC与△A1B1C1关于直线l对称,若∠B1=25°,∠A=35°,则∠C的度数为( )
A.90° B.110° C.120° D.125°
6.如图,图中由“○”和“□”组成轴对称图形,该图形的对称轴是直线 ( )
A.l1 B.l2 C.l3 D.l4
7.如图,△ABC和△ADE关于直线MN对称,BC和DE的交点F在直线MN上.
(1)图中点B的对应点是点 ,∠E的对应角是 .
(2)若ED=9,BF=6,则EF= .
(3)连接BD和EC,则BD和EC的位置关系为 .
与轴对称有关的画图
8.如图所示,作出下面已知图形以直线l为对称轴的对称图形.
1.下列选项中,直线l是四边形的对称轴的是 ( )
A B C D
2.下列图形中,不是轴对称图形的是 ( )
① ② ③ ④ ⑤
A.①⑤ B.②⑤ C.④⑤ D.①③
3.(2025辛集期中)下列轴对称图形中,对称轴条数只有1条的是 ( )
A B C D
4.如图为一张锐角三角形纸片ABC,小明想要通过折纸的方式折出如下线段:①BC边上的中线AD;②∠A的平分线AE;③BC边上的高AF.根据所学知识与相关活动经验可知,上述三条线中,能够通过折纸折出的有( )
A.①②③ B.①② C.①③ D.②③
5.(新考法)如图所示,正方形ABCD的边长为4 cm,AC是正方形的对角线,则图中阴影部分的面积为 cm2.
6.如图,在2×4的正方形网格中,△ABC的顶点在小正方形的格点上,这样的三角形称为格点三角形,则在网格中能画出与△ABC成轴对称的格点三角形一共有 个.
7.如图,直线a⊥b,请你设计两个不同的轴对称图形,使a,b都是它的对称轴.
微专题5 镜面对称与水面对称问题
镜面对称
已知镜面中的影像求实际影像时,可以将镜面中的影像写到纸上,将纸向左(或向右)翻折,从背面看到的影像即为实际影像.
1.小明从镜子中看到对面电子钟如图所示,这时的时刻应是 .
水面对称
已知水面中的影像求实际影像时,可以将水面中的影像写到纸上,将纸向上(或向下)翻折,从背面看到的影像即为实际影像.
2.路面上有水,小红看到一个汽车车牌在水中的倒影为,它的实际车牌号是 .
【详解答案】
基础达标
1.C 2.C
3.1 3 是 4.A 5.C 6.C
7.(1)D ∠C (2)3 (3)平行
8.解:如图所示.
能力提升
1.C 解析:利用对称轴是任何一对对应点所连线段的垂直平分线,可对各选项进行判断.故选C.
2.A 解析:根据题意可知,①⑤不是轴对称图形,②③④是轴对称图形.故选A.
3.A 解析:A.图中只有1条对称轴,如图1,符合题意;B.图中有3条对称轴,如图2,不符合题意;C.图中有3条对称轴,如图3,不符合题意;D.图中有无数条对称轴,不符合题意.故选A.
4.A 解析:①如图1,使点B,C重合,中点为点D,连接AD,此时AD即为BC边上的中线;②如图2,折叠三角形纸片ABC,使AB与AC重叠,此时AE即为∠A的平分线;③如图3,沿直线AF折叠,使BF与CF重合,此时AF即为BC边上的高.综上所述,能够通过折纸折出的有①②③.故选A.
图1 图2 图3
5.8 解析:因为正方形是轴对称图形,其对角线所在的直线是它的一条对称轴,因此阴影部分的面积等于正方形ABCD的面积的一半,即阴影部分的面积=×4×4=8(cm2).
6.3 解析:与△ABC成轴对称的所有格点三角形如图所示.
7.解:如图所示.(答案不唯一)
微专题5
1.10:51 解析:∵是从镜子中看,∴对称轴为竖直方向的直线,∵2的对称数字是5,镜子中数字的顺序与实际数字顺序相反,∴这时的时刻应是10:51.
2.K62897 解析:将水中的倒影写到纸上,将纸向上(或向下)翻折,由此得到实际车牌号是K62897.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
