16.4 中心对称 同步练(含答案)2025-2026学年数学冀教版(2024)八年级上册
文档属性
| 名称 | 16.4 中心对称 同步练(含答案)2025-2026学年数学冀教版(2024)八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 287.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-08 23:22:01 | ||
图片预览

文档简介
16.4中心对称
中心对称图形
1.下列四个字母中,属于中心对称图形的是 ( )
A B
C D
2.剪纸又称刻纸,是中国最古老的民间艺术之一,它是以纸为加工对象,以剪刀(或刻刀)为工具进行创作的艺术.民间剪纸往往通过谐音、象征、寓意等手法提炼、概括自然形态,构成美丽的图案.下列剪纸中,既是轴对称图形,又是中心对称图形的是 ( )
A B
C D
成中心对称
3.下列各组图形中,△A'B'C'与△ABC成中心对称的是 ( )
A B
C D
4.如图所示的兔子的卡通图片中,成中心对称的有 组.
成中心对称的性质
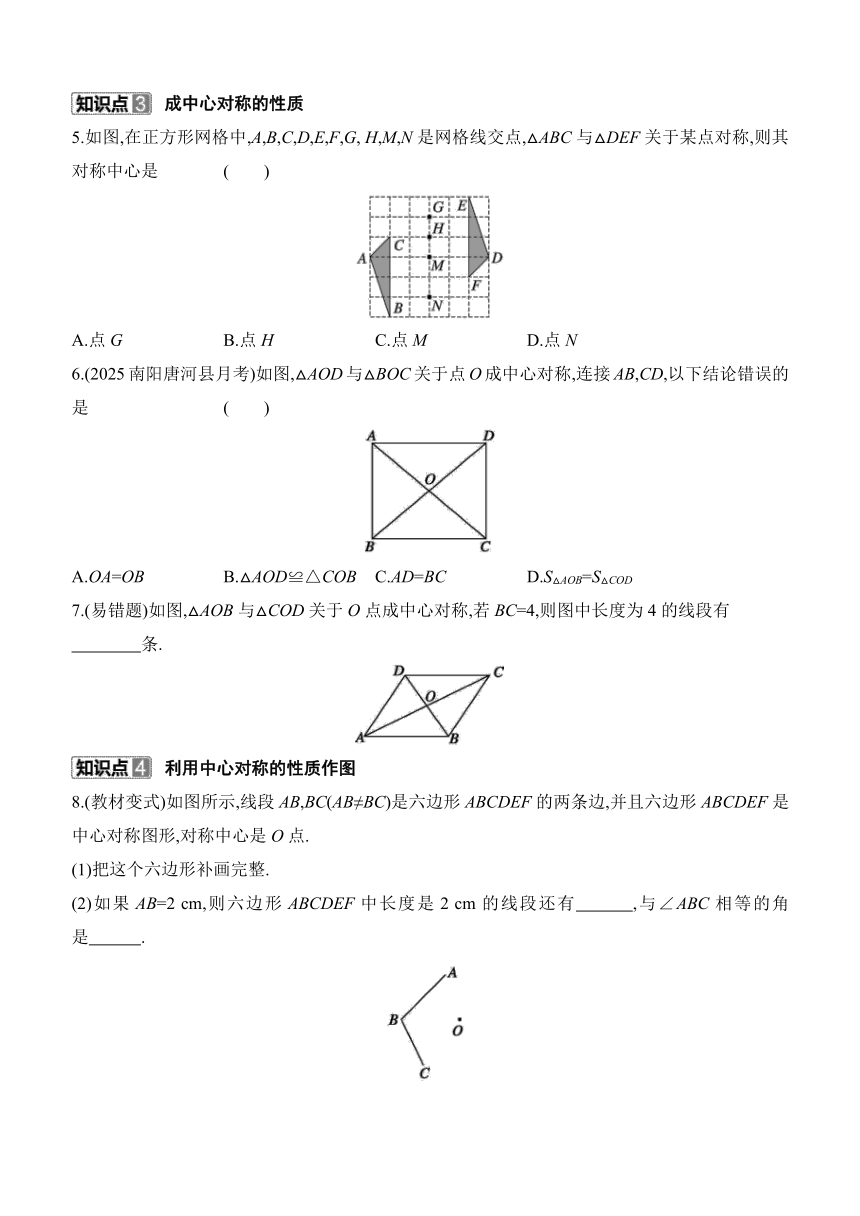
5.如图,在正方形网格中,A,B,C,D,E,F,G, H,M,N是网格线交点,△ABC与△DEF关于某点对称,则其对称中心是 ( )
A.点G B.点H C.点M D.点N
6.(2025南阳唐河县月考)如图,△AOD与△BOC关于点O成中心对称,连接AB,CD,以下结论错误的是 ( )
A.OA=OB B.△AOD≌△COB C.AD=BC D.S△AOB=S△COD
7.(易错题)如图,△AOB与△COD关于O点成中心对称,若BC=4,则图中长度为4的线段有
条.
利用中心对称的性质作图
8.(教材变式)如图所示,线段AB,BC(AB≠BC)是六边形ABCDEF的两条边,并且六边形ABCDEF是中心对称图形,对称中心是O点.
(1)把这个六边形补画完整.
(2)如果AB=2 cm,则六边形ABCDEF中长度是2 cm的线段还有 ,与∠ABC相等的角是 .
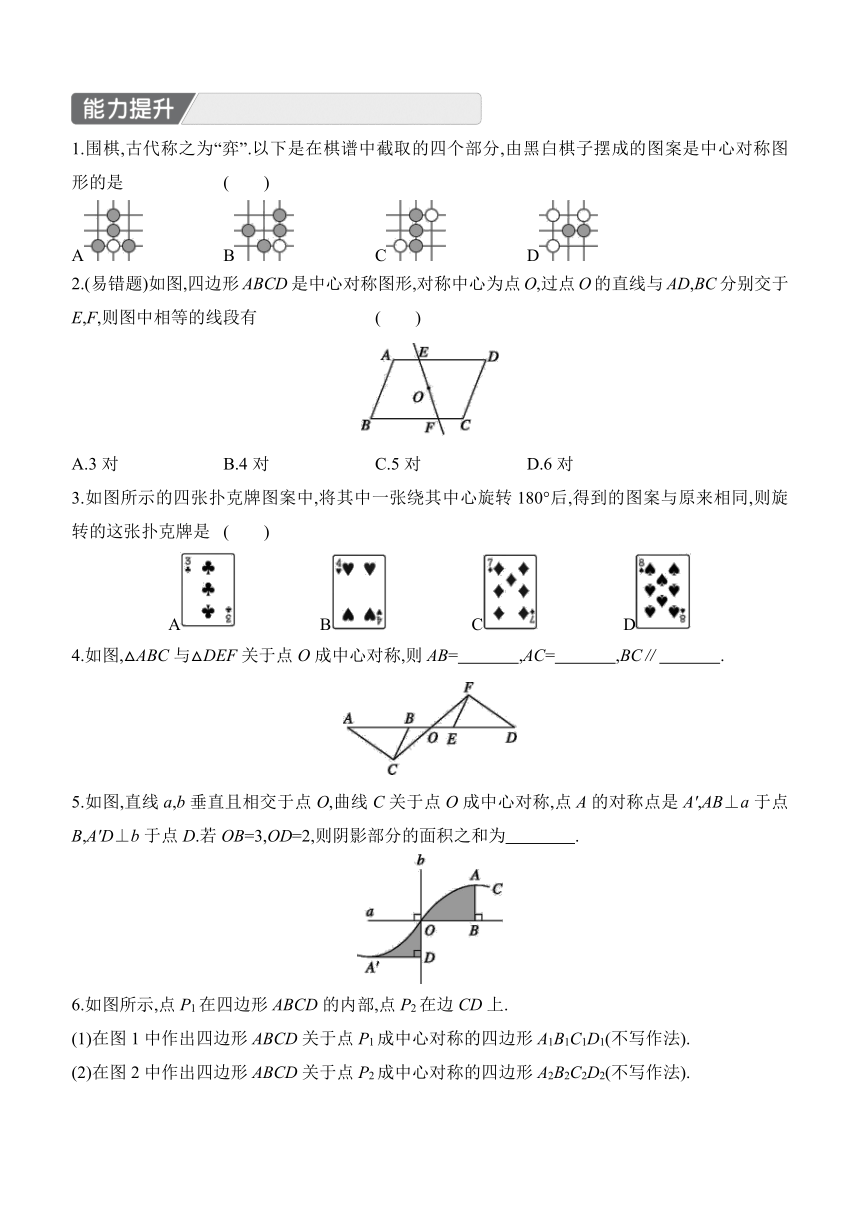
1.围棋,古代称之为“弈”.以下是在棋谱中截取的四个部分,由黑白棋子摆成的图案是中心对称图形的是 ( )
A B C D
2.(易错题)如图,四边形ABCD是中心对称图形,对称中心为点O,过点O的直线与AD,BC分别交于E,F,则图中相等的线段有 ( )
A.3对 B.4对 C.5对 D.6对
3.如图所示的四张扑克牌图案中,将其中一张绕其中心旋转180°后,得到的图案与原来相同,则旋转的这张扑克牌是 ( )
A B C D
4.如图,△ABC与△DEF关于点O成中心对称,则AB= ,AC= ,BC∥ .
5.如图,直线a,b垂直且相交于点O,曲线C关于点O成中心对称,点A的对称点是A',AB⊥a于点B,A'D⊥b于点D.若OB=3,OD=2,则阴影部分的面积之和为 .
6.如图所示,点P1在四边形ABCD的内部,点P2在边CD上.
(1)在图1中作出四边形ABCD关于点P1成中心对称的四边形A1B1C1D1(不写作法).
(2)在图2中作出四边形ABCD关于点P2成中心对称的四边形A2B2C2D2(不写作法).
图1 图2
7.如图,在四边形ABCD中,AD∥BC,E是CD上一点,点D与点C关于点E成中心对称,连接AE并延长,与BC的延长线交于点F.
(1)E是线段CD的 ,点A与点F关于点 成中心对称.
(2)若AB=AD+BC,求证:AB=BF.
8.(几何直观)如图所示的是由5个全等的正方形组成的图案,请按下列要求画图:
(1)在图1中添加1个正方形,使它成轴对称图形但不是中心对称图形.
(2)在图2中添加1个正方形,使它成中心对称图形但不是轴对称图形.
(3)在图3中添加1个正方形,使它既成轴对称图形,又成中心对称图形.
【详解答案】
基础达标
1.D 2.C 3.D 4.1 5.C 6.A
7.1
8.解:(1)画法如下:
①连接AO并延长,在AO的延长线上截取OD=OA,得到点A关于点O的对应点D;
②用同样的画法,分别画出点B,C关于点O的对应点E,F;
③顺次连接CD,DE,EF,FA,则得到所要求画出的六边形ABCDEF,如图所示.
(2)DE ∠DEF
能力提升
1.C 解析:∵在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形与原图形重合,则这个图形为中心对称图形,∴C选项中的图形为中心对称图形.故选C.
2.C 解析:观察可知,根据中心对称的性质,可知AB=CD,BC=AD,OE=OF,AE=CF,BF=DE,相等的线段共有5对.故选C.
3.B 解析:在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫作中心对称图形.∵B图案是中心对称图形,其余图案都不是中心对称图形,∴旋转的这张扑克牌是B.故选B.
4.DE DF EF 解析:∵△ABC与△DEF关于点O成中心对称,∴△ABC≌△DEF.∴AB=DE,AC=DF.又∵BO=EO,∠BOC=∠EOF,CO=FO,∴△BOC≌△EOF(SAS).∴∠BCO=∠EFO.∴BC∥EF.
5.6 解析:如图,根据题意,得图形①与图形②是全等图形.∴阴影部分的面积之和=长方形ABOE的面积=3×2=6.
6.解:(1)四边形A1B1C1D1如图1所示.
图1 图2
(2)四边形A2B2C2D2如图2所示.
7.解:(1)中点 E
(2)证明:由(1)可知AD=CF,∵AB=AD+BC,
∴AD+BC=CF+BC=BF,
∴AB=BF.
8.解:(1)添加1个正方形后的图形如图1所示.(答案不唯一)
(2)添加1个正方形后的图形如图2所示.
(3)添加1个正方形后的图形如图3所示.
中心对称图形
1.下列四个字母中,属于中心对称图形的是 ( )
A B
C D
2.剪纸又称刻纸,是中国最古老的民间艺术之一,它是以纸为加工对象,以剪刀(或刻刀)为工具进行创作的艺术.民间剪纸往往通过谐音、象征、寓意等手法提炼、概括自然形态,构成美丽的图案.下列剪纸中,既是轴对称图形,又是中心对称图形的是 ( )
A B
C D
成中心对称
3.下列各组图形中,△A'B'C'与△ABC成中心对称的是 ( )
A B
C D
4.如图所示的兔子的卡通图片中,成中心对称的有 组.
成中心对称的性质
5.如图,在正方形网格中,A,B,C,D,E,F,G, H,M,N是网格线交点,△ABC与△DEF关于某点对称,则其对称中心是 ( )
A.点G B.点H C.点M D.点N
6.(2025南阳唐河县月考)如图,△AOD与△BOC关于点O成中心对称,连接AB,CD,以下结论错误的是 ( )
A.OA=OB B.△AOD≌△COB C.AD=BC D.S△AOB=S△COD
7.(易错题)如图,△AOB与△COD关于O点成中心对称,若BC=4,则图中长度为4的线段有
条.
利用中心对称的性质作图
8.(教材变式)如图所示,线段AB,BC(AB≠BC)是六边形ABCDEF的两条边,并且六边形ABCDEF是中心对称图形,对称中心是O点.
(1)把这个六边形补画完整.
(2)如果AB=2 cm,则六边形ABCDEF中长度是2 cm的线段还有 ,与∠ABC相等的角是 .
1.围棋,古代称之为“弈”.以下是在棋谱中截取的四个部分,由黑白棋子摆成的图案是中心对称图形的是 ( )
A B C D
2.(易错题)如图,四边形ABCD是中心对称图形,对称中心为点O,过点O的直线与AD,BC分别交于E,F,则图中相等的线段有 ( )
A.3对 B.4对 C.5对 D.6对
3.如图所示的四张扑克牌图案中,将其中一张绕其中心旋转180°后,得到的图案与原来相同,则旋转的这张扑克牌是 ( )
A B C D
4.如图,△ABC与△DEF关于点O成中心对称,则AB= ,AC= ,BC∥ .
5.如图,直线a,b垂直且相交于点O,曲线C关于点O成中心对称,点A的对称点是A',AB⊥a于点B,A'D⊥b于点D.若OB=3,OD=2,则阴影部分的面积之和为 .
6.如图所示,点P1在四边形ABCD的内部,点P2在边CD上.
(1)在图1中作出四边形ABCD关于点P1成中心对称的四边形A1B1C1D1(不写作法).
(2)在图2中作出四边形ABCD关于点P2成中心对称的四边形A2B2C2D2(不写作法).
图1 图2
7.如图,在四边形ABCD中,AD∥BC,E是CD上一点,点D与点C关于点E成中心对称,连接AE并延长,与BC的延长线交于点F.
(1)E是线段CD的 ,点A与点F关于点 成中心对称.
(2)若AB=AD+BC,求证:AB=BF.
8.(几何直观)如图所示的是由5个全等的正方形组成的图案,请按下列要求画图:
(1)在图1中添加1个正方形,使它成轴对称图形但不是中心对称图形.
(2)在图2中添加1个正方形,使它成中心对称图形但不是轴对称图形.
(3)在图3中添加1个正方形,使它既成轴对称图形,又成中心对称图形.
【详解答案】
基础达标
1.D 2.C 3.D 4.1 5.C 6.A
7.1
8.解:(1)画法如下:
①连接AO并延长,在AO的延长线上截取OD=OA,得到点A关于点O的对应点D;
②用同样的画法,分别画出点B,C关于点O的对应点E,F;
③顺次连接CD,DE,EF,FA,则得到所要求画出的六边形ABCDEF,如图所示.
(2)DE ∠DEF
能力提升
1.C 解析:∵在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形与原图形重合,则这个图形为中心对称图形,∴C选项中的图形为中心对称图形.故选C.
2.C 解析:观察可知,根据中心对称的性质,可知AB=CD,BC=AD,OE=OF,AE=CF,BF=DE,相等的线段共有5对.故选C.
3.B 解析:在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫作中心对称图形.∵B图案是中心对称图形,其余图案都不是中心对称图形,∴旋转的这张扑克牌是B.故选B.
4.DE DF EF 解析:∵△ABC与△DEF关于点O成中心对称,∴△ABC≌△DEF.∴AB=DE,AC=DF.又∵BO=EO,∠BOC=∠EOF,CO=FO,∴△BOC≌△EOF(SAS).∴∠BCO=∠EFO.∴BC∥EF.
5.6 解析:如图,根据题意,得图形①与图形②是全等图形.∴阴影部分的面积之和=长方形ABOE的面积=3×2=6.
6.解:(1)四边形A1B1C1D1如图1所示.
图1 图2
(2)四边形A2B2C2D2如图2所示.
7.解:(1)中点 E
(2)证明:由(1)可知AD=CF,∵AB=AD+BC,
∴AD+BC=CF+BC=BF,
∴AB=BF.
8.解:(1)添加1个正方形后的图形如图1所示.(答案不唯一)
(2)添加1个正方形后的图形如图2所示.
(3)添加1个正方形后的图形如图3所示.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
